ಗಣಿತ

ಗಣಿತ ಎಂಬುದು ಪ್ರಮಾಣ, ವಿನ್ಯಾಸ, ಅವಕಾಶ, ಪ್ರದೇಶ, ಬದಲಾವಣೆ ಮುಂತಾದ ಪರಿಕಲ್ಪನೆಗಳ ಬಗ್ಗೆ ಜ್ಞಾನವನ್ನು ಸಂಪಾದಿಸುವ ಅಧ್ಯಯನ ವಿಭಾಗ. ಗಣಿತದ ನಿಖರ ಅರ್ಥದ ಬಗ್ಗೆ ಅನೇಕ ಭಿನ್ನಮತೀಯ ಅಭಿಪ್ರಾಯಗಳಿವೆ. ಗಣಿತ 'ವಿಜ್ಞಾನದ ಪ್ರಕಾರವೆ?', 'ನೈಜತೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆಯೆ?' ಇತ್ಯಾದಿ ಕ್ಲಿಷ್ಟ ಪ್ರಶ್ನೆಗಳ ಬಗ್ಗೆ ಅಭಿಮತವಿಲ್ಲ.
ಪ್ರಗತಿ ಪಥದಲ್ಲಿರುವ ಯಾವುದೇ ಶಾಸ್ತ್ರದ ಚಟುವಟಿಕೆಗಳನ್ನಾಗಲಿ ಸ್ಥಿರೀಕೃತ ವ್ಯಾಖ್ಯೆಯೊಂದರ ಚೌಕಟ್ಟಿನೊಳಗೆ ಬಂಧಿಸಿಡಲು ಸಾಧ್ಯವಿಲ್ಲ. ಗಣಿತಶಾಸ್ತ್ರದ ಚಟುವಟಿಕೆಗಳಾದರೂ ಈ ಮಾತಿಗೆ ಅಪವಾದವಾಗದೆ ಇರುವುದರಲ್ಲಿ ಅಚ್ಚರಿಯೇನಿಲ್ಲ. ಅನೇಕ ಸಹಸ್ರಮಾನಗಳ ದೀರ್ಘ ವೈವಿಧ್ಯಮಯ ಇತಿಹಾಸದುದ್ದಕ್ಕೂ ಈ ಶಾಸ್ತ್ರದ ಚೈತನ್ಯಪೂರ್ಣತೆ ಅವಿಚ್ಛಿನ್ನವಾಗಿ ವರ್ಧಿಸುತ್ತಲೇ ಬಂದಿದೆ. ಏನನ್ನೊ ಎಣಿಸುವ ಸಲುವಾಗಿ ಪ್ರಾಣಿಗಳ ಎಲುಬುಗಳ ಮೇಲೆ ಆದಿಮಾನವನು ಕಚ್ಚುಗಳ ಸಾಲುಗಳನ್ನು ಕೆತ್ತಿಟ್ಟಿರುವ ಗತಕಾಲದ ದಾಖಲೆಗಳು ಇಂದಿಗೂ ಅಲ್ಲಲ್ಲಿ ಉಳಿದಿವೆ; ಮೊರೇವಿಯದಲ್ಲಿ (ಚೆಕೊಸ್ಲೊವಾಕಿಯ) ದೊರೆತ ಅಂಥ ಒಂದು ಮೂಳೆಯ ಮೇಲೆ (ಅದು ಮರಿತೋಳವೊಂದರ ಅಸ್ಥಿ) ಐವತ್ತೈದು ಕಚ್ಚುಗಳಿದ್ದವು.[೧] ಈ ದಾಖಲೆಗಳು ಸುಮಾರು ಮೂವತ್ತು ಸಹಸ್ರ ವರ್ಷಗಳಷ್ಟು ಪ್ರಾಚೀನವಾದವು. ಅಲ್ಲಿಗೆ ಮಾನವನಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಗಣಿತಪ್ರಜ್ಞೆ ಉಗಮಿಸಿದ್ದು ಮೂಲತಃ ಎಣಿಕೆಯ ದಾಖಲೆಗಳ ನಿರ್ಮಾಣದೊಂದಿಗೆ ಎಂದು ಭಾವಿಸಬಹುದಾದರೆ ಆ ಉಗಮ ನಮಗೆ ತಿಳಿದಿರುವ ಎಲ್ಲ ನಾಗರಿಕತೆಗಳಿಗಿಂತ ಕನಿಷ್ಠ ಕೆಲವು ದಶಸಹಸ್ರ ವರ್ಷಗಳಷ್ಟು ಹಿಂದೆಯೇ ಜರುಗಿದ ಘಟನೆ ಎಂದಾಯಿತು. ತರುವಾಯ ಪ್ರಾಚೀನ ನಾಗರಿಕತೆಗಳ ಕಾಲದಲ್ಲಿ ಗಣಿತಶಾಸ್ತ್ರದ ಅಧ್ಯಯನ ವಸ್ತು ವಿಶಿಷ್ಟವಾಗಿ ಎಣಿಕೆಯ ಸಂಖ್ಯೆಗಳು, ಅಳತೆಯ ರಾಶಿಗಳು ಹಾಗೂ ದೃಗ್ಗೊಚರ ಆಕೃತಿಗಳು ಎಂಬ ಭಾವನೆ ರೂಪುಗೊಂಡಿತು. ಇದೇ ಮನೋಭಿಪ್ರಾಯ ಗಣಿತರಂಗದಿಂದ ತುಸು ದೂರ ಉಳಿದಿರುವ ಅನೇಕ ಜನರಲ್ಲಿ ಇಂದೂ ಬೇರೂರಿಯೇ ಇದೆ. ಆದರೆ ಹತ್ತೊಂಬತ್ತನೆಯ ಶತಮಾನದಲ್ಲಿ ಕುಡಿಯೊಡೆದ ಅಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿ (ನಾನ್ - ಯೂಕ್ಲಿಡಿಯನ್ ಜೊಮಿಟ್ರಿ), ಬೂಲೀಯ ಬೀಜಗಣಿತ (ಬೂಲಿಯನ್ ಆಲ್ಜಿಬ್ರ) ಮುಂತಾದ ಕೆಲ ನವ್ಯ ಶಾಖೆಗಳು ಗಣಿತಶಾಸ್ತ್ರದ ವ್ಯಾಪ್ತಿಗೆ ಅನಿರೀಕ್ಷಿತ ಆಯಾಮಗಳನ್ನು ನೀಡತೊಡಗಿದವು. ಅಲ್ಲಿಂದೀಚೆಗೆ ಸಂಖ್ಯೆ, ರಾಶಿ ಮತ್ತು ಗೋಚರಾಕೃತಿಗಳ ವ್ಯಾಸಂಗ ಗಣಿತಾಭ್ಯಾಸದ ಮೊದಲ ಹೆಜ್ಜೆಯಾಗಬಲ್ಲದೆ ವಿನಾ ಸಮಗ್ರ ಗಣಿತವಾಗಲಾರದು ಎಂಬ ಅಭಿಪ್ರಾಯಪಲ್ಲಟ ಅಧಿಕೃತ ಗಣಿತ ವಲಯಗಳಲ್ಲಿ ಕ್ರಮೇಣ ಮೂಡಿಬಂದಿತು. ತಾತ್ತ್ವಿಕ ಮನೋವೃತ್ತಿಯ ಹಲವಾರು ಗಣಿತಜ್ಞರು ತಮ್ಮ ಶಾಸ್ತ್ರದ ನಿಷ್ಕೃಷ್ಟ ಸ್ವರೂಪವನ್ನು ಈ ಬೆಳವಣಿಗೆಯ ಹೊಸ ಬೆಳಕಿನಲ್ಲಿ ಪುನರ್ನಿರ್ಣಯಿಸುವ ಪ್ರಯತ್ನಗಳನ್ನು ಸ್ಬಾಭಾವಿಕವಾಗಿಯೇ ಕೈಗೊಂಡರು. ತತ್ಫಲವಾಗಿ ಗಣಿತದ ನೈಜಸ್ವರೂಪ ಅಡಗಿರುವುದು ಬಹುಮಟ್ಟಿಗೆ ಅದರ ಚಿಂತನಮಾರ್ಗದಲ್ಲೇ ಹೊರತು ವಸ್ತುವಿನಲ್ಲಲ್ಲ ಎಂಬ ಅಂಶ ಹೆಚ್ಚು ಹೆಚ್ಚು ಮಂದಿ ಗಣಿತಜ್ಞರಿಗೆ ಮನವರಿಕೆಯಾಗತೊಡಗಿತು. ಯಾವ ಯಾವ ಉಕ್ತಿಗಳನ್ನು ಸತ್ಯವೆಂದು ಅಂಗೀಕರಿಸಿದಲ್ಲಿ ಮತ್ತೆ ಯಾವ ಯಾವ ಉಕ್ತಿಗಳು ಸತ್ಯವೆಂದು ಸಿದ್ಧಪಡುತ್ತವೆ ಎಂದು ಜನರು ವಿವೇಚಿಸುವಾಗಲೆಲ್ಲ ಗಣಿತ ಅಂಕುರಿಸುತ್ತದೆ, ಹಾಗೂ ಗಣಿತದ ಬಹುಭಾಗವೆಲ್ಲ ಅಂಕುರಿಸಿರುವುದು ಇಂಥ ವಿವೇಚನೆಯ ಪರಿಣಾಮವಾಗಿಯೇ. ಆದಿಯಲ್ಲಿ ಅಂಗೀಕರಿಸಲಾಗುವ ಉಕ್ತಿಗಳೇ ಆದ್ಯುಕ್ತಿಗಳು (ಆಕ್ಸಿಯಂಸ್/ ಪಾಸ್ಟ್ಯುಲೇಟ್ಸ್). ಅವುಗಳಿಂದ ಸಿದ್ಧಪಡುವ ಉಕ್ತಿಗಳೇ ಪ್ರಮೇಯಗಳು (ಥಿಯರಂಸ್). ಹೀಗೆಂದ ಮಾತ್ರಕ್ಕೆ ಗಣಿತದ ದೃಷ್ಟಿಯಲ್ಲಿ ಪರಿಕಲ್ಪನೆಗಳನ್ನು (ಕಾನ್ಸೆಪ್ಟ್ಸ್) ಕುರಿತ ಅರ್ಥ ಪ್ರಜ್ಞೆ ಯಾವ ಪಾತ್ರವನ್ನೂ ವಹಿಸುವುದಿಲ್ಲವೆಂದಾಗಲಿ, ಇಲ್ಲವೇ ಯಾವುದೋ ಒಂದು ಗೌಣವಾದ ಪಾತ್ರವನ್ನು ವಹಿಸುತ್ತದೆಂದಾಗಲಿ ಬಗೆಯಲಾಗದು. ಉತ್ತಮ ಆದ್ಯುಕ್ತಿಗಳ ಆಯ್ಕೆಗೂ, ವಿಶ್ವಾಸಾರ್ಹ ಸಾಧನಕ್ರಮಗಳ ರೂಪಣೆಗೂ ಹಿಂದಾಗಲಿ, ಇಂದಾಗಲಿ ಪರಿಕಲ್ಪನೆಗಳ ಅರ್ಥಪ್ರಜ್ಞೆಯೇ ಪ್ರಧಾನ ನಿರ್ಣಾಯಕ; ಅನಂತರ ಬರುವ ಯಾಂತ್ರಿಕ ಪರಿಕರ್ಮಗಳ ನಿರ್ವಹಣೆಯಲ್ಲಿ ಮಾತ್ರ ಅರ್ಥ ಹಿನ್ನೆಲೆಗೆ ಹಿಮ್ಮೆಟ್ಟಬಹುದು, ಅಷ್ಟೆ.
ವಿಭಾಗಗಳು
[ಬದಲಾಯಿಸಿ]ಪ್ರಮಾಣ
[ಬದಲಾಯಿಸಿ]ವಿನ್ಯಾಸ
[ಬದಲಾಯಿಸಿ]ಪ್ರದೇಶ
[ಬದಲಾಯಿಸಿ] |
 |
 |
 |
|
| ರೇಖಾಗಣಿತ | ತ್ರಿಕೋಣಮಿತಿ | ಭೇದಾತ್ಮಕ ರೇಖಾಗಣಿತ | ಸ್ಥಳಶಾಸ್ತ್ರ | ಭಾಗಶಃ ರೇಖಾಗಣಿತ |
ಬದಲಾವಣೆ
[ಬದಲಾಯಿಸಿ] |
 |
 |

| |
| ಕಲನಶಾಸ್ತ್ರ | ಸದಿಶ ಕಲನಶಾಸ್ತ್ರ | ಭೇದಾತ್ಮಕ ಸಮೀಕರಣಗಳು | ಕ್ರಿಯಾತ್ಮಕ ವ್ಯವಸ್ಥೆಗಳು | ಗೊಂದಲೆ ಸಿದ್ಧಾಂತ |
ಆಧಾರ ಸೂತ್ರಗಳು ಮತ್ತು ತತ್ವಗಳು
[ಬದಲಾಯಿಸಿ]ಪ್ರತ್ಯೇಕ ಗಣಿತ
[ಬದಲಾಯಿಸಿ]ಉಪಯುಕ್ತ ಗಣಿತ
[ಬದಲಾಯಿಸಿ]- ಗಣಿತದ ಭೌತಶಾಸ್ತ್ರ • ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಯಂತ್ರಶಾಸ್ತ್ರ • ಗಣಿತದ ದ್ರವಿಕ ಚಲನಶೀಲತೆ • ಸಂಖ್ಯಾತ್ಮಕ ವಿಶ್ಲೇಷಣೆ • ಉತ್ತಮಗೊಳಿಸುಕರಣ(ಗಣಿತ) • ಸಂಭವನೀಯತೆ • ಸಂಖ್ಯಾ ಶಾಸ್ತ್ರ • ಗಣಿತದ ಅರ್ಥಶಾಸ್ತ್ರ • ಆರ್ಥಿಕ ಗಣಿತಶಾಸ್ತ್ರ • ಆಟದ ಸಿದ್ಧಾಂತ • ಗಣಿತದ ಜೀವಶಾಸ್ತ್ರ • ಗುಪ್ತಲಿಪಿಶಾಸ್ತ್ರ • ಕಾರ್ಯಾಚರಣೆಗಳ ಸಂಶೋಧನೆ
ಧನ ಪೂರ್ಣಾಂಕಗಳು
[ಬದಲಾಯಿಸಿ]ಆದಿಮಾನವ ಎಣಿಕೆಯ ಧನ ಪೂರ್ಣಾಂಕಗಳನ್ನು (positive integers) ಕಚ್ಚುಗಳು, ಬೊಟ್ಟುಗಳು ಮುಂತಾದ ಏಕರೂಪ ಪ್ರತೀಕಗಳ ಸಾಲುಗಳಿಂದ ವ್ಯಕ್ತಪಡಿಸುತ್ತಿದ್ದನಷ್ಟೇ. ಹಿಂದೂ - ಅರ್ಯಾಬಿಕ್ ದಶಮಾನ ಪದ್ಧತಿ ಎಂದು ಪ್ರಸಿದ್ಧವಾಗಿರುವ ಆಧುನಿಕ ಪ್ರತೀಕಯೋಜನೆಯಲ್ಲಾದರೋ[೨][೩] ಈ ಸಂಖ್ಯೆಗಳನ್ನು 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ಎಂಬ ಹತ್ತು ಪ್ರತೀಕಗಳ ವಿವಿಧ ಕ್ರಮಸಂಯೋಜನೆಗಳಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಧನ ಪೂರ್ಣಾಂಕಗಳ ಆಧುನಿಕ ಲಿಖಿತರೂಪಗಳು ಪ್ರತೀಕ ಭಾಷೆಯೊಂದರ ಪದ ಅಥವಾ ವಾಕ್ಯಗಳೆಂದೂ 0, 1, 2, ..........9 ಎಂಬ ಗುರುತುಗಳು (ಅಂಕಿಗಳು) ಆ ವಾಕ್ಯಗಳಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳುವ ಬಿಡಿ ಬಿಡಿ ಅಕ್ಷರಗಳೆಂದೂ ಭಾವಿಸಬಹುದು.[೪] ಆದಿಮಾನವನ ಲಿಖಿತಸಂಖ್ಯೆಗಳೂ ವಾಕ್ಯಗಳೇ; ಆದರೆ ಅವೆಲ್ಲವೂ ಒಂದೇ ಒಂದು ಅಕ್ಷರದಿಂದ ರಚಿತವಾದ ವಾಕ್ಯಗಳು. ಆದಿಮಾನವ ನಿಯೋಜಿಸಿಕೊಂಡ ಸರಳ ಸಂಖ್ಯಾಭಾಷೆಗೆ ಇಂದೂ ಮೂಲಭೂತ ತಾತ್ತ್ವಿಕ ಮಹತ್ತ್ವವಿರುವುದರಿಂದ ಅದಕ್ಕೂ, ಧನ ಪೂರ್ಣಾಂಕಗಳ ಆಧುನಿಕ ಅಭಿವ್ಯಕ್ತಿ ವ್ಯವಸ್ಥೆಗೂ ಇರುವ ಸಂಬಂಧವನ್ನು ಗುರುತಿಸುವುದು ಅತಿ ಮುಖ್ಯ. ಈ ಸಲುವಾಗಿ ಕಚ್ಚು ಅಥವಾ ಬೊಟ್ಟಿನ ಗುರುತನ್ನು T ಎಂದು ಬರೆಯೋಣ. ತತ್ಫಲವಾಗಿ ಒಂದು, ಎರಡು, ಮೂರು ಇತ್ಯಾದಿ ಸಂಖ್ಯೆಗಳು ಆದಿಮಾನವನ ಪ್ರತೀಕಯೋಜನೆಯಲ್ಲಿ T, TT, TTT ಮೊದಲಾದ ರೂಪಗಳನ್ನು ತಾಳುತ್ತವೆ. ಇವೇ ಧನ ಪೂರ್ಣಾಂಕಗಳ ಆದಿಮರೂಪಗಳು. ಆದಿಮಾನವನ TTTTTTTTTT ಇಂದು 10 ಎಂಬ ಹೊಸ ರೂಪವನ್ನು ತಾಳಿದೆಯಷ್ಟೆ; ಎಂತಲೇ TTTTTTTTTT ಎಂಬುದು ಆಧುನಿಕ ಸಂಖ್ಯಾಭಿವ್ಯಕ್ತಿ ಪದ್ಧತಿಯ ಪಾದ (ರ್ಯಾಡಿಕ್ಸ್/ ಬೇಸ್) ಎಂದು ಹೇಳುತ್ತೇವೆ. ಮಿಕ್ಕ ಧನ ಪೂರ್ಣಾಂಕಗಳೆಲ್ಲವನ್ನೂ ಬಿಟ್ಟು ಇದನ್ನೇ ಆಧುನಿಕ ಪದ್ಧತಿಯ ಪಾದವನ್ನಾಗಿ ಆಯ್ಕೆ ಮಾಡಿಕೊಳ್ಳುವುದಕ್ಕೆ ಈ TTTTTTTTTT ಎಣಿಸಲು ಸಹಜವಾಗಿ ಒಗ್ಗಿಬರುವ ಮಾನವನ ಕೈಬೆರಳುಗಳ ಸಂಖ್ಯೆಯಾಗಿರುವುದೇ ಚಾರಿತ್ರಿಕ ಕಾರಣವಾಯಿತೆಂದು ನಂಬಲಾಗಿದೆ. ಆದರೆ ಶುದ್ಧ ಗಣಿತದ ದೃಷ್ಟಿಯಿಂದ ಇದು ಅನಂತ ಸಂಖ್ಯೆಯಷ್ಟು ಸಾಧ್ಯ ಆಯ್ಕೆಗಳ ಪೈಕಿ ಒಂದು ಮಾತ್ರ. ಪ್ರಸಕ್ತ ವಿವರಣೆಯ ದೃಷ್ಟಿಕೋನದಿಂದ TTTTTTTTTT ಯ ಉದ್ದ ತೀರ ಪ್ರತಿಕೂಲಕರವಾಗುವ ಕಾರಣ ಆಧುನಿಕ ದಶಮಾನ ಪದ್ಧತಿಯ (ಡೆಸಿಮಲ್ ಸಿಸ್ಟಮ್) ಬದಲಾಗಿ ಪ್ರಧಾನಾಂಶಗಳಲ್ಲಿ ಅದನ್ನೇ ಹೋಲುವ, ಆದರೆ ಲಾಂಬಿಕ TTTTTTTTTT ಯ ಬದಲು ಸಾಕಷ್ಟು ಮೊಟಕಾಗಿರುವ TTT ಯಷ್ಟನ್ನೇ ಪಾದವಾಗಿ ಉಳ್ಳ, ತ್ರಿಮಾನ ಪದ್ಧತಿಯನ್ನು (ಟರ್ನರಿ ಸಿಸ್ಟಮ್) ಕುರಿತು ಮೊದಲು ವಿವೇಚಿಸೋಣ. ಈ ತ್ರಿಮಾನ ಪದ್ದತಿಯಲ್ಲಿ ಆದಿಮಾನವನ TTT ಯನ್ನು 10 ಎಂದೂ, ಅದಕ್ಕಿಂತ ಕಡಿಮೆಯಾದ TT ಮತ್ತು T ಗಳನ್ನು ಅನುಕ್ರಮವಾಗಿ 2 ಮತ್ತು 1 ಎಂದೂ ಬರೆಯಲಾಗುವುದು. (ಇಲ್ಲಿ ಕಾಣಿಸಿಕೊಂಡಿರುವ 0, 2 ಮತ್ತು 1 ಯಾವುದಾದರೂ ಮೂರು ಯಾದೃಚ್ಛಿಕ ಗುರುತುಗಳು; ಅವಕ್ಕೆ ಬದಲು ಬೇರೆ ಯಾವುದಾದರೂ ಮೂರು ಗುರುತುಗಳನ್ನು ಸುಸಂಗತ ರೀತಿಯಲ್ಲಿ ಬಳಸಲು ಅಡ್ಡಿಯಿಲ್ಲ.) ಈಗ ಆದಿಮಾನವನ ಧನ ಪೂರ್ಣಾಂಕಗಳಿಗೆ (ಅಂದರೆ T ಗಳ ಸಾಲುಗಳಿಗೆ) ಅನುರೂಪವಾದ ತ್ರಿಮಾನ ಪೂರ್ಣಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಕೆಳಗಿನ ನಾಲ್ಕು ವಿಧಿಗಳ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂ ವಿಧಾನವನ್ನು ಪ್ರಯೋಗಿಸಬಹುದು:
- ವಿಧಿ 1: OTTT ಯನ್ನು TO ಎಂದು ಬದಲಾಯಿಸಿ.
- ವಿಧಿ 2: OTT ಯನ್ನು 2 ಎಂದು ಬದಲಾಯಿಸಿ.
- ವಿಧಿ 3: OT ಯನ್ನು 1 ಎಂದು ಬದಲಾಯಿಸಿ.
- ವಿಧಿ 4: ಪರಿಶೀಲಿತ ವಾಕ್ಯದ ಅತ್ಯಂತ ಎಡಗಡೆಯಲ್ಲಿ T ಇರುವುದಾದರೆ ಅದನ್ನು OT ಎಂದು ಬದಲಾಯಿಸಿ.
ಈ ವಿಧಿಗಳನ್ನು ಎಲ್ಲಿಯವರೆಗೆ ಸಾಧ್ಯವಾಗುತ್ತದೋ ಅಲ್ಲಿಯವರೆಗೆ ಅವನ್ನು ಬರೆದಿರುವ ಕ್ರಮದ ಆದ್ಯತೆಗೆ ಅನುಗುಣವಾಗಿ ಪ್ರಯೋಗಿಸುತ್ತ ಹೋಗುವುದೇ ಪ್ರಸ್ತುತ ಅಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ. ಉದಾಹರಣೆಗೆ ಆದಿಮಾನವನ
TTT TTT TTT TTT TTT
ಸಂಖ್ಯೆಗೆ ಅನುರೂಪವಾದ ತ್ರಿಮಾನಾಭಿವ್ಯಕ್ತಿಯನ್ನು ಕಂಡುಹಿಡಿಯುವ ಮಾರ್ಗವನ್ನು ಪರಿಶೀಲಿಸಬಹುದು. ಮೇಲಿನ ವಾಕ್ಯದಲ್ಲಿ O ಇರದ ಕಾರಣ ಅದರ ಮೇಲೆ 1,2 ಮತ್ತು 3ನೆಯ ವಿಧಿಗಳ ಪ್ರಯೋಗ ಅಸಾಧ್ಯ. ಆದ್ದರಿಂದ ಅದನ್ನು ಮೊದಲಿಗೆ 4ನೆಯ ವಿಧಿ ಪ್ರಯೋಗಕ್ಕೆ ಗುರಿಪಡಿಸಬೇಕು.
OTTT TTT TTT TTT TTT
ಯನ್ನು ಪಡೆಯುತ್ತೇವೆ. ಇದರಲ್ಲಿ ಅಡಿಗೆರೆ ಹಾಕಿ ಸೂಚಿಸಿರುವ ವಿಭಾಗವನ್ನು ಗಮನಿಸಿದಾಗ ಇದರ ಮೇಲೆ 1,2 ಮತ್ತು 3ನೆಯ ವಿಧಿಗಳ ಪೈಕಿ ಯಾವೊಂದನ್ನು ಬೇಕಿದ್ದರೂ ಪ್ರಯೋಗಿಸಲು ಶಕ್ಯವಿದೆಯೆಂದು ಗೊತ್ತಾಗುವುದು. ಆದರೆ 1ನೆಯ ವಿಧಿಗೇ. ಈ ಪ್ರಕಾರ ಮತ್ತೆ ಮತ್ತೆ 1ನೆಯ ವಿಧಿಯನ್ನೆ ಬಳಸುತ್ತ ಹೋದರೆ ಕ್ರಮವಾಗಿ TT OTTT TTT TTT:
TTT OTTT TTT;
TTTT OTTT ಮತ್ತು TT TTTO
ಎಂಬ ವಾಕ್ಯಗಳು ಫಲಿಸುತ್ತವೆ. ಕೊನೆಯ ವಾಕ್ಯವನ್ನು 1, 2 ಮತ್ತು 3ನೆಯ ವಿಧಿಪ್ರಯೋಗಗಳಿಗೆ ಗುರಿಪಡಿಸಲು ಸಾಧ್ಯವಿಲ್ಲದ ಕಾರಣ ಅದರ ಮೇಲೆ 4ನೆಯ ವಿದಿಯನ್ನು ಪ್ರಯೋಗಿಸಿ OTTT TTO ವನ್ನೂ ಬಳಿಕ 1ನೆಯ ವಿಧಿಯ ಪ್ರಯೋಗದಿಂದ T OTT O ವನ್ನೂ ರಚಿಸುತ್ತೇವೆ. T OTT O ನ ಮೇಲೆ 1ನೆಯ ವಿಧಿಪ್ರಯೋಗ ಅಸಾಧ್ಯ. ಮಿಕ್ಕೆಲ್ಲ ವಿಧಿಗಳ ಪ್ರಯೋಗ ಸಾಧ್ಯ. ನಿಷ್ಕರ್ಷಿತ ಆದ್ಯತೆಯಂತೆ ಅದರ ಮೇಲೆ 2ನೆಯ ವಿಧಿಯನ್ನು ಪ್ರಯೋಗಿಸಿ ಈಗ T 20 ಎಂಬ ವಾಕ್ಯವನ್ನು ಪಡೆಯುತ್ತೇವೆ. ಇನ್ನೂ ಕೊನೆಯ ಎರಡು ಹೆಜ್ಜೆಗಳಲ್ಲಿ ಮೊದಲು 4ನೆಯ ವಿಧಿಯನ್ನು ಉಪಯೋಗಿಸಿ OT 20 ಯನ್ನೂ ತರುವಾಯ 3ನೆಯ ವಿಧಿಯನ್ನು ಉಪಯೋಗಿಸಿ 120 ಯನ್ನೂ ರಚಿಸಬಹುದಷ್ಟೆ. ನಮೂದಾಗಿರುವ ಯಾವೊಂದು ವಿಧಿಯನ್ನೂ ಈ 120 ಮೇಲೆ ಪ್ರಯೊಗಿಸಲು ಸಾಧ್ಯವಿಲ್ಲದ ಕಾರಣ ಅಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ಇಲ್ಲಿಗೆ ಕೊನೆಗೊಂಡಿತು. ಅಂದ ಮೇಲೆ ಆದಿಮಾನವನ TTT TTT TTT TTT TTT ಗೆ ಅನುರೂಪವಾದ ತ್ರಿಮಾನ ಪದ್ಧತಿಯ ಸಂಖ್ಯಾಪ್ರತೀಕ 120. ಇದೇ ಪ್ರಕಾರ ಆಧಿಮಾನವನ ಇತರ ಎಲ್ಲ ಸಂಖ್ಯಾಪ್ರತೀಕಗಳನ್ನೂ ತ್ರಿಮಾನ ಪದ್ಧತಿಗೆ ರೂಪಾಂತರಿಸಬಹುದು. ತ್ರಿಮಾನ ಪದ್ಧತಿಯ ಧನ ಪೂರ್ಣಾಂಕ (ಸೂಚಕ) ಪ್ರತೀಕಗಳೆಲ್ಲವೂ 0, 1, 2 ಎಂಬ ಮೂರೇ ಗುರುತುಗಳ ಕ್ರಮಸಂಯೋಜನೆಗಳಾಗಿರುತ್ತದೆ.
ಆದಿಮಾನವ ಸಂಖ್ಯಾಪ್ರತೀಕಗಳನ್ನು ಆಧುನಿಕ ದಶಮಾನ ಪದ್ಧತಿಗೆ ಪರಿವರ್ತಿಸಲು ಅನುಸರಿಸಬೇಕಾದ ಮಾರ್ಗವೂ ಈಗ ತಿಳಿಸಿರುವ ವಿಧಾನಕ್ಕೆ ಸದೃಶವಾದುದೇ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ಮೇಲೆ ನಮೂದಿಸಿರುವ ನಾಲ್ಕೇ ವಿಧಿಗಳ ಆಲ್ಗಾರಿತಮಿನ ಬದಲು ಕೆಳಗಿನ ಹನ್ನೊಂದು ವಿಧಿಗಳ ಹೊಸ ಆಲ್ಗಾರಿತಮನ್ನು ಬಳಸಬೇಕಾಗುತ್ತದೆ, ಅಷ್ಟೆ:
- ವಿಧಿ 1: OTTTTTTTTTT ಯನ್ನು TO ಎಂದು ಮಾರ್ಪಡಿಸಿ.
- ವಿಧಿ 2: OTTTTTTTTT ಯನ್ನು 9 ಎಂದು ಬದಲಿಸಿ.
- ವಿಧಿ 3: OTTTTTTTT ಯನ್ನು 8 ಎಂದು ಬದಲಿಸಿ.
..........................................
- ವಿಧಿ 9: OTT ಯನ್ನು 2 ಎಂದು ಬದಲಿಸಿ.
- ವಿಧಿ 10: OT ಯನ್ನು 1 ಎಂದು ಬದಲಿಸಿ.
- ವಿಧಿ 11: ಪರಿಶೀಲಿತ ವಾಕ್ಯದ ಅತ್ಯಂತ ಎಡಗಡೆಯಲ್ಲಿ T ಇರುವುದಾದರೆ ಅದನ್ನು OT ಎಂದು ಮಾರ್ಪಡಿಸಿ.
ದಶಮಾನ ಮತ್ತು ತ್ರಿಮಾನಗಳಂಥ ಸಂಖ್ಯಾಪ್ರತೀಕ ಪದ್ಧತಿಗಳ ನಿಯೋಜನೆಯಲ್ಲಿ O ಚಿಹ್ನೆ ಅತಿ ಮುಖ್ಯವಾದ ಪಾತ್ರವನ್ನು ವಹಿಸಿರುವುದು ಇದೀಗ ಸ್ಪಷ್ಟವಾಗಿರಬೇಕು. ಕ್ರಿ.ಶ. ಸುಮಾರು 5 ರಿಂದ 8 ನೆಯ ಶತಮಾನಗಳ ನಡುವೆ ಹಿಂದೂ ಗಣಿತಜ್ಞರು ಈ ಚಿಹ್ನೆಯ ಅಗತ್ಯತೆಯನ್ನು ಪರಿಪೂರ್ಣವಾಗಿ ಮನಗಂಡು ಅದನ್ನು ಏನೂ ಇಲ್ಲದಿರುವಿಕೆ ಎಂಬ ಅಭಿಪ್ರಾಯದ ಶೂನ್ಯ ಪದದಿಂದ ನಿರ್ದೇಶಿಸಿದರೆ. ಅದಕ್ಕೂ ಕೆಲ ಶತಮಾನಗಳ ಹಿಂದೆ ಪ್ರಾಚೀನ ಬ್ಯಾಬಿಲೋನಿಯನ್ನರೂ ಮಧ್ಯ ಅಮೆರಿಕದ ಮಾಯ ಜನಾಂಗದವರೂ 0 ಗೆ ಸಮಾನವಾದ ಚಿಹ್ನೆಗಳನ್ನು ಅವರ ಸಂಖ್ಯಾಪ್ರತೀಕಗಳ ಮಧ್ಯಸ್ಥಾನಗಳಲ್ಲಿ (ಉದಾಹರಣೆಗೆ 120), ಅವರ ಪ್ರತೀಕಪದ್ಧತಿ ಇಪ್ಪತ್ತು ಮತ್ತು ಅರವತ್ತು ಎಂಬ ಎರಡೆರಡು ಪಾದಗಳನ್ನು ಅವಲಂಬಿಸುವ ಮಿಶ್ರತಳಿಯಾಗಿತ್ತು. ಮಾಯ ಜನಾಂಗದವರು ಬಳಸುತ್ತಿದ್ದ ಶೂನ್ಯ ಪ್ರತೀಕಗಳ ಪೈಕಿ ಕೆಲವಷ್ಟು ಇಪ್ಪತ್ತನ್ನೂ ನಿರ್ದೇಶಿಸುತ್ತಿದ್ದವು. ಅವರ ಪ್ರತೀಕಪದ್ಧತಿಯಲ್ಲಿ ಐದು, ಇಪ್ಪತ್ತು ಹಾಗೂ ಹದಿನೆಂಟು ಎಂಬ ಮೂರು ಪಾದಗಳ ಕೈವಾಡವಿರುತ್ತಿತ್ತು. ಇಂಥ ಕ್ಲಿಷ್ಟತೆಗಳಿಲ್ಲದೆ ಶೂನ್ಯ ಪ್ರತೀಕದ ಪೂರ್ಣ ಸುಸಂಗತ ಬಳಕೆಯನ್ನೂ, ಜೊತೆಗೆ ಹತ್ತು ಮಾತ್ರವೇ ಪಾದವಾಗಿರುವ ಶುದ್ಧ ದಶಮಾನ ಪದ್ಧತಿಯನ್ನೂ ರೂಢಿಗೆ ತರುವಲ್ಲಿ ಮೊಟ್ಟಮೊದಲಿಗೆ ಹಿಂದೂ ಗಣಿತಜ್ಞರು ಯಶಸ್ವಿಯಾದರು. 9ನೆಯ ಶತಮಾನದಲ್ಲಿ ಹಿಂದೂ ಗಣಿತವನ್ನು ಅರಬ್ಬರು ಕಲಿತು ಅದನ್ನು ಮತ್ತಷ್ಟು ಸಂಸ್ಕರಿಸಿ ಯೂರೋಪಿಗೂ ರವಾನಿಸಿದರು. [೫] ಧನಪೂರ್ಣಂಕಗಳ ಆಧುನಿಕ ದಶಮಾನ ಸಂಜ್ಞಾಪದ್ಧತಿಗೆ ಹಿಂದೂ-ಅರ್ಯಾಬಿಕ್ ಪದ್ಧತಿ ಎಂದು ಹೆಸರಾಗಲು ಇದೇ ಕಾರಣ.
ಆದಿಮಾನವನ ಧನಪೂರ್ಣಾಂಕಗಳಿಗೆ ಅನುರೂಪವಾದ ತ್ರಿಮಾನ ಹಾಗೂ ದಶಮಾನ ಪ್ರತೀಕಗಳನ್ನು ಗೊತ್ತುಮಾಡಿದಂತೆ ತ್ರಿಮಾನ, ದಶಮಾನಗಳಂಥ ಪದ್ಧತಿಗಳ ಧನಪೂರ್ಣಾಂಕಗಳನ್ನು ಆದಿಮಾನವನ ಪ್ರತೀಕಗಳಾಗಿ ಪುನಾರೂಪಾಂತರಿಸುವುದೂ ಅಪೇಕ್ಷಣೀಯವಷ್ಟೆ. ಈ ದಿಶೆಯಲ್ಲೂ ಸರಳ ಆಲ್ಗಾರಿತಮಂಗಳ ಯೋಜನೆ ಸಾಧ್ಯ. ಉದಾಹರಣೆಗೆ ತ್ರಿಮಾನ ಪದ್ಧತಿಯ ಧನಪೂರ್ಣಾಂಕಗಳನ್ನು T ಗುರುತುಗಳ ಸಾಲುಗಳನ್ನಾಗಿ ಮರುಪರಿವರ್ತಿಸಲು ಕೆಳಗಿನ ಆರು ವಿಧಿಗಳ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂ ಉಪಯುಕ್ತವಾಗುತ್ತದೆ. (ಇಲ್ಲಿ S ಒಂದು ಸಹಾಯಕ ಅಕ್ಷರ).
- ವಿಧಿ 1: TS ನ್ನು STTT ಎಂದು ಬದಲಾಯಿಸಿ.
- ವಿಧಿ 2: OS ನ್ನು SS ಎಂದು ಮಾರ್ಪಡಿಸಿ.
- ವಿಧಿ 3: 1S ನ್ನು SST ಎಂದು ಮಾರ್ಪಡಿಸಿ.
- ವಿಧಿ 4: 2S ನ್ನು SSTT ಎಂದು ಮಾರ್ಪಡಿಸಿ.
- ವಿಧಿ 5: ಎಲ್ಲ S ಗಳನ್ನೂ ಅಳಿಸಿಬಿಡಿ.
- ವಿಧಿ 6: ಪರಿಶೀಲಿತ ವಾಕ್ಯದ ಅತ್ಯಂತ ಬಲಗಡೆಯಲ್ಲಿ O ಇದ್ದರೆ ಅದನ್ನು OS ಎಂದೂ, 1 ಇದ್ದರೆ ಅದನ್ನು 1S ಎಂದೂ, 2 ಇದ್ದರೆ ಅದನ್ನು 2S ಎಂದೂ ಬದಲಾಯಿಸಿ
ಈ ಆಲ್ಗಾರಿತಂ ಮೇರೆಗೆ ತ್ರಿಮಾನ ಪದ್ಧತಿಯ 122 ಎಂಬ ಧನಪೂರ್ಣಾಂಕವನ್ನು T ಗಳ ಸಾಲನ್ನಾಗಿ ರೂಪಾಂತರಿಸುವ ಹೆಜ್ಜೆಗಳನ್ನು ಕೆಳಗೆ ತೋರಿಸಲಾಗಿದೆ. (ಒಂದೊಂದು ಹೆಜ್ಜೆಯ ವಾಕ್ಯದ ಮೇಲೂ ಪ್ರಯೋಗಿಸಬೇಕಾದ ವಿಧಿಯ ವಿವರವನ್ನು ಆವರಣದಲ್ಲಿ ನಮೂದಿಸಿದೆ.)
- 122 [ದತ್ತತ್ರಿಮಾನ ಧನಪೂರ್ಣಾಂಕ; ಇದರ ಮೇಲೆ 6ನೆಯ ವಿಧಿಯನ್ನು ಪ್ರಯೋಗಿಸಬೇಕು.]
- 122 S [ಈಗ ವಿಧಿ 4]
- 12S STT [ ಪುನ: ವಿಧಿ 4]
- 1SS TTS TT [ಈಗ ವಿಧಿ 1]
- 1SS TST TTT T [ ಪುನಃ ವಿಧಿ 1]
- 1SS STT TTT TTT [ ವಿಧಿ 3]
- SST SST TTT TTT T [ ವಿಧಿ 1]
- SSS TTT STT TTT TTT [ ಮತ್ತೆ ವಿಧಿ 1]
- SS TTS TTT TTT TTT TT [ ಮತ್ತೆ ವಿಧಿ 1]
- SSS TST TTT TTT TTT TTT T [ ಪುನಃ ವಿಧಿ 1]
- SSS STT TTT TTT TTT TTT TTT [ಕೊನೆಗೆ ವಿಧಿ 5]
- TTT TTT TTT TTT TTT TT [ಪರಿಸಮಾಪ್ತಿ]
ಮೇಲಿನ ವ್ಯುತ್ಪತ್ತಿಯನ್ನು ಗಮನಿಸಿದರೆ 122 ರ ಬಲತುದಿಯಲ್ಲಿರುವ 2 ಎಂಬ ಅಂಕೆ ಮೂರನೆಯ ಹೆಜ್ಜೆಯಲ್ಲಿ TT ಗೂ, ಮಧ್ಯದ 2 ಆರನೆಯ ಹೆಜ್ಜೆಯಲ್ಲಿ TTTTTT ಗೂ, ಎಡತುದಿಯ 1 ಹನ್ನೊಂದನೆಯ ಹೆಜ್ಜೆಯಲ್ಲಿ ಇನ್ನುಳಿದ TTTTTTTTT ಗೂ ಜನ್ಮ ನೀಡಿರುವುದು ವೇದ್ಯವಾಗುತ್ತದೆ. ಈ ಫಲಿತಾಂಶಗಳನ್ನು ಹೀಗೆ ವ್ಯಕ್ತಪಡಿಸಬಹುದು:
122 = TTT TTT TTT TTTTTT TT (ತ್ರಿಮಾನ ಪದ್ಧತಿ) 1 ರ ಕೊಡುಗೆ ಮಧ್ಯದ 2 ರ ಕೊಡುಗೆ ಬಲತುದಿಯ 2ರ ಕೊಡುಗೆ
ಮಧ್ಯದ 2 ರ ಕೊಡುಗೆ ಬಲತುದಿಯ 2 ರ ಕೊಡುಗೆಗಿಂತ ಅಧಿಕವಾಗಿರುವುದನ್ನು ಗಮನಿಸಬೇಕು. ಅಂದಮೇಲೆ ತ್ರಿಮಾನ ಪದ್ಧತಿಯ ಸಂಖ್ಯಾಪ್ರತೀಕಗಳಲ್ಲಿ ಬಿಡಿ ಅಂಕೆಗಳ ಮೌಲ್ಯ ಆ ಅಂಕೆಗಳಷ್ಟನ್ನೇ ಅಲ್ಲದೆ ಅವುಗಳ ಸ್ಥಾನವನ್ನೂ ಅವಲಂಬಿಸಿದೆ ಎಂದಾಯಿತು. ಈ ಲಕ್ಷಣವಿರುವ ಸಂಖ್ಯಾಸೂಚಕಪದ್ಧತಿಗಳಿಗೆ ಸ್ಥಾನಿಕ ಮೌಲ್ಯ ವ್ಯವಸ್ಥೆಗಳು (ಪೊಸಿಷನ್ ವ್ಯಾಲ್ಯು ಸಿಸ್ಟಮ್ಸ್) ಎಂದು ಹೆಸರು. ತ್ರಿಮಾನ ಪದ್ಧತಿಯಂತೆ ದಶಮಾನ ಪದ್ಧತಿಯೂ ಒಂದು ಸ್ಥಾನಿಕ ಮೌಲ್ಯ ವ್ಯವಸ್ಥೆಯೇ. ಕ್ರಿ.ಪೂ. 20 - 25 ನೆಯ ಶತಮಾನಗಳಷ್ಟು ಹಿಂದೆಯೇ ಯೂಫ್ರಟಿಸ್ ಟೈಗ್ರಿಸ್ ಕಣಿವೆಯ ಸುಮೇರಿಯನ್ ಜನರು ಅರವತ್ತನ್ನು ಪ್ರಧಾನ ಪಾದವಾಗಿ ಉಳ್ಳ, ಆದರೆ ಶೂನ್ಯ ಚಿಹ್ನೆಯಿಲ್ಲದೆ ಸ್ಥಾನಿಕ ಮೌಲ್ಯ ಸಂಖ್ಯಾಸೂಚಕ ವ್ಯವಸ್ಥೆಯೊಂದನ್ನು ನಿಯೋಜಿಸಿ ಬಳಸುತ್ತಿದ್ದರು. ಇದಕ್ಕೆ ವ್ಯತಿರಿಕ್ತವಾಗಿ ಅದಕ್ಕಿಂತ ತುಸು ಪ್ರಾಚೀನ ಕಾಲದ ಈಜಿಪ್ಟಿನ ಹೈಎರೊಗ್ಲಿಫಿಕ್ ಬರಹಗಾರರಾದರೋ ಬಿಡಿ, ಹತ್ತು, ನೂರು ಇತ್ಯಾದಿಗಳನ್ನು (ಕೋಟಿಯವರೆಗೆ ಮಾತ್ರ) ಸೂಚಿಸಲು ಕೆಲವು ಭಿನ್ನ ಚಿಹ್ನೆಗಳನ್ನೇ ಇಟ್ಟುಕೊಂಡಿದ್ದರು. ಉದಾಹರಣೆಗೆ ಇನ್ನೂರಿಪ್ಪತ್ತೆರಡು ಎಂಬ ಸಂಖ್ಯೆಯನ್ನು ಅವರು ಚಿತ್ರ (2) ರಲ್ಲಿ ಕಾಣಿಸಿರುವಂತೆ ಬರೆಯುತ್ತಿದ್ದರು; ಮತ್ತು ಇದನ್ನೇ ಚಿತ್ರ (3) ಮತ್ತು ಚಿತ್ರ (4) ರಲ್ಲಿನಂತೆ ಹಲವಾರು ಪರ್ಯಾಯ ಕ್ರಮಗಳಲ್ಲಿ ಬರೆದರೂ ಸಲ್ಲುತ್ತಿತ್ತು.
ವ್ಯಾವಹಾರಿಕ ಲೆಕ್ಕಾಚಾರಗಳಿಗೆ ದಶಮಾನ ಪದ್ಧತಿ ಕಲ್ಪಿಸಿಕೊಟ್ಟಿರುವ ಉತ್ತೇಜಕ ಸೌಲಭ್ಯಗಳು ನಿಜಕ್ಕೂ ಅಪಾರ. ಧನಪೂರ್ಣಾಂಕಗಳ ಅಭಿವ್ಯಕ್ತಿಗಾಗಿ ಇಂಥದೊಂದು ಪದ್ಧತಿ ನಿಯೋಜಿತವಾಗದಿದ್ದಲ್ಲಿ ಸಂಖ್ಯಾಕಲನಶಾಸ್ತ್ರ (ಸ್ಟ್ಯಾಟಿಸ್ಟಿಕ್ಸ್), ಅನ್ವಯಿಕ ಅರ್ಥಶಾಸ್ತ್ರ (ಅಪ್ಲೈಯ್ಡ್ ಇಕನಾಮಿಕ್ಸ್), ವಾಣಿಜ್ಯೋದ್ಯಮ (ಕಾಮರ್ಸ್), ತಂತ್ರಜ್ಞಾನ (ಟೆಕ್ನಾಲಜಿ) ಮುಂತಾದ ನವನಾಗರಿಕತೆಯ ಅವಶ್ಯ ಚಟುವಟಿಕೆಗಳಾವುವೂ ಹೆಚ್ಚು ಪ್ರವರ್ಧಿಸಲು ಅವಕಾಶವೇ ಆಗುತ್ತಿರಲಿಲ್ಲ. ಆದಾಗ್ಯೂ ಶುದ್ಧ ಗಣಿತದ (ಪ್ಯೂರ್ ಮ್ಯಾಥ್ಮ್ಯಾಟಿಕ್ಸ್) ದೃಷ್ಟಿಯಿಂದ ದಶಮಾನ, ತ್ರಿಮಾನ, ದ್ವಿಮಾನ (ಈ ಕೊನೆಯದರ ಪಾದ TT) ಮುಂತಾದ ಪ್ರತೀಕ ಯೋಜನೆಗಳ ನಿರ್ಮಾಣ ಕೇವಲ ಒಂದು ತಾಂತ್ರಿಕ ಪ್ರಗತಿಯೋ ಇಲ್ಲವೇ ನಿಜವಾದ ತಾತ್ತ್ವಿಕ ಪ್ರಗತಿಯೋ ಎಂಬ ಪ್ರಶ್ನೆ ಪರಿಶೀಲನಾರ್ಹ. ಬಹುಸಂಖ್ಯಾತ ಗಣಿತಜ್ಞರಲ್ಲಿ ಇಂದಿನವರೆಗೆ ಬೆಳೆದು ಬಂದಿರುವ ಚಿಂತನ ಪ್ರವೃತ್ತಿಗಳ ಪ್ರಕಾರ ಅದು ತಾಂತ್ರಿಕ ಪ್ರಗತಿ ಮಾತ್ರ ಆದೀತೇ ಹೊರತು ತಾತ್ತ್ವಿಕವಲ್ಲ (ಕೊನೆಯ ಪಕ್ಷಕ್ಕೆ ಇದು ಈ ಬಹುಸಂಖ್ಯಾತ ಗಣಿತಜ್ಷರ ಸುಪ್ತ ಅಥವಾ ಪ್ರಬುದ್ಧ ಮನೋಭಿಪ್ರಾಯ). ಏಕೆಂದರೆ ಆಧುನಿಕ ದಶಮಾನಾಂಕಗಳನ್ನು ಬಳಸಿ ನಾವಿಂದು ಯಾವ ಯಾವ ಗಣಿತ ಚಟುವಟಿಕೆಗಳಲ್ಲಿ ತೊಡಗಬಹುದೋ ಅವೆಲ್ಲವನ್ನೂ ಆದಿಮಾನವನ ಕಚ್ಚು, ಬೊಟ್ಟುಗಳ ನೆರವಿನಿಂದಲೇ ನಿರ್ವಹಿಸಲು ತತ್ತ್ವಶಃ ಸಾಧ್ಯವಿದೆ. ಉದಾಹರಣೆಗೆ 4 ನ್ನೂ 3 ನ್ನೂ ಕೂಡುವುದಕ್ಕೆ ಪ್ರತಿಯಾಗಿ TTTT ಯನ್ನೂ TTT ಯನ್ನೂ ಒಟ್ಟುಗೂಡಿಸಿ TTTTTTT ಯನ್ನು ರಚಿಸಬಹುದಷ್ಟೆ; ಅಂದರೆ ಎರಡು T ಸಾಲುಗಳನ್ನು ಕೂಡಲು ಅವುಗಳ ನಡುವಿನ + ಚಿಹ್ನೆಯನ್ನು ಕೈಬಿಟ್ಟರಾಯಿತು:
TTTT + TTT = TTTTTTT
ಮತ್ತೆ TTTT x TTT ಮಾದರಿಯ ಎರಡು T ಸಾಲುಗಳ ಗುಣಲಬ್ಧವನ್ನು ರಚಿಸಲು ಕೆಳಗಿನ ಏಳು ವಿಧಿಗಳ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಮನ್ನೂ ಬಳಸಿಕೊಳ್ಳಬಹುದು (ಇಲ್ಲಿ x ಗುಣಾಕಾರದ ಚಿಹ್ನೆ, Q, R, S ಸಹಾಯಕ ಅಕ್ಷರಗಳು):
- ವಿಧಿ 1: Q x TT ಯನ್ನು R x T ಎಂದು ಬದಲಾಯಿಸಿ.
- ವಿಧಿ 2: Q x T ಯನ್ನು ಅಳಿಸಿಬಿಡಿ.
- ವಿಧಿ 3: TR ನ್ನು RST ಎಂದು ಬದಲಾಯಿಸಿ.
- ವಿಧಿ 4: SR ನ್ನು RS ಎಂದು ಮಾರ್ಪಡಿಸಿ.
- ವಿಧಿ 5: TX ನ್ನು TQX ಎಂದು ಬದಲಾಯಿಸಿ.
- ವಿಧಿ 6: S ಗಳನ್ನೆಲ್ಲ T ಗಳಾಗಿ ಪರಿವರ್ತಿಸಿ.
- ವಿಧಿ 7: R ಗಳನ್ನೆಲ್ಲ ಅಳಿಸಿಬಿಡಿ.
ಈ ಆಲ್ಗಾರಿತಮನ್ನು TTTT x TTT ಯ ಮೇಲೆ ಪ್ರಯೋಗಿಸಿದಾಗ TTTTTTTTTTTT ಎಂಬ ಸರಿಯದ ಗುಣಲಬ್ಧ ಫಲಿಸುತ್ತದೆ. ಇದೇ ಪ್ರಕಾರ ಅಂಕಗಣಿತದ ಇತರ ಎಲ್ಲ ಲೆಕ್ಕಚಾರಗಳನ್ನೂ ಯಶಸ್ವಿಯಾಗಿ T ಸಾಲುಗಳ ಮಾಧ್ಯಮದಲ್ಲೇ ತತ್ತ್ವಶಃ ಕೈಗೊಳ್ಳಬಹುದು ಎಂದೆನಿಸುವುದು ಸಹಜ. ಮೇಲಾಗಿ ಆದಿಮಾನವನ T ಸಾಲುಗಳಿಗೆ, ಹಾಗೂ ಅವನ್ನೊಳಗೊಳ್ಳುವ ಲೆಕ್ಕಾಚಾರ ಕ್ರಮಗಳಿಗೆ, ಪ್ರಶ್ನಾತೀತ ತಾತ್ತ್ವಿಕ ಸರಳತೆ ಸಹ ಇರುವುದನ್ನು ಯಾರೂ ಅಲ್ಲಗಳೆಯುವಂತಿಲ್ಲ. ಆದರೂ ಧನಪೂರ್ಣಾಂಕಗಳ ಗಣಿತವನ್ನು ಆದಿಮಾನವನ ಪ್ರತೀಕಗಳಿಂದಲೇ ನಿರ್ಮಾಣಮಾಡುವ ಕಾರ್ಯಕ್ರಮ ನಿಜಕ್ಕೂ ಒಂದು ಅಪ್ರಕಟಿತ ವಿಶ್ವಾಸವನ್ನು ಅವಲಂಬಿಸಿ ನಿಂತಿದೆ: ಮನಬಂದಷ್ಟು ಉದ್ದುದ್ದವಾದ T (ಹಾಗೂ ಇತರ) ಗುರುತುಗಳ ಸಾಲುಗಳನ್ನು ರಚಿಸಿಡಲು ಯಾವ ತಾತ್ತ್ವಿಕ ಆತಂಕವೂ ಇಲ್ಲ ಎಂಬುದೇ ಆ ಅಪ್ರಕಟಿತ ವಿಶ್ವಾಸ. (ದಶಮಾನ ಪ್ರತೀಕಗಳಿಂದ ಇಲ್ಲವೇ ಮತ್ತಾವುದೇ ಪೂರ್ವನಿಶ್ಚಿತ ಸಾಲುಗುರುತು ಪ್ರತೀಕಗಳಿಂದ, ಧನ ಪೂರ್ಣಾಂಕಗಳ ಸಂಪೂರ್ಣ ಗಣಿತವನ್ನು ನಿರ್ಮಿಸುವ ಪ್ರೌಢತರ ಕಾರ್ಯಕ್ರಮಗಳಿಗೆ ಸಹ ಈ ಮಾತು ಅನ್ವಯಿಸದೆ ಇಲ್ಲ). ಇತ್ತೀಚೆಗೆ (ಮುಖ್ಯವಾಗಿ ಮಾಹಿತಿ ಸಿದ್ಧಾಂತದ --- ಇನ್ಫರ್ಮೇಷನ್ ಥಿಯರಿ --- ಸಂಸ್ಥಾಪನೆಯ ಬಳಿಕ) ಈ ವಿಶ್ವಾಸದ ಬಗ್ಗೆ ತುಸು ಪುನರಾಲೋಚನೆ ನಡೆಸುವ ಅಗತ್ಯ ಕಂಡುಬರುತ್ತದೆ. ಇಲ್ಲಿ ಉದ್ಭವಿಸುವ ಪ್ರಶ್ನೆಗಳು ಎರಡು. ಮೊದಲನೆಯದಾಗಿ, ಒಂದು ಪಕ್ಷ ಇಡೀ ವಿಶ್ವದಲ್ಲಿರುವ ಮೂಲಭೂತ ದ್ರವ್ಯಕಣಗಳೆಲ್ಲ ಸ್ವಭಾವತಃ ಅವಿಭಾಜ್ಯವೂ ಅವುಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆ ಸ್ವಭಾವತಃ ಸಾಂತವೂ (ಫೈನೈಟ್) ಆಗಿದ್ದಲ್ಲಿ ಆ ಸಂಖ್ಯೆಗಿಂತಲೂ ಉದ್ದವಾದ T ಸಾಲುಗಳನ್ನು ರಚಿಸಬಹುದೆಂಬ ಕಲ್ಪನೆಗೆ ತಾತ್ತ್ವಿಕ ಆಸರೆ ಉಳಿದಿತೇ? ಎರಡನೆಯದಾಗಿ, ಯಾವುದೇ ನಿರ್ದಿಷ್ಟ ಗುರುತುಗಳ ತೀರ ಉದ್ದವಾದ ಸಾಲೊಂದನ್ನು ರಚಿಸತೊಡಗಿದರೂ ಅಂಥ ಸಾಲಿನ ಪ್ರಾರಂಭದಲ್ಲಿ ಲಿಖಿತವಾದ ಗುರುತುಗಳು ಕಾಲಕ್ರಮೇಣ ಮಸಕಾಗುತ್ತ ಬಂದು ರಚನೆ ಪೂರ್ಣಗೊಳ್ಳುವ ಮುನ್ನವೇ ಪರಿಸರದೊಂದಿಗೆ ಲೀನವಾಗಿಬಿಡುವುದಿಲ್ಲವೇ? ಮೂವತ್ತನಾಲ್ಕನ್ನು 34 ಎಂಬ ದಶಮಾನ ರೂಪದಲ್ಲಿ ಯಾವ ಪ್ರಯಾಸವೂ ಇಲ್ಲದೆ ನೆನಪಿಟ್ಟುಕೊಳ್ಳಬಹುದಾದರೂ ಅದನ್ನು TTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT ಎಂಬ ರೂಪದಲ್ಲಿ ಗ್ರಹಿಸಲು ಲೇಖನಿ, ಕಾಗದಗಳನ್ನು ಮರೆಹೋಗದೆ ವಿಧಿಯಲ್ಲ. ಇಷ್ಟೊಂದು ಉದ್ದವಿರುವ T ಸಾಲಿನ ರಚನೆ ನಮ್ಮ ಮಿದುಳಿನೊಳಗಡೆಯಲ್ಲಿ ಇನ್ನೂ ಅಪೂರ್ಣವಾಗಿರುವಾಗಲೇ ಆದಿಯ T ಗಳು ಅಳಿಸುತ್ತ ಬರುವುದು ಇದಕ್ಕೆ ಕಾರಣ. ಇದೇ ಪ್ರಕಾರ 9999999999999999999999999999999999 ಎಂಬ ದಶಮಾನ ಪೂರ್ಣಾಂಕದ ವ್ಯಾಪ್ತಿಯನ್ನು ಗ್ರಹಿಸಬೇಕಾದರೂ ಕಾಗದ, ಲೇಖನಿಗಳು ಅಗತ್ಯವಾಗುವುವು. ಈಗ ಈ ದಶಮಾನ ಪೂರ್ಣಾಂಕವನ್ನು ಒಂದು ಅನುರೂಪ T ಸಾಲನ್ನಾಗಿ ಬರೆಯತೊಡಗಿದರೆ ಸೆಕೆಂಡ್ ಒಂದಕ್ಕೆ ಹಲವಾರು ಸಹಸ್ರಕೋಟಿ T ಗಳನ್ನು ಬರೆದರೂ ಸಾಲಿನ ರಚನೆ ಪೂರ್ಣವಾಗುವುದಕ್ಕೆ ಒಂದಷ್ಟು ಕೋಟಿಕೋಟಿ ವರ್ಷಗಳು ಅವಶ್ಯವಾಗುತ್ತವೆ. ರಚನೆಯ ಅವಧಿ ಇಷ್ಟೊಂದು ದೀರ್ಘವಿರುವಾಗ ಮಿದುಳಿನೊಳಗಡೆ ನಡೆದಂಥ ವಿದ್ಯಮಾನವೇ ಅತ್ಯುತ್ತಮ ದಾಖಲೆ ಮಾಧ್ಯಮಗಳಲ್ಲಿಯೂ ಸಂಭವಿಸುವುದು ಅನಿವಾರ್ಯ. ಅಂದ ಮೇಲೆ ಮೇಲಿನ ದಶಮಾನ ಪೂರ್ಣಾಂಕಕ್ಕೆ ಅನುರೂಪವಾದ T ಸಾಲನ್ನು ಬಹುಶಃ ಎಲ್ಲು ರಚಿಸಲು ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ. ಇನ್ನು ಇದೇ ಬಗೆಯ ತೊಡಕು ಸಾಕಷ್ಟು ದೊಡ್ಡವಾದ A ,B ಎಂಬ ದಶಮಾನ ಧನ ಪೂರ್ಣಾಂಕಗಳೆರಡರ ಚರಘಾತಾಂಕೀಯ ಸಂಯೋಜನೆ (ಎಕ್ಸ್ಪೊನೆನ್ಷಿಯಲ್ ಕಾಂಪೊಸಿಷನ್) AB ಯನ್ನು ಒಂದು ನೇರ ದಶಮಾನ ಪೂರ್ಣಾಂಕವಾಗಿ ಬರೆಯ ಹೊರಟಾಗಲೂ ಉದ್ಭವಿಸಿಯೇ ತೀರುವುದು. ಅಲ್ಲಿಗೆ ನಾವು ಯಾವುದೇ ಪ್ರತೀಕ ಯೋಜನೆಯನ್ನು ಅನುಸರಿಸಿದರೂ ಎಲ್ಲ ಧನ ಪೂರ್ಣಾಂಕಗಳ ಎಲ್ಲ ಸುಸಂಬದ್ಧ ಸಂಯೋಜನೆಗಳನ್ನೂ ಮತ್ತೆ ಪೂರ್ಣಾಂಕಗಳ ಮೂಲರೂಪಕ್ಕೆ ಪರಿವರ್ತಿಸುವುದು ಬಹುಶಃ ಅಸಾಧ್ಯವೇ ಆಗುತ್ತದೆ ಎಂದಾಯಿತು. ಮೊದಲ ನೋಟಕ್ಕೆ ಈ ತೊಡಕುಗಳು ತಾತ್ತ್ವಿಕ ಚರ್ಚೆಗೆ ಅಪ್ರಕೃತವಾದ ವ್ಯಾವಹಾರಿಕ ಸ್ವರೂಪವೆನಿಸಿದರೂ ಇವುಗಳಲ್ಲಿ ನಿಜಕ್ಕೂ ಮೂಲಭೂತ ನಿಸರ್ಗ ನಿಯಮಗಳ ಕೈವಾಡವಿರುವ ಸಾಧ್ಯತೆಯನ್ನು ನಾವು ಅಲಕ್ಷಿಸುವಂತಿಲ್ಲ. ಆದಾಗ್ಯೂ ಇಂಥ ಸಂಕೀರ್ಣತೆಗಳನ್ನೆಲ್ಲ ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡು ಗಣಿತವನ್ನು ಸಮರ್ಪವಾಗಿ ಪುನಾರಚಿಸಲು ಇದುವರೆಗೆ ಯಾರಿಂದಲೂ ಸಾಧ್ಯವಾಗಿಲ್ಲ. ಇಂತಿರುವಾಗ ತಾತ್ಕಾಲಿಕವಾಗಿಯಾದರೂ ಕ್ಲಿಷ್ಟತೆಯಿಂದ ಪಾರಾಗುವ ವಿಮೋಚನ ಮಾರ್ಗಗಳನ್ನು ಅರಸುವುದು ಸೂಕ್ತವಷ್ಟೆ. T ಹಾಗೂ ಇತರ ಗುರುತುಗಳ ಸಾಲುಗಳನ್ನು ಮನಬಂದಷ್ಟು ದೀರ್ಘವಾಗಿ ವೃದ್ಧಿಸುತ್ತ ಹೋಗುವ ಸೌಲಭ್ಯವುಂಟೆಂಬ ಸಾಂಪ್ರದಾಯಿಕ ವಿಶ್ವಾಸ ಅಂಥ ಒಂದು ಸರಳ ವಿಮೋಚನ ಮಾರ್ಗವನ್ನು ನಮ್ಮ ಪಾಲಿಗೆ ಕಲ್ಪಿಸಿಕೊಡುತ್ತದೆ. ಎಂತಲೇ ಇನ್ನು ಹೆಚ್ಚಿನ ಚರ್ಚೆಯಲ್ಲದೆ ನಾವು ಅದನ್ನು ಮುಂದೆ ಎಲ್ಲೆಡೆಯಲ್ಲೂ ಅಂಗೀಕರಿಸುತ್ತೇವೆ. [ಈ ಮಾತುಗಳಲ್ಲಿ ಅನಪೆಕ್ಷಣೀಯ ಕ್ಷಮಾಯಾಚಕ ಧ್ವನಿ ಇದೆಯೆಂದು ಕಳವಳಪಡುವವರು ಧನಪೂರ್ಣಾಂಕಗಳು ನಿಜಕ್ಕೂ ಮಾನವರ ಚಟುವಟಿಕೆಗಳನ್ನೇ ಅವಲಂಬಿಸದ ಒಂದು ಸ್ವತಂತ್ರ ಆದರ್ಶಲೋಕದ ಸಾಮಗ್ರಿಗಳೆಂದಾಗಲಿ, ಇಲ್ಲವೆ ಮಾನವರ ಸ್ವತ್ತೇ ಆದಾಗ್ಯೂ ಅವರ ಅಂತರ್ಬೋಧೆಯ ಅಮೂರ್ತ ಸೃಷ್ಟಿಫಲಗಳೆಂದಾಗಲಿ ಘೋಷಿಸಿ, ಅವುಗಳ ದಿವ್ಯಸ್ವರೂಪವನ್ನು T ಸಾಲುಗಳಂಥ ಪಾಮರ ಪ್ರತೀಕಗಳ ಮೂಲಕ ಪರಿಪೂರ್ಣವಾಗಿ ಪ್ರತಿನಿಧಿಸಲು ಸಾಧ್ಯವಾಗದೆ ಹೋಗುವುದರಲ್ಲಿ ಅಚ್ಚರಿಯಿಲ್ಲವೆಂದು ಸಮಾಧಾನ ತಂದುಕೊಳ್ಳಬಹುದು. ಸಾಕಷ್ಟು ಗೌರವ ಗಳಿಸಿರುವ ಇವೆರಡು ದೃಷ್ಟಿಕೋನಗಳಿಗೆ ಕ್ರಮವಾಗಿ ಪ್ಲೇಟೋವಾದ (ಪ್ಲೇಟಾನಿಸಂ) ಮತ್ತು ಅಂತರ್ಬೋಧನವಾದ (ಇಂಟ್ಯುಇಷನಿಸಂ) ಎಂಬ ಹೆಸರುಗಳು ಬಂದಿದೆ]
ಸಾಲು ಪ್ರತೀಕಗಳ ಉದ್ದದ ಕ್ಲಿಷ್ಟಪ್ರಶ್ನೆಯನ್ನು ಹೀಗೆ ಸ್ಥಗಿತಗೊಳಿಸಿದ ತರುವಾಯ ಆದಿಮಾನವನ T ಸಾಲುಗಳು ಮಾಧ್ಯಮದಲ್ಲಿ ಧನಪೂರ್ಣಾಂಕಗಳ ಸಮಸ್ತ ಗಣಿತವನ್ನೂ ನಿರ್ಮಿಸುವ ಕಾರ್ಯಕ್ರಮವನ್ನು ಚಿತ್ರಿಸಬಹುದು. ಇದರ ವಿವರಗಳನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಪಟ್ಟಿ ಮಾಡುವುದು ವಾಡಿಕೆ:
- T ಯನ್ನು ಒಂದು ಧನಪೂರ್ಣಾಂಕವೆಂದು ಸ್ವೀಕರಿಸುವುದು.
- x ಯಾವುದೇ ಪ್ರತೀಕವಾಗಿರಲಿ ಅದರ ನಕಲಿನ ಮುಂದೆ T ಗುರುತನ್ನು ಬರೆದು xT ಎಂಬ ಪ್ರತೀಕವನ್ನು ರಚಿಸುವ ಶಕ್ಯತೆಯನ್ನು ಒಪ್ಪುವುದು; ಹಾಗೂ x ಧನಪೂರ್ಣಾಂಕವೆಂದು ಸ್ವೀಕೃತವಾಗಿರುವ ಸಂದರ್ಭಗಳಲ್ಲೆಲ್ಲ xT ಯನ್ನು ಮತ್ತೆ ಒಂದು ಧನಪೂರ್ಣಾಂಕವೆಂದು ಸ್ವೀಕರಿಸುವುದು; (ಇದರ ಪ್ರಕಾರ TT, TTT ಮುಂತಾದ T ಸಾಲುಗಳೆಲ್ಲವೂ ಧನಪೂರ್ಣಾಂಕಗಳಾಗುತ್ತವೆ)
- T ≠ xT ಎಂದು ಅಂಗೀಕರಿಸುವುದು (x ಚರ ಧನಪೂರ್ಣಾಂಕ, ≠ ಅಸಮತೆಯ ಚಿಹ್ನೆ).
- x≠y ಆದಾಗ xT ≠ yT ಎಂದು ಅಂಗೀಕರಿಸುವುದು (x, y ಚರ ಧನಪೂರ್ಣಾಂಕಗಳು.)
- x ಗೆ ಇದ್ದೊಡನೆ xT ಗೂ ಇರಲೇಬೇಕಾಗಿ ಬರುವಂಥ ಪ್ರತಿಯೊಂದು ಲಕ್ಷಣವೂ T ಗೆ ಇದ್ದೊಡನೆ ಸಮಸ್ತ ಧನಪೂರ್ಣಾಂಕಗಳಿಗೂ ಇದ್ದೇ ಇರುತ್ತದೆಂದು ತರ್ಕಿಸುವುದು (x ಚರ ಧನಪೂರ್ಣಾಂಕ).
ಈ ತತ್ತ್ವಗಳು ಇಂದು ಪಿಯಾನೋ ಆದ್ಯುಕ್ತಿಗಳು (ಪಿಯಾನೋ ಆ್ಯಕ್ಸಿಯಂಸ್, 1889) ಎಂದು ಪ್ರಸಿದ್ಧವಾಗಿರುವವುಗಳಿಗೆ ವಸ್ತುತಃ ಸಮಾನವಾದವು. ರಿಚರ್ಡ್ ಡೆಡೆಕಿಂಟ್ (1831-1916) ಎಂಬ ಗಣಿತಜ್ಞನಿಂದ ಪ್ರಭಾವಿತನಾದ ಗೈಸೆಪೆ ಪಿಯಾನೋ (1858-1932) ಇವನ್ನು ನಿರ್ದಿಷ್ಟ ಆದ್ಯುಕ್ತಿ ರೂಪದಲ್ಲಿ ಮೊಟ್ಟ ಮೊದಲಿಗೆ ಪ್ರಕಟಿಸಿದ. ಇವುಗಳಲ್ಲಿ ಕೊನೆಯದಕ್ಕೆ (೫) ಗಣಿತಾನುಮಿತಿ ತತ್ತ್ವ (ಪ್ರಿನ್ಸಿಪಲ್ ಆಫ್ ಮ್ಯಾಥ್ಮ್ಯಾಟಿಕಲ್ ಇಂಡಕ್ಷನ್) ಎಂದು ಹೆಸರು. ಇದನ್ನು ಕುರಿತು ತುಸು ಚಿಂತನೆ ಅವಶ್ಯ. A ಎಂಬುದು x ಗೆ ಇದ್ದೊಡನೆ xT ಗೂ ಇರಲೇಬೇಕಾಗಿರುವ ಯಾವುದಾದರೊಂದು ಲಕ್ಷಣವಾಗಿರಲಿ. ಈ ಲಕ್ಷಣ T ಗೆ ಇರುವುದಾದರೆ TT ಗೂ ಇರಲೇಬೇಕಷ್ಟೆ. ಅದು ಯಾವಾಗ TT ಗೆ ಪ್ರಾಪ್ತವಾಗಬೇಕಾಯಿತೋ TTT ಗೂ ಪ್ರಾಪ್ತವಾಗದೆ ವಿಧಿಯಿಲ್ಲ (ಇದನ್ನು ಮನಗಾಣಲು T T ಯನ್ನು X ಎಂದು ಪರಿಗಣಿಸಬೇಕು); ಇತ್ಯಾದಿ. ಹೀಗೆಯೇ ಮುಂದುವರಿದರೆ ಪರೀಶೀಲಿತ A ಲಕ್ಷಣ ಸಮಸ್ತ T ಸಾಲುಗಳಿಗೂ ಇದ್ದೇ ತೀರಬೇಕೆಂದು ಮನವರಿಕೆಯಾಗುವುದು. ಆದ್ದರಿಂದ T ಸಾಲುಗಳ ವಿನಾ ಬೇರಾವ ಧನಪೂರ್ಣಾಂಕಗಳೂ ಇಲ್ಲವೆಂಬ ಬೆಳಕಿನಲ್ಲಿ ಆಲೋಚಿಸುವವರಿಗೆ ಎಲ್ಲ ಧನಪೂರ್ಣಾಂಕಗಳಿಗೂ A ಲಕ್ಷಣ ಇದ್ದೇ ಇರುವ ಸಂಗತಿ ಒಡನೆಯೇ ಗೋಚರಿಸಿ ಗಣಿತಾನುಮಿತಿ ತತ್ತ್ವದ ಆದ್ಯುಕ್ತೀಕರಣ ಅನವಶ್ಯವಾಗುವುದು. ಆದರೆ ಆದ್ಯುಕ್ತೀಯ ಮನೋಧರ್ಮದ ಪ್ರಕಾರ ಸಮಸ್ತ ಚಿಂತನೆಗಳೂ ಪ್ರಕಟಿತ ಆದ್ಯುಕ್ತಿಗಳ ಚೌಕಟ್ಟಿನೊಳಗೆ ಸಾಗಬೇಕೇ ವಿನಾ ಆ ಚೌಕಟ್ಟಿನ ಹೊರಗಡೆ ಉಗಮಿಸುವ ಬೆಳಕನ್ನು ಆಶ್ರಯಿಸುವಂತಿಲ್ಲ. ಈ ಮನೋಧರ್ಮದ ಒತ್ತಡಕ್ಕೆ ಸಿಲುಕಿದ ಗಣಿತಜ್ಞರು ಧನಪೂರ್ಣಾಂಕಗಳ ವ್ಯಾಪ್ತಿಯನ್ನು ಆದ್ಯುಕ್ತಿ ಮಾರ್ಗದಿಂದಲೇ ನಿಖರಗೊಳಿಸುವ ಸಲುವಾಗಿ ಗಣಿತಾನುಮಿತಿ ತತ್ತ್ವವನ್ನು ಮೇಲಿನಂತೆ ಆದ್ಯುಕ್ತೀಕರಿಸಿಟ್ಟರು. ಹೀಗೆ ಮಾಡುವಾಗ ಪಿಯಾನೋ ಆದ್ಯುಕ್ತಿಗಳಿಗೆ ಬದ್ಧವಾಗಿರುವ ಯಾವುದೇ ಬಗೆಯ ಗಣಿತೀಯ ಧಾತುಗಳಾಗಲಿ ವಸ್ತುತಃ T ಗಳ ಸಾಲುಗಳಿಗೇ ಸಮಾನವಾಗಿರುತ್ತವೆಂಬುದು ಅವರ ಎಣಿಕೆಯಾಗಿತ್ತು. ಇತ್ತೀಚಿನ ಸಂಶೋಧನೆಗಳ ಫಲವಾಗಿ ಈ ಎಣಿಕೆಯಲ್ಲಿ ಕೆಲ ನಿಗೂಢ ಅಸಮರ್ಪಕತೆಗಳಿರುವುದು ಗೋಚರಕ್ಕೆ ಬಂದಿದೆ. ಆದಾಗ್ಯೂ ಆ ಅಸಮರ್ಪಕತೆಗಳು ಇಂದು ಗಣಿತದ ಪ್ರಗತಿಯನ್ನು ಕುಂಠಿತಗೊಳಿಸುವುದಕ್ಕೆ ಪ್ರತಿಯಾಗಿ ಶಿಷ್ಟೇತರ ವಿಶ್ಲೇಷಣೆ (ನಾನ್ - ಸ್ಟ್ಯಾಂಡರ್ಡ್ ಅನ್ಯಾಲಿಸಿಸ್) ಮುಂತಾದ ನವ್ಯ ಅಧ್ಯಯನಗಳಿಗೆ ಮೂಲ ಪ್ರೇರಣೆಯಾಗಿ ನಿಂತಿರುವ ವಿಚಾರ ಗಮನಾರ್ಹ.
T, TT, TTT ಮೊದಲಾದ ಧನಪೂರ್ಣಾಂಕಗಳ ಅರ್ಥವೇನು ಎಂಬ ಪ್ರಶ್ನೆ ಹಲವಾರು ತಾತ್ತ್ವಿಕರನ್ನೂ, ತಾರ್ಕಿಕರನ್ನೂ ಕಾಡಿ ನಾನಾ ಬಗೆಯ ಉತ್ತರಗಳನ್ನು ಹೊರಗೆಡಹಿದೆ. ಎಫ್. ಎಲ್. ಜಿ. ಫ್ರೇಜ್ (1848-1925) ಎಂಬಾತನ ದೃಷ್ಟಿಯಲ್ಲಿ ಎಲ್ಲ ಏಕಧಾತು ಗಣಗಳ ಸಮುದಾಯವೇ T, ಎಲ್ಲ ದ್ವಿಧಾತು ಗಣಗಳ ಸಮುದಾಯವೇ TT, ಎಲ್ಲ ತ್ರಿಧಾತು ಗಣಗಳ ಸಮುದಾಯವೇ TTT, ಇತ್ಯಾದಿ ಆದುವು. ಅರ್ನ್ಸ್ಟ್ ಟ್ಸರ್ಮಲೀಜ್ (1871-1956) ಎಂಬಾತನ ಪಾಲಿಗೆ T ಶೂನ್ಯಗಣವನ್ನೊಳಗೊಂಡ ಏಕಧಾತುಗಣ, TT ಶೂನ್ಯಗಣವನ್ನೊಳಗೊಂಡ ಏಕಧಾತುಗಣವನ್ನೊಳಗೊಂಡ ಏಕಧಾತುಗಣ, TTT ಶೂನ್ಯಗಣವನ್ನೊಳಗೊಂಡ ಏಕಧಾತುಗಣವನ್ನೊಳಗೊಂಡ ಏಕಧಾತುಗಣವನ್ನೊಳಗೊಂಡ ಏಕಧಾತುಗಣ, ಹೀಗೆಲ್ಲ ಆಗಿ ನಿಂತವು. ವಾಸ್ತವವಾಗಿ ಎಲುಬುಗಳ ಮೇಲೆ ಕಚ್ಚುಗಳನ್ನು ಕೆತ್ತಿದಾಗ ಆದಿಮಾನವನು ಗಣಸಿದ್ಧಾಂತದ ಅಂತರ್ಬೋಧೆಗಾಗಲಿ, ಬಹಿರ್ಬೋಧೆಗಾಗಲಿ ಗುರಿಯಾಗಿದ್ದಿರಲಾರನಷ್ಟೆ. ಅಮೂರ್ತ ಸ್ವರೂಪದ ಕೆಲ ನಿರ್ದಿಷ್ಟ ಮಾಹಿತಿಗಳನ್ನು ದಾಖಲೆ ಮಾಡಿಸುವುದಕ್ಕಾಗಿ ಆತ ಬಳಸಿದ ಪದಗಳೇ ಈ T, TT ಮುಂತಾದ ಧನಪೂರ್ಣಾಂಕಗಳು. ಪದಗಳ ವಿಚಾರದಲ್ಲಿ ನಿಜವಾದ ತರಬೇತಿಯ ಅಗತ್ಯವಿರುವುದು ಅವು ನೀಡುವ ಮಾಹಿತಿಗಳನ್ನು ಹೇಗೆ ಬಳಸಿಕೊಳ್ಳಬೇಕು ಎಂಬ ಬಗ್ಗೆ ಮಾತ್ರವೇ. ಇದಕ್ಕೆ ಬದಲು ಪದಗಳನ್ನು ಮತ್ತಷ್ಟು ಪದಗಳ ಮೂಲಕ ವರ್ಣಿಸತೊಡಗಿದರೆ ನಾವು ಅನತಿ ಕಾಲದಲ್ಲೇ ವಿಷವರ್ತುಲಕ್ಕೆ (ವಿಷಸ್ ಸರ್ಕಲ್) ಸಿಲುಕಿ ನರಳಬೇಕಾಗುವುದು. ಸಿಹಿಯ ನಿಜವಾದ ಅರ್ಥ ಬೇಕಿದ್ದರೆ ಸಕ್ಕರೆಯನ್ನು ತಿನ್ನುವುದು ಜಾಣತನ, ನಿಘಂಟನ್ನು ಶೋಧಿಸಿ ಸಿಹಿ = ಸಕ್ಕರೆಯ ರುಚಿ, ಸಕ್ಕರೆ = ಸಿಹಿಯಾದ ಪದಾರ್ಥ ಎಂಬಂಥ ವರ್ಣನೆಗಳನ್ನು ಆವಿಷ್ಕರಿಸುವುದು ಹಾಸ್ಯಾಸ್ಪದ. ದರ್ಜಿಯೊಬ್ಬ ತನ್ನ ಗಿರಾಕಿಯ ಹಸ್ತಗಳನ್ನು ವೀಕ್ಷಿಸಿ TT (ಎರಡು ಕೈಗಳಿವೆ) ಎಂದು ಮನದಟ್ಟು ಮಾಡಿಕೊಂಡು ಆತನಿಗಾಗಿ TT ಯಷ್ಟೇ (ಎರಡೇ) ತೋಳುಗಳಿರುವ ಅಂಗಿಯನ್ನು ಹೊಲಿದುಕೊಡಬಲ್ಲನಾದರೆ TT ಯಿಂದ ಅಭಿವ್ಯಕ್ತವಾದ ಮಾಹಿತಿಯನ್ನು ಸದುಪಯೋಗ ಮಾಡಿಕೊಂಡಂತಾಗುವುದು, ಮತ್ತು TT ಯ ನಿಜವಾದ ಅರ್ಥ ಅಡಗಿರುವುದು ಅಂಥ ಸದುಪಯೋಗದಲ್ಲೇ. ಇನ್ನು ಇಂಥ ಅರ್ಥಪ್ರಜ್ಞೆಯ ಆವಶ್ಯಕತೆ ಹೊಲಿಗೆ ಮುಂತಾದ ಪ್ರಾಪಂಚಿಕ ಉದ್ಯಮಗಳಿಗೆ ಮಾತ್ರ ಸೀಮಿತವೋ ಇಲ್ಲವೆ ಶುದ್ಧ ಗಣಿತದ ಪಾಲಿಗೂ ಉಂಟೋ ಎಂಬ ಪ್ರಶ್ನೆ ಸಹ ಇದೇ ಸಂದರ್ಭದಲ್ಲಿ ಪರಿಶೀಲನಾರ್ಹ. ಗಣಿತ ಪರಿಕಲ್ಪನೆಗಳ ಸುತ್ತ ಗಣಿತಜ್ಞರು ಹೆಣೆಯಬಹುದಾದ ಆದ್ಯುಕ್ತಿಗಳ ಚೌಕಟ್ಟಿನಿಂದ ಹೊರತಾಗಿಯೇ ಆ ಪರಿಕಲ್ಪನೆಗಳ ಅರ್ಥ ಉಳಿದುಹೋಗುವುದರಿಂದ ಶುದ್ಧಗಣಿತದಲ್ಲಿ ಅರ್ಥ ಪ್ರಜ್ಞೆಯ ಕೈವಾಡವಿರುವುದನ್ನೇ ಆದ್ಯುಕ್ತಿಮಾರ್ಗಿಗಳು ಮೊದಲಲ್ಲಿ ವಿರೋಧಿಸತೊಡಗಿದರು. ಆದ್ಯುಕ್ತೀಯ ದೃಷ್ಟಿಕೋನದ ಪ್ರಕಾರ ಗಣಿತೀಯ ಪ್ರತೀಕಗಳ ಅರ್ಥದ ಪಾತ್ರವೇನಿದ್ದರೂ ಸೂಕ್ತ ಆದ್ಯುಕ್ತಿಗಳ ಆಯ್ಕೆಯವರೆಗೆ ಮಾತ್ರವೇ; ಅನಂತರ ಅವುಗಳ ಅರ್ಥ ಅಪ್ರಕೃತವಾಗಬೇಕು. ಅವುಗಳಿಂದ ನೆರವೇರುವ ಆದ್ಯುಕ್ತಿ ಪಾಲನೆಯೇ ಸರ್ವಸ್ವವಾಗಬೇಕು; ಅನೇಕ ವೇಳೆ ಆದ್ಯುಕ್ತಿಗಳ ಆಯ್ಕೆ ಕೂಡ ಅರ್ಥಸಾಧ್ಯತೆಗಳನ್ನು ಲೇಶಮಾತ್ರವೂ ಅವಲಂಬಿಸದೆ ಸೌಂದರ್ಯಸೃಷ್ಟಿ ಮೊದಲಾದ ಉನ್ನತ ಉದ್ದೇಶಗಳಿಂದಷ್ಟೇ ಪ್ರೇರಿತವಾಗಬೇಕು. ಈ ವಿಪರೀತ ಮನೋಧರ್ಮವನ್ನು ಧನಪೂರ್ಣಾಂಕಗಳಿಗೆ ಅನ್ವಯಿಸುವುದಾದರೆ ಶುದ್ಧ ಗಣಿತದ ಪಾಲಿಗೆ ಆ ಪೂರ್ಣಾಂಕ ಪ್ರತೀಕಗಳ ಅರ್ಥದ ಗೊಡವೆ ಅನವಶ್ಯ. ಅವು ಪಿಯಾನೋ ಆದ್ಯುಕ್ತಿಗಳನ್ನು ಪರಿಪಾಲಿಸುತ್ತವೆಂಬ ವಿಶ್ವಾಸವಷ್ಟೇ ಸಾಕು ಎಂದಾಗುತ್ತದೆ. ಅಲ್ಲಿಗೆ ಆ ಆದ್ಯುಕ್ತಿಗಳ ಆಧಾರದಿಂದಲೇ ಧನಪೂರ್ಣಾಂಕಗಳನ್ನು ಕುರಿತ ಪ್ರಮೇಯಗಳೆಲ್ಲವನ್ನೂ ಶುದ್ಧ ಗಣಿತಜ್ಞ ಸಾಧಿಸಬೇಕಾಗುವುದು. ಆದರೆ ಸಮಸ್ತ ಗಣಿತವನ್ನೂ ಆದ್ಯುಕ್ತಿಕರಿಸಬೇಕೆಂಬ ಆದ್ಯುಕ್ತಿಮಾರ್ಗಿಗಳ ಈ ಬಗೆಯ ತೀವ್ರಗಾಮಿ ಚಳವಳಿ ಸಲ್ಲುವಂತದಲ್ಲವೆಂದು ಕಳೆದ ನಾಲ್ಕು ದಶಕಗಳಲ್ಲಿ ನಡೆದಿರುವ ಗಣಿತ ತರ್ಕಶಾಸ್ತ್ರದ ಕೆಲ ಮಹತ್ತ್ವಪೂರ್ಣ ಸಂಶೋಧನೆಗಳು ತೋರಿಸಿಕೊಟ್ಟಿವೆ. ವಿಶಿಷ್ಟವಾಗಿ, ಧನಪೂರ್ಣಾಂಕಗಳ ಅರ್ಥವನ್ನು ಆಧರಿಸಿ ಅವುಗಳ ಬಗ್ಗೆ ಮನಗಾಣಬಹುದಾದ ಸತ್ಯಾಂಶಗಳೆಲ್ಲವನ್ನೂ ವ್ಯುತ್ಪಾದಿಸಿ ಕೊಡುವಂಥ ಆದ್ಯುಕ್ತಿ ವ್ಯವಸ್ಥೆಯೊಂದನ್ನು ಯಾರಾದರೂ ನಿಯೋಜಿಸ ಹೊರಟರೆ ವಿರೋಧಾಭಾಸಗಳ ಅನಿವಾರ್ಯ ಪ್ರವೇಶದಿಂದ ಆ ವ್ಯವಸ್ಥೆ ಕುಸಿದು ಬೀಳಬೇಕಾಗಿ ಬರುವುದು (ಗೊಯ್ಡಲ್ ಪ್ರಮೇಯ, 1931). ಅಂದಮೇಲೆ ಧನಪೂರ್ಣಾಂಕಗಳ ಬಗ್ಗೆ ನೇರ ಅರ್ಥ ಪ್ರಜ್ಞೆ ಚೆಲ್ಲುವಷ್ಟು ಬೆಳಕನ್ನು ಯಾವೊಂದು ಸುಸಂಗತ ಆದ್ಯುಕ್ತಿ ವ್ಯವಸ್ಥೆಯೂ ಚೆಲ್ಲಲಾರದು ಎಂದಾಯಿತು. ಇದರಿಂದ ಶುದ್ಧ ಗಣಿತಕ್ಕೂ ಅರ್ಥದ ಆವಶ್ಯಕತೆ ಇರುವುದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ. ಆದರೆ ನಿರ್ದಿಷ್ಟ ಪರಿಮಿತಿಗಳೊಳಗಡೆ ಆದ್ಯುಕ್ತಿಯ ಪ್ರವೃತ್ತಿಯಿಂದ ಗಣಿತದ ಬೆಳವಣಿಗೆಗೆ ಒಳ್ಳೆಯ ಲಾಭವಾಗಿದೆ ಎಂಬುದೂ ನಿಜವೇ. ಗಣಿತದ ಸರ್ವತೋಮುಖ ಪ್ರಗತಿ ಸಿದ್ಧಿಸುವುದು ಅರ್ಥಪ್ರಜ್ಞೆ ಹಾಗೂ ಆದ್ಯುಕ್ತಿ ವಿಧಾನಗಳ ಸೂಕ್ತ ಸಮನ್ವಯದಿಂದಲೇ.
ಪರಿಮೇಯಗಳು ಮತ್ತು ಸರಳ ಬೀಜಗಣಿತ (ರ್ಯಾಷನಲ್ಸ್ ಅಂಡ್ ಸಿಂಪಲ್ ಆಲ್ಜಿಬ್ರ)
[ಬದಲಾಯಿಸಿ]ಧನ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಮಾನವ T ಸಾಲು ಮತ್ತು ಇತರ ರೂಪಗಳಲ್ಲಿ ಉಪಜ್ಞಿಸಿ ಪದಾರ್ಥಗಳನ್ನು ಎಣಿಸಲು ಸಮರ್ಥನಾದನಷ್ಟೆ. ಕಾಲಕ್ರಮೇಣ ಆತನ ದೈನಂದಿನ ವ್ಯವಹಾರಗಳಲ್ಲಿ ಎಣಿಕೆಯೊಂದಿಗೆ ಅಳತೆಯ ಆವಶ್ಯಕತೆಯೂ ಉಂಟಾಯಿತು. ಅಳತೆಗಳನ್ನು ಕೇವಲ ಧನ ಪೂರ್ಣಾಂಕಗಳ ಮಾಧ್ಯಮದಲ್ಲಿ ನಿರ್ವಹಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ. ಉದಾಹರಣೆಗೆ ಹಾಲಿನ ಅಳತೆಯನ್ನು ಪರಿಶೀಲಿಸಬಹುದು. ಇದಕ್ಕಾಗಿ ನಿರ್ದಿಷ್ಟ ಗಾತ್ರದ ಪಾತ್ರೆಯೊಂದನ್ನು ಮೂಲ ಮಾನವನ್ನಾಗಿ (ಯೂನಿಟ್) ಆಯ್ಕೆ ಮಾಡಿಕೊಳ್ಳಬಹುದು. ನಮ್ಮ ಬಳಿ ಇಂಥ ಮೂರು ಮಾನಪಾತ್ರೆಗಳ ತುಂಬಾ ಹಾಲು ಇದೆಯೆಂದು ಭಾವಿಸೋಣ. ಈ ಹಾಲಿನ ರಾಶಿಯನ್ನೇನೋ TTT ಇಲ್ಲವೆ 3 ಎಂಬ ಧನ ಪೂರ್ಣಾಂಕ ವ್ಯಕ್ತಪಡಿಸಬಲ್ಲದು. ಆದರೆ ಇದೇ ಹಾಲನ್ನು ಇಬ್ಬರು ಸಮವಾಗಿ ಹಂಚಿಕೊಂಡಾಗ ಒಬ್ಬೊಬ್ಬರಿಗೂ ದೊರಕುವ ಹಾಲಿನ ರಾಶಿಯನ್ನು ನಮ್ಮ ಅಂಗೀಕೃತ ಮಾನದಲ್ಲಿ ಯಾವ ಧನ ಪೂರ್ಣಾಂಕವೂ ಸೂಚಿಸಲಾರದು. ಈ ಮಾಹಿತಿಯ ಅಭಿವ್ಯಕ್ತಿಗೆ TTT/TT ಅಥವಾ 3/2 ಎಂಬ ಭಿನ್ನರಾಶಿಯ ಉಪಜ್ಞೆ ಅವಶ್ಯ. ಇದೇ ಮೇರೆಗೆ p ಮತ್ತು q ಎರಡು ಧನಪೂರ್ಣಾಂಕಗಳಾದಲ್ಲಿ p ಮಾನಗಳನ್ನು q ಸಮಭಾಗಗಳಾಗಿ ವಿಭಜಿಸಿದಾಗ ಫಲಿಸುವ ಪ್ರತಿಯೊಂದು ಭಾಗದ ಅಳತೆಯನ್ನು ವ್ಯಕ್ತಪಡಿಸುವುದಕ್ಕಾಗಿ ಮಾನವ p/q ಭಿನ್ನರಾಶಿ ಪ್ರತೀಕವನ್ನು ಸೃಷ್ಟಿಸಬೇಕಾಯಿತು. ಧನ ಪೂರ್ಣಾಂಕಗಳನ್ನು (ಉದಾಹರಣೆಗೆ TT, TTT) ಒಂದೇ T ಅಕ್ಷರದಿಂದಾದ ಪದಗಳು ಎಂಬುದಾಗಿ ಪರಿಗಣಿಸಬಹುದೆಂದು ಆಗಲೇ ಮನಗಂಡಿದ್ದೇವೆ. ಇದೇ ದೃಷ್ಟಿಕೋನದಿಂದ ನೋಡಿದಾಗ ಭಿನ್ನರಾಶಿಗಳು (ಉದಾಹರಣೆಗೆ TTT/TT) T ಮತ್ತು / ಎಂಬ ಎರಡು ಅಕ್ಷರಗಳಿಂದಾದ ಪದಗಳಾಗುತ್ತವೆ. (ಅಂಥ ಒಂದೊಂದು ಪದದಲ್ಲೂ / ಪ್ರತೀಕದ ಪ್ರವೇಶ ಒಂದು ಸಲಕ್ಕೆ ಮಾತ್ರವೇ ಸೀಮಿತವಾಗಿರಬೇಕು. p/q ಭಿನ್ನರಾಶಿಯಲ್ಲಿ p ಗೆ ಅಂಶ (ನ್ಯೂಮರೇಟರ್) ಎಂದೂ, q ಗೆ ಛೇದ (ಡಿನಾಮೀನೇಟರ್) ಎಂದೂ ಹೆಸರು. ಪ್ರಾಚೀನ ಗಣಿತಜ್ಞರು ಕೇವಲ 1 ನ್ನು ಅಂಶವಾಗಿ ಉಳ್ಳ ಏಕಮಾನ ಭಿನ್ನರಾಶಿಗಳನ್ನು (ಯೂನಿಟ್ ಫ್ರ್ಯಾಕ್ಷನ್ಸ್) ಮಾತ್ರ ಮೊದಲು ಬಳಕೆಗೆ ತಂದರು. ಇಂದಿನ 1/3 ನ್ನು (ಅಥವಾ 1/3) ಪುರಾತನ ಈಜಿಪ್ಟಿಯನ್ನರು ಮತ್ತು ಗ್ರೀಕರು ಅನುಕ್ರಮವಾಗಿ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಬರೆಯುತ್ತಿದ್ದರು. 1/3 ರಲ್ಲಿನ ಅಡ್ಡ ಗೀಟಿನ ಬಳಕೆಯನ್ನು ಅರಬ್ಬರು ರೂಢಿಗೆ ತಂದರು. ಪ್ರಾಚೀನ ಹಿಂದೂ ಗಣಿತಜ್ಞರು ಅದನ್ನು 1/3 ಎಂಬ ರೂಪದಲ್ಲಿ ಪ್ರದರ್ಶಿಸುತ್ತಿದ್ದರು.
ಭಿನ್ನರಾಶಿಗಳ ಸೃಷ್ಟಿಯ ಬಳಿಕ ಅವನ್ನು ಕುರಿತ ವಿವಿಧ ಪರಿಕರ್ಮಗಳ ನಿಯೋಜನೆಯೂ ಅವಶ್ಯವಾಯಿತು. ಮೂರು ಮಾನಪಾತ್ರೆಗಳ ಹಾಲನ್ನು ಇಬ್ಬರಿಗೆ ಸಮವಾಗಿ ಹಂಚಲು ಎಲ್ಲ ಹಾಲನ್ನು ಒಟ್ಟಿಗೆ ಬೆರೆಸಿ ಎರಡು ಸಮ ಭಾಗಗಳನ್ನು ಮಾಡುವುದು ಒಂದು ಕ್ರಮವಾದರೆ ಒಂದೊಂದು ಪಾತ್ರೆಯ ಹಾಲನ್ನು ಎರಡೆರಡು ಸಮಭಾಗಗಳನ್ನಾಗಿ ಪ್ರತ್ಯೇಕಿಸಿ ಒಬ್ಬೊಬ್ಬನಿಗೂ ಅಂಥ ಮೂರು ಭಾಗಗಳನ್ನು ಕೊಡುವುದು ಇನ್ನೊಂದು ಕ್ರಮ. ಅಲ್ಲದೆ ಇವೆರಡಕ್ಕೂ ಪರ್ಯಾಯವಾಗಿ ಒಂದೊಂದು ಪಾತ್ರೆಯ ಹಾಲನ್ನು ಇಪ್ಪತ್ತಿಪ್ಪತ್ತು ಸಮಭಾಗಗಳನ್ನಾಗಿ ಪ್ರತ್ಯೇಕಿಸಿ ಒಬ್ಬೊಬ್ಬ ವ್ಯಕ್ತಿಗೂ ಅಂಥ ಮೂವತ್ತು ಭಾಗಗಳನ್ನು ಕೊಟ್ಟರೂ ಸಲ್ಲುತ್ತದಷ್ಟೆ. ಆದರೆ ಈ ಕೊನೆಯ ಕ್ರಮದ ಅಳತೆಯನ್ನು ಅಭಿವ್ಯಕ್ತಿಸುವ ಭಿನ್ನರಾಶಿ 30/20. ಇದರಿಂದ (3/2) = (30/20) = [(3 x 10)/(2 x 10)] ಎಂದು ಸ್ಪಷ್ಟವಾಗುವುದು. ಇದೇ ಪ್ರಕಾರ p, q ಮತ್ತು n ಯಾವುದೇ ಮೂರು ಧನ ಪೂರ್ಣಾಂಕವಾಗಿರಲಿ. p/q = (p x n) / (q x n) ಆಗುವುದು. p/q ಮತ್ತು r/s ಎಂಬ ಎರಡು ಭಿನ್ನರಾಶಿಗಳು ಸಮವಾಗಬೇಕಾದರೆ p x s = r x q ಆದರೆ ಸಾಕೆಂದು ತೋರಿಸಬಹುದು. ಈಗ p/q ಮತ್ತು r/s ಗಳನ್ನು ಕೂಡಿಸುವ ಬಗೆಯನ್ನು ಕುರಿತು ವಿವೇಚಿಸೋಣ. p/q = (ps)/(qs) ಹಾಗೂ r/s = (rq)/(sq) ಆದ ಕಾರಣ (p/q) + (r/s) ಗೆ ಬದಲು [(p x s) / (q x s)] + [(r x q) / (q x s)] ನ್ನು ಪರಿಶೀಲಿಸಬಹುದೆಂದು ನಮಗೆ ಹೊಳೆಯುತ್ತದೆ. ಒಂದು ಮಾನವನ್ನು (q x s) ಸಮಭಾಗಗಳನ್ನಾಗಿ ವಿಭಜಿಸಿ ಅಂಥ (p x s) ಭಾಗಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸಿದಾಗ (p x s) / (q x s) ರಾಶಿಯೂ, ಅಂಥ (r x q) ಭಾಗಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸಿದಾಗ (r x q) / (q x s) ರಾಶಿಯೂ ಲಭಿಸುತ್ತವೆ. ಇವೆರಡು ರಾಶಿಗಳನ್ನು ಕೂಡಿಸಿದಾಗ (p x s) + (r x q) ಭಾಗಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸಿದಂತಾಗುತ್ತದೆ. ತತ್ಫಲವಾಗಿ ಲಭಿಸುವ ರಾಶಿ [(p x s) + (r x q)] / (q x s) ಆದ್ದರಿಂದ
(p/q) + (r/s) = [(p x s) + (r x q)] / (q x s) ... (1)
ಎಂಬ ಸೂತ್ರವನ್ನು ವ್ಯಾಖ್ಯೆಯಾಗಿ ಅಂಗೀಕರಿಸಬಹುದು.
ಇನ್ನು ಗುಣಾಕಾರದ ಪ್ರಶ್ನೆ. ಒಂದು ಮಾನವನ್ನು s ಸಮಭಾಗಗಳನ್ನಾಗಿ ವಿಭಜಿಸಿ ಅಂಥ r ಭಾಗಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸಿದಾಗ r/s ಫಲ ಲಭಿಸುತ್ತದಷ್ಟೆ. ಈ ಫಲವನ್ನು ಮತ್ತೆ q ಸಮಭಾಗಗಳನ್ನಾಗಿ ವಿಭಜಿಸಿ ಅಂಥ p ಭಾಗಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸಿದಾಗ ದೊರೆಯುವ ರಾಶಿಯೇ (p/q) x (r/s) ಗುಣಲಬ್ಧ ಎಂದು ಅರ್ಥವಿಸಬಹುದು. ತುಸು ಚಿಂತನೆಯಿಂದ ಮೇಲೆ ವಿವರಿಸಿರುವ ಕ್ರಿಯೆಗಳ ಅಂತಿಮ ಫಲಿತಾಂಶ (p x r) / (q x s) ಆಗುತ್ತದೆಂದು ಮನಗಾಣಲು ಶಕ್ಯವಿದೆ. ಎಂತಲೇ ಕೆಳಗಿನ ವ್ಯಾಖ್ಯೆ ಅಂಗೀಕಾರ ಯೋಗ್ಯ:
(p/q) x (r/s) = (p x r) / (q x s) .......(2)
ನಿತ್ಯ ವ್ಯವಹಾರದಲ್ಲಿ ಜಮಾ, ಖರ್ಚು; ಲಾಭ, ನಷ್ಟ; ಭೂತಕಾಲ, ಭವಿಷ್ಯತ್ಕಾಲ; ಹಿಂಚಲನೆ, ಮುಂಚಲನೆ ಇವೇ ಮೊದಲಾದ ಪರಸ್ಪರ ವಿರುದ್ಧ ರಾಶಿಗಳು ಪದೆ ಪದೇ ಉದ್ಭವಿಸುತ್ತಿರುತ್ತವೆ. ಒಂದು ಸಹಸ್ರ ರೂಪಾಯಿ ಲಾಭವನ್ನೂ ಅಷ್ಟೇ ನಷ್ಟವನ್ನೂ 1000 ಎಂಬ ಒಂದೇ ಪ್ರತೀಕದಿಂದ ಸೂಚಿಸುವ ಬದಲು ಅನೇಕ ವೇಳೆ ಲಾಭವನ್ನು ಮಾತ್ರ ಈ ಪ್ರತೀಕದಿಂದ ಸೂಚಿಸಿ ನಷ್ಟವನ್ನು –1000 (ಋಣ ಸಹಸ್ರ ಎಂದು ಓದಬೇಕು) ಎಂಬ ಪರಿವರ್ತಿತ ಪ್ರತೀಕದಿಂದ ಅಭಿವ್ಯಕ್ತಿಸಿದ್ದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಸೌಲಭ್ಯಗಳು ಒದಗಿಬರುತ್ತವೆ. ಇತರ ವಿರುದ್ಧ ರಾಶಿಗಳ ವಿಚಾರದಲ್ಲೂ ಅಂತೆಯೇ. –1000 ದಂಥ ಪ್ರತೀಕಗಳಿಗೆ ಋಣಸಂಖ್ಯೆಗಳು (ನೆಗೆಟಿವ್ ನಂಬರ್ಸ್) ಎಂದು ಹೆಸರು.[೬] [ಇವು ಭಿನ್ನರಾಶಿಗಳೂ ಆಗಲು ಸಾಧ್ಯ. ಉದಾ, (–3/2); ಇಂಥವಕ್ಕೆ ಋಣ ಭಿನ್ನರಾಶಿಗಳು ಎಂದು ಹೆಸರು.] ಈಗ ಋಣ ಹಾಗೂ ಮಾಮೂಲು (ಧನ) ಸಂಖ್ಯೆಗಳನ್ನೊಳಗೊಳ್ಳುವ ಕೆಲವು ಪರಿಕರ್ಮಗಳನ್ನು ಉದಾಹರಿಸುತ್ತೇವೆ. 5 ರೂಪಾಯಿ ನಷ್ಟ ಹಾಗೂ 3 ರೂಪಾಯಿ ಲಾಭ ಇವುಗಳ ನಿವ್ವಳ ಫಲ 2 ರೂಪಾಯಿ ನಷ್ಟವಷ್ಟೆ. ಈ ಸನ್ನಿವೇಶವನ್ನು (– 5)+3=(– 2) ಎಂಬ ಸಂಕಲನ ಪರಿಕರ್ಮ ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ. ಅಂತೆಯೇ 5+ (–3)=2 ಮತ್ತು (–5)+(–3)= (–8). ವ್ಯವಕಲನದ ನಿದರ್ಶನವಾಗಿ –2 ರಲ್ಲಿ –5 ನ್ನು ಕಳೆಯೋಣ. ಇದಕ್ಕಾಗಿ –5 ಕ್ಕೆ ಏನನ್ನು ಕೂಡಿಸಿದರೆ –2 ಲಭಿಸುತ್ತದೆ ಎಂದು ಆಲೋಚಿಸಬೇಕು. 5 ರೂಪಾಯಿಯಷ್ಟು ನಷ್ಟವನ್ನು 2 ರೂಪಾಯಿಯಷ್ಟು ನಷ್ಟಕ್ಕೆ ತಗ್ಗಿಸಲು 3 ರೂಪಾಯಿ ಲಾಭಗಳಿಸಬೇಕೆಂಬುದು ಸುಸ್ಪಷ್ಟ. ಎಂತಲೇ (–2)–(–5)=3. (ಇಲ್ಲಿ ಗೋಚರಿಸುವ ಮೂರು - ಚಿಹ್ನೆಗಳ ಪೈಕಿ ಮಧ್ಯದ್ದು ವ್ಯವಕಲನ ಸೂಚಕ. ತುದಿಯವು ನಷ್ಟಸೂಚಕ; ಇವೆರಡು ಭಿನ್ನಗಳ ಪರಿಕಲ್ಪನೆಗಳಿಗೆ ಒಂದೇ ಪ್ರತೀಕವನ್ನು ಬಳಸುವ ರೂಢಿ ಬೋಧನೆಯ ದೃಷ್ಟಿಕೋನದಿಂದ ಮೊದಮೊದಲು ಗೊಂದಲಕಾರಿಯೆನಿಸಿದರೂ ಬರುಬರುತ್ತ ಉಪಯುಕ್ತವೇ ಆಗುವುದು.) ಇದೇ ಪ್ರಕಾರ 2–5=–3; -2 - 5=-7; ಮತ್ತು 2-(-5)=7. ಇನ್ನು ಗುಣಾಕಾರವನ್ನು ಕುರಿತು ವಿವೇಚಿಸುವ ಸಲುವಾಗಿ ವಾಹನಸಂಚಾರಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ವೇಗ x ಪ್ರಯಾಣದ ಅವಧಿ = ಕ್ರಮಿಸಿದ ದೂರ ಎಂಬ ಸೂತ್ರವನ್ನು ಪರಿಶೀಲಿಸಬೇಕು. ಇದರಂತೆ ಗಂಟೆಗೆ v ಕಿಲೋಮೀಟರು ವೇಗದಿಂದ ಚಲಿಸುತ್ತಿರುವ ವಾಹನವೊಂದು t1 ವೇಳೆಯಲ್ಲಿ s1 ಕಿಮೀ, ಕಲ್ಲನ್ನೂ t2 ವೇಳೆಯಲ್ಲಿ s2 ಕಿಮೀ., ಕಲ್ಲನ್ನು ಹಾದುಹೋದರೆ v x (t2 - t1) = (s2 - s1) ಆಗಬೇಕು. ವಾಹನ ಚಲಿಸುವ ದಿಕ್ಕಿನಲ್ಲಿ ಕಿಮೀ. ಕಲ್ಲುಗಳ ಮೇಲೆ ನಮೂದಾಗಿರುವ ಸಂಖ್ಯೆಗಳು ಏರುತ್ತ ಹೋದರೆ ವಾಹನದ ವೇಗವನ್ನು ಧನಾತ್ಮಕವೆಂದೂ ಆ ಸಂಖ್ಯೆಗಳು ಇಳಿಯುತ್ತ ಹೋದರೆ ಅದರ ವೇಗವನ್ನು ಋಣಾತ್ಮಕವೆಂದೂ ಪರಿಗಣಿಸುವುದು ಸ್ವಾಭಾವಿಕ. ಈಗ v = - 50, t1= ಸಂಜೆ 5 ಗಂಟೆ, t2= ಅಪರಾಹ್ನ 2 ಗಂಟೆ, s2= 400 ಎಂದು ಭಾವಿಸೋಣ. ಈ ಉದಾಹರಣೆಯಲ್ಲಿ ಗಂಟೆಗೆ 50 ಕಿಮೀ. ಗಳಂತೆ ಅಪರಾಹ್ನ 2 ಗಂಟೆಯಿಂದ ಸಂಜೆ 5 ಗಂಟೆಯವರೆಗಿನ 3 ಗಂಟೆಗಳ ಅವಧಿಯಲ್ಲಿ ವಾಹನ 150 ಕಿಮೀ. ದೂರವನ್ನು ಕ್ರಮಿಸಿ 400 ನೆಯ ಕಿಮೀ. ಕಲ್ಲಿನಿಂದ 250 ನೆಯ ಕಿಮೀ. ಕಲ್ಲಿಗೆ ಚಲಿಸಿರುತ್ತದೆ. (ವೇಗ ಋಣಾತ್ಮಕವಿರುವುದರಿಂದ ಕಿಮೀ. ಕಲ್ಲಿನ ಕ್ರಮಸಂಖ್ಯೆ ಕಡಿಮೆಯಾಗಬೇಕು). ಆದ್ದರಿಂದ s1=250. ಈ ಬೆಲೆಗಳನ್ನು v x (t2 - t1) = (s2 - s1) ಸೂತ್ರದಲ್ಲಿ ಆದೇಶಿಸಿದರೆ (-50) x (2 - 5) = (400-250) ಅಥವಾ (- 50) x (- 3)=150 ಆಗುತ್ತದೆ. ಅಂದಮೇಲೆ ಎರಡು ಋಣ ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧವನ್ನು ಮಾಮೂಲು ಧನ ಸಂಖ್ಯೆ ಎಂದೇ ಪರಿಗಣಿಸುವುದು ಉಪಯುಕ್ತವೆಂದಾಯಿತು; ಇದನ್ನೇ ಶಾಲಾ ಬೀಜಗಣಿತದಲ್ಲಿ (-) x (-) = (+) ಎಂಬುದಾಗಿ ಸೂತ್ರೀಕರಿಸುತ್ತಾರೆ. ವಾಹನಸಂಚಾರದ ನಿದರ್ಶನವನ್ನೇ ಬಳಸಿಕೊಂಡು (- 50) x 3 = (–150), 50 x (–3)=(–150) ಎಂದು ಸಹ ಸುಲಭವಾಗಿ ಮನಗಾಣಬಹುದು. ಶಾಲಾಬೀಜಗಣಿತದ ಸೂತ್ರೀಕರಣದಲ್ಲಿ, (-) x (+) = (-) ಮತ್ತು (+) x (-) = (-). ಕೊನೆಯದಾಗಿ ಭಾಗಾಹಾರ ಪರಿಕರ್ಮ ಗುಣಾಕಾರದ ವ್ಯುತ್ಕ್ರಮವಾದ್ದರಿಂದ [(–50) x (–3)]=150 ಆದ ಕಾರಣ 150 ÷ (–50) = (–3); (–50) x 3 = (–150) ಆದ ಕಾರಣ (–150) ÷ 50=–3; 50 x (–3) = –150 ಆದ ಕಾರಣ (–150) ÷ 50=(–3) ಇಂಥವೇ ಸೂತ್ರಗಳು ಭಾಗಾಹಾರಕ್ಕೂ ಅನ್ವಯಿಸುತ್ತವೆ; (-) ÷ (-) = (+); (-) ÷ (+) = (-); (+) ÷ (-) = (-).
ಇದೇ ಸಂದರ್ಭದಲ್ಲಿ ಸೊನ್ನೆಯ ಪರಿಕಲ್ಪನೆಯ ಬಗ್ಗೆ ಒಂದೆರಡು ಮಾತುಗಳು ಅವಶ್ಯ. (–2) +2 ಎಂಬ ಸಂಕಲನವನ್ನು ಪರಿಶೀಲಿಸಬೇಕು. ಇಲ್ಲಿ ಲಾಭ ಮತ್ತು ನಷ್ಟಗಳು ಪರಸ್ಪರ ಸಮವಾಗಿರುವುದರಿಂದ ಒಟ್ಟಿನಲ್ಲಿ ಲಾಭವೂ ಇಲ್ಲ ನಷ್ಟವೂ ಇಲ್ಲ ಎಂಬುದು ಸುವೇದ್ಯ. ಇಂಥ ಸನ್ನಿವೇಶವನ್ನು ಅಭಿವ್ಯಕ್ತಿಸಲು ನಾವು ಸೊನ್ನೆಯನ್ನು ಉಪಜ್ಞಿಸುತ್ತೇವೆ (–2) + 2 = 0. ಯಾವುದೇ ರಾಶಿಯನ್ನು ಸೊನ್ನೆಯೊಂದಿಗೆ ಕೂಡಿದಾಗ ಅದೇ ರಾಶಿ ಬರುತ್ತದೆ ಹಾಗೂ ಸೊನ್ನೆಯಿಂದ ಗುಣಿಸಿದಾಗ ಸೊನ್ನೆಯೇ ಬರುತ್ತದೆ: a + 0 = a = 0 + a; a x 0 = 0 = 0 x a. ಸೊನ್ನೆಯ ಇನ್ನು ಕೆಲವು ಗಮನಾರ್ಹ ಗುಣಗಳೆಂದರೆ a - 0 = 0, 0 - a = -a, a - a = 0; ಮತ್ತು a ಯೂ ಸೊನ್ನೆ ಅಲ್ಲದೆ ಇರುವಾಗ 0 ÷ a = 0. ಸೊನ್ನೆಯಿಂದ ಯಾವುದೇ ಸಂಖ್ಯೆಯ ಭಾಗಾಕಾರ ನಿಷಿದ್ಧ.[೭] ಸೊನ್ನೆ ಮಾಮೂಲು ಧನವೂ ಅಲ್ಲ, ಋಣವೂ ಅಲ್ಲ;[೮] ಆದರೆ ಅದನ್ನು ಒಂದು ಪೂರ್ಣಾಂಕವೆಂದು ಪರಿಗಣಿಸಲಾಗುವುದು.
ಧನ ಭಿನ್ನರಾಶಿಗಳು, ಋಣ ಭಿನ್ನರಾಶಿಗಳು ಹಾಗೂ ಸೊನ್ನೆ ಇವಿಷ್ಟನ್ನೂ ಒಟ್ಟಾಗಿ ಗಣಿತಜ್ಞರು ಪರಿಮೇಯಗಳು (ರ್ಯಾಷನಲ್ ನಂಬರ್ಸ್) ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಪರಿಮೇಯಗಳ ಸಾರ್ವತ್ರಿಕ ರೂಪ p/q; ಇಲ್ಲಿ q ಒಂದು ಧನ ಅಥವಾ ಋಣ ಪೂರ್ಣಾಂಕ, p ಒಂದು ಧನ ಅಥವಾ ಋಣ ಪೂರ್ಣಾಂಕ ಅಥವಾ ಸೊನ್ನೆ.[೯] p, q ಧನ ಪೂರ್ಣಾಂಕಗಳಾದಲ್ಲಿ (-p)/(-q) ವನ್ನು ಮಾಮೂಲು ಧನ ಭಿನ್ನರಾಶಿ (p/q) ವಿನೊಂದಿಗೂ, (-p)/q ಹಾಗೂ p/(-q) ಗಳನ್ನು ಋಣ ಭಿನ್ನರಾಶಿ [-(p/q)] ವಿನೊಂದಿಗೂ ಸಮೀಕರಿಸುತ್ತೇವೆ. p ಯಾವುದೇ ಪೂರ್ಣಾಂಕವಾದಲ್ಲಿ p/1 = p ಆಗುವ ಕಾರಣ (ಸೊನ್ನೆಯೂ ಸೇರಿದಂತೆ) ಪೂರ್ಣಾಂಕಗಳೆಲ್ಲವೂ ಪರಿಮೇಯಗಳೇ. ಯಾವುದೇ ಪರಿಮೇಯ p/q ವಿನಲ್ಲಿ ಛೇದ q ಸೊನ್ನೆ ಆಗುವುದು ನಿಷಿದ್ಧ. ps=qr ಆದಲ್ಲಿ (p/q) = (r/s) ಎಂದು ಅಂಗೀಕರಿಸುತ್ತೇವೆ. ಯಾವುದೇ ಎರಡು ಪರಿಮೇಯ p/q ಮತ್ತು r/s ಗಳನ್ನು ಮೇಲೆ ಪ್ರದರ್ಶಿಸುವ (1) ಮತ್ತು (2) ಸೂತ್ರಗಳ ಮೇರೆಗೆ ಕೂಡಿಸಬಹುದು ಹಾಗೂ ಗುಣಿಸಬಹುದು (ಈಗ p, q, r, s ಧನ ಪೂರ್ಣಾಂಕಗಳಾಗಿರಬೇಕಾದುದೇನಿಲ್ಲ). ಅಲ್ಲದೇ ಕೆಳಗಿನ ಸೂತ್ರದಂತೆ ಅವನ್ನು ವ್ಯವಕಲನ ಪರಿಕರ್ಮಕ್ಕೆ ಸಹ ಗುರಿಪಡಿಸಲು ಸಾಧ್ಯವಿದೆ:
(p/q) - (r/s) = [(p x s) - (r x q)]/(q x s)
ಕೊನೆಯದಾಗಿ r ಸೊನ್ನೆಯಲ್ಲದಿರುವಾಗ p/q ವನ್ನು r/s ನಿಂದ ಭಾಗಿಸಲೂಬಹುದು: (p/q) ÷ (r/s) = (p x s) /(q x r). ಈ ಪರಿಕರ್ಮಗಳು [(p/q) ÷ (r/s)] x (r/s) = p/q (p/q) x [(r/s) + (t/u)] = [(p/q) x (r/s)] + [(p/q) x (t/u)] ಮುಂತಾದ ಕೆಲವು ವಿಶಿಷ್ಟ ನಿಯಮಗಳನ್ನು ಪರಿಪಾಲಿಸುವುದರಿಂದ ಪರಿಮೇಯಗಳ ವ್ಯವಸ್ಥೆ ಒಂದು ಕ್ಷೇತ್ರ (ಫೀಲ್ಡ್) ಎಂದೆನಿಸಿಕೊಂಡಿದೆ.[೧೦]
ನಿರ್ದಿಷ್ಟ ಮೌಲ್ಯಗಳಿರುವ 0, 1, (-2), (3/2) ಮುಂತಾದ ಪ್ರತೀಕಗಳೊಂದಿಗೆ ಚರ ಅಥವಾ ಅಜ್ಞಾತ ಮೌಲ್ಯಗಳನ್ನು ಸೂಚಿಸುವ ಇತರ ಪ್ರತೀಕ ಇಲ್ಲವೆ ಪದಗುಚ್ಛಗಳನ್ನು ಗಣಿತಜ್ಞರು ಬಳಸತೊಡಗಿದಾಗ ಸರಳ ಬೀಜಗಣಿತದ (ಎಲೆಮೆಂಟರಿ ಆಲ್ಜಿಬ್ರ) ಉದ್ಭವವಾಯಿತು. ಡಯೊಫಾಂಟಸ್ (ಗ್ರೀಸ್, ಕ್ರಿ. ಶ. 250), ಆರ್ಯಭಟ (ಭಾರತ, ಕ್ರಿ.ಶ. 628), ಆಲ್ ಖ್ವಾರಿಜ್ಮೀ (ಅರೇಬಿಯ, ಕ್ರಿ. ಶ. 825), ಮಹಾವೀರ (ಭಾರತ ಕ್ರಿ. ಶ. 850), ಭಾಸ್ಕರಾಚಾರ್ಯ (ಭಾರತ, ಕ್ರಿ. ಶ. 1150) ಮುಂತಾದ ಪ್ರಾಚೀನ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರ ಕೊಡುಗೆ ಈ ದಿಶೆಯಲ್ಲಿ ಮಹತ್ತರವಾದುದು. ಇವರು ಸಮಸ್ಯೆಗಳನ್ನು ಸಮೀಕರಣಗಳನ್ನಾಗಿ ರೂಪಿಸಿ ಅವನ್ನು ಬಿಡಿಸುವುದರ ಮುಲಕ ಅಜ್ಞಾತ ಉತ್ತರಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದರಲ್ಲಿ ಯಶಸ್ವಿಯಾದರು. ಅನಂತರ ಯೂರೋಪಿನ ಗಣಿತಜ್ಞರು ಸರಳ ಬೀಜಗಣಿತದ ತಂತ್ರಗಳನ್ನು ಇನ್ನಷ್ಟು ವಿಸ್ತರಿಸಿ ಸಂಸ್ಕರಿಸಿದರು. ಇಂದು ಚರ ಅಥವಾ ಅಜ್ಞಾತ ರಾಶಿಗಳನ್ನು x, y ಮುಂತಾದ ಅಕ್ಷರ ಪ್ರತೀಕಗಳಿಂದ ಸೂಚಿಸುವ ಪದ್ಧತಿ ರೂಢಿಗೆ ಬಂದಿದೆ. ಗುಣಲಬ್ಧವನ್ನು ಸಂಕ್ಷೇಪವಾಗಿ x . y ಅಥವಾ ಕೇವಲ x y ಎಂದು ಈಗ ಸೂಚಿಸುತ್ತೇವೆ. ಮುಂತಾದ ಗುಣಲಬ್ಧಗಳನ್ನು ಅಭಿವ್ಯಕ್ತಿಸಲು ಅನುಕ್ರಮವಾಗಿ x2, x3 ಮುಂತಾದ ಹ್ರಸ್ವ ಪ್ರತೀಕಗಳು ರೂಪಿತವಾಗಿವೆ. ಸರಳ ಬೀಜಗಣಿತದಲ್ಲಿ ಬಹಳಷ್ಟು ವೇಳೆ x, y ಗಳಂಥ ಚರ ಇಲ್ಲವೆ ಅಜ್ಞಾತಗಳಿಗೆ ಸಂದಾಯವಾಗುವ ಬೆಲೆಗಳು ಪರಿಮೇಯಗಳೇ ಆಗಿರುತ್ತವೆ. ಉದಾಹರಣೆಗೆ (x + y)2 = x2 + 2xy + y2 ಎಂಬುದು ಸರಳ ಬೀಜಗಣಿತದ ಒಂದು ಸುಪರಿಚಿತ ಸೂತ್ರ; x, y ಗಳಿಗೆ (ಮುಖ್ಯವಾಗಿ) ಯಾವುದೋ ಪರಿಮೇಯ ಬೆಲೆಗಳನ್ನು ಕೊಟ್ಟರೂ ಇದು ಒಂದು ನಿತ್ಯ ಸಮತ್ವವನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆಂಬುದೇ ಈ ಸೂತ್ರೀಕರಣದ ಅಭಿಪ್ರಾಯ. 2x + 5 = 12 ಎಂಬುದು ಒಂದು ಸರಳ ಸಮೀಕರಣ; ಇಲ್ಲಿ x ಅಜ್ಞಾತ; ಸಮೀಕರಣ ಸತ್ಯವಾಗಲು ಈ ಅಜ್ಞಾತಕ್ಕೆ (7/2) ಎಂಬ ಪರಿಮೇಯ ಬೆಲೆ ಸಲ್ಲಬೇಕಾಗುತ್ತದೆ x2 -2x = 1, x2 + 4x + 5 = 0 ಮುಂತಾದ ವರ್ಗಾತ್ಮಕ ಸಮೀಕರಣಗಳನ್ನು (ಕ್ವಾಡ್ರ್ಯಾಟಿಕ್ ಈಕ್ವೇಷನ್ಸ್) ಪ್ರಸ್ತಾವಿಸುವಾಗ ಮಾತ್ರ ಸರಳ ಬೀಜಗಣಿತದ ಅಧ್ಯಯನ ವ್ಯಾಪ್ತಿ ಪರಿಮೇಯಗಳ ಎಲ್ಲೆಯನ್ನು ದಾಟಿ ರಂಥ ಅಪರಿಮೇಯಗಳನ್ನೂ (ಇರ್ಯಾಷನಲ್ಸ್), ರಂಥ ಮಿಶ್ರ ಸಂಖ್ಯೆಗಳನ್ನೂ (ಕಾಂಪ್ಲೆಕ್ಸ್ ನಂಬರ್ಸ್) ಒಳಗೊಳ್ಳಬೇಕಾಗುವುದು.
ಜ್ಯಾಮಿತಿ
[ಬದಲಾಯಿಸಿ]ಸಂಖ್ಯೆಗಳು ಪ್ರಾಚೀನ ಗಣಿತಾಧ್ಯಯನದ ಒಂದು ಮುಖವಾದರೆ, ಆಕೃತಿಗಳು ಅದರ ಇನ್ನೊಂದು ಮುಖ. ಆದಿಮ ಶಿಲಾಯುಗದ ಮಾನವನಿಗೆ (ಕ್ರಿ.ಪೂ. 25,000) ಜ್ಯಾಮಿತೀಯ ವಿನ್ಯಾಸಗಳ ಪ್ರಜ್ಞೆ ಇತ್ತು. ಇನ್ನು ಪುರಾತನ ನಾಗರಿಕತೆಗಳ ಕಾಲವನ್ನು ಸಮೀಕ್ಷಿಸಿದರೆ ಈಜಿಪ್ಟಿನಲ್ಲಿ ಅದ್ಭುತ ಪಿರಮಿಡ್ಡುಗಳನ್ನು ಕಟ್ಟಿದ್ದು ಕ್ರಿ.ಪೂ. 3,000 ವೇಳೆಗೆ. ಅದಕ್ಕೂ ಹಿಂದೆ ಮಡಿಕೆಗಳನ್ನು ತಯಾರಿಸುವಲ್ಲಿ, ಹಾಗೂ ವಾಹನಗಳನ್ನು ನಿರ್ಮಿಸುವಲ್ಲಿ, ಚಕ್ರಗಳ ಉಪಯೋಗವನ್ನು ಜನರು ಅರಿತಿದ್ದರು. ಕ್ರಿ.ಪೂ 2,000ದ ವೇಳೆಗೆ ಕೆಲವಷ್ಟು ಏಕತಲಾಕೃತಿಗಳ ಸಲೆಗಳನ್ನೂ (ಏರಿಯಾಸ್), ಘನಾಕೃತಿಗಳ ಘನಗಾತ್ರಗಳನ್ನೂ (ವಾಲ್ಯೂಮ್ಸ್) ಲೆಕ್ಕಮಾಡಲು ಈಜಿಪ್ಷಿಯನರು ಕಲಿತಿದ್ದರು.[೧೧][೧೨]: 116 ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯ ಮತ್ತು ತಾಲಿಸ್ ಪ್ರಮೇಯ ಎಂಬುದಾಗಿ ಇಂದು ಪ್ರಸಿದ್ಧವಾಗಿರುವ ಜ್ಯಾಮಿತೀಯ ಫಲಿತಾಂಶಗಳು ಕ್ರಿ.ಪೂ. 1500 ಕ್ಕೂ ಮುಂಚೆ ಬ್ಯಾಬಿಲೋನಿಯನ್ನರಿಗೆ ಪರಿಚಿತವಾಗಿದ್ದವು.[೧೩][೧೪][೧೫][೧೬][೧೭] ABC ತ್ರಿಭುಜದಲ್ಲಿ A ಲಂಬಕೋನಗಳು BC2 = AB2 + AC2 ಆಗಬೇಕೆಂಬ ಸಂಗತಿಯೇ ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯ.[೧೮] ಅರ್ಧವೃತ್ತವೊಂದರೊಳಗಿನ ಕೋನಗಳೆಲ್ಲವೂ ಲಂಬಕೋನಗಳು ಎಂಬುದು ತಾಲಿಸ್ ಪ್ರಮೇಯ. ತಾಲಿಸ್ ಮತ್ತು ಪೈಥಾಗೊರಸ್ ಈ ಪ್ರಮೇಯಗಳನ್ನು ಪ್ರಪ್ರಥಮವಾಗಿ ಅವಿಷ್ಕರಿಸಿದವರೇನಲ್ಲ. ನಿಜಕ್ಕೂ ಅವರಿಬ್ಬರೂ ಕ್ರಿ.ಪೂ. 6ನೆಯ ಶತಮಾನದ ತಾತ್ತ್ವಿಕರು.
ಭಾರತದಲ್ಲಿ ಕ್ರಿ.ಪೂ. 8ನೆಯ ಶತಮಾನದ ವೇಳೆಗೆ ದೇವಸ್ಥಾನಗಳ ವಿನ್ಯಾಸ, ಯಜ್ಞಯಾಗಾದಿಗಳ ನಿರ್ವಹಣೆ ಮೊದಲಾದ ಸಂಬಂಧಗಳಲ್ಲಿ ಅನೇಕ ರೀತಿಯ ವಿಶಿಷ್ಟೀಕೃತ ಜ್ಯಾಮಿತೀಯ ರಚನಾವಿಧಿಗಳು ಅನುಷ್ಠಾನಕ್ಕೆ ಬಂದಿದ್ದವು. ಈ ವಿಧಿಗಳನ್ನು ಆಪಸ್ತಂಬ (ಶುಲ್ವ ಸೂತ್ರಗಳು) ಎಂಬ ಕೃತಿಯಲ್ಲಿ ಶ್ಲೋಕಗಳ ಮೂಲಕ ವರ್ಣಿಸಲಾಗಿದೆ.[೧೯][೨೦] (ಆಪಸ್ತಂಬರದೂ ಸೇರಿದಂತೆ ಏಳು ಶುಲ್ವ ಸೂತ್ರಗಳು ಇಂದು ತಿಳಿದಿವೆ). ಶುಲ್ವ ಸೂತ್ರಗಳಲ್ಲೂ ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯದ ವ್ಯಾಪಕ ಬಳಕೆ ಕಂಡುಬರುವುದು.[೨೧] ಇಷ್ಟೆಲ್ಲ ಆದರೂ ಕ್ರಿ.ಪೂ. 6ನೆಯ ಶತಮಾನದಕ್ಕಿಂತ ಹಿಂದಿನ ಜ್ಯಾಮಿತಿ ಭೌತಶಾಸ್ತ್ರದಂತೆ ಪ್ರಧಾನತಃ ಒಂದು ಅನುಭವಜನ್ಯ (ಎಂಪಿರಿಕಲ್) ವಿಜ್ಞಾನವಾಗಿದ್ದಿತೇ ವಿನಾ ತರ್ಕಮಾರ್ಗವನ್ನು ಅನುಸರಿಸುವ ವ್ಯವಸ್ಥಿತ ಗಣಿತವಾಗಿರಲಿಲ್ಲ. ವಾಸ್ತನಿಕ ರಚನೆಗಳ ಅನುಭವದಿಂದ ಸಿದ್ಧಿಸಿದ ಉಕ್ತಿಗಳೇ ಆ ಭೌತ ಜ್ಯಾಮಿತಿಯ ಪ್ರಮೇಯಗಳು. ಪ್ರಮೇಯಗಳ ಸತ್ಯತೆಯನ್ನು ಸ್ಪಷ್ಟೀಕರಿಸುವ ಸಲುವಾಗಿ ಅದರಲ್ಲಿ ಅಪರೂಪಕ್ಕೆ ಅಲ್ಲೊಮ್ಮೆ ಇಲ್ಲೊಮ್ಮೆ ಕೆಲವೊಂದು ಸಮರ್ಥ ವಾದಗಳನ್ನು ಹೂಡಿರಬಹುದಾದರೂ ಅಂಥ ವಾದಗಳು ಆ ಜ್ಯಾಮಿತಿಯ ಅವಿಭಾಜ್ಯ ಅಂಗಗಳೆನಿಸಲಿಲ್ಲ. ಬದಲು, ಆಕೃತಿಗಳ ಪರಿಧಿ (ಪೆರಿಮಿಟರ್), ಸಲೆ ಮೊದಲಾದವನ್ನು ಅಳತೆ ಮಾಡಿ ಸಂಖ್ಯೆಗಳ ಮೂಲಕ ವ್ಯಕ್ತಪಡಿಸುವ ಕಾರ್ಯವಾದರೋ ಭೌತ ಜ್ಯಾಮಿತಿಯ ಮೂಲಭೂತ ಪರಿಪಾಠವಾಗಿತ್ತು. ವ್ಯಾವಹಾರಿಕ ಅಳತೆಗಳು ಸರಿಸುಮಾರಾಗಿರಬಲ್ಲವೇ ವಿನಾ ಪೂರ್ಣ ನಿಖರವಾಗಲಾರವೆಂಬುದು ಆ ಜ್ಯಾಮಿತಿಯ ಕೃಷಿಕಾರರ ದೃಷ್ಟಿಯಲ್ಲಿ ತಾತ್ತ್ವಿಕ ಮಹತ್ತ್ವವಿಲ್ಲದ ಒಂದು ಗೌಣ ಅಂಶವಾಗಿ ತೋರಿತು. ತತ್ಫಲವಾಗಿ ಜ್ಯಾಮಿತಿಯ ಅನ್ವೇಷಣೆಗಳೆಲ್ಲವನ್ನು ಸಂಖ್ಯೆಗಳ (ಅಂದರೆ ಧನಪೂರ್ಣಂಕಗಳ, ಇಲ್ಲವೆ ಪರಿಮೇಯಗಳ) ಮಾಧ್ಯಮದಲ್ಲೇ ಕೈಗೊಳ್ಳಬಹುದೆಂಬ ದೃಢವಿಶ್ವಾಸಕ್ಕೆ ಮನ್ನಣೆ ಉಂಟು; ಆದರೆ ಕನಿಷ್ಠ ಪಕ್ಷ ನೈಜಸಂಖೈಗಳನ್ನು-ರಿಯಲ್ ನಂಬರ್ಸ್-ಒಳಗೊಳ್ಳುವ ಆಧುನಿಕ ಸಂಖ್ಯಾಮಾಧ್ಯಮದ ವ್ಯಾಪ್ತಿ ಪರಿಮೇಯಗಳಿಗಷ್ಟೇ ಸೀಮಿತವಲ್ಲ. ಪ್ರಾಚೀನ ಕಾಲದಲ್ಲಾದರೋ ನೈಜಸಂಖ್ಯೆಯ ಪರಕಲ್ಪನೆ ಇಲ್ಲದಿದ್ದ ಕಾರಣ ಸಂಖ್ಯೆ ಎಂದರೆ ಪೂರ್ಣಾಂಕ ಇಲ್ಲವೆ ಪರಿಮೇಯ ಎಂದು ಮಾತ್ರ ಅರ್ಥವಿಸಬೇಕಾಗಿತ್ತು. ಗ್ರೀಕ್ ತಾತ್ತ್ವಿಕ ಪೈಥಾಗೊರಸ್ ಮತ್ತು ಅವನ ಅನುಯಾಯಿಗಳಾದರೂ ಈ ವಿಶ್ವಾಸದಲ್ಲಿ ಪಾಲ್ಗೊಂಡವರೇ ಆಗಿದ್ದರು. ಆದರೆ ಕ್ರಿ.ಪೂ. 6 ಮತ್ತು 4ನೆಯ ಶತಮಾನಗಳ ನಡುವೆ ಕೊನೆಯ ಪಕ್ಷ ಗ್ರೀಕ್ ಜ್ಯಾಮಿತಿಶಾಸ್ತ್ರಜ್ಞರ ಮಟ್ಟತೆ ಇಂಥ ಸಂಖ್ಯಾಶ್ರದ್ಧೆಯನ್ನು ಬುಡಮೇಲಾಗಿಸುವ ಕೆಲವು ಸಂಗತಿಗಳು ಆವಿಷ್ಕೃತವಾದುವು.
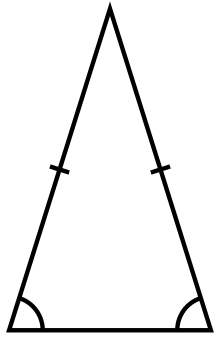
ಚಿತ್ರದ ABC ತ್ರಿಭುಜ ಈ ಬಗೆಯ ಅಂದೋಲಕ ವಿದ್ಯಮಾನವೊಂದನ್ನು ನಿದರ್ಶಿಸುತ್ತದೆ. ಇದರಲ್ಲಿ A,B,C ಕೋನಗಳು ಅನುಕ್ರಮವಾಗಿ 360, 720, 720, ಆಗಿವೆ. (ಇಂಥ ತ್ರಿಭುಜಗಳನ್ನು ರಚಿಸಲು ನಿಜಕ್ಕೂ ಸಾಧ್ಯವುಂಟೆಂದು ಗ್ರೀಕರಿಗೆ ವೇದ್ಯವಾಗಿತ್ತು). AB, BC ಗಳೆರಡರ ಉದ್ದಗಳನ್ನೂ ಪರಿಮೇಯಗಳಿಂದ ವ್ಯಕ್ತಪಡಿಸಲು ಸಾಧ್ಯವೇ ಎಂಬುದು ಈಗ ನಮ್ಮ ಮುಂದಿರುವ ಪ್ರಶ್ನೆ. ಪರ್ಯಾಲೋಚನೆಯ ದೃಷ್ಟಿಯಿಂದ ಅದು ಸಾಧ್ಯವೆಂದು ಕಲ್ಪಿಸಿಕೊಳ್ಳೋಣ. ಆಗ ಅಳತೆಯ ಮೂಲಮಾನವನ್ನು ಸೂಕ್ತವಾಗಿ ಬದಲಿಸುವುದರಿಂದ AB, BC ಗಳ ಉದ್ದಗಳು (ಧನ) ಪೂರ್ಣಾಂಕಗಳಾಗುವಂತೆ ಏರ್ಪಡಿಸಲೂ ಸಾಧ್ಯವಾಗುವುದು. (ಉದಾಹರಣೆಗೆ ಯಾವುದೋ ಒಂದು ಅಳತೆಯ ಮೂಲಮಾನವನ್ನಿಟ್ಟುಕೊಂಡಾಗ AB ಯ ಉದ್ದ 29/3, BC ಯ ಉದ್ದ 32/5 ಆಗಿರಬಹುದು. ಈ ಮೂಲಮಾನದ 1/(3x5)= 1/15 ಭಾಗವನ್ನು ಹೊಸ ಮೂಲಮಾನವನ್ನಾಗಿ ಆಯ್ಕೆ ಮಾಡಿದಲ್ಲಿ AB=15x29/3=145, BC=15x32/5=96 ಆಗುತ್ತದೆ. (145 ಮತ್ತು 96 ಎರಡೂ ಪೂರ್ಣಾಂಕಗಳು.) ಆದ್ದರಿಂದ AB = ಒಂದು ಧನಪೂರ್ಣಾಂಕ n1, BC = ಅದಕ್ಕಿಂತ ಕಿರಿದಾದ ಇನ್ನೊಂದು ಧನಪೂರ್ಣಾಂಕ n2 ಎಂದು ಭಾವಿಸಬಹುದು. ಇದಾದ ಬಳಿಕ CD=AB-BC-AD=n1-n2-n3 ಎಂದು ಕರೆಯಬಹುದಾದ ಮತ್ತೊಂದು ಧನಪೂರ್ಣಾಂಕ ಎಂದೂ ಮನಗಾಣುವುದು ಸುಲಭ. ಅಲ್ಲದೆ CBD ಯು ABC ಗೆ ಸಮರೂಪವಾಗಿರುವುದರಿಂದ (ಸಿಮಿಲರ್) AB/BC = CB/BD ಅಥವಾ n1/n2 = n2/n3 ಎಂದಾಗುವುದು. ಇಲ್ಲಿ n1>n2>n3 ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು. ಈಗ CBD ಯೂ ABC ಯಂಥದೇ ತ್ರಿಭುಜವಾದ್ದರಿಂದ ABC ಯ ಮೇಲೆ ಎಸಗಿದ ರಚನೆಯನ್ನೇ CBD ಯನ್ನೂ ಕುರಿತಂತೆಯೂ ಪುನರಾವರ್ತಿಸಲು ಅಡ್ಡಿಯೇನಿಲ್ಲ. ಹಾಗೆ ಮಾಡಿದಲ್ಲಿ ಮತ್ತೆ ಇನ್ನೊಂದು ಧನಪೂರ್ಣಾಂಕ {n1,n2,n3,n4,n5,n6........} ಫಲಿಸಿ ಅದರ ಉದ್ದಕ್ಕೂ {n1>n2>n3>n4>n5>n6>....... ಆಗಬೇಕಾಗುವುದು. ಇದು ಸ್ಪಷ್ಟವಾಗಿ ಅಸಾದ್ಯ. ಆದ್ದರಿಂದ ಚಿತ್ರದ AB, BC ಉದ್ದಗಳೆರಡನ್ನೂ ಪರಿಮೇಯಗಳಿಂದ ಅಳೆಯಬಹುದೆಂಬ ನಮ್ಮ ಕಲ್ಪನೆ ಮಿಥ್ಯೆಯೇ ಸರಿ. ಪೈಥಾಗೊರಸನ ಅನಂತರ ಜ್ಯಾಮಿತಿಯನ್ನು ಅಭ್ಯಸಿಸಿದ ಅನೇಕ ಗ್ರೀಕ್ ಸಂಶೋಧಕರು ಇಂಥ ವಿದ್ಯಮಾನಗಳ ಫಲವಾಗಿ ರೇಖಾಖಂಡಗಳು (ಲೈನ್ ಸೆಗ್ಮೆಂಟ್ಸ್) ವೃತ್ತಚಾಪಗಳು (ಸರ್ಕ್ಯುಲರ್ ಆರ್ಕ್ಸ್), ಸಲೆಗಳೇ ಮೊದಲಾದ ಜ್ಯಾಮಿತೀಯ ಧಾತುಗಳು ನಿಜಕ್ಕೂ ಸಂಖ್ಯೆಗಳಿಗಿಂತ ಮೂಲಭೂತ ಸಾಮಗ್ರಿಗಳೆಂಬ ಪ್ರಾಮಾಣಿಕ ತೀರ್ಮಾನಕ್ಕೆ ಬಂದರು. ಅವರ ಅಭಿಮತದ ಪ್ರಕಾರ ಈ ಜ್ಯಾಮಿತೀಯ ಧಾತುಗಳ ಮಾಧ್ಯಮದಲ್ಲಿ ಸಂಖ್ಯೆಗಳನ್ನು ವ್ಯಕ್ತಪಡಿಸಬಹುದೇ ವಿನಾ ಸಂಖ್ಯೆಗಳಿಂದ ಜ್ಯಾಮಿತೀಯ ಧಾತುಗಳನ್ನಲ್ಲ. (ಇಂದಿನ ನೈಜಸಂಖ್ಯೆಗಳು ಆಧುನಿಕ ಶಾಲೆಗಳಿಲ್ಲಿ ವಿದ್ಯಾರ್ಥಿಗಳತ್ತ ಪ್ರಪ್ರಥಮವಾಗಿ ಇಣುಕಿ ನೋಡುವುದಾದರೂ ಕಪ್ಪುಹಲಗೆಯ ಮೇಲೆ ಎಳೆದ ಸರಳರೇಖೆಯೊಂದರ ಆಶ್ರಯವನ್ನು ಗಳಿಸಿದ ಬಳಿಕವೇ; ಆದ್ದರಿಂದ ಪ್ರಾಚೀನ ಗ್ರೀಕರ ಅಭಿಮತಕ್ಕೆ ಇಂದೂ ಕನಿಷ್ಠ ಪಕ್ಷ ಶೈಕ್ಷಣಿಕ ಸಲುವಳಿ ಇದೆ ಎನ್ನಬಹುದು.)
ಜ್ಯಾಮಿತಿಯನ್ನು ಸ್ಥೂಲವಾಗಿ ಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿ ಮತ್ತು ಅಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿ ಎಂದು ಭಾಗಗಳಾಗಿ ವಿಂಗಡಿಸಲಾಗಿದೆ. ಜ್ಯಾಮಿತಿ ನಡೆದುಬಂದ ದಾರಿಯಲ್ಲಿ ಯೂಕ್ಲಿಡನ ಸ್ಥಾನ ಮಹತ್ತ್ವದ್ದು ಎನ್ನುವುದು ಇದರಿಂದ ಅರಿವಾಗುತ್ತದೆ. ಗಮನಾರ್ಹವಾದ ಹೆಚ್ಚಿನ ಅನ್ವೇಷಣೆಗಳನ್ನು ಯೂಕ್ಲಿಡ್ ಮಾಡದಿದ್ದರೂ ಅವನ ಹೆಸರು ಜ್ಯಾಮಿತಿಯೊಂದಿಗೆ ಸೇರಿಹೋಗಿರುವುದು ಅವನಿಗೆ ಸಂದಾಯವಾದ ಸರಿಯಾದ ಪುರಸ್ಕಾರವಾಗಿದೆ. ತನಗೆ ತಿಳಿದದ್ದನ್ನು ಅನ್ಯರಿಗೆ ಅರ್ಥವಾಗುವ ರೀತಿಯಲ್ಲಿ ತಿಳಿಯಪಡಿಸುವ ಅಪೂರ್ವ ಸಾಮರ್ಥ್ಯ ಅವನಿಗಿತ್ತು. ದಿ ಎಲಿಮೆಂಟ್ಸ್ ಎಂಬ ಆತನ ಗಣಿತ ಗ್ರಂಥ ಇದರ ಪ್ರತ್ಯಕ್ಷ ನಿದರ್ಶನ. ತನ್ನ ಕಾಲದವರೆಗೂ ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ ನಡೆದಿದ್ದ ಚಟುವಟಿಕೆಗಳನ್ನು ಸುಲಭ ಪಾಠಗಳು ('ದಿ ಎಲಿಮೆಂಟ್ಸ್), ಆಕೃತಿಗಳ ವಿಭಾಗೀಕರಣ (ದ ಡಿವಿಷನ್ ಆಫ್ ಫಿಗರ್ಸ್) ಇವೇ ಮುಂತಾದ ಗ್ರಂಥಗಳಲ್ಲಿ ಅವನು ಅಳವಡಿಸಿದ್ದಾನೆ. ಸುಲಭ ಪಾಠಗಳೂ ಎನ್ನುವ ಪುಸ್ತಕ ಯೂಕ್ಲಿಡ್ಗಿಂತ ಮುಂಚೆ ಆಗಿಹೋದವರ ಬೌದ್ಧಿಕ ಹಿರಿಮೆಗಳ ಫಲಗಳನ್ನು ಒಳಗೊಂಡ ಒಂದು ಸಂಕಲನವೇ ವಿನಾ ಒಂದು ಸಂಶೋಧನಾ ಗ್ರಂಥವಲ್ಲ. ಅದರಲ್ಲಿ ಅಂದಿನ ಗಣಿತಶಾಸ್ತ್ರದ ಪ್ರತಿಯೊಂದು ಉಕ್ತಿಯ ಸ್ಥಾನವನ್ನು ಗುರುತಿಸಿ, ಆಯಾ ಸ್ಥಾನಗಳಲ್ಲಿ ಅದನ್ನು ಅಳವಡಿಸಲಾಗಿದೆ; ಅಲ್ಲದೆ ಸಾಧನೆಗಳಿಲ್ಲದ ಉಕ್ತಿಗಳಿಗೆ ಹೊಸ ಸಾಧನೆಗಳನ್ನು ಸಹ ನಿರೂಪಿಸಲಾಗಿದೆ. ಹೀಗೆ ಜ್ಯಾಮಿತಿಯ ಪುನರುಜ್ಜೀವನಕ್ಕೆ ಯೂಕ್ಲಿಡ್ ಮುಖ್ಯವಾಗಿ ಕಾರಣನಾದ.
ಸಾಧನೆಗಳನ್ನು ರೂಪಿಸಲು ಚಿತ್ರಗಳು ಸಹಾಯಕವಾಗಬಲ್ಲವೇ ವಿನಾ ಸಾಧನೆಗಳ ಸತ್ಯತೆಗೆ ಅವು ಅನಿವಾರ್ಯವಲ್ಲ ಎನ್ನುವುದು ಯೂಕ್ಲಿಡನಿಗೆ ತಿಳಿದಿತ್ತು. ಸಾಧನೆಗಳನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಚಿತ್ರಗಳು ಸಹಾಯಕವಾಗುತ್ತವೆ ಮಾತ್ರ. ಸರಿಯಾದ ಪರಿಕಲ್ಪನೆ ಇಲ್ಲವೆ ಚಿತ್ರಗಳನ್ನು ರಚಿಸುವುದರಿಂದ ಕೆಲವು ವೇಳೆ ಅಸಂಬದ್ಧತೆಗಳನ್ನು ಸಮರ್ಥಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ ತ್ರಿಭುಜಗಳೆಲ್ಲವೂ ಸಮಬಾಹು ತ್ರಿಭುಜಗಳು ಎಂಬುದಕ್ಕೆ ಒಂದು ಅಣಕಸಾಧನೆ ಈ ರೀತಿ ಇದೆ.
△ MRA ≡ △ MPA
∴ MR = MP
AR = AP .... (1)
ಈಗ MB = MC ಮತ್ತು
∠MRB = ∠MPC = 900
∴ △ MBR ≡ △ MCP
∴ RB = PC .... (2)
(1) ಮತ್ತು (2) ರಿಂದ AB = AC
ಇದೇ ರೀತಿ AB = BC ಎಂದು ಸಾಧಿಸಬಹುದು. M ಬಿಂದು ತ್ರಿಭುಜದ ಒಳಗಡೆ ಇರುವಂತೆ ಚಿತ್ರವನ್ನು ರಚಿಸಿರುವುದು ಗಮನಾರ್ಹ. ಆದರೆ ಅದು ನಿಜವಾಗಿ ತ್ರಿಭುಜದ ಹೊರಗಡೆ ಇರುತ್ತದೆ. ಮೇಲಿನ ಸಾಧನೆಗೆ ಅಸ್ತಿತ್ವವಿರಬೇಕಾದರೆ M ತ್ರಿಭುಜದ ಒಳಗಡೆ ಇರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಬೇಕು. ಇದು ಅಸಾಧ್ಯ.
ದಿ ಎಲಿಮೆಂಟ್ಸ್ ಗ್ರಂಥದ ವಿವರಗಳು
[ಬದಲಾಯಿಸಿ]ಯಾವುದೇ ಒಂದು ಶಾಸ್ತ್ರದ ತಳಪಾಯದಲ್ಲಿ ಅದರ ಬೆಳೆವಣಿಗೆಗೆ ಅನಿವಾರ್ಯವಾದ ಮತ್ತು ಸಾಧಿಸಲು ಸಾಧ್ಯವಾಗದ ಕೆಲವು ಮೂಲ ಉಕ್ತಿಗಳು ಇರಬೇಕು. ಶಾಸ್ತ್ರದ ಬೆಳೆವಣಿಗೆಯಲ್ಲಿ ಅಡ್ಡ ಸಿಕ್ಕುವ ಎಲ್ಲ ನಿರೂಪಣೆಗಳೂ ಈ ಮೂಲ ಉಕ್ತಿಗಳಿಂದ ನಿರೂಪಿತವಾಗಿರುತ್ತವೆ. ಜ್ಯಾಮಿತಿ ಕೂಡ ಇದಕ್ಕೆ ಹೊರತಾದುದಲ್ಲ. ಅಂತೆಯೇ ಮೊದಲನೆಯ ಅಧ್ಯಾಯದಲ್ಲಿ ಇಪ್ಪತ್ತುಮೂರು ವ್ಯಾಖ್ಯೆಗಳಾದ ಬಳಿಕ ಐದು ಆದ್ಯುಕ್ತಿಗಳನ್ನು (ಪಾಸ್ಟ್ಯುಲೇಟ್ಸ್) ಮತ್ತು ಐದು ಸಾಮಾನ್ಯ ಗ್ರಹಿಕೆಗಳನ್ನು (ಕಾಮನ್ ನೋಷನ್ಸ್) ಯೂಕ್ಲಿಡ್ ಅಂಗೀಕರಿಸುತ್ತಾನೆ. ಆದ್ಯುಕ್ತಿಗಳು ಜ್ಯಾಮಿತಿಗೆ ಮಾತ್ರ ಸೀಮಿತವಾಗಿದ್ದರೆ ಸಾಮಾನ್ಯ ಗ್ರಹಿಕೆಗಳು ಎಲ್ಲ ಶಾಸ್ತ್ರಗಳಿಗೂ ಅನ್ವಯಿಸುತ್ತವೆ. ಆದ್ದರಿಂದಲೇ, ಮೂಲ ಉಕ್ತಿಗಳನ್ನು ಆದ್ಯುಕ್ತಿಗಳು ಮತ್ತು ಸಾಮಾನ್ಯ ಗ್ರಹಿಕೆಗಳು ಎಂದು ಎರಡು ಗುಂಪುಗಳಾಗಿ ವಿಂಗಡಿಸಿದ್ದಾನೆ. (ಇಂದಾದರೋ ಇಂಥ ವಿಂಗಡಣೆಗೆ ಅಷ್ಟೇನೂ ಮಾನ್ಯತೆ ಇಲ್ಲ; ಎಲ್ಲ ಮೂಲ ಉಕ್ತಿಗಳನ್ನೂ ಆದ್ಯುಕ್ತಿಗಳೆಂದೇ ಪರಿಗಣಿಸುವುದು ವಾಡಿಕೆ ಆಗಿದೆ. ಅಲ್ಲದೆ ತರ್ಕಬದ್ಧತೆಯ ಇಂದಿನ ಮಾನಕಗಳಿಗೆ ಸರಿಹೊಂದಲು ಈ ಹತ್ತೇ ಉಕ್ತಿಗಳು ಸಾಲುವುದೂ ಇಲ್ಲ.) ನೇರ ಅಂಚು (ಸ್ಟ್ರೇಟ್ಎಡ್ಜ್) ಮತ್ತು ಕೈವಾರಗಳ ನೆರವಿನಿಂದ ಮಾಡಬಹುದಾದಂಥ ರಚನೆಗಳು, ತ್ರಿಕೋನಗಳ ಸರ್ವಸಮತೆ, ಸಮಾಂತರ ಸರಳರೇಖೆಗಳ ಲಕ್ಷಣಗಳು (ತ್ರಿಕೋನದಲ್ಲಿನ ಕೋನಗಳ ಮೊತ್ತ ಎರಡು ಲಂಬಕೋನಗಳಿಗೆ ಸಮ ಎನ್ನುವುದೂ ಸೇರಿದಂತೆ), ಸಮಾಂತರ ಚತುರ್ಭುಜಗಳು (ಒಂದು ತ್ರಿಭುಜ ಅಥವಾ ಒಂದು ಸರಳರೇಖಾಕೃತಿಯ ಸಲೆಗೆ ಸಮವಾಗಿರುವಂತೆ ಮತ್ತು ಗೊತ್ತಾದ ಕೋನಗಳಿರುವಂತೆ ಒಂದು ಸಮಾಂತರ ಚತುರ್ಭುಜದ ರಚನೆಯೂ ಸೇರಿದಂತೆ) ಇವಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಪ್ರಮೇಯಗಳು ಮೊದಲನೆಯ ಅಧ್ಯಾಯದಲ್ಲಿವೆ. ಈ ಅಧ್ಯಾಯ ಪೈಥಾಗೊರಸನ ಪ್ರಮೇಯ ಮತ್ತು ಅದರ ವಿಲೋಮದ ಸಾಧನೆಗಳೊಂದಿಗೆ ಪೂರ್ಣಗೊಳ್ಳುತ್ತದೆ.

ಲಂಬಕೋನ ತ್ರಿಕೋನದ ವಿಕರ್ಣಕ್ಕೆ ಶಿರದಿಂದ ಲಂಬವನ್ನು ಎಳೆಯುವುದರಿಂದ ಉಂಟಾಗುವ ಸಮರೂಪ ತ್ರಿಕೋನಗಳಲ್ಲಿ ಸರಳ ಅನುಪಾತದ ಬಳಕೆಯಿಂದ ಪೈತಾಗೊರಸನ ಪ್ರಮೇಯವನ್ನು ಸಾಧಿಸಬಹುದು. ಈಚಿನ ಬಹಳಷ್ಟು ಪುಸ್ತಕಗಳಲ್ಲಿ ಈ ರೀತಿಯ ಸಾಧನೆಯನ್ನು ಕಾಣಬಹುದು. ಆದರೆ ಯೂಕ್ಲಿಡನ ಸಾಧನೆ ಇದಕ್ಕೆ ಹೊರತಾಗಿದೆ. ಆತನ ಸಾಧನೆ ಈ ರೀತಿ ಇದೆ.
DE ಗೆ CL ಲಂಬವಾಗಿದೆ.
△ CBE ≡ △ ABK = 1/2 BK.HK = 1/2 CB2
∴ CB2 = 2 △ CBE = ಆಯತ BL
ಇದೇ ರೀತಿ AC2 = ಆಯತ AL
ಈಗ ಆಯತ BL + ಆಯತ AL = AB2
∴ AC2 + CB2 = AB2
ಈ ಸಾಧನೆಯಲ್ಲಿ ವಿಕರ್ಣದ ವರ್ಗವನ್ನು ವಿಕರ್ಣದ ಉದ್ದದ ಅಂಕಗಣಿತ ರೀತಿಯ ಸಾಮಾನ್ಯವರ್ಗವೆಂದು ಪರಿಗಣಿಸದೆ ಅದರ ಮೇಲೆ ರಚಿಸಿದ ಒಂದು ವರ್ಗದ ಸಲೆಯೆಂದು ತಿಳಿದು ಅದನ್ನು ಇನ್ನೆರಡು ಬಾಹುಗಳ ಮೇಲೆ ರಚಿಸಿದ ವರ್ಗಗಳ ಸಲೆಗೆ ಸಮವಾದ ಎರಡು ಆಯತಗಳ ಸಲೆಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮವೆಂದು ಸಾಧಿಸಿರುವುದು ಗಮನಾರ್ಹವಾದ ಅಂಶ.[೨೨][೨೩]
a ಮತ್ತು b ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧವೆಂದರೆ a ಮತ್ತು b ಗಳು ಬಾಹುಗಳಾಗಿ ಇರುವ ಒಂದು ಆಯತದ ಸಲೆ ಎಂಬುದಾಗಿ ಗ್ರೀಕರು ತಿಳಿದಿದ್ದರು. ಅವರು ಇಂಥ ಜ್ಯಾಮಿತೀಯ ಬೀಜಗಣಿತವನ್ನು ಬೆಳೆಸಿದರು. ಸುಲಭಪಾಠಗಳು (ದಿ ಎಲಿಮೆಂಟ್ಸ್) ಪುಸ್ತಕದ ಎರಡನೆಯ ಅಧ್ಯಾಯದಲ್ಲಿ ಜ್ಯಾಮಿತೀಯ ಬೀಜಗಣಿತವನ್ನು ಚರ್ಚಿಸಿದೆ. ಮೂರು ಮತ್ತು ನಾಲ್ಕನೆಯ ಅಧ್ಯಾಯಗಳು ವೃತ್ತದ ಜ್ಯಾಮಿತಿಗೆ ಮೀಸಲಾಗಿದ್ದರೆ ಪ್ರಮಾಣ ಮತ್ತು ಅನುಪಾತದ ಚರ್ಚೆಯನ್ನು ಸಾಕಷ್ಟು ಮುಂದೂಡಿ ಐದನೆಯ ಅಧ್ಯಾಯದಲ್ಲಿ ಸಾಧ್ಯವಾದಷ್ಟು ಮಟ್ಟಿಗೆ ವಿಶದವಾಗಿ ವಿವರಿಸಿದೆ. ಈ ಅಧ್ಯಾಯದಲ್ಲಿ ಇಪ್ಪತ್ತು ಪ್ರಮೇಯಗಳಿವೆ. ಏಳು, ಎಂಟು ಮತ್ತು ಒಂಬತ್ತನೆಯ ಅಧ್ಯಾಯಗಳು ಸಂಖ್ಯಾಸಿದ್ಧಾಂತವನ್ನು (ಥಿಯರಿ ಆಫ್ ನಂಬರ್ಸ್) ಕುರಿತು ಇವೆ. ಆಗಲೇ ತಿಳಿಸಿರುವಂತೆ ನೈಜ ಸಂಖ್ಯೆಗಳ ಪರಿಕಲ್ಪನೆ ಇಲ್ಲದಿದ್ದ ಕಾರಣ ಗ್ರೀಕರು ಪ್ರತಿಯೊಂದನ್ನೂ ಜ್ಯಾಮಿತೀಯ ಪರಿಧಿಯೊಳಗೆ ಅಳವಡಿಸಿಕೊಳ್ಳುತ್ತಿದ್ದರು. ಅವರಿಗೆ ಸಂಖ್ಯೆಗಳಿಗಿಂತ ಜ್ಯಾಮಿತೀಯ ಆಕೃತಿಗಳೇ ಮೂಲಭೂತವಾಗಿ ಕಾಣುತ್ತಿದ್ದವು. ಕರಣಿಗಳಿಗೆ (ಸರ್ಡ್ಸ್) ಜ್ಯಾಮಿತೀಯ ಸಮಾನಗಳನ್ನು ಒದಗಿಸುವ ಪ್ರಮೇಯಗಳನ್ನು ಹತ್ತನೆಯ ಅಧ್ಯಾಯದಲ್ಲಿ ಕೊಟ್ಟಿದೆ. ಹನ್ನೊಂದನೆಯ ಅಧ್ಯಾಯದಲ್ಲಿ ಒಂದು ಘನಾಕೃತಿಯನ್ನು ಉದ್ದ, ಅಗಲ ಮತ್ತು ದಪ್ಪಗಳಿರುವ ಒಂದು ಆಕೃತಿ ಎಂದೂ, ಅದರ ಎಲ್ಲೆಯನ್ನು ಮೇಲ್ಮೈ ಎಂದೂ ನಿರೂಪಿಸಿದೆ. ಹನ್ನೆರಡನೆಯ ಅಧ್ಯಾಯದಲ್ಲಿ ಆಕೃತಿಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ಸಲೆ ಮುಂತಾದ ಅಳತೆಗಳ ಮಾಪನವನ್ನು ನಿಶ್ಶೇಷೀಕರಣ ವಿಧಾನದಿಂದ (ಮೆಥಡ್ ಆಫ್ ಎಕ್ಸಾಷನ್) ತಿಳಿಸಲಾಗಿದೆ. ಹದಿಮೂರನೆಯ (ಕೊನೆಯ) ಅಧ್ಯಾಯ ಐದು ಕ್ರಮ ಘನಾಕೃತಿಗಳ (regular solid) ಲಕ್ಷಣಗಳ ಚರ್ಚೆಗೆ ಮೀಸಲಾಗಿದೆ.
ಕೊನೆಯ ಪ್ರಮೇಯಗಳು ಪ್ರತಿಯೊಂದು ಕ್ರಮ ಘನಾಕೃತಿಯ ಅಳತೆಗಳನ್ನು ಪರಿಗೋಲದ (ಸರ್ಕಮ್ಸ್ಫಿಯರ್) ಅಳತೆಗಳ ಚೌಕಟ್ಟಿನಲ್ಲಿ ಹುದುಗಿಸುವ ಧ್ಯೇಯವನ್ನು ಇಟ್ಟುಕೊಂಡಿವೆ. ಕ್ರಮ ಚತುಷ್ಫಲಕ (ರೆಗ್ಯುಲರ್ ಟೆಟ್ರಹೆಡ್ರನ್), ಘನ (ಕ್ಯೂಬ್ ಅಥವಾ ರೆಗ್ಯುಲರ್ ಹೆಕ್ಸಹೆಡ್ರನ್), ಕ್ರಮ ಅಷ್ಟಫಲಕ (ರೆಗ್ಯುಲರ್ ಆಕ್ಟಹೆಡ್ರನ್), ಕ್ರಮ ದ್ವಾದಶಫಲಕ (ರೆಗ್ಯುಲರ್ ಡೊಡೆಕಹೆಡ್ರನ್) ಮತ್ತು ಕ್ರಮವಿಂಶತಿ ಫಲಕ (ರೆಗ್ಯುಲರ್ ಐಕೊಸಹೆಡ್ರನ್) ಇವೇ ಐದು ಕ್ರಮ ಘನಾಕೃತಿಗಳು. ಇದನ್ನು ಕುರಿತು ಕೆಲವು ಮಾಹಿತಿಗಳನ್ನು ಕೆಳಗೆ ಕೋಷ್ಟೀಕರಿಸಲಾಗಿದೆ.
ಕ್ರ. ಸಂ. ಬಹುಫಲಕದ ಹೆಸರು ಅಂಚುಗಳ ಸಂಖ್ಯೆ E ಶೃಂಗಗಳ ಸಂಖ್ಯೆ V ಫಲಕಗಳ ಸಂಖ್ಯೆ F ಫಲಕದ ಆಕಾರ 1 ಚತುಷ್ಫಲಕ 6 4 4 ತ್ರಿಭುಜ 2 ಘನ ಅಥವಾ ಷಷ್ಠಫಲಕ 12 8 6 ಚೌಕ 3 ಅಷ್ಟಫಲಕ 12 6 8 ತ್ರಿಭುಜ 4 ದ್ವಾದಶಫಲಕ 30 20 12 ಪಂಚಭುಜ 5 ವಿಂಶತಿಫಲಕ 30 12 20 ತ್ರಿಭುಜ
ಪ್ರತಿಯೊಂದರಲ್ಲೂ V + F = E + 2 ಎಂಬುದನ್ನು ಗಮನಿಸಬಹುದು. ಇದಕ್ಕೆ ಆಯ್ಲರ್ ಸೂತ್ರ ಎಂದು ಹೆಸರು.[೨೪] ಈ ಸೂತ್ರ ಎಲ್ಲ ಸರಳ ಸಂಯೋಜಿತ (ಸಿಂಪ್ಲಿ ಕನೆಕ್ಟಡ್) ಬಹುಫಲಕಗಳಿಗೂ ಅನ್ವಯಿಸುತ್ತದೆ.
ಅಪಲೋನಿಯಸ್
[ಬದಲಾಯಿಸಿ]ಯಾವುದಾದರೂ ಶಂಕುವನ್ನು ಒಂದು ತಲದಿಂದ ಛೇದಿಸಿದಾಗ ಏರ್ಪಡುವ ಈ ವಕ್ರರೇಖೆಗಳಿಗೆ (ಕರ್ವ್ಸ್) ಶಂಕುಜಗಳು (ಕಾನಿಕ್ಸ್) ಎಂದು ಹೆಸರು. ಇವುಗಳ ಪರಿಚಯ ಯೂಕ್ಲಿಡ್ ಮುಂತಾದವರಿಗೆ ಇದ್ದರೂ ಇವನ್ನು ಕ್ರಮವಾಗಿ ಅಭ್ಯಸಿಸಿದಾತ ಆ ತರುವಾಯ ಬಂದ ಅಪಲೋನಿಯಸ್. ಶಿರಃಕೋನಗಳು (vertical angle) ವಿಶಾಲ, ಲಂಬ ಮತ್ತು ಲಘುಕೋನಗಳಿರುವಂತೆ ಮೂರು ಲಂಬವೃತ್ತೀಯ ಶಂಕುಗಳನ್ನು (right circular cone) ಆಯ್ದು ಒಂದೊಂದರ ಅಕ್ಷದೊಡನೆಯೂ 450 ಕೋನವನ್ನುಂಟುಮಾಡುವ ಒಂದು ತಲದಿಂದ ಆ ಶಂಕುವನ್ನು ಛೇದಿಸಿದಾಗ ಅನುಕ್ರಮವಾಗಿ ದೀರ್ಘವೃತ್ತ, ಪರವಲಯ ಮತ್ತು ಅತಿಪರವಲಯಗಳು ದೊರೆಯುತ್ತವೆಂದು ಅಪಲೋನಿಯಸನ ಪೂರ್ವಜರು ತಿಳಿದಿದ್ದರು. ಆದರೆ ಛೇದಕತಲದ ಭಾಗವನ್ನೇ ಸೂಕ್ತವಾಗಿ ಬದಲಾವಣೆ ಮಾಡುವುದರಿಂದ ಒಂದೇ ಶಂಕುವಿನಿಂದ ಈ ಮೂರು ಶಂಕುಜಗಳನ್ನು ಪಡೆಯಬಹುದು ಮತ್ತು ಶಂಕು ಲಂಬವೃತ್ತೀಯವಾಗಿರದೆ ಕೇವಲ ವೃತ್ತೀಯ ಶಂಕುವಾಗಿದ್ದರೆ ಸಾಕೆಂದು ಅಪಲೋನಿಯಸ್ ತೋರಿಸಿಕೊಟ್ಟ. ಮೇಲಾಗಿ ಅಪಲೋನಿಯಸ್ ಶಂಕುವಿನ ಪರಿಕಲ್ಪನೆಯನ್ನು ಮಾರ್ಪಡಿಸಿ ಅತಿಪರವಲಯ ನಿಜಕ್ಕೂ ಎರಡು ಕವಲುಗಳ ವಕ್ರರೇಖೆ ಎಂದು ತೋರಿಸಿಕೊಟ್ಟ. ಅಪಲೋನಿಯಸ್ ನಿರ್ದೇಶಕ ಜ್ಯಾಮಿತಿಗೆ ಬಹಳ ಹತ್ತಿರ ಬಂದಿದ್ದ. ಆದರೆ ಅದನ್ನು ಶಾಸ್ತ್ರೀಯವಾಗಿ ನಿರೂಪಿಸಲು ಮಾತ್ರ ಆತನಿಗೆ ಸಾಧ್ಯವಾಗಲಿಲ್ಲ.

ಪರಿವರ್ತನ ಜ್ಯಾಮಿತಿ
[ಬದಲಾಯಿಸಿ]ಜ್ಯಾಮಿತಿ ಆಕೃತಿಗಳ ಲಕ್ಷಣಗಳನ್ನು ಅಭ್ಯಸಿಸುತ್ತದೆ. ಈ ಲಕ್ಷಣಗಳು ಅಸಂಖ್ಯಾತವಾದುವು. ಆದ್ದರಿಂದ ಜ್ಯಾಮಿತಿಯ ಆಧ್ಯಯನದಲ್ಲಿ ಒಂದು ವ್ಯವಸ್ಥೆಯನ್ನು ತರಬೇಕಾದರೆ ಈ ಲಕ್ಷಣಗಳ ವಿಂಗಡಣೆ ಅನಿವಾರ್ಯವಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ ಮೆದುಮರದ ಒಂದು ಆಯತಾಕಾರದ ಘನಾಕೃತಿಯ ಮೇಲೆ ಒಂದು ವೃತ್ತವನ್ನೂ ಪರಸ್ಪರ ಲಂಬವಾಗಿರುವ ಅದರ ವ್ಯಾಸಗಳನ್ನೂ ರಚಿಸಬೇಕು. ಇದನ್ನು ಒಂದು ಬಲವಾದ ತಿರಡಿನಲ್ಲಿ (ವೈಸ್) ಸಿಕ್ಕಿಸಿ ಘನಾಕೃತಿಯ ಅಗಲ ಮೊದಲಿನ ಅಗಲದ ಅರ್ಧದಷ್ಟಾಗುವ ತನಕ ಅದುಮಿದರೆ ರಚಿಸಿದ್ದ ವೃತ್ತ ದೀರ್ಘವೃತ್ತವಾಗಿ ಪರಿವರ್ತನೆಯಾಗುತ್ತದೆ ಮತ್ತು ಆಗ ಅದರ ವ್ಯಾಸಗಳು ಪರಸ್ಪರ ಲಂಬವಾಗಿರುವುದಿಲ್ಲ. ಘನಾಕೃತಿಗೆ ಇದ್ದ ಮೊದಲಿನ ಎಲ್ಲ ಜ್ಯಾಮಿತೀಯ ಲಕ್ಷಣಗಳೂ ನಾಶವಾದಂತೆ ಕಾಣುತ್ತವೆ. ಆದರೆ ಇದು ಪೂರ್ಣ ಸತ್ಯವಲ್ಲ; ಉದಾಹರಣೆಗೆ ಕೇಂದ್ರ ವ್ಯಾಸವನ್ನು ಅರ್ಧಿಸುತ್ತದೆ ಎನ್ನುವ ಗುಣ ವೃತ್ತ ಮತ್ತು ದೀರ್ಘವೃತ್ತ ಎರಡಕ್ಕೂ ಅನ್ವಯಿಸುತ್ತದೆ. ಅಂದರೆ ಈ ಕ್ರಿಯೆಯಲ್ಲಿ ಆಕೃತಿಗಳ ಮೂಲ ಅಳತೆಗಳು ವ್ಯತ್ಯಾಸವಾದರೂ ಕೆಲವು ಲಕ್ಷಣಗಳು ಹಾಗೆಯೇ ಉಳಿಯುತ್ತವೆ. ಈ ರೀತಿಯ ಪರಿವರ್ತನೆಯಲ್ಲಿ ಜ್ಯಾಮಿತೀಯ ಲಕ್ಷಣಗಳನ್ನು ಬದಲಾಗುವ ಲಕ್ಷಣಗಳು ಎಂದು ವಿಂಗಡಿಸಬೇಕಾಗುತ್ತದೆ. ಪರಿವರ್ತನೆಯಲ್ಲಿ ಬದಲಾಗುವ ಲಕ್ಷಣಗಳನ್ನು ಕುರಿತಾದ ಜ್ಯಾಮಿತಿಯನ್ನು ಪರಿವರ್ತನ ಜ್ಯಾಮಿತಿ ಎಂದು ಕರೆಯಬಹುದು. ಫೆಲಿಕ್ಸ್ ಕ್ಲೈನ್ (1849-1925) ಎಂಬಾತ 1872ರಲ್ಲಿ ಮಾಡಿದ ಪ್ರಮುಖ ಭಾಷಣ ಒಂದರಲ್ಲಿ ಪರಿವರ್ತನ ಜ್ಯಾಮಿತಿಯ ಮುನ್ನುಡಿಯನ್ನು ಕೊಟ್ಟಿದ್ದ.
ವಿಕ್ಷೇಪ ಜ್ಯಾಮಿತಿ
[ಬದಲಾಯಿಸಿ]
ಮೂಲ ಮೂರ್ತಿಯೊಂದುಂಟು; ಕಾಗದದ ಹಾಳೆಯ ಮೇಲೆ ಅದರ ಚಿತ್ರ ಉಂಟು ಎಂದು ಭಾವಿಸೋಣ. ಈ ಚಿತ್ರವನ್ನು, ಹಾಳೆಯ ಮೇಲೆ ಮೂರ್ತಿಯ ವಿಕ್ಷೇಪ (ಪ್ರೊಜೆಕ್ಷನ್) ಎಂದು ಭಾವಿಸಬಹುದು. ಮೂಲ ಮೂರ್ತಿಯ ಅಳತೆಗಳು ಈ ವಿಕ್ಷೇಪ ಕ್ರಿಯೆಯಲ್ಲಿ ವ್ಯತ್ಯಾಸವಾಗಿವೆ. ಇದರಲ್ಲೂ ಮೂಲದ ಕೆಲವು ಜ್ಯಾಮಿತೀಯ ಲಕ್ಷಣಗಳು ಇದ್ದಂತೆಯೇ ಇರುತ್ತವೆ ಎಂದು ತೋರಿಸಬಹುದು. ವಿಕ್ಷೇಪ ಕ್ರಿಯೆಯಲ್ಲಿ ಬದಲಾಗದ ಲಕ್ಷಣಗಳನ್ನು ಕುರಿತಾದ ಜ್ಯಾಮಿತಿಗೆ ವಿಕ್ಷೇಪ ಜ್ಯಾಮಿತಿ (ಪ್ರೊಜೆಕ್ಟಿವ್ ಜ್ಯಾಮಿತಿ) ಎಂದು ಹೆಸರು. ಅಂದರೆ ಈ ಜ್ಯಾಮಿತಿಯಲ್ಲಿನ ಪ್ರಮೇಯಗಳು ಆಕೃತಿಗಳ ಉದ್ದ, ಕೋನಗಳು ಅಥವಾ ಸರ್ವಸಮತೆ ಮುಂತಾದವನ್ನು ಕುರಿತಾಗಿರುವುದಿಲ್ಲ. ಹದಿನೇಳನೆಯ ಶತಮಾನದ ಹೊತ್ತಿಗೆ ವಿಕ್ಷೇಪ ಜ್ಯಾಮಿತಿ ಜನಿಸಿದ್ದರೂ ಅದು ಪ್ರೌಢಿಮೆಯನ್ನು ಗಳಿಸಿದ್ದು ಹದಿನೆಂಟನೆಯ ಶತಮಾನದ ಕೊನೆ ಮತ್ತು ಹತ್ತೊಂಬತ್ತನೆಯ ಶತಮಾನದಲ್ಲಿ. ಮೊದಮೊದಲು ಸಂಖ್ಯೆಗಳು ಮತ್ತು ಬೀಜಗಣಿತದ ಬಳಕೆಯಲ್ಲದೆ ಜ್ಯಾಮಿತಿಯನ್ನು ಅದರದೇ ಆದ ಪರಿಸರದಲ್ಲಿ ಬೆಳೆಸಬೇಕೆಂಬ ಮನೋಭಾವ ಬೆಳೆದು ಬಂದಿತ್ತು. ಆದರೆ ಜ್ಯಾಮಿತಿಯ ಪರಿಧಿ ಬೆಳೆದಂತೆ ಅದಕ್ಕೆ ಸಂಖ್ಯೆಗಳು ಮತ್ತು ಬೀಜಗಣಿತ ಇವುಗಳ ಸಂಬಂಧ ಅನಿವಾರ್ಯವಾಗುತ್ತ ಬಂತು. ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿನ ಚಿಂತನೆಗಳು ಸಂಖ್ಯಾ ಪರಿಕಲ್ಪನೆಯನ್ನು ಅವಲಂಬಿಸಿರಬೇಕೆಂಬ ಹೊಸ ರೀತಿಯ ಚಿಂತನ ಮಾರ್ಗ ಫರ್ಮಾ (1601-1665) ಮತ್ತು ಡೇಕಾರ್ಟೆ (1596-1650) ಅವರಿಂದ ಪ್ರಾರಂಭವಾಯಿತು.

ನಿರ್ದೇಶಕ ಜ್ಯಾಮಿತಿ
[ಬದಲಾಯಿಸಿ]ಇದು ನಿರ್ದೇಶಕ ಜ್ಯಾಮಿತಿಯ ಜನನಕ್ಕೆ ಕಾರಣವಾಯಿತು. ಒಂದು ಜ್ಯಾಮಿತಿಯ ವಸ್ತುವನ್ನು ಏಕೈಕವಾಗಿ (ಯೂನಿಕ್ಲಿ) ಗುರುತಿಸಲು ನೆರವಾಗುವ ಯಾವುದಾದರೂ ಒಂದು ಸಂಖ್ಯಾಗಣಕ್ಕೆ ನಿರ್ದೇಶಕಗಳ ಗಣವೆಂದು ಹೆಸರು. ಒಂದು ತಲದಲ್ಲಿನ ಯಾವುದಾದರೂ ಬಿಂದು P ಗೆ ಎರಡು ನಿರ್ದೇಶಕಗಳಿವೆ. ತಲದಲ್ಲಿನ ಯಾವುದಾದರೂ ಎರಡು ಸರಳರೇಖೆಗಳು O ಬಿಂದುವಿನಲ್ಲಿ ಪರಸ್ಪರ ಛೇದಿಸಲಿ. ಇವನ್ನು x-ಅಕ್ಷ ಮತ್ತು y-ಅಕ್ಷ ಎಂದು ಕರೆಯೋಣ. P ಯ ಮೂಲಕ y-ಅಕ್ಷಕ್ಕೆ ಎಳೆದ ಸಮಾಂತರ x-ಅಕ್ಷವನ್ನು L ನಲ್ಲೂ x-ಅಕ್ಷಕ್ಕೆ ಎಳೆದ ಸಮಾಂತರ y-ವನ್ನು M ನಲ್ಲೂ ಸಂಧಿಸಲಿ. OL ದೂರವನ್ನು P ಯ x-ನಿರ್ದೇಶಕವೆಂದೂ, OM ದೂರವನ್ನು y-ನಿರ್ದೇಶಕವೆಂದೂ ಕರೆಯಬಹುದು. ಅಂದರೆ x-ಅಕ್ಷದ ಮೇಲೆ OL ದೂರವನ್ನು ಗಮಿಸಿ ಅಲ್ಲಿಂದ y-ಅಕ್ಷಕ್ಕೆ ಸಮಾಂತರವಾಗಿ OM = LP ದೂರ ಸಾಗಿದರೆ P ಬಿಂದು ಸಿಕ್ಕುತ್ತದೆ. P ಯನ್ನು ನಿರ್ದೇಶಕ ಜ್ಯಾಮಿತಿಯಲ್ಲಿ P(x, y) ಎಂದು ಬರೆಯುತ್ತೇವೆ. (ಇಲ್ಲಿ x ಮತ್ತು y ಗಳು P ಯ ನಿರ್ದೇಶಕಗಳು). ax+by+c = 0 ಸಮೀಕರಣದಲ್ಲಿ x, y ಚರ ನಿರ್ದೇಶಕಗಳು ಮತ್ತು a, b, c ನೈಜಸಂಖ್ಯೆಗಳು. ಒಂದು ಬಿಂದುವಿನ ನಿರ್ದೇಶಕಗಳನ್ನು ಈ ಸಮೀಕರಣದ x ಮತ್ತು y ಜಾಗಗಳಲ್ಲಿ ಅನುಕ್ರಮವಾಗಿ ಆದೇಶಿಸಿದಾಗ ಅದರ ಸತ್ಯತೆ ನಾಶವಾಗದಿದ್ದರೆ ಅಂಥ ಬಿಂದುವಿನ ಪಥ ಸರಳರೇಖೆ ಆಗಿರುತ್ತದೆ. x ಗೆ ಬೆಲೆಗಳನ್ನು ಕೊಡುವುದರಿಂದ y ಯ ಬೆಲೆಗಳನ್ನು ax+by+c = 0 ಸಮೀಕರಣದಿಂದ ಪಡೆದು ಒಂದು ನಿರ್ದಿಷ್ಟ ಸರಳರೇಖೆಯನ್ನು ಗುರುತಿಸಬಹುದು. ಅಂದರೆ ax+by+c = 0 ಸಮೀಕರಣ ಒಂದು ಸರಳ ರೇಖೆಯನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ನಿರ್ಧರಿಸುತ್ತದೆ. ಹೀಗೆಯೇ x2/a2 + y2/b2 = 1 ದೀರ್ಘವೃತ್ತವನ್ನೂ,[೨೫] x2/a2 - y2/b2 = 1 ಅತಿಪರವಲಯವನ್ನೂ, y2 = 4ax ಪರವಲಯವನ್ನೂ ನಿರ್ಧರಿಸುತ್ತವೆ. ಒಟ್ಟಿನಲ್ಲಿ x, y ಚರಗಳಿರುವ ಒಂದು ಸಮೀಕರಣ ಒಂದು ಗೊತ್ತಾದ ವಕ್ರರೇಖೆಯನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ. ಜ್ಯಾಮಿತೀಯ ವಸ್ತುಗಳ ಎಲ್ಲ ಲಕ್ಷಣಗಳನ್ನೂ ನಿರ್ದೇಶಕ ಜ್ಯಾಮಿತಿಯ ಸಹಾಯದಿಂದ ಅಭ್ಯಸಿಸಬಹುದು.
ಯೂಕ್ಲಿಡ್ನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿ ಮತ್ತು ಅಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯ ಉದ್ಭವ
[ಬದಲಾಯಿಸಿ]ಗ್ರೀಕರಿಗೆ ಜ್ಯಾಮಿತಿ ಮನುಷ್ಯನ ಸಾಮಾನ್ಯ ಅನುಭವಗಳಿಂದ ಉದ್ಭವಿಸಿದ ಶಾಸ್ತ್ರವಾಗಿತ್ತು ಮತ್ತು ಜ್ಯಾಮಿತಿಯಲ್ಲಿನ ಯಾವುದೇ ಉಕ್ತಿಯ ಸತ್ಯತೆಯನ್ನು ಇದೇ ರೀತಿಯ ಅನುಭವಗಳಿಂದ ಸ್ಟಷ್ಟೀಕರಿಸಬೇಕಾಗಿತ್ತು. ಅಂದರೆ ಜ್ಯಾಮಿತಿ ಒಂದು ಸ್ವತಂತ್ರ ಶಾಸ್ತ್ರವಾಗಿರದೆ ಅದು ಮನುಷ್ಯನ ಅನುಭವಗಳನ್ನು ಬಹಳಷ್ಟು ಅವಲಂಬಿಸಿತ್ತು. ಈ ರೀತಿಯ ಪರಿಕಲ್ಪನೆ 18ನೆಯ ಶತಮಾನದವರೆಗೂ ನಡೆದುಬಂದಿತ್ತು. ಆ ಶತಮಾನದ ಕೊನೆಯ ಮತ್ತು 19ನೆಯ ಶತಮಾನದ ಆದಿಯ ಕೆಲವು ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರು ಜ್ಯಾಮಿತಿ ತನ್ನದೇ ಆದ ಒಂದು ಚೌಕಟ್ಟಿನಲ್ಲಿ ಮಾನವನ ಅನುಭವಗಳಿಂದ ಸ್ವತಂತ್ರವಾಗಿ ಇರಬಲ್ಲುದು ಎನ್ನುವ ಚಿಂತನೆಗೆ ದಾರಿ ಮಾಡಿಕೊಟ್ಟರು. ಇಂದು ಬಳಕೆಯಲ್ಲಿರುವ ನಾನಾರೀತಿಯ ಆಕಾಶಗಳು (ಸ್ಪೇಸಸ್) ಈ ಧಾಟಿಯ ಚಿಂತನೆಯ ಫಲವಾಗಿ ಜನಿಸಿದವುಗಳು. ಯೂಕ್ಲಿಡ್ ತನ್ನ ಜ್ಯಾಮಿತಿಗೆ ತಳಪಾಯವಾಗಿ ಐದು ಆದ್ಯುಕ್ತಿಗಳನ್ನು ಮತ್ತು ಐದು ಮೂಲ ಗ್ರಹಿಕೆಗಳನ್ನು ಸ್ವೀಕರಿಸಿದ್ದನಷ್ಟೆ. ಐದನೆಯ ಆದ್ಯುಕ್ತಿ ಇತರ ಆದ್ಯುಕ್ತಿಗಳಿಗಿಂತ ಮಹತ್ತರವಾದ ಸ್ಥಾನವನ್ನು ಗಳಿಸಿಕೊಂಡಿದೆ. ಏಕೆಂದರೆ ಈ ಆದ್ಯುಕ್ತಿ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರ ಚಿಂತನೆಯ ಮಾರ್ಗವನ್ನೇ ಬದಲಾಯಿಸಿತು. ಒಂದು ದತ್ತ ಸರಳ ರೇಖೆಯ ಮೇಲಿರದ ಒಂದು ದತ್ತಬಿಂದುವಿನ ಮೂಲಕ ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಸರಳ ರೇಖೆಗಳನ್ನು ದತ್ತ ಸರಳರೇಖೆಗೆ ಸಮಾಂತರವಾಗಿರುವಂತೆ ಎಳೆಯಲು ಸಾಧ್ಯವಿಲ್ಲ. ಇದು ಯೂಕ್ಲಿಡನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯ ಆಧುನಿಕ ರೂಪ.[೨೬] ಇಲ್ಲಿ ಒಂದು ಸಮಸ್ಯೆ ಹುಟ್ಟುತ್ತದೆ-ದತ್ತ ಬಿಂದುವಿನ ಮೂಲಕ ಎಳೆದ ಸರಳರೇಖೆ ದತ್ತ ಸರಳರೇಖೆಗೆ ಸಮಾಂತರವಾಗಿದೆ ಎಂದು ತಿಳಿಯುವ ಬಗೆ ಯಾವುದು? ಇದನ್ನು ಪರಿಹರಿಸಲು ಈ ಎರಡು ಸರಳರೇಖೆಗಳನ್ನು ಎರಡು ದಿಶೆಗಳಲ್ಲಿಯೂ ಅನಂತವಾಗಿ ವೃದ್ಧಿಸಬೇಕು. ಇವು ಒಂದನ್ನೊಂದನ್ನು ಛೇದಿಸದಿದ್ದರೆ ಆಗ ಅವು ಸಮಾಂತರವಾಗಿವೆ ಎಂದು ಹೇಳಬಹುದು. ಆದರೆ ಇದು ಪ್ರಯೋಗಾತೀತ. ಇದನ್ನು ಪರಿಹರಿಸುವ ಸಲುವಾಗಿ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯನ್ನು ಒಂದು ಪ್ರಮೇಯವೆಂದು ಪರಿಗಣಿಸಿ ಇನ್ನುಳಿದ ಆದ್ಯುಕ್ತಿಗಳು ಮತ್ತು ಮೂಲ ಉಕ್ತಿಗಳ ಸಹಾಯದಿಂದ ಅದಕ್ಕೆ ಸಾಧನೆಯನ್ನು ಒದಗಿಸುವ ಮಾರ್ಗದಲ್ಲಿ ಚಿಂತನೆ ಮಾಡಲು 18ನೆಯ ಶತಮಾನದ ಕೊನೆಯ ಮತ್ತು 19ನೆಯ ಶತಮಾನದ ಆದಿಯ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರು ಪ್ರಾರಂಭಿಸಿದರು. ಬಹಳಷ್ಟು ಸಾಧನೆಗಳೂ ಬಂದವು. ಆದರೆ ಅವೆಲ್ಲವೂ ಒಂದಲ್ಲ ಒಂದು ಅಪ್ರಕಟಿತ ಉಕ್ತಿಯನ್ನು ಸಮರ್ಥನೆ ಇಲ್ಲದೆ ಬಳಸಿಕೊಂಡಿರುತ್ತಿದ್ದವು. ಹೀಗೆ ಬಳಸಿಕೊಂಡಂಥ ಉಕ್ತಿಗಳಿಗೆ ಸಾಧನೆಗಳನ್ನು ಒದಗಿಸುವುದು ಐದನೆಯ ಆದ್ಯುಕ್ತಿಗೆ ಸಾಧನೆಯನ್ನು ಸೃಷ್ಟಿಸುವಷ್ಟೇ ಕಷ್ಟವಾಗಿರುತ್ತಿತ್ತು. ಸಮಾಂತರ ಸರಳರೇಖೆಗಳ ಸಿದ್ಧಾಂತ 19 ನೆಯ ಶತಮಾನದ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರ ಒಂದು ಪ್ರಮುಖ ಸಮಸ್ಯೆಯಾಗಿ ಗೌಸ್, ಲಗ್ರಾಂಜ್, ಡಾಲಂಬರ್ಟ, ಲಝಾಂಡರ್ ಇನ್ನೂ ಮುಂತಾದ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರನ್ನು ಆಕರ್ಷಿಸಿತು. ಆದರೂ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಗೆ ಸಮರ್ಪಕ ಸಾಧನೆ ಮಾತ್ರ ದೊರೆಯಲೇ ಇಲ್ಲ. ಆ ಬಳಿಕ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರು ಸಾಧನೆಯ ದೃಷ್ಟಿಯ ಕಡೆಗಿದ್ದ ತಮ್ಮ ಗಮನವನ್ನು ಸಮಸ್ಯೆಯ ನಿರೂಪಣೆ ಸರಿಯಾಗಿದೆಯೇ ಇಲ್ಲವೇ ಎನ್ನುವುದನ್ನು ತಿಳಿಯಲು ಹರಿಯಬಿಟ್ಟರು. ಈ ರೀತಿಯ ಚಿಂತನೆಯಲ್ಲಿ ಪ್ರಮುಖ ಪಾತ್ರ ವಹಿಸಿದವರು ಗೌಸ್, ಶ್ವೈಕಾರ್ಟ್ ಮತ್ತು ಟೌರಿನಸ್. ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯನ್ನು ಗೌಸ್ ಪೂರ್ತಿಯಾಗಿ ಕೈಬಿಟ್ಟು ಅದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿರುವಂತೆ ಕೆಲವು ಪ್ರಮೇಯಗಳನ್ನು ಸೃಷ್ಟಿಸಿ ಯಾವ ಕಾರಣಕ್ಕೋ ಏನೋ ಗುಪ್ತವಾಗಿರಿಸಿದ್ದ.[೨೭][೨೮] ಆದರೆ ಟೌರಿನಸ್ ಮಾತ್ರ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯ ಅಸತ್ಯತೆಯನ್ನು ಅವಲಂಬಿಸಿದ ಹೊಸ ಜ್ಯಾಮಿತಿಯನ್ನು ಸೃಷ್ಟಿಸಲು ಪ್ರಯತ್ನ ಪಟ್ಟು ಅದು ಅಸಾಧ್ಯವೆಂದು ತಪ್ಪಾಗಿ ತಿಳಿದ. ಅಂದರೆ ಇವರ್ಯಾರೂ ಸಮಸ್ಯೆಯನ್ನು ಬಿಡಿಸಲಿಲ್ಲ. ಆದರೆ ಲೊಬಾಚಿವ್ಸ್ಕಿ (1793-1856) ಮಾತ್ರ ಈ ಸಮಸ್ಯೆಯನ್ನು ಒಂದು ನೂತನ ಧಾಟಿಯಲ್ಲಿ ವೀಕ್ಷಿಸಿ ಅದನ್ನು ಬಿಡಿಸುವುದಲ್ಲದೆ ಜ್ಯಾಮಿತಿ ಮತ್ತು ಗಣಿತಶಾಸ್ತ್ರದ ಇತರ ವಿಭಾಗಗಳ ಬಗ್ಗೆ ಇದ್ದ ಪರಿಕಲ್ಪನೆಯನ್ನೇ ಬದಲಾಯಿಸಿದ.[೨೯] ಯೂಕ್ಲಿಡನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಗೆ ವಿರುದ್ಧ ಆಗುವಂತೆ, ಒಂದು ದತ್ತ ಸರಳರೇಖೆಯ ಮೇಲಿಂದ ಒಂದು ದತ್ತ ಬಿಂದುವಿನ ಮೂಲಕ ಕಡೆಯ ಪಕ್ಷ ಎರಡು ಸರಳರೇಖೆಯನ್ನು ದತ್ತ ಸರಳರೇಖೆಗೆ ಸಮಾಂತರವಾಗಿರುವಂತೆ ಎಳೆಯಬಹುದೆಂಬ ಆದ್ಯುಕ್ತಿಯನ್ನು ಊಹಿಸಿಕೊಂಡ. ಈ ಹೊಸ ಆದ್ಯುಕ್ತಿ ಒಂದು ವೇಳೆ ಜ್ಯಾಮಿತಿಯ ಇತರ ಉಕ್ತಿಗಳೊಂದಿಗೆ ಹೊಂದಿಕೊಳ್ಳದಿದ್ದರೆ ಅಸಂಬಂಧವಾದ ಉಕ್ತಿಗಳನ್ನು ಸೃಷ್ಟಿಸಲು ಸಾಧ್ಯವಾಗಬೇಕು. ಈ ಅಸಂಬದ್ಧತೆಗಳ ಸೃಷ್ಟಿ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಗೆ ವಿರುದ್ಧವಾಗಿರುವ ಲೊಬಾಚೆವ್ಸ್ಕಿಯ ಹೊಸ ಆದ್ಯುಕ್ತಿಯ ಅಸ್ತಿತ್ವವನ್ನು ಅಳಿಸಿಹಾಕುವುದರ ಮೂಲಕ ಪರೋಕ್ಷವಾಗಿ ಯೂಕ್ಲಿಡ್ನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯನ್ನು ಸ್ಥಾಪಿಸುತ್ತದೆ. ಆದರೆ ಲೊಬಾಚೆವ್ಸ್ಕಿ ಎಣಿಸಿದಂತೆ ಯಾವ ರೀತಿಯ ಅಸಂಬದ್ಧತೆಗಳು ಜನಿಸಲಿಲ್ಲ. ಆದ್ದರಿಂದ ಆತ ಎರಡು ರೀತಿಯ ನಿರ್ಣಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬೇಕಾಯಿತು:
- ಯೂಕ್ಲಿಡನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ (ನಾಟ್ ಪ್ರೂವೆಬಲ್),
- ಐದನೆಯ ಆದ್ಯುಕ್ತಿಗೆ ವಿರುದ್ಧವಾದ ಒಂದು ಆದ್ಯುಕ್ತಿಯನ್ನು ಜ್ಯಾಮಿತಿಯ ಮೂಲ ಉಕ್ತಿಗಳೊಂದಿಗೆ ಬಳಸಿಕೊಂಡು ಹೊಸ ರೀತಿಯ ಸುಸಂಬದ್ಧವಾದ ಕೆಲವು ಉಕ್ತಿಗಳನ್ನು ಸೃಷ್ಟಿಸಬಹುದು.
ಈ ಹೊಸ ಉಕ್ತಿಗಳ ಜನನಕ್ಕೆ ನೈಜವಾದ ಒಂದು ಅರ್ಥವನ್ನು ಒದಗಿಸಲು ಆತ ಅಸಮರ್ಥನಾಗಿದ್ದರಿಂದ ಅವನ್ನು ಕಾಲ್ಪನಿಕ ಎಂದು ಪರಿಗಣಿಸಿದ್ದ. ಆದರೆ ಈ ಹೊಸ ಕಾಲ್ಪನಿಕ ಉಕ್ತಿಗಳಿಂದ ಪ್ರಾರಂಭವಾದ ಜ್ಯಾಮಿತಿಯೇ ಇಂದು ಬಳಕೆಯಲ್ಲಿರುವ ಅಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿ. ಯೂಕ್ಲಿಡನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಗೆ ಹೊಸ ರೀತಿಯ ಜ್ಯಾಮಿತಿಯ ಸೃಷ್ಟಿಗೆ ಕಾರಣವಾಯಿತು.

ಕೇವಲ ಪ್ರಮೇಯಗಳ ಸೃಷ್ಟಿ ಅಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯ ಇರುವಿಕೆಗೆ ಬುನಾದಿ ಆಗುವುದಿಲ್ಲ. ಈ ಪ್ರಮೇಯಗಳನ್ನು ಒಳಗೊಳ್ಳುವಂಥ ಜ್ಯಾಮಿತೀಯ ಪ್ರಪಂಚ ಅಥವಾ ಪ್ರತಿರೂಪಗಳನ್ನೂ (ಮೋಡೆಲ್ಸ್) ಒದಗಿಸಬೇಕಾಗುತ್ತದೆ. ಫೆಲಿಕ್ಸ್ ಕ್ಲೈನ್ ಮತ್ತು ಹೆನ್ರಿ ಪಾನ್ಕ್ವಾರೆಯವರು (1854-1912) ಇಂಥ ಎರಡು ಪ್ರತಿರೂಪಗಳನ್ನು ಸೃಷ್ಟಿಸಿದರು. ಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯ ವಸ್ತುಗಳನ್ನು ತೆಗೆದುಕೊಂಡು ಅವನ್ನು ಅಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತೀಯ ಅಸ್ತಿತ್ವಕ್ಕೆ ಸೂಕ್ತವಾಗುವಂತೆ ಹೊಸದಾಗಿ ನಿರೂಪಿಸಿದರು. ಕ್ಲೈನ್ ಮಾದರಿಯಲ್ಲಿ ತಲ ಒಂದು ಯೂಕ್ಲಿಡೀಯ ವೃತ್ತದ ಅಭ್ಯಂತರ ಭಾಗ (ಇಂಟೀರಿಯರ್) ಎಂದು ಆಗಿದೆ. ವೃತ್ತದ ಒಳಗಿನ ಪ್ರತಿಯೊಂದು ಬಿಂದುವನ್ನೂ ಅಯೂಕ್ಲಿಡೀಯ ಬಿಂದು ಎಂದೂ, ಪ್ರತಿಯೊಂದು ಜ್ಯಾ ಅಯೂಕ್ಲಿಡೀಯ ಸರಳರೇಖೆ ಎಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ.
ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವುದು ಮತ್ತು ಅಯೂಕ್ಲಿಡೀಯ ಸರಳರೇಖೆಗಳ ಪರಸ್ಪರ ಛೇದನೆ ಇವು ಕ್ಲೈನ್ ಪ್ರತಿರೂಪದಲ್ಲಿ ಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯ ಧಾಟಿಯಲ್ಲೇ ಇವೆ. ಈ ಪ್ರತಿರೂಪ ಯೂಕ್ಲಿಡನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯನ್ನುಳಿದು ಇವೆಲ್ಲವನ್ನೂ ಒಳಗೊಂಡಿರುತ್ತದೆ ಎಂದು ತೋರಿಸಬಹುದು. ಪಾನ್ಕ್ವಾರೆ ಪ್ರತಿರೂಪದಲ್ಲೂ ತಲ ಒಂದು ಯೂಕ್ಲಿಡೀಯ ವೃತ್ತ C ಯ ಅಭ್ಯಂತರ ಭಾಗವಾಗಿದೆ. C ಮತ್ತು C' ಎರಡನೆಯ ಲಂಬಕೋನೀಯ ವೃತ್ತಗಳು (ಆರ್ಥಾಗನಲ್ ಸರ್ಕಲ್ಸ್); R ಮತ್ತು S ಅವುಗಳ ಛೇದನ ಬಿಂದುಗಳು. ಈ ಪ್ರತಿರೂಪದಲ್ಲಿ ಅಯೂಕ್ಲಿಡೀಯ ಬಿಂದುಗಳು ಅ ವೃತ್ತದ ಅಭ್ಯಂತರ ಭಾಗದ ಯೂಕ್ಲಿಡೀಯ ಬಿಂದುಗಳಾಗಿವೆ. ಅ ವೃತ್ತದ ಅಭ್ಯಂತರ ಭಾಗ ಮತ್ತು C' ರೀತಿಯ ಯಾವುದಾದರೂ ವೃತ್ತ ಇವೆರಡರ ಛೇದನವನ್ನು ಯೂಕ್ಲಿಡೀಯ ಸರಳರೇಖೆ ಎಂದು ಪರಿಗಣಿಸಿದೆ. ಈ ಪ್ರತಿರೂಪ ಯೂಕ್ಲಿಡನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯನ್ನು ಉಳಿದು ಇನ್ನೆಲ್ಲವನ್ನೂ ಒಳಗೊಂಡಿದೆ ಎಂದು ತೋರಿಸಬಹುದು. ಲೊಬಾಚೆವ್ಸ್ಕಿಯ ಈ ಜ್ಯಾಮಿತಿಗೆ ಹೈಪರ್ಬೋಲಿಕ್ ಜ್ಯಾಮಿತಿ ಎಂದು ಹೆಸರು. ರೀಮಾನ್ ಕೂಡ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಗೆ ಬದಲಾಗಿ ಒಂದೇ ತಲದಲ್ಲಿರುವ ಯಾವ ಎರಡು ಸರಳರೇಖೆಗಳೂ ಸಮಾಂತರವಾಗಿರುವುದಿಲ್ಲ ಎಂದು ಇಟ್ಟುಕೊಂಡು ಬೇರೊಂದು ಅಯೂಕ್ಲಿಡೀಯ ಜ್ಯಾಮಿತಿಯನ್ನು ಸೃಷ್ಟಿಸಿದ. ಇದಕ್ಕೆ ಎಲಿಪ್ಟಿಕ್ ಅಥವಾ ರೀಮಾನಿಯನ್ ಜ್ಯಾಮಿತಿ ಎಂದು ಹೆಸರು.
ವಿಶ್ಲೇಷಣೆ
[ಬದಲಾಯಿಸಿ]ಅನಂತ ಕ್ರಿಯೆ ಅಥವಾ ಪರಿಮಿತಿಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ್ದುದನ್ನು ವಿಶ್ಲೇಷಿಸುವ ಗಣಿತಶಾಸ್ತ್ರದ ಶಾಖೆಯೇ ವಿಶ್ಲೇಷಣೆ (ಅನಾಲಿಸಿಸ್).[೩೦][೩೧] ಇದರ ಉಗಮ ಪರೋಕ್ಷವಾಗಿ ಆರ್ಕಿಮಿಡೀಸ್ ಮತ್ತು ಯುಡೋಕ್ಸಸ್ ಅವರ ಕಾಲದಲ್ಲಿಯೇ ಆಗಿತ್ತು. ಅನಂತರ ಬಹಳಷ್ಟು ಮಂದಿ ಅದರ ಬಗ್ಗೆ ಚಿಂತನೆ ಮಾಡಿದರೂ ಅದು ಒಂದು ನಿರ್ದಿಷ್ಟ ರೂಪಕ್ಕೆ ಬಂದದ್ದು 19ನೆಯ ಶತಮಾನದಲ್ಲಿಯೇ. ವಿಶ್ಲೇಷಣೆಯಲ್ಲಿ ಉತ್ಪನ್ನ (ಫಂಕ್ಷನ್) ಬಹು ಮುಖ್ಯಪಾತ್ರವನ್ನು ವಹಿಸುತ್ತದೆ.
A ಮತ್ತು B ಎರಡು ಗಣಗಳಾಗಿರಲಿ. x, A ಯ ಒಂದು ಧಾತುವನ್ನೂ, y, B ಯ ಒಂದು ಧಾತುವನ್ನೂ ಸೂಚಿಸಲಿ. ಪ್ರತಿಯೊಂದು x ∈ A ಗೆ ಗೊತ್ತಾದ ಒಂದು y ∈ B ಯನ್ನು ನಿಗದಿಮಾಡಲು ಸಾಧ್ಯವಾದರೆ ಆಗ A ಯಿಂದ B ಗೆ ಒಂದು ಉತ್ಪನ್ನ ಇದೆ ಎಂದು ಹೇಳುತ್ತೇವೆ.[೩೨] ಈ ಪರಿಕಲ್ಪನೆಗೆ ಬಹಳಷ್ಟು ಹತ್ತಿರ ಬರುವಂತೆ ಪಿ.ಜಿ.ಎಲ್.ಡೀರಿಕ್ಲೇ (1805-1859) ಎಂಬಾತ ಉತ್ಪನ್ನವನ್ನು ಹೀಗೆ ನಿರೂಪಿಸುತ್ತಾನೆ: x ಮತ್ತು y ಗಳು ಎರಡು ಚರಗಳು; x ಗೆ ಒಂದು ಸಂಖ್ಯಾಬೆಲೆಯನ್ನು ಆದೇಶಿಸಿದಾಗ y ಯ ಬೆಲೆಯನ್ನು ಏಕೈಕವಾಗಿ ನಿರ್ಧರಿಸುವ x ನ್ನು ಒಳಗೊಂಡ ಒಂದು ಸೂತ್ರವಿದ್ದರೆ ಆಗ y ಯು x ಎಂಬ ಸ್ವತಂತ್ರ ಚರದ ಉತ್ಪನ್ನವಾಗಿರುತ್ತದೆ.[೩೩] ಡೀರಿಕಲೇಯ ಈ ಕೆಳಗಿನ ಉದಾಹರಣೆಯಿಂದ y ಯ ಬೆಲೆಯನ್ನು ನಿರ್ಧರಿಸುವ ಸೂತ್ರ ಯಾವುದೇ ಅಭಿಜಾತ (ಕ್ಲ್ಯಾಸಿಕಲ್) ಸೂತ್ರೀಕರಣಕ್ಕೂ ಒಳಪಡಬೇಕಾಗಿಲ್ಲ ಎನ್ನುವುದು ಅರಿವಾಗುತ್ತದೆ. x ಪರಿಮೇಯ ಆಗಿದ್ದರೆ y=c ಆಗಿರಲಿ; ಮತ್ತು x ಅಪರಿಮೇಯ ಆಗಿದ್ದರೆ y=d≠c ಆಗಿರಲಿ. c ಮತ್ತು d ಗಳು ಎರಡು ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಗಳು. ಸಂಖ್ಯಾಸಿದ್ಧಾಂತ ಸಾಮಾನ್ಯವಾಗಿ ಪರಿಮೇಯಗಳ ಚರ್ಚೆಯನ್ನು ಮಾಡುತ್ತದೆ. ಪರಿಮೇಯ ax+b = 0 ಎಂಬ ಸಮೀಕರಣದ ಮೂಲ ಆಗಿರುತ್ತದೆ. ಇಲ್ಲಿ a,b ಪೂರ್ಣಾಂಕಗಳು. ನೈಜ ವಿಶ್ಲೇಷಣೆ (ರಿಯಲ್ ಅನಾಲಿಸಿಸ್) ಪರಿಮೇಯ ಮತ್ತು ಅಪರಿಮೇಯ ಎರಡರೊಂದಿಗೆ ವ್ಯವಹರಿಸುತ್ತದೆ. ax2+bx+c = 0 (a,b ಮತ್ತು c ಗಳು ಪೂರ್ಣಾಂಕಗಳು) ಎಂಬ ಸಮೀಕರಣದ ಮೂಲಗಳಿಗೆ ಯೂಕ್ಲಿಡೀಯ ಸಲಕರಣೆಗಳಿಂದ (ನೇರ ಅಂಚು ಮತ್ತು ಕೈವಾರ) ಜ್ಯಾಮಿತೀಯ ಸಮಾನಗಳನ್ನೂ ಕೊಡಬಹುದು. ಆದರೆ ಸಮೀಕರಣದ ಡಿಗ್ರಿ ಎರಡಕ್ಕಿಂತ ಹೆಚ್ಚಾದರೆ ಈ ಸಲಕರಣೆಗಳಿಂದ ಮೂಲಗಳಿಗೆ ಜ್ಯಾಮಿತಿಯ ಸಮಾನಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ. ಪರಿಮೇಯ ಗುಣಾಂಕಗಳುಳ್ಳ (ಕೋಎಫಿಶೆಂಟ್ಸ್) ಯಾವುದೇ ಬೀಜಗಣಿತದ ಸಮೀಕರಣದ (ಆಲ್ಜಿಬ್ರೇಕ್ ಇಕ್ವೇಷನ್) ಮೂಲಗಳಿಗೆ ಬೀಜಗಣಿತೀಯ ಸಂಖ್ಯೆಗಳು; ಆದರೆ ಎಲ್ಲ ಪರಿಮೇಯಗಳೂ ಬೀಜಗಣಿತದ ಸಂಖ್ಯೆಗಳಲ್ಲ ಏಕೆಂದರೆ π ಮತ್ತು e ಗಳು ಎರಡು ಅಪರಿಮೇಯಗಳು; ಇವು ಬೀಜಗಣಿತದ ಸಂಖ್ಯೆಗಳಲ್ಲ ಎಂದು ಸಾಧಿಸಬಹುದು. ಬೀಜಗಣಿತೀಯ ಅಲ್ಲದ ಅಪರಿಮೇಯ ಸಂಖ್ಯೆಗಳಿಗೆ ಬೀಜಾತೀತ (ಟ್ರಾನ್ಸೆಂಡೆಂಟಲ್) ಸಂಖ್ಯೆಗಳೆಂದು ಹೆಸರು.[೩೪][೩೫] eπ, πe, π+e ಮತ್ತು πe ಗಳಲ್ಲಿ eπ ಮಾತ್ರ ಬೀಜಾತೀತ ಎಂದು ಸಾಧಿಸಲು ಸಾಧ್ಯವಾಗಿದೆ. ಇನ್ನುಳಿದ ಮೂರರ ಸ್ವರೂಪ ಇನ್ನೂ ನಿರ್ಧರಿತವಾಗಿಲ್ಲ. πe ಮತ್ತು π+e ಗಳಲ್ಲಿ ಕೊನೆಯ ಪಕ್ಷ ಯಾವುದಾದರೂ ಒಂದು ಬೀಜಾತೀತ ಎಂದು x2-(π+e)x+πe = 0 ಎಂಬ ಸಮೀಕರಣದ ಸಹಾಯದಿಂದ ಸುಲಭವಾಗಿ ನಿರ್ಧರಿಸಬಹುದು. ಆದರೆ πe ಮತ್ತು π+e ಗಳಲ್ಲಿ ಯಾವೊಂದು ಅಥವಾ ಎರಡೂ ಬೀಜಾತೀತ ಎಂದು ತೋರಿಸುವುದು ಸಾಧ್ಯವಾಗದೆ ಹಾಗೆಯೇ ಇಂದು ಉಳಿದಿದೆ.
ಗಣಿತಶಾಸ್ತ್ರದ ಶೈಶವಾವಸ್ಥೆಯಲ್ಲಿ ಕಲನಶಾಸ್ತ್ರ ಮತ್ತು ವಿಶ್ಲೇಷಣೆ ಎರಡೂ ಒಂದೇ ಆಗಿ ಕಾಣುತ್ತಿದ್ದವು. ಕಲನಶಾಸ್ತ್ರಕ್ಕೂ ಜ್ಯಾಮಿತಿಗೂ ಇದ್ದ ನಿಕಟ ಸಂಬಂಧವನ್ನು ಬೇರ್ಪಡಿಸಿ ಕಲನಶಾಸ್ತ್ರವು ನೈಜಸಂಖ್ಯೆಗಳನ್ನು ಅವಲಂಬಿಸಿರುವಂತೆ ಮಾರ್ಪಾಡು ಮಾಡಲು ಹೊರಟಾಗ ಕಲನಶಾಸ್ತ್ರ ವಿಶ್ಲೇಷಣೆಯ ಒಂದು ಅಂಗ ಮಾತ್ರ ಎಂದು ಗೋಚರವಾಯಿತು.
ಈ ದಿಶೆಯಲ್ಲಿ ಕೆಲಸ ಮಾಡಿದ ಪ್ರಮುಖರು ಕಾರ್ಲ್ ವೈರ್ಸ್ಟ್ರಾಸ್ (1815-1897), ಬಾರ್ನರ್ಡ್ ಬೊಲ್ಜನೋ (1781-1848) ಮುಂತಾದವರು.
ನೈಜಸಂಖ್ಯೆಗಳ ನಿರೂಪಣೆ
[ಬದಲಾಯಿಸಿ]ಮೊಟ್ಟಮೊದಲು ನೈಜಸಂಖ್ಯೆಗಳ ಸರಿಯಾದ ನಿರೂಪಣೆಯ ಆವಶ್ಯಕತೆ ಇತ್ತು. ಈ ಕೊರತೆಯನ್ನು ತುಂಬಿದವ ಜೆ. ಡಬ್ಲ್ಯು. ಆರ್. ಡೆಡಿಕೆಂಟ್ (1831-1916). ಈತನ ಹೆಸರಿನ ವಿಭಜನೆಗಳು ನೈಜಸಂಖ್ಯೆಗಳನ್ನು ನಿರೂಪಿಸುತ್ತವೆ.[೩೬] ಡೆಡಿಕೆಂಟ್ ವಿಭಜನೆಗಳಿಗೆ ಸಮವಾದ ಮತ್ತು ಅದಕ್ಕಿಂತ ಸುಲಭರೂಪದ ರಸಲ್ನ ನಿರೂಪಣೆ ಈ ರೀತಿ ಇದೆ: ಪರಿಮೇಯ ಸಂಖ್ಯೆಗಳ ಗಣ R ನ ನೀಚಖಂಡ (ಲೋಯರ್ ಸೆಗ್ಮೆಂಟ್) ಈ ಕೆಳಗೆ ನಮೂದಿಸಿರುವ ಲಕ್ಷಣಗಳಿರುವ L ಗಣ ಎಂದು ತಿಳಿಯೋಣ:
- L ಅಶೂನ್ಯ ಗಣ
- x ∈ L ಮತ್ತು y<x ಆಗಿದ್ದರೆ y ಕೂಡ L ನಲ್ಲಿ ಇರುತ್ತದೆ.
- x ∈ L ಆದಾಗ z > x ಮತ್ತು z ∈ L ಆಗುವಂತೆ ಮತ್ತೊಂದು x ನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು.
ಇದೇ ರೀತಿ ಉಚ್ಚಖಂಡ (ಅಪ್ಪರ್ ಸೆಗ್ಮೆಂಟ್) U ನ ಲಕ್ಷಣಗಳು ಇಂತಿವೆ:
- U ಅಶೂನ್ಯ ಗಣ.
- x ∈ U ಮತ್ತು y > x ಆಗಿದ್ದರೆ y ಕೂಡ U ನಲ್ಲಿ ಇರುತ್ತದೆ.
- x ∈ U ಆದಾಗ z < x ಮತ್ತು z ∈ L ಆಗುವಂತೆ ಮತ್ತೊಂದು z ನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು.
ಇಂಥ ಖಂಡಗಳು ನೈಜಸಂಖ್ಯೆಗಳನ್ನು ನಿರ್ಧರಿಸುತ್ತವೆ.
ಉದಾಹರಣೆಗೆ: 1. U = {x | x >2} ಎನ್ನುವ ಉಚ್ಚಖಂಡ 2 ಎಂಬ ನೈಜಸಂಖ್ಯೆಗಳನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ.
2. U = {x | x2 > 2 ಮತ್ತು x > 0} ಎನ್ನುವ ಉಚ್ಚಖಂಡ ಎಂಬ ನೈಜಸಂಖ್ಯೆಯನ್ನು (ಅಪರಿಮೇಯ) ನಿರ್ಧರಿಸುತ್ತದೆ.
ನೈಜಸಂಖ್ಯೆಯ ಈ ನಿರೂಪಣೆಯಲ್ಲಿ ಕೂಡಿಸುವುದು ಗುಣಿಸುವುದು ಮುಂತಾದ ಪರಿಕರ್ಮಗಳನ್ನು ಸೂಕ್ತವಾಗಿ ನಿರೂಪಿಸಬಹುದು.
ನೈಜಸಂಖ್ಯೆಯನ್ನು ಕೌಷಿ ಲಕ್ಷಣವಿರುವ ಪರಿಮೇಯಗಳ ಒಂದು ಶ್ರೇಢಿ ಎಂದು ನಿರೂಪಿಸುವುದು ಉಂಟು. ಕೌಷಿ ಲಕ್ಷಣ ಈ ರೀತಿ ಇದೆ: (Rn) ಪರಿಮೇಯಗಳ ಒಂದು ಶ್ರೇಢಿಯಾಗಿರಲಿ. ಪ್ರತಿಯೊಂದು ε > 0 ಗೆ (ε ಪರಿಮೇಯ) m,n > N ಆದಾಗೆಲ್ಲ -ε < Rm-Rn < ε ಆಗುವಂತೆ N ನ್ನು ಗೊತ್ತುಮಾಡಲು ಸಾಧ್ಯವಾಗುವುದಾದರೆ (Rn) ಗೆ ಕೌಷಿ ಶ್ರೇಢಿ ಎಂದು ಹೆಸರು. ಈ ನಿರೂಪಣೆಯಲ್ಲೂ ಸಮತೆ ಮತ್ತು ಎಲ್ಲ ಪರಿಕರ್ಮಗಳನ್ನು ಸೂಕ್ತವಾಗಿ ನಿರೂಪಿಸಲು ಸಾಧ್ಯ.
ನೈಜಸಂಖ್ಯೆಗಳ ಹೊಸ ಪರಕಲ್ಪನೆ, ಪರಿಮಿತಿ ಮುಂತಾದ ಪರಿಕಲ್ಪನೆಗಳನ್ನು ಜ್ಯಾಮಿತಿಯ ಆಧಾರವಿಲ್ಲದೆಯೇ ವರ್ಣಿಸಲು ಅವಕಾಶ ಮಾಡಿಕೊಟ್ಟಿತು. ಈ ತಳಹದಿಯ ಮೇಲೆ ವಿಶ್ಲೇಷಣೆ ಬೆಳೆಯುತ್ತ ಬಂದು ಇದರಿಂದಾಗಿ ಸಮ್ಮಿಶ್ರ ಸಂಖ್ಯಾ ಚರಗಳ ವಿಶ್ಲೇಷಣೆ ಮತ್ತು ಅವಕಲನ ಸಮೀಕರಣ ಸಿದ್ಧಾಂತ ಇವು ಹುಟ್ಟಿಕೊಂಡವು. ಇಂದು ಅನ್ವಯ ಗಣಿತಕ್ಕೆ ವಿಶ್ಲೇಷಣೆ ಅನಿವಾರ್ಯವಾಗಿದೆ.
ಟಾಪಾಲಜಿ
[ಬದಲಾಯಿಸಿ]19ನೆಯ ಶತಮಾನದ ಮಧ್ಯಭಾಗದಲ್ಲಿ ಜ್ಯಾಮಿತಿಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಒಂದು ಹೊಸಬಗೆಯ ಬೆಳೆವಣಿಗೆ ಅಂಕುರಿಸಿತು. ಇದು ಜ್ಯಾಮಿತಿಯಿಂದ ಸ್ವತಂತ್ರವಾಗಿ ನಿಂತು ಟಾಪಾಲಜಿ ಎಂಬ ಹೆಸರಿನಿಂದ ಗಣಿತಶಾಸ್ತ್ರದ ಒಂದು ಶಾಖೆಯಾಗಿ ಬೆಳೆಯುತ್ತ ಬಂದಿದೆ. ಆದ್ಯುಕ್ತಿಗಳನ್ನು ಪ್ರಾರಂಭದಲ್ಲಿ ಅವಲಂಬಿಸಲು ಇದಕ್ಕೆ ಸಾಧ್ಯವಿಲ್ಲ. ಅದಕ್ಕೆ ಬದಲು ಇದು ಮನುಷ್ಯನ ಜ್ಯಾಮಿತೀಯ ಅಂತರ್ಬೋಧೆಯನ್ನು ಬಹಳವಾಗಿ ಅವಲಂಬಿಸಿತ್ತು.
ಇದರ ಉಗಮ ಕಳೆದ ನೂರು ವರ್ಷಗಳಲ್ಲಿ ಆದಂತೆ ಅನಿಸಿದರೂ ಬಹುಫಲಕಗಳ ಭುಜಗಳು, ಶೃಂಗಗಳು ಮತ್ತು ಮುಖಗಳು ಇವುಗಳ ಪರಸ್ಪರ ಸಂಬಂಧವನ್ನು ಡೇಕಾರ್ಟೆ (1596-1650) ಮತ್ತು ಆಯ್ಲರ್ (1707-1783) ಅಭ್ಯಸಿಸಿದ್ದರಿಂದ 17 ಮತ್ತು 18ನೆಯ ಶತಮಾನದಲ್ಲಿ ಟಾಪಾಲಜಿಯ ಸುಳಿವು ಇವರಿಗೆ ಸಿಕ್ಕಿತು. ಇದರ ಕ್ಷೇತ್ರದಲ್ಲಿ ಪ್ರಮುಖನಾದ ಪಾನ್ಕ್ವಾರೆ (1854-1912) ಎಂಬಾತ ಡೇಕಾರ್ಟೆ ಮತ್ತು ಆಯ್ಲರ್ ಅವರ ಅನಿಸಿಕೆಗಳನ್ನು ಟಾಪಾಲಜಿಯ ಕೇಂದ್ರ ಪ್ರಮೇಯವನ್ನಾಗಿ ಪರಿವರ್ತಿಸಿದ್ದಾನೆ.[೩೭] ವಸ್ತುವಿನ ಒಂದು ಭಾಗಕ್ಕೂ ಅದರ ಪಕ್ಕದ ಭಾಗಕ್ಕೂ ಇರುವ ದೈಹಿಕ ಪಾರ್ಶ್ವಸಂಪರ್ಕ ವಸ್ತುವಿನ ಒಂದು ಪ್ರಮುಖ ಲಕ್ಷಣ. ಲೊಬಾಚೆವ್ಸ್ಕಿ (1793-1856) ಈ ಪಾರ್ಶ್ವಸಂಪರ್ಕವನ್ನು ಒಂದು ಜ್ಯಾಮಿತೀಯ ಲಕ್ಷಣ ಎಂದು ಪರಿಗಣಿಸಿದ್ದ; A ಮತ್ತು B ಗಳು ಒಂದಕ್ಕೊಂದು ಅಂಟಿಕೊಂಡು C ಎಂಬ ಜ್ಯಾಮಿತೀಯ ಆಕೃತಿ ಆಗಿದೆ. ವಿಲೋಮವಾಗಿ C ಎಂಬ ಆಕೃತಿಯನ್ನು ವಿಭಜಿಸಿದಾಗ A ಮತ್ತು B ಗಳೆಂಬ ಎರಡು ಭಾಗಗಳಾಗುತ್ತವೆ. C ಯನ್ನು ಒಂದೇ ಆಕೃತಿ ಎಂದು ಪರಿಗಣಿಸಿದಾಗ A ಮತ್ತು B ಗಳಿಗೆ ಪಾರ್ಶ್ವಸಂಪರ್ಕ ಇರುತ್ತದೆ. ಜ್ಯಾಮಿತೀಯ ವಸ್ತುಗಳನ್ನು ಪರಿವರ್ತನೆಗೆ ಒಳಪಡಿಸಿದಾಗ ವಸ್ತುಗಳ ಪಾರ್ಶ್ವಸಂಪರ್ಕ ನಾಶವಾಗದಿದ್ದರೆ ಆ ಪರಿವರ್ತನೆಗೆ ಅವಿಚ್ಛಿನ್ನ ಪರಿವರ್ತನೆಯೆಂದೂ, ಪಾರ್ಶ್ವಸಂಪರ್ಕಗಳು ನಾಶವಾಗದಿರುವ ಜೊತೆಗೆ ವಸ್ತುವಿನಲ್ಲಿ ಹೊಸ ಪಾರ್ಶ್ವಸಂಪರ್ಕಗಳು ಉಂಟಾಗದಿದ್ದರೆ ಅಂಥ ಪರಿವರ್ತನೆಗಳಿಗೆ ಟಾಪಾಲಜೀಯ ಪರಿವರ್ತನೆಯೆಂದೂ ಹೆಸರು. ಅಂದರೆ ಟಾಪಾಲಜೀಯ ಪರಿವರ್ತನೆಯಲ್ಲಿ ವಸ್ತುವಿನ ಭಾಗಗಳ ವಿಭಜನೆ ಅಥವಾ ಬೆಸುಗೆಗಳು ಆಗುವುದಿಲ್ಲ. ಆದ್ದರಿಂದ ಇಂಥ ಪರಿವರ್ತನೆಗಳು ಒಂದು-ಒಂದು ಸಂವಾದಿತ್ವವನ್ನು ವ್ಯಾಖ್ಯಿಸುತ್ತವೆ. ರಬ್ಬರಿನ ಒಂದು ವರ್ತುಲ ಉಂಗುರವನ್ನು ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ಅದನ್ನು ನಿತಂತರ ಪರಿವರ್ತನೆಗೆ ಗುರಿಪಡಿಸಿದಾಗ ಚಿತ್ರದಲ್ಲಿ ಕೊಟ್ಟಿರುವ ನಮೂನೆಯ ಆಕೃತಿಗಳು ದೊರೆಯುತ್ತವೆ.

ಇವುಗಳಲ್ಲಿ (d) ಯನ್ನುಳಿದು ಇನ್ನೆಲ್ಲವೂ ಟಾಪಾಲಜೀಯ ಪರಿವರ್ತನೆಗಳು. ಈ ಚಿತ್ರ ಅಡ್ಡವಿಟ್ಟ 8 ರ ಆಕಾರದಲ್ಲಿದೆ. ಇದರ ನಡುವೆ ಇರುವ ಗಂಟಿನಲ್ಲಿ ಹೊಸ ಸಂಪರ್ಕ ಏರ್ಪಟ್ಟಿದೆ. ಆದ್ದರಿಂದ ಇದು ಅವಿಚ್ಛಿನ್ನ ಪರಿವರ್ತನೆಯೇ ಹೊರತು ಟಾಪಾಲಜೀಯ ಪರಿವರ್ತನೆ ಅಲ್ಲ. ಕೆಲವು ಲಕ್ಷಣಗಳು ನಾಶವಾಗದೆ ಹಾಗೆಯೇ ಇರುತ್ತವೆ. ಇಂಥವುಗಳಿಗೆ ವಸ್ತುವಿನ ಟಾಪಾಲಜೀಯ ಲಕ್ಷಣಗಳೆಂದು ಹೆಸರು. ಉದಾಹರಣೆಗೆ ಒಂದು ವಸ್ತುವಿನಲ್ಲಿ A ಮತ್ತು B ಬಿಂದುಗಳು ಅಕ್ಕಪಕ್ಕದಲ್ಲಿದ್ದರೆ ಯಾವುದೇ ಟಾಪಾಲಜೀಯ ಪರಿವರ್ತನೆಗಳಲ್ಲಿ ಅವು ಅಕ್ಕಪಕ್ಕದಲ್ಲಿಯೇ ಇರುತ್ತವೆ.
ಹೀಗೆ A ಮತ್ತು B ಗಳ ಪರಸ್ಪರ ಅಕ್ಕಪಕ್ಕದಲ್ಲಿರುವಿಕೆ ವಸ್ತುವಿನ ಒಂದು ಟಾಪಾಲಜೀಯ ಲಕ್ಷಣ. ಹಿಟ್ಟಿನಿಂದ ಮಾಡಿದ ಒಂದು ಮಿದುವಾದ ಗೋಳವನ್ನು ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವ ಯಾವುದಾದರೂ ರೂಪಕ್ಕೆ ಈ ಗೋಳವನ್ನು ಮುರಿಯದೇ ಬದಲಾಯಿಸಬಹುದು. ಇದು ಒಂದು ಟಾಪಾಲಜೀಯ ಪರಿವರ್ತನೆಯಾಗಿದೆ. ಗೋಳವನ್ನು ಒಂದು ಘನವನ್ನಾಗಿ ಪರಿವರ್ತಿಸೋಣ. ಈಗ ಗೋಳಕ್ಕೆ ಅಂಚುಗಳಿಲ್ಲ. ಆದರೆ ಘನಕ್ಕೆ ಅಂಚುಗಳಿವೆ. ಅಂಚುಗಳಿರುವ ಅಥವಾ ಅಂಚುಗಳಿಲ್ಲದಿರುವುದು ಟಾಪಾಲಜೀಯ ಲಕ್ಷಣಗಳಲ್ಲ. ಏಕೆಂದರೆ ಪರಿವರ್ತನೆಯಲ್ಲಿ ಈ ಲಕ್ಷಣಗಳು ಬದಲಾಗಿವೆ. ಮೇಲಿನ ಯಾವುದೇ ಆಕೃತಿ ಮತ್ತು ಗೋಳ ಟಾಪಾಲಜೀಯವಾಗಿ ಸಮವಾಗಿವೆಯೆಂದು ತಿಳಿಯಬಹುದು. ಎರಡು ವಸ್ತುಗಳಲ್ಲಿ ಒಂದನ್ನು ಇನ್ನೊಂದಕ್ಕೆ ಟಾಪಾಲಜೀಯ ಪರಿವರ್ತನೆಯಿಂದ ಮಾರ್ಪಾಡು ಮಾಡಲು ಸಾಧ್ಯವಾದರೆ ಅಂಥ ವಸ್ತುಗಳು ಪರಸ್ಪರ ಹೋಮಿಯೋಮಾರ್ಫಿಕ್ ಆಗಿವೆ ಅನ್ನುತ್ತೇವೆ. ಈಗ ಒಂದು ಪ್ರಶ್ನೆ ಏಳುತ್ತದೆ: ಯಾವುದಾದರೂ ಒಂದು ವಸ್ತುವಿನ ಮೇಲ್ಮೈಗೆ ಒಂದೇ ಪಾರ್ಶ್ವ ಇರುವುದು ಸಾಧ್ಯವೇ? ಇದಕ್ಕೆ ಉತ್ತರ ಹೌದು. ಉದಾಹರಣೆಗೆ ಮೋಬಿಯಸ್ ಪಟ್ಟಿ.

ಇದೊಂದು ಆಯತಾಕಾರದ ಕಾಗದದ ಪಟ್ಟಿ ABCD. ಇದರಲ್ಲಿ D ಬಿಂದು B ಯೊಂದಿಗೆ C ಬಿಂದು A ಯೊಂದಿಗೆ ಐಕ್ಯವಾಗುವಂತೆ CD ತುದಿಯನ್ನು AB ತುದಿಯ ಮೇಲೆ ಅಂಟಿಸಬೇಕು. ಈ ಆಕೃತಿಗೆ ಒಂದೇ ಪಾರ್ಶ್ವವಿರುವ ಮೇಲ್ಮೈ ಇರುತ್ತದೆ. ಇದನ್ನು ಖಚಿತಪಡಿಸುವುದು ಬಹಳ ಸುಲಭ. ಪಟ್ಟಿಯ ಮಧ್ಯರೇಖೆಯ ಮೇಲೆ E ಯಾವುದಾದರೂ ಒಂದು ಬಿಂದು ಆಗಿರಲಿ. E ಯಿಂದ ಪ್ರಾರಂಭಿಸಿ ಮಧ್ಯರೇಖೆಯ ಮೇಲೆ ಹೋದರೆ ಕೊನೆಗೆ ಆಯತಾಕಾರದ ಪಟ್ಟಿಯ ಎರಡು ಪಾರ್ಶ್ವಗಳನ್ನೂ ಬಳಸಿಕೊಂಡು ಇನ್ನೊಂದು ಮೇಲ್ಮೈಯಲ್ಲಿ ಬಂದು ಸೇರುತ್ತವೆ. ಒಂದು ವೇಳೆ ಮೋಬಿಯಸ್ ಪಟ್ಟಿಗೆ ದ್ವಿಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ಇದ್ದಿದ್ದರೆ E ಬಿಂದುವನ್ನೂ ಅದು ಇರುವ ಪಾರ್ಶ್ವದಲ್ಲಿಯೇ ತಲುಪಬೇಕಾಗಿದ್ದಿತು.
ಇದೇ ರೀತಿ ಏಕಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ಇರುವುದರೊಂದಿಗೆ ಸಂವೃತ ಸಹ ಆಗಿರುವ ಆಕೃತಿಗೆ ಕ್ಲೈನ್ ಕುಪ್ಪಿ ಒಂದು ಉದಾಹರಣೆ ಆಗಿದೆ. ಎರಡು ಮೋಬಿಯಸ್ ಪಟ್ಟಿಗಳ ಭುಜಗಳನ್ನು ಒಂದಕ್ಕೊಂದು ಅಂಟಿಸುವುದರಿಂದ ಏರ್ಪಡುವ ಆಕೃತಿಯೇ ಕ್ಲೈನ್ ಕುಪ್ಪಿ.

ಬೀಜಗಣಿತ
[ಬದಲಾಯಿಸಿ]19ನೆಯ ಶತಮಾನ ಗಣಿತಶಾಸ್ತ್ರದ ಇತಹಾಸದಲ್ಲಿ ಒಂದು ಮಹತ್ತರವಾದ ಕಾಲ. ಈ ಶತಮಾನದಲ್ಲಿ ಚಿಂತನೆಯ ಚೌಕಟ್ಟು ಲಭಿಸಿತಲ್ಲದೆ ಆ ಶಾಸ್ತ್ರದ ಪ್ರತಿಯೊಂದು ಶಾಖೆಯಲ್ಲಿಯೂ ಅತೀವವಾದ ಬೆಳೆವಣಿಗೆ ಉಂಟಾಯಿತು. ಒಟ್ಟಿನಲ್ಲಿ ಗಣಿತಶಾಸ್ತ್ರ ಈ ಕಾಲದಲ್ಲಿ ಒಂದು ಆರೋಗ್ಯಕರವಾದ ಪ್ರೌಢಿಮೆಯನ್ನು ಗಳಿಸಿ ವಿವಿಧ ಶಾಖೆಗಳಲ್ಲಿ ತನ್ನ ಮುಂದಿನ ಗತಿಯನ್ನು ನಿರ್ಧರಿಸಿಕೊಂಡಿತು. 19ನೆಯ ಶತಮಾನ ಬೀಜಗಣಿತದ (ಮಾಡರ್ನ್ ಆಲ್ಜಿಬ್ರ) ಶತಮಾನ ಎಂದು ಕರೆಯುವ ವಾಡಿಕೆ ಇತ್ತು. ಆಧುನಿಕ ಬೀಜಗಣಿತದ ಅಂಗವಾಗಿ ಅಮೂರ್ತ ಬೀಜಗಣಿತವೂ ಸೇರಿಕೊಂಡಿದೆ. 19ನೆಯ ಶತಮಾನದ ಕಾಲದಲ್ಲಿ ಆಧುನಿಕ ಬೀಜಗಣಿತ ಆಧುನಿಕ ಆಗಿದ್ದಿತೇ ವಿನಾ ಇಂದು ಆಧುನಿಕ ಎಂಬ ಪದವನ್ನು ಬಿಟ್ಟು ಕೇವಲ ಬೀಜಗಣಿತ ಎಂದು ಕರೆಸಿಕೊಳ್ಳುವಷ್ಟು ಹಳೆಯದಾಗಿದೆ. ಇನ್ನು ಮುಂದೆ ಬೀಜಗಣಿತ ಅಂದರೆ ಆಧುನಿಕ ಬೀಜಗಣಿತ ಎಂದು ಭಾವಿಸಬೇಕು. ಜಾರ್ಜ್ ಪೀಕಾಕ್ (1791-1858), ವಿಲಿಯಂ ಹ್ಯಾಮಿಲ್ಟನ್ (1805-1865), ಆರ್ಥರ್ ಕೇಲೀ (1821-1895), ಸಿಲ್ವಿಸ್ಟರ್ (1814-1897), ಜಾರ್ಜ್ ಬೂಲ್ (1815-1864) ಮತ್ತು ಗ್ಯಾಲ್ವ (1811-1832) ಇವರು ಬೀಜಗಣಿತದ ಕ್ರಾಂತಿ ಪುರುಷರು. ಋಣಸಂಖ್ಯೆಗಳಿಗೆ ಬೆಲೆ ಇದೆ ಎಂದು ಹೇಳುವುದು ಅಪರಾಧವೆಂದು ತಿಳಿಯುತ್ತಿದ್ದ ಕಾಲವದು. ಹೊಸ ಚಿಂತನೆಗೆ ಅವಕಾಶಮಾಡಿಕೊಳ್ಳಲು ಬಯಸದೆ ಹಳೆಯದಕ್ಕೆ ಇನ್ನಷ್ಟು ಬಲವಾಗಿ ಅಂಟಿಕೊಳ್ಳುವ ಪ್ರವೃತ್ತಿಯನ್ನು ಬೆಳೆಸಿಕೊಂಡಿದ್ದ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞರಿಂದ ಕೂಡಿದ ವಾತಾವರಣವಿತ್ತು. ಅಂಥ ಕಾಲದಲ್ಲಿ ಪೀಕಾಕ್ ಕೇಂಬ್ರಿಜಿನ ಟ್ರಿನಿಟಿ ಕಾಲೇಜಿನ ಅಧಿಕಾರ ವರ್ಗದಲ್ಲಿದ್ದುಕೊಂಡು ಬೀಜಗಣಿತದ ಬೆಳೆವಣಿಗೆಗೆ ಬಹಳಷ್ಟು ಶ್ರಮಿಸಿದ. ಟ್ರೀಟೈಸ್ ಆನ್ ಆಲ್ಜಿಬ್ರ ಎನ್ನುವ ಗ್ರಂಥವನ್ನು ಬರೆದು (1830) ಬೀಜಗಣಿತಕ್ಕೆ ತಾರ್ಕಿಕ ಸ್ವರೂಪವನ್ನು ಕೊಡಲು ಪ್ರಯತ್ನಪಟ್ಟ. ವ್ಯತ್ಯಯ ನಿಯಮ (ಕಾಮ್ಯೂಟೇಟಿವ್ ಲಾ), ಸಾಹಚರ್ಯ ನಿಯಮ (ಅಸೋಸಿಯೇಟಿವ್ ಲಾ) ಇತ್ಯಾದಿ ಮೂಲನಿಯಮಗಳನ್ನು ಇಂದು ಬಳಕೆಯಲ್ಲಿರುವ ರೀತಿಯಲ್ಲಿ ನಿರೂಪಿಸಲು ಈತನಷ್ಟು ಯಶಸ್ವಿಯಾಗಿ ಯಾರೂ ಪ್ರಯತ್ನಿಸಲಿಲ್ಲ. ಮೊದಲು ಈ ನಿಯಮಗಳನ್ನು ಸಂಖ್ಯೆಗಳ ಮೇಲೆ ಪ್ರಯೋಗಿಸಿದ. ಹೀಗೆಯೇ ಮುಂದುವರಿದು ಇವನ್ನು ಸಾಮಾನ್ಯ ರಾಶಿಗಳ ಮೇಲೂ ಪ್ರಯೋಗಿಸಿ ಪ್ರತೀಕಾತ್ಮಕ ಬೀಜಗಣಿತದ (ಸಿಂಬಾಲಿಕ್ ಆಲ್ಜಿಬ್ರ) ಜನನಕ್ಕೆ ಕಾರಣನಾದ. ಮುಂಚೆ ಈ ನಿಯಮಗಳನ್ನು ಸಂಖ್ಯೆಗಳ ಮೇಲೆ ಪ್ರಯೋಗಿಸಿದಾಗ + ಮತ್ತು - ಚಿಹ್ನೆಗಳಿಗೆ ಅವುಗಳ ಸರ್ವೆಸಾಮಾನ್ಯವಾದ ಅರ್ಥವಿತ್ತು. ಉದಾಹರಣೆಗೆ: 2-1 ಕ್ಕೆ ಅರ್ಥವಿರುತ್ತಿತ್ತೇ ವಿನಾ 1-2 ಕ್ಕೆ ಅಲ್ಲ. ಆದರೆ ಪ್ರತೀಕಾತ್ಮಕ ಬೀಜಗಣಿತದಲ್ಲಿ ಪರಿಮಾಣಗಳ (ಮ್ಯಾಗ್ನಿಟ್ಯೂಡ್ಸ್) ಮೇಲೆ ನಿಬಂಧನೆಗಳನ್ನು ಹಾಕದೆ ಚಿಹ್ನೆಗಳನ್ನು ಬಳಸಬಹುದೆಂದು ಪ್ರತಿಪಾದಿಸಲಾಯಿತು. ಪೀಕಾಕ್ + ಮತ್ತು - ಚಿಹ್ನೆಗಳ ಈ ರೀತಿಯ ವಿಸ್ತಾರವಾದ ಬಳಕೆ ಯಾವ ಸಮಜಾಯಿಸಿಕೆಯನ್ನೂ ಕೊಡಲಿಲ್ಲ. ಆತನ ಹೊಸ ಚಿಂತನಮಾರ್ಗಕ್ಕೆ ಬೆಂಬಲ ಕೊಟ್ಟವ ಭಾರತದಲ್ಲಿ ಜನಿಸಿ ಇಂಗ್ಲೆಂಡಿನಲ್ಲಿ ಬೆಳೆದ ಡಿ' ಮಾರ್ಗನ್ (1806-1871). ಚಿಹ್ನೆಗಳು ಪೀಕಾಕನಿಗೆ ಸಂಖ್ಯೆಗಳು ಅಥವಾ ಪರಿಮಾಣಗಳು ಆಗಿದ್ದರೆ ಡಿ' ಮಾರ್ಗನನಿಗೆ ಅವು ಅಮೂರ್ತವಾಗಿದ್ದವು. ತಾನು ಬಳಸಿದ ಪರಿಕರ್ಮಗಳ ಪ್ರತೀಕಗಳನ್ನೂ, ಅಕ್ಷರಗಳನ್ನೂ ಆತ ಅಮೂರ್ತವಾಗಿರಿಸಿದ. ನೈಜ ಸಂಖ್ಯೆಗಳ ಮತ್ತು ಮಿಶ್ರ ಸಂಖ್ಯೆಗಳ ಬೀಜಗಣಿತ ಎರಡಕ್ಕೂ ಒಂದೇ ಬಗೆಯ ಪರಿಕರ್ಮ ಪದ್ಧತಿಗಳ ಇರುವಿಕೆಯನ್ನು ಕಂಡುಕೊಂಡ. ಬೀಜಗಣಿತದ ಮೂಲ ನಿಯಮಗಳು ಎಲ್ಲ ಬೀಜಗಣಿತೀಯ ವ್ಯವಸ್ಥೆಗಳಿಗೂ ಹೊಂದಿಕೊಳ್ಳುವುವು ಎಂಬ ಪರಿಕಲ್ಪನೆಗೆ ಬಹಳ ಹತ್ತಿರ ಬಂದರೂ ಆತ ನೈಜ ಸಂಖ್ಯೆಗಳ ಬೀಜಗಣಿತ ಮತ್ತು ಮಿಶ್ರ ಸಂಖ್ಯೆಗಳ ಬೀಜಗಣಿತ ಎಂಬ ಎರಡು ಬೀಜಗಣಿತಗಳು ಮಾತ್ರ ಇರಬಲ್ಲವು ಎಂದು ನಂಬಿದ್ದ. ಡಿ' ಮಾರ್ಗನನ ಈ ಗ್ರಹಿಕೆ ತಪ್ಪು ಎಂದು ಡಬ್ಲಿನ್ನಿನ ಟ್ರಿನಿಟಿ ಕಾಲೇಜಿನಲ್ಲಿದ್ದ ಹ್ಯಾಮಿಲ್ಟನ್ ತೋರಿಸಿದ. ಈತ ನೈಜಸಂಖ್ಯೆಗಳ ಸಕ್ರಮಯಗ್ಮಗಳ ಬೀಜಗಣಿತವನ್ನು ಸೃಷ್ಟಿಸಿದ. (a,b) ಮತ್ತು (α,β) ಎಂಬ ನೈಜಸಂಖ್ಯೆಗಳ ಎರಡು ಸಕ್ರಮ ಯಗ್ಮಗಳ ಗುಣಲಬ್ಧವನ್ನು (a,b) . (α,β) = (aα-bβ, aβ+bα) ಎಂದು ನಿರೂಪಿಸುತ್ತಾನೆ. ಈ ಸಕ್ರಮಯುಗ್ಮಗಳ ಮಾಧ್ಯಮದಲ್ಲಿ ಇಡೀ ಮಿಶ್ರಸಂಖ್ಯೆಗಳ ಪರಿಕರ್ಮಗಳನ್ನು ಅಳವಡಿಸಲು ಅವನಿಗೆ ಸಾಧ್ಯವಾಯಿತು. ಇನ್ನೂ ಮುಂದುವರಿದು ನೈಜಸಂಖ್ಯೆಗಳ ಸಕ್ರಮಯುಗ್ಮಗಳನ್ನು ಒಂದೇ ತಲದಲ್ಲಿರುವ ಸದಿಶ ಪರಿಮಾಣಗಳು ಎಂದು ಗ್ರಹಿಸಿ ಇದೇ ಪರಿಕಲ್ಪನೆಯನ್ನು ಮೂರು ಆಯಾಮಗಳ ಆಕಾಶಕ್ಕೂ ಮುಂದುವರಿಸಿದ. ಮೂರು ಆಯಾಮಗಳ ಆಕಾಶದಲ್ಲಿ ಸದಿಶ ಪರಿಮಾಣವನ್ನು ಮೂರು ನೈಜ ಸಂಖ್ಯೆಗಳ ಸಕ್ರಮಗಣಗಳಿಂದ ಸೂಚಿಸುತ್ತಾನೆ: (a+bi+cj) ಅಥವಾ (a,b,c). ಆದರೆ ಮೂರು ನೈಜಸಂಖ್ಯೆಗಳ ಸಕ್ರಮಗಣಗಳ ಗುಣಲಬ್ಧವನ್ನು ನಿರೂಪಿಸುವುದು ಆತನಿಗೆ ಕೂಡಲೆ ಸಾಧ್ಯವಾಗಲಿಲ್ಲ. 10 ವರ್ಷಗಳ ಬಳಿಕ ಒಂದು ದಿವಸ ಮೂರು ನೈಜಸಂಖ್ಯಾಸಕ್ರಮಗಣದ ಬದಲು 4 ನೈಜ ಸಂಖ್ಯಾಸಕ್ರಮಗಣವನ್ನು ಉಪಯೋಗಿಸಿ i2=j2=k2=-1 ಮತ್ತು ij=k=-ji, jk=i=-kj ಮತ್ತು ki=j=-ik ಎಂದು ಊಹಿಸಿಕೊಂಡರೆ (a+bi+cj+dk) ರೂಪದ ಪರಿಮಾಣಗಳ ಗುಣಲಬ್ಧವನ್ನು ನಿರೂಪಿಸಬಹುದು ಎಂದು ತಿಳಿಸಿದ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ವ್ಯತ್ಯಯ ನಿಯಮವನ್ನು ಆತ ಕೈಬಿಟ್ಟಿರುವುದು ಗಮನಾರ್ಹ. ಉದಾಹರಣೆಗೆ ij≠ji. ಯುಕ್ಲಿಡ್ನ ಐದನೆಯ ಆದ್ಯುಕ್ತಿಯನ್ನು ಕೈಬಿಟ್ಟು ಲೊಬಾಚಿವ್ಸ್ಕಿ ಹೊಸ ಜ್ಯಾಮಿತಿಗೆ ಜನನವಿತ್ತರೆ ಹ್ಯಾಮಿಲ್ಟನ್ ವ್ಯತ್ಯಯ ನಿಯಮವನ್ನು ಕೈಬಿಟ್ಟು ಒಂದು ಹೊಸ ಬೀಜಗಣಿತವನ್ನು ಸೃಷ್ಟಿಸಿದ.[೩೮]: 210 ನಾಲ್ಕು ನೈಜಸಂಖ್ಯೆಗಳ ಗಣಗಳ ಬೀಜಗಣಿತ ವ್ಯತ್ಯಯ ನಿಯಮವಿಲ್ಲದ ಒಂದು ಬೀಜಗಣಿತ. ಪರಿವರ್ತನ ಸಿದ್ಧಾಂತದಿಂದ ಉದ್ಭವಿಸಿದ ಮಾತೃಕೆಗಳ ಬೀಜಗಣಿತ ಇನ್ನೊಂದು ಉದಾಹರಣೆ. ಇದರ ಕರ್ತೃ ಕೇಲಿ. ಜಾರ್ಜ್ ಬೂಲ್ ಎಂಬ ಬ್ರಿಟಿಷ ಗಣಿತಜ್ಞ ಇನ್ನೊಂದು ಬಗೆಯ ಬೀಜಗಣಿತವನ್ನು ಸೃಷ್ಟಿಸಿದ. ಯಾವುದೇ ವಿಷಯ ತನ್ನ ಅಸ್ತಿತ್ವಕ್ಕೆ ಬೇಕಾಗುವ ಸೂಕ್ತ ಪರಿಕರ್ಮ ಸೂತ್ರಗಳು ಮತ್ತು ಇವುಗಳಿಗೆ ಗುರಿಯಾಗುವ ಪ್ರತೀಕಗಳು ಇವನ್ನು ಇಟ್ಟುಕೊಂಡರೆ ಅದು ಗಣಿತಶಾಸ್ತ್ರದ ಒಂದು ಅಂಗವಾಗಿರುತ್ತದೆ ಎನ್ನುವ ಗಣಿತಶಾಸ್ತ್ರದ ಸರಿಯಾದ ಪರಿಕಲ್ಪನೆಯನ್ನು ಆತ ಗ್ರಹಿಸಿದ. ಇಂದು ಗಣಿತಶಾಸ್ತ್ರದ ಪ್ರತಿಯೊಂದು ಶಾಖೆಯಲ್ಲಿಯೂ ಮೂಲಭೂತವಾಗಿ ಕಾಣುವ ಗಣ ಎಂಬ ಪರಿಕಲ್ಪನೆಯನ್ನು ಮೊದಲು ಗ್ರಹಿಸಿದಾತ ಬೂಲ್. A ಮತ್ತು B ಗಳು ಯಾವುದಾದರೂ ಒಂದು ವಿಶ್ವಗಣ U ವಿನ ಎರಡು ಉಪಗಣಗಳಾದರೆ A U B ಅನ್ನುವುದು ಇನ್ನೊಂದು ಗಣ; ಇದರಲ್ಲಿ A ಯಲ್ಲಿರುವ ಎಲ್ಲ ಧಾತುಗಳು, B ಯಲ್ಲಿರುವ ಎಲ್ಲ ಧಾತುಗಳೂ ಇವೆ. A ∩ B ಅನ್ನುವುದು ಮತ್ತೊಂದು ಗಣ. ಇದರಲ್ಲಿ A ಮತ್ತು B ಎರಡಕ್ಕೂ ಉಭಯಸಾಮನ್ಯವಾಗಿರುವ ಧಾತುಗಳು ಮಾತ್ರ ಇವೆ. O ಪ್ರತೀಕವನ್ನು ಧಾತುಗಳೇ ಇಲ್ಲದ ಗಣವನ್ನು ಸೂಚಿಸಲು ಬಳಸುತ್ತಾನೆ. ಇದಕ್ಕೆ ಶೂನ್ಯಗಣ ಎಂದು ಹೆಸರು (ಇದಕ್ಕೆ ಪ್ರಚಲಿತ ಪ್ರತೀಕ ∅). ಇಂದು ಬಳಕೆಯಲ್ಲಿರುವ U ಮತ್ತು ∩ ಚಿಹ್ನೆಗಳ ಬದಲು + ಮತ್ತು x ಚಿಹ್ನೆಗಳನ್ನು ಬೂಲ್ ಬಳಸುತ್ತಿದ್ದ. + ಮತ್ತು x ಗಳನ್ನೊಳಗೊಂಡ ಗಣಗಳನ್ನು ಕುರಿತ ಬೂಲೀಯ ಬೀಜಗಣಿತವನ್ನು ಆತ ಸೃಷ್ಟಿಸಿದ. ವ್ಯತ್ಯಯ ನಿಯಮ, ಸಾಹಚರ್ಯ ನಿಯಮ ಮತ್ತು ವಿತರಣ ನಿಯಮಗಳು ಈ ಬೀಜಗಣಿತದಲ್ಲಿ ಸಿದ್ಧಿಸುತ್ತವೆ. ಕೆಳಗೆ ಕೊಟ್ಟಿರುವ ಈ ಬೀಜಗಣಿತದ ಕೆಲವು ವಿಶೇಷ ಲಕ್ಷಣಗಳನ್ನು ಗಮನಿಸಬೇಕು.
- A+A=A, (2A ಅಲ್ಲ).
- A x B = A x C, A ≠ 0 ಆಗಿದ್ದರೆ B=C ಆಗಬೇಕಾದ ಆವಶ್ಯಕತೆ ಇಲ್ಲ.
- A x B = 0 ಆಗಿದ್ದರೆ A ಅಥವಾ B ಯಾವುದಾದರೂ ಶೂನ್ಯಗಣ ಆಗಬೇಕಾದ ಆವಶ್ಯಕತೆ ಇಲ್ಲ. (A=B ಅಂದರೆ A ಮತ್ತು B ಯಲ್ಲಿರುವ ಧಾತುಗಳು ಒಂದೇ ಆಗಿವೆ ಎಂದು ಅರ್ಥ).
ಇದು (ಅಮೂರ್ತ) ಬೀಜಗಣಿತದ ಕಡೆಗಿಟ್ಟ ಮೊದಲ ಹೆಜ್ಜೆ ಆಗಿದೆ. ಗ್ರೂಪ್, ವಲಯ (ರಿಂಗ್) ಮತ್ತು ಕ್ಷೇತ್ರ (ಫೀಲ್ಡ್) ಎಂಬ ಪರಿಕಲ್ಪನೆಗಳು ಬೆಳೆದು ಬಂದು ಅಮೂರ್ತಬೀಜಗಣಿತ ಬೃಹದಾಕಾರವಾಗಿ ಬೆಳೆಯುತ್ತ ಇದೆ.
ಗಣಿತಶಾಸ್ತ್ರದ ತಳಹದಿ (ಫ಼ೌಂಡೇಶನ್ಸ್ ಆಫ಼್ ಮ್ಯಾತ್ಮ್ಯಾಟಿಕ್ಸ್)
[ಬದಲಾಯಿಸಿ]ಶಾಸ್ತ್ರವೊಂದರ ಆಯಕಟ್ಟಿನಲ್ಲಿ ಪರಸ್ಪರ ವ್ಯತಿರಿಕ್ತವಾದ ಫಲಿತಾಂಶಗನ್ನು ಸಮರ್ಥಿಸಲು ಶಕ್ಯವಾಗುವುದಾದರೆ ಅಂಥ ಶಾಸ್ತ್ರ ಅಸಂಗತ (ಇನ್ಕನ್ಸಿಸ್ಟೆಂಟ್) ಎನಿಸುವುದು. ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ ಈ ಬಗೆಯ ಸನ್ನಿವೇಶ ಉದ್ಭವಿಸಲು ಸಾಧ್ಯವಿಲ್ಲವೆಂದು ನಂಬಲಾಗಿದೆ. ಈ ನಂಬಿಕೆಯನ್ನೇ ಒಂದು ಖಚಿತ ಪ್ರಮೇಯವಾಗಿ ಸಾಧಿಸಬಹುದೇ ಎಂಬ ಪ್ರಶ್ನೆ ವಿವೇಚನಾರ್ಹ. ಗಣಿತದ ಸುಸಾಂಗತ್ಯವನ್ನು (ಕನ್ಸಿಸ್ಟೆನ್ಸಿ) ಸಾಧಿಸುವ ಪ್ರಯತ್ನಗಳು ವಸ್ತುತಃ ಗಣಿತೀಯ ಮಾರ್ಗಗಳನ್ನೇ ಅನುಸರಿಸಬೇಕಾಗುವುದರಿಂದ ಅಂಥ ಸಾಧನೆಗಳ ವಿಶ್ವಸನೀಯತೆಗೆ ಭಂಗ ತಗಲುವುದು ಅನಿವಾರ್ಯ. ಆದಾಗ್ಯೂ ಹೆಚ್ಚು ವಿಶ್ವಸನೀಯವೆಂದು ತೋರುವ ಒಂದು ಗಣಿತ ಶಾಖೆಯ ಆಧಾರದ ಮೇಲೆ ಪ್ರಾರಂಭದಲ್ಲಿ ಕಡಿಮೆ ವಿಶ್ವಸನೀಯವೆನಿಸಬಹುದಾದ ಮತ್ತೊಂದು ಗಣಿತ ಶಾಖೆಯ ಸುಸಾಂಗತ್ಯವನ್ನು ಸಮರ್ಥಿಸುವ ಪ್ರಯತ್ನಗಳು ನಡೆಯದೆ ಇಲ್ಲ. ಬಹಳಷ್ಟು ಮಂದಿ ಕಾರ್ಯನಿರತ ಗಣಿತಜ್ಞರಾದರೋ (ವರ್ಕಿಂಗ್ ಮ್ಯಾಥ್ಮ್ಯಾಟಿಷಿಯನ್ಸ್) ಗಣಿತದ ಸುಸಾಂಗತ್ಯವನ್ನು ಅನುಭವಸಿದ್ಧವೆಂದು ಪರಿಗಣಿಸಿ ತಮ್ಮ ದೈನಂದಿನ ಸಂಶೋಧನೆಗಳನ್ನು ಮುಂದುವರಿಸುತ್ತಾರೆ. ಗಣಿತದಲ್ಲಿ ಒಂದು ವೇಳೆ ಗೌಣ ಅಸಾಂಗತ್ಯಗಳು ತಲೆದೋರಿದರೂ ಅವು ಸಂಶೋಧನೆಗಳ ಅಪರಿಪೂರ್ಣತೆಯನ್ನು ಪ್ರತಿಫಲಿಸುತ್ತವೆಂದೂ, ಚಿಕ್ಕಪುಟ್ಟ ಸುಧಾರಣೆಗಳಿಂದ ಅವನ್ನೆಲ್ಲ ನಿವಾರಿಸಬಹುದೆಂದೂ ಅವರು ದೃಢವಾಗಿ ನಂಬುತ್ತಾರೆ.
ಗಣಿತಮಾರ್ಗಗಳ ಬಗ್ಗೆ ಜನಸಾಮಾನ್ಯರ ನಿಲುವು ಇಂದು ನಿಜಕ್ಕೂ ಭಕ್ತಿಪೂರ್ಣವಾಗಿದೆ. ಶಾಶ್ವತ ಸತ್ಯಗಳ ಆಗರ ಎಂದು ಕಲ್ಪಿಸಲಾಗಿರುವ ಗಣಿತವನ್ನು ಕುರಿತಂತೆ ಅದಾವ ಸಂಶಯಗಳು ತಾನೆ ಜನಿಸಲು ಶಕ್ಯ ಎಂದು ಅವರು ಅಚ್ಚರಿಪಡುವುದು ಸಹಜ. ಇದಕ್ಕೆ ಉತ್ತರವಾಗಿ ನಾವು ಪ್ರಧಾನತಃ ಮೂರು ಪರಿಕಲ್ಪನೆಗಳ ಕಡೆ ಬೆರಳು ತೋರಿಸಬೇಕಾಗಿಬರುತ್ತದೆ. ಅನಂತ (ಇನ್ಫಿನಿಟಿ), ಸಾರ್ವತ್ರಿಕತೆ (ಜನರ್ಯಾಲಿಟಿ)ಮತ್ತು ನಿಷೇಧ (ನೆಗೇಷನ್). ಆಧುನಿಕ ಪ್ರೌಢ ಗಣಿತದಲ್ಲಿ ಚರ್ಚೆಗೆ ಬರುವ ಬಹಳಷ್ಟು ಗಣಗಳೆಲ್ಲ ಅನಂತವಾದವು (ಉದಾಹರಣೆಗೆ ಸಮಸ್ತ ಧನಪೂರ್ಣಾಂಕಗಳ ಗಣ); ಇವುಗಳಲ್ಲಿನ ಧಾತುಗಳನ್ನು ಬಿಡಿಬಿಡಿಯಾಗಿ ಎಣಿಸುವುದಕ್ಕಾಗಲಿ, ವಿಶಿಷ್ಟ ಪರೀಕ್ಷೆಗಳಿಗೆ ಗುಪಡಿಸುವುದಕ್ಕಾಗಲಿ ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ. ಒಂದು ಚೀಲದಲ್ಲಿ ಕೆಂಪು ಬಣ್ಣದ ಹತ್ತು ಗೋಲಿಗಳಿವೆಯೆಂದು ಭಾವಿಸೋಣ. ಈಗ
A. ಚೀಲದಲ್ಲಿರುವ ಯಾವುದೇ ಗೋಲಿಯ ಬಣ್ಣ ಕೆಂಪು (ಅರ್ಥಾತ್ ಚೀಲದಲ್ಲಿರುವ ಗೋಲಿಗಳೆಲ್ಲ ಕೆಂಪುಬಣ್ಣದವು) ಎಂಬ ಉಕ್ತಿಯನ್ನು
B. ಯಾವುದೇ ಧನ ಪೂರ್ಣಾಂಕಕ್ಕೆ ಅದರ ಮುಂದಿನ ಪೂರ್ಣಾಂಕವನ್ನು ಕೂಡಿಸಿದಾಗ ಬರುವ ಫಲ ಒಂದು ಬೆಸ ಪೂರ್ಣಾಂಕ.
ಎಂಬುದರೊಡನೆ ಹೋಲಿಸಿನೋಡಬೇಕು. A ಯನ್ನು ಸಮರ್ಥಿಸಲು ಚೀಲದಲ್ಲಿರುವ ಗೋಲಿಗಳನ್ನು ಒಂದೊಂದಾಗಿ ತೆಗೆದು ಪ್ರದರ್ಶಿಸಬಹುದು. B ಯ ಸತ್ಯತೆಯನ್ನು ಮನಗಾಣಲು 1+2=3= ಬೆಸ ಪೂರ್ಣಾಂಕ, 2+3=5= ಬೆಸ ಪೂರ್ಣಾಂಕ, 3+4=7 ಬೆಸ ಪೂರ್ಣಾಂಕ ಎಂದು ಮುಂತಾಗಿ ಧನಪೂರ್ಣಾಂಕಗಳನ್ನು ಬಿಡಿಬಿಡಿ ಪರೀಕ್ಷೆಗಳಿಗೆ ಗುರಿಮಾಡುತ್ತ ಸಾಗಲು ಸಾಧ್ಯವಿಲ್ಲ. ಬದಲು ಅದಕ್ಕೆ ಗಣಿತೀಯ ಮಾರ್ಗದ ಒಂದು ಸಮಗ್ರ ಸಾಧನೆಯೇಬೇಕು. ಆದ್ದರಿಂದ ನಾವು ಬಳಸುವ ಭಾಷೆಯ ಅಪರಿಪೂರ್ಣತೆಯಿಂದಾಗಿ A, B ಗಳೊಂದೊಂದೂ ಉಕ್ತಧಾತುಗಳನ್ನು ಕುರಿತ ಒಂದೊಂದು ಲಕ್ಷಣದ ಸಾರ್ವತ್ರಿಕತೆಯನ್ನು ತಿಳಿಯಪಡಿಸುವಂತೆ ತೋರಿದಾಗ್ಯೂ A ಯಲ್ಲಿರುವ ಸಾರ್ವತ್ರಿಕತೆಯ ಸ್ವರೂಪವೇ ಬೇರೆ, B ಯಲ್ಲಿರುವ ಸಾರ್ವತ್ರಿಕತೆಯ ಸ್ವರೂಪವೇ ಬೇರೆ. ಇವೆರಡು ಸಂದರ್ಭಗಳಲ್ಲೂ ಸಾರ್ವತ್ರಿಕತೆ ಎಂಬ ದ್ವಂದ್ವಾರ್ಥ ಯುಕ್ತ ಏಕಪದವನ್ನೇ ಪ್ರಯೋಗಿಸುವುದು ನಮ್ಮ ವಾಗ್ಭಂಡಾರದ ದಾರಿದ್ರ್ಯವನ್ನು ಪ್ರತಿಬಿಂಬಿಸುತ್ತದೆ. ಗಣಿತಶಾಸ್ತ್ರದ ಸಾಂಪ್ರದಾಯಿಕದ ಬೋಧನೆಯಲ್ಲಿ ಇಂಥ ದಾರಿದ್ರ್ಯವನ್ನೇ ಒಂದು ಸೌಲಭ್ಯವನ್ನಾಗಿ ಸ್ವೀಕರಿಸಿ B ಯಂಥ ಸನ್ನಿವೇಶಗಳಲ್ಲೂ A, B ಮಾದರಿ ಸಾರ್ವತ್ರಿಕತೆಯ ಅರ್ಥಛಾಯೆಯನ್ನು ವಿಕ್ಷೇಪಿಸುವ ಮೂಲಕ ವಿವಿಧ ಪ್ರಮೇಯಗಳನ್ನು ಸಾಧಿಸಲಾಗುವುದು. ಈ ಬಗೆಯ ಪ್ರಶ್ನಾಸ್ಪದ ಸಾಧನಕ್ರಮಗಳಲ್ಲಿ ಬಳಸಲಾಗುವ ಕೇಂದ್ರೀಯ ಉಪಕರಣವೆಂದರೆ ನಾವು ಹೆಸರಿಸಿರುವ ಮೂರನೆಯ ಪರಿಕಲ್ಪನೆ ನಿಷೇಧ. ಅಂಥ ಸಾಧನೆಗಳಿಗೆ ನಿಷೇಧದಿಂದ ಒದಗಿಬರುವ ಆಸರೆಯನ್ನು ಬಹಿರಂಗಪಡಿಸುವ ಸಲುವಾಗಿ ಪೆಟ್ಟಿಗೆಯೊಂದರಲ್ಲಿ ಕೆಂಪು ಸೇರಿದಂತೆ ವಿವಿಧ ಬಣ್ಣಗಳ ಗೋಲಿಗಳಿವೆಯೆಂದೂ ಆ ಪೆಟ್ಟಿಗೆಯಿಂದ ಬಣ್ಣವನ್ನು ನೋಡದೆ ಎರಡು ಮೂರು ಗೋಲಿಗಳನ್ನು ಮೇಲೆ ಹೇಳಿದ ಚೀಲಕ್ಕೆ ವರ್ಗಾಯಿಸುತ್ತೇವೆಂದೂ ಭಾವಿಸೋಣ. ಈಗ ಕೆಳಗಿನ ಉಕ್ತಿಗಳನ್ನು ಪರಶೀಲಿಸಬೇಕು.
(~A) ಚೀಲದಲ್ಲಿರುವ ಗೋಲಿಗಳೆಲ್ಲ ಕೆಂಪು ಬಣ್ಣದವಲ್ಲ
(C) ಕೆಂಪು ಬಣ್ಣವಿರದ ಒಂದು ಗೋಲಿಯಾದರೂ ಚೀಲದಲ್ಲಿ ಇದೆ
(D) n-1+101000 ಮತ್ತು n+1+101000 ಇವುಗಳ ಪೈಕಿ ಒಂದನ್ನಾದರೂ ವಿಭಾಜ್ಯ ಪೂರ್ಣಾಂಕವನ್ನಾಗಿಸುವ ಗುಣ ಎಲ್ಲ ಧನಪೂರ್ಣಾಂಕ n ಗಳಿಗೂ ಇದೆ. [ಸೂಚನೆ: ಒಂದು ಪೂರ್ಣಾಂಕ m ಗೆ ±m ಹಾಗೂ ±1 ಇವುಗಳಲ್ಲದೆ ಬೇರೆ ಅಪವರ್ತನಗಳೂ ಇರುವುದಾದರೆ ಆ m ವಿಭಾಜ್ಯ ಪೂರ್ಣಾಂಕ (ಕಾಂಪೊಸಿಟ್ ಇಂಟಿಜರ್) ಎನಿಸುತ್ತದೆ.[೩೯][೪೦]]
(~D) n-1+101000 ಮತ್ತು n+1+101000 ಇವುಗಳ ಪೈಕಿ ಒಂದನ್ನಾದರೂ ವಿಭಾಜ್ಯ ಪೂರ್ಣಾಂಕವನ್ನಾಗಿಸುವ ಗುಣ ಎಲ್ಲ ಧನಪೂರ್ಣಾಂಕ n ಗಳಿಗೂ ಇಲ್ಲ.
(E) n-1+101000 ಮತ್ತು n+1+101000 ಇವುಗಳ ಪೈಕಿ ಒಂದನ್ನಾದರೂ ವಿಭಾಜ್ಯ ಪೂರ್ಣಾಂಕವನ್ನಾಗಿಸದೆ ಹೋಗುವಂಥ ಕನಿಷ್ಠಪಕ್ಷ ಒಂದು ಧನಪೂರ್ಣಾಂಕ n ಇದೆ.
(~A) ಉಕ್ತಿ (A) ಉಕ್ತಿಯ ನಿಷೇಧ; ಅಂತೆಯೇ (~D) ಉಕ್ತಿ (D)ಉಕ್ತಿಯ ನಿಷೇಧ. (A) ಯನ್ನಾಗಲಿ (~A) ಯನ್ನಾಗಲಿ ಸಮರ್ಥಿಸಬೇಕಾದರೆ ಚೀಲದಲ್ಲಿರುವ ಗೋಲಿಗಳನ್ನೆಲ್ಲ ಒಂದೊಂದಾಗಿ ತೆಗೆದು ಪ್ರದರ್ಶಿಸಿದರಾಯಿತು. ಆಗ ಕೊನೆಯವರೆಗೂ ಕೆಂಪು ಗೋಲಿಗಳೇ ಗೋಚರಿಸುತ್ತಲಿರುತ್ತವೆ. ಇಲ್ಲವೆ ಒಂದಲ್ಲ ಒಂದು ಸಲ ಕೆಂಪಲ್ಲದ ಗೋಲಿಯೊಂದು ಕಣ್ಣಿಗೆ ಬೀಳುತ್ತದೆ ಎನ್ನುವುದು ಅನುಭವವೇದ್ಯ. ಪ್ರಥಮ ಪ್ರಸಂಗದಲ್ಲಿ (A) ಯೂ, ಎರಡನೆಯ ಪ್ರಸಂಗದಲ್ಲಿ (~A) ಯೂ ಸಮರ್ಥಿತವಾಗುವುವು. ಒಂದು ವೇಳೆ (~A) ಸಮರ್ಥಿತವಾಗುವುದಾದರೆ ಅದಕ್ಕೂ ಮುಂಚೆ (ಅಂದರೆ ಕೆಂಪಲ್ಲದ ಗೋಲಿ ಕಾಣಿಸಿದ ತತ್ಕ್ಷಣವೇ) (C) ಸಮರ್ಥಿತವಾಗಿರುತ್ತದೆಂಬ ಅಂಶವನ್ನು ಗಮನಿಸಬೇಕು. (~A) ಊರ್ಜಿತವಾಗುವುದು (C) ಮೂಲಕವೇ. ಈ ಅನುಭವದಿಂದ ನಾವು ಎರಡು ತೀರ್ಮಾನಗಳಿಗೆ ಬರುತ್ತೇವೆ:
- (A) ಮತ್ತು (~A)ಗಳ ಪೈಕಿ ಒಂದಲ್ಲ ಒಂದು ಸಮರ್ಥಿತವಾಗಲೇಬೇಕು;
- (C) ಮತ್ತು (~A) ಸಮಾನಾರ್ಥಕ ಉಕ್ತಿಗಳು.
ಈಗ ಸಾದೃಶ್ಯತರ್ಕದಿಂದ ಸಾಂಪ್ರದಾಯಿಕ ಗಣಿತ ಕೆಳಗಿನ ಎರಡು ಶ್ರದ್ಧೆಗಳನ್ನು ಅಂಗೀಕರಿಸುತ್ತದೆ:
- (D) ಮತ್ತು (~D) ಗಳ ಪೈಕಿ ಒಂದಲ್ಲ ಒಂದು ಸಮರ್ಥಿತವಾಗಲೇಬೇಕು.;
- (E) ಮತ್ತು (~D) ಸಮಾನಾರ್ಥಕ ಉಕ್ತಿಗಳು. ಅವುಗಳ ಪೈಕಿ ಒಂದು ಸಮರ್ಥಿತವಾದರೆ ಇನ್ನೊಂದು ಸಮರ್ಥಿತವಾದಂತೆಯೇ.
ಗೋಲಿಗಳ ವಿಚಾರದಲ್ಲಿ (1), (2) ಆ ಗೋಲಿಗಳನ್ನು ಒಂದೊಂದಾಗಿ ಪರೀಕ್ಷಿಸುವ ಸಾಧ್ಯತೆಯ ನೇರ ಫಲಿತಾಂಶಗಳು. ಧನಪೂರ್ಣಾಂಕಗಳನ್ನು ಹಾಗೆ ಪರೀಕ್ಷಿಸುವ ಸಾಧ್ಯತೆ ಇಲ್ಲದಿರುವುದರಿಂದ ಅವನ್ನು ಕುರಿತ (1), (2) ಕೇವಲ ಭಾಷಾಸಾದೃಶ್ಯದಿಂದ ಜನಿಸಿದ ಮಿಥ್ಯೆಗಳಿರಬಹುದು. ನಿಜಕ್ಕೂ (D) ಯನ್ನಾಗಲಿ (~D) ಯನ್ನಾಗಲಿ ಸಮರ್ಥಿಸಲು ಗಣಿತೀಯ ಮಾರ್ಗದ ಸಾಧನೆಯನ್ನೇ ನಿಯೋಜಿಸಬೇಕಾಗುವುದು. (D) ಇಲ್ಲವೆ (~D) ಗೆ ಸಾಧನೆಯೊಂದನ್ನು ನಿಯೋಜಿಸಲು ಸಾಧ್ಯವಾಗಲೇಬೇಕೆಂಬ ನಿಸರ್ಗನಿಯಮ ಎಲ್ಲಿದೆ? ಒಂದು ನಿರ್ದಿಷ್ಟ ಗಣಿತಶಾಖೆಯ ಆಯಕಟ್ಟಿನಲ್ಲಿ (D) ಯನ್ನು ಸಾಧಿಸಲೂ ಸಾಧ್ಯವಾಗದಿರಬಹುದು; (~D)ಯನ್ನು ಸಾಧಿಸಲೂ ಸಾಧ್ಯವಾಗದಿರಬಹುದು. ವಾಸ್ತವವಾಗಿ ಇದುವರೆಗೆ ಯಾರೂ (D) ಯನ್ನಾಗಲಿ, (~D) ಯನ್ನಾಗಲಿ ಸಾಧಿಸಿಯೂ ಇಲ್ಲವೆಂಬ ಸಂಗತಿಯನ್ನು ಇಲ್ಲಿ ಪ್ರಾಸಂಗಿಕವಾಗಿ ಗಮನಿಸಬಹುದಾಗಿದೆ. ಒಂದು ಪಕ್ಷ ಮುಂದೆ ಯಾವಾಗಲಾದರೂ (~D) ಯನ್ನು ಪರೋಕ್ಷ ಮಾರ್ಗದಲ್ಲಿ (ಇಂಡೈರೆಕ್ಟ್ ಮೆಥಡ್) ಸಾಧಿಸಲಾಗುವುದೆಂದು ಭಾವಿಸೋಣ. ಗೋಲಿಗಳನ್ನು ಕುರಿತಾಗಿ ನೇರಮಾರ್ಗದಲ್ಲಿ (C) ಮೂಲಕ (~A) ಫಲಿಸಿದಂತೆ ಧನ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಕುರಿತ ಅಂಥ ಪರೋಕ್ಷ ಸಾಧನೆಯಲ್ಲಿ (E) ಮೂಲಕ (~D) ಸಿದ್ಧಿಸಿರುವುದಿಲ್ಲ; ಆ ಪರೋಕ್ಷ ಸಾಧನೆಯ ಪೂರ್ಣ ಅಧ್ಯಯನದ ಬಳಿಕವೂ n ± 1± 101000 ಗಳೆರಡನ್ನೂ ಅವಿಭಾಜ್ಯವಾಗಿಸುವ ಒಂದು ಧನ ಪೂರ್ಣಾಂಕ n ನ್ನು ಗೊತ್ತುಮಾಡಿ ತೋರಿಸಲು ಸಾಧ್ಯವಾಗದಿರಬಹುದು. ಅಂದಮೇಲೆ (~D) ಗೆ (ಪರೋಕ್ಷ) ಸಾಧನೆಯೊಂದು ಇದ್ದಾಗಲೂ (E) ಗೆ ಸಾಧನೆ ಇಲ್ಲದೆ ಹೋಗಬಹುದು. ಇಂತಿರುವಾಗ (~D), (E) ಗಳನ್ನು ಸಮಾನಾರ್ಥಕ ಉಕ್ತಿಗಳು ಎಂದು ಬಗೆಯಲು ಆಧಾರವಾದರೂ ಏನಿದೆ?
ಆದರೆ ಮೇಲಿನ ಟೀಕೆಗಳು ಬಹುಸಂಖ್ಯಾತ ಗಣಿತಜ್ಞರನ್ನು ತೀವ್ರವಾಗಿ ಬಾಧಿಸಿವೆಯೆಂದು ತಿಳಿಯಲಾಗದು. ಕಾರ್ಯನಿರತ ಗಣಿತಜ್ಞರನೇಕರಿಗೆ ಇವುಗಳ ಬಗ್ಗೆ ನಿರ್ದಿಷ್ಟ ಅರಿವೇ ಇಲ್ಲದಿರುವುದು ಹೆಚ್ಚು ಸಂಭವನೀಯ. ಸಾಂಪ್ರದಾಯಿಕ ಗಣಿತವನ್ನು ಕುರಿತ ಈ ಟೀಕೆಗಳು ಪ್ರಧಾನವಾಗಿ ಅಂತರ್ಬೋಧನವಾದಿಗಳೆಂಬ (ಇಂಟ್ಯುಇಷನಿಸ್ಟ್ಸ್) ಕೆಲ ಗಣಿತ ತಾತ್ತ್ವಿಕರ ಅಭಿಮತವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತವೆ. ಲಿಯೊಪೋಲ್ಡ್ ಕ್ರೋನೆಕರ್ (1823-1891) ಎಂಬ ಗಣಿತಜ್ಞನ ಆಲೋಚನೆಗಳಿಂದ ಅಸ್ಪಷ್ಟವಾಗಿ ಪ್ರಾರಂಭವಾದ ಅಂತರ್ಬೋಧನವಾದವನ್ನು ಪ್ರಸಕ್ತ ಶತಮಾನದ ಆದಿಯಲ್ಲಿ ಎಲ್.ಇ.ಜೆ. ಬ್ರುವರ್ (1882-1966) ಸ್ಫುಟ ರೂಪರೇಖೆಗಳಿನ್ನಿತ್ತು ಬೆಳೆಸಿದ. ಅಂತರ್ಬೋಧನವಾದಿಗಳ ಟೀಕೆಗಳನ್ನು ಸಾಂಪ್ರದಾಯಿಕ ಗಣಿತಜ್ಞರು ಸಾಧಾರಣವಾಗಿ ಅಲಕ್ಷಿಸಿದರೂ ಅವರಲ್ಲಿ ಅತಿ ಪ್ರಮುಖನಾಗಿದ್ದ ಡೇವಿಡ್ ಹಿಲ್ಬರ್ಟ್ನಿಗೆ (1862-1943) ಮಾತ್ರ ಅವು ತಕ್ಕ ಉತ್ತರವನ್ನು ಕೊಡಬೇಕಾದ ಸವಾಲುಗಳೆನಿಸಿದ್ದು ಗಮನಾರ್ಹ.[೪೧] ಈ ಸಂಬಂಧದಲ್ಲಿ ಹಿಲ್ಬರ್ಟ್ನ ಮನೋಭಿಪ್ರಾಯ ಹೀಗಿದ್ದಿತು: ಧನ ಪೂರ್ಣಾಂಕಗಳೇ ಮೊದಲಾದ ಅನಂತ ಗಣಗಳ ಧಾತುಗಳನ್ನು ಕುರಿತಂತೆ (1), (2) ರಂಥ ಸಾಂಪ್ರದಾಯಿಕ ಶ್ರದ್ಧೆಗಳ ಪರಿಣಾಮವಾಗಿ ಗಣಿತದಲ್ಲಿ ಅಸಾಂಗತ್ಯಗಳು ಜನಿಸದೆ ಇರುವ ಪಕ್ಷದಲ್ಲಿ ಅವನ್ನು ಅಂಗೀಕರಿಸುವ ಜನ್ಮಸಿದ್ಧ ಹಕ್ಕಿನಿಂದ ಗಣಿತಜ್ಞರನ್ನು ಯಾರೂ ವಂಚಿಸಲಾಗದು; ಆದ್ದರಿಂದ ಟೀಕೆಗೆ ಗುರಿಯಾಗಿರುವ ಶ್ರದ್ಧೆಗಳಿಂದ ಅಸಾಂಗತ್ಯಗಳು ತಲೆದೋರುವುದಿಲ್ಲ ಎಂಬುದನ್ನು ಒಂದು ನಿರ್ದಿಷ್ಟ ಪ್ರಮೇಯ ರೂಪದಲ್ಲಿ ಸರ್ವಸಮ್ಮತವಾಗುವಂತೆ ಸಮರ್ಥಿಸುವುದೇ ಅಂತರ್ಬೋಧನವಾದಿಗಳ ಸವಾಲಿಗೆ ಸಾಂಪ್ರದಾಯಿಕರು ನೀಡಬೇಕಾದ ಉತ್ತರ. (ಈ ವಿಶ್ಲೇಷಣೆಯನ್ನೂ ಬ್ರುವರ್ ಒಪ್ಪಲಿಲ್ಲ; ಅರ್ಥಕ್ಕೆ ವಿಮುಖವಾದ ಚಿಂತನೆಗಳು ಸುಸಂಗತವಾಗಿದ್ದಾಗ್ಯೂ ಅಪರಿಗ್ರಾಹ್ಯ ಎಂಬುದು ಬ್ರುವರ್ ವಾದ. ಆದರೆ ನಮ್ಮ ಪ್ರಸಕ್ತ ಚರ್ಚೆಗೆ ಇದು ಅನವಶ್ಯ.) ಹೀಗೆಂದು ಆಲೋಚಿಸಿ ಸಾಂಪ್ರದಾಯಿಕ ಗಣಿತವನ್ನು ಸಂರಕ್ಷಿಸುವ ಗಂಭೀರ ಪ್ರಯತ್ನಕ್ಕೆ (1920ರ ವೇಳೆ) ಹಿಲ್ಬರ್ಟ್ ಕೈಹಾಕಿದ. ಧನಪೂರ್ಣಾಂಕಗಳನ್ನು ಕುರಿತ ಸಾಂಪ್ರದಾಯಿಕ ಗಣಿತದ ಶಾಖೆ ಮಿಕ್ಕೆಲ್ಲವಕ್ಕೂ ಮೂಲಭೂತವಾದ ಕಾರಣ ಮೊದಲಿಗೆ ಸಹಜವಾಗಿಯೇ ಕರೆಯಿತ್ತರು. ಈ ಕಾರ್ಯದಲ್ಲಿ ಸಮರ್ಪಕ ಯಶಸ್ಸು ಲಭಿಸಬಹುದೆಂಬ ಪೂರ್ಣ ವಿಶ್ವಾಸ ಅಂದು ಅವರಿಗೆ ಇದ್ದಂತಿತ್ತು. ಆದರೆ ಹಿಲ್ಬರ್ಟ್ನ ಈ ಎಣಿಕೆ ತಪ್ಪು ಎಂಬ ಅನಿರೀಕ್ಷಿತ ಫಲಿತಾಂಶ 1931ರಲ್ಲಿ ಕುರ್ಟ್ ಗೊಯ್ಡಲ್ನ (1906-1978) ಸಂಶೋಧನೆಗಳಿಂದ ಬೆಳಕಿಗೆ ಬಂದಿತು.
ಧನಪೂರ್ಣಾಂಕಗಳನ್ನು ಕುರಿತ ಸಾಂಪ್ರದಾಯಿಕ ಗಣಿತಶಾಖೆಯನ್ನು ಇನ್ನು ಮುಂದೆ N ಎಂದು ಸಂಕ್ಷೇಪವಾಗಿ ಸೂಚಿಸೋಣ. ಈ N ಒಂದು ಆದ್ಯುಕ್ತೀಯ ಸಿದ್ಧಾಂತ (ಆ್ಯಕ್ಸಿಯಮ್ಯಾಟಿಕ್ ಥಯೊರಿ); ಅದು ಪಿಯಾನೊ ಆದ್ಯುಕ್ತಿಗಳನ್ನೂ, ಧನ ಪೂರ್ಣಾಂಕಗಳ ಬಗ್ಗೆ (1), (2) ರಂಥ ಶ್ರದ್ಧೆಗಳನ್ನೂ ಅವಲಂಬಿಸಿ ನಿಲ್ಲುತ್ತದೆ. ಆದರೆ N ನ್ನು ಕನ್ನಡದಂಥ ಯಾವುದಾದರೊಂದು ನಿತ್ಯ ವ್ಯವಹಾರದ ಭಾಷೆಯಲ್ಲಿ ನಿರೂಪಿಸ ಹೊರಟರೆ ಆದಿಯಲ್ಲೇ ಅಸಾಂಗತ್ಯಗಳು ಕಾಣಿಸಿಕೊಂಡು ಸಿದ್ಧಾಂತವನ್ನು ಕೈಬಿಡಬೇಕಾಗಿ ಬರಬಹುದು. ಉದಾಹರಣೆಗೆ (ಗಿ) ಪಿಯಾನೊ ಆದ್ಯುಕ್ತಿಯಲ್ಲಿ ಸುಳಿದಿರುವ ಲಕ್ಷಣ ಎಂಬ ಪದವನ್ನು ಗಮನಿಸಬೇಕು. ಯಾವುದಾದರೊಂದು ಲಕ್ಷಣ a ಎಲ್ಲ ಧನಪೂರ್ಣಾಂಕಗಳಿಗೂ ಇಲ್ಲದಿರುವ ಪಕ್ಷದಲ್ಲಿ ಆ a ಲಕ್ಷಣವಿರದ ಧನಪೂರ್ಣಾಂಕಗಳ ಗಣದಲ್ಲಿ ಒಂದು ಕನಿಷ್ಠ ಧಾತು ಇರುತ್ತದೆ ಎಂದು ಪಿಯಾನೊ ಆದ್ಯುಕ್ತಿಗಳನ್ನೂ, ಸಾಧಾರಣ ಗಣಪರಿಕಲ್ಪನೆಗಳನ್ನೂ ಆಧರಿಸಿ ತೋರಿಸಬಹುದು. ಈಗ ಹತ್ತಕ್ಕಿಂತ ಕಡಿಮೆ ಕನ್ನಡ ಪದಗಳಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಲು ಶಕ್ಯವಿರುವುದೂ ಕೆಲ ಧನ ಪೂರ್ಣಾಂಕಗಳಿರುವ ಒಂದು ಲಕ್ಷಣವಷ್ಟೆ. ಕನ್ನಡ ಪದಗಳ ಗಣ ಸಾಂತ; ಧನ ಪೂರ್ಣಾಂಕಗಳ ಗಣವಾದರೋ ಅನಂತ. ಆದ್ದರಿಂದ ಈ ಲಕ್ಷಣ ಎಲ್ಲ ಧನಪೂರ್ಣಾಂಕಗಳಿಗೂ ಇರಲು ಸಾಧ್ಯವಿಲ್ಲ. ತತ್ಫಲವಾಗಿ ಹತ್ತಕ್ಕಿಂತ ಕಡಿಮೆ ಕನ್ನಡ ಪದಗಳಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಲು ಶಕ್ಯವಾಗದೆ ಇರುವ ಧನಪೂರ್ಣಾಂಕಗಳ ಗಣದಲ್ಲಿ ಒಂದು ಕನಿಷ್ಠ ಧಾತು b ಇರಬೇಕು. ಆದರೆ ಕನ್ನಡ ಭಾಷೆಯ ಮಾದ್ಯಮದಲ್ಲಿ ಇದೇ b ಯನ್ನು ಹತ್ತಕ್ಕಿಂತ ಕಡಿಮೆ ಕನ್ನಡ ಪದಗಳಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಲು 1 2 3 4 5 ಶಕ್ಯವಾಗದ ಕನಿಷ್ಠ ಧನ ಪೂರ್ಣಾಂಕ 6 7 8 9
ಎಂಬುದಾಗಿ ವ್ಯಕ್ತಪಡಿಸಬಹುದು. ಈ ಅಭಿವ್ಯಕ್ತಿಯಲ್ಲಿರುವ ಪದಗಳನ್ನು ಅವುಗಳ ಅಡಿಯಲ್ಲೇ ಎಣಿಸಿದ್ದೇವೆ. ಆ ಪದಗಳ ಸಂಖ್ಯೆ ಒಂಬತ್ತು ಮಾತ್ರವೇ ಆಗಿದೆ (ಜಿ. ಜಿ. ಬೆರಿ ಎಂಬಾತನ ಆಭಾಸ). ಇಂಥ ಅಸಾಂಗತ್ಯವನ್ನು ವ್ಯುತ್ಪಾದಿಸುವುದಕ್ಕಾಗಿ ವ್ಯಾವಹಾರಿಕ ಭಾಷೆಯೊಂದರ ವಾಕ್ಯರಚನಾ ಶೈಲಿಯ (ಸಿಂಟ್ಯಾಕ್ಸ್) ಸ್ವಚ್ಛಂದತೆಯನ್ನೂ, ಅದರ ಪದಗಳನ್ನು ಕುರಿತು ನಮಗಿರುವ ಅರ್ಥ ಪ್ರಜ್ಞೆಯನ್ನೂ ಇಲ್ಲಿ ಬಳಸಿಕೊಳ್ಳಲಾಗಿದೆ. ಆದ್ದರಿಂದಲೇ ಅಸಾಂಗತ್ಯಗಳ ಬಹಿಷ್ಕರಣ ದೃಷ್ಟಿಯಿಂದ ಗಣಿತಶಾಖೆ N ನ ನಿರೂಪಣಮಾಧ್ಯಮ ಆಖ್ಯಾತಕಲನದಂಥ (ಪ್ರೆಡಿಕೇಟ್ ಕ್ಯಾಲ್ಕ್ಯುಲಸ್; ತಾರ್ಕಿಕ ಕಲನಕ್ರಿಯೆಗಳು) ಶಿಸ್ತಿನ ಭಾಷೆಯೇ ಆಗಬೇಕು. ಮತ್ತು ಆ ನಿರೂಪಣೆಯಲ್ಲಿ ಅರ್ಥಪ್ರಜ್ಞೆಗೆ ಎಡೆಯಿರಲೇಬಾರದು ಎಂಬ ನಿಬಂಧನೆಗಳನ್ನು ಹಿಲ್ಬರ್ಟ್ ಹಾಕಿಕೊಳ್ಳುತ್ತಾನೆ. ಹೀಗೆ ರೂಪಿತವಾಗುವ N ನಲ್ಲಿ ಪ್ರಮೇಯಗಳ ಸಾಧನೆಗಳೆಲ್ಲವೂ ಕೆಲ ನಿರ್ದಿಷ್ಟ ವಿಧಿಗಳ ಮೇರೆಗೆ ಆಡಿದ ಕೆಲ ನಿರ್ದಿಷ್ಟ ಪ್ರತೀಕಗಳ ಆಟದಂತೆ ಕಾಣಿಸುತ್ತದೆ. ಇಂಥ N ನಲ್ಲಿ ಯಾವ ಅಸಾಂಗತ್ಯಗಳೂ ಇದುವರೆಗೆ ಗೋಚರಿಸಿಲ್ಲ; ಇನ್ನು ಮುಂದೆಯೂ ಗೋಚರಿಸಲಾರವು ಎಂಬ ವ್ಯಾಪಕವಾದ ಒಂದು ನಂಬಿಕೆ ಗಣಿತಜ್ಞವಲಯಗಳಲ್ಲಿದೆ. ಈಗ ಈ N ನ ಚೌಕಟ್ಟಿನೊಳಗೇ (ಪ್ರತೀಕಗಳ ಒಂದು ವಿಧ್ಯುಕ್ತ ಕ್ರೀಡೆಯಾಗಿ) ಅದರ ಸುಸಾಂಗತ್ಯವನ್ನು ಒಂದು ಪಕ್ಷ ಸಾಧಿಸಿದರೆ ಸಾಧನೆಗೆ ಮುಂಚೆಯೇ ಸಾದಿಸಬೇಕಾದುದನ್ನು ಅಂಗೀಕರಿಸಿದಂತಾಗುತ್ತದಷ್ಟೆ. ಇದು ನಿಷ್ಪ್ರಯೋಜಕವಾದ ಕಾರಣ N ನ ಸುಸಾಂಗತ್ಯದ ಸಮರ್ಥನೆ ಮಾತ್ರ ಶುದ್ಧ ಮಾರ್ಗ ಅನುಸರಿಸಬೇಕೆಂದೂ (1), (2)ರಂಥ ವಿವಾದಾಸ್ಪದ ಶ್ರದ್ಧೆಗಳನ್ನು ಕಟ್ಟುನಿಟ್ಟಾಗಿ ತೊರೆದೇ ಅದು ಸಾಗಬೇಕೆಂದೂ ಹಿಲ್ಬರ್ಟ್ ಉದ್ದೇಶಿಸಿದ. N ನೊಳಗಡೆ ನಡೆಯುವ ಪ್ರತೀಕಗಳ ಅರ್ಥವಿಮುಖಕ್ರೀಡೆ ಗಣಿತವಾದರೆ ಆ ಕ್ರೀಡೆಯ ಸುಸಾಂಗತ್ಯವನ್ನು ಕುರಿತು N ನ ಹೊರಗಡೆ ನಡೆಯುವ ಅರ್ಥಾವಲಂಬಿ ವಿವೇಚನೆ ಹಿಲ್ಬರ್ಟ್ನ ಪರಿಭಾಷೆಯಲ್ಲಿ ಅಧಿಗಣಿತ (ಮೆಟಾಮ್ಯಾಥಮ್ಯಾಟಿಕ್ಸ್) ಎಂದೆನಿಸುತ್ತದೆ.
1931ರ ಗೊಯ್ಡಲ್ ಸಂಶೋಧನೆಗಳ ಬಗ್ಗೆ ಒಂದು ಸ್ಥೂಲಪರಿಚಯವನ್ನು ಈಗ ಕಲ್ಪಿಸಿಕೊಡಬಹುದು. ಈ ಸಂಬಂಧದಲ್ಲಿ ಗೊಯ್ಡಲ್ನ ಮೂಲ ನಿರೂಪಣೆಯನ್ನು ಅನುಸರಿಸುವ ಬದಲು ಪ್ರಸಕ್ತ ಲೇಖನದಲ್ಲಿ ಒದಗಿಬಂದಿರುವ ಸಿದ್ಧತೆಗಳ ಪರಿಮಿತಿಯನ್ನು ಗಮನಿಸಿ ಸೂಕ್ತ ಮಾರ್ಪಾಡುಗಳನ್ನು ಮಾಡಿಕೊಳ್ಳುತ್ತೇವೆ. N ನಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳುವ ಬಿಡಿ ಪ್ರತೀಕ (ಅಕ್ಷರ)ಗಳ ಮಾಲೆ ಸಾಂತವಾದ ಕಾರಣ ಅವೆಲ್ಲಕ್ಕೂ ನಾವು ಯಾವುದಾದರೊಂದು ವಾದಸರಣಿಯಲ್ಲಿ ಕ್ರಮಾಂಕಗಳನ್ನು ಆರೋಪಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ, N ನ ಅಕ್ಷರಮಾಲೆಯಲ್ಲಿ S, T, X ಎಂಬ ಮೂರೇ ಅಕ್ಷರಗಳಿವೆಯೆಂದು ಭಾವಿಸೋಣ. (ನಿಜಕ್ಕೂ ಅದರಲ್ಲಿ ಇನ್ನೂ ಹೆಚ್ಚು ಅಕ್ಷರಗಳಿರಬಹುದು; ಇದರಿಂದ ತಾತ್ತ್ವಿಕ ವ್ಯತ್ಯಾಸವೇನೂ ಉಂಟಾಗುವುದಿಲ್ಲ.) ಇದಕ್ಕೆ ಅನುಕ್ರಮವಾಗಿ 0, 1, 2 ಎಂಬ ಕ್ರಮಾಂಕಗಳನ್ನು ನೀಡಬಹುದಷ್ಟೆ. N ನ ಸೂತ್ರಗಳು, ಸಾಧನೆಗಳು, ಪ್ರಮೇಯಗಳು, ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂಗಳು ಮುಂತಾದವೆಲ್ಲವೂ S, T, X ಅಕ್ಷರಗಳ ಸಾಂತಕ್ರಮ ಸಂಯೋಜನೆಗಳಾಗಿರುತ್ತವೆ. (ಫೈನೈಟ್ ಸ್ಟ್ರಿಂಗ್ಸ್) ಉದಾಹರಣೆಗೆ
TTSTTTXXSTSTXSSSTSSTTX
ಎಂಬುದು N ನ ಯಾವುದೇ ಒಂದು ಸೂತ್ರವಾಗಿರಬಹುದು. ಇದರಲ್ಲಿ ಅಕ್ಷರಗಳಿಗೆ ಬದಲು ಆಯಾ ಕ್ರಮಾಂಕಗಳನ್ನು ಆದೇಶಿಸಿದರೆ
1101112201012000100112
ಎಂಬ ಪ್ರತೀಕ ಲಭಿಸುತ್ತದೆ. ಈ ಕೊನೆಯ ಪ್ರತೀಕವನ್ನು ಒಂದು ತ್ರಿಮಾನ ಪೂರ್ಣಾಂಕವೆಂದು ಪರಿಗಣಿಸಬಹುದು. N ನಲ್ಲಿಯಾದರೂ ಧನ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಇಂಥ ತ್ರಿಮಾನ ಪ್ರತೀಕ ಯೋಜನೆಯಿಂದ ಸೂಚಿಸಿರುವುದಿಲ್ಲ. ಪ್ರಾಯಶಃ ಅಲ್ಲಿ ಅವನ್ನು T, TT, TTT ಮೊದಲಾದ T ಸಾಲುಗಳಿಂದ ವ್ಯಕ್ತಪಡಿಸುವ ಪರಿಪಾಠ ಅಂಗೀಕೃತವಾಗಿರಬಹುದು. ಹಾಗಿದ್ದಲ್ಲಿ ಮೇಲಿನ ತ್ರಿಮಾನ ಪೂರ್ಣಾಂಕವನ್ನು ಒಂದು ಉದ್ದವಾದ T ಸಾಲನ್ನಾಗಿ (ತತ್ತ್ವಶಃ) ಪರಿವರ್ತಿಸಿಡಬಹುದಷ್ಟೆ. (ಈ ಸರಳ ನಿದರ್ಶನದಲ್ಲೇ ತ್ರಿಮಾನ ಪೂರ್ಣಾಂಕದ ಅನುರೂಪ T ಸಾಲು ಒಂದು ಸಹಸ್ರ ಕೋಟಿಗಿಂತಲೂ ಹೆಚ್ಚು T ಗಳನ್ನೊಳಗೊಳುತ್ತದೆ; ಆದರೆ ನಮ್ಮ ಚರ್ಚೆ ತಾತ್ತ್ವಿಕ ತಲಕ್ಕೆ ಸೀಮಿತವಾಗಿರುವ ಕಾರಣ ಇಂಥ ಬೃಹತ್ಸರಣಿಗಳನ್ನು ನೆನೆದು ಧೃತಿಗೆಡಬೇಕಾಗಿಲ್ಲ). ಆ ಪ್ರಕಾರ ಫಲಿಸುವ T ಸಾಲನ್ನು ಮೇಲೆ ನಮೂದಿಸಿರುವ TTS... ... TX ಸೂತ್ರದ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆ ಎಂದು ಕರೆಯೋಣ. (ಮೂಲ ಸಂಶೋಧನೆಯ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಗಳು ಬೇರೆ ರೀತಿಯವಾಗಿದ್ದವು.) ಹೀಗೆ N ನ ಒಂದೊಂದು ಸೂತ್ರ, ಸಾಧನೆ, ಪ್ರಮೇಯ, ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂಗೂ N ನ ಅಕ್ಷರಮಾಲೆಯಲ್ಲೇ ವ್ಯಕ್ತಪಡಿಸಿದ ಒಂದೊಂದು ನಿರ್ದಿಷ್ಟ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆ ಇರುತ್ತದೆ, ಹಾಗೂ ಯಾವುದಾದರೊಂದು ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಯನ್ನು ಕೊಟ್ಟಾಗ ಅದಕ್ಕೆ ಅನುರೂಪವಾದ ಸೂತ್ರ ಮುಂತಾದವನ್ನು (ತತ್ತ್ವಶಃ) ಯಾಂತ್ರಿಕವಾಗಿ ಗೊತ್ತುಮಾಡಬಹುದು. N ನಲ್ಲಿ ನಿಯೋಜಿಸಲು ಸಾಧ್ಯವಿರುವ ವಿವಿಧ ಉಕ್ತಿಗಳ ವಿವಿಧ ಸಾಧನೆಗಳೆಲ್ಲವನ್ನೂ ಅವುಗಳ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಗಳನ್ನು ಆಧರಿಸಿ ಒಂದನೆಯ ಸಾಧನೆ, ಎರಡನೆಯ ಸಾಧನೆ, ಮೂರನೆಯ ಸಾಧನೆ ಎಂದು ಮೊದಲಾಗಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಅನುಕ್ರಮದಲ್ಲಿ ಬರೆಯುತ್ತ ಹೋಗಬಹುದು. ಹಾಗೆ ಬರೆಯುವಾಗ ಒಂದೊಂದು ಹೆಜ್ಜೆಯಲ್ಲೂ N ನ ಯಾವುದೇ ದತ್ತಸೂತ್ರ (ಉಕ್ತಿ)ಗಳು ಸಾಧಿತವಾದವೋ ಇಲ್ಲವೋ ಎಂಬುದನ್ನು ತಾಳೆ ನೋಡುತ್ತಲೂ ಹೋಗಬಹುದು. ಈ ಕಾರ್ಯ ಕೇವಲ ಯಾಂತ್ರಿಕವಾದ್ದರಿಂದ ಇದನ್ನು ನಿರ್ವಹಿಸಬಲ್ಲ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂಗಳನ್ನು ವಿಯೋಜಿಸಲು ಸಾಧ್ಯವಾಗಬೇಕು; ನಿಜಕ್ಕೂ ಅಂಥ ನಿಯೋಜನೆ ಶಕ್ಯವೆಂಬುದಕ್ಕೆ ಅಧಿಗಣಿತದಲ್ಲಿ ನಿಷ್ಕೃಷ್ಟ ಸಮರ್ಥನೆಯನ್ನು ನೀಡಬಹುದು.
N ವ್ಯವಸ್ಥೆಯನ್ನು ಕುರಿತಂತೆ ಅದರ ಇಂಥಿಂಥ ಸೂತ್ರಗಳಿಗೆ ಇಂಥಿಂಥ ಸಾಧನೆಗಳಿವೆ; ಮತ್ತೆ ಇಂಥಿಂಥ ಸೂತ್ರಗಳನ್ನು ಸಾಧಿಸುವುದು ಅಸಾಧ್ಯ, ಇಂಥಿಂಥ ವಾಕ್ಯ(ಪದ)ಗಳ ಮೇಲೆ ಇಂಥಿಂಥ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂಗಳನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಇಂಥಿಂಥ ಫಲಿತಾಂಶಗಳು ಲಭಿಸುತ್ತವೆ ಎಂದು ಮುಂತಾಗಿ ಮಾತನಾಡಿಕೊಳ್ಳಬಹುದಷ್ಟೆ. ಈ ಬಗೆಯ ವರ್ಣನೆಗಳೆಲ್ಲವೂ ಅಧಿಗಣಿತದ ಪ್ರಾಂತಕ್ಕೆ ಸೇರಿದವು. ನಮ್ಮ ದೃಷ್ಟಿಯನ್ನು ಇವುಗಳಲ್ಲಿ ಉಲ್ಲೇಖವಾಗುವ ಸೂತ್ರ, ಸಾಧನೆ, ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂ ಮುಂತಾದವುಗಳಿಂದ ಅವುಗಳ ಅನುರೂಪ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಗಳತ್ತ ಹೊರಳಿಸಿದರೆ ಈ ವಿದ್ಯಮಾನಗಳೆಲ್ಲ ಆ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಗಳ ನಡುವೆ ಏರ್ಪಡುವ ಕೆಲವಷ್ಟು ಸಂಬಂಧಗಳಾಗಿ ಗೋಚರಿಸುತ್ತವೆ. ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಗಳು ಕೇವಲ ಧನ ಪೂರ್ಣಾಂಕಗಳಾದ ಕಾರಣ N ವ್ಯವಸ್ಥೇ ಸಾಕಷ್ಟು ಸತ್ತ್ವಯುತವಾಗಿದ್ದಲ್ಲಿ ಅವುಗಳ ನಡುವಿನ ಇಂಥ ಸಂಬಂಧಗಳನ್ನು N ನ ಪ್ರತೀಕಾತ್ಮಕ ಅಂತರ್ಭಾಷೆಯಲ್ಲೇ ಅಭಿವ್ಯಕ್ತಿಸಲು ಶಕ್ಯವಾಗಬೇಕು. N ಭಾಷೆಗೆ ನಿಜಕ್ಕೂ ಈ ರೀತಿಯ ಸಾಮರ್ಥ್ಯವಿದೆಯೆಂದು ಇನ್ನು ಮುಂದೆಲ್ಲ ಭಾವಿಸುತ್ತೇವೆ. ಅಂದಮೇಲೆ, ಮೇಲೆ ನಿದರ್ಶಿಸಿರುವಂಥ ಸುಸ್ಪಷ್ಟ ಅರ್ಥದ ಅಧಿಗಣಿತೀಯ ವರ್ಣನೆಗಳೊಂದೊಂದಕ್ಕೂ ಅನುರೂಪವಾಗಿ N ಭಾಷೆಯಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಗಳನ್ನು ಕುರಿತ ಒಂದೊಂದು ಪ್ರತೀಕಾತ್ಮಕ ಸೂತ್ರ (ಉಕ್ತಿ) ಇರುತ್ತದೆಂದಾಯಿತು. ಪ್ರತೀಕಾತ್ಮಕ ಸೂತ್ರಗಳನ್ನು ಆಯಾ ಅಧಿಗಣಿತೀಯ ವರ್ಣನೆಗಳ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರಗಳು ಎಂದು ಕರೆಯೋಣ. ಸ್ಪಷ್ಟಾರ್ಥಯುಕ್ತ ಅಧಿಗಣಿತೀಯ ವರ್ಣನೆಯೊಂದರ ಬಗ್ಗೆ ನಿತ್ಯವ್ಯವಹಾರದ ಕನ್ನಡ ಭಾಷೆಯಲ್ಲಿ ಒಂದು ಸಮರ್ಥನೆಯನ್ನು ನೀಡಲು ಸಾಧ್ಯವಾಗುವ ಸಂದರ್ಭಗಳಲ್ಲೆಲ್ಲ ಅದರ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರವನ್ನು ಕುರಿತು N ನಲ್ಲಿ ಒಂದು ವಿಧ್ಯುಕ್ತ ಸಾಧನೆಯನ್ನು ರೂಪಿಸುವುದಕ್ಕೂ ಸಾಧ್ಯವಾಗುವುದೆಂದು ಭಾವಿಸುತ್ತೇವೆ. ಈಗ x ಎಂಬುದು N ನ ಯಾವುದಾದರೊಂದು ವಾಕ್ಯ(ಪದ)ವೂ M ಎಂಬುದು ಇದೇ ವ್ಯವಸ್ಥೆಯ ಒಂದು ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಮೂ ಆದಲ್ಲಿ
(Mx). x ನ ಮೇಲೆ M ನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರುತ್ತದೆ
(~Mx). x ನ ಮೇಲೆ M ನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರುವುದಿಲ್ಲ
ಎಂಬ ಎರಡು ಅಧಿಗಣಿತೀಯ ವರ್ಣನೆಗಳಿಗೆ ವಿಶೇಷ ಪ್ರಾಶಸ್ತ್ಯವುಂಟು. ಇವುಗಳ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರಗಳನ್ನು ಅನುಕ್ರಮವಾಗಿ M(x) ಮತ್ತು ~M(x) ಎಂಬುದಾಗಿ ಸೂಚಿಸೋಣ. (Mx), (~Mx) ಕನ್ನಡದ ವಾಕ್ಯಗಳು; M(x), ~M(x) ಆದರೋ N ನ ಸಂಕೇತಗಳ ಸರಪಣಿಗಳು ಎಂಬುದನ್ನು ಗಮನಿಸಬೇಕು. ಅಷ್ಟೇ ಅಲ್ಲದೆ M(x), ~M(x) ಗಳಿಗೆ ಅಧಿಗಣಿತ ಪ್ರಾಂತದಲ್ಲಿ ಅರ್ಥ ಕಲ್ಪಿಸಿದರೂ ಅವು (Mx), (~Mx) ಆಗಿ ಮರುಪರಿವರ್ತಿತವಾಗುವ ಬದಲು ಒಂದಷ್ಟು ಧನಪೂರ್ಣಾಂಕಗಳ ನಡುವಿನ ಕೆಲವು ನಿರ್ದಿಷ್ಟ ಸಂಬಂಧಗಳನ್ನು ಮಾತ್ರವೇ ಪ್ರತಿಫಲಿಸುತ್ತವೆ. M(x) ಇಲ್ಲವೇ ~M(x) ನ್ನು N ನಲ್ಲಿ ಸಾಧಿಸಲು ಸಾಧ್ಯವಾದರೂ ಆಗಬಹುದು, ಇಲ್ಲದಿದ್ದರೂ ಇಲ್ಲ; ಒಂದು ವೇಳೆ ಅಲ್ಲಿ ಅವೆರಡನ್ನೂ ಸಾಧಿಸಲು ಶಕ್ಯವಾದರೆ N ಅಸಂಗತವೆನಿಸಿಕೊಳ್ಳುತ್ತದೆ.
ಈಗ x ಎಂಬುದು N ನ ಅಕ್ಷರಮಾಲೆಯಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಿರುವ ಒಂದು ಧನ ಪೂರ್ಣಾಂಕವಾಗಿರಲಿ. ಈ x ಯಾವುದಾದರೂ ಒಂದು ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂನ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆ ಆಗಿರಬಹುದು; ಅಂಥ ಸಂದರ್ಭದಲ್ಲಿ ಆ ನಿರ್ದಿಷ್ಟ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂನ್ನು x* ಎಂಬ ಪ್ರತೀಕದಿಂದ ಸೂಚಿಸೋಣ. ಒಂದು ವೇಳೆ x ಯಾವೊಂದು ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂನ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆಯೂ ಆಗಿಲ್ಲದಿದ್ದರೆ x* ಎಂಬುದು ಯಾವುದೇ ಪದ y ಯನ್ನು yT, yTT, yTTT ಎಂದು ಮೊದಲಾಗಿ ಕೊನೆಯೇ ಇಲ್ಲದಂತೆ ಲಂಬಿಸುತ್ತ ಹೋಗುವ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂನ್ನು ನಿರ್ದೇಶಿಸಲಿ. ಅಧಿಗಣಿತೀಯ ಉಕ್ತಿಗಳಾದ
(x*x). x ಮೇಲೆ x* ವನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರುತ್ತದೆ;
(~x*x). x ಮೇಲೆ x* ವನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರುವುದಿಲ್ಲ
ಎಂಬವಕ್ಕೆ ಅನುರೂಪವಾಗಿ N ನಲ್ಲಿ x*(x) ಮತ್ತು ~x*(x) ಎಂಬ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರಗಳಿರುತ್ತವಷ್ಟೆ. ಆಗಲೇ ತಿಳಿಸಿರುವಂತೆ N ನ ಸಾಧನೆಗಳೆಲ್ಲವನ್ನೂ ಒಂದು ವ್ಯವಸ್ಥಿತ ಅನುಕ್ರಮದಲ್ಲಿ ಬರೆಯುತ್ತ ಹೋದಾಗ x*(x) ಮತ್ತು ~x(*x) ಗಳ ಸಾಧನೆಗಳು ಗೋಚರಕ್ಕೆ ಬರುತ್ತವೋ ಇಲ್ಲವೋ ಎಂಬ ಬಗ್ಗೆ ಹೆಜ್ಜೆ ಹೆಜ್ಜೆಗೂ ಯಾಂತ್ರಿಕವಾಗಿ ತನಿಖೆ ನಡೆಸಬಹುದು. ಹೀಗೆ ಮಾಡುವಾಗ x*(x) ನದಕ್ಕಿಂತ ಮುನ್ನ ~x*(x) ನ ಒಂದು ಸಾಧನೆ ಕಾಣಿಸಿಕೊಂಡರೆ ನಮ್ಮ ತನಿಖೆಯನ್ನು ಅಷ್ಟಕ್ಕೇ ನಿಲ್ಲಿಸೋಣ. ಬದಲು ~x*(x) ನದಕ್ಕಿಂತ ಮುಂಚೆ x*(x) ನ ಸಾಧನೆ ಕಣ್ಣಿಗೆ ಬಿದ್ದರೆ ಆ ಸಾಧನೆಯ ಮುಂದೆ T, TT, TTT ಎಂದು ಮೊದಲಾಗಿ ಕೊನೆಯೇ ಇಲ್ಲದಂತೆ ಬರೆಯುತ್ತ ಹೋಗೋಣ. ಯಾಂತ್ರಿಕವಾದ ಈ ಕಾರ್ಯವನ್ನೂ x ಮೇಲೆ ಪ್ರಯೋಗಿಸಬಹುದಾದ ಒಂದು ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂ L ನಿಂದ ನಿರ್ವಹಿಸಲು ಶಕ್ಯವಾಗುವುದು. x ಮೇಲೆ L ನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರಬೇಕಿದ್ದರೆ N ನ ಸಾಧನೆಗಳ ಅನುಕ್ರಮದಲ್ಲಿ ~x*(x) ನ ಒಂದು ಸಾಧನೆ ಇರಬೇಕಲ್ಲದೆ ಆ ಸಾಧನೆಗಿಂತ ಮುಂಚೆ x*(x) ನ ಯಾವ ಸಾಧನೆಯೂ ಕಾಣಿಸಿಕೊಳ್ಳಬಾರದು. (ಗೊಯ್ಡಲ್ನ ಮೂಲ ಸಂಶೋಧನೆಯಲ್ಲಿ ಈ L ಗೆ ಅನುರೂಪವಾದ ಪರಿಕರ್ಮಕ್ಕೆ ಬದಲಾಗಿ ಬೇರೊಂದು ಪರಿಕರ್ಮ ಪ್ರಮುಖ ಪಾತ್ರವನ್ನು ವಹಿಸಿತ್ತು; L ಗೆ ಅನುರೂಪವಾದ ಪರಿಕರ್ಮಕ್ಕೆ ಅಧಿಕತರ ಉಪಯುಕ್ತತೆ ಇರುವುದನ್ನು 1936ರಲ್ಲಿ ಬಾರ್ಕ್ಲೆ ರಾಸರ್ ಪತ್ತೆ ಹಚ್ಚಿದ.) ಈ L ನ ಗೊಯ್ಡಲ್ ಸಂಖ್ಯೆ g ಆಗಿರಲಿ. ಅಂದಮೇಲೆ L ಎಂದರೂ ಒಂದೇ, g* ಎಂದರೂ ಒಂದೇ: g* = L. ಸ್ವಾರಸ್ಯಕರ ಪ್ರಶ್ನೆಯೊಂದು ಈಗ ನಮ್ಮ ಮುಂದೆ ಏಳುತ್ತದೆ: L(g) = g*(g) ಮತ್ತು ~L(g) = ~g*(g) ಇವೆರಡು ಉಕ್ತಿಗಳ ಪೈಕಿ N ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಯಾವುದನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯ? ಈ ಬಗ್ಗೆ ವಿವೇಚಿಸಲು g*(g) ಗೆ ಒಂದು ಸಾಧನೆ P ಯನ್ನು ರೂಪಿಸುವುದಕ್ಕೆ ಸಾಧ್ಯವಾಗುವುದೆಂದು ಭಾವಿಸೋಣ. N ನ ಸಾಧನೆಗಳ ಅನುಕ್ರಮದೊಳಗೆ ಈ P ಯಾವುದೋ ಒಂದು ಸ್ಥಾನದಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ. ಆಗ ಆದಿಯಿಂದ P ವರೆಗಿನ ಸಾಧನೆಗಳನ್ನು (ಇವುಗಳ ಸಂಖ್ಯೆ ಸಾಂತವೆನ್ನುವುದನ್ನು ಗಮನಿಸಬೇಕು) ಒಂದೊಂದಾಗಿ ಪರಿಶೀಲಿಸಿ N ಸಾಧನೆಗಳ ಅನುಕ್ರಮದಲ್ಲಿ ಮೊದಲು ಸಾಧಿತವಾಗುವುದು g*(g) ಯೋ ಇಲ್ಲವೇ ~g*(g) ಯೋ ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸಬಹುದಷ್ಟೆ. ಹಾಗೆ ಮೊದಲು ಸಾಧಿತವಾಗುವುದು ~g*(g) ಆದ ಪಕ್ಷದಲ್ಲಿ N ನೊಳಗೆ g*(g) ಮತ್ತು ~g*(g) ಗಳೆರಡರ ಸಾಧನೆಗಳೂ ಕಾಣಿಸಿಕೊಂಡು N ಅಸಂಗತವಾಗುವುದು. ಇದಕ್ಕೆ ಪ್ರತಿಯಾಗಿ ಮೊದಲು ಸಾಧಿತವಾಗುವುದು g*(g) ಎಂದು ಭಾವಿಸಿದರೆ g ಯ ಮೇಲೆ L ನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಸಾಧನೆಗಳ ತನಿಖೆಯಲ್ಲಿ g*(g) ಯ ಸಾಧನೆ ಮುಂಚಿತವಾಗಿ ಗೋಚರಕ್ಕೆ ಬಂದು L ಕ್ರಿಯೆಯಿಂದ ಆ ಸಾಧನೆಯ ಮುಂದೆ T, TT, TTT ಇತ್ಯಾದಿ ಅಕ್ಷರಗಳು ಕೊನೆಯೇ ಇಲ್ಲದಂತೆ ಲಿಖಿತವಾಗುತ್ತ ಹೋಗುವುವು. ಅಂದ ಮೇಲೆ ಈ ಸಂದರ್ಭದಲ್ಲಿ g ಯನ್ನು ಕುರಿತಂತೆ L ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರುವುದೇ ಇಲ್ಲ. ಇದರಿಂದ ಅಧಿಗಣಿತೀಯ ಉಕ್ತಿ (~Lg) ಸಮರ್ಥಿತವಾದಂತಾಯಿತು. N ವ್ಯವಸ್ಥೆ ಸಾಕಷ್ಟು ಸತ್ತ್ವಯುತವಿರುವಾಗ ಇದೇ ಸಮರ್ಥನೆಯನ್ನು N ನ ಅಧಿಕೃತ ಭಾಷೆಯಲ್ಲಿ ~L(g) [ = ~g*(g)] ಉಕ್ತಿಯ ಸಾಧನೆಯನ್ನಾಗಿ ಪರಿವರ್ತಿಸಬಹುದು. ಅಂದರೆ ಈಗಲೂ N ನೊಳಗೆ g*(g) ಮತ್ತು ~g*(g) ಗಳೆರಡರ ಸಾಧನೆಗಳೂ ಗೋಚರಿಸಿ N ಅಸಂಗತವಾಗುತ್ತದೆ ಎಂದಾಯಿತು. ಅಲ್ಲಿಗೆ N ನಲ್ಲಿ g*(g) ಗೆ ಸಾಧನೆಯೊಂದನ್ನು ನಿಯೋಜಿಸಲು ಶಕ್ಯವಿರುವಾಗಲೆಲ್ಲ N ಅಸಂಗತವಾಗಿಯೇ ತೀರುವುದು. ಇದೇ ಮೇರೆಗೆ N ನಲ್ಲಿ ~g*(g) ಯನ್ನು ಕುರಿತು ಸಾಧನೆ ನೀಡಲು ಶಕ್ಯವಾದಾಗಲೂ N ಅಸಂಗತವಾಗುತ್ತದೆಂದು ಸುಲಭವಾಗಿ ತೋರಿಸಬಹುದು. N ನಿಜಕ್ಕೂ ಸುಸಂಗತ ಎಂಬ ವಿಶ್ವಾಸ ನಮಗಿದ್ದರೆ ಅದರ ಚೌಕಟ್ಟಿನೊಳಗೆ g*(g) ಯನ್ನೂ ಸಾಧಿಸಲು ಶಕ್ಯವಿಲ್ಲ, ~g*(g) ಯನ್ನೂ ಸಾಧಿಸಲು ಶಕ್ಯವಿಲ್ಲ ಎಂದು ನಂಬಲು ಸಹ ನಾವು ಸಿದ್ಧರಿರಬೇಕು. ಒಂದು ಉಕ್ತಿ ಮತ್ತು ಅದರ ನಿಷೇಧ ಇವೆರಡರ ಪೈಕಿ ಒಂದಲ್ಲ ಒಂದನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯವಾಗಲೇಬೇಕೆಂಬ ಎಣಿಕೆ ಇಲ್ಲಿ ತಪ್ಪಾಗಿಬಿಟ್ಟಿತು. ಇದೇ ಗೊಯ್ಡಲ್ನ ಸುಪ್ರಸಿದ್ಧ ಪ್ರಥಮ ಪ್ರಮೇಯ.
ಮೇಲಿನ ಪರಿಸ್ಥಿತಿಗೆ ಒಂದು ಸ್ಥೂಲ ಉಪಮಾನವನ್ನು ನೀಡುವ ಸಲುವಾಗಿ (F), ಕೆಳಗೆ ಲಿಖಿತವಾಗಿರುವ (~F) ಉಕ್ತಿಯನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯವಿದೆ; (~F). (~F) ಎಂಬ ಈ ಉಕ್ತಿಯನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ ಎಂಬ ನಿತ್ಯವ್ಯಾವಹಾರಿಕ ಭಾಷೆಯ ವಾಕ್ಯಗಳನ್ನು ಆಯ್ಕೆಮಾಡಿಕೊಳ್ಳುವುದು ಜನಪ್ರಿಯವಾಗಿದೆ. ಇವುಗಳ ಪೈಕಿ (F) ಗೆ ಸಾಧನೆಯೊಂದನ್ನು ರೂಪಿಸಬೇಕಾದಲ್ಲಿ (~F) ನ್ನು ಹೇಗೆ ಸಾಧಿಸಬಹುದೆಂದು ಅದರಲ್ಲಿ ತಿಳಿಸಬೇಕಾಗುವ ಕಾರಣ ಆ (F) ನ ಸಾಧನೆಯಲ್ಲಿ (~F) ನ ಸಾಧನೆಯೂ ಅಡಕವಾಗಿ ಅಸಾಂಗತ್ಯ ತಲೆದೋರುವುದು; ಬದಲು (~F) ಗೆ ಸಾಧನೆ ಕೊಡಲು ಶಕ್ಯವಿದ್ದಲ್ಲಿ ಆ ಸಾಧನೆಯೇ (F) ನ ಸಾಧನೆಯೂ ಆಗಿ ಪರಿಣಮಿಸಿ ಮತ್ತೆ ಅಸಾಂಗತ್ಯ ಉದ್ಭವಿಸುತ್ತದೆ. ಆದರೆ ನಿಜಕ್ಕೂ ಈ ಉಪಮಾನ ತೀರ ಸರಳೀಕೃತವೆನ್ನದೆ ವಿಧಿಯಿಲ್ಲ. ಇದರ ಪರಿಶೀಲನೆಯಿಂದ ಗೊಯ್ಡಲ್ ಪ್ರಮೇಯ ಪೂರ್ಣಾಂಕಗಳ ಗಣಿತಕ್ಕೆ ದೂರವೂ ಮಹತ್ತ್ವರಹಿತವೂ ಆದ ಕೇವಲ ಒಂದು ಚಮತ್ಕಾರಿಕ ಭಾಷಾಶ್ಲೇಷೆ (ಕ್ವಿಬ್ಲಿಂಗ್) ಎಂಬ ಅಭಿಪ್ರಾಯ ಮೂಡಬಹುದು. (F) ಮತ್ತು (~F) ಗಳು ಹೆಚ್ಚೆಂದರೆ ಅಧಿಗಣಿತೀಯ (g*g) ಮತ್ತು (~g*g) ಗಳಿಗೆ ಸದೃಶ್ಯವಾಗಬಹುದೇ ವಿನಾ ಅವುಗಳ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರ g*(g) ಮತ್ತು ~g*(g) ಗಳಿಗಿಲ್ಲ. ಅಧಿಗಣಿತ ಪ್ರಾಂತದಲ್ಲಿ ಈ g*(g) ಮತ್ತು ~g*(g) ಗಳಿಗೆ ಮತ್ತೆ ಅರ್ಥಕಲ್ಪಿಸಿದಾಗ ಅವು ಯಾವುದೇ ಶ್ಲೇಷೆಯ ಸೋಂಕಿಲ್ಲದೆ ಧನಪೂರ್ಣಾಂಕಗಳ ನಡುವಿನ ನೂರಕ್ಕೆ ನೂರರಷ್ಟು ಅಪ್ಪಟ ಗಣಿತ ಸಂಬಂಧಗಳನ್ನು ಮಾತ್ರ ವ್ಯಕ್ತಪಡಿಸುವುವು. ಇಂಥ ಸದಭಿವ್ಯಕ್ತಿ ಸಂಬಂಧಗಳನ್ನು N ನಲ್ಲಿ ವಿಧ್ಯುಕ್ತವಾಗಿ ಸಾಧಿಸಲು ಇಲ್ಲವೆ ನಿರಾಕರಿಸಲು ಪ್ರಯತ್ನಿಸುವುದೂ ಒಂದೇ, N ವ್ಯವಸ್ಥೆಯೇ ಅಸಂಗತ ಎಂದು ತೋರಿಸಲು ಯತ್ನಿಸುವುದೂ ಒಂದೇ ಎಂಬ ಅನಿರೀಕ್ಷಿತ ಆವಿಷ್ಕಾರ ಇಪ್ಪತ್ತನೆಯ ಶತಮಾನದ ಆದಿಭಾಗದವರೆಗೂ ಗಣಿತಜ್ಞ ವಲಯಗಳಲ್ಲಿ ಬೇರೂರಿ ನಿಂತಿದ್ದ ಪ್ರಬಲ ತಾತ್ತ್ವಿಕ ಶ್ರದ್ಧೆಯೊಂದನ್ನು ಬುಡಮೇಲಾಗಿಸಿತು.
ಕೊನೆಯದಾಗಿ ಈಗ (G) N ವ್ಯವಸ್ಥೆ ನಿಜಕ್ಕೂ ಸುಸಂಗತ ಎಂಬ ಅಧಿಗಣಿತೀಯ ಉಕ್ತಿಯಲ್ಲಿ ವಿಶ್ವಾಸವಿರಿಸಿ g*(g), ~g*(g) ಗಳ ಗೊಯ್ಡಲ್ಪೂರ್ವ ರೂಪಗಳಾದ g*g, ~g*g ಗಳ ಬಗ್ಗೆ ತುಸು ಆಲೋಚಿಸೋಣ:
(g*g). g ಮೇಲೆ g*[=L] ಎಂಬ ಮಾರ್ಕಫ್ ಆಲ್ಗಾರಿತಂನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರುತ್ತದೆ;
(~ g*g). g ಮೇಲೆ g*[=L] ನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರುವುದಿಲ್ಲ.
x ಮೇಲೆ L ನ್ನು ಪ್ರಯೋಗಿಸಿದಾಗ ಆಲ್ಗಾರಿತಂ ಕ್ರಿಯೆ ನಿಲುಗಡೆಗೆ ಬರಬೇಕಿದ್ದಲ್ಲಿ N ನೊಳಗೆ ~x*(x) ನ ಒಂದು ಸಾಧನೆ ಇರಬೇಕೆಂಬ ಅಂಶವನ್ನು ಸ್ಮರಿಸಿಕೊಳ್ಳಬೇಕು. ಆದ್ದರಿಂದ ಮೇಲಿನ ಉಕ್ತಿಗಳ ಪೈಕಿ g*(g) ಸಾಧಿತವಾಗುವುದಲ್ಲದೆ ಇನ್ನೊಂದು ಕಡೆ N ನ ಸಾಧನೆಗಳ ಅನುಕ್ರಮದಲ್ಲಿ ~g*(g) ಯ ಸಾಧನೆಯೂ ಗೋಚರಿಸಬೇಕಾಗುತ್ತದೆ. ನಮ್ಮ ವಿಶ್ವಾಸ (G) ಗೆ ಇದು ವ್ಯತಿರಿಕ್ತವಾದ ಕಾರಣ (g*g) ನಿರಾಕರಣೀಯ, (~g*g) ಸಮರ್ಥನೀಯ. ಅಂದಮೇಲೆ (G) ಸಮರ್ಥನೀಯವಾದಲ್ಲಿ (~g*g) ಕೂಡ ಸಮರ್ಥನೀಯ ಎಂದಾಯಿತು. ಇದರಿಂದ N ವ್ಯವಸ್ಥೆಯೊಳಗೆ (G) ಯ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರವನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯವಾಗುವುದಾದರೆ ~g*(g) ನ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರ ~g*(g) ಯನ್ನೂ ಅಲ್ಲಿ ಸಾಧಿಸಲು ಶಕ್ಯವಾಗುತ್ತದೆಂದು ತೀರ್ಮಾನಿಸಬಹುದು. ಆದರೆ ಪ್ರಥಮ ಗೊಯ್ಡಲ್ ಪ್ರಮೇಯದಿಂದ ~g*(g) ಸಾಧಿತವಾದೊಡನೆಯೇ N ಅಸಂಗತವಾಗಿಬಿಡುವುದು. ಆದ್ದರಿಂದ ನಾವು (G) ಯನ್ನು ಸಾಧಿಸಲು ಪ್ರಯತ್ನಿಸುವುದೂ ಒಂದೇ [ಅಧಿಗಣಿತದಲ್ಲಿ (G) ಸಮರ್ಥಿತವಾದ ಕೂಡಲೇ N ನಲ್ಲಿ ಅದರ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರವೂ ಸಾಧಿತವಾಗುವುದು] N ವ್ಯವಸ್ಥೆ ಅಸಂಗತವೆಂದು ತೋರಿಸಲು ಯತ್ನಿಸುವುದೂ ಒಂದೇ. ಈ ಅನಿರೀಕ್ಷಿತ ಫಲಿತಾಂಶವೇ ಗೊಯ್ಡಲ್ ದ್ವಿತೀಯ ಪ್ರಮೇಯ. ಹಿಲ್ಬರ್ಟ್ ಸಂಶಯಾತೀತವಾದ ಅರ್ಥಾವಲಂಬಿ ಮಾರ್ಗಗಳಿಂದ N ನ ಸುಸಾಂಗತ್ಯವನ್ನು [ಅಂದರೆ (G) ಉಕ್ತಿಯನ್ನು] ಸಮರ್ಥಿಸ ಹೊರಟನಷ್ಟೆ. ಅವನು ಆಲೋಚಿಸಿದಂಥ ಮಾರ್ಗಗಳಿರಲಿ, ಅವುಗಳ ಜೊತೆಗೆ N ನಲ್ಲಿ ಅಂಗೀಕೃತವಾಗಿರುವ ಇನ್ನುಳಿದ ಸಂದೇಹಪೀಡಿತ ಮಾರ್ಗಗಳೆಲ್ಲವನ್ನೂ ಬಳಸಿಕೊಂಡರೂ N ನಿಜಕ್ಕೂ ಸುಸಂಗತವಾಗಿರುವುದಾದರೆ ಅದರ ಸುಸಾಂಗತ್ಯವನ್ನು ಯಾರೂ ಸಾಧಿಸಲು ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ. ಇದಾವುದೇ ಮಾರ್ಗಗಳಿಂದ (G) ಸಾಧಿತವಾಗುವುದಾದರೆ ಏಕಕಾಲೀಯವಾಗಿ (~G). N ವ್ಯವಸ್ಥೆ ನಿಜಕ್ಕೂ ಅಸಂಗತ ಎಂಬುದೂ ಸಾಧಿತವಾಗಿಬಿಡುವುದು.
N ನಲ್ಲಿ g*(g), ~g*(g) ಯ ಗೊಯ್ಡಲ್ ರೂಪಾಂತರ ಇವೇ ಮೊದಲಾದ ಉಕ್ತಿಗಳಿಗೆ ಅನಿರ್ಧರಣೀಯ ಸೂತ್ರಗಳು (ಅನ್ಡಿಸೈಡಬಲ್ ಫಾರ್ಮ್ಯುಲೇ) ಎಂದು ಹೆಸರು. ಇವುಗಳ ನಿರುಪಾಧಿಕ ಸತ್ಯಾಸತ್ಯತೆಗಳ ಬಗ್ಗೆ ವಿವಾದ ತಲೆದೋರುವುದು ಸ್ವಾಭಾವಿಕ. ಧನ ಪೂರ್ಣಾಂಕಗಳಿಗೆ ಅವನ್ನು ಕುರಿತು ಚಿಂತಿಸುವ ಯಾವುದೇ ಬುದ್ಧಿಶಕ್ತಿಯಿಂದ ಸ್ವತಂತ್ರವಾದ ಅಸ್ತಿತ್ವವುಂಟು ಎಂದು ಗೊಯ್ಡಲ್ನೂ ಸೇರಿದಂತೆ ಒಂದು ಗುಂಪಿನ ಗಣಿತ ತಾತ್ತ್ವಿಕರು ನಂಬುತ್ತಾರೆ. ಇಂಥವರಿಗೆ ಪ್ಲೇಟೋವಾದಿಗಳು ಎನ್ನಬಹುದು. ಇವರ ಪ್ರಕಾರ ಅನಿರ್ಧರಣೀಯ ಸೂತ್ರಗಳೂ ದಿಟ ಇಲ್ಲವೆ ಸಟೆ ಆಗಿರಲೇಬೇಕು; N ನಂಥ ವ್ಯವಸ್ಥೆಗಳ ಚೌಕಟ್ಟಿನಲ್ಲಿ ಅವು ದಿಟವೊ ಸಟೆಯೊ ತೀರ್ಮಾನಿಸಲು ಸಾಧ್ಯವಾಗದೆ ಇರುವುದಕ್ಕೆ ಆ ವ್ಯವಸ್ಥೆಗಳು ಒಳಗೊಳ್ಳುವ ಆದ್ಯುಕ್ತಿಗಳ ಹಾಗೂ ಸಾಧನಮಾರ್ಗಗಳ ಅಪರಿಪೂರ್ಣತೆಯೇ ಕಾರಣ. ಉದಾಹರಣೆಗೆ (G) ಉಕ್ತಿಯಲ್ಲಿ ವಿಶ್ವಾಸವಿರಿಸಿ ಮೇಲಿನ ~g*(g) ಸಮರ್ಥನೀಯವೆಂದು ಮನಗಂಡೆವಷ್ಟೆ. ಇದು ನೇರ ಅರ್ಥ ಪ್ರಜ್ಞೆಯ ಫಲ ಎಂದು ಪರಿಗಣಿಸಿ ಆ ಮೂಲಕ ನಿಜವಾದ ಧನ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಕುರಿತಂತೆ ~g*(g) ಸತ್ಯವೆಂದೂ, g*(g) ಅಸತ್ಯವೆಂದೂ ಈ ಮೊದಲನೆಯ ಗುಂಪಿನ ತಾತ್ತ್ವಿಕರು ನಂಬಬಹುದು. ನೇರ ಅರ್ಥಪ್ರಜ್ಞೆ ಚೆಲ್ಲುವಷ್ಟು ಬೆಳಕನ್ನು N ವ್ಯವಸ್ಥೆಯ ಆದ್ಯುಕ್ತೀಯ ಸಾಧನಮಾರ್ಗಗಳು ಚೆಲ್ಲಲಾರವೇ ಹೊರತಾಗಿ ಆ ಬೆಳಕೇ ಇಲ್ಲವೆನ್ನಲಾಗದು ಎಂಬುದು ಇವರ ಅಭಿಮತ. ಮತ್ತೊಂದು ಗುಂಪಿನ ಗಣಿತತಾತ್ತ್ವಿಕರಾದರೋ ಅನಂತದ ಪ್ರಾಂತದಲ್ಲಿ ಮೇಲಿನಂಥ ನೇರ ಅರ್ಥಪ್ರಜ್ಞೆಯ, ಹಾಗೂ ನಿರುಪಾಧಿಕ ಸತ್ಯಾಸತ್ಯತೆಗಳ, ಪರಿಕಲ್ಪನೆಯೇ ಮಿಥ್ಯ ಎಂದು ಅಭಿಪ್ರಾಯ ಪಡುತ್ತಾರೆ. ಇವರ ಪ್ರಕಾರ ಧನ ಪೂರ್ಣಾಂಕಗಳು ಕೇವಲ ಒಂದು ಬೌದ್ಧಿಕ ಉಪಜ್ಞೆಯೇ (ಇನ್ವೆನ್ಷನ್) ಹೊರತು ಸ್ವತಂತ್ರ ಅಸ್ತಿತ್ವವಿರುವ ಧಾತುಗಳಲ್ಲ; ಅವು ನಾವು ಹೇಗೆ ನಿರ್ಮಿಸುತ್ತೇವೋ ಹಾಗೆ ರೂಪತಾಳುತ್ತವೆ. ಮೇಲಾಗಿ ಅನಂತ ಪ್ರಾಂತದಲ್ಲಿ ಮಾನವನ ಸೃಷ್ಟಿಕ್ರಿಯೆ ಎಂದೂ ಪೂರ್ಣಗೊಳ್ಳುವುದೇ ಇಲ್ಲ. ಅಪೂರ್ಣ ಕಾದಂಬರಿಯೊಂದರಲ್ಲಿ ನಾಯಕನ ಭವಿಷ್ಯವನ್ನು ಕುರಿತು ಪ್ರಶ್ನೆ ಇನ್ನೂ ಅನಿರ್ಧರಿತವಾಗಿಯೇ ಉಳಿದಿರಬಹುದಷ್ಟೆ. ಅಂತೆಯೇ N ನಂಥ ಉಪಜ್ಞಿತ ವ್ಯವಸ್ಥೆಗಳಲ್ಲೂ ~g*(g) ಮಾದರಿಯ ಅನಿರ್ಧರಣೀಯ ಸೂತ್ರಗಳು ಗೋಚರಿಸುವುದರಲ್ಲಿ ಅಚ್ಚರಿಯೇನಿಲ್ಲ. ಧನ ಪೂರ್ಣಾಂಕಗಳ ಕಾದಂಬರಿಯನ್ನು ಕನ್ನಡದಂಥ ನಿತ್ಯವ್ಯಾವಹಾರಿಕ ಭಾಷೆಯಲ್ಲಿ ರಚಿಸತೊಡಗಿದಾಗ ಪಿಯಾನೊ ಆದ್ಯುಕ್ತಿಗಳು ಅದನ್ನು ಅಂತಿಮ ಪರಿಸಮಾಪ್ತಿಯವರೆಗೂ ಕೊಂಡೊಯುತ್ತವೆಂಬ ಮಿಥ್ಯೆ ಉದ್ಭವಿಸುತ್ತದೆ. ಆದರೆ ಹಾಗೆ ರಚಿಸಿದ ಕಾದಂಬರಿ ಅಸಂಗತವೂ ಆಗುವ ಅಪಾಯವನ್ನು ಈಗಾಗಲೇ ಮನಗಂಡಿದ್ದೇವೆ. ವ್ಯಾವಹಾರಿಕ ಭಾಷೆಗೆ ಪ್ರತಿಯಾಗಿ ಸೂಕ್ತ ಪ್ರತೀಕಾತ್ಮಕ ಭಾಷೆಯೊಂದನ್ನು (ಸಿಂಬಾಲಿಕ್ ಲ್ಯಾಂಗ್ವೇಜ್) ಬಳಸಿ ಈ ಅಪಾಯವನ್ನು ತಡೆಗಟ್ಟಲು ಪ್ರಯತ್ನಿಸಿದಾಗ ಕಾದಂಬರಿ ಎಂದೆಂದೂ ಅಪೂರ್ಣವಾಗಿಯೇ ಉಳಿದುಕೊಳ್ಳುವುದು. ಅಪೂರ್ಣ ಕಾದಂಬರಿಯನ್ನು ಬೇರೆ ಬೇರೆ ರೀತಿಗಳಲ್ಲಿ ಮುಂದುವರಿಸಬಹುದಷ್ಟೆ. ಎಂತಲೇ N ನ್ನೂ ವಿವಿಧ ಮಾರ್ಗಗಳಲ್ಲಿ ವಿಸ್ತರಿಸಬಹುದು. ಅಂಥ ಕೆಲವು ವಿಸ್ತರಣೆಗಳಲ್ಲಿ ~g*(g) ಯನ್ನು ಸಾಧಿಸಲು ಶಕ್ಯವಾಗಬಹುದು, ಇನ್ನು ಕೆಲವು ವಿಸ್ತರಣೆಗಳಲ್ಲಿ g*(g) ಯನ್ನು ಸಾಧಿಸಲು ಶಕ್ಯವಾಗಬಹುದು, ಮತ್ತೆ ಕೆಲವಲ್ಲಿ ಇವೆರಡೂ ಮುಂಚಿನಂತೆ ಅನಿರ್ಧರಣೀಯವಾಗಿಯೇ ಉಳಿದುಕೊಳ್ಳಬಹುದು. ಅಂದಮೇಲೆ ಪಿಯಾನೊ ಆದ್ಯುಕ್ತಿಗಳ ಚೌಕಟ್ಟಿನಲ್ಲೇ ಒಂದಕ್ಕೊಂದು ಐಸೊಬಿಂಬಗಳಾಗದೆ ಇರುವಂಥ ಬೇರೆ ಬೇರೆ ಧನಪೂರ್ಣಾಂಕ ವ್ಯವಸ್ಥೆಗಳನ್ನು ರೂಪಿಸಲು ಸಾಧ್ಯವೆಂದಾಯಿತು. [ಎರಡು ಗಣಿತೀಯ ವ್ಯವಸ್ಥೆಗಳಿಗೆ ಏಕ ರೀತಿಯ ರಚನೆ ಇದ್ದಲ್ಲಿ ಅಂಥವನ್ನು ಪರಸ್ಪರ ಐಸೊಬಿಂಬಗಳೆಂದು (ಐಸೊಮಾರ್ಫಿಕ್ ಇಮೇಜಸ್) ವರ್ಣಿಸುತ್ತೇವೆ, ಉದಾಹರಣೆಗೆ T ಸಾಲುಗಳ ವ್ಯವಸ್ಥೆ ಮತ್ತು ದಶಮಾನ ಧನ ಪೂರ್ಣಾಂಕಗಳ ವ್ಯವಸ್ಥೆ.] ಇದೇ ಮೇರೆಗೆ ಪರಸ್ಪರ ಐಸೊಬಿಂಬಗಳಾಗದೆ ಇರುವ ಬೇರೆ ಬೇರೆ ನೈಜಸಂಖ್ಯಾವ್ಯವಸ್ಥೆಗಳನ್ನು ಸಹ ರೂಪಿಸಲು ಸಾಧ್ಯ. ಈ ಸಾಧ್ಯತೆಗಳನ್ನು ಉಪಯೋಗಿಸಿಕೊಂಡು ಅಬ್ರಹಾಂ ರಾಬಿನ್ಸನ್ ಸಾಂಪ್ರದಾಯಿಕ ಗಣಿತ ವಿಶ್ಲೇಷಣೆಯನ್ನೂ (ನೈಜಸಂಖ್ಯೆಗಳ ಸಿದ್ಧಾಂತ) ವಿಸ್ತರಿಸಿ ಶಿಷ್ಟೇತರ ವಿಶ್ಲೇಷಣೆ (ನಾನ್ಸ್ಟ್ಯಾಂಡರ್ಡ್ ಅನ್ಯಾಲಿಸಿಸ್) ಎಂಬ ಹೊಸ ಗಣಿತಶಾಖೆಯನ್ನು ಸೃಷ್ಟಿಸಿದ (1966).[೪೨][೪೩] ಈಚೆಗೆ ಗಣಿತಜ್ಞರ ಒಲವು, ನವರೂಪವಾದಿಗಳು (ನಿಯೊಫಾರ್ಮಲಿಸ್ಟ್ಸ್) ಎಂದು ಕರೆಯಬಹುದಾದ, ಈ ಎರಡನೆಯ ಗುಂಪಿನ ತಾತ್ತ್ವಿಕರ ಪರ ತುಸು ಹೆಚ್ಚಾಗಿ ಒಲಿದಿರುವಂತಿದೆ.
ಗಣಿತಶಾಸ್ತ್ರದ ತಳಹದಿಯನ್ನು ಕುರಿತ ನಮ್ಮ ವಿವೇಚನೆ ಈ ಶಾಸ್ತ್ರದ ಒಂದು ಉಕ್ತಿ (D) ಮತ್ತು ಅದರ ನಿಷೇಧರೂಪ (~D) ಇವುಗಳ ಪೈಕಿ ಒಂದಲ್ಲ ಒಂದನ್ನು ಸಾಧಿಸಲು ಶಕ್ಯವಿರಲೇಬೇಕೆಂಬ ಸಾಂಪ್ರದಾಯಿಕ ಶ್ರದ್ಧೆಯನ್ನು ಪ್ರಶ್ನಿಸುವ ಮೂಲಕ ಪ್ರಾರಂಭವಾಯಿತಷ್ಟೆ. ಒಂದು ದೃಷ್ಟಿಯಲ್ಲಿ 1931ರ ಗೊಯ್ಡಲ್ ಸಂಶೋಧನೆಗಳು ಹಾಗೆ ಪ್ರಶ್ನಿಸುವುದರ ಸಾಧುತ್ವವನ್ನು ಪುರಸ್ಕರಿಸುತ್ತವೆನ್ನುವುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಆದರೆ ಪ್ಲೇಟೋವಾದಿ ಗಣಿತಜ್ಞರು ಉಕ್ತಿಗಳ ಅನಿರ್ಧರಣೀಯತೆಗೆ N ನಂಥ ವ್ಯವಸ್ಥೆಯಲ್ಲಿನ ಸಾಧನಾಮಾರ್ಗಗಳ ಸತ್ತ್ವಹೀನತೆ ಕಾರಣವೇ ವಿನಾ ಆ ಉಕ್ತಿಗಳಲ್ಲ ಎಂದು ಸಾರಿ ಸಾಂಪ್ರದಾಯಿಕ ಶ್ರದ್ಧೆಯನ್ನು ಎತ್ತಿ ಹಿಡಿಯಬಯಸುತ್ತಾರೆ. ಅತ್ತ ನವರೂಪವಾದಿಗಳೂ ಬೇರೊಂದು ನಿಗೂಢ ರೀತಿಯಲ್ಲಿ ಸಾಂಪ್ರದಾಯಿಕ ಶ್ರದ್ಧೆಗೆ ಬೆಂಬಲ ನೀಡುತ್ತಾರೆ. ಅವರ ಪ್ರಕಾರ (D) ಮತ್ತು (~D) ಗಳಲ್ಲಿ ಒಂದಲ್ಲ ಒಂದನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯವಾಗಬೇಕೆಂಬ ನಿಯಮವಿಲ್ಲದಿದ್ದಾಗ್ಯೂ (D) ಇಲ್ಲವೆ (~D) ಸತ್ಯವಾಗಿರಬೇಕು. ಇಲ್ಲಿ ಉದ್ದರಣ ಚಿಹ್ನೆಗಳಲ್ಲಿರುವ ಇಲ್ಲವೆ ಹಾಗೂ ಸತ್ಯ ಎಂಬ ಪದಗಳಿಗೆ ನಿತ್ಯ ವ್ಯಾವಹಾರಿಕ ಅರ್ಥವನ್ನು ಆರೋಪಿಸಬಾರದು: ಅವು ಗಣಿತ ಕ್ರೀಡೆಯ ಅರ್ಥವಿಮುಖ ಪಗಡೆಕಾಯಿಗಳು ಮಾತ್ರ. [ಉದಾಹರಣೆಗೆ (D) ಸತ್ಯವೋ (~D) ಸತ್ಯವೋ ಎಂದು ಪ್ರಶ್ನಿಸುವಂತಿಲ್ಲ; ಹಾಗೆ ಪ್ರಶ್ನಿಸಿದರೆ ಇಲ್ಲವೆ ಎಂಬ ಪದಕ್ಕೆ ಸಲ್ಲದ ರೂಢಿಯ ಅರ್ಥ ಕೊಟ್ಟಂತಾಗುತ್ತದೆ.] ಈ ಪಗಡೆ ಕಾಯಿಗಳನ್ನು ಅಂಗೀಕೃತ ನಿಯಮಗಳ ಪ್ರಕಾರ ನಡೆಸುತ್ತ ಹೋದಾಗ (D), (~D) ಗಳೆರಡೂ ಸತ್ಯವಾಗಿರಬೇಕು ಎಂಬ ಮಾದರಿಯ ಅಸಾಂಗತ್ಯ ಎಂದೂ ತಲೆದೋರದೆ ಇರುವುದೇ ರೂಪವಾದಿಗಳ ಪಾಲಿಗೆ ಗಣಿತಕ್ರೀಡೆಯ ಸಾರ್ಥಕ್ಯ ನಿರ್ಣಾಯಕ. ಪ್ರಸ್ತಕ ವಿಭಾಗದ ಆದಿಯಲ್ಲೇ ಹೆಸರಿಸಿದ ಅಂತರ್ಬೋಧನವಾದಿಗಳಾದರೋ ರೂಪವಾದಿಗಳ ಅಂತರ್ವಿಮುಖ ಸತ್ಯವನ್ನೂ ಪ್ಲೇಟೋವಾದಿಗಳ ನಿರುಪಾಧಿಕ ಸತ್ಯವನ್ನು ತಿರಸ್ಕರಿಸಿ ಯಾವುದನ್ನು ಶುದ್ಧ ಅರ್ಥಪ್ರಜ್ಞೆಯ ಆಧಾರದಿಂದ ಸಾಧಿಸಲು ಶಕ್ಯವೋ ಅದು ಮಾತ್ರವೇ ಸತ್ಯ ಎಂದು ನಿಶ್ಚಯಿಸುತ್ತಾರೆ. ಇಂಥ ಹಲವಾರು ತಾತ್ತ್ವಿಕ ಪಂಥಗಳಲ್ಲಿ ಗಣಿತಜ್ಞನೊಬ್ಬನ ಒಲವು ಯಾವೆಡೆಗೇ ಇದ್ದರೂ ಆತನ ಗಣಿತ ಚಟುವಟಿಕೆಗಳಲ್ಲಿ ಅಸಾಂಗತ್ಯಗಳು ಉದ್ಭವಿಸುವುದಿಲ್ಲ ಎಂಬ ವಿಶ್ವಾಸಕ್ಕೆ ಆತನ ಅನುಭವ ಮಾತ್ರ ಆಸರೆಯಾಗಬಲ್ಲದೇ ವಿನಾ ಅಂಥ ವಿಶ್ವಾಸವನ್ನು ಗಣಿತೀಯ ಮಾರ್ಗಗಳಿಂದ ಸಾಧಿಸಲು ಎಂದೆಂದೂ ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ. ಗೊಯ್ಡಲ್ ನೆರವೇರಿಸಿದ ಈ ಅನಿರೀಕ್ಷಿತ ಪರಿಸ್ಥಿತಿಯ ಆವಿಷ್ಕಾರ ಗಣಿತಶಾಸ್ತ್ರದ ತಳಹದಿಯ ಇತಿಹಾಸದಲ್ಲಿ ಒಂದು ಅತ್ಯಂತ ಮಹತ್ತ್ವಪೂರ್ಣ ಮೈಲಿಗಲ್ಲಾಗಿ ಬಹುಕಾಲ ಉಳಿಯಲಿದೆ.
ಇದನ್ನೂ ನೋಡಿ
[ಬದಲಾಯಿಸಿ]ಉಲ್ಲೇಖಗಳು
[ಬದಲಾಯಿಸಿ]- ↑ Beckmann, Petr (1971). A History of π (PI). Boulder, Colorado: The Golem Press. p. 8. ISBN 978-0-911762-12-9.
- ↑ Audun Holme, Geometry: Our Cultural Heritage, 2000
- ↑ William Darrach Halsey, Emanuel Friedman (1983). Collier's Encyclopedia, with bibliography and index.
When the Arabian empire was expanding and contact was made with India, the Hindu numeral system and the early algorithms were adopted by the Arabs
- ↑ In some countries, such as Arabic-speaking ones, other glyphs are used for the digits
- ↑ Smith & Karpinski 1911, Ch. 7, pp. 99–127.
- ↑ "Integers are the set of whole numbers and their opposites.", Richard W. Fisher, No-Nonsense Algebra, 2nd Edition, Math Essentials, ISBN 978-0999443330
- ↑ Cheng 2017, p. 47.
- ↑ Weisstein, Eric W. "Zero". Wolfram (in ಇಂಗ್ಲಿಷ್). Archived from the original on 1 June 2013. Retrieved 4 April 2018.
- ↑ Rosen, Kenneth (2007). Discrete Mathematics and its Applications (6th ed.). New York, NY: McGraw-Hill. pp. 105, 158–160. ISBN 978-0-07-288008-3.
- ↑ Biggs, Norman L. (2002). Discrete Mathematics. India: Oxford University Press. pp. 75–78. ISBN 978-0-19-871369-2.
- ↑ Treese, Steven A. (2018). History and Measurement of the Base and Derived Units. Cham, Switzerland: Springer Science+Business Media. ISBN 978-3-319-77577-7. LCCN 2018940415. OCLC 1036766223.
- ↑ Imhausen, Annette (2016). Mathematics in Ancient Egypt: A Contextual History. Princeton University Press. ISBN 978-1-4008-7430-9. OCLC 934433864.
- ↑ Neugebauer 1969: p. 36 "In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse."
- ↑ Friberg, Jöran (1981). "Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations". Historia Mathematica. 8: 277–318. doi:10.1016/0315-0860(81)90069-0.: p. 306 "Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean theorem was well known to the mathematicians of the Old Babylonian period."
- ↑ Høyrup, Jens. "Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics". In Renger, Johannes (ed.). Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. pp. 393–407., p. 406, "To judge from this evidence alone it is therefore likely that the Pythagorean rule was discovered within the lay surveyors’ environment, possibly as a spin-off from the problem treated in Db2-146, somewhere between 2300 and 1825 BC." (Db2-146 is an Old Babylonian clay tablet from Eshnunna concerning the computation of the sides of a rectangle given its area and diagonal.)
- ↑ Robson, E. (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press.: p. 109 "Many Old Babylonian mathematical practitioners … knew that the square on the diagonal of a right triangle had the same area as the sum of the squares on the length and width: that relationship is used in the worked solutions to word problems on cut-and-paste ‘algebra’ on seven different tablets, from Ešnuna, Sippar, Susa, and an unknown location in southern Babylonia."
- ↑ de Laet, Siegfried J. (1996). History of Humanity: Scientific and Cultural Development. UNESCO, Volume 3, p. 14. ISBN 92-3-102812-X
- ↑ Judith D. Sally; Paul Sally (2007). "Chapter 3: Pythagorean triples". Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. p. 63. ISBN 978-0-8218-4403-8.
- ↑ Robert Lingat 1973, p. 21.
- ↑ Patrick Olivelle 1999, p. 3.
- ↑ Thibaut (1875), pp. 232–238
- ↑ Heiberg, J.L. "Euclid's Elements of Geometry" (PDF). pp. 46–47.
- ↑ "Euclid's Elements, Book I, Proposition 47". See also a web page version using Java applets by Prof. David E. Joyce, Clark University.
- ↑ Richeson (2008)
- ↑ "Ellipse - from Wolfram MathWorld". Mathworld.wolfram.com. 2020-09-10. Retrieved 2020-09-10.
- ↑ "Euclid's Elements, Book I, Proposition 30". aleph0.clarku.edu. Retrieved 13 June 2023.
- ↑ Klein 1979, pp. 57–60.
- ↑ Stäckel 1917, pp. 19–20.
- ↑ Stephen Hawking. God Created the Integers: The Mathematical Breakthroughs that Changed History. Running Press. 2007. pp. 697–703.
- ↑ Edwin Hewitt and Karl Stromberg, "Real and Abstract Analysis", Springer-Verlag, 1965
- ↑ Stillwell, John Colin. "analysis | mathematics". Encyclopædia Britannica. Archived from the original on 2015-07-26. Retrieved 2015-07-31.
- ↑ Halmos 1970, p. 30; the words map, mapping, transformation, correspondence, and operator are sometimes used synonymously.
- ↑ Dirichlet 1889, p. 135 as quoted in Medvedev 1991, pp. 60–61.
- ↑ Pickover, Cliff. "The 15 most famous transcendental numbers". sprott.physics.wisc.edu. Retrieved 2020-01-23.
- ↑ Shidlovskii, Andrei B. (June 2011). Transcendental Numbers. Walter de Gruyter. p. 1. ISBN 9783110889055.
- ↑ "Lecture #1" (PDF). 18.095 Lecture Series in Mathematics. 2015-01-05.
- ↑ Aleksandrov, P S (28 February 1972). "Poincaré and topology". Russian Mathematical Surveys. 27 (1): 157–168. doi:10.1070/RM1972v027n01ABEH001365. ISSN 0036-0279.
- ↑ Bruno (2003)
- ↑ Pettofrezzo & Byrkit 1970, pp. 23–24.
- ↑ Long 1972, p. 16.
- ↑ cf. Reid 1996, pp. 148–149.
- ↑ Non-standard Analysis. By Abraham Robinson. Princeton University Press, 1974.
- ↑ Abraham Robinson and Nonstandard Analysis Archived 15 April 2014 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.: History, Philosophy, and Foundations of Mathematics. By Joseph W. Dauben. www.mcps.umn.edu.
ಗ್ರಂಥಸೂಚಿ
[ಬದಲಾಯಿಸಿ]- Smith, David Eugene; Karpinski, Louis Charles (1911). The Hindu–Arabic Numerals. Boston: Ginn.
- Cheng, Eugenia (2017). Beyond Infinity: An Expedition to the Outer Limits of Mathematics. Basic Books. ISBN 978-1-5416-4413-7.
- Robert Lingat (1973). The Classical Law of India. University of California Press. ISBN 978-0-520-01898-3.
- Patrick Olivelle (1999). Dharmasutras: The Law Codes of Ancient India. Oxford University Press. ISBN 978-0-19-283882-7.
- Thibaut, George (1875). "On the Śulvasútras". The Journal of the Asiatic Society of Bengal. 44: 227–275.
- Richeson, D.S. (2008). Euler's Gem: The polyhedron formula and the birth of topology. Princeton University Press.
- Klein, Felix (1979) [1926]. Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. Teil 1 [Lectures on the Development of Mathematics in the 19th Century]. Grundlehren der mathematischen Wissenschaften 24 (in ಜರ್ಮನ್). Berlin, Heidelberg, New York: Springer-Verlag. ISBN 3-540-09234-X.
- Stäckel, Paul (1917). "Gauss als Geometer". In Königlich Preußische Akademie der Wissenschaften (ed.). Carl Friedrich Gauss. Werke (in ಜರ್ಮನ್). Vol. X, 2 (Abhandlung 4).
- Halmos, Paul R. (1970). Naive Set Theory. Springer-Verlag. ISBN 978-0-387-90092-6.
- Dirichlet, G. P. Lejeune (1889). Gesammelte Werke, Bd. I. Berlin. ISBN 9780828402255.
{{cite book}}: CS1 maint: location missing publisher (link) - Medvedev, Fyodor A. (1991). Scenes from the History of Real Functions. Birkhauser. ISBN 9780817625726.
- Bruno, Leonard C. (2003) [1999]. Math and mathematicians: the history of math discoveries around the world. Baker, Lawrence W. Detroit, Mich.: U X L. ISBN 0787638137. OCLC 41497065.
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77-171950
- Reid, Constance. (1996). Hilbert. New York: Springer. ISBN 0-387-94674-8. The definitive English-language biography of Hilbert.




















