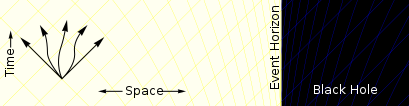
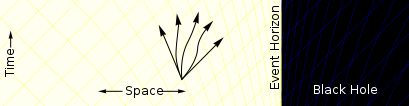
ಕಪ್ಪು ಕುಳಿ

ದೊಡ್ಡ ಮೆಗೆಲ್ಯಾನಿಕ್ ಮೋಡದ ಎದುರು ಕಪ್ಪು ಕುಳಿಯ ಅನುಕರಣೆಯ ದೃಶ್ಯ. ಕಪ್ಪು ಕುಳಿ ಸ್ಕೆವಾರ್ಜ್ಸ್‌‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯ ಮತ್ತು ವೀಕ್ಷಕರ ದೂರದ ನಡುವೆ ಅನುತಾಪವು 1:9. ಐನ್‌ಸ್ಟೈನ್ ಉಂಗುರ ಎಂದು ಹೆಸರಾದ ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್ ಪರಿಣಾಮವು ಮೋಡದ ಕೋನೀಯ ಗಾತ್ರಕ್ಕೆ ಹೋಲಿಸಿದಾಗ ಎರಡು ಪ್ರಕಾಶಮಾನವಾದ ಮತ್ತು ದೊಡ್ಡದಾದ ಮೋಡದ ವಿರೂಪ ಚಿತ್ರಗಳನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ.

ಕಪ್ಪು ಕುಳಿ ಬಾಹ್ಯಾಕಾಶದ ಪ್ರದೇಶವಾಗಿದ್ದು, ಅದರಿಂದ ಬೆಳಕು ಸೇರಿದಂತೆ ಯಾವುದೂ ತಪ್ಪಿಸಿಕೊಂಡು ಹೋಗುವುದು ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ. ಇದು ತೀರಾ ಸಾಂದ್ರೀಕೃತ ದ್ರವ್ಯರಾಶಿಯಿಂದ ಉಂಟಾದ ಸ್ಪೇಸ್‌ಟೈಮ್‌(ದೇಶ-ಕಾಲ)(ದೇಶದ ಮೂರು ಆಯಾಮ ಮತ್ತು ಕಾಲದ ಒಂದು ಆಯಾಮದ ಕಲ್ಪನೆ) ರೂಪವಿಕೃತಿಯ ಫಲಿತಾಂಶವಾಗಿದೆ. ಕಪ್ಪು ಕುಳಿಯ ಸುತ್ತ ಗುರುತಿಸಲಾಗದ ಹೊರಮೈಯಿದ್ದು, ಇದು ಹಿಂತಿರುಗಲಾರದ ಬಿಂದುವನ್ನು ಸಂಕೇತಿಸುತ್ತದೆ. ಈ ಹೊರಮೈಯನ್ನು ಈವೆಂಟ್ ಹಾರಿಜಾನ್(ಬೆಳಕು ಹಾದುಹೋಗದ ಕಪ್ಪುಕುಳಿಯ ಸುತ್ತಲಿನ ಪ್ರದೇಶ) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಇದನ್ನು "ಕಪ್ಪು " ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಏಕೆಂದರೆ ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ಪರಿಪೂರ್ಣ ಕಪ್ಪು ಕಾಯದ ರೀತಿಯಲ್ಲಿ ಅದಕ್ಕೆ ಬಡಿಯುವ ಎಲ್ಲ ಬೆಳಕನ್ನು ಹೀರಿಕೊಂಡು, ಏನನ್ನೂ ಬಿಂಬಿಸುವುದಿಲ್ಲ. ಕಪ್ಪು ಕುಳಿಗಳು ಕೂಡ ಪರಿಮಿತಿಯ ಉಷ್ಣಾಂಶದೊಂದಿಗಿರುವ ಕಪ್ಪು ಕಾಯದ ರೀತಿಯಲ್ಲಿ ವಿಕಿರಣವನ್ನು ಸೂಸುತ್ತವೆ ಎಂದು ಕ್ವಾಂಟಮ್ ಯಂತ್ರಶಾಸ್ತ್ರ ಮುಂಗಂಡಿದೆ. ಈ ಉಷ್ಣಾಂಶವು ಕಪ್ಪುಕುಳಿಯ ದ್ರವ್ಯರಾಶಿಯೊಂದಿಗೆ ಇಳಿಮುಖವಾಗುತ್ತದೆ. ಇದರಿಂದ ನಾಕ್ಷತ್ರಿಕ ದ್ರವ್ಯರಾಶಿಯ ಕಪ್ಪುಕುಳಿಯ ವಿಕಿರಣವನ್ನು ಗಮನಿಸಲು ಕಷ್ಟವಾಗುತ್ತದೆ.

ಇದರ ಅದೃಶ್ಯ ಒಳಪ್ರದೇಶದ ನಡುವೆಯೂ, ಕಪ್ಪು ಕುಳಿಯನ್ನು ಇತರ ಭೌತಶಾಸ್ತ್ರದ ಜತೆ ಪರಸ್ಪರ ಕಾರ್ಯದ ಮೂಲಕ ವೀಕ್ಷಿಸಬಹುದು. ಬಾಹ್ಯಾಕಾಶದ ಪ್ರದೇಶದಲ್ಲಿ ಪರಿಭ್ರಮಣೆ ಮಾಡುವ ನಕ್ಷತ್ರದ ಗುಂಪಿನ ಚಲನೆಯ ಜಾಡು ಹಿಡಿಯುವ ಮೂಲಕ ಕಪ್ಪು ಕುಳಿಯನ್ನು ನಿರ್ಣಯಿಸಬಹುದು. ಪರ್ಯಾಯವಾಗಿ ನಾಕ್ಷತ್ರಿಕ ಕಪ್ಪು ಕುಳಿಯಲ್ಲಿ ಜೊತೆ ನಕ್ಷತ್ರದಿಂದ ಅನಿಲ ಬಿದ್ದಾಗ, ಅನಿಲವು ಒಳಮುಖವಾಗಿ ಸುರುಳಿಯಾಗಿ ಸುತ್ತುತ್ತದೆ. ಅತ್ಯಂತ ಉಷ್ಣಾಂಶಕ್ಕೆ ಬಿಸಿಯಾಗಿ ದೊಡ್ಡ ಪ್ರಮಾಣದ ವಿಕಿರಣವನ್ನು ಹೊಮ್ಮಿಸುತ್ತದೆ. ಇದನ್ನು ಭೂಮಿಯಿಂದ ಅಥವಾ ಭೂಮಿಯನ್ನು ಸುತ್ತುವ ದೂರದರ್ಶಕಗಳಿಂದ ಗುರುತಿಸಬಹುದು.

ಖಗೋಳವಿಜ್ಞಾನಿಗಳು ಅಸಂಖ್ಯಾತ ನಾಕ್ಷತ್ರಿಕ ಕಪ್ಪು ಕುಳಿಗಳನ್ನು ಗುರುತಿಸಿದ್ದಾರೆ ಹಾಗು ಗ್ಯಾಲಕ್ಸಿಗಳ ಮಧ್ಯದಲ್ಲಿ ಬೃಹತ್ ಗಾತ್ರದ ಕಪ್ಪುಕುಳಿಗಳ ಬಗ್ಗೆ ಸಾಕ್ಷ್ಯವನ್ನು ಪತ್ತೆಮಾಡಿದ್ದಾರೆ. ೧೯೮೮ರಲ್ಲಿ ಖಗೋಳವಿಜ್ಞಾನಿಗಳು ಕ್ಷೀರಪಥದ ಗ್ಯಾಲಕ್ಸಿಯ ಮಧ್ಯದ ಪ್ರದೇಶದಲ್ಲಿ ಸ್ಯಾಗಿಟ್ಟಾರಿಯಸ್ A* ಬಳಿ ೨ ದಶಲಕ್ಷ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳಿಗಿಂತ ದೊಡ್ಡದಾದ ಬೃಹತ್ ಕಪ್ಪುಕುಳಿಯ ಅಸ್ತಿತ್ವದ ಬಗ್ಗೆ ಸಾಕ್ಷ್ಯಾಧಾರವನ್ನು ಪತ್ತೆಹಚ್ಚಿದ್ದಾರೆ. ಹೆಚ್ಚುವರಿ ದತ್ತಾಂಶವನ್ನು ಬಳಸಿದ ಇತ್ತೀಚಿನ ಹೆಚ್ಚಿನ ಫಲಿತಾಂಶಗಳು ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಯು ೪ ದಶಲಕ್ಷ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳಿಗಿಂತ ದೊಡ್ಡದಾಗಿದೆಯೆಂದು ಸೂಚಿಸಿವೆ.

ಇತಿಹಾಸ

ಕಪ್ಪು ಕುಳಿಯ ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್‌ನ ಅನುಕರಣೆಯು ಹಿನ್ನೆಲೆಯಲ್ಲಿ ಗ್ಯಾಲಕ್ಸಿಯ ಚಿತ್ರವನ್ನು ವಿರೂಪಗೊಳಿಸುತ್ತದೆ(ದೊಡ್ಡ ಆನಿಮೇಷನ್‌ಗಾಗಿ ಇಲ್ಲಿ ಕ್ಲಿಕ್ ಮಾಡಿ)

ಬೃಹತ್ ಗಾತ್ರದ ಕಾಯದಲ್ಲಿ ಬೆಳಕು ಕೂಡ ತಪ್ಪಿಸಿಕೊಳ್ಳದಿರುವ ಕಲ್ಪನೆಯನ್ನು ಮೊದಲಿಗೆ ಭೂವಿಜ್ಞಾನಿ ಜಾನ್ ಮಿಚೆಲ್ ಮಂಡಿಸಿದ್ದಾರೆ. ೧೭೮೩ರಲ್ಲಿ ರಾಯಲ್ ಸೊಸೈಟಿಗೆ ಹೆನ್ರಿ ಕ್ಯಾವೆಂಡಿಶ್ ಅವರನ್ನು ಉದ್ದೇಶಿಸಿ ಬರೆದಿರುವ ಪತ್ರದಲ್ಲಿ ಇದನ್ನು ಪ್ರಸ್ತಾಪಿಸಿದ್ದಾರೆ.

If the semi-diameter of a sphere of the same density as the Sun were to exceed that of the Sun in the proportion of 500 to 1, a body falling from an infinite height towards it would have acquired at its surface greater velocity than that of light, and consequently supposing light to be attracted by the same force in proportion to its vis inertiae, with other bodies, all light emitted from such a body would be made to return towards it by its own proper gravity.

— John Michell

೧೭೯೬ರಲ್ಲಿ, ಗಣಿತಶಾಸ್ತ್ರಜ್ಞ ಪೀರೆ-ಸೈಮನ್ ಲ್ಯಾಪ್ಲೇಸ್ ತಮ್ಮ ಪುಸ್ತಕ Exposition du système du Monde (ನಂತರದ ಆವೃತ್ತಿಗಳಿಂದ ಇದನ್ನು ತೆಗೆಯಲಾಗಿದೆ.)ದ ಪ್ರಥಮ ಅಥವಾ ಎರಡನೇ ಆವೃತ್ತಿಗಳಲ್ಲಿ ಇದೇ ರೀತಿಯ ಕಲ್ಪನೆಯನ್ನು ಉತ್ತೇಜಿಸಿದ್ದಾರೆ. ಇಂತಹ "ಕಪ್ಪು ನಕ್ಷತ್ರ"ಗಳನ್ನು ೧೯ನೇ ಶತಮಾನದಲ್ಲಿ ಕಡೆಗಣಿಸಲಾಗಿತ್ತು. ಏಕೆಂದರೆ ದ್ರವ್ಯರಾಶಿರಹಿತ ಅಲೆಯಾದ ಬೆಳಕು ಗುರುತ್ವಶಕ್ತಿಯ ಪ್ರಭಾವಕ್ಕೆ ಒಳಗಾಗುವುದು ಹೇಗೆಂದು ಅರ್ಥವಾಗಿರಲಿಲ್ಲ.

ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ

ಸ್ಕವಾರ್ಜ್ಸ್ಚೈಲ್ಡ್‌ನ ತ್ರಿಜ್ಯ

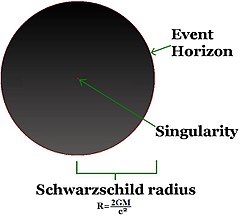
೧೯೧೫ರಲ್ಲಿ, ಆಲ್ಬರ್ಟ್ ಐನ್‌ಸ್ಟೀನ್ ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ ಸಿದ್ಧಾಂತವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು.ಇದಕ್ಕೆ ಮುಂಚೆ ಬೆಳಕಿನ ಚಲನೆಯ ಮೇಲೆ ಗುರುತ್ವ ಪ್ರಭಾವ ಬೀರುತ್ತದೆಂದು ತೋರಿಸಿದ್ದರು. ಕೆಲವು ತಿಂಗಳ ನಂತರ, ಕಾರ್ಲ್ ಸ್ಕವಾರ್ಜ್ಸ್ಚೈಲ್ಡ್ ಬಿಂದು ದ್ರವ್ಯರಾಶಿ ಮತ್ತು ವೃತ್ತಾಕಾರದ ದ್ರವ್ಯರಾಶಿಯ ಗುರುತ್ವ ಕ್ಷೇತ್ರಕ್ಕೆ ವಿವರಣೆ ನೀಡಿದರು.

ಸ್ಕವಾರ್ಜ್ಸ್ಚೈಲ್ಡ್ ನಂತರ ಕೆಲವು ತಿಂಗಳ ನಂತರ, ಹೆಂಡ್ರಿಕ್ ಲೋರೆಂಟ್ಜ್ ವಿದ್ಯಾರ್ಥಿ ಜೋಹಾನ್ಸ್ ಡ್ರಾಸ್ಟ್, ಸ್ವತಂತ್ರವಾಗಿ ಬಿಂದು ದ್ರವ್ಯರಾಶಿಗೆ ಅದೇ ರೀತಿಯ ವಿವರಣೆ ನೀಡಿದರು ಮತ್ತು ಅದರ ಗುಣಲಕ್ಷಣಗಳ ಬಗ್ಗೆ ವ್ಯಾಪಕವಾಗಿ ಬರೆದರು. ಈ ವಿವರಣೆಯು ವಿಶಿಷ್ಟ ನಡವಳಿಕೆಯನ್ನು ಹೊಂದಿದ್ದು, ಅದಕ್ಕೆ ಸ್ಕೆವಾರ್ಜ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅಲ್ಲಿ ಅದು ಸಿಂಗ್ಯುಲರ್‌ ಆಗುತ್ತದೆ. ಅಂದರೆ, ಐನ್‌ಸ್ಟೈನ್ ಸಮೀಕರಣದಲ್ಲಿ ಕೆಲವು ಪದಗಳು ಅನಂತವಾಗಿರುತ್ತದೆಂದು ಅರ್ಥ. ಆ ಸಮಯದಲ್ಲಿ ಆ ಮೇಲ್ಮೈನ ಸ್ವರೂಪವನ್ನು ಅರ್ಥಮಾಡಿಕೊಂಡಿರಲಿಲ್ಲ. ೧೯೨೪ರಲ್ಲಿ ನಿರ್ದೇಶಾಂಕಗಳ ಬದಲಾವಣೆಗಳ ನಂತರ ಏಕತ್ವವು ಅದೃಶ್ಯವಾಗಿದ್ದನ್ನು ಆರ್ಥರ್ ಎಡ್ಡಿಂಗ್‌ಟನ್ ತೋರಿಸಿದರು.(ನೋಡಿ ಎಡ್ಡಿಂಗ್‌ಟನ್ ನಿರ್ದೇಶಾಂಕಗಳು) ಆದರೂ ಸ್ಕೆವಾರ್ಜ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದ ನಿರ್ದೇಶಾಂಕವು ಅಭೌತ ನಿರ್ದೇಶಾಂಕ ಏಕತ್ವ(ಅತೀ ಸಾಂದ್ರತೆಯ ಸಣ್ಣ ಗಾತ್ರದ ಬಿಂದು)ವೆಂದು ಅರ್ಥ ಎಂದು ಅರಿವು ಜಾರ್ಜ್ಸ್ ಲೆಮೈಟರ್‌ಅವರಿಗೆ ೧೯೩೩ರಲ್ಲಿ ಉಂಟಾಯಿತು.

೧೯೩೧ರಲ್ಲಿ ಸುಬ್ರಮಣ್ಯನ್ ಚಂದ್ರಶೇಖರ್ ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತವನ್ನು ಬಳಸಿ, ೧.೪೪ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳಿಗಿಂತ ಹೆಚ್ಚಿನ ಎಲೆಕ್ಟ್ರಾನ್ ಕಳೆದುಕೊಂಡ ಭೌತವಸ್ತುವಿನ ತಿರುಗದಿರುವ ಕಾಯವು(ಚಂದ್ರಶೇಖರ್ ಮಿತಿ)ಕುಸಿಯುತ್ತದೆಎಂದು ಲೆಕ್ಕಹಾಕಿದರು. ಅವರ ವಾದಗಳನ್ನು ಎಡ್ಡಿಂಗ್‌ಟನ್ ಮತ್ತು ಲೆವ್ ಲಾಂಡೋವ್ ಮುಂತಾದ ಅನೇಕ ಮಂದಿ ಸಮಕಾಲೀನರು ವಿರೋಧಿಸಿದರು. ಕೆಲವು ಅಜ್ಞಾತ ಕ್ರಿಯಾತಂತ್ರ ಕುಸಿತವನ್ನು ತಡೆಯುತ್ತದೆಂದು ವಾದಿಸಿದರು. ಅವರ ಪ್ರತಿಪಾದನೆ ಆಂಶಿಕವಾಗಿ ನಿಜವಾಗಿತ್ತು. ಚಂದ್ರಶೇಖರ್ ಮಿತಿಗಿಂತ ಸ್ವಲ್ಪ ಹೆಚ್ಚು ಬೃಹತ್ತಾದ ಶ್ವೇತ ಕುಬ್ಜ ತಾರೆ ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರವಾಗಿ ಕುಸಿಯುತ್ತದೆ, ಪಾಲಿ ಎಕ್ಸ್‌ಕ್ಲೂಷನ್ ತತ್ವದ ಪ್ರಕಾರ ಸ್ವತಃ ಅದು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ. ಆದರೆ, ೧೯೩೯ರಲ್ಲಿ ರಾಬರ್ಟ್ ಓಪನ್‌ಹೈಮರ್ ಮತ್ತಿತರರು ಅಂದಾಜು ಮೂರು ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳಿಗಿಂತ ಹೆಚ್ಚಿರುವ ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರಗಳು(ಟೋಲ್ಮಾನ್-ಓಪನ್‌ಹೈಮರ್-ವೋಲ್ಕೋಫ್ ಮಿತಿ)ಚಂದ್ರಶೇಖರ್ ಮಂಡಿಸಿದ ಕಾರಣಗಳಿಂದ ಕಪ್ಪು ಕುಳಿಗಳಾಗಿ ಕುಸಿಯುತ್ತವೆ. ಕೆಲವು ನಕ್ಷತ್ರಗಳು ಕಪ್ಪು ಕುಳಿಗಳಾಗಿ ಕುಸಿಯಲು ಯಾವುದೇ ಭೌತಶಾಸ್ತ್ರದ ನಿಯಮಗಳು ಮಧ್ಯಪ್ರವೇಶಿಸಿ ನಿಲ್ಲಿಸುವ ಸಂಭವವಿಲ್ಲ ಎಂದು ತೀರ್ಮಾನಿಸಿದರು.

ಓಪ್ಪನ್‌ಹೈಮರ್ ಮತ್ತು ಅವರ ಸಹ ಲೇಖಕರು ಸ್ಕೆವಾರ್ಜ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದ ಗಡಿಯಲ್ಲಿನ ಏಕತ್ವವನ್ನು(ಅನಂತ ಸಾಂದ್ರತೆ ಮತ್ತು ಅತೀ ಸೂಕ್ಷ್ಮ ಗಾತ್ರದ ಬಿಂದು) ಕಾಲವು ಸ್ಥಗಿತಗೊಂಡ ಗುಳ್ಳೆಯ ಗಡಿ ಎಂದು ಸೂಚಿಸುವ ಮೂಲಕ ವ್ಯಾಖ್ಯಾನಿಸಿದರು. ಇದು ಬಾಹ್ಯ ವೀಕ್ಷಕರಿಗೆ ಕ್ರಮಬದ್ಧ ದೃಷ್ಟಿಕೋನವಾಗಿದೆ. ಆದರೆ ಒಳಬೀಳುವ ವೀಕ್ಷಕರಿಗೆ ಕ್ರಮಬದ್ಧ ದೃಷ್ಟಿಕೋನವಾಗಿರಲಿಲ್ಲ. ಈ ಗುಣಲಕ್ಷಣದ ಕಾರಣದಿಂದಾಗಿ, ಕುಸಿದ ನಕ್ಷತ್ರಗಳನ್ನು ಹೆಪ್ಪುಗಟ್ಟಿದ ನಕ್ಷತ್ರಗಳು ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಏಕೆಂದರೆ ಸ್ಕೆವಾರ್ಜ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದಲ್ಲಿ ಅದರ ಕುಸಿತ ಆರಂಭವಾದ ಕ್ಷಣದಲ್ಲೇ ಬಾಹ್ಯ ವೀಕ್ಷಕ ನಕ್ಷತ್ರದ ಮೇಲ್ಮೈ ಹೆಪ್ಪುಗಟ್ಟಿದ್ದನ್ನು ಕಾಣುತ್ತಾರೆ. ಇದು ಆಧುನಿಕ ಕಪ್ಪು ಕುಳಿಗಳ ಗೊತ್ತಾದ ಲಕ್ಷಣವಾಗಿದೆ. ಆದರೆ ಹೆಪ್ಪುಗಟ್ಟಿದ ನಕ್ಷತ್ರದ ಮೇಲ್ಮೈನ ಬೆಳಕು ವೇಗವಾಗಿ ಕೆಂಪುಪಲ್ಲಟವಾಗಿ, ಕಪ್ಪುಕುಳಿಯನ್ನು ಶೀಘ್ರವಾಗಿ ಕಪ್ಪುಬಣ್ಣಕ್ಕೆ ಪರಿವರ್ತಿಸುತ್ತದೆ ಎನ್ನುವುದಕ್ಕೆ ಪ್ರಾಧಾನ್ಯತೆ ನೀಡಬೇಕಾಗುತ್ತದೆ. ಅನೇಕ ಬೌತವಿಜ್ಞಾನಿಗಳು ಸ್ಕವಾರ್ಜ್ಸ್‌‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದಲ್ಲಿ ಕಾಲವು ಸ್ಥಗಿತಗೊಳ್ಳುವ ಕಲ್ಪನೆಯನ್ನು ಸ್ವೀಕರಿಸಲು ಸಾಧ್ಯವಾಗಲಿಲ್ಲ. ಆ ವಿಷಯದ ಬಗ್ಗೆ ಸುಮಾರು ೨೦ವರ್ಷಗಳವರೆಗೆ ಯಾವುದೇ ಆಸಕ್ತಿ ಉಳಿದಿರಲಿಲ್ಲ.

ಸುವರ್ಣ ಯುಗ (Golden age of general relativity)

೧೯೫೮ರಲ್ಲಿ ಡೇವಿಡ್ ಫಿಂಕಲ್‌ಸ್ಟೈನ್ ಸ್ಕೆವಾರ್ಜ್ಸ್‌‌ಚೈಲ್ಡ್ ಮೇಲ್ಮೈ r = ೨m ಯನ್ನು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಆಗಿ ಗುರುತಿಸಿದರು.[ ಜ್ಯಾಮಿತೀಯ ಏಕಾಂಶಗಳಲ್ಲಿ i.e. 2Gm/c ², r ಮೇಲ್ಮೈನ ತ್ರಿಜ್ಯವಾಗಿದ್ದು, m ಕಪ್ಪುಕುಳಿಯ ದ್ರವ್ಯರಾಶಿ] ಪರಿಪೂರ್ಣ ಏಕದಿಕ್ಕಿನ ಪದರವಾಗಿದ್ದು, ಸಾಂದರ್ಭಿಕ ಪ್ರಭಾವಗಳು ಅದರ ಒಂದು ದಿಕ್ಕಿನಲ್ಲಿ ಮಾತ್ರ ಹಾದುಹೋಗಬಹುದು". ಇದು ಓಪನ್‌ಹೈಮರ್ಸ್ ಫಲಿತಾಂಶಗಳಿಗೆ ಕಟ್ಟುನಿಟ್ಟಾಗಿ ವಿರೋಧಿಯಾಗಿರಲಿಲ್ಲ. ಆದರೆ ಕಪ್ಪುಕುಳಿಯ ಗುರುತ್ವದ ಪ್ರಭಾವಕ್ಕೆ ಒಳಗಾಗಿ ಅದರತ್ತ ಬೀಳುವ ವೀಕ್ಷಕರ ದೃಷ್ಟಿಕೋನವನ್ನು ಸೇರಿಸಲು ಅದು ವಿಸ್ತರಿಸಿತು. ಫಿಂಕಲ್‌ಸ್ಟೈನ್ಸ್ ವಿವರಣೆಯು ಕಪ್ಪು ಕುಳಿಯಲ್ಲಿ ಗುರುತ್ವದ ಪ್ರಭಾವಕ್ಕೆ ಮುಕ್ತವಾಗಿ ಒಳಗಾಗಿ ಬೀಳುವ ವೀಕ್ಷಕರ ಭವಿಷ್ಯಕ್ಕೆ ಸ್ಕವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ವಿವರಣೆ(ಪರಿಹಾರ)ಯನ್ನು ವಿಸ್ತರಿಸಿತು. ಸಂಪೂರ್ಣ ವಿಸ್ತರಣೆಯನ್ನು ಮಾರ್ಟಿನ್ ಕ್ರುಸ್ಕಾಲ್ ಈಗಾಗಲೇ ಪತ್ತೆಮಾಡಿದ್ದು, ಅದನ್ನು ಪ್ರಕಟಿಸುವಂತೆ ಒತ್ತಾಯಿಸಲಾಯಿತು.

ಈ ಫಲಿತಾಂಶಗಳು ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತದ ಸುವರ್ಣ ಯುಗದ ಆರಂಭದಲ್ಲಿ ಬಂದವು. ಇದು ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತ ಮತ್ತು ಕಪ್ಪುಕುಳಿಗಳು ಸಂಶೋಧನೆಯ ಮುಖ್ಯವಾಹಿನಿ ವಿಷಯಗಳಾಗಿ ಗುರುತಿಸಲಾಗಿತ್ತು. ಈ ಪ್ರಕ್ರಿಯೆಗೆ ೧೯೬೭ರಲ್ಲಿ ಪಲ್ಸಾರ್‌ಗಳ ಶೋಧನೆಗೆ ನೆರವಾಯಿತು. ಇದು ಶೀಘ್ರವಾಗಿ ತಿರುಗುವ ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರಗಳೆಂದು ಕೆಲವೇ ವರ್ಷಗಳಲ್ಲಿ ತೋರಿಸಲಾಯಿತು. ಅಲ್ಲಿಯವರೆಗೆ, ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರಗಳು ಕಪ್ಪು ಕುಳಿಯ ರೀತಿಯಲ್ಲಿ ಕೇವಲ ಸೈದ್ಧಾಂತಿಕ ಕುತೂಹಲಗಳೆಂದು ಪರಿಗಣಿಸಲಾಗಿತ್ತು. ಆದರೆ ಪಲ್ಸಾರ್‌ಗಳ ಶೋಧನೆಯಿಂದ ಅವುಗಳ ಬೌತಿಕ ಉಪಸ್ಥಿತಿಯನ್ನು ತೋರಿಸಿತು ಮತ್ತು ಗುರುತ್ವಬಲದ ಕುಸಿತದಿಂದ ರಚನೆಯಾಗಿರಬಹುದಾದ ಎಲ್ಲ ರೀತಿಯ ಸಾಂದ್ರ ವಸ್ತುಗಳ ವಿಧಗಳ ಬಗ್ಗೆ ಮತ್ತಷ್ಟು ಆಸಕ್ತಿಯನ್ನು ಕೆರಳಿಸಿತು.

ಈ ಅವಧಿಯಲ್ಲಿ ಅನೇಕ ಸಾಮಾನ್ಯ ಕಪ್ಪು ಕುಳಿ ವಿವರಣೆ(ಪರಿಹಾರ)ಗಳನ್ನು ಪತ್ತೆಮಾಡಲಾಯಿತು. ೧೯೬೩ರಲ್ಲಿ ರಾಯ್ ಕೆರ್ ತಿರುಗುವ ಕಪ್ಪು ಕುಳಿಗೆ ನಿಖರ ವಿವರಣೆಯನ್ನು ಕಂಡುಹಿಡಿದರು. ಎರಡು ವರ್ಷಗಳ ನಂತರ ಎಜ್ರಾ ಟಿ. ನ್ಯೂಮ್ಯಾನ್ ಪರಿಭ್ರಮಿಸುವ ಮತ್ತು ವಿದ್ಯುತ್ ಆವೇಶದ ಕಪ್ಪುಕುಳಿಗೆ ಆಕ್ಸಿಸಿಮಿಟ್ರಿಕ್(ಕಕ್ಷೆಯ ಸುತ್ತ ಸಮ್ಮಿತಿ) ಪರಿಹಾರ(ವಿವರಣೆ)ವನ್ನು ಕಂಡುಕೊಂಡರು. ವರ್ನರ್ ಇಸ್ರೇಲ್, ಬ್ರಾಂಡನ್ ಕಾರ್ಟರ್ ಮತ್ತು ಡಿ.ಸಿ. ರಾಬಿನ್ಸ್‌ಸನ್ ಕೆಲಸಗಳ ಮೂಲಕ ನೊ-ಹೇರ್ ಪ್ರಮೇಯ ಹೊಮ್ಮಿತು. ಸ್ಥಗಿತಗೊಂಡ ಕಪ್ಪುಕುಳಿ ವಿವರಣೆಯನ್ನು ಕೆರ್-ನ್ಯೂಮ್ಯಾನ್ ಮೆಟ್ರಿಕ್‌ ಮೂರು ಮಾನದಂಡಗಳಾದ ದ್ರವ್ಯರಾಶಿ, ಕೋನೀಯ ಆವೇಗ ಮತ್ತು ವಿದ್ಯುದಾವೇಶದಿಂದ ಸಂಪೂರ್ಣವಾಗಿ ವಿವರಿಸಲಾಗಿದೆ ಎಂದು ಇದು ತಿಳಿಸಿದೆ.

ಕಪ್ಪು ಕುಳಿಯ ವಿವರಣೆಗಳ ವಿಚಿತ್ರ ಲಕ್ಷಣಗಳು ಸಮ್ಮಿತಿ ಸ್ಥಿತಿಗಳು ಹೇರಿದ ಅಸಹಜ ಕೃತಕಗಳಾಗಿದ್ದು, ಸಾಮಾನ್ಯ ಪರಿಸ್ಥಿತಿಗಳಲ್ಲಿ ಏಕತ್ವಗಳು ಕಾಣುವುದಿಲ್ಲ ಎಂದು ಸುದೀರ್ಘಾವಧಿವರೆಗೆ ಶಂಕಿಸಲಾಗಿತ್ತು. ಈ ಅಭಿಪ್ರಾಯವನ್ನು ನಿರ್ದಿಷ್ಟವಾಗಿ ಬೆಲಿನ್‌ಸ್ಕಿ, ಖಾಲಾಟ್ನಿಕೋವ್, ಮತ್ತುಲಿಫ್‌ಶಿಟ್ಜ್‌ಹೊಂದಿದ್ದರು. ಸಾಮಾನ್ಯ ವಿವರಣೆಗಳಲ್ಲಿ ಯಾವುದೇ ಏಕತ್ವಗಳು ಕಾಣುವುದಿಲ್ಲ ಎಂದು ಸಾಬೀತು ಪಡಿಸಲು ಅವರು ಯತ್ನಿಸಿದರು. ಆದಾಗ್ಯೂ, ೬೦ರ ದಶಕದ ಕೊನೆಯಲ್ಲಿರೋಜರ್ ಪೆನ್ರೋಸ್ ಮತ್ತು ಸ್ಟೀಫನ್ ಹಾಕಿಂಗ್ ಏಕತ್ವಗಳು ಸಾಮಾನ್ಯವೆಂದು ಸಾಬೀತು ಮಾಡಲು ಜಾಗತಿಕ ತಂತ್ರಗಳನ್ನು ಬಳಸಿದರು.

ಜೇಮ್ಸ ಬಾರ್ಡೀನ್, ಜಾಕೋಬ್ ಬೆಕೆನ್‌ಸ್ಟೈನ್, ಕಾರ್ಟರ್, ಮತ್ತು ಹಾಕಿಂಗ್‌ರ ೧೯೭೦ರ ದಶಕದಲ್ಲಿನ ಕೆಲಸಗಳು ಕಪ್ಪು ಕುಳಿ ರಚನಾವಿಧಾನದ ನಿಯಮಗಳ ರಚನೆಗೆ ದಾರಿ ಕಲ್ಪಿಸಿತು. ಈ ನಿಯಮಗಳು ಕಪ್ಪು ಕುಳಿಯ ನಡವಳಿಕೆಯನ್ನು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ನಿಯಮಗಳ ಜತೆ ಸಮೀಪದ ಸಾದೃಶ್ಯದಿಂದ ವಿವರಿಸುತ್ತದೆ. ದ್ರವ್ಯರಾಶಿಯನ್ನು ಶಕ್ತಿಯೊಂದಿಗೆ, ಪ್ರದೇಶವನ್ನು ಜಡೋಷ್ಣ(ಜಡೋಷ್ಣ) ಮೇಲ್ಮೈ ಗುರುತ್ವವನ್ನು ಉಷ್ಣಾಂಶದೊಂದಿಗೆ ಸಂಬಂಧ ಕಲ್ಪಿಸುತ್ತದೆ.೧೯೭೪ರಲ್ಲಿ ಕಪ್ಪು ಕುಳಿಗಳ ಮೇಲ್ಮೈ ಗುರುತ್ವಕ್ಕೆ ಪ್ರಮಾಣಾನುಗುಣವಾದ ಉಷ್ಣಾಂಶದೊಂದಿಗೆ ಕಪ್ಪು ಕಾಯದ ರೀತಿಯಲ್ಲಿ ವಿಕಿರಣವನ್ನು ಹೊರಸೂಸುತ್ತದೆ ಎಂದು ಕ್ವಾಂಟಮ್ ಕ್ಷೇತ್ರ ಸಿದ್ಧಾಂತವು ಮುಂಗಂಡಿರುವುದನ್ನು ೧೯೭೪ರಲ್ಲಿ ಹಾಕಿಂಗ್ ತೋರಿಸಿದಾಗ ಈ ಸಾದೃಶ್ಯವು ಸಂಪೂರ್ಣವಾಯಿತು.

ಕಪ್ಪು ಕುಳಿ ಪದವನ್ನು ಜಾನ್ ವೀಲರ್ ೧೯೬೭ರ ಉಪನ್ಯಾಸದ ಸಂದರ್ಭದಲ್ಲಿ ಸಾರ್ವಜನಿಕವಾಗಿ ಮೊಟ್ಟಮೊದಲು ಬಳಸಿದರು. ಈ ಪದವನ್ನು ಹುಟ್ಟುಹಾಕಿದ ಹಿರಿಮೆ ಅವರಿಗೆ ಸಲ್ಲುತ್ತದೆಯಾದರೂ, ಅದು ಬೇರಾರೊ ತಮಗೆ ಸಲಹೆ ಮಾಡಿದ್ದು ಎಂದು ಸದಾ ಹೇಳುತ್ತಿದ್ದರು. ಅಮೆರಿಕನ್ ಅಸೋಸಿಯೇಷ್ ಫಾರ್ ದಿ ಅಡ್ವಾನ್ಸ್‌ಮೆಂಟ್ ಆಫ್ ಸೈನ್ಸ್‌ಗೆ ಆನ್ನೆ ಈವಿಂಗ್ ೧೯೬೪ರಲ್ಲಿ ಬರೆದ ಪತ್ರದಲ್ಲಿ ಈ ಪದವನ್ನು ಮೊಟ್ಟಮೊದಲಿಗೆ ಬಳಸಿದ ದಾಖಲೆ ಸಿಗುತ್ತದೆ. ವೀಲರ್ ಈ ಪದವನ್ನು ಬಳಸಿದ ನಂತರ, ಇದನ್ನು ಸಾಮಾನ್ಯ ಬಳಕೆಯಲ್ಲಿ ಅಳವಡಿಸಲಾಯಿತು.

ಲಕ್ಷಣಗಳು ಮತ್ತು ರಚನೆ

ಕಪ್ಪು ಕುಳಿಯು ಒಂದೊಮ್ಮೆ ರಚನೆಯ ಬಳಿಕ ಸ್ಥಿರ ಸ್ಥಿತಿಯನ್ನು ಸಾಧಿಸಿದರೆ, ಕಪ್ಪು ಕುಳಿಯು ಮೂರು ಸ್ವತಂತ್ರ ಬೌತಿಕ ಲಕ್ಷಣಗಳನ್ನು ಮಾತ್ರ ಒಳಗೊಂಡಿರುತ್ತದೆ ಎಂದು ನೋ-ಹೇರ್ ಪ್ರಮೇಯವು ಹೇಳುತ್ತದೆ.ಅವು ದ್ರವ್ಯರಾಶಿ, ವಿದ್ಯುದಾವೇಶ ಮತ್ತು ಕೋನೀಯ ಆವೇಗ. ಈ ಲಕ್ಷಣಗಳಿಗೆ ಅಥವಾ ಮಾನದಂಡಗಳಿಗೆ ಒಂದೇ ಮೌಲ್ಯಗಳನ್ನು ಹಂಚಿಕೊಳ್ಳುವ ಯಾವುದೇ ಎರಡು ಕಪ್ಪು ಕುಳಿಗಳು ಪ್ರಾಚೀನ(ಕ್ವಾಂಟಂ ಅಲ್ಲದ)ಯಂತ್ರಶಾಸ್ತ್ರದ ಪ್ರಕಾರ ಸಾದೃಶ್ಯದಿಂದ ಕೂಡಿರುತ್ತದೆ.

ಈ ಲಕ್ಷಣಗಳು ವಿಶೇಷವಾಗಿದೆ. ಏಕೆಂದರೆ ಅವು ಕಪ್ಪುಕುಳಿಯ ಹೊರಗಿನಿಂದ ಕಾಣಬಹುದಾಗಿದೆ. ಉದಾಹರಣೆಗೆ, ವಿದ್ಯುದಾವೇಶದ ಕಪ್ಪುಕುಳಿಯು ಬೇರಾವುದೇ ವಿದ್ಯುದಾವೇಶದ ವಸ್ತುವಿನ ರೀತಿಯಲ್ಲಿ ಸಾದೃಶ್ಯದ ವಿದ್ಯುದಾವೇಶಗಳಿಂದ ವಿಕರ್ಷಿಸುತ್ತದೆ. ಇದೇ ರೀತಿ, ಕಪ್ಪುಕುಳಿಯನ್ನು ಒಳಗೊಂಡಿರುವ ಗೋಳದೊಳಗಿನ ಒಟ್ಟು ದ್ರವ್ಯರಾಶಿಯನ್ನು ಕಪ್ಪು ಕುಳಿಯಿಂದ ದೂರದಲ್ಲಿ ಗಾಸ್`ಸ್ ನಿಯಮ,ADM ದ್ರವ್ಯರಾಶಿಯ ಗುರುತ್ವ ಸಾದೃಶ್ಯವನ್ನು ಬಳಸಿ ಕಂಡುಹಿಡಿಯಬಹುದು. ಇದೇ ರೀತಿ, ಕೋನೀಯ ಆವೇಗವನ್ನು ದೂರದಿಂದಲೇ ಗುರುತ್ವಕಾಂತೀಯ ಕ್ಷೇತ್ರದಿಂದ ಫ್ರೇಮ್ ಡ್ರಾಗಿಂಗ್(ದೇಶಕಾಲವನ್ನು ತನ್ನತ್ತ ಎಳೆಯುವುದು)ಬಳಸಿಕೊಳ್ಳುವ ಮೂಲಕ ಅಳೆಯಬಹುದು.

ಒಂದು ವಸ್ತುವು ಕಪ್ಪು ಕುಳಿಯೊಳಗೆ ಬಿದ್ದಾಗ, ಆ ವಸ್ತುವಿನ ಆಕಾರದ ಬಗ್ಗೆ ಅಥವಾ ಅದಕ್ಕೆ ವಿದ್ಯುದಾವೇಶ ವಿತರಣೆಯ ಬಗ್ಗೆ ಮಾಹಿತಿಯು ಕಪ್ಪು ಕುಳಿಯ ವ್ಯಾಪ್ತಿಯೊಳಗೆ ಸಮನಾಗಿ ಹಂಚಿಹೋಗಿರುತ್ತದೆ ಹಾಗು ಹೊರಗಿನ ವೀಕ್ಷಕರಿಗೆ ಕಾಣುವುದಿಲ್ಲ. ಈ ಪರಿಸ್ಥಿತಿಯಲ್ಲಿ ಹಾರಿಜಾನ್ ನಡವಳಿಕೆಯು ಘರ್ಷಣೆ ಮತ್ತು ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧದೊಂದಿಗೆ ವಾಹಕದ ಹಿಗ್ಗಿಸುವ ಪದರಕ್ಕೆ ಸಮೀಪದ ಹೋಲಿಕೆಯಿಂದ ಕೂಡಿದ್ದು, ಡಿಸ್ಸಿಪೇಟಿವ್( ಚದರಿಸುವ) ವ್ಯವಸ್ಥೆಯಾಗಿದೆ.(ನೋಡಿ ಪದರ ಮಾದರಿ) ಇದು ವಿದ್ಯುತ್ಕಾಂತತೆ ಮುಂತಾದ ಇತರೆ ಕ್ಷೇತ್ರ ಪ್ರಮೇಯಗಳಿಗಿಂತ ವ್ಯತ್ಯಾಸದಿಂದ ಕೂಡಿದೆ. ಅವು ಸೂಕ್ಷ್ಮದರ್ಶಕೀಯ ಮಟ್ಟದಲ್ಲಿ ಯಾವುದೇ ಘರ್ಷಣೆ ಅಥವಾ ಪ್ರತಿರೋಧ ಹೊಂದಿರುವುದಿಲ್ಲ. ಏಕೆಂದರೆ ಅವು ಟೈಮ್ ರಿವರ್ಸಿಬಲ್(ಟಿ-ಸಮ್ಮಿತಿ)ನಿಂದ ಕೂಡಿರುತ್ತದೆ. ಏಕೆಂದರೆ ಕಪ್ಪು ಕುಳಿ ತರುವಾಯ ಕೇವಲ ಮೂರು ಮಾನದಂಡಗಳ ಜತೆಯಲ್ಲಿ ಸ್ಥಿರವಾದ ಸ್ಥಿತಿಯನ್ನು ಸಾಧಿಸುತ್ತದೆ. ಆರಂಭಿಕ ಸ್ಥಿತಿಗಳ ಬಗ್ಗೆ ಮಾಹಿತಿ ಕಳೆದುಕೊಳ್ಳುವುದನ್ನು ತಪ್ಪಿಸುವ ಯಾವುದೇ ಮಾರ್ಗವಿಲ್ಲ. ಕಪ್ಪು ಕುಳಿಯ ಗುರುತ್ವ ಮತ್ತು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರಗಳು ಒಳಗೆ ಏನು ಪ್ರವೇಶಿಸಿತು ಎಂಬ ಬಗ್ಗೆ ತೀರಾ ಕಡಿಮೆ ಮಾಹಿತಿ ಒದಗಿಸುತ್ತದೆ. ಕಪ್ಪು ಕುಳಿಯ ಹಾರಿಜಾನ್‌ನಿಂದ ದೂರದಲ್ಲಿ ಮಾಪನ ಮಾಡಲು ಸಾಧ್ಯವಿಲ್ಲದ ಪ್ರತಿ ಪರಿಮಾಣವನ್ನು ಕಳೆದುಹೋದ ಮಾಹಿತಿಯು ಒಳಗೊಂಡಿದೆ. ಇದರಲ್ಲಿ ಒಟ್ಟು ಬಾರ್ಯಾನ್ ಸಂಖ್ಯೆ, ಲೆಪ್ಟಾನ್ ಸಂಖ್ಯೆ ಮತ್ತು ಕಣ ಬೌತಶಾಸ್ತ್ರದ ಹುಸಿ ವಿದ್ಯುದಾವೇಶಗಳನ್ನು ಒಳಗೊಂಡಿವೆ. ಈ ನಡವಳಿಕೆಯು ಗೊಂದಲದಿಂದ ಕೂಡಿದ್ದು, ಕಪ್ಪು ಕುಳಿ ಮಾಹಿತಿ ನಷ್ಟ ವಿರೋಧಾಭಾಸ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಭೌತಿಕ ಗುಣಲಕ್ಷಣಗಳು

ಅತ್ಯಂತ ಸರಳ ಕಪ್ಪು ಕುಳಿ ದ್ರವ್ಯರಾಶಿಯಿಂದ ಕೂಡಿರುತ್ತದೆ. ಆದರೆ ಅದಕ್ಕೆ ವಿದ್ಯುದಾವೇಶ ಅಥವಾ ಕೋನೀಯ ಆವೇಗ ಇರುವುದಿಲ್ಲ. ಈ ಕಪ್ಪು ಕುಳಿಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಸ್ಕವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ಕಪ್ಪು ಕುಳಿ ಎಂದು ಉಲ್ಲೇಖಿಸಲಾಗುತ್ತದೆ. ವಿಜ್ಞಾನಿ ಕಾರ್ಲ್ ಸ್ಕವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ೧೯೧೫ರಲ್ಲಿ ಈ ವಿವರಣೆಯನ್ನು ರೂಪಿಸಿದರು. ಬರ್ಕಾಫ್`ಸ್ ಪ್ರಮೇಯದ ಪ್ರಕಾರ, ದುಂಡಾಗಿ ಸಮ್ಮಿತೀಯ ಆಗಿರುವುದು ಈ ನಿರ್ವಾತ ವಿವರಣೆ ಮಾತ್ರ. ಇದರ ಅರ್ಥ ಇಂತಹ ಕಪ್ಪು ಕುಳಿಯ ಗುರುತ್ವ ಕ್ಷೇತ್ರ ಮತ್ತು ಯಾವುದೇ ದುಂಡಾದ ಇದೇ ದ್ರವ್ಯರಾಶಿಯ ವಸ್ತುವಿನ ನಡುವೆ ಗಮನಿಸಬಹುದಾದ ವ್ಯತ್ಯಾಸವಿರುವುದಿಲ್ಲ. ಕಪ್ಪು ಕುಳಿ ಅದರ ಸುತ್ತಮುತ್ತಲಿನ ಎಲ್ಲವನ್ನೂ ಹೀರಿಕೊಳ್ಳುವ ಜನಪ್ರಿಯ ಕಲ್ಪನೆಯು ಕಪ್ಪು ಕುಳಿ ವ್ಯಾಪ್ತಿಯಲ್ಲಿ ಮಾತ್ರ ಸರಿಯಾಗಿರುತ್ತದೆ. ದೂರದಲ್ಲಿ ಬಾಹ್ಯ ಗುರುತ್ವ ಕ್ಷೇತ್ರವು ಅಷ್ಟೇ ದ್ರವ್ಯರಾಶಿಯ ಯಾವುದೇ ಕಾಯಕ್ಕೆ ಸದೃಶವಾಗಿರುತ್ತದೆ.

ಹೆಚ್ಚು ಸಾಮಾನ್ಯ ಕಪ್ಪು ಕುಳಿಗಳನ್ನು ವಿವರಿಸುವ ಸಿದ್ಧಾಂತಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ. ವಿದ್ಯುದಾವೇಶದ ಕಪ್ಪು ಕುಳಿಯನ್ನು ರೈಸ್ನರ್-ನಾರ್ಡ್‌ಸ್ಟ್ರಾಮ್ ಮೆಟ್ರಿಕ್‌ನಿಂದ ವಿವರಿಸಲಾಗಿದೆ. ಕೆರ್ ಮೆಟ್ರಿಕ್ ಪರಿಭ್ರಮಿಸುವ ಕಪ್ಪು ಕುಳಿಯನ್ನು ವಿವರಿಸುತ್ತದೆ. ಅತ್ಯಂತ ಸಾಮಾನ್ಯ ಸ್ಥಿರ ಕಪ್ಪು ಕುಳಿ ಸಿದ್ಧಾಂತವು ಕೆರ್-ನಿವ್‌ಮ್ಯಾನ್ ಮ್ಯಾಟ್ರಿಕ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಇದು ಕಪ್ಪು ಕುಳಿಯನ್ನು ವಿದ್ಯುದಾವೇಶ ಮತ್ತು ಕೋನೀಯ ಆವೇಗದಿಂದ ವಿವರಿಸುತ್ತದೆ.

ಕಪ್ಪು ಕುಳಿಯ ದ್ರವ್ಯರಾಶಿ ಯಾವುದೇ ಸಕಾರಾತ್ಮಕ ಮೌಲ್ಯ ಪಡೆಯಬಹುದಾಗಿದ್ದು, ವಿದ್ಯುದಾವೇಶ ಮತ್ತು ಕೋನೀಯ ಆವೇಗವು ದ್ರವ್ಯರಾಶಿಯ ನಿರ್ಬಂಧಕ್ಕೆ ಒಳಗಾಗಿದೆ. ಪ್ಲಾಂಕ್ ಯೂನಿಟ್‌ಗಳಲ್ಲಿ ಒಟ್ಟು ವಿದ್ಯುದಾವೇಶ Q ಮತ್ತು ಒಟ್ಟು ಕೋನೀಯ ಆವೇಗ J ಕೆಳಗಿನ ಅಗತ್ಯವನ್ನು ಪೂರೈಸುತ್ತದೆ.

$Q^{2}+\left({\tfrac {J}{M}}\right)^{2}\leq M^{2}\,$

ದ್ರವ್ಯರಾಶಿM ಯಿಂದ ಕೂಡಿದ ಕಪ್ಪು ಕುಳಿ ಅಸಮಾನತೆಯನ್ನು ಭರ್ತಿ ಮಾಡಿದರೆ ಅದು ಪರಮಾವಧಿ ಎನಿಸುತ್ತದೆ. ಅಸಮಾನತೆಗಳನ್ನು ಉಲ್ಲಂಘಿಸುವ ಐನ್‌ಸ್ಟೈನ್ ಸಮೀಕರಣಗಳ ವಿವರಣೆಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೂ ಅವು ಹಾರಿಜಾನ್(ವ್ಯಾಪ್ತಿ) ಹೊಂದಿರುವುದಿಲ್ಲ. ಈ ವಿವರಣೆಗಳು ಸ್ಫುಟ ಏಕತ್ವಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ ಮತ್ತು ಅಬೌತ ವೆಂದು ಕಾಣಲಾಗುತ್ತದೆ. ಕಾಸ್ಮಿಕ್ ನಿರೋಧಕ ಊಹನವು ಶಕ್ತಿ ಸ್ಥಿತಿ(ರಿಯಲ್ಯಾಸ್ಟಿಕ್ ಮ್ಯಾಟರ್) ಗುರುತ್ವ ಕುಸಿತದ ಮೂಲಕ ಇಂತಹ ಏಕತ್ವ(ಅಪರಿಮಿತ ಸಾಂದ್ರತೆ)ಗಳ ರಚನೆಯನ್ನು ತಳ್ಳಿಹಾಕುತ್ತದೆ. ಇದು ಸಾಂಖ್ಯಿಕ ಅನುಕರಣೆಗಳಿಂದ ಬೆಂಬಲಿತವಾಗಿದೆ.‌

ವಿದ್ಯುತ್‌ಕಾಂತೀಯ ಬಲದ ದೊಡ್ಡ ಶಕ್ತಿಯ ಕಾರಣದಿಂದ ನಕ್ಷತ್ರಗಳ ಕುಸಿತದಿಂದ ರಚನೆಯಾಗುವ ಕಪ್ಪು ಕುಳಿಗಳು ನಕ್ಷತ್ರದ ತಟಸ್ಥ ವಿದ್ಯುದಾವೇಶವನ್ನು ಹೆಚ್ಚುಕಡಿಮೆ ಉಳಿಸುವುದೆಂದು ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ. ಪರಿಭ್ರಮಣೆಯು ಸಾಂದ್ರ ವಸ್ತುಗಳ ಸಾಮಾನ್ಯ ಲಕ್ಷಣವೆಂದು ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ. ಕಪ್ಪು ಕುಳಿಯ ದ್ವಿ ಎಕ್ಸರೆ ಮೂಲ GRS ೧೯೧೫+೧೦೫ ಗರಿಷ್ಠ ಅವಕಾಶದ ಮೌಲ್ಯದ ಬಳಿ ಕೋನೀಯ ಆವೇಗವನ್ನು ಹೊಂದಿರುವುದಾಗಿ ಕಾಣುತ್ತದೆ.

ವರ್ಗ	ದ್ರವ್ಯರಾಶಿ	ಗಾತ್ರ
ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿ	~105–109 M Sun	~0.001–10 AU
ಮಧ್ಯಮ ದ್ರವ್ಯರಾಶಿಯ ಕಪ್ಪು ಕುಳಿ	~೧೦೩ M ಸೂರ್ಯ	~೧೦೩ km = R ಭೂಮಿ
ನಾಕ್ಷತ್ರಿಕ ಕಪ್ಪು ಕುಳಿ	~೧೦ M ಸೂರ್ಯ	~೩೦ ಕಿಮೀ
ಸೂಕ್ಷ್ಮ ಕಪ್ಪು ಕುಳಿ	~M ಚಂದ್ರ ನವರೆಗೆ	~೦.೧ mmವರೆಗೆ

ಕಪ್ಪು ಕುಳಿಗಳು ಸಾಮಾನ್ಯವಾಗಿ ಅವುಗಳ ದ್ರವ್ಯರಾಶಿ ಪ್ರಕಾರ ವಿಂಗಡಿಸಲಾಗುತ್ತದೆ. ಕೋನೀಯ ಆವೇಗ J ಅಥವಾ ವಿದ್ಯುದಾವೇಶQ ದಿಂದ ಇದು ಮುಕ್ತವಾಗಿರುತ್ತದೆ. ಕಪ್ಪು ಕುಳಿಯ ಗಾತ್ರವು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಅಥವಾ ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ಇದು ಸರಿಸುಮಾರು ದ್ರವ್ಯರಾಶಿ M ಗೆ ಈ ಮೂಲಕ ಪ್ರಮಾಣಾನುಗುಣವಾಗಿರುತ್ತದೆ.

$r_{\mathrm {sh} }={\frac {2GM}{c^{2}}}\approx 2.95\,{\frac {M}{M_{\mathrm {Sun} }}}~\mathrm {~} \mathrm {km,}$

ಅಲ್ಲಿ r _shಸ್ಕವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯ ಮತ್ತು M_{ಸೂರ್ಯ} ಸೂರ್ಯನ ದ್ರವ್ಯರಾಶಿಯಾಗಿರುತ್ತದೆ. ಈ ಸಂಬಂಧವು ಶೂನ್ಯ ವಿದ್ಯುದಾವೇಶ ಮತ್ತು ಕೋನೀಯ ಆವೇಗದ ಕಪ್ಪು ಕುಳಿಗಳಲ್ಲಿ ನಿಖರವಾಗಿರುತ್ತದೆ. ಹೆಚ್ಚಿನ ಸಾಮಾನ್ಯ ಕಪ್ಪು ಕುಳಿಗಳಿಗೆ ಇದು ಅಂಶ ೨ರಷ್ಟು ವ್ಯತ್ಯಾಸದಿಂದ ಕೂಡಿರುತ್ತದೆ. ಬಲಭಾಗದ ಕೋಷ್ಠಕವು ವಿಶಿಷ್ಟ ಕಪ್ಪು ಕುಳಿಗಳ ವಿವಿಧ ವರ್ಗಗಳನ್ನು ಪಟ್ಟಿಮಾಡುತ್ತದೆ.

ಈವೆಂಟ್ ಹಾರಿಜಾನ್ (Event horizon)

• [ಸರಿಯಾದ ಉಚ್ಛಾರ- ಈವೆಂಟ್ ಹೊರೈಝನ್]

ಕಪ್ಪು ಕುಳಿಯಿಂದ ದೂರದಲ್ಲಿ ಕಣವೊಂದು ಯಾವುದೇ ದಿಕ್ಕಿನಲ್ಲಿ ಚಲಿಸಬಹುದು. ಇದು ಬೆಳಕಿನ ವೇಗದಿಂದ ಮಾತ್ರ ನಿರ್ಬಂಧಿತವಾಗಿದೆ.

ಕಪ್ಪು ಕುಳಿಯ ಸಮೀಪದಲ್ಲಿ ದೇಶಕಾಲ ಕಲ್ಪನೆಯು ವಿರೂಪಗೊಳ್ಳಲು ಆರಂಭಿಸುತ್ತದೆ. ಕಪ್ಪು ಕುಳಿಯಿಂದ ದೂರ ಹೋಗುವ ಪಥಗಳಿಗಿಂತ ಕಪ್ಪು ಕುಳಿಯತ್ತ ಸಾಗುವ ಹೆಚ್ಚು ಪಥಗಳಿವೆ.

ಈವೆಂಟ್ ಹಾರಿಜಾನ್(ಬೆಳಕು ಹಾದುಹೋಗದ ಕಪ್ಪುಕುಳಿಯ ಸುತ್ತಲಿನ ಪ್ರದೇಶ)ನ ಒಳಗೆ ಎಲ್ಲ ಪಥಗಳು ಕಣವನ್ನು ಕಪ್ಪು ಕುಳಿಯ ಮಧ್ಯಕ್ಕೆ ಸಮೀಪದಲ್ಲಿ ತರುತ್ತವೆ. ಇದರಿಂದ ಕಣವು ತಪ್ಪಿಸಿಕೊಳ್ಳುವುದು ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ.

ಕಪ್ಪು ಕುಳಿಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವ ಲಕ್ಷಣವು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಕಾಣಿಸುವುದಾಗಿದೆ. ಇದು ದೇಶಕಾಲದ ಗಡಿಯಾಗಿದ್ದು, ಇದರ ಮೂಲಕ ವಸ್ತು ಮತ್ತು ಬೆಳಕು ಕಪ್ಪುಕುಳಿಯ ದ್ರವ್ಯರಾಶಿಯತ್ತ ಒಳಮುಖವಾಗಿ ಸಾಗುತ್ತದೆ. ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಒಳಪ್ರದೇಶದಿಂದ ಬೆಳಕು ಅಥವಾ ಬೇರಾವುದೇ ವಸ್ತು ತಪ್ಪಿಸಿಕೊಳ್ಳಲು ಸಾಧ್ಯವಿಲ್ಲ. ಈವೆಂಟ್ ಹಾರಿಜಾನ್‌ನನ್ನು ಹಾಗೆ ಕರೆಯುವುದು ಏಕೆಂದರೆ, ಅದರ ಗಡಿಯೊಳಗೆ ಯಾವುದೇ ಘಟನೆ ಸಂಭವಿಸಿದರೂ, ಆ ಘಟನೆಯ ಮಾಹಿತಿಯು ಬಾಹ್ಯ ವೀಕ್ಷಕನನ್ನು ಮುಟ್ಟಲು ಸಾಧ್ಯವಿಲ್ಲ. ಅಂತಹ ಘಟನೆ ನಡೆದರೆ ಅದನ್ನು ನಿರ್ಧರಿಸುವುದು ಅಸಾಧ್ಯವಾಗುತ್ತದೆ.

ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ ಮುಂಗಾಣುವಂತೆ, ದೊಡ್ಡ ದ್ರವ್ಯರಾಶಿಯ ಉಪಸ್ಥಿತಿಯು ದೇಶಕಾಲವನ್ನು ಯಾವ ರೀತಿ ವಿರೂಪಗೊಳಿಸುತ್ತದೆಂದರೆ, ಕಣಗಳು ಸಾಗುವ ಪಥಗಳು ದ್ರವ್ಯರಾಶಿಯತ್ತ ವಾಲುತ್ತವೆ. ಕಪ್ಪು ಕುಳಿಯ ಈವೆಂಟ್ ಹಾರಿಜಾನ್‌ನಲ್ಲಿ ಈ ವಿರೂಪವು ಪ್ರಬಲವಾಗಿದ್ದು, ಕಪ್ಪು ಕುಳಿಯಿಂದ ದೂರ ಯಾವುದೇ ಪಥ ಹೋಗುವುದಿಲ್ಲ.

ದೂರದಲ್ಲಿರುವ ವೀಕ್ಷಕನಿಗೆ, ಕಪ್ಪು ಕುಳಿಯ ಹತ್ತಿರವಿರುವ ಗಡಿಯಾರಗಳು ಕಪ್ಪುಕುಳಿಯಿಂದ ದೂರವಿರುವ ಗಡಿಯಾರಗಳಿಗಿಂತ ಹೆಚ್ಚು ನಿಧಾನವಾಗಿ ಟಿಕ್‌ ಶಬ್ದ ಮಾಡುವುದು ಕಾಣುತ್ತದೆ. ಗುರುತ್ವ ಕಾಲ ಹಿಗ್ಗುವಿಕೆ ಪರಿಣಾಮವಾಗಿ, ಕುಪ್ಪು ಕುಳಿಯೊಳಗೆ ಬೀಳುವ ವಸ್ತು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಸಮೀಪಿಸುತ್ತಿದ್ದಂತೆ ನಿಧಾನವಾಗಿ ಚಲಿಸುತ್ತಿರುವ ಹಾಗೆ ಮತ್ತು ಅದನ್ನು ಮುಟ್ಟಲು ಅನಂತ ಕಾಲವನ್ನು ತೆಗೆದುಕೊಳ್ಳುವಂತೆ ಕಾಣುತ್ತದೆ. ಇದೇ ಸಮಯದಲ್ಲಿ, ಈ ವಸ್ತುವಿನ ಎಲ್ಲ ಪ್ರಕ್ರಿಯೆಗಳು ನಿಧಾನವಾಗುತ್ತದೆ ಮತ್ತು ಹೊರಹೊಮ್ಮಿಸುವ ಬೆಳಕು ಕೆಂಪು ಮತ್ತು ಮಂದವಾಗಿ ಕಾಣುತ್ತದೆ. ಈ ಪರಿಣಾಮವನ್ನು ಗುರುತ್ವದ ಕೆಂಪು ಪಲ್ಲಟ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ತರುವಾಯ, ಅದು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಮುಟ್ಟುವುದಕ್ಕೆ ಸ್ವಲ್ಪ ಮುಂಚಿನ ಹಂತದಲ್ಲಿ, ಬೀಳುವ ವಸ್ತು ಅತೀ ಮಸುಕಾಗಿ ಕಾಣದಾಗುತ್ತದೆ.

ಆದರೆ, ಕಪ್ಪುಕುಳಿಯೊಳಗೆ ಬೀಳುವ ವೀಕ್ಷಕ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಹಾದುಹೋಗುವಾಗ ಇದ್ಯಾವ ಪರಿಣಾಮಗಳನ್ನು ಗಮನಿಸುವುದಿಲ್ಲ. ಅವನದೇ ಗಡಿಯಾರದ ಪ್ರಕಾರ,ಅವನು ಅನಂತ ಕಾಲದ ನಂತರ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ದಾಟುತ್ತಾನೆ. ಆದರೆ ಯಾವ ಕಾಲದಲ್ಲಿ ಅದನ್ನು ಹಾದುಹೋಗುತ್ತಾನೆಂದು ನಿರ್ಧರಿಸಲು ಅಸಮರ್ಥನಾಗುತ್ತಾನೆ. ಏಕೆಂದರೆ ಸ್ಥಳೀಯ ವೀಕ್ಷಣೆಗಳಿಂದ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಸ್ಥಳವನ್ನು ನಿರ್ಧರಿಸುವುದು ಅಸಾಧ್ಯ.

ಪರಿಭ್ರಮಣೆಯಿಲ್ಲದ(ಸ್ಥಿರವಾದ)ಕಪ್ಪು ಕುಳಿ, ಸ್ಕವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯವು ಗುಂಡಗಿನ ಈವೆಂಟ್ ಹಾರಿಜಾನ್‌ನ ಮೇರೆ ನಿರ್ಧರಿಸುತ್ತದೆ. ಒಂದು ವಸ್ತುವಿನ ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯವು ದ್ರವ್ಯರಾಶಿಗೆ ಪ್ರಮಾಣಾನುಗುಣವಾಗಿದೆ. ಪರಿಭ್ರಮಿಸುವ ಕಪ್ಪುಕುಳಿಯು ವಿಕೃತ, ಗುಂಡಗಿಲ್ಲದ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಹೊಂದಿರುತ್ತದೆ. ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ವಸ್ತುವಿನ ಮೇಲ್ಮೈಯಾಗಿರದೇ, ಕೇವಲ ಗಣಿತೀಯವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಿದ ಗಡಿಗುರುತಾಗಿದ್ದು, ಯಾವುದೇ ವಸ್ತು ಅಥವಾ ವಿಕಿರಣವು ಕಪ್ಪು ಕುಳಿಯನ್ನು ಹಾದುಹೋಗದಂತೆ ತಪ್ಪಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ. ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ ನೀಡಿರುವ ಕಪ್ಪು ಕುಳಿಯ ವಿವರಣೆಯು ಅಂದಾಜು ವಿವರಣೆಯೆಂದು ಹೇಳಲಾಗಿದ್ದು, ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಸುತ್ತಮುತ್ತ ಕ್ವಾಂಟಂ ಗುರುತ್ವದ ಪರಿಣಾಮಗಳು ಮಹತ್ವದ್ದಾಗಿರುತ್ತದೆಂದು ಕೆಲವು ವಿಜ್ಞಾನಿಗಳು ನಿರೀಕ್ಷಿಸುತ್ತಾರೆ. ಇದು ಕಪ್ಪು ಕುಳಿಯ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಬಳಿ ವಸ್ತುವಿನ ವೀಕ್ಷಣೆಗಳನ್ನು ಪರೋಕ್ಷವಾಗಿ ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ ಮತ್ತು ಉದ್ದೇಶಿತ ವಿಸ್ತರಣೆಗಳ ಅಧ್ಯಯನಕ್ಕೆ ಬಳಸಲು ಅವಕಾಶವಾಗುತ್ತದೆ.

ಏಕತ್ವ (Gravitational singularity)

ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆಯ ಮೂಲಕ ವಿವರಿಸಿರುವಂತೆ ಕಪ್ಪು ಕುಳಿಯ ಮಧ್ಯದಲ್ಲಿ ಗುರುತ್ವ ಏಕತ್ವವಿರುತ್ತದೆ. ಇದರಲ್ಲಿ ದೇಶಕಾಲ ತಿರುವುಗಳು ಅನಂತವಾಗಿರುತ್ತದೆ. ಪರಿಭ್ರಮಿಸದಿರುವ ಕಪ್ಪು ಕುಳಿಗೆ ಈ ಪ್ರದೇಶವು ಏಕಾಂಶದ ಆಕಾರವನ್ನು ತಳೆಯುತ್ತದೆ ಹಾಗೂ ಪರಿಭ್ರಮಿಸುವ ಕಪ್ಪು ಕುಳಿಯು ಪರಿಭ್ರಮಿಸುವ ಸಮತಲದಲ್ಲಿರುವ ಉಂಗುರ ಏಕತ್ವವಾಗಿ ರೂಪುಗೊಳ್ಳುತ್ತದೆ. ಎರಡೂ ಪ್ರಕರಣಗಳಲ್ಲಿ ಏಕತ್ವ ಪ್ರದೇಶವು ಶೂನ್ಯ ಗಾತ್ರವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಏಕತ್ವ ಪ್ರದೇಶವು ಕಪ್ಪು ಕುಳಿ ವಿವರಣೆಯ ಎಲ್ಲ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆಂದು ತೋರಿಸಬಹುದು. ಏಕತ್ವ ಪ್ರದೇಶವು ಅನಂತ ಸಾಂದ್ರತೆಯನ್ನು ಹೊಂದಿರುವ ಪ್ರದೇಶವೆಂದು ಭಾವಿಸಲಾಗಿದೆ.

ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ಕಪ್ಪುಕುಳಿ(ಪರಿಭ್ರಮಿಸದಿರುವ,ವಿದ್ಯುದಾವೇಶ ರಹಿತ)ಯೊಳಗೆ ಬೀಳುವ ವೀಕ್ಷಕ ಏಕತ್ವದಿಂದ ತಪ್ಪಿಸಿಕೊಳ್ಳಲು ಸಾಧ್ಯವಿಲ್ಲ. ಹಾಗೆ ತಪ್ಪಿಸಿಕೊಳ್ಳಲು ಯತ್ನಿಸಿದರೆ, ಅಲ್ಲಿಗೆ ಹೋಗುವ ಸಮಯ ಮಾತ್ರ ಕಡಿಮೆಯಾಗುತ್ತದೆ. ಒಂದೊಮ್ಮೆ ಅವರು ಏಕತ್ವ ಮುಟ್ಟಿದಾಗ, ಅವರು ಅನಂತ ಸಾಂದ್ರತೆಯಲ್ಲಿ ಅಪ್ಪಳಿಸುತ್ತಾರೆ ಹಾಗು ಅವರ ದ್ರವ್ಯರಾಶಿಯು ಒಟ್ಟು ಕಪ್ಪು ಕುಳಿಯಲ್ಲಿ ಸೇರ್ಪಡೆಯಾಗುತ್ತದೆ. ಇದು ಸಂಭವಿಸುವ ಮುಂಚೆ, ಬೆಳೆಯುವ ಗುರುತ್ವ ಶಕ್ತಿಯಿಂದ ಅವರ ಛಿದ್ರತೆ ಉಂಟಾಗಬಹುದು. ಈ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಕೆಲವು ಬಾರಿ ಸ್ಪಗೆಟಿಫಿಕೇಶನ್ ಅಥವಾ ನೂಡಲ್ ಪರಿಣಾಮ ಎಂದು ಉಲ್ಲೇಖಿಸಲಾಗುತ್ತದೆ.

ವಿದ್ಯುದಾವೇಶದ(ರೈಸ್ನರ್–ನಾರ್ಡ್‌ಸ್ಟ್ರಾಮ್ )ಅಥವಾ ಪರಿಭ್ರಮಿಸುವ(ಕೆರ್) ಕಪ್ಪು ಕುಳಿ ಪ್ರಕರಣದಲ್ಲಿ ಏಕತ್ವವನ್ನು ತಪ್ಪಿಸಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ. ಈ ವಿವರಣೆಗಳನ್ನು ಸಾಧ್ಯವಾದಷ್ಟು ವಿಸ್ತರಿಸಿದಾಗ, ವರ್ಮ್‌ಹೋಲ್ ರೀತಿಯಲ್ಲಿ ಕಪ್ಪುಕುಳಿ ಕಾರ್ಯನಿರ್ವಹಿಸಿ, ಅದು ಭಿನ್ನ ದೇಶಕಾಲದ ವ್ಯಾಪ್ತಿಯೊಳಗೆ ನಿರ್ಗಮಿಸುವ ಕಾಲ್ಪನಿಕ ಸಾಧ್ಯತೆಯನ್ನು ಬಹಿರಂಗಪಡಿಸುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಇನ್ನೊಂದು ಬ್ರಹ್ಮಾಂಡದೊಳಗೆ ಪ್ರಯಾಣಿಸುವ ಸಾಧ್ಯತೆಯು ಕೇವಲ ಸೈದ್ಧಾಂತಿಕವಾಗಿದ್ದು, ಯಾವುದೇ ಪ್ರಕ್ಷುಬ್ಧತೆಯು ಈ ಸಾಧ್ಯತೆಯನ್ನು ಹಾಳುಮಾಡುತ್ತದೆ. ಕೆರ್ ಏಕತ್ವದ ಸುತ್ತ ಮುಚ್ಚಿದ ಟೈಮ್‌ಲೈಕ್ ರೇಖೆ(ಒಬ್ಬರ ಭೂತಕಾಲಕ್ಕೆ ಹಿಂತಿರುಗುವುದು)ಯನ್ನು ಅನುಸರಿಸುವಂತೆ ಅದು ಕಾಣುತ್ತದೆ ಹಾಗು ಗ್ರಾಂಡ್‌ಫಾದರ್ ವಿರೋಧಾಭಾಸ(ಕಾಲದ ವಿವಿಧ ಹಂತಗಳಲ್ಲಿ ಸಂಚರಿಸುವುದು)ಮುಂತಾದ ಕಾರಣತ್ವದ ಸಮಸ್ಯೆಗಳಿಗೆ ದಾರಿ ಕಲ್ಪಿಸುತ್ತದೆ. ಯಾವುದೇ ವಿಚಿತ್ರ ಪರಿಣಾಮಗಳು ಪರಿಭ್ರಮಿಸುವ ಮತ್ತು ವಿದ್ಯುದಾವೇಶದ ಕಪ್ಪುಕುಳಿಗಳ ಸೂಕ್ತ ಕ್ವಾಂಟಂ ಯಾಂತ್ರಿಕ ಸಂಸ್ಕರಣೆಯಲ್ಲಿ ಉಳಿಯುವುದಿಲ್ಲ ಎಂದು ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ.

ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆಯಲ್ಲಿ ಏಕತ್ವಗಳ ದರ್ಶನವು ಸಿದ್ಧಾಂತದ ಕುಸಿತವನ್ನು ಸಂಕೇತಿಸುತ್ತದೆಂದು ಗ್ರಹಿಸಲಾಗಿದೆ. ಈ ಕುಸಿತವನ್ನು ಆದಾಗ್ಯೂ ನಿರೀಕ್ಷಿಸಲಾಗಿತ್ತು. ತೀವ್ರ ಹೆಚ್ಚು ಸಾಂದ್ರತೆ ಮತ್ತು ಕಣದ ಪರಸ್ಪರ ಕ್ರಿಯೆಗಳಿಂದ ಕ್ವಾಂಟಂ ಮೆಕಾನಿಕಲ್ ಪರಿಣಾಮಗಳು ಈ ಕಾರ್ಯಗಳನ್ನು ವಿವರಿಸುತ್ತದೆ. ಇದುವರೆಗೆ ಕ್ವಾಂಟಂ ಮತ್ತು ಗುರುತ್ವದ ಪರಿಣಾಮಗಳನ್ನು ಏಕ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಸಂಯೋಜಿಸಲು ಸಾಧ್ಯವಾಗಿಲ್ಲ. ಕ್ವಾಂಟಂ ಗುರುತ್ವದ ಸಿದ್ಧಾಂತವು ಯಾವುದೇ ಏಕತ್ವಗಳಿಲ್ಲದೇ ಕಪ್ಪು ಕುಳಿಗಳ ವೈಶಿಷ್ಠ್ಯಗಳನ್ನು ತೋರಿಸುತ್ತದೆಂದು ಸಾಮಾನ್ಯವಾಗಿ ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ.

ದ್ಯುತಿಗೋಳ (Photon sphere)

ದ್ಯುತಿಗೋಳವು ಶೂನ್ಯದಷ್ಟು ದಪ್ಪಗಿರುವ ವೃತ್ತಾಕಾರದ ಗಡಿಯಾಗಿದ್ದು, ಸ್ಪರ್ಶ ರೇಖೆಗಳಲ್ಲಿ ವೃತ್ತದತ್ತ ಚಲಿಸುವ ಫೋಟೊನ್‌ಗಳು ವೃತ್ತಾಕಾರದ ಕಕ್ಷೆಯಲ್ಲಿ ಸಿಕ್ಕಿಕೊಳ್ಳುತ್ತವೆ. ಪರಿಭ್ರಮಿಸದಿರುವ ಕಪ್ಪು ಕುಳಿಗಳಿಗೆ, ದ್ಯುತಿಗೋಳವು ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದ ೧ .೫ಪಟ್ಟು ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಕಕ್ಷೆಗಳು ಕ್ರಿಯಾಶೀಲವಾಗಿ ಅಸ್ಥಿರವಾಗಿದೆ. ಆದ್ದರಿಂದ ಯಾವುದೇ ಸಣ್ಣ ಕ್ಷೋಬೆ(ಒಳಗೆ ಬೀಳುವ ವಸ್ತುವಿನ ಕಣ ಮುಂತಾದವು)ಕಾಲಕ್ರಮೇಣ ಬೆಳೆದು, ಕಪ್ಪುಕುಳಿಯಿಂದ ತಪ್ಪಿಸಿಕೊಂಡು ಹೊರಭಾಗದ ಪಥದಲ್ಲಿ ಅಥವಾ ಒಳಭಾಗದ ಸುರುಳಿಯಲ್ಲಿ ಸ್ಥಾಪನೆಯಾಗುತ್ತದೆ, ಹಾಗು ಕೊನೆಯಲ್ಲಿ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ದಾಟುತ್ತದೆ.

ದ್ಯುತಿಗೋಳದ ಒಳಗಿನಿಂದ ಬೆಳಕು ತಪ್ಪಿಸಿಕೊಳ್ಳಬಹುದಾಗಿದ್ದು, ಒಳಮುಖದ ಪಥದಲ್ಲಿ ದ್ಯುತಿಗೋಳ ದಾಟಿದ ಯಾವುದೇ ಬೆಳಕನ್ನು ಕಪ್ಪು ಕುಳಿಯು ಸೆರೆಹಿಡಿಯುತ್ತದೆ. ಆದರೆ ದ್ಯುತಿಗೋಳದ ಒಳಗಿನಿಂದ ಬಾಹ್ಯ ವೀಕ್ಷಕನಿಗೆ ಮುಟ್ಟುವ ಬೆಳಕು ದ್ಯುತಿಗೋಳದ ಒಳಗಿನ ವಸ್ತುಗಳಿಂದ ಹೊಮ್ಮಿದ್ದರೂ, ಅದು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಹೊರಗಿರುತ್ತವೆ.

ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರಗಳು ಮುಂತಾದ ಇತರ ಸಾಂದ್ರ ವಸ್ತುಗಳು ಕೂಡ ದ್ಯುತಿಗೋಳ ಒಳಗೊಂಡಿರಬಹುದು. ವಸ್ತುವಿನ ಗುರುತ್ವ ಕ್ಷೇತ್ರವು ಅದರ ವಾಸ್ತವ ಗಾತ್ರವನ್ನು ಅವಲಂಬಿಸಿಲ್ಲ ಎಂಬ ವಾಸ್ತವಾಂಶವನ್ನು ಇದು ಆಧರಿಸಿದೆ. ಆದ್ದರಿಂದ ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯಕ್ಕಿಂತ ೧ .೫ಪಟ್ಟು ಚಿಕ್ಕದಾದ ಯಾವುದೇ ವಸ್ತು ಅದರ ದ್ರವ್ಯರಾಶಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ದ್ಯುತಿಗೋಳ ಹೊಂದಿರುತ್ತದೆ.

ಎರ್ಗೊಸ್ಪಿಯರ್ (Ergosphere)

ಎರ್ಗೊಸ್ಪಿಯರ್ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಹೊರಗೆ ವಿಲಕ್ಷಣ ಅಂಡಗೋಳ ಪ್ರದೇಶವಾಗಿದ್ದು, ವಸ್ತುಗಳು ಸ್ಥಿರವಾಗಿ ನಿಲ್ಲಲು ಸಾಧ್ಯವಿಲ್ಲ.

ಪರಿಭ್ರಮಿಸುವ ಕಪ್ಪು ಕುಳಿಗಳು ದೇಶಕಾಲದ ಪ್ರದೇಶದಿಂದ ಸುತ್ತುವರಿದಿದೆ. ಅಲ್ಲಿ ಸ್ಥಿರವಾಗಿ ನಿಲ್ಲುವುದು ಅಸಾಧ್ಯವಾಗಿದ್ದು, ಅದಕ್ಕೆ ಎರ್ಗೋಸ್ಪಿಯರ್ ಎನ್ನಲಾಗುತ್ತದೆ. ಇದು ಫ್ರೇಮ್‌ಡ್ರ್ಯಾಗಿಂಗ್(ದೇಶಕಾಲ ಸೆಳೆಯುವ)ಪ್ರಕ್ರಿಯೆಯ ಫಲವಾಗಿದೆ. ಯಾವುದೇ ಪರಿಭ್ರಮಿಸುವ ದ್ರವ್ಯರಾಶಿಯು ತನ್ನನ್ನು ಸುತ್ತುವರಿದಿರುವ ದೇಶಕಾಲದತ್ತ ಸ್ವಲ್ಪಮಟ್ಟಿಗೆ ಎಳೆಯಲ್ಪಡುತ್ತದೆ ಎಂದು ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ ಮುಂಗಂಡಿದೆ. ಪರಿಭ್ರಮಿಸುವ ದ್ರವ್ಯರಾಶಿಯ ಬಳಿಯಿರುವ ಯಾವುದೇ ವಸ್ತುವು ಪರಿಭ್ರಮಣೆಯ ದಿಕ್ಕಿನತ್ತ ಚಲಿಸಲು ಆರಂಭಿಸುತ್ತದೆ. ಪರಿಭ್ರಮಿಸುವ ಕಪ್ಪು ಕುಳಿಗೆ ಈ ಪರಿಣಾಮವು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಬಳಿ ಅತೀ ಪ್ರಬಲವಾಗಿದ್ದು, ವಸ್ತುವು ಚಲನೆ ಸ್ಥಗಿತಗೊಳಿಸಲು ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಬೆಳಕಿನ ವೇಗಕ್ಕಿಂತ ಹೆಚ್ಚು ಚಲಿಸಬೇಕಾಗುತ್ತದೆ.

ಕಪ್ಪು ಕುಳಿಯ ಎರ್ಗೊಸ್ಪಿಯರ್ ಒಳಗಿನಿಂದ(ಹೊರ)ಈವೆಂಟ್ ಹಾರಿಜಾನ್‌ನಿಂದ ಮತ್ತು ಆಬ್ಲೇಟ್ ಅಂಡಗೋಳದಿಂದ ಸುತ್ತುವರಿದಿದೆ. ಇವು ಧ್ರುವಗಳಲ್ಲಿ ಈವೆಂಟ್ ಹಾರಿಜಾನ್‌ ಜತೆ ಒಂದಾಗುತ್ತದೆ ಹಾಗು ಸಮಭಾಜಕವೃತ್ತದಲ್ಲಿ ಅಗಲವಾಗಿರುವುದನ್ನು ಗಮನಿಸಬಹುದು. ಹೊರಗಿನ ಗಡಿಯನ್ನು ಕೆಲವು ಬಾರಿ ಎರ್ಗೋಸರ್ಫೇಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಎರ್ಗೋಸ್ಪಿಯರ್‌ನಿಂದ ವಸ್ತುಗಳು ಮತ್ತು ವಿಕಿರಣಗಳು ಸಾಮಾನ್ಯವಾಗಿ ತಪ್ಪಿಸಿಕೊಳ್ಳುತ್ತವೆ. ಪೆನ್ರೋಸ್ ಪ್ರಕ್ರಿಯೆ ಮೂಲಕ, ವಸ್ತುಗಳು ಎರ್ಗೋಸ್ಪಿಯರ್‌ನಿಂದ ಅವು ಪ್ರವೇಶಿಸಿದ ಶಕ್ತಿಗಿಂತ ಹೆಚ್ಚು ಶಕ್ತಿಯೊಂದಿಗೆ ಹೊರಚಿಮ್ಮುತ್ತವೆ. ಈ ಶಕ್ತಿಯನ್ನು ಕಪ್ಪು ಕುಳಿಯ ಪರಿಭ್ರಮಿಸುವ ಶಕ್ತಿಯಿಂದ ತೆಗೆದುಕೊಳ್ಳಲಾಗಿದ್ದು, ಅದು ನಿಧಾನವಾಗಲು ಕಾರಣವಾಗುತ್ತದೆ.

ರಚನೆ ಮತ್ತು ವಿಕಾಸ

ಕಪ್ಪು ಕುಳಿಗಳ ವಿಲಕ್ಷಣ ಸ್ವಭಾವವನ್ನು ಪರಿಗಣಿಸಿ, ಇಂತಹ ವಿಲಕ್ಷಣ ವಸ್ತುಗಳು ನಿಸರ್ಗದಲ್ಲಿ ಅಸ್ತಿತ್ವದಲ್ಲಿರಲು ಸಾಧ್ಯವೇ ಅಥವಾ ಐನ್‌ಸ್ಟೈನ್ ಸಮೀಕರಣಗಳಿಗೆ ಕೇವಲ ವಿವರಣೆಗಳೇ ಎಂಬ ಪ್ರಶ್ನೆ ಸಹಜವಾಗಿ ಉದ್ಭವಿಸುತ್ತದೆ. ಐನ್‌ಸ್ಟೈನ್ ಸ್ವತಃ ಕಪ್ಪುಕುಳಿಗಳು ರಚನೆಯಾಗುವುದಿಲ್ಲ ಎಂದು ತಪ್ಪಾಗಿ ಭಾವಿಸಿದ್ದರು. ಏಕೆಂದರೆ ಕುಸಿಯುವ ಕಣಗಳ ಕೋನೀಯ ಆವೇಗವು ಕೆಲವು ತ್ರಿಜ್ಯದಲ್ಲಿ ಚಲನೆಯನ್ನು ಸ್ಥಿರಗೊಳಿಸುತ್ತದೆಂದು ಅವರು ತೀರ್ಮಾನಿಸಿದ್ದರು. ಇದು ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ ಸಮುದಾಯವು ಅನೇಕ ವರ್ಷಗಳವರೆಗೆ ಎಲ್ಲ ಫಲಿತಾಂಶಗಳನ್ನು ತಳ್ಳಿಹಾಕಲು ದಾರಿ ಕಲ್ಪಿಸಿತು. ಆದಾಗ್ಯೂ, ಸಾಪೇಕ್ಷತಾ ವಾದಿಗಳಲ್ಲಿ ಕೆಲವರು ಕಪ್ಪು ಕುಳಿಗಳು ಬೌತಿಕ ವಸ್ತುಗಳಾಗಿವೆ ಎಂದು ವಾದಿಸಲಾರಂಭಿಸಿದರು ಹಾಗು ೧೯೬೦ರ ದಶಕದ ಕೊನೆಯಲ್ಲಿ, ಆ ಕ್ಷೇತ್ರದಲ್ಲಿ ಬಹುತೇಕ ಮಂದಿ ಸಂಶೋಧಕರನ್ನು ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ರಚನೆಗೆ ಯಾವುದೇ ಅಡ್ಡಿಯಿಲ್ಲ ಎಂಬ ಬಗ್ಗೆ ಮನವೊಲಿಸಿದರು.

ಒಂದೊಮ್ಮೆ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ರಚನೆಯಾದ ನಂತರ, ಅದರಲ್ಲಿ ಒಂದು ಕಡೆ ಏಕತ್ವವು ರೂಪುಗೊಳ್ಳುತ್ತದೆ ಎಂದು ರೋಜರ್ ಪೆನ್ರೋಸ್ ಸಾಬೀತು ಮಾಡಿದರು. ಸ್ವಲ್ಪ ಕಾಲದ ನಂತರ, ಮಹಾ ಸ್ಫೋಟವನ್ನು ವಿವರಿಸುವ ಅನೇಕ ವಿಶ್ವವಿಜ್ಞಾನ ವಿವರಣೆಗಳು ಸದಿಶ ಕ್ಷೇತ್ರಗಳು ಅಥವಾ ವಿಲಕ್ಷಣ ವಸ್ತುವಿಲ್ಲದೇ ಏಕತ್ವಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ ಎಂದು ಸ್ಟೀಫನ್ ಹಾಕಿಂಗ್ ತೋರಿಸಿದರು.(ನೋಡಿ ಪೆನ್‌ರೋಸ್-ಹಾಕಿಂಗ್ ಏಕತ್ವ ಪ್ರಮೇಯಗಳು). ಕೆರ್ ವಿವರಣೆ, ನೊ-ಹೇರ್ ಪ್ರಮೇಯ ಮತ್ತು ಕಪ್ಪು ಕುಳಿ ಉಷ್ಣಬಲವಿಜ್ಞಾನದ ನಿಯಮಗಳು, ಕಪ್ಪುಕುಳಿಗಳ ಬೌತಿಕ ಲಕ್ಷಣಗಳು ಸರಳ ಮತ್ತು ಗ್ರಹಿಸಬಹುದಾಗಿದ್ದು, ಸಂಶೋಧನೆಗೆ ಗೌರವಾನ್ವಿತ ವಸ್ತುವನ್ನಾಗಿ ಮಾಡಿದೆಯೆಂದು ತೋರಿಸಿವೆ. ನಕ್ಷತ್ರಗಳು ಮುಂತಾದ ಭಾರವಾದ ವಸ್ತುಗಳ ಗುರುತ್ವ ಕುಸಿತವು ಕಪ್ಪು ಕುಳಿಗಳ ಪ್ರಾಥಮಿಕ ರಚನೆ ಪ್ರಕ್ರಿಯೆ ಎಂದು ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ. ಆದರೆ ಕಪ್ಪುಕುಳಿಗಳ ರಚನೆಗೆ ಎಡೆಯಾಗುವ ವಿಲಕ್ಷಣ ಪ್ರಕ್ರಿಯೆಗಳು ಕೂಡ ಇವೆ.

ಗುರುತ್ವ ಕುಸಿತ (Gravitational collapse)

ಒಂದು ವಸ್ತುವಿನ ಸ್ವಯಂ ಗುರುತ್ವಬಲವನ್ನು ಪ್ರತಿರೋಧಿಸುವ ವಸ್ತುವಿನ ಆಂತರಿಕ ಒತ್ತಡವು ಸಾಕಷ್ಟಿಲ್ಲದಿದ್ದರೆ ಗುರುತ್ವ ಕುಸಿತವು ಉಂಟಾಗುತ್ತದೆ. ನಕ್ಷತ್ರ ಬೀಜಕಣಗಳ ಸಂಶ್ಲೇಷಣೆ ಮೂಲಕ ಉಷ್ಣಾಂಶವನ್ನು ಕಾಯ್ದುಕೊಳ್ಳಲು ನಕ್ಷತ್ರದಲ್ಲಿ ಅತೀ ಕಡಿಮೆ ಇಂಧನ ಉಳಿದಿರುತ್ತದೆ ಅಥವಾ ಸ್ಥಿರವಾಗಿರಬೇಕಿದ್ದ ನಕ್ಷತ್ರ ಹೆಚ್ಚುವರಿ ಬೌತವಸ್ತುವನ್ನು ಸ್ವೀಕರಿಸುವ ರೀತಿಯಲ್ಲಿ, ಅದರ ಮುಖ್ಯಉಷ್ಣಾಂಶವು ಏರಿಕೆಯಾಗುವುದಿಲ್ಲ. ಎರಡೂ ಪ್ರಕರಣದಲ್ಲಿ, ನಕ್ಷತ್ರದ ಉಷ್ಣಾಂಶವು ಅದರ ಸ್ವಂತ ಭಾರದಿಂದ ಕುಸಿತ ಉಂಟಾಗುವುದನ್ನು ತಪ್ಪಿಸುವಷ್ಟು ಹೆಚ್ಚಾಗಿರುವುದಿಲ್ಲ. ಆದರ್ಶ ಅನಿಲ ನಿಯಮವು ಒತ್ತಡ, ಉಷ್ಣಾಂಶ ಮತ್ತು ಘನಅಳತೆಯ ಮಧ್ಯೆ ಸಂಬಂಧವನ್ನು ವಿವರಿಸುತ್ತದೆ.

ನಕ್ಷತ್ರದ ಭಾಗಗಳ ಶಿಥಿಲತೆಯ ಒತ್ತಡದಿಂದ ಕುಸಿತವನ್ನು ತಡೆಯಬಹುದು. ಬೌತವಸ್ತುವನ್ನು ವಿಲಕ್ಷಣ ಸಾಂದ್ರೀಕೃತ ಸ್ಥಿತಿಯಲ್ಲಿ ಸಾಂದ್ರೀಕರಿಸುವ ಮೂಲಕ ಇದನ್ನು ಸಾಧಿಸುತ್ತದೆ. ಇದರ ಫಲಿತಾಂಶವು ಸಾಂದ್ರ ನಕ್ಷತ್ರದ ವಿವಿಧ ವಿಧಗಳಲ್ಲಿ ಒಂದಾಗಿರುತ್ತದೆ. ಯಾವ ವಿಧದ ಸಾಂದ್ರ ನಕ್ಷತ್ರ ರಚನೆಯಾಗುತ್ತದೆ ಎನ್ನುವುದು ಅಲ್ಪಾವಶೇಷದ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ-ಕುಸಿತದಿಂದ ಉಂಟಾದ ಬದಲಾವಣೆಗಳಿಂದ ಉಳಿದ ಬೌತವಸ್ತು(ಉದಾಹರಣೆಗೆ ಸೂಪರ್‌ನೋವಾ ಅಥವಾ ಗ್ರಹನೀಹಾರಿಕೆಗೆ ದಾರಿ ಕಲ್ಪಿಸುವ ಕಂಪನಗಳು)ಹೊರ ಪದರಗಳನ್ನು ಹಾರಿಸುತ್ತವೆ. ಇದು ಮೂಲ ನಕ್ಷತ್ರಕ್ಕಿಂತ ಗಾತ್ರದಲ್ಲಿ ಗಣನೀಯವಾಗಿ ಕಡಿಮೆಯಿರುತ್ತದೆ. ನಕ್ಷತ್ರಗಳಿಂದ ೫ ಸೌರದ್ರವ್ಯರಾಶಿಗಳನ್ನು ಮೀರಿದ ಅಲ್ಪಾವಶೇಷಗಳು ಉತ್ಪಾದನೆಯಾಗುತ್ತದೆ. ಕುಸಿತಕ್ಕೆ ಮುಂಚೆ ೨೦ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳನ್ನು ನಕ್ಷತ್ರಗಳು ಹೊಂದಿದ್ದವು.

ಮೂಲ ನಕ್ಷತ್ರವು ಅತೀ ಬಾರವಾಗಿದ್ದು ಅಥವಾ ಸಂಗ್ರಹಿಸಿದ ಅವಶೇಷವು ಬೌತದ್ರವ್ಯ ಸಂಚಯದ ಮೂಲಕ ಹೆಚ್ಚುವರಿ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಸಂಗ್ರಹಿಸುವ ಕಾರಣದಿಂದ, ಅವಶೇಷದ ದ್ರವ್ಯರಾಶಿಯು ೩ -೪ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳನ್ನು ಮೀರಿದರೆ( ಟೋಲ್ಮಾನ್–ಓಪ್ಪೆನ್‌ಹೈಮರ್–ವೋಲ್ಕೋಫ್ ಮಿತಿ) ಕುಸಿತವನ್ನು ತಡೆಯಲು ನ್ಯೂಟ್ರಾನ್‌ಗಳ ಶಿಥಿಲತೆಯ ಒತ್ತಡ ಕೂಡ ಸಾಕಾಗುವುದಿಲ್ಲ. ಇದಾದ ನಂತರ,ಯಾವುದೇ ಗೊತ್ತಾದ ವಿಧಾನವು(ಕ್ವಾರ್ಕ್ ಶಿಥಿಲತೆ ಒತ್ತಡ ಹೊರತುಪಡಿಸಿ, ನೋಡಿ ಕ್ವಾರ್ಕ್ ನಕ್ಷತ್ರ) ಕುಸಿತವನ್ನು ತಡೆಯುವಷ್ಟು ಪ್ರಬಲವಾಗಿರುವುದಿಲ್ಲ ಮತ್ತು ವಸ್ತುವು ಕಪ್ಪು ಕುಳಿಯಾಗಿ ಕುಸಿಯುವುದು ಅನಿವಾರ್ಯವಾಗುತ್ತದೆ.

ಈ ಭಾರೀ ನಕ್ಷತ್ರಗಳ ಗುರುತ್ವ ಕುಸಿತವು ನಾಕ್ಷತ್ರಿಕ ದ್ರವ್ಯರಾಶಿಯ ಕಪ್ಪು ಕುಳಿ ರಚನೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ ಎಂದು ಭಾವಿಸಲಾಗಿದೆ. ಎಳೆಯ ಬ್ರಹ್ಮಾಂಡದಲ್ಲಿ ನಕ್ಷತ್ರದ ರಚನೆಯಿಂದ ಅತೀ ದೊಡ್ಡ ನಕ್ಷತ್ರಗಳನ್ನು ಸೃಷ್ಟಿಸಿರಬಹುದು. ಅವುಗಳ ಕುಸಿತದಿಂದ ೧೦^೩ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳ ಕಪ್ಪು ಕುಳಿಗಳನ್ನು ಉತ್ಪಾದಿಸಿರಬಹುದು. ಈ ಭಾರವಾದ ಕಪ್ಪು ಕುಳಿಗಳು ಅನೇಕ ಗ್ಯಾಲಕ್ಸಿಗಳ ಮಧ್ಯದಲ್ಲಿ ಪತ್ತೆಯಾಗುವ ಬೃಹತ್ ಕಪ್ಪುಕುಳಿಗಳ ಬೀಜಗಳಾಗಿರಬಹುದು.

ಗುರುತ್ವ ಕುಸಿತದ ಸಂದರ್ಭದಲ್ಲಿ ಬಿಡುಗಡೆಯಾಗುವ ಬಹುತೇಕ ಶಕ್ತಿಯು ಅತೀ ವೇಗವಾಗಿ ಹೊಮ್ಮುತ್ತದೆ. ಆದರೆ ಈ ಪ್ರಕ್ರಿಯೆಯ ಅಂತ್ಯವನ್ನು ಬಾಹ್ಯ ವೀಕ್ಷಕ ವಾಸ್ತವವಾಗಿ ಗಮನಿಸುವುದಿಲ್ಲ. ಕುಸಿತವು ಒಳಗೆ ಬೀಳುವ ವಸ್ತುವಿನ ಉಲ್ಲೇಖದ ಚೌಕಟ್ಟಿನಿಂದಪರಿಮಿತ ಮೊತ್ತದ ಕಾಲವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ದೂರದ ವೀಕ್ಷಕ ಒಳಬೀಳುವ ವಸ್ತು ನಿಧಾನವಾಗಿ ಗುರುತ್ವ ಕಾಲ ಹಿಗ್ಗುವಿಕೆ ಕಾರಣದಿಂದ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಸ್ವಲ್ಪ ಮೇಲೆ ನಿಲ್ಲುವುದನ್ನು ಕಾಣುತ್ತಾನೆ. ಕುಸಿಯುವ ವಸ್ತುವಿನಿಂದ ಬೆಳಕು ವೀಕ್ಷಕನನ್ನು ಮುಟ್ಟಲು ಹೆಚ್ಚೆಚ್ಚು ಸಮಯ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಈವೆಂಟ್ ಹಾರಿಜಾನ್‌ ರಚನೆಗೆ ಸ್ವಲ್ಪ ಮುಂಚಿತವಾಗಿ ಹೊಮ್ಮುವ ಬೆಳಕಿನೊಂದಿಗೆ ಅನಂತ ಕಾಲದ ಮೊತ್ತ ವಿಳಂಬವಾಗುತ್ತದೆ. ಹೀಗೆ ಬಾಹ್ಯ ವೀಕ್ಷಕ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ರಚನೆಯನ್ನು ವೀಕ್ಷಿಸುವುದೇ ಇಲ್ಲ. ಬದಲಿಗೆ, ಕುಸಿಯುವ ವಸ್ತು ಮಬ್ಬಾಗುವಂತೆ ಕಂಡುಬಂದು, ಹೆಚ್ಚೆಚ್ಚು ಕೆಂಪು-ಪಲ್ಲಟವಾಗಿ ತರುವಾಯ ಕಳೆಗುಂದುವಂತೆ ಕಾಣುತ್ತದೆ.

ಮಹಾ ಸ್ಫೋಟದಲ್ಲಿ ಆದ್ಯಸ್ವರೂಪದ ಕಪ್ಪು ಕುಳಿಗಳು

ಗುರುತ್ವ ಕುಸಿತಕ್ಕೆ ಹೆಚ್ಚಿನ ಸಾಂದ್ರತೆಗಳ ಅಗತ್ಯವಿರುತ್ತದೆ. ಬ್ರಹ್ಮಾಂಡದ ಪ್ರಸಕ್ತ ಯುಗದಲ್ಲಿ ಇಂತಹ ಹೆಚ್ಚಿನ ಸಾಂದ್ರತೆಗಳು ಕೇವಲ ನಕ್ಷತ್ರಗಳಲ್ಲಿ ಮಾತ್ರ ಕಾಣಸಿಗುತ್ತದೆ. ಆದರೆ ಪೂರ್ವದ ಬ್ರಹ್ಮಾಂಡದಲ್ಲಿ ಮಹಾ ಸ್ಫೋಟದ ಸ್ವಲ್ಪ ನಂತರ ಸಾಂದ್ರತೆಗಳು ಅತೀ ಹೆಚ್ಚಾಗಿ, ಕಪ್ಪು ಕುಳಿಗಳ ರಚನೆಗೆ ಅವಕಾಶ ನೀಡಿರಬಹುದು. ಅತೀ ಸಾಂದ್ರತೆ ಮಾತ್ರ ಕಪ್ಪು ಕುಳಿಗಳ ರಚನೆಗೆ ಅವಕಾಶ ನೀಡಲು ಸಾಕಾಗುವುದಿಲ್ಲ.ಸಮಾನರೂಪದ ದ್ರವ್ಯರಾಶಿ ವಿತರಣೆಯು ದ್ರವ್ಯರಾಶಿಯು ಒಟ್ಟುಗೂಡಲು ಅವಕಾಶ ನೀಡುವುದಿಲ್ಲ. ಆದಿಸ್ವರೂಪದ ಕಪ್ಪು ಕುಳಿಗಳು ಅಂತಹ ಸಾಂದ್ರ ಮಾಧ್ಯಮದಲ್ಲಿ ರಚನೆಯಾಗಲು, ಅಲ್ಲಿ ಆರಂಭಿಕ ಸಾಂದ್ರತೆಯ ಪ್ರಕ್ಷುಬ್ಧತೆಗಳು ಇರಬೇಕಾಗುತ್ತದೆ. ನಂತರ ಅವುಗಳ ಗುರುತ್ವದಿಂದ ಬೆಳೆಯಬಹುದು. ಪೂರ್ವದ ಬ್ರಹ್ಮಾಂಡದ ವಿವಿಧ ಮಾದರಿಗಳು ಈ ಪ್ರಕ್ಷುಬ್ಧತೆಗಳ ಗಾತ್ರದ ಊಹಿಸುವಿಕೆಗಳಲ್ಲಿ ವ್ಯಾಪಕ ವ್ಯತ್ಯಾಸಗಳನ್ನು ಹೊಂದಿವೆ. ವಿವಿಧ ಮಾದರಿಗಳು ಪ್ಲಾಂಕ್ ದ್ರವ್ಯರಾಶಿಯಿಂದ ಹಿಡಿದು ನೂರಾರು ಸಾವಿರ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳ ಕಪ್ಪು ಕುಳಿಗಳ ಸೃಷ್ಟಿಯ ಬಗ್ಗೆ ಊಹಿಸಿವೆ. ಆದ್ಯಸ್ವರೂಪದ ಕಪ್ಪು ಕುಳಿಯು ಯಾವುದೇ ವಿಧದ ಕಪ್ಪುಕುಳಿಯ ಸೃಷ್ಟಿಗೆ ಕಾರಣ ನೀಡುತ್ತದೆ.

ಅತೀ ಶಕ್ತಿಯ ಡಿಕ್ಕಿಗಳು

CMSಶೋಧಕದಲ್ಲಿ ಅನುಕರಣೆಯ ವಿದ್ಯಮಾನವಾದ ಡಿಕ್ಕಿಯಲ್ಲಿ ಸೂಕ್ಷ್ಮ ಕಪ್ಪುಕುಳಿಯು ಸೃಷ್ಟಿಯಾಗಬಹುದು.

ಗುರುತ್ವ ಕುಸಿತ ಮಾತ್ರ ಕಪ್ಪು ಕುಳಿಗಳ ರಚನೆ ಸಾಧ್ಯವಾಗುವ ಪ್ರಕ್ರಿಯೆ ಮಾತ್ರವಲ್ಲ. ತಾತ್ವಿಕವಾಗಿ,ಅತೀ ಶಕ್ತಿಯ ಡಿಕ್ಕಿಗಳು ಕೂಡ ಸಾಕಷ್ಟು ಸಾಂದ್ರತೆಯನ್ನು ಉಂಟುಮಾಡಿ, ಕಪ್ಪು ಕುಳಿಗಳು ರಚನೆಯಾಗಬಹುದು. ಆದಾಗ್ಯೂ, ಇಲ್ಲಿಯವರೆಗೆ, ಇಂತಹ ಯಾವುದೇ ಘಟನೆಗಳನ್ನು ನೇರವಾಗಿ ಅಥವಾ ಪರೋಕ್ಷವಾಗಿ ಕಣದ ವೇಗವರ್ಧಕ ಪ್ರಯೋಗಗಳಲ್ಲಿ ದ್ರವ್ಯರಾಶಿಯ ಸಮತೋಲನದ ಕೊರತೆಯಾಗಿ ಗುರುತಿಸಲಾಗಿಲ್ಲ. ಇದು ಕಪ್ಪು ಕುಳಿಗಳ ದ್ರವ್ಯರಾಶಿಗೆ ಕಡಿಮೆ ಮಿತಿ ಹೊಂದಿರುವುದನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಸೈದ್ಧಾಂತಿಕವಾಗಿ, ಈ ಗಡಿಯು ಪ್ಲಾಂಕ್ ಮಾಸ್ (m _P = √ħc/G ≈ ≈ 1.2×10¹⁹ GeV/c² ≈ 2.2×10⁻⁸ kg),ಸುತ್ತ ಆವರಿಸಿರುವ ನಿರೀಕ್ಷೆಯಿದೆ. ಅಲ್ಲಿ ಕ್ವಾಂಟಂ ಪರಿಣಾಮಗಳು ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆ ಸಿದ್ಧಾಂತ ಸಂಪೂರ್ಣವಾಗಿ ಕುಸಿದುಬೀಳುವಂತೆ ಮಾಡುವುದನ್ನು ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ. ಇದು ಕಪ್ಪು ಕುಳಿಗಳ ಸೃಷ್ಟಿಯನ್ನು ಭೂಮಿ ಅಥವಾ ಅದರ ಬಳಿ ಸಂಭವಿಸುವ ಅಧಿಕ ಶಕ್ತಿ ಪ್ರಕ್ರಿಯೆಯಿಂದ ದೂರವಿರಿಸುತ್ತದೆ. ಕ್ವಾಂಟಂ ಗುರುತ್ವದಲ್ಲಿ ಕೆಲವು ಬೆಳವಣಿಗೆಗಳು ಪ್ಲಾಂಕ್ ಮಾಸ್ ಇನ್ನಷ್ಟು ಕಡಿಮೆಯಿರಬಹುದೆಂದು ಸೂಚಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ ಕೆಲವು ಬ್ರೇನ್‌ವರ್ಲ್ಡ್ ಸನ್ನಿವೇಶಗಳು ಇದನ್ನು ಇನ್ನಷ್ಟು ಕಡಿಮೆಯಿರಿಸುತ್ತದೆ. ಬಹುಶಃ1 TeV/c² ಇದರಷ್ಟು ಕಡಿಮೆ ಇರಿಸಿರಬಹುದು. ಇದರಿಂದ ಕಾಸ್ಮಿಕ್ ಕಿರಣಗಳು ಭೂಮಿಯ ವಾತಾವರಣವನ್ನು ಪ್ರವೇಶಿಸಿದಾಗ ಅತೀ ಪ್ರಬಲ ಡಿಕ್ಕಿಗಳಲ್ಲಿ ಸೂಕ್ಷ್ಮ ಕಪ್ಪು ಕುಳಿಗಳು ಸೃಷ್ಟಿಯಾಗಿರುವ ಸಾಧ್ಯತೆಯಿದೆ ಅಥವಾ CERNನ ಹೊಸ ದೊಡ್ಡ ಹ್ಯಾಡ್ರಾನ್ ಕೊಲೈಡರ್‌ನಲ್ಲಿ ಸೃಷ್ಟಿಯಾಗುವ ಸಂಭವವಿದೆ. ಈ ಪ್ರಮೇಯಗಳು ಅತ್ಯಂತ ಊಹಾತ್ಮಕವಾಗಿದ್ದು, ಈ ಪ್ರಕ್ರಿಯೆಗಳಲ್ಲಿ ಕಪ್ಪುಕುಳಿಗಳ ರಚನೆಯು ಅಸಂಭವ ಎಂದು ಅನೇಕ ತಜ್ಞರು ಭಾವಿಸಿದ್ದಾರೆ. ಈ ಡಿಕ್ಕಿಗಳಿಂದ ಸೂಕ್ಷ್ಮ ಕಪ್ಪು ಕುಳಿಗಳು ರಚನೆಯಾದರೂ ಕೂಡ,ಅವು ೧೦^−೨೫ ಸೆಕೆಂಡುಗಳಲ್ಲಿ ಆವಿಯಾಗಿ, ಭೂಮಿಗೆ ಯಾವುದೇ ಗಂಡಾಂತರ ಉಂಟುಮಾಡುವುದಿಲ್ಲ.

ಬೆಳವಣಿಗೆ

ಒಂದೊಮ್ಮೆ ಕಪ್ಪು ಕುಳಿ ರಚನೆಯಾದ ನಂತರ, ಹೆಚ್ಚುವರಿ ಬೌತದ್ರವ್ಯಗಳನ್ನು ಹೀರಿಕೊಳ್ಳುವ ಮೂಲಕ ಬೆಳವಣಿಗೆಯನ್ನು ಮುಂದುವರಿಸುತ್ತದೆ. ಯಾವುದೇ ಕಪ್ಪು ಕುಳಿ ನಿರಂತರವಾಗಿ ತನ್ನ ನೇರ ಸುತ್ತಮುತ್ತಲಿಂದ ಮತ್ತು ಸರ್ವವ್ಯಾಪಿ ಕಾಸ್ಮಿಕ್ ಹಿನ್ನೆಲೆಯ ವಿಕಿರಣದಿಂದ ಅನಿಲ ಮತ್ತು ಅಂತರ ನಕ್ಷತ್ರೀಯ ಧೂಳನ್ನು ನಿರಂತರವಾಗಿ ಹೀರಿಕೊಳ್ಳುತ್ತದೆ.ಇದು ಪ್ರಾಥಮಿಕ ಪ್ರಕ್ರಿಯೆಯಾಗಿದ್ದು, ಈ ಮೂಲಕ ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಗಳು ಬೆಳೆಯುವಂತೆ ಕಾಣುತ್ತದೆ. ನಕ್ಷತ್ರಗಳ ವೃತ್ತಾಕಾರದ ಗೊಂಚಲಿನಲ್ಲಿ ಮಧ್ಯವರ್ತಿ ದ್ರವ್ಯರಾಶಿ ಕಪ್ಪು ಕುಳಿಗಳ ರಚನೆಗೆ ಇದೇ ರೀತಿಯ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸೂಚಿಸಲಾಗಿದೆ.

ಇನ್ನೊಂದು ಸಾಧ್ಯತೆಯು ಕಪ್ಪು ಕುಳಿಗಳು ನಕ್ಷತ್ರಗಳು ಮುಂತಾದ ಇತರೆ ಕಾಯಗಳ ಜತೆ ಅಥವಾ ಇತರೆ ಕಪ್ಪುಕುಳಿಗಳ ಜತೆ ವಿಲೀನವಾಗುವುದು. ಬೃಹತ್ ಕಪ್ಪುಕುಳಿಗಳ ಮುಂಚಿನ ಅಭಿವೃದ್ಧಿಗೆ ವಿಶೇಷವಾಗಿ ಇದು ಮುಖ್ಯವೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಇವುಗಳನ್ನು ಅನೇಕ ಸಣ್ಣ ವಸ್ತುಗಳ ಘನೀಕರಣದಿಂದ ರಚನೆಯಾಗಿದೆಯೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಈ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಕೆಲವು ಮಧ್ಯವರ್ತಿ ದ್ರವ್ಯರಾಶಿ ಕಪ್ಪು ಕುಳಿಯ ಹುಟ್ಟಿಗೆ ಕೂಡ ಪ್ರಸ್ತಾಪಿಸಲಾಗಿದೆ.

ಬಾಷ್ಪೀಕರಣ (ಆವಿಯಾಗುವಿಕೆ)(Hawking radiation)

೧೯೭೪ರಲ್ಲಿ ಕಪ್ಪು ಕುಳಿಗಳು ಸಂಪೂರ್ಣವಾಗಿ ಕಪ್ಪು ಬಣ್ಣದ್ದಲ್ಲ, ಆದರೆ ಉಷ್ಣವಿಕಿರಣವನ್ನು ಸ್ವಲ್ಪ ಪ್ರಮಾಣದಲ್ಲಿ ಸೂಸುತ್ತವೆ ಎಂದು ಸ್ಟೀಫನ್ ಹಾಕಿಂಗ್ ತೋರಿಸಿದರು. ಕ್ವಾಂಟಂ ಕ್ಷೇತ್ರ ಸಿದ್ಧಾಂತವನ್ನು ಸ್ಥಿರ ಕಪ್ಪು ಕುಳಿ ಹಿನ್ನೆಲೆಯಲ್ಲಿ ಬಳಸುವ ಮೂಲಕ ಅವರು ಈ ಫಲಿತಾಂಶವನ್ನು ಪಡೆದರು. ಈ ಲೆಕ್ಕಾಚಾರಗಳ ಫಲಿತಾಂಶವು ಕಪ್ಪು ಕುಳಿಯು ಸಂಪೂರ್ಣ ಕಪ್ಪು ಕಾಯ ಲೋಹಿತದಲ್ಲಿ ಕಣಗಳನ್ನು ಹೊರಸೂಸಬೇಕು ಎನ್ನುವುದಾಗಿದೆ. ಈ ಪರಿಣಾಮವನ್ನು ಹಾಕಿಂಗ್ ವಿಕಿರಣ ಎನ್ನಲಾಗುತ್ತದೆ. ಹಾಕಿಂಗ್ ಫಲಿತಾಂಶದ ನಂತರ, ಅನೇಕ ಮಂದಿ ವಿವಿಧ ವಿಧಾನಗಳ ಮೂಲಕ ಪರಿಣಾಮವನ್ನು ಪರಿಶೀಲಿಸಿದರು. ಅವರ ಕಪ್ಪು ಕುಳಿ ವಿಕಿರಣ ಸಿದ್ಧಾಂತ ಸರಿಯಾಗಿದ್ದರೆ, ಕಪ್ಪುಕುಳಿಗಳು ವಿಕಿರಣದ ಉಷ್ಣ ರೋಹಿತವನ್ನು ಸೂಸುತ್ತದೆಂದು ನಿರೀಕ್ಷಿಸಲಾಗುತ್ತದೆ. ಆ ಮೂಲಕ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಕಳೆದುಕೊಳ್ಳುತ್ತದೆ. ಸಾಪೇಕ್ಷತೆ ಸಿದ್ಧಾಂತದ ಪ್ರಕಾರ ದ್ರವ್ಯರಾಶಿ ಅತೀ ಸಾಂದ್ರೀಕರಿಸಿದ ಶಕ್ತಿಯಾಗಿದೆ(E = mc ^೨). ಕಪ್ಪುಕುಳಿಗಳು ಕಾಲಕ್ರಮೇಣ ಕುಗ್ಗಿ, ಆವಿಯಾಗುತ್ತವೆ. ಈ ಲೋಹಿತದ ಉಷ್ಣಾಂಶವಾದ ಹಾಕಿಂಗ್ ಉಷ್ಣಾಂಶವು ಕಪ್ಪು ಕುಳಿಯ ಮೇಲ್ಮೈ ಉಷ್ಣಾಂಶಕ್ಕೆ ಪ್ರಮಾಣಾನುಗುಣವಾಗಿರುತ್ತದೆ. ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ಕಪ್ಪು ಕುಳಿಯು ದ್ರವ್ಯರಾಶಿಗೆ ವಿಲೋಮಾನುಪಾತವಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ ದೊಡ್ಡ ಕಪ್ಪು ಕುಳಿಗಳು ಸಣ್ಣ ಕಪ್ಪುಕುಳಿಗಳಿಗಿಂತ ಕಡಿಮೆ ವಿಕಿರಣವನ್ನು ಹೊರಸೂಸುತ್ತವೆ.

ಒಂದು ಸೌರ ದ್ರವ್ಯರಾಶಿಯ ನಾಕ್ಷತ್ರಿಕ ಕಪ್ಪುಕುಳಿಯು ೧೦೦ ನ್ಯಾನೊಕೆಲ್ವಿನ್‌ಗಳಷ್ಟು ಹಾಕಿಂಗ್ ಉಷ್ಣಾಂಶವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ಇದು ಕಾಸ್ಮಿಕ್ ಮೈಕ್ರೊತರಂಗ ಹಿನ್ನೆಲೆಯ ೨ .೭ಉಷ್ಣಾಂಶಕ್ಕಿಂತ ತೀರಾ ಕಡಿಮೆ. ನಾಕ್ಷತ್ರಿಕ ದ್ರವ್ಯರಾಶಿ(ಮತ್ತು ದೊಡ್ಡದು)ಕಪ್ಪುಕುಳಿಗಳು ಹಾಕಿಂಗ್ ವಿಕಿರಣದ ಮೂಲಕ ಸೂಸುವುದಕ್ಕಿಂತ ಹೆಚ್ಚು ದ್ರವ್ಯರಾಶಿಯನ್ನು ಕಾಸ್ಮಿಕ್ ಮೈಕ್ರೋತರಂಗ ಹಿನ್ನೆಲೆಯ ವಿಕಿರಣದಿಂದ ಸ್ವೀಕರಿಸುತ್ತದೆ. ಹೀಗೆ ಅದು ಕುಗ್ಗುವಿಕೆ ಬದಲಿಗೆ ಬೆಳೆಯುತ್ತದೆ. ೨.೭ (ಬಾಷ್ಪೀಕರಣ ಸಾಧ್ಯ)ಗಿಂತ ಹೆಚ್ಚು ಹಾಕಿಂಗ್ ಉಷ್ಣಾಂಶ ಹೊಂದಬೇಕಾದರೆ, ಕಪ್ಪು ಕುಳಿಯು ಚಂದ್ರನಿಗಿಂತ ಹಗುರವಾಗಿರಬೇಕಾಗುತ್ತದೆ(ಆದ್ದರಿಂದ ಮಿಲಿಮೀಟರ್‌ನ ಹತ್ತನೇ ಒಂದು ಭಾಗದ ವ್ಯಾಸಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ).

ಆದರೆ ಕಪ್ಪು ಕುಳಿಯು ಅತೀ ಸಣ್ಣದಾಗಿದ್ದರೆ, ವಿಕಿರಣ ಪರಿಣಾಮಗಳು ತೀರಾ ಪ್ರಬಲವಾಗಿರುತ್ತದೆಂದು ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ. ಮಾನವನಿಗೆ ಹೋಲಿಸಿದರೆ ಭಾರವಾದ ಕಪ್ಪು ಕುಳಿ ಕೂಡ ಕ್ಷಣಾರ್ದದಲ್ಲಿ ಆವಿಯಾಗುತ್ತದೆ. ಕಾರಿನಷ್ಟು (~೧೦^−೨೪ m) ತೂಕವಿರುವ ಕಪ್ಪುಕುಳಿ ಕೂಡ ಆವಿಯಾಗಲು ನ್ಯಾನೊಸೆಕೆಂಡ್ ಮಾತ್ರ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಈ ಕಾಲದಲ್ಲಿ ಸೂರ್ಯನಿಗಿಂತ ೨೦೦ ಪಟ್ಟು ಹೆಚ್ಚು ಪ್ರಕಾಶಮಾನತೆಯನ್ನು ಸಂಕ್ಷಿಪ್ತವಾಗಿ ಹೊಂದಿರುತ್ತದೆ. ಹಗುರವಾದ ಕಪ್ಪುಕುಳಿಗಳು ಇನ್ನೂ ಹೆಚ್ಚು ವೇಗವಾಗಿ ಆವಿಯಾಗುತ್ತದೆಂದು ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ. ಉದಾಹರಣೆಗೆ ೧ TeV/c ^೨ದ್ರವ್ಯರಾಶಿಯ ಕಪ್ಪುಕುಳಿ ಸಂಪೂರ್ಣವಾಗಿ ಆವಿಯಾಗಲು ೧೦^−೮೮ಸೆಕೆಂಡುಗಳಿಗಿಂತ ಕಡಿಮೆ ಕಾಲಾವಧಿ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಇಂತಹ ಸಣ್ಣ ಕಪ್ಪು ಕುಳಿಯ ಕ್ವಾಂಟಂ ಗುರುತ್ವ ಪರಿಣಾಮಗಳು ಪ್ರಮುಖ ಪಾತ್ರವಹಿಸುವುದು ಹಾಗು – ಕೂಡ ನಿರೀಕ್ಷಿಸಲಾಗಿದೆ. ಆದರೆ ಕ್ವಾಂಟಂ ಗುರುತ್ವದಲ್ಲಿ ಪ್ರಸಕ್ತ ಬೆಳವಣಿಗೆಗಳು ಹಾಗೆ ಸೂಚಿಸುವುದಿಲ್ಲ.– ಊಹನೆಯಾಗಿ ಇಂತಹ ಸಣ್ಣ ಕಪ್ಪುಕುಳಿಯನ್ನು ಸ್ಥಿರಗೊಳಿಸುತ್ತದೆ.

ಕಪ್ಪುಕುಳಿಯ ವೀಕ್ಷಿತ ಸಾಕ್ಷಿಗಳು

ಅವುಗಳ ಸ್ವಭಾವದಿಂದ, ಕಪ್ಪು ಕುಳಿಗಳು ಉಹಾತ್ಮಕ ಹಾಕಿಂಗ್ ವಿಕಿರಣ ಹೊರತುಪಡಿಸಿ, ಯಾವುದೇ ಸಂಕೇತಗಳನ್ನು ನೇರವಾಗಿ ಸೂಸುವುದಿಲ್ಲ. ಖಬೌತಿಕ ಕಪ್ಪು ಕುಳಿಯ ಹಾಕಿಂಗ್ ವಿಕಿರಣವು ಅತೀ ದುರ್ಬಲವೆಂದು ಮುಂಗಾಣಲಾಗಿದ್ದು, ಭೂಮಿಯಿಂದ ಖಬೌತಿಕ ಕಪ್ಪು ಕುಳಿಗಳನ್ನು ನೇರವಾಗಿ ಗುರುತಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ. ಹಾಕಿಂಗ್ ವಿಕಿರಣವು ದುರ್ಬಲವಾಗುವುದಕ್ಕೆ ಹೊರತಾದ ಹಂತವು ಬೆಳಕಿನ(ಆದ್ಯರೂಪದ)ಕಪ್ಪು ಕುಳಿಗಳ ಬಾಷ್ಪೀಕರಣದ ಕೊನೆಯ ಹಂತವಾಗಿದೆ. ಇಂತಹ ಬೆಳಕುಗಳಿಗೆ ಹಿಂದಿನ ಶೋಧವು ಯಶಸ್ವಿಯಾಗಿಲ್ಲ ಮತ್ತು ಬೆಳಕು ಆದ್ಯರೂಪದ ಕಪ್ಪು ಕುಳಿಗಳ ಅಸ್ತಿತ್ವದ ಸಾಧ್ಯತೆ ಬಗ್ಗೆ ಕಟ್ಟುನಿಟ್ಟಿನ ಮಿತಿಗಳನ್ನು ಒದಗಿಸುತ್ತದೆ. ೨೦೦೮ರಲ್ಲಿ ಉಡಾವಣೆ ಮಾಡಿದ NASAದ ಫರ್ಮಿ ಗಾಮಾ-ಕಿರಣ ಬಾಹ್ಯಾಕಾಶ ದೂರದರ್ಶಕವು ಈ ಬೆಳಕುಗಳಿಗಾಗಿ ಶೋಧವನ್ನು ಮುಂದುವರಿಸುತ್ತದೆ.

ಹೀಗೆ ಕಪ್ಪುಕುಳಿಗಳ ಕಬೌತಿಕ ಶೋಧವು ಪರೋಕ್ಷ ವೀಕ್ಷಣೆಗಳನ್ನು ಅವಲಂಬಿಸಬೇಕಾಗುತ್ತದೆ. ಕಪ್ಪು ಕುಳಿಯ ಅಸ್ತಿತ್ವವನ್ನು ಅದರ ಸುತ್ತಮುತ್ತಲಿನ ಜತೆ ಗುರುತ್ವ ಪರಸ್ಪರ ಕಾರ್ಯಗಳನ್ನು ವೀಕ್ಷಿಸುವ ಮೂಲಕ ಗಮನಿಸಬಹುದು.

2019 ರಲ್ಲಿ ವೀಕ್ಷಿತ ಸಾಕ್ಷಿ

• 'ಪೋವೆಹಿ' ಎಂಬ ಕಪ್ಪು ಕುಳಿ('ಆಸ್ಟ್ರಾಫಿಸಿಕಲ್‌ ಜರ್ನಲ್‌ ಲೆಟರ್ಸ್‌'ನಲ್ಲಿ ಪ್ರಕಟವಾದ ವಿಷಯ- ಬೇರೆಉಯವರಿಗೆ ಕಾಪಿರೈಟ್ ಇಲ್ಲ ಪತ್ರಿಕೆ ವಿಷಯವನ್ನು ಸಾರ್ವಜನಿಕರಿಗೆ ಬಿಡುಗಡೆ ಮಾಡಿದೆ);ನೋಡಿನಕ್ಷತ್ರ,; ಆಕಾಶ ಗಂಗೆ-ಬ್ರಹ್ಮಾಂಡ
• ಜಗತ್ತಿನ ಹಲವೆಡೆ 8 ರೇಡಿಯೊ ಟೆಲಿಸ್ಕೋಪ್‌ಗಳನ್ನು ಏಕಕಾಲಕ್ಕೆ ಬಳಸಿ ಇದುವರೆಗೂ ಚಿದಂಬರ ರಹಸ್ಯವಾಗಿ ಉಳಿದಿದ್ದ ಮತ್ತು ಕೇವಲ ಕಾಲ್ಪನಿಕ ಚಿತ್ರಗಳಿಗಷ್ಟೇ ಸೀಮಿತವಾಗಿದ್ದ ಕಪ್ಪುಕುಳಿಯನ್ನು 10-4-2019 ರಂದು ನೈಜವಾಗಿ ಸೆರೆ ಹಿಡಿಯಲಾತ್ತು.
• ಕಪ್ಪು ಕುಳಿಯು ಭೂಮಿಯಿಂದ 55೦ ಕೋಟಿ ಜ್ಯೋತಿರ್ವರ್ಷಗಳಷ್ಟು ದೂರದಲ್ಲಿದೆ. ಸೂರ್ಯನಗಿಂತಲೂ 65೦ ಕೋಟಿ ಪಟ್ಟು ಹೆಚ್ಚು ತೂಕ ಹೊಂದಿದೆ. ಇದು ‘ಕಪ್ಪು ಕುಳಿಯ ಬಗ್ಗೆ ಮೊದಲ ಬಾರಿ ಅಧಿಕೃತವಾದ ಸಾಕ್ಷ್ಯ. " ಇದರ ಅಸ್ತಿತ್ವದ ಬಗೆಗೆ ಯಾವುದೇ ಬಗೆಯ ಸಂದೇಹಗಳು ಈಗ ಉಳಿದಿಲ್ಲ. ಈ ಹಿಂದೆ, ನಮಗೆ ಶೇಕಡ 99ರಷ್ಟು ಸಾಕ್ಷ್ಯಗಳಿದ್ದರೂ ಕೆಲವು ಸಂದೇಹಗಳು ಉಳಿದಿದ್ದವು. ಈಗ ಶೇಕಡ 100ರಷ್ಟು ಖಚಿತವಾಗಿದೆ," ಎಂದು ಮುಂಬೈನ ಟಾಟಾ ಇನ್‌ಸ್ಟಿಟ್ಯೂಟ್‌ ಆಫ್‌ ಫಂಡಮೆಂಟಲ್‌ ರಿಸರ್ಚ್‌ (ಟಿಐಎಫ್‌ಆರ್‌) ಸಹಾಯಕ ಪ್ರಾಧ್ಯಾಪಕ ಸುದೀಪ್‌ ಭಟ್ಟಾಚಾರಾರ್ಯ ವಿವರಿಸಿದ್ದಾರೆ.
• 'ಎಂ87' ಹೆಸರಿನ ನಕ್ಷತ್ರಪುಂಜದಲ್ಲಿ ಈ ದೈತ್ಯ ಗಾತ್ರದ ಕಪ್ಪುಕುಳಿ ಮೊದಲ ಬಾರಿಗೆ ಕ್ಯಾಮರಾ ಕಣ್ಣಿಗೆ ದೊರೆತಿದೆ. ಕಪ್ಪು ಕುಳಿವೊಂದರ ಸುತ್ತಲೂ ಪ್ರಕಾಶಮಾನವಾಗಿ ಕೆಂಪು ಮಿಶ್ರಿತ ಕಿತ್ತಳೆ ಬಣ್ಣದಲ್ಲಿ ಹೊಳೆಯುವ ಬೃಹತ್‌ ಬೆಂಕಿಯ ಬಳೆ ಚಿತ್ರದಲ್ಲಿ ಕಂಡುಬಂದಿದೆ. ಜಗತ್ತಿನ ಹಲವೆಡೆ 8 ರೇಡಿಯೊ ಟೆಲಿಸ್ಕೋಪ್‌ಗಳನ್ನು ಏಕಕಾಲಕ್ಕೆ ಬಳಸಿ ಇದುವರೆಗೂ ಚಿದಂಬರ ರಹಸ್ಯವಾಗಿ ಉಳಿದಿದ್ದ ಮತ್ತು ಕೇವಲ ಕಾಲ್ಪನಿಕ ಚಿತ್ರಗಳಿಗಷ್ಟೇ ಸೀಮಿತವಾಗಿದ್ದ ಕಪ್ಪುಕುಳಿಯನ್ನು ೧೦-೪-೨೦೧೯ ರಂದು ನೈಜವಾಗಿ ಸೆರೆ ಹಿಡಿಯಲಾಗಿತ್ತು.
• ಬಾಹ್ಯಾಕಾಶ ವಿಜ್ಞಾನ ನಿಯತಕಾಲಿಕೆ 'ಆಸ್ಟ್ರಾಫಿಸಿಕಲ್‌ ಜರ್ನಲ್‌ ಲೆಟರ್ಸ್‌'ನಲ್ಲಿ ಈ ಐತಿಹಾಸಿಕ ಚಿತ್ರವನ್ನು ಪ್ರಕಟಿಸಲಾಗಿದೆ. ಬಲವಾದ ಗುರುತ್ವಾಕರ್ಷಣೆ ಹೊಂದಿರುವ ಕಪ್ಪು ಕುಳಿಯಲ್ಲಿ ಬೆಳಕು ಸಹ ಪಾರಾಗಲು ಸಾಧ್ಯವಿಲ್ಲ. ಹೀಗಾಗಿ, ಕಪ್ಪು ಕುಳಿಗಳು ವಿಶಿಷ್ಟ ಮತ್ತು ವಿಭಿನ್ನವಾಗಿವೆ.
• ‘ಸುಮಾರು 200ಕ್ಕೂ ಹೆಚ್ಚು ಸಂಶೋಧಕರು ಕಪ್ಪುಕುಳಿಯ ವೈಜ್ಞಾನಿಕ ವಿಶ್ಲೇಷಣೆಯಲ್ಲಿ ತೊಡಗಿದ್ದಾರೆ’ ಎಂದು ಇವೆಂಟ್‌ ಹಾರಿಜಾನ್‌ ಟೆಲಿಸ್ಕೋಪ್‌ನ ಯೋಜನಾ ನಿರ್ದೇಶಕ ಶೆಫರ್ಡ್‌ ಎಸ್‌. ಡೊಲೆಮಾನ್‌ ತಿಳಿಸಿದ್ದಾರೆ.

ಬೌತದ್ರವ್ಯದ ಸಂಚಯ (Accretion disc)

ಕಪ್ಪುಕುಳಿಯ ಸಂಚಯ ತಟ್ಟೆಯಿಂದ ಗ್ಯಾಲಕ್ಸಿಯೇತರ ಜೆಟ್‌ಗಳ ರಚನೆ

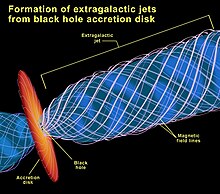
ಕೋನೀಯ ಆವೇಗದ ಸಂರಕ್ಷಣೆಯ ಕಾರಣದಿಂದ ಬೃಹತ್ ವಸ್ತುವಿನಿಂದ ಸೃಷ್ಟಿಯಾದ ಗುರುತ್ವದ ಸೆಳೆತಕ್ಕೆ ಬೀಳುವ ಅನಿಲವು ಆ ವಸ್ತುವಿನ ಸುತ್ತ ತಟ್ಟೆ ಆಕಾರದ ರಚನೆಯನ್ನು ಸಾಧಾರಣವಾಗಿ ಸೃಷ್ಟಿಸುತ್ತದೆ. ತಟ್ಟೆಯೊಳಗೆ ಉಂಟಾಗುವ ಘರ್ಷಣೆಯು ಕೋನೀಯ ಆವೇಗವನ್ನು ಹೊರಭಾಗಕ್ಕೆ ಸಾಗಿಸುತ್ತದೆ. ಇದರಿಂದ ಬೌತವಸ್ತು ಇನ್ನಷ್ಟು ಕೆಳಭಾಗಕ್ಕೆ ಬಿದ್ದು, ಸಂಭಾವ್ಯ ಶಕ್ತಿಯನ್ನು ಬಿಡುಗಡೆ ಮಾಡುತ್ತದೆ ಮತ್ತು ಅನಿಲದ ಉಷ್ಣಾಂಶವನ್ನು ವರ್ಧಿಸುತ್ತದೆ. ಶ್ವೇತ ಕುಬ್ಜ ನಕ್ಷತ್ರಗಳು, ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರಗಳು ಮತ್ತು ಕಪ್ಪು ಕುಳಿಗಳು ಮುಂತಾದ ಸಾಂದ್ರ ವಸ್ತುವಿನಲ್ಲಿ, ಒಳಪ್ರದೇಶದ ಅನಿಲವು ಅತ್ಯಂತ ಬಿಸಿಯಾಗಿ, ಅಪಾರ ಪ್ರಮಾಣದ ವಿಕಿರಣ(ಮುಖ್ಯವಾಗಿ ಎಕ್ಸರೆ ಕಿರಣಗಳು)ಗಳನ್ನು ಹೊರಸೂಸುತ್ತವೆ. ಇದನ್ನು ದೂರದರ್ಶಕಗಳಿಂದ ಗುರುತಿಸಬಹುದು. ಹೆಚ್ಚುವರಿ ಸಂಚಯದ ಈ ಪ್ರಕ್ರಿಯೆಯು ಅತ್ಯಂತ ದಕ್ಷ ಶಕ್ತಿ ಉತ್ಪಾದನೆ ಕ್ರಿಯೆಯಾಗಿದ್ದು, ಬೆಳವಣಿಗೆಯಾದ ವಸ್ತುವಿನ ೪೦%ದ್ರವ್ಯರಾಶಿ ವಿಕಿರಣದ ಮೂಲಕ ಉತ್ಸರ್ಜಿಸಬಹುದು. (ಬೈಜಿಕ ಸಮ್ಮಿಳನದಲ್ಲಿ ಉಳಿದ ದ್ರವ್ಯರಾಶಿಯ ೦.೭%ಮಾತ್ರ ಶಕ್ತಿಯಾಗಿ ಉತ್ಸರ್ಜಿಸುತ್ತದೆ.) ಅನೇಕ ಪ್ರಕರಣಗಳಲ್ಲಿ, ಸಂಚಯದ ತಟ್ಟೆಗಳು ಧ್ರುವಗಳಲ್ಲಿ ಉತ್ಸರ್ಜಿಸುವ ಸಾಪೇಕ್ಷತಾ ಜೆಟ್‌ಗಳನ್ನು ಜತೆಗೂಡಿರುತ್ತದೆ. ಇದು ಹೆಚ್ಚಿನ ಶಕ್ತಿಯನ್ನು ಒಯ್ಯುತ್ತದೆ. ಈ ಜೆಟ್‌ಗಳ ಸೃಷ್ಟಿಯ ಕಾರ್ಯವಿಧಾನವು ಪ್ರಸಕ್ತ ಸರಿಯಾಗಿ ಅರ್ಥವಾಗಿಲ್ಲ.

ಕಪ್ಪು ಕುಳಿಗಳಲ್ಲಿ ಬೌತದ್ರವ್ಯದ ಸಂಚಯಕ್ಕೆ ಬ್ರಹ್ಮಾಂಡದ ಹೆಚ್ಚು ಶಕ್ತಿಶಾಲಿ ವಿದ್ಯಮಾನ ಕಾರಣವಾಗಿದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ, ಸಕ್ರಿಯ ಗ್ಯಾಲಕ್ಸಿಯ ಬೀಜಕಣಗಳು ಮತ್ತು ಕ್ವಾಸಾರ್‌ಗಳು ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಗಳ ಸಂಚಯ ತಟ್ಟೆಗಳೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಇದೇ ರೀತಿ ಎಕ್ಸರೆ ಬೈನರಿಗಳು ದ್ವಿನಕ್ಷತ್ರ ವ್ಯವಸ್ಥೆಯೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಅದರಲ್ಲಿ ಎರಡು ನಕ್ಷತ್ರಗಳಲ್ಲೊಂದು ಸಾಂದ್ರ ವಸ್ತುವಾಗಿದ್ದು, ಅದರ ಜೊತೆ ನಕ್ಷತ್ರದಿಂದ ಬೌತದ್ರವ್ಯವನ್ನು ಸಂಚಯ ಮಾಡುತ್ತದೆ. ಕೆಲವು ಅಲ್ಟ್ರಾಲುಮಿನಸ್ ಎಕ್ಸರೆ ಮೂಲಗಳು ಮಧ್ಯವರ್ತಿ ದ್ರವ್ಯರಾಶಿಯ ಕಪ್ಪು ಕುಳಿಗಳಾಗಿರಬಹುದು ಎಂದು ಕೂಡ ಸೂಚಿಸಲಾಗಿದೆ.

ಎಕ್ಸರೆ ಬೈನರಿಗಳು

(X-ray binary) ಎಕ್ಸರೆ ಬೈನರಿಗಳು ಜೋಡಿ ತಾರೆ(ಯುಗಳ ನಕ್ಷತ್ರ)ಗಳಾಗಿದ್ದು, ಲೋಹಿತದ ಎಕ್ಸರೆ ಭಾಗದಲ್ಲಿ ಪ್ರಕಾಶಿಸುತ್ತದೆ. ಈ ಎಕ್ಸರೆ ಉತ್ಸರ್ಜನೆಗಳು ಸಾಂದ್ರ ವಸ್ತುವಾದ ನಕ್ಷತ್ರಗಳ ಒಂದು ಭಾಗದಿಂದ ಸಂಭವಿಸಿದೆಯೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಇನ್ನೊಂದು ನಿಯಮಿತ ನಕ್ಷತ್ರದಿಂದ ಬೌತದ್ರವ್ಯವನ್ನು ಸಂಚಯ ಮಾಡುವ ಮೂಲಕ ಇಂದು ಉಂಟಾಗಿದೆ. ಈ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಸಾಮಾನ್ಯ ನಕ್ಷತ್ರದ ಉಪಸ್ಥಿತಿಯಿಂದ ಕೇಂದ್ರ ವಸ್ತುವನ್ನು ಅಧ್ಯಯನ ಮಾಡುವ ಹಾಗೂ ಅದು ಕಪ್ಪು ಕುಳಿಯಾಗಿರುವುನ್ನು ನಿರ್ಧರಿಸುವ ವಿಶಿಷ್ಟ ಅವಕಾಶ ಒದಗಿಸುತ್ತದೆ.

ಜೊತೆ ನಕ್ಷತ್ರದಿಂದ ಬೌತದ್ರವ್ಯವನ್ನು ಪೂರೈಸುವ ಸಾಂದ್ರ ವಸ್ತುವಿನ ಸುತ್ತಲಿರುವ ಸಂಚಯ ತಟ್ಟೆಯೊಂದಿಗೆ ಯುಗನಕ್ಷತ್ರದ ಕಲಾವಿದನ ಕಲ್ಪನೆ.

ಇಂತಹ ವ್ಯವಸ್ಥೆಯು ಸಾಂದ್ರ ವಸ್ತುವಿಗೆ ನೇರವಾಗಿ ಹೋಲುವ ಸಂಕೇತಗಳನ್ನು ಉತ್ಸರ್ಜನೆ ಮಾಡಿದರೆ, ಅದು ಕಪ್ಪು ಕುಳಿಯಾಗುವುದಿಲ್ಲ. ಇಂತಹ ಸಂಕೇತಗಳ ಅನುಪಸ್ಥಿತಿಯಿಂದ, ಸಾಂದ್ರ ವಸ್ತುವು ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರವೆಂಬ ಸಾಧ್ಯತೆಯನ್ನು ಹೊರತಾಗಿಸುವುದಿಲ್ಲ. ಜೊತೆ ನಕ್ಷತ್ರವನ್ನು ಅಧ್ಯಯನ ಮಾಡುವ ಮೂಲಕ ವ್ಯವಸ್ಥೆಯ ಕಕ್ಷೀಯ ಮಾನದಂಡಗಳನ್ನು ಪಡೆಯಲು ಹಾಗು ಸಾಂದ್ರ ವಸ್ತುವಿನ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಪಡೆಯಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ. ಇದು ಟೋಲ್ಮಾನ್-ಓಪನ್‌ಹೈಮರ್ ವೋಲ್ಕಾಫ್ ಮಿತಿಗಿಂತ ಹೆಚ್ಚಿಗಿದ್ದರೆ(ಕುಸಿತಕ್ಕೆ ಮುಂಚೆ ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರದ ಗರಿಷ್ಠ ದ್ರವ್ಯರಾಶಿ) ವಸ್ತುವು ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರವಾಗಲು ಸಾಧ್ಯವಿಲ್ಲ ಮತ್ತು ಸಾಮಾನ್ಯವಾಗಿ ಕಪ್ಪು ಕುಳಿಯೆಂದು ನಿರೀಕ್ಷಿಸಲಾಗುತ್ತದೆ.

ಕಪ್ಪು ಕುಳಿಯ ಪ್ರಥಮ ಪ್ರಬಲ ಪರೀಕ್ಷಾರ್ಥಿ, ಸೈಗ್ನಸ್ X-೧ನ್ನು ೧೯೭೨ರಲ್ಲಿ ಚಾರ್ಲ್ಸ್ ಥಾಮಸ್ ಬೋಲ್ಟನ್ ಮತ್ತು ವೆಬ್‌ಸ್ಟರ್ ಹಾಗು ಮುರ್‌ಡಿನ್ ಈ ರೀತಿ ಶೋಧನೆ ಮಾಡಿದರು. ಆದಾಗ್ಯೂ, ಪರೀಕ್ಷಾರ್ಥಿ ಕಪ್ಪು ಕುಳಿಗಿಂತ ಜೊತೆ ನಕ್ಷತ್ರವು ಹೆಚ್ಚು ಭಾರವಾಗಿರುವ ಫಲವಾಗಿ ಉಂಟಾದ ಅನಿಶ್ಚಿತತೆಗಳಿಂದ ಕೆಲವು ಅನುಮಾನಗಳು ಉಳಿದಿವೆ. ಪ್ರಸಕ್ತ ಕಪ್ಪು ಕುಳಿಗಳಿಗೆ ಉತ್ತಮ ಪರೀಕ್ಷಾರ್ಥಿಗಳನ್ನು ಎಕ್ಸರೇ ಬೈನರಿಗಳ ವರ್ಗದಲ್ಲಿ ಕಾಣಬಹುದು. ಇದನ್ನು ಹಗುರ ಎಕ್ಸರೆ ಟ್ರಾನ್ಸಿಯೆಂಟ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ವ್ಯವಸ್ಥೆಯ ವರ್ಗದಲ್ಲಿ ಜೊತೆ ನಕ್ಷತ್ರವು ಕಡಿಮೆ ದ್ರವ್ಯರಾಶಿಯಿಂದ ಕೂಡಿದ್ದು, ಕಪ್ಪು ಕುಳಿ ದ್ರವ್ಯರಾಶಿಯಲ್ಲಿ ಹೆಚ್ಚು ನಿಖರ ಅಂದಾಜುಗಳಿಗೆ ಅವಕಾಶ ನೀಡುತ್ತದೆ. ಇದಲ್ಲದೇ ಈ ವ್ಯವಸ್ಥೆಗಳು ಪ್ರತಿ ೧೦ -೫೦ವರ್ಷಗಳ ಕಾಲ ಅನೇಕ ವರ್ಷಗಳವರೆಗೆ ಎಕ್ಸರೆನಲ್ಲಿ ಸಕ್ರಿಯವಾಗಿರುತ್ತದೆ. ಕಡಿಮೆ ಎಕ್ಸರೆ ಉತ್ಸರ್ಜನೆಯ ಅವಧಿಯಲ್ಲಿ(ನಿಶ್ಚಲತೆ ಎನ್ನಲಾಗುತ್ತದೆ),ಸಂಚಯ ತಟ್ಟೆಯು ತೀವ್ರ ಮಸುಕಾಗಿ, ಈ ಅವಧಿಯಲ್ಲಿ ಜೊತೆ ನಕ್ಷತ್ರದ ವಿವರವಾದ ವೀಕ್ಷಣೆಗೆ ಅವಕಾಶ ನೀಡುತ್ತದೆ. ಇಂತಹ ದರ್ಜೆಗಳಲ್ಲಿ ಅತ್ಯಂತ ಉತ್ತಮವಾದುದು V೪೦೪ Cyg.

ನಿಶ್ಚಲತೆ ಮತ್ತು ಹಾರಿಜ ವಹನ(ಅಡ್ವೆಕ್ಷನ್)-ಪ್ರಾಬಲ್ಯದ ಸಂಚಯ ಹರಿವು

ನಿಶ್ಚಲತೆ ಸಮಯದಲ್ಲಿ ಸಂಚಯ ತಟ್ಟೆ(ಮಂಡಲ)ಯ ಮಸುಕಾಗಿರುವಿಕೆಯು ಒಂದು ಕ್ರಮದೊಳಗೆ ಪ್ರವೇಶಿಸುವ ಹರಿವಾಗಿದ್ದು, ಇದನ್ನು ಹಾರಿಜ ವಹನ ಪ್ರಾಬಲ್ಯದ ಸಂಚಯ ಹರಿವು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. (ADAF). ಈ ಕ್ರಮದಲ್ಲಿ ತಟ್ಟೆ(ಮಂಡಲ)ಯಲ್ಲಿ ಉಂಟಾಗುವ ಘರ್ಷಣೆಯಿಂದ ಉತ್ಪಾದನೆಯಾಗುವ ಎಲ್ಲ ಶಕ್ತಿಯು ವಿಕಿರಣವಾಗುವ ಬದಲಿಗೆ ಹರಿವಿನ ಜತೆ ಸಾಗುತ್ತದೆ. ಈ ಮಾದರಿಯು ಸರಿಯಾಗಿದ್ದರೆ, ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಉಪಸ್ಥಿತಿಗೆ ಪ್ರಬಲ ಗುಣಾತ್ಮಕ ಸಾಕ್ಷ್ಯವನ್ನು ಒದಗಿಸುತ್ತದೆ. ತಟ್ಟೆಯ ಮಧ್ಯದಲ್ಲಿನ ವಸ್ತು ಘನ ಮೇಲ್ಮೈ ಹೊಂದಿದ್ದರೆ, ಮೇಲ್ಮೈ ಮೇಲೆ ಅತೀ ಶಕ್ತಿಯುತ ಅನಿಲ ಅಪ್ಪಳಿಸಿದರೆ, ಇದು ದೊಡ್ಡ ಪ್ರಮಾಣದ ವಿಕಿರಣವನ್ನು ಸೂಸುತ್ತದೆ. ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರಗಳಿಗೆ ಇದೇ ಸ್ಥಿತಿಯಲ್ಲಿನ ಪರಿಣಾಮವನ್ನು ಗಮನಿಸಬಹುದು.

ಅರೆ ಆವರ್ತಕ ತೂಗಾಟಗಳು (Quasi-periodic oscillations)

ಸಂಚಯ ತಟ್ಟೆಗಳಿಂದ ಎಕ್ಸರೆ ಉತ್ಸರ್ಜನೆಯು ನಿರ್ದಿಷ್ಟ ಆವರ್ತನಗಳಲ್ಲಿ ಕೆಲವು ಬಾರಿ ಹೊಳೆಯುತ್ತವೆ. ಈ ಸಂಕೇತಗಳನ್ನು ಅರೆ ಆವರ್ತಕ ತೂಗಾಟಗಳು ಎನ್ನಲಾಗುತ್ತದೆ. ಸಂಚಯ ತಟ್ಟೆಯ ಒಳತುದಿಯಲ್ಲಿ ವಸ್ತು ಚಲಿಸುವುದರಿಂದ(ಒಳ ಸ್ಥಿರ ವೃತ್ತಾಕಾರದ ಕಕ್ಷೆ) ಉಂಟಾಗುತ್ತದೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಅವುಗಳ ಆವರ್ತನವನ್ನು ಸಾಂದ್ರ ವಸ್ತುವಿನ ದ್ರವ್ಯರಾಶಿಗೆ ಕೊಂಡಿ ಕಲ್ಪಿಸಲಾಗಿದೆ. ಹೀಗೆ ಸಂಭಾವ್ಯ ಕಪ್ಪು ಕುಳಿಗಳ ದ್ರವ್ಯರಾಶಿಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಅವುಗಳನ್ನು ಪರ್ಯಾಯ ಮಾರ್ಗವಾಗಿ ಬಳಸಬಹುದು.

ಗಾಮಾ ಕಿರಣ ಸ್ಫೋಟಗಳು

ತೀವ್ರ, ಆದರೆ ಒಂದು ಬಾರಿಯ ಗಾಮಾ ಕಿರಣ ಸ್ಫೋಟಗಳು(GRBs) ಹೊಸ ಕಪ್ಪು ಕುಳಿಗಳ ಹುಟ್ಟಿನ ಸಂಕೇತವಾಗಿರಬಹುದು. ಏಕೆಂದರೆ GRBಗಳು ದೈತ್ಯ ನಕ್ಷತ್ರಗಳ ಗುರುತ್ವ ಕುಸಿತ ಅಥವಾ ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರಗಳ ನಡುವೆ ಡಿಕ್ಕಿಗಳಿಂದ ಉಂಟಾಗಬಹುದು ಎಂದು ಖಬೌತಿಕವಿಜ್ಞಾನಿಗಳು ಭಾವಿಸಿದ್ದಾರೆ. ಎರಡೂ ರೀತಿಯ ವಿದ್ಯಮಾನವು ಕಪ್ಪು ಕುಳಿಗಳನ್ನು ಉತ್ಪಾದಿಸಲು ಸಾಕಷ್ಟು ದ್ರವ್ಯರಾಶಿ ಮತ್ತು ಒತ್ತಡ ಒಳಗೊಂಡಿರುತ್ತದೆ. ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರ ಮತ್ತು ಕಪ್ಪು ಕುಳಿ ನಡುವೆ ಡಿಕ್ಕಿಯಿಂದ ಕೂಡ GRB ಉಂಟಾಗಬಹುದೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಆದರೆ ಹೊಸ ಕಪ್ಪುಕುಳಿ ರಚನೆಯಾಗಿರುವುದಕ್ಕೆ GRBಸಾಕ್ಷ್ಯವಲ್ಲ. ಎಲ್ಲ ಗೊತ್ತಿರುವ GRBಗಳು ನಮ್ಮದೇ ಗೆಲಾಕ್ಸಿಯ ಹೊರಗಿನಿಂದ ಉಂಟಾಗುತ್ತವೆ. ಬಹುತೇಕ ಬಿಲಿಯನ್‌ಗಳಷ್ಟು(ಶತಕೋಟಿಗಳು) ಜ್ಯೋತಿರ್ವರ್ಷಗಳ ದೂರದಿಂದ ಬಂದಿರುತ್ತವೆ. ಆದ್ದರಿಂದ ಅವುಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ಕಪ್ಪು ಕುಳಿಗಳು ಬಿಲಿಯನ್‌ಗಳಷ್ಟು ವರ್ಷಗಳಷ್ಟು ಪ್ರಾಚೀನವಾಗಿದೆ.

ಗ್ಯಾಲಕ್ಸಿಯ ಬೀಜಕಣಗಳು (Active galactic nucleus)

ಈ ಚಿತ್ರದಲ್ಲಿ M87 ಮಧ್ಯದಿಂದ ಹುಟ್ಟುವ ಜೆಟ್ ಸಕ್ರಿಯ ಗ್ಯಾಲಕ್ಸಿಯ ಬೀಜಕಣದಿಂದ ಬಂದಿದೆ. ಇದು ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಯನ್ನು ಹೊಂದಿರಬಹುದು.ಕೃಪೆ:ಹಬ್ಬಲ್ ಬಾಹ್ಯಾಕಾಶ ದೂರದರ್ಶಕ/NASA/ESA

ಪ್ರತಿ ಗ್ಯಾಲಕ್ಸಿಯ ಮಧ್ಯದಲ್ಲಿ ಅಥವಾ ಪ್ರತಿ ಗ್ಯಾಲಕ್ಸಿಯ ಬಳಿ ಅತೀ ಬೃಹತ್ತಾದ ಕಪ್ಪು ಕುಳಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ ಎಂದು ವ್ಯಾಪಕವಾಗಿ ಒಪ್ಪಿಕೊಳ್ಳಲಾಗಿದೆ M-ಸಿಗ್ಮಾ ಸಂಬಂಧವೆಂದು ಹೆಸರಾದ ಕುಳಿಯ ದ್ರವ್ಯರಾಶಿ ಮತ್ತು ಗ್ಯಾಲಕ್ಸಿಯ ನಕ್ಷತ್ರಗಳ ಗುಂಪಿನ ವೇಗದ ಪ್ರಸರಣದ ನಡುವೆ ನಿಕಟ ವೀಕ್ಷಣೆಯ ಸಹಸಂಬಂಧವು ಕಪ್ಪು ಕುಳಿ ಮತ್ತು ಸ್ವತಃ ಗ್ಯಾಲಕ್ಸಿಯ ರಚನೆಯ ನಡುವೆ ಸಂಬಂಧವನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ದಶಕಗಳ ಕಾಲ, ಖಗೋಳವಿಜ್ಞಾನಿಗಳು ಅಸಾಮಾನ್ಯ ಲಕ್ಷಣಗಳ ಗ್ಯಾಲಕ್ಸಿಗಳನ್ನು ವರ್ಣಿಸಲು ಸಕ್ರಿಯ ಗ್ಯಾಲಕ್ಸಿ ಪದವನ್ನು ಬಳಸಿದ್ದಾರೆ. ಉದಾಹರಣೆಗೆ ರೋಹಿತದ ಗೆರೆ ಉತ್ಸರ್ಜನೆ ಮತ್ತು ಅತೀ ಪ್ರಬಲ ರೇಡಿಯೊ ತರಂಗಗಳ ಉತ್ಸರ್ಜನೆ. ಆದಾಗ್ಯೂ, ಸೈದ್ಧಾಂತಿಕ ಮತ್ತು ವೀಕ್ಷಣೆಯ ಅಧ್ಯಯನಗಳು ಈ ಗ್ಯಾಲಕ್ಸಿಗಳಲ್ಲಿ ಸಕ್ರಿಯ ಗ್ಯಾಲಕ್ಸಿಯ ಬೀಜಕಣಗಳು(AGN)ಬೃಹತ್ತಾದ ಕಪ್ಪು ಕುಳಿಗಳನ್ನು ಹೊಂದಿರಬಹುದೆಂದು ತೋರಿಸಿದೆ. ಈ AGNಗಳ ಮಾದರಿಗಳು ಕೇಂದ್ರ ಕಪ್ಪು ಕುಳಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ.ಅದು ಸೂರ್ಯನಿಗಿಂತ ಲಕ್ಷಾಂತರ ಅಥವಾ ಕೋಟ್ಯಂತರ ಪಟ್ಟು ದೊಡ್ಡದಿರಬಹುದು. ಅನಿಲ ಮತ್ತು ಧೂಳಿನ ತಟ್ಟೆಯಾದ ಸಂಚಯ ತಟ್ಟೆ ಮತ್ತು ಎರಡು ಸಂಚಯ ತಟ್ಟೆಗೆ ಲಂಬವಾಗಿರುವ ಎರಡು ಜೆಟ್‌ಗಳನ್ನು ಕೂಡ ಹೊಂದಿರುತ್ತವೆ.

ಬಹುತೇಕ AGNಗಳಲ್ಲಿ ಅತೀ ಬೃಹತ್ತಾದ ಕಪ್ಪು ಕುಳಿಗಳು ಸಿಗುತ್ತದೆಂದು ನಿರೀಕ್ಷಿಸಲಾಗಿದ್ದರೂ, ಕೆಲವು ಗ್ಯಾಲಕ್ಸಿಗಳ ಬೀಜಕಣಗಳನ್ನು ಎಚ್ಚರಿಕೆಯಿಂದ ಅಧ್ಯಯನ ಮಾಡಲಾಗಿದೆ. ಈ ಅಧ್ಯಯನಗಳಲ್ಲಿ ಕೇಂದ್ರ ಅತೀ ಬೃಹತ್ತಾದ ಕಪ್ಪು ಕುಳಿ ಪರೀಕ್ಷಾರ್ಥಿಗಳ ನಡುವಿನ ವಾಸ್ತವ ದ್ರವ್ಯರಾಶಿಗಳನ್ನು ಅಳೆಯುವ ಮತ್ತು ಗುರುತಿಸುವ ಪ್ರಯತ್ನಗಳನ್ನು ಮಾಡಲಾಗಿದೆ. ಬೃಹತ್ತಾದ ಕಪ್ಪು ಕುಳಿ ದರ್ಜೆಗಳ ಅತ್ಯಂತ ಗಮನಾರ್ಹ ಗ್ಯಾಲಕ್ಸಿಗಳಲ್ಲಿ ಕೆಲವು ಆಂಡ್ರೋಮೆಡಾ ಗ್ಯಾಲಕ್ಸಿ,M೩೨, M೮೭, NGC ೩೧೧೫, NGC ೩೩೭೭, NGC ೪೨೫೮, ಮತ್ತು ಸಾಂಬ್ರೆರೊ ಗ್ಯಾಲಕ್ಸಿ.

ಪ್ರಸಕ್ತ ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಗಳಿಗೆ ಅತ್ಯುತ್ತಮ ಸಾಕ್ಷ್ಯವು ನಮ್ಮ ಕ್ಷೀರ ಪಥದ ಮದ್ಯದಲ್ಲಿ ನಕ್ಷತ್ರಗಳ ಸೂಕ್ತ ಚಲನೆಯನ್ನು ಅಧ್ಯಯನ ಮಾಡುವುದರಿಂದ ಸಿಗುತ್ತದೆ. ೧೯೯೫ರಿಂದ ಖಗೋಳವಿಜ್ಞಾನಿಗಳು ಸ್ಯಾಗಿಟ್ಟಾರಿಯಸ್ A* ಪ್ರದೇಶದಲ್ಲಿ ೯೦ ನಕ್ಷತ್ರಗಳ ಚಲನೆಯ ಜಾಡು ಹಿಡಿದಿದ್ದಾರೆ. ಅವುಗಳ ಚಲನೆಯನ್ನು ಕೆಪ್ಲೇರಿಯನ್ ಕಕ್ಷೆಗಳಿಗೆ ಹೊಂದಿಕೆ ಮಾಡುವ ಮೂಲಕ ೦.೦೨ ಜ್ಯೋತಿವರ್ಷಗಳ ತ್ರಿಜ್ಯದ ಘನಅಳತೆಯಲ್ಲಿ ೨ .೬ದಶಲಕ್ಷ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳನ್ನು ಹೊಂದಿರಬಹುದೆಂದು ೧೯೯೮ರಲ್ಲಿ ತೀರ್ಮಾನಿಸಲು ಸಮರ್ಥರಾದರು. ಆಗಿನಿಂದ ನಕ್ಷತ್ರಗಳಲ್ಲಿ ಒಂದಾದ S೨ ಪೂರ್ಣ ಪರಿಭ್ರಮಣೆಯನ್ನು ಪೂರ್ಣಗೊಳಿಸಿದೆ. ಕಕ್ಷೆಯ ದತ್ತಾಂಶದಿಂದ ಸ್ಯಾಗಿಟ್ಯಾರಿಯಸ್ A*ಪ್ರದೇಶದಲ್ಲಿ ನಕ್ಷತ್ರಗಳ ಕಕ್ಷೀಯ ಚಲನೆಯನ್ನು ಉಂಟುಮಾಡುವ ವಸ್ತುವಿನ ದ್ರವ್ಯರಾಶಿ ಮತ್ತು ಗಾತ್ರವನ್ನು ಕುರಿತು ಉತ್ತಮ ನಿರ್ಬಂಧಗಳನ್ನು ಇರಿಸಲು ಅವರು ಸಮರ್ಥರಾದರು. ೦.೦೦೨ ಜ್ಯೋತಿರ್ವರ್ಷಗಳಿಗಿಂತ ಕಡಿಮೆ ತ್ರಿಜ್ಯದಲ್ಲಿ ೪ .೩ ದಶಲಕ್ಷ ಸೌರ ದ್ರವ್ಯರಾಶಿಗಳ ವೃತ್ತಾಕಾರದ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಪತ್ತೆಹಚ್ಚಿದರು. ಆ ದ್ರವ್ಯರಾಶಿಗೆ ಸಂಬಂಧಿಸಿದ ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದ ೩೦೦೦ ಪಟ್ಟು ಇದು ಹೆಚ್ಚಿಗಿದ್ದರೂ, ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಯಾಗಿ ಕೇಂದ್ರ ವಸ್ತುವಿಗೆ ಇದು ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ ಹಾಗು ಯಾವುದೇ ವಾಸ್ತವಿಕ ನಕ್ಷತ್ರಗಳ ಗೊಂಚಲು ಬೌತಿಕವಾಗಿ ಸಮರ್ಥನೀಯವಲ್ಲ."

ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್ (Gravitational lens

ಬೃಹತ್ ವಸ್ತುವಿನ ಸುತ್ತ ದೇಶಕಾಲದ ವಿಕಲ್ಪದಿಂದ ಬೆಳಕಿನ ಕಿರಣಗಳು ದ್ಯುತಿಮಸೂರದಲ್ಲಿ ಹಾಯುವಾಗ ಬಾಗುವ ರೀತಿಯಲ್ಲಿ ಬಾಗುತ್ತವೆ. ಈ ವಿದ್ಯಮಾನವನ್ನು ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ದುರ್ಬಲ ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್ ಬಗ್ಗೆ ಅವಲೋಕನಗಳನ್ನು ನಡೆಸಲಾಗಿದೆ.ಇವುಗಳಲ್ಲಿ ಬೃಹತ್ ವಸ್ತುವಿನ ಸುತ್ತ ದೇಶಕಾಲದ ವಿಕಲ್ಪದಿಂದ ಬೆಳಕಿನ ಕಿರಣಗಳು ದ್ಯುತಿಮಸೂರದಲ್ಲಿ ಹಾಯುವಾಗ ಬಾಗುವ ರೀತಿಯಲ್ಲಿ ಬಾಗುತ್ತವೆ. ಈ ವಿದ್ಯಮಾನವನ್ನು ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ದುರ್ಬಲ ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್ ಬಗ್ಗೆ ಅವಲೋಕನಗಳನ್ನು ನಡೆಸಲಾಗಿದೆ.ಇವುಗಳಲ್ಲಿ ಫೋಟೊನ್‌ಗಳು ಕೆಲವು ಆರ್ಕ್‌ಸೆಕೆಂಡುಗಳಿಂದ ವಿಚಲಿಸುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಕಪ್ಪು ಕುಳಿಗಾಗಿ ನೇರವಾಗಿ ವೀಕ್ಷಣೆ ನಡೆಸಲಾಗಿಲ್ಲ. ಕಪ್ಪು ಕುಳಿಯಿಂದ ಗುರುತ್ವ ಲೆನ್ಸಿಂಗ್ ವೀಕ್ಷಿಸುವ ಒಂದು ಸಾಧ್ಯತೆಯು ಕಪ್ಪು ಕುಳಿಯ ಸುತ್ತ ಪರಿಭ್ರಮಿಸುವ ನಕ್ಷತ್ರವನ್ನು ಗಮನಿಸುವುದಾಗಿದೆ. ಇಂತಹ ಅವಲೋಕನಗಳಿಗೆ ಸ್ಯಾಗಿಟ್ಟಾರಿಯಸ್ A* ಸುತ್ತ ಕಕ್ಷೆಯಲ್ಲಿ ಅನೇಕ ಪರೀಕ್ಷಾರ್ಥಿಗಳಿದ್ದಾರೆ.

ಪರ್ಯಾಯಗಳು

ನಾಕ್ಷತ್ರಿಕ ಕಪ್ಪುಕುಳಿಗೆ ಸಾಕ್ಷ್ಯವು ನ್ಯೂಟ್ರಾನ್ ನಕ್ಷತ್ರ ದ್ರವ್ಯರಾಶಿಯ ಗರಿಷ್ಠ ಮಿತಿಯ ಅಸ್ತಿತ್ವದ ಮೇಲೆ ಪ್ರಬಲವಾಗಿ ಅನ್ವಯಿಸಿದೆ. ಆ ಮಿತಿಯ ಗಾತ್ರವು ದಟ್ಟ ಬೌತದ್ರವ್ಯದ ಗುಣಗಳ ಬಗ್ಗೆ ಊಹೆಗಳನ್ನು ತೀವ್ರವಾಗಿ ಅವಲಂಬಿಸಿದೆ. ಹೊಸ ವಿಲಕ್ಷಣ ಬೌತದ್ರವ್ಯದ ಹಂತಗಳು ಈ ಮಿತಿಯನ್ನು ಮೇಲೆತ್ತಬಹುದು. ಅತ್ಯಧಿಕ ಸಾಂದ್ರತೆಯಲ್ಲಿ ಮುಕ್ತ ಕ್ವಾರ್ಕ್‌ಗಳ ಹಂತವು ದಟ್ಟ ಕ್ವಾರ್ಕ್ ನಕ್ಷತ್ರಗಳ ಅಸ್ತಿತ್ವಕ್ಕೆ ಅವಕಾಶ ನೀಡಬಹುದು. ಕೆಲವು ಸೂಪರ್‌ಮೆಟ್ರಿಕ್ ಮಾದರಿಗಳು Q ನಕ್ಷತ್ರಗಳ ಅಸ್ತಿತ್ವವನ್ನು ಮುಂಗಾಣಬಹುದು. ಪ್ರಮಾಣಕ ಮಾದರಿಯ ಕೆಲವು ವಿಸ್ತರಣೆಗಳು ಕ್ವಾರ್ಕ್‌ಗಳ ಮೂಲಭೂತ ನಿರ್ಮಾಣ ಬ್ಲಾಕ್‌ಗಳಾಗಿ ಪ್ರಿಯಾನ್‌ಗಳು ಹಾಗು ಪ್ರಿಯಾನ್ ನಕ್ಷತ್ರಗಳನ್ನು ರಚಿಸುವುದೆಂದು ಊಹಿಸಲಾಗಿರುವ ಲೆಪ್ಟಾನ್‌ಗಳ ಅಸ್ತಿತ್ವವನ್ನು ಸ್ಥಾಪಿಸುತ್ತವೆ. ಈ ಊಹಾತ್ಮಕ ಮಾದರಿಗಳು ನಾಕ್ಷತ್ರಿಕ ಕಪ್ಪು ಕುಳಿ ಪರೀಕ್ಷಾರ್ಥಿಗಳ ಅನೇಕ ವೀಕ್ಷಣೆಗಳ ಬಗ್ಗೆ ವಿವರಿಸಲು ಸಮರ್ಥವಾಗಿವೆ. ಆದಾಗ್ಯೂ, ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆಯ ಸಾಮಾನ್ಯ ವಾದಗಳಿಂದ ಇಂತಹ ಯಾವುದೇ ವಸ್ತು ಗರಿಷ್ಠ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆಂದು ತೋರಿಸಬಹುದು.

ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ತ್ರಿಜ್ಯದೊಳಗಿರುವ ಕಪ್ಪು ಕುಳಿಯ ಸರಾಸರಿ ಸಾಂದ್ರತೆಯು ಅದರ ಚದರದ್ರವ್ಯರಾಶಿಗೆ ವಿಲೋಮಾನುಪಾತವಾಗಿರುವುದರಿಂದ, ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಗಳು ನಾಕ್ಷತ್ರಿಕ ಕಪ್ಪುಕುಳಿಗಳಿಗಿಂತ ಕಡಿಮೆ ಸಾಂದ್ರತೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆ.(೧೦^೮ಸೌರ ದ್ರವ್ಯರಾಶಿ ಕಪ್ಪು ಕುಳಿಯ ಸರಾಸರಿ ಸಾಂದ್ರತೆಯನ್ನು ನೀರಿನ ಸಾಂದ್ರತೆ ಜತೆ ಹೋಲಿಸಬಹುದು). ಪರಿಣಾಮವಾಗಿ, ಕಪ್ಪು ಕುಳಿಯನ್ನು ರಚನೆ ಮಾಡುವ ಬೌತದ್ರವ್ಯದ ಬೌತವಿಜ್ಞಾನವನ್ನು ಉತ್ತಮವಾಗಿ ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲಾಗಿದೆ ಹಾಗು ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿ ವೀಕ್ಷಣೆಗಳಿಗೆ ಪರ್ಯಾಯ ವಿವರಣೆಗಳು ಹೆಚ್ಚು ಮಾಮೂಲಿಯಾಗಿದೆ. ಉದಾಹರಣೆಗೆ, ಬೃಹತ್ ಕಪ್ಪುಕುಳಿಗಳು ಅತೀ ಮಸುಕಾದ ವಸ್ತುಗಳ ದೊಡ್ಡ ಗೊಂಚಲಿನಿಂದ ರೂಪುಗೊಳ್ಳಬಹುದು. ಆದಾಗ್ಯೂ, ಸಾಧಾರಣವಾಗಿ ಇಂತಹ ಪರ್ಯಾಯಗಳು ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿ ಪರೀಕ್ಷಾರ್ಥಿಗಳನ್ನು ವಿವರಿಸಲು ಸಾಕಷ್ಟು ಸ್ಥಿರವಾಗಿಲ್ಲ.

ಕಪ್ಪು ಕುಳಿಗಳು ರಚನೆಯಾಗದಿರಲು ಗುರುತ್ವ ಸಿದ್ಧಾಂತವಾಗಿ ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆಯು ವಿಫಲವಾಗಬೇಕು ಎಂದು ನಾಕ್ಷತ್ರಿಕ ಮತ್ತು ಬೃಹತ್ ಕಪ್ಪು ಕುಳಿಗಳಿಗೆ ಸಾಕ್ಷ್ಯವು ಸೂಚಿಸುತ್ತದೆ. ಬಹುಶಃ ಕ್ವಾಂಟಂ ಮೆಕಾನಿಕಲ್ ತಿದ್ದುಪಡಿಗಳ ಪ್ರಾರಂಭದಿಂದ ಇದು ಉಂಟಾಗಬಹುದು. ಕ್ವಾಂಟಂ ಗುರುತ್ವ ಸಿದ್ಧಾಂತದ ಹೆಚ್ಚು ನಿರೀಕ್ಷಿತ ಲಕ್ಷಣವೆಂದರೆ ಅದು ಏಕತ್ವಗಳು ಅಥವಾ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಲಕ್ಷಣಗಳನ್ನು ತೋರಿಸುವುದಿಲ್ಲ(ಆದ್ದರಿಂದ ಕಪ್ಪು ಕುಳಿಗಳಲ್ಲ). ಇತ್ತೀಚಿನ ವರ್ಷಗಳಲ್ಲಿ,ಸ್ಟ್ರಿಂಗ್ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಫಜ್‌ಬಾಲ್ ಮಾದರಿಯು ಹೆಚ್ಚಿನ ಗಮನವನ್ನು ಸೆಳೆದಿದೆ. ಸ್ಟ್ರಿಂಗ್ ಸಿದ್ಧಾಂತದ ನಿರ್ದಿಷ್ಟ ಪರಿಸ್ಥಿತಿಗಳ ಲೆಕ್ಕಾಚಾರಗಳ ಆಧಾರದ ಮೇಲೆ, ಕಪ್ಪು ಕುಳಿ ವಿವರಣೆಯ ಪ್ರತ್ಯೇಕ ಸ್ಥಿತಿಗಳಲ್ಲಿ ಸಾಮಾನ್ಯವಾಗಿ ಈವೆಂಟ್ ಹಾರಿಜಾನ್ ಅಥವಾ ಏಕತ್ವವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ(ಆದ್ದರಿಂದ ಅದು ಕಪ್ಪು ಕುಳಿಯೆಂದು ನಿಜವಾಗಿ ಪರಿಗಣಿಸಲು ಆಗುವುದಿಲ್ಲ),ಆದರೆ ದೂರದ ವೀಕ್ಷಕನಿಗೆ ಇಂತಹ ಸ್ಥಿತಿಗಳ ಸಾಂಖ್ಯಿಕ ಸರಾಸರಿಯು ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆಯಲ್ಲಿರುವ ಸಾಮಾನ್ಯ ಕಪ್ಪು ಕುಳಿಯ ರೀತಿಯಲ್ಲಿ ಕಾಣುತ್ತದೆ.

ತೆರೆದ ಪ್ರಶ್ನೆಗಳು

ಜಡೋಷ್ಣ(ಎಂಟ್ರಪಿ) ಮತ್ತು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನ

೧೯೭೧ರಲ್ಲಿ, ಸ್ಟೀಫನ್ ಹಾಕಿಂಗ್ ಸಾಮಾನ್ಯ ಪರಿಸ್ಥಿತಿಗಳ ಅಡಿಯಲ್ಲಿ, ಯಾವುದೇ ಪ್ರಾಚೀನ ಕಪ್ಪು ಕುಳಿಗಳ ಸಂಗ್ರಹದ ಈವೆಂಟ್ ಹಾರಿಜಾನ್‌ (event horizon)ಗಳ ಒಟ್ಟು ಪ್ರದೇಶವು ಡಿಕ್ಕಿಯಾಗಿ ವಿಲೀನಗೊಂಡರೂ ಸಹ ಕುಂಠಿತಗೊಳ್ಳುವುದಿಲ್ಲ ಎಂದು ತೋರಿಸಿದರು. ಈ ಫಲಿತಾಂಶವು ಕಪ್ಪು ಕುಳಿ ಯಂತ್ರಶಾಸ್ತ್ರಗಳ ಎರಡನೇ ನಿಯಮ ಎಂದು ಹೆಸರಾಗಿದೆ ಹಾಗು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ಎರಡನೇ ನಿಯಮವನ್ನು ಹೋಲುತ್ತದೆ. ವ್ಯವಸ್ಥೆಯ ಒಟ್ಟು ಜಡೋಷ್ಣವು ಕುಂಠಿತಗೊಳ್ಳುವುದಿಲ್ಲ ಎಂದು ಅದು ವಿವರಿಸುತ್ತದೆ. ಸಂಪೂರ್ಣ ಶೂನ್ಯ ಉಷ್ಣಾಂಶದ ಪ್ರಾಚೀನ ವಸ್ತುಗಳಲ್ಲಿ ಕಪ್ಪು ಕುಳಿಗಳು ಶೂನ್ಯ ಜಡೋಷ್ಣಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆಂದು ಭಾವಿಸಲಾಗಿದೆ. ಪ್ರಕರಣವು ಹೀಗಿದ್ದಾಗ ಉಷ್ಣಬಲವಿಜ್ಞಾನದ ಎರಡನೇ ನಿಯಮವು ಕಪ್ಪು ಕುಳಿಯನ್ನು ಪ್ರವೇಶಿಸುವ ಜಡೋಷ್ಣ ಹೊತ್ತ ಬೌತದ್ರವ್ಯದಿಂದ ಭಂಗವಾಗುತ್ತದೆ.ಇದು ಬ್ರಹ್ಮಾಂಡದ ಒಟ್ಟು ಜಡೋಷ್ಣವನ್ನು ಕುಂಠಿತಗೊಳಿಸುವಲ್ಲಿ ಫಲ ನೀಡುತ್ತದೆ. ಆದ್ದರಿಂದ ಕಪ್ಪುಕುಳಿ ಜಡೋಷ್ಣವನ್ನು ಹೊಂದಿರಬೇಕು ಹಾಗು ಅದರ ವ್ಯಾಪ್ತಿಯ ಪ್ರದೇಶಕ್ಕೆ ಪ್ರಮಾಣಾನುಗುಣವಾಗಿರಬೇಕು ಎಂದು ಜಾಕೋಬ್ ಬೆಕೆನ್‌ಸ್ಟೈನ್ ಪ್ರಸ್ತಾಪಿಸಿದರು.

ಕಪ್ಪು ಕುಳಿಯು ಕಪ್ಪುಕಾಯ ವಿಕಿರಣವನ್ನು ಸ್ಥಿರ ಉಷ್ಣಾಂಶದಲ್ಲಿ ಸೂಸುತ್ತದೆ ಎಂಬ ಕ್ವಾಂಟಂ ಕ್ಷೇತ್ರ ಸಿದ್ಧಾಂತದ ಮುಂಗಾಣ್ಕೆಯ ಹಾಕಿಂಗ್ಸ್ ಶೋಧನೆಯಿಂದ ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ನಿಯಮಗಳ ಜತೆ ಕೊಂಡಿಯು ಮತ್ತಷ್ಟು ಬಲಗೊಂಡಿದೆ. ಇದು ಕಪ್ಪು ಕುಳಿ ರಚನಾವಿಧಾನದ ಎರಡನೇ ನಿಯಮದ ಉಲ್ಲಂಘನೆಯಂತೆ ಕಾಣುತ್ತದೆ. ಏಕೆಂದರೆ ವಿಕಿರಣವು ಕಪ್ಪು ಕುಳಿಯಿಂದ ಶಕ್ತಿಯನ್ನು ಒಯ್ದು, ಅದು ಕುಗ್ಗಲು ಕಾರಣವಾಗುತ್ತದೆ. ಈ ವಿಕಿರಣವು,ಜಡೋಷ್ಣವನ್ನು ಕೂಡ ಒಯ್ಯುತ್ತದೆ. ಕಪ್ಪು ಕುಳಿಯನ್ನು ಸುತ್ತುವರಿದಿರುವ ಜಡೋಷ್ಣ ವಸ್ತು ಹಾಗು ಪ್ಲಾಂಕ್ ಯೂನಿಟ್‌ಗಳಲ್ಲಿ ಅಳೆಯುವ ಹಾರಿಜಾನ್ ಪ್ರದೇಶದ ಕಾಲುಭಾಗದ ಮೊತ್ತವು ವಾಸ್ತವವಾಗಿ ಸದಾ ವರ್ಧಿಸುತ್ತದೆ. ಇದು ಕಪ್ಪು ಕುಳಿ ರಚನಾವಿಧಾನದ ಪ್ರಥಮ ನಿಯಮದ ರಚನೆಗೆ ಅವಕಾಶ ಕಲ್ಪಿಸುತ್ತದೆ. ದ್ರವ್ಯರಾಶಿಯು ಶಕ್ತಿಯಾಗಿ, ಮೇಲ್ಮೈ ಗುರುತ್ವವು ಉಷ್ಣಾಂಶವಾಗಿ ಮತ್ತು ಪ್ರದೇಶವು ಜಡೋಷ್ಣವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ಪ್ರಥಮ ನಿಯಮಕ್ಕೆ ಇದು ಸದೃಶವಾಗಿದೆ.

ಒಂದು ಗೊಂದಲದ ಲಕ್ಷಣವೆಂದರೆ, ಕಪ್ಪು ಕುಳಿಯ ಜಡೋಷ್ಣವು ಅದರ ಗಾತ್ರದಿಂದ ವರ್ಧಿಸುವ ಬದಲಿಗೆ ಪ್ರದೇಶದೊಂದಿಗೆ ವರ್ಧಿಸುತ್ತದೆ. ಜಡೋಷ್ಣವು ಸಾಮಾನ್ಯವಾಗಿ ವಿಸ್ತರಿತ ಪ್ರಮಾಣವಾಗಿದ್ದು, ವ್ಯವಸ್ಥೆಯ ಗಾತ್ರದೊಂದಿಗೆ ರೇಖೀಯವಾಗಿ ವರ್ಧಿಸುತ್ತದೆ. ಈ ವಿಚಿತ್ರ ಲಕ್ಷಣವು 'ಟಿ ಹೂಫ್ಟ್‌ಮತ್ತು ಸಸ್‌ಕಿಂಡ್‌ಗೆ ಪೂರ್ಣಲೇಖೀ ತತ್ವವನ್ನು ಮಂಡಿಸಲು ದಾರಿ ಕಲ್ಪಿಸಿತು. ದೇಶಕಾಲದ ಗಾತ್ರದಲ್ಲಿ ಯಾವುದೇ ಸಂಭವಿಸಿದರೂ,ಆ ಗಾತ್ರದ ಗಡಿಯನ್ನು ಕುರಿತ ದತ್ತಾಂಶದಿಂದ ವಿವರಿಸಬಹುದು ಎಂದು ಇದು ಸೂಚಿಸುತ್ತದೆ.

ಸಾಮಾನ್ಯ ಸಾಪೇಕ್ಷತೆಯನ್ನು ಕಪ್ಪು ಕುಳಿ ಜಡೋಷ್ಣದ ಅರೆ ಪ್ರಾಚೀನ ಲೆಕ್ಕಾಚಾರವನ್ನು ನಿರ್ವಹಿಸಲು ಬಳಸಬಹುದಾದರೂ, ಈ ಪರಿಸ್ಥಿತಿಯು ಸೈದ್ಧಾಂತಿಕವಾಗಿ ತೃಪ್ತಿನೀಡದು. ಸಾಂಖ್ಯಿತ ಚಲನಶಾಸ್ತ್ರದಲ್ಲಿ ಒಂದೇ ಸ್ಥೂಲಗೋಚರ ಗುಣಗಳಿರುವ ವ್ಯವಸ್ಥೆಯ ಸೂಕ್ಷ್ಮದರ್ಶಕೀಯ ವಿನ್ಯಾಸಗಳ ಸಂಖ್ಯೆಯನ್ನು ಎಣಿಸುವುದು ಎಂದು ಜಡೋಷ್ಣವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲಾಗಿದೆ.( ಉದಾ-ದ್ರವ್ಯರಾಶಿ, ವಿದ್ಯುದಾವೇಶ, ಒತ್ತಡ ಮುಂತಾದವು). ಕ್ವಾಂಟಂ ಗುರುತ್ವದ ತೃಪ್ತಿಕರ ಸಿದ್ಧಾಂತವಿಲ್ಲದೇ, ಕಪ್ಪು ಕುಳಿಗಳ ಗಣನೆಯನ್ನು ನಿರ್ವಹಿಸುವುದು ಸಾಧ್ಯವಿಲ್ಲ. ಕ್ವಾಂಟಂ ಗುರುತ್ವಕ್ಕೆ ವಿವಿಧ ವಿಧಾನಗಳಲ್ಲಿ ಕೆಲವು ಪ್ರಗತಿಗಳನ್ನು ಕೈಗೊಳ್ಳಲಾಗಿದೆ. ೧೯೯೫ರಲ್ಲಿ,ಸ್ಟ್ರಿಂಗ್ ಸಿದ್ಧಾಂತದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಮಹಾಸಮ್ಮಿತೀಯ ಕಪ್ಪು ಕುಳಿಯನ್ನು ಎಣಿಸುವುದು ಬೆಕಿನ್‌ಸ್ಟೈನ್-ಹಾಕಿಂಗ್ ಜಡೋಷ್ಣವನ್ನು ಪುನರುತ್ಪಾದಿಸಿತು ಎಂದು ೧೯೯೫ರಲ್ಲಿ ಸ್ಟ್ರಾಮಿಂಜರ್ ಮತ್ತು ವಾಫಾ ತೋರಿಸಿದರು. ಆಗಿನಿಂದ,ಸ್ಟ್ರಿಂಗ್ ಸಿದ್ಧಾಂತ ಮತ್ತು ಲೂಪ್ ಕ್ವಾಂಟಂ ಗುರುತ್ವ ಮುಂತಾದ ಕ್ವಾಂಟಂ ಗುರುತ್ವದ ಇತರ ವಿಧಾನಗಳು ಎರಡರಲ್ಲೂ ವಿವಿಧ ಕಪ್ಪು ಕುಳಿಗಳಿಗೆ ಒಂದೇ ರೀತಿಯ ಫಲಿತಾಂಶಗಳು ವರದಿಯಾಗಿದೆ.

ಕಪ್ಪು ಕುಳಿ ಏಕಾತ್ಮಕತೆ

ಮೂಲ ಬೌತಶಾಸ್ತ್ರದಲ್ಲಿ ಮಾಹಿತಿ ನಷ್ಟ ವಿರೋಧಾಭಾಸ ಅಥವಾ ಕಪ್ಪು ಕುಳಿ ಏಕಾತ್ಮಕತೆವಿರೋಧಾಭಾಸವು ತೆರೆದ ಪ್ರಶ್ನೆಯಾಗಿದೆ. ಸಾಂಪ್ರದಾಯಿಕ ರೀತಿಯಲ್ಲಿ,ಬೌತಶಾಸ್ತ್ರದ ನಿಯಮಗಳು ಒಂದೇ ತೆರನಾದ ಮುಂದೆ ಹೋಗುವ ಅಥವಾ ಹಿಂದುಮುಂದಾಗಿರುತ್ತದೆ.(T-ಸಮ್ಮಿತೀಯ). ಲಿಯೊವಿಲ್ಲೆ'ಸ್ ಪ್ರಮೇಯವು ಫೇಸ್ ಸ್ಪೇಸ್(ಸ್ಥಳದ ಅವಸ್ಥೆಯ)ಗಾತ್ರದ ಸ್ಥಾಯಿತ್ವವನ್ನು ನಿರ್ದೇಶಿಸುತ್ತದೆ. ಅದನ್ನು ಮಾಹಿತಿಯ ಸ್ಥಾಯಿತ್ವ ಎಂದು ಭಾವಿಸಲಾಗಿದ್ದು,ಪ್ರಾಚೀನ ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ ಕೂಡ ಕೆಲವು ಸಮಸ್ಯೆಯಿದೆ. ಕ್ವಾಟಂ ಯಂತ್ರಶಾಸ್ತ್ರದಲ್ಲಿ ಇದು ಮುಖ್ಯ ಗುಣಲಕ್ಷಣವಾದಏಕಾತ್ಮಕತೆಗೆ ಸಂಬಂಧಿಸಿದ್ದು,ಸಂಭಾವ್ಯತೆ ಸ್ಥಾಯಿತ್ವ ನಿಭಾಯಿಸುತ್ತದೆ(ಇದನ್ನು ಸಾಂದ್ರತೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನಿಂದ ಅಭಿವ್ಯಕ್ತಗೊಳಿಸುವ ಕ್ವಾಂಟಂ ಫೇಸ್ ಸ್ಪೇಸ್(ಸ್ಥಳದ ಅವಸ್ಥೆಯ) ಗಾತ್ರದ ಸ್ಥಾಯಿತ್ವ ಎಂದು ಕೂಡ ಭಾವಿಸಲಾಗಿದೆ).

ಇವನ್ನೂ ಗಮನಿಸಿ

• ಕಲ್ಪನೆಯಲ್ಲಿ ಕಪ್ಪು ಕುಳಿ
• ಬ್ಲಾಕ್ ಸ್ಟ್ರಿಂಗ್
• ಕುಗೇಲ್‌ಬ್ಲಿಟ್ಜ್(ಖಭೌತ ವಿಜ್ಞಾನ)
• ಕಪ್ಪು ಕುಳಿಗಳ ಪಟ್ಟಿ
• ಸಸ್‌ಕೈಂಡ್–ಹಾಕಿಂಗ್ ಕದನ

• ಕಪ್ಪು ಕುಳಿ ಭೌತಶಾಸ್ತ್ರದ ಘಟನೆಗಳ ಅನುಕ್ರಮ
• ಶ್ವೇತ ಕುಳಿ
• ವರ್ಮ್‌ಹೋಲ್

ಹೆಚ್ಚಿನ ಓದಿಗಾಗಿ

ಜನಪ್ರಿಯ ಓದಿಗಾಗಿ

• Ferguson, Kitty (1991). Black Holes in Space-Time. Watts Franklin. ISBN 0-531-12524-6..
• Hawking, Stephen (೧೯೮೮). A Brief History of Time. Bantam Books, Inc. ISBN ೦-೫೫೩-೩೮೦೧೬-೮. {{cite book}}: Check |isbn= value: invalid character (help).
• Hawking, Stephen; Penrose, Roger (1996). The Nature of Space and Time. Princeton University Press. ISBN 0-691-03791-2. {{cite book}}: Check |isbn= value: checksum (help).
• Melia, Fulvio (೨೦೦೩). The Black Hole at the Center of Our Galaxy. Princeton U Press. ISBN ೯೭೮-೦-೬೯೧-೦೯೫೦೫-೯. {{cite book}}: Check |isbn= value: invalid character (help).
• Melia, Fulvio (2003). The Edge of Infinity. Supermassive Black Holes in the Universe. Cambridge U Press. ISBN 978-0-521-81405-8..
• Pickover, Clifford (1998). Black Holes: A Traveler's Guide. Wiley, John & Sons, Inc. ISBN 0-471-19704-1..
• Stern, B. (2008). "Blackhole". Archived from the original on 2011-07-27. Retrieved 2011-01-03., ಕವಿತೆ.
• Thorne, Kip S. (೧೯೯೪). Black Holes and Time Warps. Norton, W. W. & Company, Inc. ISBN ೦-೩೯೩-೩೧೨೭೬-೩. {{cite book}}: Check |isbn= value: invalid character (help).
• Wheeler, J. Craig (2007). Cosmic Catastrophes (2nd ed.). Cambridge University Press. ISBN 0-521-85714-7. {{cite book}}: Invalid |ref=harv (help)

ವಿಶ್ವವಿದ್ಯಾನಿಲಯ ಪಠ್ಯಪುಸ್ತಕಗಳು ಮತ್ತು ಪ್ರಬಂಧ

• Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley. ISBN 0-8053-8732-3. {{cite book}}: Invalid |ref=harv (help)ಸೀನ್ ಕ್ಯಾರೋಲ್ ವೆಬ್‌ಸೈಟ್ Archived 2007-06-13 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.‌ನಿಂದ ಪುಸ್ತಕ ಆಧಾರಿತ ಉಪನ್ಯಾಸ ಟಿಪ್ಪಣಿಗಳು ಉಚಿತವಾಗಿ ಲಭ್ಯವಾಗುತ್ತದೆ.
• Carter, B. (1973). "Black hole equilibrium states". In DeWitt, B.S.; DeWitt, C. (eds.). Black Holes..
• Chandrasekhar, Subrahmanyan (1999). Mathematical Theory of Black Holes. Oxford University Press. ISBN 0-19-850370-9..
• Frolov, V.P.; Novikov, I.D. (1998). "Black hole physics". {{cite journal}}: Cite journal requires |journal= (help); Invalid |ref=harv (help).
• Hawking, S.W.; Ellis, G.F.R. (1973). Large Scale Structure of space time. Cambridge University Press. ISBN 0521099064. {{cite book}}: More than one of |author= and |last1= specified (help).
• Melia, Fulvio (೨೦೦೭). The Galactic Supermassive Black Hole. Princeton U Press. ISBN ೯೭೮-೦-೬೯೧-೧೩೧೨೯-೦. {{cite book}}: Check |isbn= value: invalid character (help).
• Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes. Addison Wesley Longman. ISBN 0-201-38423-X..
• Thorne, Kip S.; Misner, Charles; Wheeler, John (1973). Gravitation. W. H. Freeman and Company. ISBN 0-7167-0344-0..
• Wald, Robert M. (1992). Space, Time, and Gravity: The Theory of the Big Bang and Black Holes. University of Chicago Press. ISBN 0-226-87029-4..

ಪುನರ್ಪರಿಶೀಲನೆ ಪತ್ರಗಳು

• Gallo, Elena; Marolf, Donald (2009). "Resource Letter BH-2: Black Holes". American Journal of Physics. 77: 294. doi:10.1119/1.3056569.
• Hughes, Scott A. (2005). "Trust but verify: The case for astrophysical black holes". arXiv:hep-ph/0511217v2 [hep-ph].  ೨೦೦೫ SLAC ಸಮ್ಮರ್ ಇನ್‌ಸ್ಟಿಟ್ಯೂಟ್ ಉಪನ್ಯಾಸ ಟಿಪ್ಪಣಿಗಳು.

ಬಾಹ್ಯ ಕೊಂಡಿಗಳು

• ಸ್ಟಾನ್‌ಪೋರ್ಡ್ ಎನ್‌ಸೈಕ್ಲೋಪೀಡಿಯ ಆಫ್ ಫಿಲಾಸಫಿ: "ಸಿಂಗ್ಯುಲ್ಲಾರಿಟೀಸ್ ಎಂಡ್ ಬ್ಲಾಕ್ ಹೋಲ್ಸ್" ಎರಿಕ್ ಕುರಿಯಲ್ ಎಂಡ್ ಪೀಟರ್ ಬೋಕುಲಿಚ್ ಅವರಿಂದ.
• "ಬ್ಲಾಕ್ ಹೋಲ್" ಆನ್ ಸ್ಕೊಲಾರ್‌ಪೀಡಿಯ
• ಬ್ಲಾಕ್‌ಹೋಲ್ಸ್: ಗ್ರಾವಿಟಿ`ಸ್ ರಿಲೆಂಟ್‌ಲೆಸ್ ಪುಲ್ –

ಸ್ಪೇಸ್ ಟೆಲಿಸ್ಕೋಪ್ ಸೈನ್ಸ್ ಇನ್‌ಸ್ಟಿಟ್ಯೂಟ್‌ನಿಂದ ಕಪ್ಪು ಕುಳಿಗಳ ಬೌತಶಾಸ್ತ್ರ ಮತ್ತು ಖಗೋಳಶಾಸ್ತ್ರದ ಬಗ್ಗೆ ಅಂತರಸಂಪರ್ಕ ಬಹುಮಾಧ್ಯಮ ವೆಬ್‌ಸೈಟ್.

• FAQ ಆನ್ ಬ್ಲಾಕ್‌ಹೋಲ್ಸ್
• "ಸ್ಕೆವಾರ್ಜ್ಸ್‌ಚೈಲ್ಡ್ ಜಿಯೋಮಿಟ್ರಿ Archived 1998-01-18 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ."
• ಅಡ್ವಾನ್ಸ್ಡ್ ಮ್ಯಾಥೆಮೆಟಿಕ್ಸ್ ಆಫ್ ಬ್ಲಾಕ್ ಹೋಲ್ ಎವಾಪೊರೇಷನ್ Archived 2012-10-17 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.

ವೀಡಿಯೊಗಳು

• 16 -ಇಯರ್ ಲಾಂಗ್ ಸ್ಟಡಿ ಟ್ರಾಕ್ಸ್ ಸ್ಟಾರ್ಸ್ ಆರ್ಬಿಟಿಂಗ್ ಮಿಲ್ಕಿ ವೇ ಬ್ಲಾಕ್ ಹೋಲ್
• ಯೇಲ್ ಯೂನಿವರ್ಸಿಟಿ ವಿಡಿಯೊ ಲೆಕ್ಚರ್: ಇಂಟರೋಡಕ್ಷನ್ ಟು ಬ್ಲಾಕ್ ಹೋಲ್ಸ್ Archived 2008-01-15 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. ಎಟ್ ಗೂಗಲ್ ವಿಡಿಯೊ.
• ಮೂವಿ ಆಫ್ ಬ್ಲಾಕ್ ಹೋಲ್ ಕ್ಯಾಂಡಿಟೇಟ್ ಫ್ರಂ ಮ್ಯಾಕ್ಸ್ ಪ್ಲಾಂಕ್ ಇನ್‌ಸ್ಟಿಟ್ಯೂಟ್ Archived 2006-09-04 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.