ಶಕ್ತಿ

ಶಕ್ತಿ ಎಂದರೆ ಕೆಲಸ (ಅಥವಾ ಕಾರ್ಯ) ಮಾಡಲು ಇರುವ ಅಳವು. ಗ್ರೀಕ್ನ ಮೂಲ ಪದಗಳಾದ ἐνέργεια ಅಂದರೆ ಎನರ್ಜೀಯಾ (ಚಟುವಟಿಕೆ, ಕಾರ್ಯಾಚರಣೆ) ಮತ್ತು ἐνεργός ಎನರ್ಗೊಸ್' (ಸಕ್ರಿಯ, ಕಾರ್ಯನಿರತ) ಎಂಬ ಪದಗಳಿಂದ ಭೌತವಿಜ್ಞಾನದ ಶಕ್ತಿ ('ಎನರ್ಜಿ') ಎಂಬ ಇಂಗ್ಲಿಷ್ ಪದವು ನಿಷ್ಪನ್ನವಾಗಿದೆ. 'ಶಕ್ತಿ' ಎಂಬುದು, ಬಲವು ನಿರ್ವಹಿಸಬಲ್ಲ ಕಾರ್ಯದ ಯಾವುದೇ ಭೌತಿಕ ಅದಿಶ ಪರಿಮಾಣವನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಸಂರಕ್ಷಣಾ ನಿಯಮಕ್ಕೆ ಒಳಗಾಗುವ ವಸ್ತು ಮತ್ತು ವ್ಯವಸ್ಥೆಗಳ ಲಕ್ಷಣವೂ ಆಗಿದೆ. ಚಲನಶಕ್ತಿ, ಅಂತಸ್ಥ ಶಕ್ತಿ, ಶಾಖೋತ್ಪನ್ನ ಶಕ್ತಿ, ಗುರುತ್ವ ಶಕ್ತಿ, ಶಾಬ್ದಿಕ ಶಕ್ತಿ, ಬೆಳಕಿನ ಶಕ್ತಿ, ಸ್ಥಿತಿಸ್ಥಾಪಕ ಶಕ್ತಿ ಮತ್ತು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿ - ಹೀಗೆ ಶಕ್ತಿಯಲ್ಲಿ ಹತ್ತು ಹಲವು ರೂಪಗಳಿವೆ. ಯಾವ ಬಲದ ಆಧಾರದ ಮೇಲೆ ಶಕ್ತಿ ಉತ್ಪನ್ನವಾಗಿದೆ ಎಂಬುದನ್ನು ಆಧರಿಸಿ ಶಕ್ತಿಗೆ ಆ ಬಲದ ಹೆಸರನ್ನು ಗುಣವಾಚಿಯನ್ನಾಗಿ ಸೇರಿಸಲಾಗುತ್ತದೆ.
ಯಾವುದೇ ಶಕ್ತಿಯನ್ನು ರೂಪಾಂತರಿಸಬಹುದು. ಆದರೆ, ಶಕ್ತಿಯ ಒಟ್ಟು ಪ್ರಮಾಣ ಮಾತ್ರ ಅಷ್ಟೇ ಇರುತ್ತದೆ. ಶಕ್ತಿ-ಸಂಪನ್ಮೂಲದ ಸಂರಕ್ಷಣೆ ಎಂಬ ಈ ತತ್ವವನ್ನು 19ನೆಯ ಶತಮಾನದ ಆರಂಭದಲ್ಲಿ ಮೊದಲ ಬಾರಿಗೆ ಹೌದೆಂದು ಸಮರ್ಥಿಸಲಾಯಿತು. ಯಾವುದೇ ವ್ಯವಸ್ಥೆಯಲ್ಲೂ ಇದು ಅನ್ವಯವಾಗುತ್ತದೆ. ನೋಥರ್ ಪ್ರಮೇಯದ ಪ್ರಕಾರ, ಭೌತವಿಜ್ಞಾನದ ನಿಯಮಗಳು ಕಾಲಾಂತರದಲ್ಲಿ ಬದಲಾಗದು ಎಂಬ ಸಂಗತಿಯನ್ನು ಆಧರಿಸಿಯೇ ಶಕ್ತಿಯ ಸಂರಕ್ಷಣೆ ನಡೆದಿದೆ.[೧]
ವ್ಯವಸ್ಥೆಯ ಒಟ್ಟು ಶಕ್ತಿಯು ಕಾಲಾಂತರದಲ್ಲಿ ಬದಲಾಗದಿದ್ದರೂ, ಅದನ್ನು ಯಾತಕ್ಕಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ ಎಂಬುದರ ಮೇಲೆ ಅದರ ಮೌಲ್ಯ ನಿಂತಿರುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಚಲಿಸುತ್ತಿರುವ ವಿಮಾನದಲ್ಲಿ ಕುಳಿತಿರುವ ಪ್ರಯಾಣಿಕನೊಬ್ಬನಿಗೆ, ವಿಮಾನಕ್ಕೆ ಹೋಲಿಸಿದಾಗ ಶೂನ್ಯ ಚಲನ ಶಕ್ತಿಯಿರುತ್ತದೆ; ಆದರೆ ಭೂಮಿಗೆ ಹೋಲಿಸಿ ನೋಡಿದಾಗ ಶೂನ್ಯವಲ್ಲದ ಚಲನೆಯ ಶಕ್ತಿಯಿರುತ್ತದೆ.
ಇತಿಹಾಸ[ಬದಲಾಯಿಸಿ]
ಕ್ರಿ.ಪೂ. ನಾಲ್ಕನೆಯ ಶತಮಾನದಲ್ಲಿ, ಅರಿಸ್ಟಾಟಲ್ ರಚಿಸಿದ ನಿಕೊಮಾಕಿಯನ್ ಎಥಿಕ್ಸ್[೨] ಎಂಬ ಕೃತಿಯಲ್ಲಿ ಮೊದಲ ಬಾರಿಗೆ ಬಳಸಲಾದ ἐνέργεια (ಎನರ್ಜೀಯಾ) ಎಂಬ ಗ್ರೀಕ್ ಪದದಿಂದ ಶಕ್ತಿ (ಎನರ್ಜಿ) ಪದದ ನಿಷ್ಪನ್ನವಾಗಿದೆ. 'ಬೆಳಕಿನ ಕಿರಣಗಳು ಸೂಕ್ಷ್ಮ ಶಕ್ತಿ ಕಣಗಳ ಪ್ರವಾಹಗಳಾಗಿವೆ' ಎಂದು ಕ್ರಿ.ಶ. 1021 ನಲ್ಲಿ ಅಲ್ ಹಜನ್ ಎಂಬ ಅರಬ್ಬಿ ಭೌತವಿಜ್ಞಾನಿಯು ತನ್ನ 'ಬುಕ್ ಆಫ್ ಆಪ್ಟಿಕ್ಸ್' (ದೃಗ್ವಿಜ್ಞಾನದ ಪುಸ್ತಕ) ಗ್ರಂಥದಲ್ಲಿ ಹೇಳುತ್ತಾನೆ. ಬೆಳಕಿನ ಅತಿಸೂಕ್ಷ್ಮ ಅಂಶಗಳು ರೇಖಾಗಣಿತ ಮತ್ತು ಪ್ರಯೋಗಗಳಿಂದ ಸಂಶೋಧಿಸಬಹುದಾದ ಗುಣಗಳನ್ನು ಮಾತ್ರ ಹೊಂದಿವೆ; ಹಾಗೂ 'ಶಕ್ತಿಯನ್ನು ಬಿಟ್ಟು ಇನ್ಯಾವುದೇ ಗೋಚರ ಗುಣಗಳಿಲ್ಲ'[೩] ಎಂದು ನಿರೂಪಿಸಿದ್ದಾನೆ. ವಸ್ತುವೊಂದು ಭೂ ಕೇಂದ್ರದಿಂದ ಎಷ್ಟು ಎತ್ತರದಲ್ಲಿದೆ ಎನ್ನುವುದನ್ನು ಆಧರಿಸಿ ಗುರುತ್ವ ಶಕ್ತಿಯ ಸಾಮರ್ಥ್ಯ ಏರಿಳಿಕೆಯಾಗುತ್ತದೆ ಎಂದು 1121ರ ದ ಬುಕ್ ಆಫ್ ದ ಬ್ಯಾಲೆನ್ಸ್ ಆಫ್ ವಿಸ್ಡಮ್ ಗ್ರಂಥದಲ್ಲಿ ಅಲ್ ಕಾಜಿನಿ ಅಭಿಪ್ರಾಯ ಪಡುತ್ತಾರೆ.[೪]
ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆಯು 'ವಿಸ್ ವಿವಾ' ಎಂಬ ಕಲ್ಪನೆಯಿಂದ ಹೊರಹೊಮ್ಮಿತು. 'ವಸ್ತುವಿನ ದ್ರವ್ಯರಾಶಿ ಮತ್ತು ಅದರ ವೇಗದ ಗುಣಲಬ್ಧದ ವರ್ಗ' ಎಂದು 'ವಿಸ್ ವಿವಾ'ವನ್ನು ಲಿಬ್ನಿಜ್ ವ್ಯಾಖ್ಯಾನಿಸಿದರು. 'ವಿಸ್ ವಿವಾ'ದ ಒಟ್ಟು ಮೊತ್ತವು ಸಂರಕ್ಷಿತವಾಗಿದೆ ಎಂದು ಅವರು ನಂಬಿದ್ದರು. ಘರ್ಷಣೆಯ ಕಾರಣ ನಿಧಾನಗತಿಯನ್ನು ಲೆಕ್ಕಕ್ಕೆ ತೆಗೆದುಕೊಳ್ಳಲು, 'ಶಾಖವು ವಸ್ತುವಿನ ಅಂಶಗಳ ಯಾದೃಚ್ಛಿಕ ಚಲನವಲನವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ' ಎಂದು ಲಿಬ್ನಿಜ್ ಹೇಳಿದ್ದರು. ಈ ಅಭಿಪ್ರಾಯಕ್ಕೆ ಐಸಾಕ್ ನ್ಯೂಟನ್ರ ಸಹಮತವಿತ್ತು. ಆದರೂ ಈ ಅಭಿಪ್ರಾಯವು ಸಾರ್ವತ್ರಿಕವಾಗಿ ಸ್ವೀಕೃತವಾಗಲು ಒಂದು ಶತಮಾನಕ್ಕಿಂತಲೂ ಹೆಚ್ಚು ಕಾಲ ಬೇಕಾಯಿತು. ವಿಸ್ ವಿವಾ ಬದಲಿಗೆ, ಆಧುನಿಕ ಅರ್ಥದಲ್ಲಿ, 'ಎನರ್ಜಿ' (ಶಕ್ತಿ) ಎಂಬ ಪದವನ್ನು ಬಳಸುವುದರಲ್ಲಿ ಥಾಮಸ್ ಯಂಗ್ 1807ರಲ್ಲಿ ಮೊದಲಿಗರಾದರು.[೫] ಗಸ್ಟಾವ್-ಗಾಸ್ಪರ್ಡ್ ಕಾರಿಯಾಲಿಸ್ 'ಚಲನಶಕ್ತಿ' (ಕೈನೆಟಿಕ್ ಎನರ್ಜಿ) ಗೆ 1829ರಲ್ಲಿ ಆಧುನಿಕ ಅರ್ಥವನ್ನು ಒದಗಿಸಿದರು. 1853ರಲ್ಲಿ ವಿಲಿಯಮ್ ರಾಂಕೀನ್ 'ಅಂತಸ್ಥ ಶಕ್ತಿ' (ಪೊಟೆಂಷಿಯಲ್ ಎನರ್ಜಿ) ಎಂಬ ಪದವನ್ನು ರೂಪಿಸಿದರು. 'ಶಕ್ತಿಯೆನ್ನುವುದು ಒಂದು ವಸ್ತುವೇ (caloric), ಅಥವಾ, ಸಂವೇಗದಂತೆಯೇ ಸರಳವಾದ ಒಂದು ಭೌತಿಕ ಪರಿಮಾಣವೇ?' ಎಂಬುದರ ಬಗ್ಗೆ ಕೆಲ ವರ್ಷಗಳ ಕಾಲ ಚರ್ಚೆ ನಡೆದಿತ್ತು.
ವಿಲಿಯಮ್ ಥಾಮ್ಸನ್ (ಲಾರ್ಡ್ ಕೆಲ್ವಿನ್) ಈ ಎಲ್ಲ ನಿಯಮಗಳನ್ನು ಬೆರೆಸಿ ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ (ಥರ್ಮೊಡೈನಾಮಿಕ್ಸ್) ನಿಯಮವನ್ನು ಪ್ರತಿಪಾದಿಸಿದ. ಇದರಿಂದಾಗಿ, ರುಡಾಲ್ಫ್ ಕ್ಲಾಸಿಯಸ್, ಜೊಸಯ್ಯ ವಿಲರ್ಡ್ ಗಿಬ್ಸ್ ಮತ್ತು ವಾಲ್ಥರ್ ನೆರ್ನ್ಸ್ಟ್ ಮಂಡಿಸಿದ ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆಗಳನ್ನು ಬಳಸಿ ರಾಸಾಯನಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಬಗ್ಗೆ ವಿವರಣೆಗಳನ್ನು ನೀಡಲು ಸಾಧ್ಯವಾಯಿತು. ಜೊತೆಗೆ, ಕ್ಲಾಸಿಯಸ್ ಜಡೋಷ್ಣ (entropy=ಯಾಂತ್ರಿಕ ಬಳಕೆಗೆ ಅಲಭ್ಯವಾಗುವ ಉಷ್ಣ ಶಕ್ತಿ ಪ್ರಮಾಣ) ಪರಿಕಲ್ಪನೆಯ ಗಣಿತ ಸೂತ್ರವನ್ನು ರಚಿಸಲು ಇದು ಕಾರಣವಾಯಿತು. ಜೊಝೆಫ್ ಸ್ಟೆಫಾನ್ ವಿಕಿರಣ ಶಕ್ತಿಯ (ರೇಡಿಯಂಟ್ ಎನರ್ಜಿ) ನಿಯಮಗಳನ್ನು ಪರಿಚಯಿಸಲು ಸಹ ಸಾಧ್ಯವಾಯಿತು.
ಖ್ಯಾತ ಭೌತವಿಜ್ಞಾನ ಅಧ್ಯಾಪಕ ಮತ್ತು ನೊಬೆಲ್ ಪ್ರಶಸ್ತಿ ಪುರಸ್ಕೃತ ರಿಚರ್ಡ್ ಫೆಯ್ನ್ಮನ್ ೧೯೬೧ರಲ್ಲಿ ಕ್ಯಾಲಿಫೊರ್ನಿಯಾ ತಂತ್ರಜ್ಞಾನ ಸಂಸ್ಥೆಯ ಪದವಿಪೂರ್ವ ವಿದ್ಯಾರ್ಥಿಗಳಿಗೆ ಉಪನ್ಯಾಸ ನೀಡುತ್ತಾ, ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆಯ ಕುರಿತು ಹೀಗೆ ಹೇಳಿದರು:
There is a fact, or if you wish, a law, governing natural phenomena that are known to date. There is no known exception to this law; it is exact, so far we know. The law is called conservation of energy; it states that there is a certain quantity, which we call energy, that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity, which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.
— The Feynman Lectures on Physics[೬]
ಶಕ್ತಿಯ ಸಂರಕ್ಷಣೆಯ ನಿಯಮವು, ಶಕ್ತಿಗೆ ಸಂಯುಕ್ತವಾದ ಪ್ರಮಾಣ, ಅರ್ಥಾತ್ ಸಮಯದ ಸ್ಥಾನಾಂತರ ಚಲನಾ ಸಮರೂಪದ ನೇರ ಗಣಿತ ಫಲಶ್ರುತಿಯಾಗಿದೆ' ಎಂಬುದು ೧೯೧೮ರಿಂದಲೂ ತಿಳಿದಿರುವ ವಿಚಾರ. ಅರ್ಥಾತ್, ಭೌತವಿಜ್ಞಾನದ ನಿಯಮಗಳು 'ಸಮಯದ ಕ್ಷಣ'ಗಳ (=moment) ನಡುವಿನ ವ್ಯತ್ಯಾಸದ ಭಿನ್ನತೆಯನ್ನು ತೋರಿಸದ ಕಾರಣ ಶಕ್ತಿಯು ಸಂರಕ್ಷಿತವಾಗಿದೆ.
ವಿಶ್ವದ ಆದಿಯಿಂದಲೂ ವ್ಯಕ್ತವಾದ ಶಕ್ತಿಯ ವಿವಿಧ ಸ್ವರೂಪ[ಬದಲಾಯಿಸಿ]
ನೈಸರ್ಗಿಕ ವಿದ್ಯಮಾನಗಳನ್ನು ವಿವರಿಸಿ ಮತ್ತು ಮುಂಗಾಣುವುದರಲ್ಲಿ ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆ ಮತ್ತು ಅದರ ರೂಪಾಂತರಗಳು ಉಪಯುಕ್ತವಾಗಿವೆ. ಶಕ್ತಿಯ ರೂಪಾಂತರಗಳ ದಿಕ್ಕನ್ನು (ಯಾವ ರೀತಿಯ ಶಕ್ತಿ ಬೇರಾವ ರೀತಿಗೆ ರೂಪಾಂತರಗೊಳ್ಳುತ್ತದೆ) ಜಡೋಷ್ಣ (ಲಭ್ಯವಿರುವ ಎಲ್ಲ ರೀತಿಯಲ್ಲೂ ಸಮಾನವಾಗಿ ಪ್ರಸರಿಸಿರುವ ಶಕ್ತಿ) ಪರಿಗಣನೆಗಳ ಮೂಲಕ ವಿವರಿಸಲಾಗಿದೆ. ಕಾರ್ಯತಃ ಎಲ್ಲ ಶಕ್ತಿ ರೂಪಾಂತರಗಳಿಗೂ ಸಣ್ಣ ಪ್ರಮಾಣದಲ್ಲಿ ಅನುಮತಿಯಿದೆ. ಆದರೆ, ಶಕ್ತಿ ಅಥವಾ ವಸ್ತುವು ಸಾರಯುತ ರೂಪಗಳಿಗೆ ಅಥವಾ ಸಣ್ಣ ಜಾಗಗಳಿಗೆ ಹೋಗುವುದು ಸಂಖ್ಯಾಶಾಸ್ತ್ರ ರೀತ್ಯಾ ಅಸಂಭವವಾಗಿರುವುದರಿಂದ, ನಿರ್ದಿಷ್ಟ ದೊಡ್ಡ ಪ್ರಮಾಣದ ರೂಪಾಂತರಗಳಿಗೆ ಅನುಮತಿಯಿಲ್ಲ.
ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆಯು ವಿಜ್ಞಾನದ ಎಲ್ಲ ಶಾಖೆಗಳಲ್ಲಿಯೂ ವ್ಯಾಪಕವಾಗಿದೆ.
- ಜೀವ ವಿಜ್ಞಾನದಲ್ಲಿ, ಶಕ್ತಿ ಎಂಬುದು ಜೀವಗೋಳದಿಂದ ಹಿಡಿದು ಅತಿಸೂಕ್ಷ್ಮ ಜೀವಿಗಳವರೆಗೂ ಇರುವ ಎಲ್ಲಾ ಜೀವ ವ್ಯವಸ್ಥೆಗಳ ಲಕ್ಷಣವಾಗಿದೆ. ಜೀವಿಯೊಳಗೆ, ಜೀವಕೋಶ ಅಥವಾ ಅಂಗಕವು (=ಆರ್ಗನೆಲ್) ಬೆಳೆದು ಅಭಿವೃದ್ಧಿಯಾಗಲು ಶಕ್ತಿ ಅಗತ್ಯವಾಗಿ ಬೇಕು. ಶರ್ಕರ ಪಿಷ್ಟಗಳು (ಸಕ್ಕರೆಯೂ ಸೇರಿದಂತೆ) ಮತ್ತು ಕೊಬ್ಬುಗಳ (=ಲಿಪಿಡ್ಸ್) ಆಣ್ವಿಕ ರಚನೆಯಲ್ಲಿ ಜೀವಕೋಶಗಳು ಶೇಖರಿಸುವ ಈ ಅಂಶ ಆಮ್ಲಜನಕದೊಂದಿಗೆ ಪ್ರತಿಕ್ರಿಯಿಸಿದಾಗ ಶಕ್ತಿಯು ಹೊರಹೊಮ್ಮುತ್ತದೆ. ಮಾನವನ ದೃಷ್ಟಿಯಲ್ಲಿ ಹೇಳಬೇಕಾದರೆ, ಮಾನವ ಸಮಾನ (H-e) (ಮಾನವ ಶಕ್ತಿ ಪರಿವರ್ತನೆ) ಎನ್ನಲಾಗುತ್ತದೆ. ಇದರಂತೆ, ಮಾನವ ಶಕ್ತಿಯ ವೆಚ್ಚವು ದಿನಕ್ಕೆ 12,500kJ (kJ=ಕಿಲೊಜೌಲ್ಸ್) ಮತ್ತು 80 ವ್ಯಾಟ್ಗಳಷ್ಟು ಆಧಾರ ಚಯಾಪಚಯ ದರವೆಂದು ಊಹಿಸಿ) ನಿಗದಿತ ಶಕ್ತಿಯ ವೆಚ್ಚಕ್ಕೆ, ಮಾನವ ಚಯಾಪಚಯಕ್ಕೆ ಬೇಕಾದ ಸಂಬಂಧಿತ ಶಕ್ತಿಯ ಪ್ರಮಾಣವನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, 'ನಮ್ಮ ಶರೀರ ಸರಾಸರಿ 80 ವ್ಯಾಟ್ಗಳಷ್ಟು ಕಾರ್ಯ ನಡೆಸಿದರೆ, ಹತ್ತಿರುವ 100 ವ್ಯಾಟ್ ಬಲ್ಬ್ ಒಂದು 1.25 ಮಾನವ ಸಮಾನಗಳಲ್ಲಿ ನಡೆದಂತೆ' ಎಂದು ಭಾವಿಸಬಹುದು ((100 ÷ 80) i.e. 1.25 H-e). ಕೇವಲ ಕೆಲವೇ ಸೆಕೆಂಡುಗಳ ಅವಧಿಯ ಕಷ್ಟಕರ ಕೆಲಸಕ್ಕೆ, ವ್ಯಕ್ತಿಯೊಬ್ಬ ಸಾವಿರ ವ್ಯಾಟ್ಗಳಷ್ಟು ಶ್ರಮವನ್ನು ವ್ಯಯಿಸಬೇಕಾದೀತು - ಒಂದು ಅಶ್ವಶಕ್ತಿಯಲ್ಲೇ 746 ವ್ಯಾಟ್ಗೂ ಹಲವು ಪಟ್ಟು. ಕೆಲವೇ ನಿಮಿಷಗಳ ಕೆಲಸಕ್ಕೆ, ಸದೃಢ ಮನುಷ್ಯನೊಬ್ಬ ಬಹುಶಃ 1,000 ವ್ಯಾಟ್ಗಳಷ್ಟು ಶಕ್ತಿಯನ್ನು ಉತ್ಪಾದಿಸಬಹುದು. ಸುಮಾರು ಒಂದು ತಾಸಿನ ಚಟುವಟಿಕೆಗೆ, ಉತ್ಪಾದನೆಯು ಸುಮಾರು 300ರಷ್ಟಕ್ಕೆ ಇಳಿದರೆ, ಇಡೀ ದಿನ ನಡೆಯುವ ಚಟುವಟಿಕೆಗೆ 150 ವ್ಯಾಟ್ ಗರಿಷ್ಠ ಮಟ್ಟ ಆಗಬಹುದು.[೭] ಭೌತಿಕ ಮತ್ತು ಜೈವಿಕ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ ಶಕ್ತಿಯ ಪ್ರವಾಹವನ್ನು ಅರ್ಥೈಸಿಕೊಳ್ಳಲು ನೆರವಾಗುತ್ತದೆ. ಅದು ಶಕ್ತಿಯನ್ನು ಮಾನವ ಅಳತೆಗೋಲಿನ ಪ್ರಕಾರ ವಿವರಿಸಿ ಹೇಳುತ್ತದೆ ಮತ್ತು ನಿರ್ದಿಷ್ಟ ಶಕ್ತಿಯ ಬಳಕೆಯ 'ಸಂವೇದನೆ'ಯನ್ನೂ ನೀಡುತ್ತದೆ.[೮]
- ಭೂವಿಜ್ಞಾನದಲ್ಲಿ ಭೂಖಂಡ ಸರಿತ (= continental drift), ಪರ್ವತ ಶ್ರೇಣಿಗಳು, ಜ್ವಾಲಾಮುಖಿಗಳು ಮತ್ತು ಭೂಕಂಪಗಳು - ಇವೆಲ್ಲವೂ ಸಹ ಭೂಮಿಯ ಅಂತರಾಳದಲ್ಲಿ ನಡೆಯುವ ಶಕ್ತಿಯ ರೂಪಾಂತರಗಳ ಅರ್ಥದಲ್ಲಿ ವಿವರಿಸಬಹುದಾದ ವೈಜ್ಞಾನಿಕ ವಿಷಯಗಳಾಗಿವೆ.[೯] ಪವನ ಶಾಸ್ತ್ರಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಗಾಳಿ, ಮಳೆ, ಆಲಿಕಲ್ಲು, ಹಿಮ, ಮಿಂಚು, ಸುಂಟರಗಾಳಿ ಮತ್ತು ಚಂಡಮಾರುತ -ಈ ಎಲ್ಲ ಘಟನೆಗಳೂ ಸಹ ಭೂಮಿಯ ವಾಯುಮಂಡಲದ ಮೇಲೆ ಸೌರ ಶಕ್ತಿ ಬೀರುವಂತಹ ಶಕ್ತಿಯ ರೂಪಾಂತರಗಳು.
- ವಿಶ್ವವಿಜ್ಞಾನ ಮತ್ತು ಖಗೋಳ ವಿಜ್ಞಾನಗಳಲ್ಲಿ ನಕ್ಷತ್ರಗಳು, ನವ್ಯತಾರೆಗಳು (=ನೊವಾ), ಮಹಾನವ್ಯ ತಾರೆಗಳು (=ಸುಪರ್ನೋವಾ), ಕ್ವೇಸಾರ್ಗಳು ಮತ್ತು ಗ್ಯಾಮಾ ಕಿರಣ ಸಿಡಿತಗಳು - ಇವೆಲ್ಲ ಘಟನೆಗಳೂ ಸಹ ವಿಶ್ವದಲ್ಲಿ ಸಂಭವಿಸುವ ದ್ರವ್ಯರಾಶಿಯ ಅತಿ ಹೆಚ್ಚಿನ ಉತ್ಪಾದನೆಯ ಶಕ್ತಿ ರೂಪಾಂತರಗಳಾಗಿವೆ. ಸೌರ ಚಟುವಟಿಕೆಗಳೂ ಸೇರಿ ಎಲ್ಲ ನಾಕ್ಷತ್ರಿಕ (=ಸ್ಟೆಲಾರ್) ಘಟನೆಗಳಿಗೆ ವಿವಿಧ ರೀತಿಯ ಶಕ್ತಿ ರೂಪಾಂತರಗಳು ಕಾರಣವಾಗಿವೆ. ಖಾಗೋಳಿಕ ವಸ್ತುಗಳಾದ ನಕ್ಷತ್ರಗಳು, ಕಪ್ಪು ಕುಳಿಗಳು (=ಬ್ಲ್ಯಾಕ್ ಹೋಲ್), ಇತ್ಯಾದಿ ಸೇರಿದಂತೆ, ವಿವಿಧ ವರ್ಗಗಳೊಳಗೆ (ಸಾಮಾನ್ಯವಾಗಿ ಆಣ್ವಿಕ ಜಲಜನಕ) ದ್ರವ್ಯರಾಶಿಯ ಗುರುತ್ವದ ಕುಸಿತದಿಂದ; ಅಥವಾ ಜಲಜನಕದಂಥ ಲಘು ಪರಮಾಣು ಸಮ್ಮಿಲನದಿಂದ, ಉಂಟಾಗುವ ರೂಪಾಂತರಗಳಲ್ಲಿ ಶಕ್ತಿಯ ಉತ್ಪಾದನೆಯಾಗುತ್ತದೆ.
ಕಾಲಾಂತರದಲ್ಲಿ ವಿಶ್ವದಲ್ಲಿ ಸಂಭವಿಸುವ ಶಕ್ತಿಯ ರೂಪಾಂತರಗಳು ಹಲವು ವಿಧಗಳ ಅಂತಸ್ಥ ಶಕ್ತಿಯ ಮೂಲಕ ನಿರೂಪಿತವಾಗುತ್ತದೆ. 'ಬಿಗ್ ಬ್ಯಾಂಗ್' ಸಂಭವಿಸಿದಾಗಿಂದಲೂ ಈ ಅಂತಸ್ಥ ಶಕ್ತಿಯು ಲಭ್ಯವಿದ್ದು, ಪ್ರಚೋದನೆಯಾದಾಗ ಚಲನ ಶಕ್ತಿ ಅಥವಾ ವಿಕಿರಣ ಶಕ್ತಿ ಸೇರಿದಂತೆ ಹೆಚ್ಚು ಸಕ್ರಿಯ ಶಕ್ತಿಗಳಾಗಿ ರೂಪಾಂತರಗೊಳ್ಳುತ್ತದೆ.
ಇಂತಹ ಪ್ರಕ್ರಿಯೆಗಳ ಚಿರಪರಿಚಿತ ಉದಾಹರಣೆಗಳಲ್ಲಿ ಬೈಜಿಕ ಕ್ಷಯವೂ ಒಂದು. ಬೈಜಿಕ ಕೇಂದ್ರ ಸಂಶ್ಲೇಷಣೆಯ (=ನುಕ್ಲಿಯೊಸಿನ್ಥೆಸಿಸ್) ಮೂಲಕ ಯುರೇನಿಯಮ್ ಮತ್ತು ಥೋರಿಯಮ್ನಂತಹ ಭಾರದ ಸಮಸ್ಥಾನಿಗಳಲ್ಲಿ (=ಐಸೊಟೊಪ್) ಮೂಲತಃ ಶೇಖರಿಸಲ್ಪಟ್ಟ ಶಕ್ತಿಯು ಬಿಡುಗಡೆಯಾಗುವ ಪ್ರಕ್ರಿಯೆಗೆ 'ಬೈಜಿಕ ಕ್ಷಯ' ಎನ್ನಲಾಗುತ್ತದೆ. ಮಹಾನವ್ಯ ತಾರೆಯೊಂದರ ಪತನದಿಂದಾಗಿ ಬಿಡುಗಡೆಯಾಗುವ ಗುರುತ್ವದ ಅಂತಸ್ಥಶಕ್ತಿಯನ್ನು ಬಳಸಿ, ಭಾರದ ಧಾತುಗಳ ಸೃಷ್ಟಿಯಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ಶೇಖರಿಸುತ್ತದೆ. ಆನಂತರ ಇವುಗಳನ್ನು ಸೌರ ಮಂಡಲ ಮತ್ತು ಭೂಮಿಯಲ್ಲಿ ಒಂದಾಗಿಸಲಾಗುತ್ತದೆ. ಈ ಪ್ರಕ್ರಿಯೆಗೆ 'ಬೈಜಿಕ ಕೇಂದ್ರ ಸಂಶ್ಲೇಷಣೆ' ಎನ್ನಲಾಗುತ್ತದೆ. ಪರಮಾಣು ವಿದಳನ ಬಾಂಬ್ಗಳಲ್ಲಿ ಈ ಶಕ್ತಿಯು ಪ್ರಚೋದಿತವಾಗಿ ಬಿಡುಗಡೆಯಾಗುತ್ತದೆ. ನಿಧಾನಗತಿಯ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ, ಭೂ ಮಧ್ಯದಲ್ಲಿರುವ ಅಣುಗಳ ಬೈಜಿಕ ಕ್ಷಯದಿಂದ ಬಿಡುಗಡೆಯಾಗುವ ಉಷ್ಣವು ಪರ್ವತೋತ್ಪತ್ತಿಗೆ (=ಆರೊಜೆನೆಸಿಸ್) ಕಾರಣವಾಗುತ್ತದೆ. ಈ ನಿಧಾನಗತಿಯ ಮೇಲಕ್ಕೆತ್ತುವ ಪ್ರಕ್ರಿಯೆಯು, ಉಷ್ಣ ಶಕ್ತಿಯ ಒಂದು ಬಗೆಯ ಗುರುತ್ವದ ಅಂತಸ್ಥಶಕ್ತಿಯ ಶೇಖರಣೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಭೂಕುಸಿತವಾದಾಗ ಈ ಉಷ್ಣ ಶಕ್ತಿಯು ಸಕ್ರಿಯ ಚಲನಶಕ್ತಿಯಾಗಿ ಬಿಡುಗಡೆಯಾಗುತ್ತದೆ. ಬಂಡೆಗಳಲ್ಲಿ ಶೇಖರಣೆಯಾಗಿರುವ ಸ್ಥಿತಿಸ್ಥಾಪಕ ಅಂತಸ್ಥಶಕ್ತಿಯನ್ನು ಭೂಕಂಪಗಳು ಬಿಡುಗಡೆಗೊಳಿಸುತ್ತವೆ. ವಿಕಿರಣಶೀಲ ಉಷ್ಣ ಮೂಲಗಳಿಂದ ಈ ಶಕ್ತಿ ಸಂಚಯನವಾಗಿರುತ್ತದೆ. ಹೀಗಾಗಿ, ಭೂಮಿಯ ಗುರುತ್ವ ಕ್ಷೇತ್ರದಲ್ಲಿ ಅಂತಸ್ಥ ಶಕ್ತಿಯಾಗಿ, ಅಥವಾ, ಬಂಡೆಗಳಲ್ಲಿ ಯಾಂತ್ರಿಕ ಅಂತಸ್ಥ ಶಕ್ತಿಯಾಗಿ ಶೇಖರಣೆಗೊಂಡಿರುವ ಶಕ್ತಿಯನ್ನು ಭೂಕುಸಿತಗಳು ಮತ್ತು ಭೂಕಂಪಗಳು ಬಿಡುಗಡೆಗೊಳಿಸುತ್ತವೆ ಎಂಬುದು ಈ ತನಕದ ತಿಳಿವಳಿಕೆಯಾಗಿದೆ. ಆದರೆ ಇದಕ್ಕೂ ಮುಂಚೆ, ಎಂದೋ ಪತನಗೊಂಡ ನಕ್ಷತ್ರಗಳಿಂದ ಸೃಷ್ಟಿಯಾದ ಈ ಭಾರದ ಅಣುಗಳಲ್ಲಿ ಶೇಖರಣೆಯಾದ ಶಕ್ತಿಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ.
ವಿಶ್ವದ ಉದ್ಭವವಾದಾಗಿನಿಂದಲೂ ಆರಂಭಗೊಂಡ ಅದೇ ರೀತಿಯ ರೂಪಾಂತರಗಳ ಸರಣಿಯ ಇನ್ನೊಂದು ಉದಾಹರಣೆಯಲ್ಲಿ ಸೂರ್ಯನಲ್ಲಿ ಸಂಭವಿಸುವ ಜಲಜನಕದ ಬೈಜಿಕ ಸಮ್ಮಿಳನವು, 'ಬಿಗ್ ಬ್ಯಾಂಗ್' ಸಮಯದಲ್ಲಿ ಸೃಷ್ಟಿಯಾಗಿ ಶೇಖರಣೆಯಾದ ಅಂತಸ್ಥ ಶಕ್ತಿಯ ಬಿಡುಗಡೆಗೆ ಕಾರಣವಾಯಿತು. ಸಿದ್ಧಾಂತದ ಪ್ರಕಾರ, ಆ ಸಮಯದಲ್ಲಿ ಬಾಹ್ಯಾಕಾಶವು ವಿಸ್ತರಿಸಿತು. ಇದರಿಂದಾಗಿ ಭಾರದ ಧಾತುಗಳೊಂದಿಗೆ ಜಲಜನಕದ ಸಂಪೂರ್ಣ ಸಮ್ಮಿಳನ ಸಾಧ್ಯವಾಗದಷ್ಟು ಅತಿ ವೇಗವಾಗಿ ವಿಶ್ವವು ತಂಪಾಯಿತು. ಜಲಜನಕವು ಸಮ್ಮಿಳನದ ಮೂಲಕ ಬಿಡುಗಡೆಯಾಗಬಲ್ಲ ಅಂತಸ್ಥಶಕ್ತಿಯ ಸಂಗ್ರಹಣೆಯ ಪ್ರತೀಕವಾಗಿದೆ. ನಕ್ಷತ್ರಗಳು ಉದಯಿಸಿದಾಗ ಜಲಜನಕದ ಮೋಡಗಳು ಕುಸಿದು ಇದರಿಂದ ಉಷ್ಣ ಮತ್ತು ಒತ್ತಡವು ಸಮ್ಮಿಳನ ಪ್ರಕ್ರಿಯೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ. ಸಮ್ಮಿಳನಗೊಂಡ ಶಕ್ತಿಯ ಕೆಲವಂಶ ಸೂರ್ಯನ ಬೆಳಕಾಗಿ ರೂಪಾಂತರಗೊಳ್ಳುತ್ತದೆ. ಸೂರ್ಯನ ಬೆಳಕು ಭೂಮಿಗೆ ಬಡಿದಾಗ ಪುನಃ ಗುರುತ್ವ ಅಂತಸ್ಥ ಶಕ್ತಿಯಾಗಿ ಶೇಖರಣೆಯಾಗುತ್ತದೆ. (ಉದಾಹರಣೆಗೆ) ಸಾಗರಗಳಿಂದ ನೀರು ಆವಿಯಾಗಿ ಪರ್ವತಗಳ ಮೇಲೆ ಸಂಗ್ರಹವಾಗುತ್ತದೆ (ಆನಂತರ ಜಲಾಶಯಗಳಿಂದ ಬಿಡುಗಡೆಯಾದಾಗ ನೀರನ್ನು ಬಳಸಿ ಜಲಚಕ್ರ/ವಿದ್ಯುತ್ ಉತ್ಪಾದನಾ ಯಂತ್ರ(ಜನರೇಟರ್) ಚಲಾಯಿಸಿ ವಿದ್ಯುತ್ ಉತ್ಪಾದಿಸಬಹುದು). ಹವಾಮಾನ ಘಟನೆಗಳಿಗೆ ಸೂರ್ಯನ ಬೆಳಕು ಕಾರಣವಾಗುವುದರ ಜೊತೆಗೆ ಜ್ವಾಲಾಮುಖಿಯ ಅನಾಹುತಗಳಿಂದ ಪಾರು ಮಾಡುತ್ತದೆ. ಚಂಡಮಾರುತವೆಂಬುದು ಸೌರ-ಸಂಬಂಧೀ ಹವಾಮಾನದ ಒಂದು ವಿದ್ಯಮಾನ. ಹಲವು ತಿಂಗಳುಗಳ ಕಾಲ ಬೆಚ್ಚಗಾದ, ವಿಶಾಲವೂ ಅಸ್ಥಿರವೂ ಆದ ಸಾಗರಗಳು ಉಷ್ಣ ಶಕ್ತಿಯ ಕೆಲವಂಶವನ್ನು ಇದ್ದಕ್ಕಿದ್ದಂತೆ ಹೊರಸೂಸುತ್ತವೆ. ಇದರ ಪರಿಣಾಮವಾಗಿ ಕೆಲವು ದಿನಗಳ ಕಾಲ ಪ್ರಚಂಡ ಚಲನೆಯುಳ್ಳ ಬಿರುಸಾದ ಹವೆ ಹೊರಹೊಮ್ಮುತ್ತದೆ. ಕಾರ್ಬೊಹೈಡ್ರೇಟ್, ಕೊಬ್ಬು ಮತ್ತು ಆಮ್ಲಜನಕದ ದಹನಶೀಲ ಸಂಯುಕ್ತಗಳಾಗಿ ಇಂಗಾಲ ಡಯಾಕ್ಸೈಡ್ ಮತ್ತು ನೀರು ಪರಿವರ್ತನೆಯಾದಾಗ ಗಿಡಗಳು ಸೂರ್ಯನ ಬೆಳಕನ್ನು ರಾಸಾಯನಿಕ ಅಂತಸ್ಥಶಕ್ತಿಯ ರೂಪದಲ್ಲಿ ಗ್ರಹಿಸುತ್ತವೆ. ಇದ್ದಕ್ಕಿದ್ದಂತೆ ಸಣ್ಣ ಕಿಡಿಯಿಂದ ಉಷ್ಣ ಮತ್ತು ಬೆಳಕಿನ ರೂಪದಲ್ಲಿ ಈ ಶಕ್ತಿಯ ಬಿಡುಗಡೆಯಾಗಿ ಕಾಳ್ಗಿಚ್ಚಿಗೆ ಕಾರಣವಾಗಬಹುದು. ಅಥವಾ, ಮನುಷ್ಯರು ಮತ್ತು ಪ್ರಾಣಿಗಳಲ್ಲಿ ಚಯಾಪಚಯಕ್ಕಾಗಿ ಶಕ್ತಿಯು ನಿಧಾನವಾಗಿ ಲಭ್ಯವಾಗಬಲ್ಲದು. ಕಿಣ್ವಗಳ ಕ್ರಿಯೆಯಿಂದ ಅಪಚಯವುಂಟಾಗುತ್ತದೆ. ಈ ಎಲ್ಲ ರೂಪಾಂತರ ಸರಣಿಯುದ್ದಕ್ಕೂ, ಮಹಾಸ್ಫೋಟ ಸಮಯದಲ್ಲಿ ಸಂಗ್ರಹವಾದ ಅಂತಸ್ಥಶಕ್ತಿಯು ಆನಂತರ ಮಧ್ಯವರ್ತಿ ಘಟನಾವಳಿಗಳ ಮೂಲಕ ಬಿಡುಗಡೆಯಾಗುತ್ತದೆ. ಕೆಲವೊಮ್ಮೆ ಬಿಡುಗಡೆಗಳ ನಡುವೆ ಕಾಲಾಂತರದಲ್ಲಿ ಇನ್ನಷ್ಟು ಸಕ್ರಿಯ ಶಕ್ತಿಯಾಗಿ ವಿವಿಧ ರೀತಿಗಳಲ್ಲಿ ಶೇಖರಣೆಯಾಗುತ್ತದೆ. ಈ ಎಲ್ಲ ಘಟನೆಗಳಲ್ಲಿಯೂ ಸಹ, ಉಷ್ಣವೂ ಸೇರಿದಂತೆ ಒಂದು ಬಗೆಯ ಶಕ್ತಿಯು ಬೇರೆ ಬೇರೆ ವಿಧಗಳಿಗೆ ಪರಿವರ್ತಿತವಾಗುತ್ತದೆ.
ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆಯ ಅನ್ವಯಗಳು[ಬದಲಾಯಿಸಿ]
ಶಕ್ತಿಯು ಕಟ್ಟುನಿಟ್ಟಾದ ಜಾಗತಿಕ ಸಂರಕ್ಷಣಾ ನಿಯಮಕ್ಕೆ ಒಳಪಟ್ಟಿದೆ. ಅರ್ಥಾತ್, ಸಮಯದ ಮೇಲೆ ಸ್ಪಷ್ಟವಾಗಿ ಅವಲಂಬಿಸದ ಪರಸ್ಪರ ಕ್ರಿಯೆಯುಳ್ಳ ಕಣಗಳ ವ್ಯವಸ್ಥೆಯ ಶಕ್ತಿಯನ್ನು ಅಳತೆ ಮಾಡಿ ನೋಡಿದರೆ, ವ್ಯವಸ್ಥೆಯ ಒಟ್ಟು ಶಕ್ತಿಯು ಯಾವಾಗಲೂ ಒಂದೇ ಸಮನಾಗಿರುತ್ತದೆ.[೧೦]
- ವ್ಯವಸ್ಥೆಯೊಂದರ ಒಟ್ಟು ಶಕ್ತಿಯನ್ನು ವಿವಿಧ ರೀತಿಗಳಲ್ಲಿ ವಿಭಜಿಸಿ ವರ್ಗೀಕರಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ, (ಕೇವಲ ನಿರ್ದೇಶಾಂಕಗಳ ಫಲನವಾಗಿರುವ) ಅಂತಸ್ಥ ಶಕ್ತಿಯನ್ನು, (ಕೇವಲ ನಿರ್ದೇಶಾಂಕ ಸಮಯ ವಿಕಲಜನ್ಯದ ಫಲನವಾಗಿರುವ) ಚಲನಶಕ್ತಿಯಿಂದ ಪ್ರತ್ಯೇಕವಾಗಿ ಗುರುತಿಸಲು ಕೆಲವೊಮ್ಮೆ ಅನುಕೂಲಕರ. ಗುರುತ್ವ ಶಕ್ತಿ, ವಿದ್ಯುತ್ ಶಕ್ತಿ, ಶಾಖೋತ್ಪನ್ನ ಶಕ್ತಿ ಮತ್ತು ಶಕ್ತಿಯ ಇತರೆ ರೂಪಗಳ ನಡುವೆಯೂ ಸಹ ಭಿನ್ನತೆ ಗುರುತಿಸುವುದು ಅನುಕೂಲಕರವಾಗಿದೆ. ಈ ವರ್ಗೀಕರಣಗಳು ಒಂದರ ಮೇಲೊಂದು ಅತಿವ್ಯಾಪಿಸುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಶಾಖೋತ್ಪನ್ನ ಶಕ್ತಿಯು ಸಾಮಾನ್ಯವಾಗಿ ಅಂತಸ್ಥ ಮತ್ತು ಚಲನಶಕ್ತಿಗಳೆರಡರ ಅಂಶವನ್ನೂ ಹೊಂದಿರುತ್ತದೆ.
- ಶಕ್ತಿಯ ವರ್ಗಾವಣೆ ಯು ವಿವಿಧ ರೂಪಗಳನ್ನು ತಳೆಯಬಹುದು. ಚಿರಪರಿಚಿತ ಉದಾಹರಣೆಗಳಲ್ಲಿ ಕಾರ್ಯ, ಶಾಖದ ಹರಿವು ಮತ್ತು ಕೆಳಗೆ ಚರ್ಚಿಸಿದಂತೆ 'ಅಭಿವಹನ' (=ವಾಯುಮಂಡಲದಲ್ಲಿ ಗಾಳಿಯ ಅಡ್ಡ ಚಲನೆಯಿಂದ ತಾಪ, ಒತ್ತಡ, ಮೊದಲಾದವುಗಳ ಸಾಗಣೆ) ಸೇರಿವೆ.
- ಭೌತಶಾಸ್ತ್ರದ ಹೊರಗೂ, ಶಕ್ತಿ ಎಂಬ ಪದವನ್ನು ವಿವಿಧ ರೀತಿಯಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ. ಇದರಿಂದಾಗಿ ನಿರ್ದಿಷ್ಟಾರ್ಥದಿಂದ ಅದು ದೂರ ಉಳಿಯುತ್ತದೆ ಮತ್ತು ಶಿಥಿಲಾರ್ಥಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ. ಆಡುಮಾತಿನ ಪದ ಮತ್ತು ತಾಂತ್ರಿಕ ಪರಿಭಾಷೆ - ಒಂದಕ್ಕೊಂದು ಪೂರಕವಾಗಿಲ್ಲ. ಉದಾಹರಣೆಗೆ, ಪ್ಲೀಸ್ ಕಂಸರ್ವ್ ಎನರ್ಜಿ (=ದಯಮಾಡಿ ಶಕ್ತಿಯನ್ನು ಸಂರಕ್ಷಿಸಿ) ಎಂಬ ಸಾರ್ವಜನಿಕ ಸೇವಾ ಸೂಚನೆಯಲ್ಲಿ ಕಂಸರ್ವೇಷನ್ ಮತ್ತು ಎನರ್ಜಿ ಎಂಬ ಆಡು ಮಾತಿನ ಪದಗಳು ಸೂಚನೆಗೆ ಸಂಬಂಧಿಸಿದ ತನ್ನ ಸಾಂದರ್ಭಿಕ ಅರ್ಥ ಪಡೆಯುತ್ತದೆ, ಆದರೆ 'ಕಂಸರ್ವೇಷನ್' ಮತ್ತು 'ಎನರ್ಜಿ' ಪದಗಳ ತಾಂತ್ರಿಕ ಕಲ್ಪನೆಗೂ ಸೂಚನೆಯಲ್ಲಿ ಅವು ಪಡೆದುಕೊಂಡ ಅರ್ಥಕ್ಕೂ ಅಪಾರ ಅಂತರವಿದೆ. (ಶಕ್ತಿ ಸಂರಕ್ಷಣಾ ನಿಯಮದಲ್ಲಿ ಬಳಸಿದಂತೆ).[೧೧]
ಅಭಿಜಾತ ಭೌತವಿಜ್ಞಾನದಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ಅದಿಶ(=ದಿಕ್ಕಿಲ್ಲದ ಆದರೆ ಪರಿಮಾಣ ಇರುವ) ಪ್ರಮಾಣವೆಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ. ಇದು ಸಮಯಕ್ಕೆ ಸ್ವೀಕೃತ ಸಂಯುಕ್ತವಾಗಿದೆ. ವಿಶೇಷ ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಶಕ್ತಿಯು ಅದಿಶ ಪ್ರಮಾಣವಾಗಿದೆ (ಇದು ಲೊರೆಂಟ್ಜ್ ಅದಿಶ ಪ್ರಮಾಣವಲ್ಲ ಆದರೆ, ಶಕ್ತಿ-ಸಂವೇಗ 4-ಸದಿಶದ (=4-ವೆಕ್ಟರ್) ಕಾಲದ ಘಟಕವಾಗಿದೆ).[೧೨] ಆರ್ಥಾತ್ ಆಕಾಶದ ಪರಿಭ್ರಮಣೆಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಶಕ್ತಿಯು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ, ಆದರೆ ದೇಶ-ಕಾಲವೆಂಬ ಚತುರಾಯಾಮದ ಕಲ್ಪನೆಯ ಪರಿಭ್ರಮಣೆಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಶಕ್ತಿಯು ಸ್ಥಿರವಾಗಿರುವುದಿಲ್ಲ.
ಶಕ್ತಿಯ ವರ್ಗಾವಣೆ[ಬದಲಾಯಿಸಿ]
ಶಕ್ತಿಯು ಕಟ್ಟುನಿಟ್ಟಾಗಿ ಸಂರಕ್ಷಿತವಾಗಿರುವುದರಿಂದ ಮತ್ತು ಸ್ಥಳೀಯವಾಗಿಯೂ ಸಂರಕ್ಷಿತವಾಗಿರುವುದರಿಂದ (ವ್ಯಾಖ್ಯಾನಿಸಬಹುದಾದಲ್ಲೆಲ್ಲಾ), ಶಕ್ತಿಯ ವ್ಯಾಖ್ಯಾನದಂತೆ, ವ್ಯವಸ್ಥೆಗಳು ಮತ್ತು ಅವಕ್ಕೆ ಹೊಂದಿಕೊಂಡಿರುವ ಪ್ರದೇಶಗಳ ನಡುವಿನ ಶಕ್ತಿಯ ವರ್ಗಾವಣೆಯು ಕಾರ್ಯವಾಗಿರುತ್ತದೆ. ಯಾಂತ್ರಿಕ ಕಾರ್ಯ ಇದಕ್ಕೊಂದು ಚಿರಪರಿಚಿತ ಉದಾಹರಣೆ. ಸರಳ ಪ್ರಕರಣಗಳಲ್ಲಿ ಇದನ್ನು ಕೆಳಕಂಡಂತೆ ಬರೆಯಲಾಗುತ್ತದೆ:
- (1)
(ಬೇರಾವುದೇ ಶಕ್ತಿ-ವರ್ಗಾವಣಾ ಪ್ರಕ್ರಿಯೆಗಳು ಒಳಗೊಳ್ಳದಿದ್ದಲ್ಲಿ). E = ವರ್ಗಾವಣೆಯಾದ ಶಕ್ತಿಯ ಮೊತ್ತ; =ವ್ಯವಸ್ಥೆ ಮೇಲೆ ನಡೆಸಲಾದ ಕಾರ್ಯ.
ಹೆಚ್ಚು ಸಾಮಾನ್ಯವಾಗಿ, ಶಕ್ತಿಯ ವರ್ಗಾವಣೆಯನ್ನು ಎರಡು ವರ್ಗಗಳಾಗಿ ವಿಭಜಿಸಬಹುದು:
- (2)
ಇದರಲ್ಲಿ ಎಂಬುದು ವ್ಯವಸ್ಥೆಯೊಳಗೆ ಹರಿಯುವ ಶಾಖ.
ವಿವೃತ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಇತರೆ ರೀತಿಯಲ್ಲೂ ಶಕ್ತಿ ಆಯ ವ್ಯಯ ಎರಡೂ ಸಂಭವಿಸುತ್ತದೆ. ರಾಸಾಯನಿಕ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ, ವಿವಿಧ ಸಮರ್ಥ ರಾಸಾಯನಿಕ ವಸ್ತುಗಳನ್ನು ವ್ಯವಸ್ಥೆಯೊಂದಕ್ಕೆ ಸೇರಿಸುವುದರ ಮೂಲಕ ಆ ವ್ಯವಸ್ಥೆಗೆ ಶಕ್ತಿಯನ್ನು ತುಂಬಬಹುದು. ಆನಂತರ ಈ ರಾಸಾಯನಿಕಗಳನ್ನು ಹೊರಗೆಳೆಯಬಹುದು. (ಮೋಟಾರು ವಾಹನವೊಂದಕ್ಕೆ ಇಂಧನವನ್ನು ತುಂಬಿದಾಗ ಹೆಚ್ಚುವರಿಯಾದ ಕಾರ್ಯ ಅಥವಾ ಶಾಖವನ್ನು ಸೇರಿಸದೆಯೇ ಶಕ್ತಿಯ ಲಾಭವನ್ನು ಪಡೆಯುವುದು ಇವೆರಡೂ ಪ್ರಕ್ರಿಯೆಗಳಿಗೆ ಉದಾಹರಣೆಯಾಗಿದೆ.) ಇದೇ ರೀತಿ ಗಡಿಯಾರವೊಂದಕ್ಕೆ ಕೀಲಿ ಕೊಡುವುದು ಯಾಂತ್ರಿಕ ವ್ಯವಸ್ಥೆಗೆ ಶಕ್ತಿ ತುಂಬುವುದಕ್ಕೊಂದು ಸೂಕ್ತ ನಿದರ್ಶನ. ಮೇಲಿನ ಸಮೀಕರಣಕ್ಕೆ ಈ ಪದಗಳನ್ನು ಸೇರಿಸಬಹುದು; ಅಥವಾ, 'ಶಕ್ತಿ ಜೋಡಣಾ ಪರಿಮಾಣ ' ಎಂಬ ಪ್ರಮಾಣದೊಳಗೆ ಸಾಮಾನ್ಯವಾಗಿ ಅಂತರ್ಗತಗೊಳಿಸಬಹುದು. ನಿಯಂತ್ರಣಾ ಪ್ರಮಾಣ ಅಥವಾ ವ್ಯವಸ್ಥಾ ಪ್ರಮಾಣದ ಮೇಲೆ ಒಯ್ಯಲಾದ ಯಾವುದೇ ರೀತಿಯ ಶಕ್ತಿಯನ್ನು 'E' ಪ್ರತಿನಿಧಿಸುತ್ತೆ. ಮೇಲಿರುವ ಉದಾಹರಣೆಗಳಂತೆ ಇನ್ನಷ್ಟನ್ನು ಊಹಿಸಬಹುದು (ಉದಾಹರಣೆಗೆ, ಕಣಗಳ (ಪಾರ್ಟಿಕಲ್ಸ್) ಪ್ರವಾಹವು ವ್ಯವಸ್ಥೆಯೊಳಗೆ ಪ್ರವೇಶಿಸುತ್ತಿರುವುದು, ಅಥವಾ ಲೇಸರ್ ವಿಕಿರಣದಿಂದ ಸೂಸುವ ಶಕ್ತಿಯು (ಶಾಸ್ತ್ರೀಯ ಅರ್ಥದಲ್ಲಿ 'ಏನನ್ನೂ ಮಾಡದೇ' ಅಥವಾ 'ಶಾಖ ಸೇರಿಸದೇ') ವ್ಯವಸ್ಥೆಯ ಶಕ್ತಿ ಮೂಲಕ್ಕೆ ಸೇರಿಸುವುದು).
- (3)
ಈ ಸಾಮಾನ್ಯ ಸಮೀಕರಣದಲ್ಲಿ E ಇತರೆ ಹೆಚ್ಚುವರಿ ಅಭಿವಹನ ಶಕ್ತಿ ಪರಿಮಾಣಗಳನ್ನು ನಿರೂಪಿಸುತ್ತದೆ (ಇದು ವ್ಯವಸ್ಥೆಯ ಮೇಲಿನ ಕಾರ್ಯದ ವ್ಯಾಪ್ತಿಯ ಹೊರಗಿರುವ ಅಥವಾ ಅದಕ್ಕೆ ಸೇರಿಸದ ಶಾಖದ ಪರಿಮಾಣವೂ ಆಗಿರುತ್ತದೆ).
ಅಂತಸ್ಥಶಕ್ತಿಯಿಂದ () ಚಲನಾ ಶಕ್ತಿಗೆ () ಮತ್ತು ಚಲನಾ ಶಕ್ತಿಯಿಂದ ಪುನಃ ಅಂತಸ್ಥಶಕ್ತಿಗೆ ನಿರಂತರವಾಗಿ ಶಕ್ತಿ ಹರಿದಾಡುತ್ತಿರುತ್ತದೆ. ಇದಕ್ಕೆ 'ಶಕ್ತಿಯ ಸಂರಕ್ಷಣೆ' ಎನ್ನಲಾಗುತ್ತದೆ. ಈ ಸಂವೃತ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ಸೃಷ್ಟಿಸುವುದು ಅಥವಾ ನಾಶಪಡಿಸುವುದು ಎರಡೂ ಅಸಾಧ್ಯ. ಹೀಗಾಗಿ ಆರಂಭಿಕ ಶಕ್ತಿ ಮತ್ತು ಅಂತಿಮ ಶಕ್ತಿಯು ಪರಸ್ಪರ ಸಮಾನಾಗಿರುತ್ತವೆ. ಇದನ್ನು ಕೆಳಕಂಡ ಸಮೀಕರಣದ ಮೂಲಕ ನಿರೂಪಿಸಬಹುದಾಗಿದೆ:
(ದ್ರವ್ಯರಾಶಿ X ಗುರುತ್ವದ ಕಾರಣ ವೇಗ X ಎತ್ತರ) ಮತ್ತು (ದ್ರವ್ಯರಾಶಿಯ ಅರ್ಧಭಾಗ X ವೇಗದ ವರ್ಗ) ಎಂದು ಸಮೀಕರಣವನ್ನು ಸರಳೀಕರಿಸಬಹುದು. -ಇವುಗಳನ್ನು ಕೂಡಿಸಿದರೆ ಶಕ್ತಿಯ ಒಟ್ಟು ಮೊತ್ತ ದೊರೆಯುತ್ತದೆ.
ಶಕ್ತಿ ಮತ್ತು ಚಲನೆಯ ನಿಯಮಗಳು[ಬದಲಾಯಿಸಿ]
ಶಕ್ತಿ ಎಂಬುದು ಸಂರಕ್ಷಿತ ಪ್ರಮಾಣವಾದ್ದರಿಂದ ಅಭಿಜಾತ ಯಂತ್ರ ವಿಜ್ಞಾನದಲ್ಲಿ ಕಾಲ್ಪನಿಕವಾಗಿಯೂ ಮತ್ತು ಗಣಿತೀಯ ದೃಷ್ಟಿಯಿಂದಲೂ ಉಪಯುಕ್ತ ಗುಣಲಕ್ಷಣವಾಗಿದೆ.
ಹ್ಯಾಮಿಲ್ಟೋನಿಯನ್[ಬದಲಾಯಿಸಿ]
ವ್ಯವಸ್ಥೆಯಲ್ಲಿನ ಶಕ್ತಿಯ ಒಟ್ಟು ಮೊತ್ತಕ್ಕೆ ಕೆಲವೊಮ್ಮೆ ಹ್ಯಾಮಿಲ್ಟೋನಿಯನ್ ಎನ್ನಲಾಗುತ್ತದೆ. ಹೀಗೆನ್ನುವುದು ವಿಲಿಯಮ್ ರೊವಾನ್ ಹ್ಯಾಮಿಲ್ಟನ್ ಹೆಸರಿನ ಮೇಲೆ. ಬಹಳ ಜಟಿಲವೂ ಅಥವಾ ಆಮೂರ್ತವೂ ಆದಂಥ ವ್ಯವಸ್ಥೆಯ ಚಲನೆಯ ಅಭಿಜಾತ ಸಮೀಕರಣಗಳನ್ನು ಸಹಾ ಹ್ಯಾಮಿಲ್ಟೋನಿಯನ್ ಲೆಕ್ಕಾಚಾರದಲ್ಲಿ ಬರೆಯಬಹುದು. ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತದಿಂದ ವಿವರಿಸಿಲ್ಲದ ಕ್ವಾಂಟಮ್ ಯಂತ್ರವಿಜ್ಞಾನದಲ್ಲಿ ಈ ಅಭಿಜಾತ ಸಮೀಕರಣಗಳು ನೇರ ಸಾದೃಶ್ಯಗಳನ್ನು ಹೊಂದಿವೆ.[೧೩]
ಲ್ಯಾಗ್ರಾಂಜಿಯನ್[ಬದಲಾಯಿಸಿ]
ಲ್ಯಾಗ್ರಾಂಜಿಯನ್ ಎಂಬುದು ಶಕ್ತಿಗೆ ಸಂಬಂಧಿತ ಇನ್ನೊಂದು ಪರಿಕಲ್ಪನೆ (ಇದು ಜೊಸೆಫ್ ಲೂಯಿಸ್ ಲ್ಯಾಗ್ರಾಂಜ್ ಹೆಸರಿನಲ್ಲಿದೆ). ಇದು ಹ್ಯಾಮಿಲ್ಟೋನಿಯನ್ಗಿಂತಲೂ ಮೂಲಭೂತದ್ದಾಗಿದೆ. ಇದನ್ನು ಚಲನೆಯ ಸಮೀಕರಣಗಳ ನಿಷ್ಪತ್ತಿಗಾಗಿ ಬಳಸಬಹುದು. ಅಭಿಜಾತ ಯಂತ್ರ ವಿಜ್ಞಾನದ ಸನ್ನಿವೇಶದಲ್ಲಿ ಇದನ್ನು ಸೃಷ್ಟಿಸಲಾಯಿತು. ಆದರೆ ಇದು ಆಧುನಿಕ ಭೌತ ವಿಜ್ಞಾನ ಕ್ಷೇತ್ರದಲ್ಲೂ ಸಾಮಾನ್ಯ ಉಪಯೋಗಕ್ಕೆ ಬಂದಿದೆ. ಚಲನಶಕ್ತಿಯಿಂದ ಅಂತಸ್ಥಶಕ್ತಿಯನ್ನು ಕಳೆದಾಗ ಲ್ಯಾಗ್ರಾಂಜಿಯನ್ ದೊರೆಯುತ್ತದೆ. ಸಂರಕ್ಷಿತವಲ್ಲದ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ (ಘರ್ಷಣೆಯುಳ್ಳ ವ್ಯವಸ್ಥೆ) ಹ್ಯಾಮಿಲ್ಟೋನಿಯನ್ಗಿಂತ ಹೆಚ್ಚಾಗಿ ಗಣಿತೀಯ ನಿರೂಪಣೆಗೆ ಲ್ಯಾಗ್ರಾಂಜ್ ನಿಯಮನಿಷ್ಠೆಯು ಅನುಕೂಲಕರ.
ಶಕ್ತಿ ಮತ್ತು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನ[ಬದಲಾಯಿಸಿ]
ಆಂತರಿಕ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಆಂತರಿಕ ಶಕ್ತಿ – ವ್ಯವಸ್ಥೆಯೊಂದರ ಎಲ್ಲ ಸೂಕ್ಷ್ಮ ರೂಪದ ಶಕ್ತಿಯ ಒಟ್ಟು ಮೊತ್ತವೇ ಆಂತರಿಕ ಶಕ್ತಿ. ಇದು ಆಣ್ವಿಕ ರಚನೆಯ ಮತ್ತು ಆಣ್ವಿಕ ಚಟುವಟಿಕೆಯ ಮಟ್ಟಕ್ಕೆ ಸಂಬಂಧಿಸಿದೆ. ಇದನ್ನು ಅಣುಗಳೊಳಗಿನ ಚಲನಶಕ್ತಿ ಮತ್ತು ಅಂತಸ್ಥಶಕ್ತಿಗಳ ಒಟ್ಟು ಮೊತ್ತವೆಂದು ಪರಿಗಣಿಸಲಾಗಿದ್ದು ಇದು ಕೆಳಕಂಡ ಶಕ್ತಿಯ ರೀತಿಗಳನ್ನು ಹೊಂದಿದೆ:[೧೪]
| ವಿಧಗಳು | ಆಂತರಿಕ ಶಕ್ತಿಯ ರಚನೆ (U) |
|---|---|
| ಸಂವೇದನಾಶೀಲ ಶಕ್ತಿ | ಚಲನಶಕ್ತಿಯೊಂದಿಗೆ (ಆಣ್ವಿಕ ಸ್ಥಾನಾಂತರಣ, ತಿರುವು ಮತ್ತು ಕಂಪನ; ಋಣಕಣ ಸ್ಥಾನಾಂತರಣ ಮತ್ತು ಗಿರಕಿ; ಹಾಗೂ ಬೈಜಿಕ ಗಿರಕಿ) ಸಂಬಂಧಿತ ವ್ಯವಸ್ಥೆಯ ಆಂತರಿಕ ಶಕ್ತಿಯ ಅಂಶ. |
| ಸುಪ್ತ ಶಕ್ತಿ | ವ್ಯವಸ್ಥೆಯ ಅವಸ್ಥೆಯೊಂದಿಗೆ ಸಂಬಂಧ ಹೊಂದಿದ ಆಂತರಿಕ ಶಕ್ತಿ. |
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ | ಭೌತದ್ರವ್ಯದಲ್ಲಿ ಪರಮಾಣುಗಳ ವಿವಿಧ ರೀತಿಯ ಸಮೂಹಗಳೊಂದಿಗೆ ಸಂಬಂಧ ಉಳ್ಳ ಆಂತರಿಕ ಶಕ್ತಿ. |
| ಬೈಜಿಕ ಶಕ್ತಿ | ಪರಮಾಣುವಿನ ಬೈಜಿಕ ಕೇಂದ್ರದೊಳಗೆ ದೃಢ ಬಂಧಕಗಳೊಂದಿಗಿರುವ ಅಪಾರ ಪ್ರಮಾಣದ ಶಕ್ತಿ. |
| ಶಕ್ತಿಯ ಅಂತರಕ್ರಿಯೆಗಳು | ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಶೇಖರಿಸಿಲ್ಲದ ಶಕ್ತಿ ರೂಪಗಳು (ಉದಾಹರಣೆಗೆ ಶಾಖದ ವರ್ಗಾವಣೆ, ದ್ರವ್ಯರಾಶಿ ವರ್ಗಾವಣೆ ಮತ್ತು ಕಾರ್ಯ). ಆದರೆ ವ್ಯವಸ್ಥೆಯ ಸರಹದ್ದನ್ನು ಶಕ್ತಿಯು ದಾಟಿದಾಗ ಈ ವ್ಯವಸ್ಥೆಯು ಶಕ್ತಿಯನ್ನು ಗುರುತಿಸುತ್ತದೆ. ಇದು ಪ್ರಕ್ರಿಯೆಯ ಅವಧಿಯ ಲಾಭ ಅಥವಾ ನಷ್ಟವನ್ನು ನಿರೂಪಿಸುತ್ತದೆ. |
| ಶಾಖೋತ್ಪನ್ನ ಶಕ್ತಿ | ಆಂತರಿಕ ಶಕ್ತಿಯ ಸಂವೇದನಾಶೀಲ ಮತ್ತು ಸುಪ್ತ ರೂಪಗಳ ಒಟ್ಟು ಮೊತ್ತ. |
ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ನಿಯಮಗಳು[ಬದಲಾಯಿಸಿ]
ಕಾರ್ಯವನ್ನು ಉಷ್ಣಕ್ಕೆ ಸಂಪೂರ್ಣವಾಗಿ ಪರಿವರ್ತಿಸಬಹುದು, ಆದರೆ ಉಷ್ಣವನ್ನು ಕಾರ್ಯಕ್ಕೆ ಪರಿವರ್ತಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ ಎಂಬುದು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ಎರಡನೆಯ ನಿಯಮ. ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಯಂತ್ರವಿಜ್ಞಾನದ ಗಣಿತೀಯ ಪರಿಣಾಮವಿದು. ಶಕ್ತಿಯು ಸಂರಕ್ಷಿತವಾಗಿರುತ್ತದೆ;[೧೫] ಹಾಗೂ, ಉಷ್ಣವನ್ನು ಶಕ್ತಿಯ ವರ್ಗಾವಣೆಯ ಒಂದು ರೂಪ ಎಂದು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ಮೊದಲ ನಿಯಮವು ಹೇಳುತ್ತದೆ. ಸಾಮಾನ್ಯ ಬಳಕೆಯಲ್ಲಿರುವ ಮೊದಲ ನಿಯಮದ ಉಪಸಿದ್ಧಾಂತವು ಹೀಗೆ ಸಾರುತ್ತದೆ: 'ಕೇವಲ ಒತ್ತಡದ ಶಕ್ತಿಗಳು ಮತ್ತು ಉಷ್ಣ ವರ್ಗಾವಣೆಗೆ ಒಳಪಡುವ ವ್ಯವಸ್ಥೆಯೊಂದಕ್ಕೆ, (ಉದಾಹರಣೆ: ಅನಿಲ ತುಂಬಿರುವ ಸಿಲಿಂಡರ್), ವ್ಯವಸ್ಥೆಯ ಶಕ್ತಿಯಲ್ಲಿನ ವ್ಯತ್ಯಾಸವನ್ನು (ಶಕ್ತಿ ಗಳಿಕೆಯನ್ನು ಸೂಚಿಸುವ ಹೆಚ್ಚಿದ ಪ್ರಮಾಣ) ಕೆಳಕಂಡಂತೆ ನಿರೂಪಿಸಲಾಗಿದೆ:
- ,
ಈ ಸಮೀಕರಣದಲ್ಲಿ ಬಲಭಾಗದಲ್ಲಿರುವ ಮೊದಲ ಪರಿಮಾಣವು ವ್ಯವಸ್ಥೆಯೊಳಗೆ ಉಷ್ಣದ ವರ್ಗಾವಣೆಯಾಗಿದೆ. ಇದನ್ನು ಉಷ್ಣತೆ T ಮತ್ತು ಜಡೋಷ್ಣ S (ವ್ಯವಸ್ಥೆಯನ್ನು ಬಿಸಿ ಮಾಡಿದಾಗ, ಇದರಲ್ಲಿ ಜಡೋಷ್ಣವು ಹೆಚ್ಚಾಗಿ ಬದಲಾವಣೆ dS ಧನಾತ್ಮಕವಾಗಿರುವುದು). ಬಲದಲ್ಲಿರುವ ಎರಡನೆಯ ಪರಿಮಾಣವು ವ್ಯವಸ್ಥೆಯ ಮೇಲೆ ಮಾಡಲಾದ ಕಾರ್ಯವನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಇದರಲ್ಲಿ P=ಒತ್ತಡ ಮತ್ತು V=ಘನಗಾತ್ರ (ವ್ಯವಸ್ಥೆ ಸಂಕುಚಿತಗೊಳ್ಳಲು ಅದರ ಮೇಲೆ ಕಾರ್ಯ ನಡೆಯುವ ಅಗತ್ಯವಿದೆ. ಇದರಿಂದಾಗಿ, ವ್ಯವಸ್ಥೆಯ ಮೇಲೆ ಕಾರ್ಯ ನಡೆದಾಗ ಘನಗಾತ್ರದ ಪರಿವರ್ತನೆ dV ಋಣಾತ್ಮಕವಾಗುತ್ತದೆ). ಅಭಿಜಾತ ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದಲ್ಲಿ ಶಕ್ತಿ ಸಂರಕ್ಷಣೆಗೆ ಈ ಸಮೀಕರಣವು ಪ್ರಮಾಣಿತ ಉದಾಹರಣೆಯಾಗಿದ್ದರೂ, ಎಲ್ಲಾ ರಾಸಾಯನಿಕ, ವಿದ್ಯುತ್, ಬೈಜಿಕ ಮತ್ತು ಗುರುತ್ವ ಶಕ್ತಿಗಳನ್ನು ಉಪೇಕ್ಷಿಸುವುದು ಇಲ್ಲಿನ ವೈಶಿಷ್ಟ್ಯ. ಜೊತೆಗೆ ಉಷ್ಣ ಶಕ್ತಿಯನ್ನು ಹೊರತುಪಡಿಸಿ ಇತರೆ ಯಾವುದೇ ರೂಪದ ಶಕ್ತಿಯ ಅಭಿವಹನ ಪ್ರಭಾವವನ್ನು ಸಹ ನಿರಾಕರಿಸುತ್ತದೆ. ಏಕೆಂದರೆ ಇದು ಉಷ್ಣತೆಯನ್ನು ಅವಲಂಬಿಸುವ ಒಂದು ಪರಿಮಾಣವನ್ನು ಹೊಂದಿದೆ. ಉಷ್ಣತೆಯನ್ನು ವಿವರಿಸಲಾಗದ ಸ್ಥಿತಿಯಲ್ಲೂ ಮೊದಲ ನಿಯಮದ ಸಾಮಾನ್ಯ ಹೇಳಿಕೆಯೇ (ಶಕ್ತಿ ಸಂರಕ್ಷಣೆ) ಸಿಂಧುವಾಗಿದೆ.
ಶಕ್ತಿಯನ್ನು ಕೆಲವೊಮ್ಮೆ ಹೀಗೂ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ:
- ,
[೧೧] ಏಕೆಂದರೆ W ಅಥವಾ Q ಉಷ್ಣಬಲ ವೈಜ್ಞಾನಿಕ ಫಲನಗಳು (ಬಹುಶಃ ಗಣನೀಯವಲ್ಲದ ಪ್ರಕರಣಗಳನ್ನು ಬಿಟ್ಟು) ಈ ಸಮೀಕರಣದ ಬಲಭಾಗದಲ್ಲಿ ಅರ್ಥಪೂರ್ಣವಾಗಿರಲಾರದು. ಆದ್ದರಿಂದ ಇದನ್ನು ಒಪ್ಪುವುದು ದುಸ್ತರ.
ಶಕ್ತಿಯ ಸಮವಿತರಣ[ಬದಲಾಯಿಸಿ]
ಯಾಂತ್ರಿಕ ಆಂಶಿಕ ಆಂದೋಲಕವೊಂದರ (ಸ್ಪ್ರಿಂಗ್ ಒಂದಕ್ಕೆ ತೂಗಿಬಿಟ್ಟಿರುವ ದ್ರವ್ಯರಾಶಿ) ಶಕ್ತಿಯು ಚಲನಶಕ್ತಿಯೂ ಹೌದು ಮತ್ತು ಅಂತಸ್ಥಶಕ್ತಿಯೂ ಹೌದು. ಅವು ಒಂದಕ್ಕೊಂದು ಪರ್ಯಾಯವಾಗಿವೆ. ತೂಗಾಟದ ಪಥದಲ್ಲಿ ಎರಡೂ ಕಡೆ ಅದು ಸಂಪೂರ್ಣವಾಗಿ ಚಲನಶಕ್ತಿಯೊಂದಿಗೂ, ಪರ್ಯಾಯವಾಗಿ ಇನ್ನೆರಡು ಕಡೆಗಳಲ್ಲಿ ಅದು ಸಂಪೂರ್ಣವಾಗಿ ಅಂತಸ್ಥಶಕ್ತಿಯೊಂದಿಗೂ ಇರುತ್ತದೆ. ಇಡೀ ಪಥದಲ್ಲಿ, ಅಥವಾ ಹಲವು ಪಥಗಳಲ್ಲಿ ಒಟ್ಟು ಶಕ್ತಿಯು ಈ ರೀತಿಯಾಗಿ ಚಲನ ಮತ್ತು ಅಂತಸ್ಥಶಕ್ತಿಗಳ ನಡುವೆ ಸಮನಾಗಿ ವಿತರಣೆಯಾಗುತ್ತದೆ. ಇದಕ್ಕೆ ಸಮವಿತರಣ ತತ್ವ ಎನ್ನಲಾಗಿದೆ. ಸ್ವಾತಂತ್ರ್ಯದ ಅಂಶಗಳುಳ್ಳ ವ್ಯವಸ್ಥೆಯೊಂದರ ಒಟ್ಟು ಶಕ್ತಿಯು, ಎಲ್ಲಾ ಲಭ್ಯ ಸ್ವಾತಂತ್ರ್ಯದ ಅಂಶಗಳ ನಡುವೆಯೂ ಸಮನಾಗಿ ವಿತರಣೆಯಾಗುತ್ತದೆ.
ಜಡೋಷ್ಣ ಎಂಬ ಪ್ರಮಾಣದ ವರ್ತನೆಯನ್ನು ಅರ್ಥ ಮಾಡಿಕೊಳ್ಳಲು ಶಕ್ತಿಗೆ ಸನಿಹ ಸಂಬಂಧಿಯಾದ ಈ ತತ್ವವು ಬಹಳ ಮುಖ್ಯವಾಗಿದೆ. ವ್ಯವಸ್ಥೆಯೊಂದರಲ್ಲಿ ಶಕ್ತಿ ವಿತರಣೆಯ ಸಮಾನತೆಯ ಮಾಪನವೇ ಜಡೋಷ್ಣ. ಪ್ರತ್ಯೇಕಿತ ವ್ಯವಸ್ಥೆಯೊಂದಕ್ಕೆ ಹೆಚ್ಚು ಸ್ವಾತಂತ್ರ್ಯದ ಅಂಶಗಳನ್ನು ನೀಡಿದ್ದಲ್ಲಿ (ಅರ್ಥಾತ್ ಈಗಿರುವ ಸ್ಥಿತಿಯಂತೇ ಇರುವ ಹೊಸ ಲಭ್ಯ ಶಕ್ತಿ ಸ್ಥಿತಿಯನ್ನು ನೀಡಿದಲ್ಲಿ), ಒಟ್ಟು ಶಕ್ತಿಯು 'ಹೊಸತು' ಮತ್ತು 'ಹಳತು'ಗಳ ನಡುವೆ ಯಾವುದೇ ಭೇದ ತೋರದೆ ಎಲ್ಲ ಲಭ್ಯ ಮಟ್ಟಗಳಲ್ಲಿಯೂ ಸಮನಾಗಿ ಪ್ರಸರಿಸುತ್ತದೆ. ಈ ಗಣಿತೀಯ ಫಲಿತಾಂಶವನ್ನು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದ ಎರಡನೆಯ ನಿಯಮ ಎನ್ನಲಾಗಿದೆ.
ಆಂದೋಲಕಗಳು, ಫೊನಾನ್ಗಳು ಮತ್ತು ಫೊಟಾನ್ಗಳು[ಬದಲಾಯಿಸಿ]
ಸಮಕಾಲಿಕವಲ್ಲದ ಆಂದೋಲಕಗಳ ಸಮಷ್ಟಿಯಲ್ಲಿ ಸರಾಸರಿ ಶಕ್ತಿಯು ಚಲನಶಕ್ತಿ ಮತ್ತು ಅಂತಸ್ಥಶಕ್ತಿಗಳ ನಡುವೆ ಸಮನಾಗಿ ಹಂಚಿಕೆಯಾಗಿರುತ್ತದೆ. ಘನಾಕೃತಿಯೊಂದರಲ್ಲಿ (ಕೆಲವೊಮ್ಮೆ ಸಡಿಲವಾಗಿ ಉಷ್ಣ ಸಂಗ್ರಹ ಎನ್ನಲಾಗುತ್ತದೆ) ಯಾಂತ್ರಿಕ ಆಂದೋಲಕಗಳಂತೆ ವರ್ತಿಸುವ ಉಷ್ಣ ಫೋನಾನ್ಗಳ ಸಮಷ್ಟಿಯ ಮೂಲಕ ಉಷ್ಣ ಶಕ್ತಿಯನ್ನು ನಿಖರವಾಗಿ ವಿವರಿಸಬಹುದು. ಈ ಮಾದರಿಯಲ್ಲಿ ಉಷ್ಣ ಶಕ್ತಿಯು ಸಮನಾಗಿ ಚಲನಶಕ್ತಿಯೂ ಮತ್ತು ಅಂತಸ್ಥಶಕ್ತಿಯೂ ಆಗಿದೆ.
ಆದರ್ಶ ಅನಿಲದಲ್ಲಿ ಕಣಗಳ ನಡುವಿನ ಅಂತರಕ್ರಿಯಾ ಸಾಮರ್ಥ್ಯವು ಅಗತ್ಯವಾಗಿ ಶಕ್ತಿಯನ್ನು ಶೇಖರಿಸದೇ ಇರುವ ಡೆಲ್ಟಾ ಫಲನವಾಗಿದೆ. ಆದ್ದರಿಂದ, ಉಷ್ಣ ಶಕ್ತಿಯು ಸಂಪೂರ್ಣವಾಗಿ ಚಲನಶಕ್ತಿಯೇ ಆಗಿರುತ್ತದೆ.
ವಿದ್ಯುತ್ ಆಂದೋಲಕವು (ಎಲ್ಸಿ ವಿದ್ಯುನ್ಮಂಡಲ) ಯಾಂತ್ರಿಕ ಆಂದೋಲಕಕ್ಕೆ ಸಾದೃಶವಾಗಿರುವ ಕಾರಣ, ಅದರ ಸರಾಸರಿ ಶಕ್ತಿಯು ಸಮನಾಗಿ ಚಲನ ಮತ್ತು ಅಂತಸ್ಥಶಕ್ತಿಯಾಗಿರಲೇಬೇಕು. ಆಯಸ್ಕಾಂತೀಯ ಶಕ್ತಿಯನ್ನು ಚಲನಶಕ್ತಿ ಮತ್ತು ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಅಂತಸ್ಥಶಕ್ತಿ ಎನ್ನಬೇಕೋ ಅಥವಾ, ತಿರುವುಮುರುವಾಗಿ ಪರಿಗಣಿಸಬೇಕೋ ಎಂಬುದು ಇನ್ನೂ ನಿರ್ದಾರವಾಗದ ಸಂಗತಿ. ಅರ್ಥಾತ್, ವಿದ್ಯುತ್ ಚೋದಕವು (=ಇಂಡಕ್ಟರ್) ದ್ರವ್ಯರಾಶಿಗೆ ಸಾದೃಶವಾಗಿದ್ದು, ಸಂಚಾಯಕವು ಸ್ಪ್ರಿಂಗ್ಗೆ ಸಾದೃಶವಾಗಿದೆ; ಅಥವಾ ಸಂಚಾಯಕವು ದ್ರವ್ಯರಾಶಿಗೆ ಸಾದೃಶವಾಗಿದ್ದು, ವಿದ್ಯುತ್ ಚೋದಕವು (ಇಂಡಕ್ಟರ್) ಸ್ಪ್ರಿಂಗ್ಗೆ ಸಾದೃಶವಾಗಿದೆ.
1. ಹಿಂದೆ ತಿಳಿಸಿರುವಂತೆ, ಮುಕ್ತ ಆಕಾಶದಲ್ಲಿ ವಿದ್ಯುತ್ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು 'ಆಂದೋಲಕಗಳ ಸಮಷ್ಟಿ' ಎಂದು ಪರಿಗಣಿಸಬಹುದು. ಅರ್ಥಾತ್ ವಿಕಿರಣ ಶಕ್ತಿಯನ್ನು ಸಮನಾಗಿ ಅಂತಸ್ಥ ಮತ್ತು ಚಲನಶಕ್ತಿಯೆಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ. ವಿದ್ಯುತ್ ಕಾಂತೀಯ ಲ್ಯಾಗ್ರಾಂಜಿಯನ್ ಪ್ರಮುಖ ಆಸಕ್ತಿಯ ವಿಷಯವಾಗಿದ್ದು ಅಂತಸ್ಥ ಮತ್ತು ಚಲನಶಕ್ತಿಯಾಗಿರುವ ಉದಾಹರಣೆಗಾಗಿ ಈ ಮಾದರಿಯು ಉಪಯುಕ್ತವಾಗಿದೆ.
2. ಇನ್ನೊಂದೆಡೆ, ಸಮೀಕರಣ ರಲ್ಲಿ, ಕೊಡುಗೆ ಅನ್ನು ವಿಶ್ರಾಮ ಶಕ್ತಿ ಮತ್ತು ಶಕ್ತಿಗೆ ಇತರೆ ಎಲ್ಲಾ ಕೊಡುಗೆಗಳನ್ನೂ ಚಲನಶಕ್ತಿ ಎಂದೂ ಹೇಳಲಾಗಿದೆ. ದ್ರವ್ಯರಾಶಿ ಹೊಂದಿರುವ ಕಣವೊಂದಕ್ಕೆ, c ಗಿಂತಲೂ ಕಡಿಮೆ ವೇಗಗಳಲ್ಲಿ ಚಲನಶಕ್ತಿಯು ಎಂದು ಹೇಳಲಾಗಿದೆ. √ ಎಂದು ಬರೆದು, ಅತಿ ಕಡಿಮೆ ವರ್ಗಕ್ಕೆ ವರ್ಗಮೂಲವನ್ನು ವಿಸ್ತರಿಸುವುದರ ಮೂಲಕ ಇದನ್ನು ಸಾಧಿಸಬಹುದು. ಈ ರೀತಿ ತರ್ಕಿಸಿದರೆ, ಫೋಟಾನಿನ ಶಕ್ತಿಯು ಸಂಪೂರ್ಣವಾಗಿ ಚಲನಶಕ್ತಿಯಾಗಿದೆ. ಏಕೆಂದರೆ ಫೋಟಾನ್ಗೆ ದ್ರವ್ಯರಾಶಿಯಿಲ್ಲ, ಜೊತೆಗೆ ವಿಶ್ರಾಮ ಶಕ್ತಿಯೂ ಅದಕ್ಕಿಲ್ಲ. 'ಶಕ್ತಿ-v/s-ಸಂವೇಗ' ಸಂಬಂಧವು ಪ್ರಮುಖ ವಿಷಯವಾದಲ್ಲಿ, ಈ ಸಮೀಕರಣವು ಉಪಯುಕ್ತವಾಗಿದೆ.
ಈ ಎರಡೂ ವಿಶ್ಲೇಷಣೆಗಳು ಸಂಪೂರ್ಣವಾಗಿ ಸಂಗತವಾಗಿವೆ. ವಿಷಯ 1ರಲ್ಲಿ ವಿದ್ಯುತ್ ಮತ್ತು ಕಾಂತೀಯ ಸ್ವಾತಂತ್ರ್ಯದ ಅಂಶಗಳು ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಚಲಿಸುತ್ತವೆ. ಆದರೆ ವಿಷಯ 2ರಲ್ಲಿ ವೇಗವು ಚಲನೆಯ ಗುಂಟವೇ ಸಾಗುತ್ತದೆ. ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತದಿಂದ ವಿವರಿಸಲಾಗಿಲ್ಲದ ಕಣಗಳಿಗೆ, ಅಂತಸ್ಥ-ವಿರುದ್ಧ-ಚಲನಶಕ್ತಿಯ ಎರಡೂ ಕಲ್ಪನೆಗಳು ಸಾಂಖ್ಯಿಕವಾಗಿ ಸಮನಾಗಿದೆ. ಆದ್ದರಿಂದ ಈ ಅನಿಶ್ಚಯತೆಯಿಂದ ಯಾವುದೇ ತೊಡಕಿಲ್ಲ. ಆದರೆ, ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತದಿಂದ ವಿವರಿಸಲಾದ ಕಣಗಳಿಗೆ ಇದು ಸಮಸ್ಯೆಯೊಡ್ಡಬಹುದು.
ಕಾರ್ಯ ಮತ್ತು ವಾಸ್ತವ ಕಾರ್ಯ[ಬದಲಾಯಿಸಿ]
'ಕಾರ್ಯ'ವೆಂಬುದು 'ಬಲ' ಮತ್ತು 'ದೂರ'ದ ಗುಣಲಬ್ಧ.
ಕಾರ್ಯವು () ಪಥ C ಯುದ್ದಕ್ಕೂ ಬಲ F ದ ರೇಖಾ-ಅನುಕಲಕ್ಕೆ ಸಮನಾಗಿದೆ.
ಕಾರ್ಯ ಮತ್ತು ಅದರಿಂದಾಗಿ ಶಕ್ತಿಯು ಚೌಕಟ್ಟನ್ನು ಅವಲಂಬಿಸಿದೆ. ಉದಾಹರಣೆಗೆ, ಬ್ಯಾಟಿನಿಂದ ಚೆಂಡಿಗೆ ಹೊಡೆದಾಗ ಏನಾಗುತ್ತೆ ಗಮನಿಸಿ. ಬ್ಯಾಟಿನ ಹೊಡೆತ ಚೆಂಡಿನ ಮಧ್ಯದಲ್ಲಿ ಏನೂ ಪರಿಣಾಮ ಬೀರಿರುವುದಿಲ್ಲ. ಆದರೆ ಬೀಸುವಾತನ ಬ್ಯಾಟಿನ ಹೊಡೆತ ಚೆಂಡಿನ ಮೇಲೆ ಗಣನೀಯ ಕೆಲಸ ಮಾಡಿರುತ್ತದೆ. ಆದರೆ, ಬ್ಯಾಟ್ ಬೀಸುತ್ತಿರುವ ವ್ಯಕ್ತಿಯ ಚೌಕಟ್ಟಿನಲ್ಲಿ, ಚೆಂಡಿನ ಮೇಲೆ ಗಮನಾರ್ಹ ಕಾರ್ಯವನ್ನು ಮಾಡಲಾಗಿದೆ.
ಕ್ವಾಂಟಮ್ ಯಂತ್ರ ವಿಜ್ಞಾನ[ಬದಲಾಯಿಸಿ]
ಕ್ವಾಂಟಮ್ ಯಂತ್ರ ವಿಜ್ಞಾನದಲ್ಲಿ, ಶಕ್ತಿ ಕ್ರಿಯಾಚಿಹ್ನೆಯ ದೃಷ್ಟಿಯಿಂದ ಶಕ್ತಿಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ತರಂಗ ಫಲನದ ಕಾಲ ವಿಕಲಜನ್ಯವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ಶ್ರೋಡಿಂಗರ್ ಸಮೀಕರಣವು ಶಕ್ತಿಯ ಕ್ರಿಯಾಚಿಹ್ನೆಯನ್ನು ಕಣ ಅಥವಾ ವ್ಯವಸ್ಥೆಯೊಂದರ ಪೂರ್ಣ ಶಕ್ತಿಗೆ ಸಮೀಕರಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ, ಕ್ವಾಂಟಮ್ ಯಂತ್ರ ವಿಜ್ಞಾನದಲ್ಲಿ ಶಕ್ತಿ ಮಾಪನದ ವ್ಯಾಖ್ಯಾನ ಎಂದು ಇದನ್ನು ಪರಿಗಣಿಸಬಹುದು. ಕ್ವಾಂಟಮ್ ವ್ಯವಸ್ಥೆಯ ನಿಧಾನಗತಿಯಲ್ಲಿ ಬದಲಾಗುವ (ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತದಿಂದ ವಿವರಿಸಲಾಗಿಲ್ಲದ) ತರಂಗ ಫಲನದ ದೇಶ-ಕಾಲ ಅವಲಂಬನೆಯನ್ನು ಶ್ರೋಡಿಂಗರ್ ಸಮೀಕರಣವು ವಿವರಿಸುತ್ತದೆ. ವ್ಯವಸ್ಥೆಗಾಗಿ ಸಮೀಕರಣದ ಫಲಿತಾಂಶವು ವಿಭಿನ್ನವಾಗಿದೆ (ಬಂಧಿತವಾದ ಕ್ವಾಂಟಮ್ ಯಾಂತ್ರಿಕ ವ್ಯವಸ್ಥೆಗಳ ಒಂದು ಗುಂಪು; ಇದರಲ್ಲಿ ಪ್ರತಿಯೊಂದನ್ನೂ ಶಕ್ತಿ ಮಟ್ಟದಲ್ಲಿ ನಿರೂಪಿಸಲಾಗಿದೆ.) ಇದೇ ಕ್ವಾಂಟಾದ ಪರಿಕಲ್ಪನೆ. ನಿರ್ವಾತ ಪ್ರದೇಶದಲ್ಲಿನ ಯಾವುದೇ ಆಂದೋಲಕ (ಕಂಪಕ) ಮತ್ತು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕಿರಣಗಳಿಗಾಗಿ ಶ್ರೋಡಿಂಗರ್ ಸಮೀಕರಣದ ಫಲಿತಾಂಶದಲ್ಲಿ, ಉಗಮಿಸುವ ಶಕ್ತಿ ಸ್ಥಿತಿಗಳು ಆವರ್ತನಕ್ಕೆ ಪ್ಲ್ಯಾಂಕ್ ಸಮೀಕರಣ ಮೂಲಕ ಸಂಬಂಧ ಪಟ್ಟಿರುತ್ತೆ (ಇದರಲ್ಲಿ ಪ್ಲ್ಯಾಂಕ್ ಸ್ಥಿರಾಂಕ ಮತ್ತು ಆವರ್ತನ). ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದ ವಿಚಾರದಲ್ಲಿ ಈ ಶಕ್ತಿ ಸ್ಥಿತಿಯನ್ನು ಬೆಳಕಿನ ಅಥವಾ ಫೋಟಾನ್ಗಳ ಕ್ವಾಂಟಾ ಎನ್ನಲಾಗಿದೆ.
ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತ[ಬದಲಾಯಿಸಿ]
ನ್ಯೂಟನಿಯನ್ ಯಾಂತ್ರಿಕ ವಿಜ್ಞಾನದ ಬದಲಿಗೆ ಲೊರೆಂಟ್ಜ್ ರೂಪಾಂತರಗಳನ್ನು ಬಳಸಿ, ಕೇವಲ ಸಾಪೇಕ್ಷತಾ ಸಿದ್ಧಾಂತದಿಂದ ವಿವರಿಸಿರುವಂತೆ ಚಲನಶಕ್ತಿಯನ್ನು ಗಣನೆ ಮಾಡಿದಾಗ (= ದ್ರವ್ಯರಾಶಿಯೊಂದರ ವೇಗವನ್ನು ಶೂನ್ಯ ವೇಗದಿಂದ ಎಲ್ಲೆಯುಳ್ಳ ವೇಗಕ್ಕೆ ಹೆಚ್ಚಿಸಲು ಮಾಡಲಾದ ಕಾರ್ಯ) ಐನ್ಸ್ಟೀನ್ ಈ ಗಣನೆಗಳ ಉಪ-ಉತ್ಪನ್ನವನ್ನು ಪರಿಶೋಧಸಿದ. ಇದು ಶೂನ್ಯ ವೇಗದಲ್ಲಿ ಮಾಯವಾಗದಂತಹ ಶಕ್ತಿ ಪರಿಮಾಣವಾಗಿದೆ. ಇದನ್ನು ಅವರು ವಿಶ್ರಾಮ ದ್ರವ್ಯರಾಶಿ ಶಕ್ತಿ ಎಂದರು. ಯಾವುದೇ ದ್ರವ್ಯರಾಶಿ ವಿಶ್ರಾಮ ಸ್ಥಿತಿಯಲ್ಲಿರುವಾಗ ಈ ಶಕ್ತಿಯನ್ನು ಹೊಂದಿರತಕ್ಕದ್ದು. ಕಾಯಕ್ಕಿರುವ (=ವಸ್ತು) ಶಕ್ತಿಯು ಅದರ ದ್ರವ್ಯರಾಶಿಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿದೆ.
- ,
ಇದರಲ್ಲಿ
- m ಏನ್ನುವುದು ದ್ರವ್ಯರಾಶಿ,
- c ನಿರ್ವಾತ ಪ್ರದೇಶದಲ್ಲಿ ಬೆಳಕಿಗಿರುವ ವೇಗ,
- E ವಿಶ್ರಾಮ ದ್ರವ್ಯರಾಶಿ ಶಕ್ತಿ.
ಉದಾಹರಣೆಗೆ, ಎಲೆಕ್ಟ್ರಾನ್-ಪಾಸಿಟ್ರಾನ್ನಲ್ಲಿ ಪ್ರತಿ ಕಣದ ವಿಶ್ರಾಮ ದ್ರವ್ಯರಾಶಿಯು ನಶಿಸಿಹೋಗುತ್ತದೆ. ಆದರೆ ಎರಡೂ ಕಣಗಳ ಜಡತ್ವ ಸಮಾನ ಪರಿಮಾಣವು (ಅದರ ಸ್ಥಿರ ದ್ರವ್ಯರಾಶಿ) ಉಳಿದುಕೊಳ್ಳುತ್ತದೆ (ಏಕೆಂದರೆ ಶಕ್ತಿ ಎಂದಿಗೂ ದ್ರವ್ಯರಾಶಿಯ ಜೊತೆ ಸಂಬಂಧ ಉಳ್ಳದ್ದು); ಹಾಗೂ ಈ ಜಡತ್ವ ಮತ್ತು ಸ್ಥಿರ ದ್ರವ್ಯರಾಶಿಯನ್ನು ದ್ರವ್ಯರಾಶಿಯಿಲ್ಲದಂತಹ ಫೋಟಾನ್ಗಳು ಒಯ್ಯುತ್ತವೆ, ಆದರೆ ವ್ಯವಸ್ಥೆಯಾಗಿ ಅವು ತಮ್ಮ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಉಳಿಸಿಕೊಳ್ಳುತ್ತವೆ. ಇದು ಒಂದು ಹಿಮ್ಮೊಗವಾಗಬಲ್ಲ ಪ್ರಕ್ರಿಯೆ. ಹಿಂದುಮುಂದಾದ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಜೋಡಿ ಸೃಷ್ಟಿ ಎನ್ನಲಾಗಿದೆ. ಇದರಲ್ಲಿ, ನಿರ್ಮೂಲವಾಗುವ ಎರಡು (ಅಥವಾ ಅದಕ್ಕೂ ಹೆಚ್ಚು) ಕಣಗಳ ವಿಶ್ರಾಮ ದ್ರವ್ಯರಾಶಿಯು ಸೃಷ್ಟಿಯಾಗುತ್ತದೆ.
ಸಾರ್ವತ್ರಿಕ ಸಾಪೇಕ್ಷತೆಯಲ್ಲಿ, ಒತ್ತಡ-ಶಕ್ತಿ ಕರ್ಷಕ (ಸ್ಟ್ರೆಸ್-ಎನರ್ಜಿ-ಟೆನ್ಸಾರ್) ಗುರುತ್ವ ಕ್ಷೇತ್ರಕ್ಕೆ ಮೂಲ ಪರಿಮಾಣವಾಗುತ್ತದೆ. ಸಾಪೇಕ್ಷತೆಯ ಸಿದ್ಧಾಂತದಿಂದ ವಿವರಿಸಲಾಗಿಲ್ಲದ ನ್ಯೂಟನಿಯನ್ ಸಾಮೀಪ್ಯದಲ್ಲಿ, ದ್ರವ್ಯರಾಶಿಯು ಮೂಲ ಪರಿಮಾಣವಾಗುವ ರೀತಿಗೆ ಇದು ಸ್ಥೂಲ ಸದೃಶವಾಗಿದೆ.[೧೨]
'ಶಕ್ತಿಯು ದ್ರವ್ಯರಾಶಿಗೆ ಸಮಾನವಾಗಿದೆ' ಎಂಬ ಮಾತು ಕೇಳಿಬರುವುದು ಅಪರೂಪದ್ದೇನಲ್ಲ. 'ಪ್ರತಿಯೊಂದು ಶಕ್ತಿಗೂ ಜಡತ್ವ ಮತ್ತು ಗುರುತ್ವ ಸಮಾನವಾಗಿ ಇರುತ್ತದೆ' ಎಂದು ಹೇಳುವುದು ಹೆಚ್ಚು ನಿಖರ. ದ್ರವ್ಯರಾಶಿಯು ಶಕ್ತಿಯ ಒಂದು ರೂಪ. ಆದ್ದರಿಂದ, ದ್ರವ್ಯರಾಶಿಗೂ ಸಹ ಜಡತ್ವ ಮತ್ತು ಗುರುತ್ವ ಇದ್ದೇ ಇರುತ್ತದೆ.
ಮಾಪನ[ಬದಲಾಯಿಸಿ]
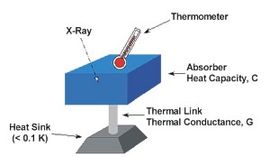
ಒಂದು ವ್ಯವಸ್ಥೆಯು ಇನ್ನೊಂದರ ಮೇಲೆ ಮಾಡುವ (ಅಥವಾ ಮಾಡಬಲ್ಲ) ಕಾರ್ಯವೆಂದು ಶಕ್ತಿಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಿರುವುದರಿಂದ ಶಕ್ತಿಗೆ ಯಾವುದೇ ಸಮಗ್ರ ಮಾಪನವಿಲ್ಲ, ಅಂದರೆ ಅದರ ಮೊತ್ತವನ್ನು ನಿರ್ದಿಷ್ಟವಾಗಿ ಅಳೆಯಲಾಗದು. ಇದರಿಂದಾಗಿ, ಒಂದು ಸ್ಥಿತಿಯಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ಆಗುವ ವ್ಯವಸ್ಥೆಯ ರೂಪಾಂತರವನ್ನು ಮಾತ್ರ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು ಮತ್ತು ಈ ರೀತಿ ಮಾಪನ ಮಾಡಬಹುದು.
ವಿಧಾನಗಳು[ಬದಲಾಯಿಸಿ]
ದ್ರವ್ಯರಾಶಿ, ದೂರ, ವಿಕಿರಣ, ಉಷ್ಣತೆ, ಸಮಯ, ವಿದ್ಯುದಾವೇಶ ಮತ್ತು ವಿದ್ಯುತ್ ಪ್ರವಾಹ-ಶಕ್ತಿಯ ಮಾಪನಕ್ಕಾಗಿ, ಆಗಾಗ್ಗೆ ವಿಜ್ಞಾನದ ಇನ್ನಷ್ಟು ಮೂಲಭೂತ ಪರಿಕಲ್ಪನೆಗಳನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
ಶಾಖಮಾಪನ (ಕ್ಯಾಲೊರಿಮೆಟ್ರಿ), ಆಗಾಗ್ಗೆ ಬಳಸಲಾಗುವ ಉಷ್ಣಬಲ ವೈಜ್ಞಾನಿಕ ತಂತ್ರ. ಉಷ್ಣಾಂಶದ ಮಾಪನಕ್ಕಾಗಿ ಉಷ್ಣಮಾಪಕವನ್ನೂ ಅಥವಾ ವಿಕಿರಣದ ತೀಕ್ಷ್ಣತೆಯ ಮಾಪನಕ್ಕಾಗಿ ವಿಕಿರಣತಾಪಮಾಪಕವನ್ನೂ (=ಬೊಲೊಮೀಟರ್) ಬಳಸಲಾಗುತ್ತದೆ.
ಏಕಮಾನಗಳು[ಬದಲಾಯಿಸಿ]
ವಿಜ್ಞಾನದ ಇತಿಹಾಸದುದ್ದಕ್ಕೂ, ಅರ್ಗ್ ಮತ್ತು ಕ್ಯಾಲೊರಿ ಸೇರಿದಂತೆ ವಿವಿಧ ಏಕಮಾನಗಳಲ್ಲಿ (=ಯೂನಿಟ್ಗಳಲ್ಲಿ) ಶಕ್ತಿಯನ್ನು ವ್ಯಕ್ತಪಡಿಸಲಾಗಿದೆ. ಪ್ರಸ್ತುತ, ಶಕ್ತಿಯನ್ನು ಮಾಪನ ಮಾಡಲು, ಜೂಲ್ ಎಂಬ ಎಸ್ಐ ಏಕಮಾನವು ಸ್ವೀಕೃತವಾಗಿದೆ. ಜೂಲ್ ಅಲ್ಲದೆ, ಶಕ್ತಿಯ ಮಾಪನ ಮಾಡಲು ಕಿಲೊವ್ಯಾಟ್ ಅವರ್ (kWh) ಮತ್ತು ಬ್ರಿಟಿಷ್ ಥರ್ಮಲ್ ಯೂನಿಟ್ (Btu) ಏಕಮಾನಗಳನ್ನೂ ಬಳಸಲಾಗಿದೆ. ಇವೆರಡೂ ಶಕ್ತಿಯ ದೊಡ್ಡ ಏಕಮಾನಗಳು. ಒಂದು kWh ನಿಖರವಾಗಿ 3.6 ದಶಲಕ್ಷ ಜೂಲ್ಗಳಿಗೆ ಸಮಾನವಾಗಿದೆ; ಒಂದು ಬಿಟಿಯು ಸುಮಾರು 1055 ಜೌಲ್ಗಳಿಗೆ ಸಮನಾಗಿದೆ.[೧೬]
ಶಕ್ತಿಯ ರೂಪಗಳು[ಬದಲಾಯಿಸಿ]

ಯಂತ್ರ ವಿಜ್ಞಾನವು, ವಸ್ತುವಿನ ಅಂತಸ್ಥ ಶಕ್ತಿ (ವಸ್ತುವಿನ ನಿಶ್ಚಲ ಸ್ಥಿತಿಯನ್ನು ಅವಲಂಬಿಸಿದೆ) ಮತ್ತು ಚಲನಶಕ್ತಿ (ವಸ್ತುವಿನ ಚಲನಾವಸ್ಥೆಯನ್ನು ಅವಲಂಬಿಸಿದೆ) ನಡುವೆ ಭಿನ್ನ ಲಕ್ಷಣಗಳನ್ನು ಗುರುತಿಸುತ್ತದೆ. ಚಲ ಮತ್ತು ಅಚಲಾವಸ್ಥೆ - ಇವೆರಡೂ ಆಧಾರ ಚೌಕಟ್ಟಿಗೆ ಸಾಪೇಕ್ಷ ಸಂಗತಿಗಳಾಗಿವೆ. ಈ ಆಧಾರ ಚೌಕಟ್ಟನ್ನು ನಮೂದಿಸತಕ್ಕದ್ದು: ಇದು ಆಗಾಗ್ಗೆ (ಮತ್ತು ಮೂಲತಃ) ಭೂಮಿಯ ಮೇಲೆ ಇಚ್ಛಾನುಸಾರವಾಗಿ ನಿಗದಿತ ಒಂದು ಸ್ಥಳ - ನೆಲದ ಚೌಕಟ್ಟು ಎಂದು ಸಹ ಹೇಳಬಹುದು. ಶಕ್ತಿಯ ಎಲ್ಲ ರೂಪಗಳನ್ನೂ ಚಲನಶಕ್ತಿ ಅಥವಾ ಅಂತಸ್ಥಶಕ್ತಿಯೆಂದು ವಿಂಗಡಿಸುವ ಯತ್ನವು ನಡೆದಿದೆ. ಫೇಯ್ನ್ಮನ್ ಹೇಳಿದಂತೆ ಇದು ಸರಿಯಲ್ಲ ಎಂದಲ್ಲ, ಆದರೂ ಸರಳತೆಯ ಬಗ್ಗೆ ಅಸ್ಪಷ್ಟತೆಯಿದೆ.
These notions of potential and kinetic energy depend on a notion of length scale. For example, one can speak of macroscopic potential and kinetic energy, which do not include thermal potential and kinetic energy. Also what is called chemical potential energy (below) is a macroscopic notion, and closer examination shows that it is really the sum of the potential and kinetic energy on the atomic and subatomic scale. Similar remarks apply to nuclear "potential" energy and most other forms of energy. This dependence on length scale is non-problematic if the various length scales are decoupled, as is often the case ... but confusion can arise when different length scales are coupled, for instance when friction converts macroscopic work into microscopic thermal energy.
| ಯಾಂತ್ರಿಕ ಶಕ್ತಿಯ ಪರಿವರ್ತನೆ | |
|---|---|
| ಈ ಶಕ್ತಿಯಾಗಿ | ಈ ಸಲಕರಣೆಗಳ ಮೂಲಕ |
| ಯಾಂತ್ರಿಕ ಶಕ್ತಿ | ಮೀಟುಗೋಲು (ಲೀವರ್) |
| ಉಷ್ಣ ಶಕ್ತಿ | ಬ್ರೇಕ್ಗಳು |
| ವಿದ್ಯುತ್ ಶಕ್ತಿ | ಡೈನಮೊ |
| ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ | ಸಿಂಕ್ರೋಟ್ರಾನ್ |
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ | ಬೆಂಕಿಕಡ್ಡಿಗಳು |
| ಬೈಜಿಕ ಶಕ್ತಿ | ಕಣ ವೇಗವರ್ಧಕ |
ಯಾಂತ್ರಿಕ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಯಾಂತ್ರಿಕ ಶಕ್ತಿಯು ಹಲವು ರೂಪಗಳಲ್ಲಿ ಪ್ರಕಟವಾಗುತ್ತದೆ; ಆದರೆ ಅದನ್ನು ಸ್ಥಿತಿಸ್ಥಾಪಕ ಅಂತಸ್ಥಶಕ್ತಿ ಹಾಗೂ ಚಲನಶಕ್ತಿ ಎಂದು ಸ್ಥೂಲವಾಗಿ ವಿಂಗಡಿಸಲಾಗಿದೆ. ಗುರುತ್ವ, ಸ್ಥಾಯೀವಿದ್ಯುತ್ ಮತ್ತು ಆಯಸ್ಕಾಂತೀಯ ಹೀಗೆ ಎಲ್ಲಾ ಶಕ್ತಿ ಕ್ಷೇತ್ರದಲ್ಲೂ ಇರುವ 'ಅಂತಸ್ಥಶಕ್ತಿ' ಎಂಬುದು ಬಹಳ ಸಾಮಾನ್ಯ ಪದ. ಬಲ ಕ್ಷೇತ್ರದಲ್ಲಿ ವಸ್ತುವೊಂದು ಅದರ ಸ್ಥಿತಿಯ ಕಾರಣದಿಂದಲೇ ಪಡೆದ ಶಕ್ತಿ ಅಂತಸ್ಥಶಕ್ತಿಯಾಗಿದೆ.
ನಿರ್ದೇಶಿತ ಸ್ಥಳದಿಂದ ಇನ್ನೊಂದು ಸ್ಥಳಕ್ಕೆ ವಸ್ತುವೊಂದನ್ನು ಸ್ಥಳಾಂತರಿಸಲು ಬಲಕ್ಕೆ ಪ್ರತಿಯಾಗಿ ಮಾಡಲಾದ ಕಾರ್ಯವನ್ನು ಅಂತಸ್ಥಶಕ್ತಿ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. (ಚಿಹ್ನೆಗಳು Ep, V ಅಥವಾ Φ). F ಬಲದ ನಿರೂಪಣೆಯಾಗಿದ್ದು s ಸ್ಥಳಾಂತರಣದ ನಿರೂಪಣೆಯಾಗಿದ್ದರೆ,
ಸಮೀಕರಣದಲ್ಲಿರುವ 'dot' (ಡಾಟ್) ಎರಡೂ ಸದಿಶಗಳ ಅದಿಶ ಗುಣಲಬ್ಧವನ್ನು ನಿರೂಪಿಸುತ್ತದೆ.
'ಕನಿಷ್ಠ ಪಕ್ಷ ಪರಿಪೂರ್ಣ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ಕಾರ್ಯದ ಮೂಲಕ ಸ್ಥಳಾಂತರಗೊಳಿಸಬಹುದು' ಎಂಬ ಕಲ್ಪನೆಯನ್ನು 'ಅಂತಸ್ಥ' ಶಕ್ತಿ ಎಂಬ ಹೆಸರು ಕಲ್ಪನೆಯನ್ನು ಮೂಲತಃ ಪ್ರತಿಪಾದಿಸಿತ್ತು (ಇದು ಹಿಮ್ಮೊಗವಾಗಬಲ್ಲ ಪ್ರಕ್ರಿಯೆ; ಕೆಳಗೆ ನೋಡಿ.) ಇದು ಯಾವುದೇ ನೈಜ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಪರಿಪೂರ್ಣ ಸತ್ಯವಲ್ಲ, ಆದರೆ ಶಾಸ್ತ್ರೀಯ ಯಂತ್ರವಿಜ್ಞಾನದಲ್ಲಿ ಇದನ್ನು ಬಹಳಷ್ಟು ಸಲ ವಿವೇಕಯುತ ಮೊದಲ ಅಂದಾಜು ಎಂದು ಭಾವಿಸಬಹುದು.
ಗಮನಾರ್ಹವಾಗಿ ಗುರುತ್ವ ಅಥವಾ ಸ್ಥಿತಿಸ್ಥಾಪಕ ಬಲಗಳ ವಿಚಾರದಲ್ಲಿ, ಮೇಲಿನ ಸಮೀಕರಣವನ್ನು ಹಲವಾರು ಸಂದರ್ಭಗಳಲ್ಲಿ ಸರಳಗೊಳಿಸಬಹುದು.
ಸ್ಥಿತಿಸ್ಥಾಪಕ ಅಂತಸ್ಥ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]

ಸ್ಪ್ರಿಂಗನ್ನು ಕುಗ್ಗಿಸುವಾಗ ಅಥವಾ ಹಿಗ್ಗಿಸುವಾಗ ಬೇಕಾಗುವ ಅಗತ್ಯ ಕಾರ್ಯವನ್ನು 'ಸ್ಥಿತಿಸ್ಥಾಪಕ ಅಂತಸ್ಥಶಕ್ತಿ'ಯೆಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ಸ್ಪ್ರಿಂಗ್, ಅಥವಾ ಹುಕ್ಸ್ ನಿಯಮವನ್ನು ಪಾಲಿಸುವ ಯಾವುದೇ ವ್ಯವಸ್ಥೆಯಲ್ಲಿನ ಬಲ F ದ ಪ್ರಮಾಣವು, ಹಿಗ್ಗುವಿಕೆ ಅಥವಾ ಕುಗ್ಗುವಿಕೆ, x ನ ಸೂಕ್ತ ಪ್ರಮಾಣಾನುಗುಣದಲ್ಲಿದೆ.
ನಿರ್ದಿಷ್ಟ ಸ್ಪ್ರಿಂಗ್ ಅಥವಾ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ k ಬಲ ಸ್ಥಿರಾಂಕವಾಗಿದೆ. ಈ ವಿಚಾರದಲ್ಲಿ, ಲೆಕ್ಕ ಹಾಕಲಾದ ಕಾರ್ಯವು ಕೆಳಕಂಡಂತೆ ವ್ಯಕ್ತವಾಗುತ್ತದೆ:
(k ನಿಯತಾಂಕವಾಗಿದ್ದಲ್ಲಿ ಮಾತ್ರ ಇದು ಸಾಧ್ಯ) ಸಾಮಾನ್ಯ ಸ್ಥಿತಿಗಳಲ್ಲಿ ರಾಸಾಯನಿಕ ಬಂಧಗಳ ವರ್ತನೆಗೆ ಹುಕ್ಸ್ ನಿಯಮವು ಸೂಕ್ತ ಅಂದಾಜಾಗಿದೆ, ಅಂದರೆ ಅವು ರಚಿತವಾಗಿರಬಾರದು ಅಥವಾ ಮುರಿದುಬಿದ್ದಿರಬಾರದು.
ಚಲನಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ನಿರ್ದಿಷ್ಟ ವೇಗಕ್ಕೆ ವಸ್ತುವೊಂದನ್ನು ತರುವ ಉದ್ದೇಶದಿಂದ ವೇಗವರ್ಧನೆಗಾಗಿ ಅಗತ್ಯವಾದ ಕಾರ್ಯಕ್ಕೆ ಚಲನಶಕ್ತಿ ಎನ್ನಲಾಗಿದೆ. (ಚಿಹ್ನೆಗಳು: Ek, T ಅಥವಾ K) ಈ ಕಾರ್ಯದ ಲೆಕ್ಕಹಾಕಿ ಕೆಳಕಂಡ ಸಮೀಕರಣವನ್ನು ಪಡೆಯಬಹುದು:
ಬೆಳಕಿನ ವೇಗ c ಗೆ ಸನಿಹವಾಗುವ ವೇಗಗಳಲ್ಲಿ, ಲೊರೆಂಟ್ಜ್ ರೂಪಾಂತರಗಳನ್ನು ಬಳಸಿ ಈ ಕಾರ್ಯವನ್ನು ಲೆಕ್ಕ ಹಾಕಬೇಕು. ಆ ರೀತಿ ಲೆಕ್ಕ ಹಾಕಿದಾಗ ಕೆಳಕಂಡಂತೆ ಫಲಿತಾಂಶ ದೊರೆಯುತ್ತದೆ:
c ವೇಗಕ್ಕೆ ಹೋಲಿಸಿದಂತೆ ಕಡಿಮೆ ವೇಗವನ್ನು ಲೆಕ್ಕಕ್ಕೆ ತೆಗೆದುಕೊಂಡಲ್ಲಿ ಈ ಸಮೀಕರಣವು ಇದರ ಮೇಲಿನದರಂತೆ ಸರಳವಾಗುತ್ತದೆ. ಈ ಕಾರ್ಯದ ಗಣಿತೀಯ ಉಪ-ಉತ್ಪನ್ನವು (ಹಿಂದಿನ ಸಮೀಕರಣದಲ್ಲಿ ಗಮನಿಸಿದಂತೆ) ವಿಶ್ರಾಮ ಸ್ಥಿತಿಯಲ್ಲಿಯೂ ಸಹ ದ್ರವ್ಯರಾಶಿಯು ಕೆಳಕಂಡ ಸಮೀಕರಣದಂತೆ ಇರುತ್ತದೆ:
ಹೀಗಾಗಿ ಈ ಶಕ್ತಿಗೆ ವಿಶ್ರಾಮ ದ್ರವ್ಯರಾಶಿ ಶಕ್ತಿ ಎನ್ನಲಾಗುತ್ತದೆ.
ಮೇಲ್ಮೈ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಮೇಲ್ಮೈಯಲ್ಲಿ ಕರ್ಷಣವಿದ್ದಲ್ಲಿ (ಉದಾಹರಣೆಗೆ ಹಿಗ್ಗಿಸಲಾದ ರಬರ್ ಅಥವಾ ವಸ್ತುವಿನ ಅಂತರಮುಖಗಳು) ಮೇಲ್ಮೈ ಶಕ್ತಿಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲು ಸಾಧ್ಯವಾಗುವುದು. ಬೆರೆಯದಿರುವ, ಏಕರೂಪದ್ದಲ್ಲದ ಬೇರೆ ಬೇರೆ ವಸ್ತುಗಳ ಮಿಲನವು ಒಂದು ರೀತಿಯ ಮೇಲ್ಮೈಕರ್ಷಣಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ. ಈ ಶಕ್ತಿಗಳು ಚಲಿಸಲು ಅವಕಾಶವಿದ್ದಲ್ಲಿ (ಉದಾಹರಣೆಗೆ, ಲೋಮನಾಳಾಕರ್ಷಣದ ಮೇಲ್ಮೈಯಲ್ಲಿ ಕಂಡಂತೆ); ಸಾಮಾನ್ಯವಾಗಿ ಕನಿಷ್ಠ ಶಕ್ತಿಯ ಅಗತ್ಯವಿರುತ್ತದೆ.
ಉದಾಹರಣೆಗೆ, ಮೇಲ್ಮೈ ಶಕ್ತಿಯು ಅದರ ವಿಸ್ತೀರ್ಣಕ್ಕೆ ಸೂಕ್ತ ಪ್ರಮಾಣಾನುಗುಣವಾಗಿದ್ದಲ್ಲಿ, ಮೇಲ್ಮೈ ಹೊಂದಬಹುದಾದ ಅತ್ಯಲ್ಪ ಶಕ್ತಿಯನ್ನು ಅಲ್ಪತಮ ಮೇಲ್ಮೈ ನಿರೂಪಿಸುತ್ತದೆ. ಈ ಕಾರಣಕ್ಕಾಗಿ, ಕಡಿಮೆ ಗಾತ್ರದ ಸಾಬೂನು ಪದರಗಳು ಅಲ್ಪತಮ ಹೊರತಲಗಳಾಗಿವೆ (ಗಾತ್ರ ಅಲ್ಪವಾದಷ್ಟೂ ಗುರುತ್ವದ ಪ್ರಭಾವ ಕಡಿಮೆಯಾಗುತ್ತದೆ; ತೆರೆದಿರುವಿಕೆಯು ಒತ್ತಡದೇರಿಕೆಯನ್ನು ತಡೆಯುತ್ತದೆ. ಗುಳ್ಳೆಯನ್ನು ಕನಿಷ್ಠ ಶಕ್ತಿಯ ಹೊರತಲವೆಂದು ಗಮನಿಸತಕ್ಕದ್ದು; ಆದರೆ ವ್ಯಾಖ್ಯಾನದಂತೆ ಅಲ್ಪತಮ ಹೊರತಲವಲ್ಲ).
ಶಬ್ದ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಶಬ್ದವು ಯಾವುದೇ ಯಾಂತ್ರಿಕ ಮಾಧ್ಯಮದ ಮೂಲಕ ಪ್ರಸರಿಸುವ ಒಂದು ರೀತಿಯ ಯಾಂತ್ರಿಕ ಕಂಪನ.
ಗುರುತ್ವ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಭೂಮಿಯ ಹೊರತಲದ ಸಮೀಪವಿರುವ ಗುರುತ್ವ ಬಲವು ಎತ್ತರ h ದೊಂದಿಗೆ ವ್ಯತ್ಯಯವಾಗುವುದು ಬಹಳ ಕಡಿಮೆ; ಹಾಗೂ, ದ್ರವ್ಯರಾಶಿ m ಯಿಂದ ಗುಣಿಸಲಾದ ಗುರುತ್ವದ ವೇಗವರ್ಧನೆ g = 9.81 m/s²ಗೆ ಸಮನಾಗಿದೆ. ಈ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಗುರುತ್ವ ಅಂತಸ್ಥಶಕ್ತಿಯ ಸಮೀಕರಣವು ಕೆಳಕಂಡಂತಿದೆ:
ರಾಶಿ ಪ್ರಮಾಣ m1 ಮತ್ತು m2 ಅನ್ನು ಹೊಂದಿರುವ ಎರಡು ವಸ್ತುಗಳ ನಡುವಿನ ನ್ಯೂಟನಿಯನ್ ಗುರುತ್ವದಿಂದ ಉಂಟಾಗುವ ಅಂತಸ್ಥಶಕ್ತಿಗೆ ಸಾಮಾನ್ಯ ಸಮೀಕರಣವು ಕೆಳಕಂಡಂತಿದೆ:
-
- ,
ಇದರಲ್ಲಿ r - ಎರಡೂ ವಸ್ತುಗಳ ನಡುವಿನ ಪ್ರತ್ಯೇಕತೆ; ಹಾಗೂ G ಗುರುತ್ವದ ನಿಯತಾಂಕ , 6.6742(10)×10−11 m3kg−1s−2.[೧೭] ಈ ವಿಚಾರದಲ್ಲಿ, ಉಲ್ಲೇಖಿತ ಸ್ಥಳವು ಎರಡೂ ವಸ್ತುಗಳ ನಡುವಿನ ಅನಂತವಾದ ಪ್ರತ್ಯೇಕತೆಯಾಗಿದೆ.
ಉಷ್ಣ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
| ಉಷ್ಣ ಶಕ್ತಿಯ ಪರಿವರ್ತನೆಯಾಗುವುದು | |
|---|---|
| ಇದರೊಳಗೆ | ಇಂದ |
| ಯಾಂತ್ರಿಕ ಶಕ್ತಿ | ಆವಿ ಚಕ್ರ |
| ಉಷ್ಣ ಶಕ್ತಿ | ತಾಪ ವಿನಿಮಯಕಾರ |
| ವಿದ್ಯುತ್ ಶಕ್ತಿ | ಉಷ್ಣಯುಗ್ಮ |
| ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ | ಶಾಖವುಳ್ಳ ವಸ್ತುಗಳು |
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ | ಊದು ಕುಲುಮೆ (ಬ್ಲಾಸ್ಟ್ ಫರ್ನೇಸ್) |
| ಬೈಜಿಕ ಶಕ್ತಿ | ಮಹಾನವ್ಯತಾರೆ |
ಮಾಧ್ಯಮವು ಒಳಗೊಂಡಿರುವ ಅತಿಸೂಕ್ಷ್ಮ ಕಣಗಳ ಯಾದೃಚ್ಛಿಕ ಚಲನವಲನದೊಂದಿಗೆ ಸಂಬಂಧಿತವಾಗಿರುವ ಶಕ್ತಿಯೇ ಉಷ್ಣಶಕ್ತಿ. (ಅನಿಲ, ಪ್ಲಾಸ್ಮಾ, ಘನ ಇತ್ಯಾದಿಗಳೇ ಕೆಲವು ಮಾಧ್ಯಮಗಳು) ಉದಾಹರಣೆಗೆ, ಏಕಾಣುವಿನ ಅನಿಲದ ವಿಚಾರದಲ್ಲಿ, ಅದು ಕೇವಲ ಅನಿಲಾಣುವಿನ ಚಲನವಲನದ ಚಲನಶಕ್ತಿಯಾಗಿದೆ. ಉಲ್ಲೇಖಿತ ಅನಿಲ ದ್ರವ್ಯರಾಶಿಯ ಕೇಂದ್ರ ಚೌಕಟ್ಟಿನಲ್ಲಿ ಇದರ ಮಾಪನ ಮಾಡಲಾಗಿದೆ. ಅಧಿಕಾಣುಗಳುಳ್ಳ ಅನಿಲವಾದರೆ, ಸುತ್ತುವ ಶಕ್ತಿಯೊಂದಿಗೆ ಕಂಪನ ಶಕ್ತಿಯೂ ಒಳಗೊಂಡಿದೆ. ದ್ರವ ಮತ್ತು ಘನಾಕೃತಿಗಳ ವಿಚಾರದಲ್ಲಿ, ಅಣುಗಳ ಅಂತರಕ್ರಿಯೆಯ ಅಂತಸ್ಥಶಕ್ತಿಯು ಅಡಕಗೊಂಡಿದೆ.
ನಿರ್ದಿಷ್ಟ ಸರಹದ್ದನ್ನು ದಾಟಿ ವರ್ಗಾವಣೆಯಾಗುವ 'ಶಾಖ'ವನ್ನು ಉಷ್ಣ ಶಕ್ತಿ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ (ಉದಾಹರಣೆಗೆ, ಕಾದ ವಸ್ತುವಿನ ಸಂಪರ್ಕದಿಂದ ತಂಪಾಗಿರುವ ವಸ್ತುವಿಗೆ ಶಾಖದ ಹರಿವು). ಸಣ್ಣ ಪ್ರಮಾಣದಲ್ಲಿ ಶಾಖದ ವರ್ಗಾವಣೆಯ ಪ್ರಾಯೋಗಿಕ ವ್ಯಾಖ್ಯಾನವು ಕೆಳಕಂಡಂತಿದೆ:
ಇದರಲ್ಲಿ C v ವ್ಯವಸ್ಥೆಯ ಶಾಖ ಸಾಮರ್ಥ್ಯವಾಗಿದೆ.
ವ್ಯವಸ್ಥೆಯು ಅವಸ್ಥಾ ರೂಪಾಂತರಕ್ಕೊಳಗಾದಲ್ಲಿ ಈ ವ್ಯಾಖ್ಯಾನವು ನಿಲ್ಲುವುದಿಲ್ಲ. (ಉದಾಹರಣೆಗೆ, ಇಬ್ಬನಿಯು ಕರಗಿ ನೀರಾಗುವಂತಹ ವಿಚಾರಗಳಲ್ಲಿ ವ್ಯವಸ್ಥೆಯು ತನ್ನ ಉಷ್ಣಾಂಶವನ್ನು ಹೆಚ್ಚಿಸಿಕೊಳ್ಳದೇ ಶಾಖವನ್ನು ಹೀರಿಕೊಳ್ಳಬಹುದು.) ಇನ್ನಷ್ಟು ಜಟಿಲವಾದ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ, ಉಷ್ಣ ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆಯ ಬದಲು ಆಂತರಿಕ ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆಯನ್ನು ಬಳಸುವುದು ಸೂಕ್ತ.
ಸೈದ್ಧಾಂತಿಕ ಸಮಸ್ಯೆಗಳಿದ್ದರೂ ಸಹ, ಶಕ್ತಿ ಬದಲಾವಣೆಗಳ ಪ್ರಾಯೋಗಿಕ ಮಾಪನದಲ್ಲಿ ಮೇಲಿನ ವ್ಯಾಖ್ಯಾನವು ತುಂಬ ಉಪಯುಕ್ತ. ವಿವಿಧ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಇನ್ನೊಂದು ವಸ್ತುವಿನ (ಉದಾಹರಣೆಗೆ: ನೀರಿನ ತೊಟ್ಟಿ) ಉಷ್ಣಾಂಶವನ್ನು ಹೆಚ್ಚಿಸಲು ವ್ಯವಸ್ಥೆಯೊಂದರಿಂದ ಬಿಡುಗಡೆಯಾದ ಶಕ್ತಿಯನ್ನು ಬಳಸಬಹುದು. (ಉದಾ:ಸ್ನಾನ ಮಾಡುವ ಸಂದರ್ಭ) ವಸ್ತುವೊಂದರ ಉಷ್ಣಾಂಶವನ್ನು ಹೆಚ್ಚಿಸಲು ಅಗತ್ಯವಾದ ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಪ್ರಮಾಣವನ್ನು ಮಾಪನ ಮಾಡಲೂ ಸಾಧ್ಯವಾಗಿದೆ.
ಒಂದು ಗ್ರಾಮ್ ನೀರಿನ ಉಷ್ಣವನ್ನು 1 °Cನಷ್ಟು ಹೆಚ್ಚಿಸಲು ಬೇಕಾದ ಶಕ್ತಿಯ ಪ್ರಮಾಣವನ್ನು ಮೂಲತಃ ಕ್ಯಾಲೊರಿ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿತ್ತು (ಸುಮಾರು 4.1855 J, ಆದರೂ ವ್ಯಾಖ್ಯಾನವು ಆನಂತರ ಬದಲಾಯಿತು). ಒಂದು ಪೌಂಡ್ ನೀರಿನ ಉಷ್ಣವನ್ನು 1 °Fನಷ್ಟು ಹೆಚ್ಚಿಸಲು ಬೇಕಾದ ಶಕ್ತಿಯನ್ನು ಬ್ರಿಟಿಷ್ ಥರ್ಮಲ್ ಯೂನಿಟ್ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿತ್ತು (ಆನಂತರ ಅದು 1055.06 J ಎಂದು ನಿಗದಿಯಾಯಿತು).
ವಿದ್ಯುತ್ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
| ವಿದ್ಯುತ್ ಶಕ್ತಿ ಪರಿವರ್ತನೆಗೊಂಡಿದೆ | |
|---|---|
| ಗೆ | ಇಂದ |
| ಯಾಂತ್ರಿಕ ಶಕ್ತಿ | ವಿದ್ಯುತ್ ಮೊಟಾರ್ |
| ಉಷ್ಣ ಶಕ್ತಿ | ರೋಧಕ |
| ವಿದ್ಯುತ್ ಶಕ್ತಿ | ಪರಿವರ್ತಕ |
| ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ | ಪ್ರಕಾಶ-ಹೊಮ್ಮಿಸುವ ಡಯೋಡ್ |
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ | ವಿದ್ಯುದ್ವಿಚ್ಛೇದನ |
| ಬೈಜಿಕ ಶಕ್ತಿ | ಸಿಂಕ್ರೋಟ್ರಾನ್ |
ಸ್ಥಾಯೀ ವಿದ್ಯುತ್ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಒಂದು ಪ್ರಮಾಣದ ಅಥವಾ ವಿನ್ಯಾಸಗೊಳಿಸಿದ ವಿದ್ಯುತ್ ಅಂತಸ್ಥ ಶಕ್ತಿ ಅಂದರೆ ಎಲ್ಲೆಯಿಲ್ಲದಂತೆ-ಮಹತ್ತರವಾಗಿ ಸಂಯೋಜನೆಗೊಂಡಿರುವ ಸಂಚಿತ ಶಕ್ತಿಯನ್ನು ವಿನ್ಯಾಸಗೊಳಿಸಿದ ಪ್ರಮಾಣಕ್ಕೆ ತರುವುದಕ್ಕೆ ವಿದ್ಯುದಾವೇಶದ ಪ್ರತಿ ಕೂಲಂಬ್ಗೆ ತಗಲುವ ಕಾರ್ಯ ಶಕ್ತಿ. (ಅಥವಾ ವಿದ್ಯದಾವೇಶದ ಪ್ರತಿ ಕೂಲಂಬ್ನಲ್ಲಿ ಎಲ್ಲೆಯಿಲ್ಲದ-ಮಹತ್ತರವಾದ ಅದರ ಸಂಯೋಜನೆಯನ್ನು ಕಳೆದುಕೊಳ್ಳಲು ಎಷ್ಟು ಪ್ರಮಾಣದ ಕಾರ್ಯವಾಗಬೇಕಿದೆ ಎಂಬುದು) Q1 ಮತ್ತು Q2 ಎಂಬ ಎರಡು ವಿದ್ಯುದಾವೇಶಗಳಿಗೆ r ನಷ್ಟು ದೂರಕ್ಕೆ ಕಾರ್ಯವು ವಿದ್ಯುತ್ ಅಂತಸ್ಥ ಶಕ್ತಿ ಮೂಲಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ:
ಇದರಲ್ಲಿ ε0 ನಿರ್ವಾತದ ವಿದ್ಯುತ್ ಸ್ಥಿರಾಂಕ 107/4πc0² ಅಥವಾ 8.854188…×10−12 F/m ಆಗಿದೆ.[೧೭] ಸಂಚಾಯಕಗಳಲ್ಲಿ ಸಂಚಯನ C ನಷ್ಟು ಅದುಮಿಟ್ಟ ಸಂಚಿತ ಶಕ್ತಿಯ ಅನುಗುಣ್ಯ ವಿನ್ಯಾಸದಲ್ಲಿ ಸಾಮಾನ್ಯವಾಗಿ ಸಂಚಿತಶಕ್ತಿಯಲ್ಲಿನ ಮೂಲ ಅಗಲಿಕೆ ಇರದಂತೆ ಮಾಡಲಾಗಿರುತ್ತದೆ.(ಆದುದರಿಂದ ಸಂಚಾಯಕದ ಪ್ಲೇಟ್ಗಳಲ್ಲಿ ಒಂದಕ್ಕೊಂದರ ಸಾಮೀಪ್ಯದಿಂದಾಗಿ ಶೂನ್ಯ ಸಂಚಿತ ಶಕ್ತಿ ಇರುತ್ತದೆ) ಈ ಆಯ್ಕೆಗೆ ಸಮರ್ಥ ಕಾರಣ - ಸಂಚಾಯಕಗಳ ಪ್ಲೇಟ್ಗಳ ಮೇಲಿರುವ ಸಂಚಿತ ಶಕ್ತಿಯ ಪ್ರಮಾಣ ಮತ್ತು ವೋಲ್ಟೇಜ್ ಅನ್ನು ಅಳೆಯುವುದಕ್ಕೆ. ಆದರೆ ಒಂದಕ್ಕೊಂದು ಸಂಚಾಯಕಗಳ ನಡುವಿನ ದೂರವು ಅದರ ಸಂಚಿತ ಶಕ್ತಿಯ ಎಲ್ಲೆಯನ್ನು ಮೀರಬಾರದು, ಬದಲಾಗಿ ಅವು ಸಂಚಿತ ಶಕ್ತಿ ಇಳಿದ ಸಂಚಾಯಕಗಳಾಗಿದ್ದು, ಇನ್ನೇನು ಸಂಚಿತ ಶಕ್ತಿ ಪ್ಲೇಟುಗಳಿಂದ ಹೊಮ್ಮಿಬಿಡುತ್ತದೆ ಎನ್ನುವಷ್ಟು ಮಾತ್ರ ಒಂದಕ್ಕೊಂದು ಹತ್ತಿರ ಇರಬೇಕಾಗುತ್ತದೆ. (ಇಲ್ಲಿ ಎಲೆಕ್ಟ್ರಾನ್ಗಳು ಮತ್ತು ಅಯಾನ್ಗಳು ಪುನಃ ಸೇರಿ ಪ್ಲೇಟ್ಗಳನ್ನು ತಟಸ್ಥಗೊಳಿಸುವುದು). ಈ ಪ್ರಸಂಗದಲ್ಲಿ ಕಾರ್ಯ ಮತ್ತು ವಿದ್ಯುತ್ ಅಂತಸ್ಥಶಕ್ತಿಯು ಹೀಗಿರುತ್ತದೆ:
ವಿದ್ಯುತ್ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ರೋಧಕದ ಮೂಲಕ ಹರಿದಾಗ ವಿದ್ಯುತ್ ಶಕ್ತಿ ಉಷ್ಣಕ್ಕೆ ಬದಲಾಗುತ್ತದೆ. ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ವಿದ್ಯುತ್ ಸಾಧನದ ಮೂಲಕ ಹರಿದಾಗ ಕೆಲ ಮಟ್ಟಿನ ವಿದ್ಯುತ್ ಶಕ್ತಿ ಬೇರೆ ಬೇರೆ ಶಕ್ತಿಯ ರೂಪ ತಾಳುವುದಿದೆ. (ಒಂದಷ್ಟು ವಿದ್ಯುತ್ ಉಷ್ಣತೆಯಲ್ಲಿ ಲಯವಾಗುವುದೂ ಇದೆ). ವಿದ್ಯುತ್ ಪ್ರವಾಹದಿಂದ ಉಂಟಾದ ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಪ್ರಮಾಣವನ್ನು ವಿವಿಧ ರೀತಿಯಲ್ಲಿ ವ್ಯಕ್ತ ಮಾಡಬಹುದು:
U ಎಂಬುದು ವಿದ್ಯುತ್ ಸಾಮರ್ಥ್ಯದ ವ್ಯತ್ಯಾಸ (ವೋಲ್ಟ್ಸ್ ಲೆಕ್ಕದಲ್ಲಿ) Q ಎಂಬುದು ಕೂಲಂಬ್ ಲೆಕ್ಕದಲ್ಲಿರುವ ವಿದ್ಯುದಾವೇಶ, ಆಂಪೀಯರ್ಸ್ ಲೆಕ್ಕದಲ್ಲಿ I ಎಂಬ ವಿದ್ಯುತ್ ಪ್ರವಾಹ, t ಎಂಬುದು ವಿದ್ಯುತ್ತು ಹರಿದ ಸಮಯ ಸೆಕೆಂಡುಗಳಲ್ಲಿ, ವಾಟ್ಸ್ ಲೆಕ್ಕದಲ್ಲಿ P ಎಂಬುದು ಪವರ್ ಮತ್ತು R ಎಂಬುದು ವಿದ್ಯುತ್ ರೋಧ (ಓಮ್ಸ್ನಲ್ಲಿ).
ಪ್ರಾಯೋಗಿಕವಾಗಿ ಶಕ್ತಿಯನ್ನು ಅಳೆಯುವುದಕ್ಕೆ ಈ ಸೂಚಿ ಬಹು ಉಪಯುಕ್ತ. ಶಕ್ತಿಯ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸ, ರೋಧ ಮತ್ತು ಸಮಯ- ಈ ಎಲ್ಲವನ್ನೂ ಕರಾರುವಾಕ್ಕಾಗಿ ಅಳೆಯಬಹುದಾಗಿದೆ.
ಆಯಸ್ಕಾಂತೀಯ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಆಯಸ್ಕಾಂತೀಯ ಶಕ್ತಿ ಹಾಗು ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ನಡುವೆ ಮೂಲಭೂತವಾಗಿ ವ್ಯತ್ಯಾಸವೇನಿಲ್ಲ: ಎರಡೂ ಸಂಗತಿಗಳು ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ಸಮೀಕರಣಕ್ಕೆ ಸಂಬಂಧಪಟ್ಟಿವೆ. ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರ B ನಲ್ಲಿ ಆಯಸ್ಕಾಂತೀಯ ಅಕ್ಷದ ಸುತ್ತದ ಮಹತ್ತ್ವ M ನ ಆಯಸ್ಕಾಂತದ ಅಂತಸ್ಥ ಶಕ್ತಿಯನ್ನು -ಆಯಸ್ಕಾಂತೀಯ ಬಲದ ಕಾರ್ಯವು (ನಿರ್ದಿಷ್ಟವಾಗಿ ಅದು ಆಯಸ್ಕಾಂತೀಯ ಭ್ರಾಮಕ) ಆಯಸ್ಕಾಂತದ ದ್ವಿಧ್ರುವ ಮಹತ್ತ್ವದ ಸದಿಶದ ಪುನರ್ ಜೋಡಣೆ ಎಂದು ವಿವರಿಸಬಹುದು ಮತ್ತು ಅದು ಈ ಕೆಳಗಿನದಕ್ಕೆ ಸಮಾನವಾಗಿರುವುದು:
L ನಷ್ಟು ಚೋದಕತೆ ಹೊಂದಿರುವ ಚೋದನಕಾರಿಯಲ್ಲಿ I ನಷ್ಟು ವಿದ್ಯುತ್ ಪ್ರವಾಹ ತನ್ಮೂಲಕ ಹರಿಯುವಾಗ ಅದು ಶೇಖರಿಸಿರುವ ಶಕ್ತಿಯು ಕೆಳಕಂಡ ಸಮೀಕರಣದಂತೆ ಲೆಕ್ಕಿಸಲಾಗಿದೆ.
ಅಧಿವಾಹಕ ಆಯಸ್ಕಾಂತೀಯ ಶೇಖರಣೆಗೆ ಈ ಎರಡನೆ ಉಕ್ತಿಯು ಅಡಿಪಾಯವಾಗಿದೆ.
ವಿದ್ಯುದ್ಕಾಂತೀಯ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
| ಪರಿವರ್ತಿತ ವಿದ್ಯುದ್ಕಾಂತೀಯ ವಿಕಿರಣ | |
|---|---|
| ಗೆ | ಇಂದ |
| ಯಾಂತ್ರಿಕ ಶಕ್ತಿ | ಸೌರ ಹಾಯಿ |
| ಉಷ್ಣ ಶಕ್ತಿ | ಸೌರ ಸಂಗ್ರಾಹಕ |
| ವಿದ್ಯುತ್ ಶಕ್ತಿ | ಸೌರ ವಿದ್ಯುತ್ಕೋಶ |
| ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ | ಅರೇಖೀಯ ದೃಗ್ವಿಜ್ಞಾನ |
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ | ದ್ಯುತಿ ಸಂಶ್ಲೇಷಣೆ |
| ಬೈಜಿಕ ಶಕ್ತಿ | ಮೋಸ್ಬೇಯರ್ ರೋಹಿತ ದರ್ಶಕ |
ಸಂಚಾಯಕಗಳಲ್ಲಾಗಲಿ ಚೋದನಕಾರಿಗಳಲ್ಲಾಗಲಿ ಒಂದು ಕನಿಷ್ಠ ಪ್ರಮಾಣದ ವಿದ್ಯುತ್ತು ಅಥವಾ ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಸೃಷ್ಟಿಸುವುದಕ್ಕೆ ಬೇಕಾಗುವ ಕಾರ್ಯ ಶಕ್ತಿಯ ಲೆಕ್ಕಾಚಾರವು ವಿದ್ಯುತ್ತು ಮತ್ತು ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳ ಶಕ್ತಿಯ ಸಾಂದ್ರತೆಯಲ್ಲಿ ಪರಿಣಮಿಸುತ್ತದೆ.
ಮತ್ತು
SI ಏಕಮಾನಗಳಲ್ಲಿ
ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣಗಳಾದ ಸೂಕ್ಷ್ಮತರಂಗ, ಗೋಚರ ಬೆಳಕು ಅಥವಾ ಗ್ಯಾಮಾ ಕಿರಣ ಇವುಗಳು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಮೇಲಿನ ಉಕ್ತಿಗಳನ್ನು ಉಪಯೋಗಿಸಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳ ಆಯಸ್ಕಾಂತೀಯ ಮತ್ತು ವಿದ್ಯುತ್ ಘಟಕಗಳ ಘನಗಾತ್ರದ ಸಾಂದ್ರತೆಯನ್ನು ಮತ್ತು ಶಕ್ತಿಯ ಹರಿವನ್ನು e/m ಕ್ಷೇತ್ರದಲ್ಲಿ ಲೆಕ್ಕ ಮಾಡಬಹುದು. ಪರಿಣಾಮವಾಗಿ ಬಂದ ಪಾಯಿಂಟಿಂಗ್ ಸದಿಶ ಹೀಗೆ ವ್ಯಕ್ತವಾಗುತ್ತದೆ:
ಶಕ್ತಿಯ ಹರಿವಿನ ಸಾಂದ್ರತೆ ಮತ್ತು ದಿಕ್ಕನ್ನು SI ಏಕಮಾನಗಳಲ್ಲಿ ಕೊಟ್ಟಿರುತ್ತದೆ.
ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣದ ಶಕ್ತಿಯು ಕ್ವಾಂಟೀಕೃತವಾಗಿದೆ (ಪ್ರತ್ಯೇಕವಾದ ಶಕ್ತಿಯ ಮಟ್ಟಗಳಿರುತ್ತವೆ) ಈ ಮಟ್ಟಗಳ ಅಂತರ ಈ ಕೆಳಗಿನದರ ಸಮಕ್ಕಿರುತ್ತದೆ:
ಇಲ್ಲಿ h ಪ್ಲಾಂಕ್ ನಿಯತಾಂಕ ಆಗಿರುತ್ತದೆ 6.6260693(11)×10−34 Js,[೧೭] ಮತ್ತು v ವಿಕಿರಣದ ಆವರ್ತನೆ. ಇಷ್ಟು ಪ್ರಮಾಣದ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯನ್ನು ಒಂದು ಫೋಟಾನ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಗೋಚರವಾಗುವ ಬೆಳಕಿನಷ್ಟಿನ ಫೋಟಾನ್ಗಳು 270-520 yJಯಷ್ಟು ಶಕ್ತಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಇದು 160-310 KJ/mol,ಗೆ ಸಮವಾಗಿರುವ ಇದು, ದುರ್ಬಲ ರಾಸಾಯನಿಕ ಬಂಧದಷ್ಟು ಶಕ್ತಿ ಹೊಂದಿರುತ್ತದೆ.
ರಾಸಾಯನಿಕ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ ಪರಿವರ್ತಿತಗೊಂಡಿದೆ | |
|---|---|
| ಗೆ | ಇಂದ |
| ಯಾಂತ್ರಿಕ ಶಕ್ತಿ | ಸ್ನಾಯು |
| ಉಷ್ಣ ಶಕ್ತಿ | ಅಗ್ನಿ |
| ವಿದ್ಯುತ್ ಶಕ್ತಿ | ಇಂಧನ ಕೋಶ |
| ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ | ಮಿಣುಕುಹುಳು |
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ | ರಾಸಾಯನಿಕ ಕ್ರಿಯೆ |
ಕಣಗಳಲ್ಲಿನ ಅಣುಗಳ ಬೆಸುಗೆ ಮತ್ತು ವಿವಿಧ ರೀತಿಯ ದ್ರವ್ಯಗಳ ಶಕ್ತಿಯ ಮೊತ್ತವೇ ರಾಸಾಯನಿಕ ಶಕ್ತಿ. ವಿದ್ಯುತ್ ಪೂರಣದ ಸಂದರ್ಭದಲ್ಲಿ, ಎಲೆಕ್ಟ್ರಾನ್ ಮತ್ತು ಪ್ರೋಟಾನ್ಗಳು ಪರಸ್ಪರ ಸ್ಥಾನ ಬದಲಾವಣೆಯ ಪುನರ್-ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಒಟ್ಟಾದಾಗಿನ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ವಿದ್ಯುತ್ ಬಲವು ಮಾಡಿದ ಕಾರ್ಯವಿದು ಎನ್ನಬಹುದು. ಮೂಲಭೂತವಾಗಿ ಇದು ವಿದ್ಯುತ್ ಪೂರಣದ ಸಂದರ್ಭದಲ್ಲಿ ಉಂಟಾಗುವ ಸ್ಥಾಯೀವಿದ್ಯುತ್ ಶಕ್ತಿ. ರಾಸಾಯನಿಕ ಕ್ರಿಯೆಯಲ್ಲಿ ರಾಸಾಯನಿಕ ಶಕ್ತಿ ಕಡಿಮೆ ಆದ ಪಕ್ಷದಲ್ಲಿ ಅನೇಕ ವೇಳೆ ಅದು ಸುತ್ತ-ಮುತ್ತಲ್ಲಿನ ಶಾಖ ಅಥವಾ ಬೆಳಕಿನ ರೂಪದಲ್ಲಿ ವರ್ಗಾವಣೆಯಿಂದಾಗಿ ಆಗಿರುತ್ತದೆ. ಅದೇ ರೀತಿ ರಾಸಾಯನಿಕ ಕ್ರಿಯೆಯಲ್ಲಿ ರಾಸಾಯನಿಕ ಶಕ್ತಿ ಹೆಚ್ಚಾದಲ್ಲಿ ಅದು ಕೂಡ ಸುತ್ತ-ಮುತ್ತಲ್ಲಿನ ಶಾಖ ಮತ್ತು ಬೆಳಕಿನ ರೂಪದಲ್ಲಿ ವರ್ಗಾವಣೆ ಆಗಿರುವುದರಿಂದ ಉಂಟಾಗಿರುತ್ತದೆ. ಉದಾಹರಣೆಗೆ,
- ಯಾವಾಗ ಎರಡು ಜಲಜನಕ ಪರಮಾಣುಗಳು ಪ್ರತಿಕ್ರಿಯಿಸಿ ದ್ವಿಜಲಜನಕ ಅಣುವಾಗುತ್ತೋ ಆಗ ರಾಸಾಯನಿಕ ಶಕ್ತಿ 724 zJ(H-H ನ ಬಂಧಕ ಶಕ್ತಿ) ಅಷ್ಟು ಕಡಿಮೆ ಆಗುತ್ತದೆ.
- ಜಲಜನಕದ ಪರಮಾಣುವಿನಿಂದ ಎಲೆಕ್ಟ್ರಾನನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ಹೊರತೆಗೆದಾಗ ಅದು ಅನಿಲ ಹಂತದ ಜಲಜನಕ ಅಯಾನ್ ಆಗಿರುತ್ತದೆ (ಅನಿಲ ಹಂತದಲ್ಲಿ), ರಾಸಾಯನಿಕ ಶಕ್ತಿ 2.18 aJ ನಷ್ಟು ವರ್ಧಿಸುತ್ತದೆ. ಇದು ಜಲಜನಕದ ಅಯಾನೀಕರಣ ಶಕ್ತಿ.
ಪ್ರಶ್ನಿತ ದ್ರವ್ಯದ ಒಂದು ಮೋಲ್ನಲ್ಲಿ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯ ಅತಿ ಸಣ್ಣ ಬದಲಾವಣೆಯನ್ನೂ ಗಮನಿಸುವುದು ಸಾಮಾನ್ಯ. ರಾಸಾಯನಿಕ ಕ್ರಿಯೆಯಲ್ಲಿ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯ ಬದಲಾವಣೆಯು ಹಂತ ಹಂತವಾಗಿ ಪ್ರತಿ ಮೋಲ್ಗೆ ಹತ್ತರಿಂದ ನೂರಾರು ಕಿಲೋಜೂಲ್ಸ್ವರೆಗೂ ವಿಶಿಷ್ಟ ಮೌಲ್ಯಗಳು ಬದಲಾಗುತ್ತವೆ.
ಮೇಲೆ ವಿವರಿಸಿದ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯನ್ನು ರಸಾಯನ ಶಾಸ್ತ್ರಜ್ಞರು ತಾಂತ್ರಿಕವಾಗಿ ಆಂತರಿಕ ಶಕ್ತಿ U ಅನ್ನುತ್ತಾರೆ. ವ್ಯವಸ್ಥೆಯ ನಿಯತಾಂಕವನ್ನು ಇಟ್ಟುಕೊಂಡು ಇದರ ಪರಿಮಾಣವನ್ನು ಅಳೆಯಬಹುದಾಗಿದೆ. ಏನೇ ಆದರೂ ಬಹಳಷ್ಟು ರಾಸಾಯನಿಕಗಳು ಕಾರ್ಯಾಚರಣೆಯಲ್ಲಿ ಒತ್ತಡವನ್ನು ಸ್ಥಿರವಾಗಿ ನಿಭಾಯಿಸುತ್ತವೆ ಮತ್ತು ಕ್ರಿಯೆಯಲ್ಲಿ ಪರಿಮಾಣ ಬದಲಾದರೆ (ಉದಾ:ಅನಿಲವನ್ನು ಹೊರ ಬಿಡುವುದಾಗಿರಬಹುದು), ಶಾಖಪ್ರಮಾಣ, H ಪಡೆಯಲು ಎಷ್ಟು ತಿದ್ದುಪಡಿ ಕಾರ್ಯ ಅಗತ್ಯವಾಗುತ್ತದೆ ಎಂದು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕಾಗುತ್ತದೆ.
-
- ΔH = ΔU + pΔV
ರಾಸಾಯನಿಕ ಕ್ರಿಯೆ ನಡೆಯುತ್ತದೆಯೋ ಇಲ್ಲವೋ ಎಂದು ಅರಿಯಲು ಮತ್ತು ಗಿಬ್ಸ್ ಮುಕ್ತ ಶಕ್ತಿ G ಅನ್ನು ಕೊಡಲು ಅಲಭ್ಯ ಪ್ರಮಾಣ S ನಲ್ಲಿಯ ಬದಲಾವಣೆಯನ್ನು ಗೊತ್ತು ಮಾಡಿಕೊಳ್ಳಲು ಎರಡನೆಯ ತಿದ್ದುಪಡಿಯು ಅಗತ್ಯವಾಗುತ್ತದೆ.
-
- ΔG = ΔH − TΔS
ಈ ತಿದ್ದುಪಡಿಗಳು ಕೆಲವೊಮ್ಮೆ ಗಣನೀಯವಲ್ಲದಂತೆ ತೋರುವುದಾದರೂ ಹಲವುವೇಳೆ ಸಂಭವಿಸುವುದಿಲ್ಲ (ಅನಿಲಗಳನ್ನು ಒಳಗೊಂಡ ಕ್ರಿಯೆಗಳಲ್ಲಿ ಇದು ವಿಶೇಷ)
ಕೈಗಾರಿಕಾ ಕ್ರಾಂತಿ ಆದಾಗಿನಿಂದ ಕಲ್ಲಿದ್ದಲು, ತೈಲ, ನಿಸರ್ಗಾನಿಲ ಅಥವಾ ಇವುಗಳಿಂದ ದೊರೆತ ಉತ್ಪಾದನೆಗಳನ್ನು ಉರಿಸುವುದರಿಂದ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯು ವಿವಿಧ ರೀತಿಯ ಶಕ್ತಿಯಾಗಿ ಸಮಾಜದ ಮೇಲೆ ಪ್ರಭಾವ ಬೀರುವ ಶಕ್ತಿಯಾಗಿ ರೂಪಾಂತರಗೊಂಡಿದೆ. ಈ ಪಳೆಯುಳಿಕೆ ಇಂಧನಗಳ ದಹನದಿಂದಾಗಿ ಬಿಡುಗಡೆಯಾಗುವ ಶಕ್ತಿ ಯಾವುದೇ ಸಮಾಜದಲ್ಲಿ ಅಥವಾ ದೇಶದಲ್ಲಿ ಶಕ್ತಿ ಕ್ಷಯ (ನಿಜವಾಗಿ ಶಕ್ತಿಯ ರೂಪಾಂತರ ಎಂದೇ ಹೇಳಬೇಕು)ದ ಸರಾಸರಿ ಬಿಡುಗಡೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ:
- 1 ಟನ್ ಕಲ್ಲಿದ್ದಿಲು ಸಮಾನವಾದದ್ದು = 29.3076 GJ = 8,141 ಕಿಲೊವ್ಯಾಟ್ ಅವರ್
- 1 ಟನ್ ತೈಲಕ್ಕೆ ಸಮಾನವಾದದ್ದು (TOE) = 41.868 GJ = 11,630 ಕಿಲೊವ್ಯಾಟ್ ಅವರ್
ಇದೇ ಆಧಾರದ ಮೇಲೆ ಪೂರ್ತಿ ತುಂಬಿದ ಒಂದು ಗ್ಯಾಸೋಲೀನ್ ಟ್ಯಾಂಕು (45 ಲೀಟರ್, 12 ಗ್ಯಾಲನ್ಸ್) ಸಮಾನವಾದದ್ದು 1.6 GJಯಷ್ಟು ರಾಸಾಯನಿಕ ಶಕ್ತಿಗೆ. ಮತ್ತೊಂದು ರಾಸಾಯನಿಕವಾಗಿ ಆಧಾರಿತ ಶಕ್ತಿಯನ್ನು ಅಳೆಯುವ ಏಕಮಾನ "ಟಿಎನ್ಟಿ ಯ ಟನ್ನು", 4.184 GJ ಎಂದು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ 1 ಟನ್ ತೈಲ ಉರಿಸಿದರೆ 1 ಟನ್ ಟಿಎನ್ಟಿ ಸ್ಫೋಟವಾದಾಗ ಬಿಡುಗಡೆ ಆಗುವುದಕ್ಕಿಂತ ಸುಮಾರು 10 ಪಟ್ಟು ಹೆಚ್ಚು ಶಕ್ತಿ ಬಿಡುಗಡೆಯಾಗುತ್ತದೆ: ಶಕ್ತಿಯು ನಿಧಾನ ಗತಿಯಲ್ಲಿ ಅತ್ಯಂತ ನಿಯಂತ್ರಿತ ರೀತಿಯಲ್ಲಿ ಬಿಡುಗಡೆ ಗೊಳ್ಳುವುದೊಂದು ಅದೃಷ್ಟ.
ಬ್ಯಾಟರಿಗಳಲ್ಲಿ ಮತ್ತು ಆಹಾರದಲ್ಲಿ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯನ್ನು ಶೇಖರಿಸುವುದೊಂದು ಸರಳ ಉದಾಹರಣೆ. ಆಹಾರ ಜೀರ್ಣಗೊಂಡಾಗ ಮತ್ತು ಚಯಾಪಚಯ ಕ್ರಿಯೆಗೆ ಒಳಗಾದಾಗ (ಹೆಚ್ಚಿನ ವೇಳೆ ಆಮ್ಲಜನಕದೊಂದಿಗೆ) ರಾಸಾಯನಿಕ ಶಕ್ತಿ ಬಿಡುಗಡೆಗೊಳ್ಳುತ್ತದೆ. ಇದು ಶಾಖ ಶಕ್ತಿ ಅಥವಾ ಸ್ನಾಯು ಶಕ್ತಿ ಆಗಿ ರೂಪಾಂತರಗೊಂಡು ಚಲನಶಕ್ತಿಯಾಗಿ ಮಾರ್ಪಡುತ್ತದೆ.
ಬೈಜಿಕ ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
| ಬೈಜಿಕ ಶಕ್ತಿ ಪರಿವರ್ತನೆ | |
|---|---|
| ಗೆ | ಇಂದ |
| ಯಾಂತ್ರಿಕ ಶಕ್ತಿ | ಆಲ್ಫಾ ವಿಕಿರಣ |
| ಉಷ್ಣ ಶಕ್ತಿ | ಸೂರ್ಯ |
| ವಿದ್ಯುತ್ ಶಕ್ತಿ | ಬೀಟಾ ವಿಕಿರಣ |
| ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ | ಗ್ಯಾಮಾ ವಿಕಿರಣ |
| ರಾಸಾಯನಿಕ ಶಕ್ತಿ | ವಿಕಿರಣಶೀಲ ಕ್ಷಯ |
| ಬೈಜಿಕ ಶಕ್ತಿ | ಬೈಜಿಕ ಸಮಾಂಗತೆ |
ಬೈಜಿಕ ವಿದಳನ ಮತ್ತು ಬೈಜಿಕ ಸಮ್ಮಿಳನದ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಬಿಡುಗಡೆಯಾಗುವ ಶಕ್ತಿ ಪರಮಾಣು ಅಂತಸ್ಥಶಕ್ತಿ, ಜೊತೆಗೆ ವಿದ್ಯುತ್ ಅಂತಸ್ಥ ಶಕ್ತಿಗೆ ಶಕ್ತಿ ಒದಗಿಬರುತ್ತದೆ. ಈ ಎರಡೂ ಪ್ರಕ್ರಿಯೆಗಳ ಫಲಿತಾಂಶಗಳೆಂದರೆ ಬೈಜಿಕ ಕೇಂದ್ರಗಳು. ತನ್ನ ಬೈಜಿಕ ಕೇಂದ್ರದಲ್ಲಿ ಪ್ರಶಸ್ತವಾಗಿ ಬೈಜಿಕ ಶಕ್ತಿಯನ್ನು (ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯ ವಿರೋಧವಿರುತ್ತದೆ) ಕ್ರಿಯೆಗಿಂತಲೂ ಹಿಂದಿಗಿಂತ ಹೆಚ್ಚು ಒತ್ತಾಗಿ ಬೈಜಿಕ ಕಣಗಳನ್ನು ಬಂಧಿಸಿರುತ್ತದೆ.
ದುರ್ಬಲ ಬೈಜಿಕ ಶಕ್ತಿ, (ಶಕ್ತಿಯುತವಾದದ್ದಕ್ಕಿಂತಲೂ ಭಿನ್ನವಾದದ್ದು) ವಿಕಿರಣ ಕ್ಷಯ ಮತ್ತು ಬೀಟಾ ಕ್ಷಯಗಳಿಗೆ ಅಂತಸ್ಥ ಶಕ್ತಿಯನ್ನು ನೀಡುತ್ತದೆ. ಬೈಜಿಕ ಪ್ರಕ್ರಿಯೆಗಳಲ್ಲಿ ಹೊರಹೊಮ್ಮುವ ಶಕ್ತಿ ಅತ್ಯಂತ ದೊಡ್ಡದಾಗಿದ್ದು, ಶಕ್ತಿ ಹೊರ ಹೊಮ್ಮಿದ ನಂತರ ದ್ರವ್ಯರಾಶಿಯ ಸಾಪೇಕ್ಷ ಬದಲಾವಣೆ ಪ್ರತಿ ಸಾವಿರಕ್ಕೆ ಅದೆಷ್ಟೊ ಭಾಗದಷ್ಟಾಗುತ್ತದೆ.
ಬೈಜಿಕ ಸಮ್ಮಿಳನ ಮತ್ತು ವಿದಳನ ಪ್ರಕ್ರಿಯೆಗಳಲ್ಲಿ ಬೈಜಿಕ ಕಣಗಳಾದ ಪ್ರೋಟಾನ್ ಮತ್ತು ನ್ಯೂಟ್ರಾನ್ಗಳು (ನ್ಯೂಕ್ಲಿಯಾನ್ಗಳು) ನಾಶವಾಗುವುದಿಲ್ಲ (ಬೇರ್ಯಾನ್ ಸಂಖ್ಯೆಯ ಸಂರಕ್ಷಣಾ ನಿಯಮ) ಕೆಲವು ಲಘು ಕಣಗಳು ಸೃಷ್ಟಿಯಾಗಬಹುದು ಅಥವಾ ನಾಶವಾಗಬಹುದು (ಉದಾ; ಬೀಟಾ ಮೈನಸ್ ಮತ್ತು ಬೀಟಾ ಪ್ಲಸ್ ಕ್ಷಯ ಅಥವಾ ಎಲೆಕ್ಟಾನ್ ಸೆರೆ ಕ್ಷಯ) ಆದರೆ ಈ ಕಿರಿದಾದ ಪ್ರಕ್ರಿಯೆಗಳು ಬೈಜಿಕ ವಿದಳನ ಮತ್ತು ಸಮ್ಮಿಳನ ಪ್ರಕ್ರಿಯೆಗಳ ಶಕ್ತಿಯ ಬಿಡುಗಡೆಗೆ ಅಷ್ಟೊಂದು ಮುಖ್ಯವಲ್ಲ. ಅದಕ್ಕಿಂತಲ್ಲೂ ಹೆಚ್ಚಾಗಿ, ಬೇರ್ಯಾನ್ (=ಭಾರಕಣ) ಸಂಗ್ರಹಗಳು ಹೆಚ್ಚು ಒತ್ತಾಗಿ ಬಂಧಿತವಾದಾಗ ವಿದಳನ ಮತ್ತು ಸಮ್ಮಿಳನ ಪ್ರಕ್ರಿಯೆಗಳಲ್ಲಿ ಹೆಚ್ಚು ಶಕ್ತಿ ಹೊರಹೊಮ್ಮುತ್ತದೆ ಮತ್ತು ಈ ಶಕ್ತಿ ಬೈಜಿಕ ಕೇಂದ್ರದ ದ್ರವ್ಯರಾಶಿಯ ಕೆಲವು ಭಾಗ (ಸಂಪೂರ್ಣವಲ್ಲ) ಕ್ರಿಯೆಯಲ್ಲಿ ಶಾಖ ಮತ್ತು ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣವನ್ನು ಹೊರಸೂಸುತ್ತದೆ. ಈ ಶಾಖ ಮತ್ತು ವಿಕಿರಣ "ಕಳೆದು ಹೋದ" ದ್ರವ್ಯರಾಶಿಯನ್ನು ಉಳಿಸಿಕೊಳ್ಳುತ್ತದೆ ಆದರೆ ದ್ರವ್ಯರಾಶಿಯು ಶಾಖ ಮತ್ತು ಬೆಳಕಿನ ರೂಪದಲ್ಲಿ ತಪ್ಪಿಸಿಕೊಂಡು ಅಳತೆಗೆ ಒಳಪಡದ ವ್ಯವಸ್ಥೆಯತ್ತ ಸಾಗುತ್ತದೆ.
ಸೌರ ಶಕ್ತಿ ಎನ್ನಲಾಗುವ ಸೂರ್ಯನ ಶಕ್ತಿಯ ಪರಿವರ್ತನೆ ಇದಕ್ಕೊಂದು ಉದಾಹರಣೆ. ಸೂರ್ಯನಲ್ಲಿ, ಪ್ರತಿ ಸೆಕೆಂಡಿಗೆ ಜಲಜನಕದ ಸಮ್ಮಿಳನ 4 ದಶಲಕ್ಷ ಮೆಟ್ರಿಕ್ ಟನ್ ಸೌರ ಭೌತದ್ರವ್ಯವನ್ನು ಬೆಳಕಾಗಿ ಪರಿವರ್ತಿಸಿ ಅಂತರಿಕ್ಷದಲ್ಲಿ ಸೂಸಲ್ಪಡುತ್ತದೆ. ಈ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಸೂರ್ಯನ ಪ್ರೋಟಾನ್ಗಳು ಮತ್ತು ನ್ಯೂಟ್ರಾನ್ಗಳ ಸಂಖ್ಯೆಯಲ್ಲಿ ಬದಲಾವಣೆಯಾಗುವುದಿಲ್ಲ. ಈ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಬೆಳಕು ದ್ರವ್ಯರಾಶಿಯ ಜಡತ್ವದ ಸಮತೆಯನ್ನ ಉಳಿಸಿಕೊಂಡಿರುತ್ತದೆ ಮತ್ತು ಆ ಯಾವ ದ್ರವ್ಯರಾಶಿಯು ಪ್ರತಿ ಸೆಕೆಂಡಿಗೆ 4 ದಶಲಕ್ಷ ಟನ್ ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೋ ಅದು ಅಂತರಿಕ್ಷದಲ್ಲಿ ಚಲಿಸುತ್ತಿರುತ್ತದೆ. ರಚನೆಗೊಂಡ ಪ್ರತಿ ಹೀಲಿಯಂ ಬೈಜಿಕ ಕೇಂದ್ರ ನಾಲ್ಕು ಪ್ರೋಟಾನ್ಗಳಿಗಿಂತ ಕಡಿಮೆ ಸಾಂದ್ರದ್ದಾಗಿದ್ದು (ಒಂದು ಅಂದಾಜಿನ ಪ್ರಕಾರ) ಆದರೆ ಸೂರ್ಯನ ಬೈಜಿಕ ಅಂತಸ್ಥಶಕ್ತಿಯಿಂದ ಬೆಳಕು ಪರಿವರ್ತನೆಯಾಗುವ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಯಾವುದೇ ಕಣಗಳಾಗಲಿ ಅಥವಾ ಪರಮಾಣುಗಳಾಗಲಿ ನಾಶವಾಗಿರುವುದಿಲ್ಲ.
ಶಕ್ತಿಯ ರೂಪಾಂತರಗಳು[ಬದಲಾಯಿಸಿ]
ಒಂದು ಪ್ರಕಾರದ ಶಕ್ತಿಯನ್ನು ಇನ್ನೊಂದು ಪ್ರಕಾರಕ್ಕೆ ಸಾಧನಗಳ ಸಹಾಯದಿಂದ ಪದೇ ಪದೇ ರೂಪಾಂತರಗೊಳಿಸಬಹುದು. ಉದಾ: ಬ್ಯಾಟರಿ- ರಾಸಾಯನಿಕ ಶಕ್ತಿಯಿಂದ ವಿದ್ಯುತ್ ಶಕ್ತಿ; ಅಣೆಕಟ್ಟು: ಗುರುತ್ವ ಅಂತಸ್ಥಶಕ್ತಿಯಿಂದ ಚಲನಶಕ್ತಿಗೂ (ನೀರು ಹಾಯಿಸಿ ಜಲಚಕ್ರ ಭ್ರಮಣೆಯಿಂದ). ಕೊನೆಗೆ ವಿದ್ಯುತ್ ಜನಕದ ಮುಖಾಂತರ ವಿದ್ಯುತ್ ಶಕ್ತಿಯಾಗಿಯೂ ರೂಪಾಂತರಿಸುವುದು ಸಾಧ್ಯ. ಅದೇ ರೀತಿ ರಾಸಾಯನಿಕ ಸ್ಫೋಟದ ವಿಚಾರದಲ್ಲಿ ಅತ್ಯಂತ ಅಲ್ಪಾವಧಿಯಲ್ಲಿ ರಾಸಾಯನಿಕ ಅಂತಸ್ಥಶಕ್ತಿಯು ಚಲನಶಕ್ತಿಯಾಗಿ ಮತ್ತು ಉಷ್ಣ ಶಕ್ತಿ ಆಗಿ ರೂಪಾಂತರವಾಗುತ್ತದೆ. ಲೋಲಕ (ಪೆಂಡ್ಯೂಲಂ) ಇದಕ್ಕೆ ಮತ್ತೊಂದು ಉದಾಹರಣೆ. ಅದರ ತುತ್ತ ತುದಿಗೆ ಚಲನ ಶಕ್ತಿ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ ಮತ್ತು ಗುರುತ್ವ ಅಂತಸ್ಥ ಶಕ್ತಿ ಗರಿಷ್ಠ ಮಟ್ಟದ್ದಾಗಿರುತ್ತದೆ. ಮತ್ತು ಅದರ ಕನಿಷ್ಠ ಬಿಂದುವಿನಲ್ಲಿ ಚಲನ ಶಕ್ತಿ ಗರಿಷ್ಠವಾಗಿದ್ದು ಅಂತಸ್ಥ ಶಕ್ತಿ ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ. ಶಕ್ತಿಯ ರೂಪಾಂತರ ಪ್ರಕ್ರಿಯೆಗಳಲ್ಲಿ ಘರ್ಷಣವಿರುವುದಿಲ್ಲ. ಅದು ಪರಿಪೂರ್ಣ ಎಂದು (ಅವಾಸ್ತವಿಕವಾಗಿ) ಅಂದುಕೊಂಡರೆ ಲೋಲಕ ಅವಿರತವಾಗಿ ಎಂದಿಗೂ ಆಡುತ್ತಲೇ ಇರಬೇಕಾಗುತ್ತದೆ.
ಶಕ್ತಿ ತೂಕವನ್ನು ಹೆಚ್ಚಿಸುತ್ತದೆ ಮತ್ತು ಅದು ದ್ರವ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ಪ್ರತಿಕ್ರಮದಲ್ಲೂ ಇದೇ ವರ್ತನೆ ಇರುತ್ತದೆ. ಆಲ್ಬರ್ಟ್ ಐನ್ಸ್ಟೈನ್ (1905) ಸಂಶೋಧಿಸಿದ ಪ್ರಕಾರ, E = mc² ಸೂತ್ರ, ದ್ರವ್ಯರಾಶಿ ಮತ್ತು ವಿಶೇಷ ಸಾಪೇಕ್ಷತೆ ಅಡಿಯಲ್ಲಿ ವಿಶ್ರಾಮ ಶಕ್ತಿಯನ್ನು ಪರಿಮಾಣಿಸುತ್ತದೆ. ಜೆ.ಜೆ.ಥಾಮ್ಸನ್ (1881), ಹೆನ್ರಿ ಪಾಯಿನ್ಕೇರ್ (1900), ಫ್ರೆಡ್ರಿಚ್ ಹಸೆನೋರೆಲ್ (1904) ಮತ್ತು ಇತರರು ವಿವಿಧ ಸಿದ್ಧಾಂತಗಳ ಚೌಕಟ್ಟಿನಲ್ಲಿ ಇದೇ ರೀತಿಯ ಸೂತ್ರಗಳನ್ನು ಸಂಶೋಧಿಸಿದ್ದಾರೆ. ಸಾಮಾನ್ಯ ಮಾನವನ ಮಾಪನಕ್ಕೆ ತೀರಾ ದೊಡ್ದದಾಗಿರುಗುವುದು. ಸರ್ವೇಸಾಧಾರಣ ಪ್ರಮಾಣದ ದ್ರವ್ಯರಾಶಿ (ಅಂದಾಜು 1 ಕೆಜಿ) ಬೇರೊಂದು ಶಕ್ತಿಗೆ ರೂಪಾಂತರವಾದಾಗ, ಬೈಜಿಕ ರಿಯಾಕ್ಟರುಗಳು ಮತ್ತು ಬೈಜಿಕ ಶಸ್ತ್ರಗಳಲ್ಲಿ ಕಾಣುವಂತೆ ಪ್ರಚಂಡ ಶಕ್ತಿ ಬಿಡುಗಡೆಯಾಗುವುದನ್ನು ಕಾಣಬಹುದು (ಜೂಲ್ಸ್). ವ್ಯತಿರಿಕ್ತವಾಗಿ, ಶಕ್ತಿಯ ಏಕಮಾನದ ದ್ರವ್ಯರಾಶಿ ಸಮಾನ ವಸ್ತುವು ತೀರಾ ಕಿರಿದು. ಅದಕ್ಕಾಗಿಯೇ ಲಯವಾದ ಶಕ್ತಿಯನ್ನು ಎಷ್ಟೋ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಭಾರೀ ಪ್ರಮಾಣದ ಶಕ್ತಿ ಲಯವಾಗದ ಹೊರತು ಅದನ್ನು ಅಳೆಯಲಾಗದು. ಶಕ್ತಿಯು ದ್ರವ್ಯರಾಶಿಯಾಗಿ (ಕಣಗಳ) ರೂಪಾಂತರಗೊಳ್ಳುವ ಉದಾಹರಣೆಗಳನ್ನು ಪ್ರಖರ ಶಕ್ತಿಯ ಬೈಜಿಕ ಭೌತವಿಜ್ಞಾನದಲ್ಲಿ ಕಾಣಬಹುದು.
ನಿಸರ್ಗದಲ್ಲಿ ಶಕ್ತಿಯ ರೂಪಾಂತರಗಳನ್ನು ಮೂಲಭೂತವಾಗಿ ಎರಡು ರೀತಿಯಲ್ಲಿ ವಿಂಗಡಿಸಲಾಗಿದೆ: ಉಷ್ಣಬಲ ವಿಜ್ಞಾನರೀತ್ಯಾ ಪೂರ್ವಸ್ಥಿತಿಗೆ ತರಬಲ್ಲ ಮತ್ತು ಉಷ್ಣಬಲ ವಿಜ್ಞಾನರೀತ್ಯಾ ಪೂರ್ವಸ್ಥಿತಿಗೆ ತರಲಾಗದ. ಉಷ್ಣಬಲ ವಿಜ್ಞಾನದಲ್ಲಿ ಪೂರ್ವಸ್ಥಿತಿಗೆ ತರಬಲ್ಲ ಶಕ್ತಿಯು ಶಕ್ತಿ ರಹಿತ ಕ್ಷೇತ್ರದಲ್ಲಿ ಹರಡಿ ಹಂಚಿಹೋಗದು. ಇನ್ನೂ ಹೆಚ್ಚಿನ ಶಕ್ತಿಯ ಪತನವಾಗದ ಹೊರತು ಅದನ್ನು ಒಟ್ಟುಗೂಡಿಸಿದ ರೀತಿಯಲ್ಲಿ ಮರಳಿ ಪಡೆಯಲಾಗದು. ಹೀಗೆ ಚೆದುರುವಿಕೆ ಘಟಿಸಿದಾಗ ಅದು ಪೂರ್ವಸ್ಥಿತಿಗೆ ತರಬಲ್ಲ ಪ್ರಕ್ರಿಯೆ. ಉದಾಹರಣೆಗೆ, ಮೇಲೆ ವಿವರಿಸಿದ ಲೋಲಕದ ರೀತಿಯಲ್ಲಿ ಒಂದು ರೀತಿಯ ಅಂತಸ್ಥ ವಲಯದಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ರೂಪಾಂತರಗೊಳ್ಳುವ ಶಕ್ತಿ ಪೂರ್ವಸ್ಥಿತಿಗೆ ತರಬಲ್ಲದ್ದಾಗಿರುತ್ತದೆ. ಎಷ್ಟೇ ಕನಿಷ್ಠ ಶಕ್ತಿಯ ಕ್ವಾಂಟಂ ಸ್ಥಿತಿಯು ಪರಮಾಣುಗಳ ನಡುವೆ ಪ್ರಚೋದಿತವಾಗಿದ್ದರೂ, ಶಾಖೋತ್ಪನ್ನವಾಗಿದ್ದ ಪಕ್ಷದಲ್ಲಿ ಅವು ಶಕ್ತಿಯ ಸ್ವಲ್ಪ ಭಾಗಕ್ಕೆ ಸಂಗ್ರಹಾಗಾರದಂತೆ ವರ್ತಿಸುತ್ತದೆ. ಶಕ್ತಿ ರೂಪಾಂತರದ ಪ್ರಕ್ರಿಯೆಗಳಲ್ಲಿ ಶೇಖಡ ನೂರು ಬದಲಾವಣೆಯಷ್ಟು ಅವನ್ನು ಮರಳಿ ಪಡೆಯಲಾಗುವುದಿಲ್ಲ. ಈ ಪರಿಸ್ಥಿಯಲ್ಲಿ ಪೂರ್ಣವಾಗಿ ಉಪಯೋಗಿಸಲ್ಪಡುವ ಶಕ್ತಿ ಆಗಲಾರದು. ಇದರಲ್ಲಿ ಆಂಶಿಕವಾಗಿ ಶಾಖದ ರೂಪದಲ್ಲಿ ಇರುತ್ತದೆ. ವಿಶ್ವದಲ್ಲಿ ಕ್ವಾಂಟಂ ಸ್ಥಿತಿಯ ಏರು-ಪೇರು ಘಟಿಸಿ (ಭೌತ ದ್ರವ್ಯ ವಿಸ್ತಾರವಾಗಿಯೋ ಅಥವಾ ಹರಳಿನಲ್ಲಿ ಯಾದೃಚ್ಛಿಕೀಕರಣ ಆಗುವ ಮುಖಾಂತರವೋ) ಭಿನ್ನ ರೀತಿಯಲ್ಲಿ ಶಾಖ ಹೆಚ್ಚಾದಾಗ ಮಾತ್ರ ಪೂರ್ಣವಾಗಿ ಶಕ್ತಿ ಉಪಯೋಗಿಸಲ್ಪಡಬಹುದು.
ಕಾಲಾನಂತರದಲ್ಲಿ ವಿಶ್ವ ವಿಕಸಿಸಿದಂತೆಲ್ಲಾ ಹೆಚ್ಚೆಚ್ಚು ಶಕ್ತಿ ಪೂರ್ವಸ್ಥಿತಿಗೆ ತರಲಾಗದ ಸ್ಥಿತಿಯಲ್ಲಿ ಸಿಕ್ಕುಬಿದ್ದಿದೆ (ಅಂದರೆ ಶಾಖ ಮತ್ತಿತ್ತರ ಅವ್ಯವಸ್ಥೆ ಅಧಿಕಗೊಳ್ಳುತ್ತದೆ). ಇದನ್ನು ಉಷ್ಣ ಶಕ್ತಿಯಿಂದ ಉಂಟಾದ ಅನಿವಾರ್ಯ ಶಾಖದಿಂದಾಗುವ ವಿಶ್ವದ ಅಂತ್ಯ ಎಂದು ಉಲ್ಲೇಖಿಸಲಾಗುತ್ತದೆ. ಈ ರೀತಿಯ ಉಷ್ಣಮರಣದಿಂದ ವಿಶ್ವದ ಶಕ್ತಿಯಲ್ಲಿ ಬದಲಾವಣೆ ಆಗುವುದಿಲ್ಲ, ಆದರೆ ಶಕ್ತಿಯಲ್ಲಿ ಸ್ವಲ್ಪ ಭಾಗ- ಶಾಖದ ಎಂಜಿನ್ ಮುಖಾಂತರ ಕಾರ್ಯ ನಿರ್ವಹಣೆಗೆ ಅಥವಾ ಉಪಯೋಗಿಸಬಹುದಾದ ಶಕ್ತಿಯನ್ನಾಗಿ ರೂಪಾಂತರಗೊಳ್ಳುವುಕ್ಕೆ (ಶಾಖದ ಎಂಜಿನ್ಗೆ ಅಳವಡಿಸಿರುವ ಜನರೇಟರ್ನಿಂದ), ಇರುವ ಪಾಲಿನ ಶಕ್ತಿ ಕಡಿಮೆ ಆಗುತ್ತಾ ಹೋಗುತ್ತದೆ.
ಶಕ್ತಿ ಸಂರಕ್ಷಣೆಯ ನಿಯಮಗಳು[ಬದಲಾಯಿಸಿ]
ಶಕ್ತಿ ಸಂರಕ್ಷಣೆಯ ನಿಯಮಕ್ಕೆ ಶಕ್ತಿಯು ಅಧೀನವಾಗಿದೆ. ಈ ನಿಯಮದ ಪ್ರಕಾರ ಶಕ್ತಿಯನ್ನು ಸೃಷ್ಟಿಸುವುದಕ್ಕಾಗಲಿ (ಉತ್ಪಾದಿಸುವುದಕ್ಕಾಗಲಿ) ಅಥವಾ ತನ್ನಷ್ಟಕ್ಕೇ ತಾನು ನಾಶವಾಗುವುದಕ್ಕಾಗಲಿ ಸಾಧ್ಯವಿಲ್ಲ. ಅದನ್ನು ಕೇವಲ ರೂಪಾಂತರಗೊಳಿಸಬಹುದಷ್ಟೇ. ಅನೇಕ ರೀತಿಯ ಶಕ್ತಿಗಳೆಲ್ಲವೂ (ಗುರುತ್ವ ಶಕ್ತಿಯ[೧೮] ಹೊರತಾಗಿ) ಕಠಿಣ ಸಂರಕ್ಷಣಾ ನಿಯಮಗಳಿಗೆ ಒಳಪಟ್ಟಿವೆ. ಈ ವಿಷಯದಲ್ಲಿ, ಬಾಹ್ಯಾಕಾಶದ ಅಕ್ಕಪಕ್ಕದ ವಲಯಗಳ ಮಧ್ಯೆ ಶಕ್ತಿಯನ್ನು ವಿನಿಮಯ ಮಾಡಿಕೊಳ್ಳಬಹುದು ಮತ್ತು ಯಾವುದೇ ಅಂತರಿಕ್ಷದ ವಿಸ್ತಾರ ಸಾಂದ್ರತೆಯೊಳಗೂ ಶಕ್ತಿಯ ಬದಲಾವಣೆ ಸಾಧ್ಯ ಎಂದು ಬಲ್ಲವರು ಒಪ್ಪುತ್ತಾರೆ. ಜಾಗತಿಕವಾದ ಶಕ್ತಿ ಸಂರಕ್ಷಣೆ ನಿಯಮದ ಪ್ರಕಾರ ವಿಶ್ವದ ಒಟ್ಟಾರೆ ಶಕ್ತಿ ಬದಲಾವಣೆ ಆಗುವುದಿಲ್ಲ; ಇದು ಸ್ಥಳೀಯ ನಿಯಮದ ಅನುಸಿದ್ಧಾಂತ, ಆದರಿದು[೬] ಅದಲು-ಬದಲು[೧೧] ಆಗಲು ಸಾಧ್ಯವಿಲ್ಲ. ಶಕ್ತಿ ಸಂರಕ್ಷಣೆ ಅಂದರೆ ಕಾಲದ ಪರಿವರ್ತನಾ ಸಮ್ಮಿತಿಯ ಗಣಿತದ ಪರಿಣಾಮ (ವಿವಿಧ ಸಮಯಗಳ ಮಧ್ಯಂತರದ ಒಟ್ಟು ಲೆಕ್ಕ[೧೯])
ವ್ಯವಸ್ಥೆಯ ಒಳಬರುವ ಒಟ್ಟು ಪ್ರಮಾಣದ ಶಕ್ತಿಯು ವ್ಯವಸ್ಥೆಯಿಂದ ಆಚೆ ಹೊಮ್ಮುವ ಒಟ್ಟು ಪ್ರಮಾಣದ ಶಕ್ತಿಯ ಜೊತೆಗೆ ವ್ಯವಸ್ಥೆಯೊಳಗಿನದ್ದೇ ಆದ ಶಕ್ತಿಯನ್ನು ಕೂಡಿದರೆ ಬರುವ ಮೊತ್ತದಷ್ಟು-ಎಂಬುದು ಶಕ್ತಿ ಸಂರಕ್ಷಣೆಯ ನಿಯಮ. ಈ ನಿಯಮ ಭೌತ ಶಾಸ್ತ್ರದ ಮೂಲಾಧಾರ ತತ್ವ. ಕಾಲದ ಪರಿವರ್ತನಾ ಸಮ್ಮಿತಿಯ ಪ್ರಕಾರ ವಿಶ್ವದಲ್ಲಿ ಗೋಚರವಾಗುವ ಅನೇಕ ವಸ್ತುಗಳು ಸಮಯದ ಸಮಭಾಗಿತ್ವದಲ್ಲಿ ಸ್ಥಳದಿಂದ ಅವು ಸ್ವತಂತ್ರವಾಗುತ್ತವೆ. ಇನ್ನೊಂದು ರೀತಿಯಲ್ಲಿ-ನಿನ್ನೆ,ಇಂದು ಮತ್ತು ನಾಳೆ ಎಂಬುದರಲ್ಲಿ ಭೌತಿಕ ಭಿನ್ನತೆಯೇ ಇಲ್ಲ.
ಇದು ಏಕೆಂದರೆ ಶಕ್ತಿ ಎಂಬುದು ಸಮಯದ ಅಂಗೀಕೃತ ಸಂಯುಗ್ಮ. ಗಣಿತದ ಬಲೆಯೊಳಗೆ ಶಕ್ತಿ ಮತ್ತು ಸಮಯವು ಅನಿಶ್ಚಯ ತತ್ವಕ್ಕೆ ಎಡೆಯಾಗಿರುತ್ತದೆ. ಯಾವುದೇ ನಿಗದಿತ ಅವಧಿಯಲ್ಲಿ ಕರಾರುವಾಕ್ಕಾಗಿ ಶಕ್ತಿಯ ಪ್ರಮಾಣವನ್ನು ಖಚಿತಗೊಳಿಸುವುದಕ್ಕೆ ಆಗುವುದಿಲ್ಲ. ಅನಿಶ್ಚಿತ ತತ್ವವನ್ನು ಶಕ್ತಿ ಸಂರಕ್ಷಣೆಯ ತತ್ವವೆಂದು ತಪ್ಪಾಗಿ ಅರ್ಥೈಸಿಕೊಳ್ಳಬಾರದು. ಏಕೆಂದರೆ, ಶಕ್ತಿ ಸಂರಕ್ಷಣಾ ತತ್ವವನ್ನು ಗಣಿತೀಯ ಮಿತಿಗಳೊಳಗೆ ಲೆಕ್ಕ ಹಾಕಿ ಬಹುತೇಕ ಶಕ್ತಿಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು ಮತ್ತು ಅಳೆಯಬಹುದು.
ಹ್ಯಾಮಿಲ್ಟೋನಿಯನ್ ಕ್ರಿಯಾಚಿಹ್ನೆಯ ಮೂಲಕ ಕ್ವಾಂಟಂ ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ವ್ಯಕ್ತ ಮಾಡಲು ಸಾಧ್ಯವಿದೆ. ಯಾವುದೇ ಸಮಯದ ಮಾಪನದಿಂದ ಶಕ್ತಿಯ ಅನಿಶ್ಚಿತತೆಯು ಹೀಗಿದೆ:
ಇದು ಹೈಸನ್ಬರ್ಗ್ ಅನಿಶ್ಚಿತತೆಯ ತತ್ವವನ್ನು ಹೋಲುತ್ತದೆ. (ಆದರೆ ಗಣಿತಶಾಸ್ತ್ರ ರೀತ್ಯ ಸಮಾನವಲ್ಲ ಏಕೆಂದರೆ H ಮತ್ತು t ಶಾಸ್ತ್ರೀಯವಾಗಿ ಆಗಲಿ ಕ್ವಾಂಟಂ ಮೆಕಾನಿಕ್ಸ್ನಲ್ಲಾಗಲಿ ಸಕ್ರಿಯವಾಗಿ ಸಂಯುಗ್ಮ ಚರಗಳಲ್ಲ).
ಆವೇಗವನ್ನು ಹೊತ್ತೊಯ್ಯುವ ಕಾರ್ಯತಃ ಸಮಯ ಚಲನೆ ಅಥವಾ ವಸ್ತುತಃ ಸಮಯ ಚಲನೆ ನೈಜ ಕಣಗಳೊಂದಿಗೆ ಬದಲಾಯಿಸಿಕೊಳ್ಳುವುದು ಮೂಲಭೂತ ಬಲದ ಸೃಷ್ಟಿಗೆ ಕಾರಣವಗುತ್ತದೆ. (ನಿರ್ದಿಷ್ಟವಾಗಿ ಮೂಲಭೂತ ಅಂತರಕ್ರಿಯೆ), ಈ ಏರು-ಪೇರುಗಳ ಗ್ರಹಿಕೆಯಿಂದ ಕಾರ್ಯತಃ ಕಣಗಳನ್ನು ಅಥವಾ ವಸ್ತುತಃ ಕಣಗಳನ್ನು ಗುಣಾತ್ಮಕವಾಗಿ ಅರ್ಥ ಮಾಡಿಕೊಳ್ಳಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ. ಮಿಥ್ಯಾ ಫೋಟಾನ್ಗಳು (ಅಲ್ಪ ಪರಿಮಾಣದ ಯಾಂತ್ರಿಕ ಶಕ್ತಿಯ ಫೋಟಾನ್ಗಳ ಶಕ್ತಿ ಸ್ಥಿತಿ) ವಿದ್ಯುದಾವೇಶಗಳ ನಡುವೆ ವಿದ್ಯುತ್ ಸ್ಥಾಯೀಮಾನದ ಅಂತರಕ್ರಿಯೆಗೆ (ಕೂಲಂಬ್ ನಿಯಮಕ್ಕೆ ಪರಿಣಮಿಸುತ್ತದೆ), ತನ್ನಷ್ಟಕ್ಕೇ ನಡೆವ ಪರಮಾಣು ಮತ್ತು ಬೈಜಿಕ ವಿಕರಣ ಕ್ಷಯಕ್ಕೆ, (ಕ್ಯಾಸಿಮಿರ್) ಬಲಕ್ಕೆ, ವ್ಯಾನ್ ಡರ್ ವಾಲ್ಸ್ ಬಂಧಕ ಬಲಕ್ಕೆ ಮತ್ತು ಇನ್ನೂ ಕೆಲವು ಸಂರಕ್ಷಣೀಯ ಸಂಗತಿಗಳಿಗೆ ಹೊಣೆಯಾಗುತ್ತದೆ.
ಶಕ್ತಿ ಮತ್ತು ಬದುಕು[ಬದಲಾಯಿಸಿ]

ಬದುಕಿರುವ ಯಾವುದೇ ಜೀವಿಯು ಬೆಳೆಯುವುದಕ್ಕೆ ಮತ್ತು ಸಂತಾನೋತ್ಪತಿಗೆ ಹೊರಗಿನ ಶಕ್ತಿಗಳ ಮೇಲೆ ಅವಲಂಬಿಸಿದೆ-ಹಸಿರು ಸಸ್ಯಗಳು ಸೂರ್ಯನ ವಿಕಿರಣ ಶಕ್ತಿಯ ಮೇಲೆ; ಪ್ರಾಣಿಗಳು ಕೆಲವು ರಾಸಾಯನಿಕ ಶಕ್ತಿಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿವೆ. ವಯಸ್ಕರಿಗೆ ಪ್ರತಿ ದಿನ 1500–2000 ಕ್ಯಾಲೋರಿಗಳಷ್ಟು (6–8 MJ) ಆಮ್ಲಜನಕ ಮತ್ತು ಆಹಾರ ಕಣಗಳ ಸಂಮಿಶ್ರಣದ ಸೇವನೆಯನ್ನು ಶಿಫಾರಸು ಮಾಡಲಾಗಿದೆ. ಆಹಾರದಲ್ಲಿ ಹೆಚ್ಚಿನಂಶ ಕಾರ್ಬೋಹೈಡ್ರೈಟ್ಸ್, ಕೊಬ್ಬಿನಾಂಶ ಮತ್ತು ಗ್ಲುಕೋಸ್ (C6H12O6) ಮತ್ತು ಸ್ಟಿಯರಿನ್ (C57H110O6) ಅತ್ಯುತ್ತಮ ಉದಾಹರಣೆಗಳು. ಮೈಟೊಕಾಂಡ್ರಿಯಾದಲ್ಲಿ ಆಹಾರ ಕಣಗಳನ್ನು ಇಂಗಾಲದ ಡಯಾಕ್ಸೈಡ್ಗೆ ಮತ್ತು ನೀರಿಗೆ ಆಕ್ಸಿಡೀಕರಿಸಲಾಗುತ್ತದೆ.
-
- C6H12O6 + 6O2 → 6CO2 + 6H2O
- C57H110O6 + 81.5O2 → 57CO2 + 55H2O
ಮತ್ತು ಸ್ವಲ್ಪ ಶಕ್ತಿಯನ್ನು ADPಯಿಂದ ATPಗೆ ಪರಿವರ್ತಿಸಲು ಉಪಯೋಗಿಸಲಾಗುತ್ತದೆ.
-
- ADP + HPO42− → ATP + H2O
ಕಾರ್ಬೋಹೈಡ್ರೈಟ್ ಮತ್ತು ಕೊಬ್ಬಿನಾಂಶದಲ್ಲಿ ಉಳಿದ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯನ್ನು ಶಾಖವಾಗಿ ಪರಿವರ್ತಿಸಲಾಗುತ್ತದೆ: ATP ಯನ್ನು ಒಂದು ರೀತಿಯ ಚಲಾವಣೆಯಲ್ಲಿರುವ ಶಕ್ತಿಯನ್ನು ಒಡೆದು ಅಥವಾ ಸಿಗಿದು ನೀರಿನೊಂದಿಗೆ ಅದು ಪ್ರತಿಕ್ರಿಯಿಸಿದಾಗ ಅದರಲ್ಲಿಯ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯನ್ನು ಚಯಾಪಚಯಕ್ಕೆ ಮತ್ತು ಈ ಪ್ರತಿ ಚಯಾಪಚಯ ಪ್ರತಿಕ್ರಿಯಾಸರಣಿಯಲ್ಲಿ ಕೆಲವು ರಾಸಾಯನಿಕ ಶಕ್ತಿಯು ಶಾಖವಾಗಿ ಪರಿವರ್ತಿತವಾಗುತ್ತದೆ. ಮೂಲ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯ ಅತ್ಯಲ್ಪ ಪ್ರಮಾಣವನ್ನು ಮಾತ್ರ ಕೆಲಸಕ್ಕೆ ಉಪಯೋಗಿಸಲಾಗುತ್ತದೆ.[೨೦]
- ಚಲನಾ ಶಕ್ತಿಯಲ್ಲಿ ಗಳಿಕೆ 100 m ಪೂರ್ಣ ವೇಗದ ಓಟಗಾರ ಓಡುವ ಸಂದರ್ಭದಲ್ಲಿ:4 kJ
- 2 ಮೀಟರ್ ಬಳಸುವ ಮೂಲಕ 150 kg ಎತ್ತಲಾದ ಗುರುತ್ವ ಅಂತಸ್ಥಶಕ್ತಿ ಗಳಿಕೆ: 3 KJ
- ಸಾಧಾರಣ ವಯಸ್ಕರು ಪ್ರತಿ ದಿನ ಸೇವಿಸಬೇಕಾದ ಆಹಾರ: 6–8 MJ
ತಮಗೆ ಒದಗಿ ಬರುವ ಶಕ್ತಿಯನ್ನು (ರಾಸಾಯನಿಕ ಶಕ್ತಿ ಅಥವಾ ವಿಕಿರಣ ಶಕ್ತಿ) ಬಳಸಿಕೊಳ್ಳುವಲ್ಲಿ ಜೀವಿಗಳು ಗಣನೀಯ ದಕ್ಷತೆಯನ್ನೇನೂ ತೋರುವುದಿಲ್ಲ (ಭೌತಿಕ ರೂಪದಲ್ಲಿ). ವಾಸ್ತವ ಸಂಗತಿ ಎಂದರೆ ಯಂತ್ರಗಳೇ ಈ ದಿಶೆಯಲ್ಲಿ ಹೆಚ್ಚು ಸಮರ್ಥವಾಗಿವೆ ಎನ್ನಬಹುದು.
ಏನೇ ಆದರೂ, ಬೆಳೆಯುವ ಅವಯವಗಳಲ್ಲಿ ಶಾಖವಾಗಿ ಪರಿವರ್ತಿತವಾದ ಶಕ್ತಿ ಮಹತ್ತರ ಕಾರ್ಯವೊಂದನ್ನು ಮಾಡುತ್ತದೆ, ತಾನು ಬೆಳೆದು ಬಂದ ಕಣಗಳ ದೃಢತೆಯನ್ನು ವರ್ಧಿಸುತ್ತದೆ. ಉಷ್ಣ ಬಲ ವಿಜ್ಞಾನದ ಎರಡನೆಯ ನಿಯಮದ ಪ್ರಕಾರ ಶಕ್ತಿ (ಮತ್ತು ಭೌತದ್ರವ್ಯ) ವಿಶ್ವಾದ್ಯಂತ ಸಮವಾಗಿ ಹರಡುವಂತೆ ಉದ್ದೇಶಿಸುತ್ತದೆ: ಶಕ್ತಿ (ಮತ್ತು ಭೌತದ್ರವ್ಯ) ನಿಶ್ಚಿತವಾದ ಎಡೆಯಲ್ಲಿ ಕೇಂದ್ರಿಕೃತಗೊಳ್ಳಬೇಕಾದರೆ ಹೆಚ್ಚಿನ ಮೊತ್ತದ ಶಕ್ತಿಯನ್ನು (ಶಾಖವಾಗಿ) ವಿಶ್ವದ ಉಳಿದೆಡೆ ಸುತ್ತ-ಮುತ್ತ ಹರಡಬೇಕಾಗುತ್ತದೆ.[೨೧] ಸರಳ ಜೀವಿಗಳು ಸಂಕೀರ್ಣ ಜೀವಿಗಳಿಗಿಂತ ಅಧಿಕ ದಕ್ಷತೆಯನ್ನು ಸಾಧಿಸುತ್ತವೆ. ಆದರೆ ಸಂಕೀರ್ಣ ಜೀವಿಗಳಿಗೆ ಲಭ್ಯವಾಗುವ ಪರಿಸರ ವಾಸ್ತವ್ಯದ ತಾಣ ಈ ಸಣ್ಣ ಭ್ರಾತೃಗಳಿಗೆ ಲಭ್ಯವಾಗುವುದಿಲ್ಲ. ಚಯಾಪಚಯ ಕ್ರಿಯೆಯ ಹಾದಿಯಲ್ಲಿ ರಾಸಾಯನಿಕ ಶಕ್ತಿಯ ಭಾಗವು ಶಾಖವಾಗಿ ಪರಿವರ್ತಿಸುವ ಪ್ರತಿ ಹೆಜ್ಜೆಯು ಅದು ಪರಿಸರದಲ್ಲಿ ಕಂಡು ಬರುವ ಒಟ್ಟು ಜೀವರಾಶಿಗೆ ಕಾರಣವಾಗಿರುತ್ತದೆ: ಆಹಾರ ಸರಪಳಿಯದ್ದೇ ತೆಗೆದುಕೊಂಡರೂ ಅದರ ಮೊದಲ ಹಂತದಲ್ಲೇ ನಿಗದಿತ ಇಂಗಾಲ 124.7 Pg/a ಕ್ಕೆ ನಿಗದಿತ ದ್ಯುತಿಸಂಶ್ಲೇಷಣೆ 64.3 Pg/a (52%)[೨೨] ಹಸಿರು ಸಸ್ಯಗಳ ಚಯಾಪಚಯಕ್ಕೆ ಉಪಯೋಗಿಸಲಾಗುತ್ತದೆ ಅಂದರೆ ಕಾರ್ಬನ್ ಡೈಆಕ್ಸೈಡಾಗಿ ಮತ್ತು ಶಾಖವಾಗಿ ಪುನರ್ ಪರಿವರ್ತಿತವಾಗುತ್ತದೆ.
ಮಾಹಿತಿ ಸಮಾಜ ಮತ್ತು ಶಕ್ತಿ[ಬದಲಾಯಿಸಿ]
ಆಧುನಿಕ ಸಮಾಜವು ಪಳೆಯುಳಿಕೆ ಇಂಧನವನ್ನೇ ಇನ್ನೂ ಆರ್ಥಿಕ ಬೆಳವಣಿಗೆ ಮತ್ತು ಇವತ್ತಿನ ಬದುಕಿನ ಮಟ್ಟವನ್ನು ಕಾಪಾಡಿಕೊಳ್ಳಲು ನಿರಂತರವಾಗಿ ನಂಬಿಕೊಂಡಿದೆ. ಏನೇ ಆಗಲಿ, ಮೊದಲ ಬಾರಿಗೆ ಭೂಮಿಯ ಭೌತಿಕ ಮಿತಿಯನ್ನು ಸೀಮಿತ ಸಾಧನಗಳ ಜೊತೆ ಮುಖಾಮುಖಿಯನ್ನಾಗಿಸಲಾಗಿದೆ, ಈ ಸೀಮಿತ ಸಾಧನಗಳ ಮೂಲವು- ತೈಲ ಹಾಗು ನೈಸರ್ಗಿಕ ಅನಿಲ ಮತ್ತು ಅದರ ಜಾಗತಿಕ ಹವಾಮಾನಕ್ಕೆ ಅಪ್ಪಳಿಸುತ್ತಿರುವ ಹಸಿರು ಮನೆಯ ಅನಿಲ ಹೊರಸೂಸುವಿಕೆಯಾಗಿದೆ. ಕೈಗಾರಿಕಾ ಪ್ರಪಂಚದಲ್ಲಿ ಮತ್ತು ಬೆಳೆಯುತ್ತಿರುವ ಆರ್ಥಿಕತೆಯಲ್ಲಿ ಶಕ್ತಿಯ ಮೇಲಿನ ನಮ್ಮ ಅವಲಂಬನೆಯನ್ನು ಕರಾರುವಾಕ್ಕಾಗಿ ಸಾರ್ವಜನಿಕ ಅಭಿವೃಧಿ ನಿಯಮಗಳಿಗೆ ಸಮಂಜಸವಾಗಿ ಸಮಾಜದ ಅಭಿವೃಧಿಯ ನಿರ್ವಹಣೆಯನ್ನು ಹಿಂದೆಂದೂ ಲೆಕ್ಕ ಹಾಕೇ ಇಲ್ಲ. ಪ್ರಸ್ತುತ, ಹಸಿರು ಮನೆಯ ಅನಿಲಗಳನ್ನು ಪ್ರಾದೇಶಿಕ ಅಸಮತೋಲನ ನೀಗಿಸುವ ಮೂಲಕ ಜಾಗತಿಕ ಹೊರಸೂಸುವಿಕೆಯನ್ನು ಮಿತಗೊಳಿಸಬೇಕಾದರೆ ಆರ್ಥಿಕ ಅಡಿಪಾಯದ ಮೇಲೆ ವಿಶ್ವಾದ್ಯಂತ ಏರುಮಿತಿ-ಮತ್ತು-ವ್ಯಾಪಾರ (=ಕಾರ್ಬನ್ ಸೂಸುವಿಕೆಯ ಮೇಲಿನ ನಿರ್ಬಂಧ) ವ್ಯವಸ್ಥೆಯ ಮೇಲೆ ಹೆಚ್ಚು ಒತ್ತು ಕೊಡಲಾಗುತ್ತಿದೆ. ಪಳೆಯುಳಿಕೆ ಇಂಧನವನ್ನು ಖಾಸಗಿ ವಲಯಗಳಲ್ಲಿ ಉತ್ಪಾದನೆ ಮತ್ತು ಸಾಗಾಣಿಕೆ ಸೇವೆಗಳಿಗೆ ನೇರವಾಗಿ ಉಪಯೋಗಿಸಲು ಸಮಾಜದ ಒಳವ್ಯಾಪ್ತಿಯವರೆಗೂ ಎಲ್ಲಾ ಹಂತಗಳಲ್ಲಿ ಮಾಹಿತಿಗಳು ವ್ಯಾಪಿಸಲಾಗುತ್ತದೆ. ಇಂದಿನ ಸಮಾಜದಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ಜ್ಞಾನಾರ್ಜನೆಗಾಗಿ, ಸುದ್ದಿಗಾಗಿ ಮತ್ತು ಮನರಂಜನೆಗಾಗಿ ಬಳಕೆ ಮಾಡುವುದರತ್ತ ಕೇಂದ್ರೀಕರಿಸಲಾಗಿದೆ. ಪಳೆಯುಳಿಕೆ ಇಂಧನದ ಮೇಲೆ ಅವಲಂಬನೆ ಶುರವಾಗಿರುವುದರಿಂದ, ವೈಯಕ್ತಿಕ ಮತ್ತು ಜಾಗತಿಕ ಮಟ್ಟದ ಸಮತೋಲನ ಕಾಪಾಡುವ ನಿಟ್ಟಿನಲ್ಲಿ ಇಂಧನ ಮಾಹಿತಿಯನ್ನು ಒದಗಿಸುವ ಸಮೂಹ ಸ್ವಾಮ್ಯದ ಮಾಧ್ಯಮವೊಂದು ಉದಯವಾಗಬಹುದು. ಇನ್ನೂ ಈ ಬೆಳವಣಿಗೆ, ಅನಿರ್ಬಂಧಿತವಾಗಿ ಅಭವೃದ್ಧಿಯಾಗಿಲ್ಲ, ಹೆಚ್ಚಾಗಿ ಖಾಸಗಿ ಸಂಗತಿಗಳೇ ಆಗಿವೆ. ರಾಷ್ಟ್ರೀಯ ಮಟ್ಟದ್ದಲ್ಲಿ ಅಳತೆ ಮಾಪನವನ್ನು ಖಾಸಗಿ ವಲಯಕ್ಕೂ ಕಡ್ಡಾಯ ಮಾಡಬೇಕೆಂಬ ನಿಯಮದ ಪ್ರಸ್ತಾವನೆಯನ್ನು ಡಚ್ ಸೆನೇಟ್ ಇತ್ತೀಚೆಗೆ ಆಂಶಿಕವಾಗಿ ತಿರಸ್ಕರಿಸಿದೆ.[೨೩]
ಉಲ್ಲೇಖಗಳು ಮತ್ತು ಪರಾಮರ್ಶೆಗಳು[ಬದಲಾಯಿಸಿ]
- ↑ Lofts, G (2004). "11 — Mechanical Interactions". Jacaranda Physics 1 (2 ed.). Milton, Queensland, Australia: John Willey & Sons Australia Ltd. p. 286. ISBN 0 7016 3777 3.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ ಆರಿಸ್ಟೋಟಲನ, "ನಿಕೊಮಾಕಿಯನ್ ನಿಯಮಗಳು", 1098b33,ಪರ್ಸ್ಯುಸ್ನಲ್ಲಿ
- ↑ Rashed, Roshdi (2007), "The Celestial Kinematics of Ibn al-Haytham", Arabic Sciences and Philosophy, Cambridge University Press, 17: 7–55 [19], doi:10.1017/S0957423907000355
- ↑ ಮೇರಿಯಂ ರೋಝಾಂಸ್ಕಯಾ ಮತ್ತು ಐ.ಎಸ್.ಲೆವಿನೋವಾ (1996),"ಸಮಸ್ಥಿತಿಶಾಸ್ತ್ರ",ಪುಟ Rashed, Roshdi & Régis Morelon (1996), [[]] ([[:Encyclopedia of the History of Arabic Science:|Encyclopedia of the History of Arabic Science]])}}, vol. 1 & 3, Routledge, 614-642, ISBN 0415124107621ರಲ್ಲಿ,
- ↑ Smith, Crosbie (1998). The Science of Energy - a Cultural History of Energy Physics in Victorian Britain. The University of Chicago Press. ISBN 0-226-76420-6.
- ↑ ೬.೦ ೬.೧ Feynman, Richard (1964). The Feynman Lectures on Physics; Volume 1. U.S.A: Addison Wesley. ISBN 0-201-02115-3.
- ↑ http://www.uic.edu/aa/college/gallery400/notions/human%20energy.htm Retrieved on May-29-09
- ↑ ಬೈಸಿಕಲ್ ಗಣಕ- ವೇಗ,ತೂಕ ಮತ್ತು ವ್ಯಾಟೇಜ್ [೧] [೨].
- ↑ ಭೂಮಿ ಶಕ್ತಿಯ ಅಂದಾಜು ಪತ್ರ
- ↑ ಬರ್ಕಲಿಯ ಭೌತಿಕ ಶಾಸ್ತ್ರದ ಕೋರ್ಸ್ ವಾಲ್ಯೂಂ. 1 ಚಾರ್ಲ್ಸ್ ಕಿಟ್ಟಲ್, ವಾಲ್ಟರ್ ಡಿ ಕ್ನೈಟ್ ಮತ್ತು ಮಾಳ್ವಿನ್ ಎ ರುಡರ್ಮಾನ್
- ↑ ೧೧.೦ ೧೧.೧ ೧೧.೨ ದಿ ಲಾಸ್ ಆಫ್ ಥರ್ಮೊಡೈನಾಮಿಕ್ಸ್ ಶಕ್ತಿ, ಮುಕ್ತ ಶಕ್ತಿ ಇತ್ಯಾದಿಗಳ ಕೂಲಂಕಷ ವ್ಯಾಖ್ಯಾನಗಳನ್ನೊಳಗೊಂಡು.
- ↑ ೧೨.೦ ೧೨.೧ Misner, Thorne, Wheeler (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0716703440.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ ದಿ ಹ್ಯಾಮಿಲ್ಟೋನಿಯನ್ Archived 2007-10-11 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. MIT ಓಪನ್ಕೋರ್ಸ್ವೇರ್ ಜಾಲತಾಣ 18.013A Chapter 16.3 ಪ್ರವೇಶ ಫೆಬ್ರುವರಿ 2007
- ↑ Cengel, Yungus, A. (2002). Thermodynamics - An Engineering Approach, 4th ed. McGraw-Hill. pp. 17–18. ISBN 0-07-238332-1.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help)CS1 maint: multiple names: authors list (link) - ↑ Kittel and Kroemer (1980). Thermal Physics. New York: W. H. Freeman. ISBN 0-7167-1088-9.
- ↑ ರಿಸ್ಟಿನೆನ್, ರಾಬರ್ಟ್ ಎ. ಮತ್ತು ಕ್ರಾವ್ಸ್ಹಾರ್, ಜ್ಯಾಕ್ ಜೆ. ಇನರ್ಜಿ ಅಂಡ್ ದಿ ಎನ್ವಿರಾನ್ಮೆಂಟ್. ನ್ಯೂ ಯಾರ್ಕ್ : ಜಾನ್ ವಿಲ್ಲಿ ಅಂಡ್ ಸನ್ಸ್, ಇಂಕಾರ್ಪೊರೇಟೆಡ್, 2006.
- ↑ ೧೭.೦ ೧೭.೧ ೧೭.೨ Mohr, Peter J. (2008). "CODATA Recommended Values of the Fundamental Physical Constants: 2006". Rev. Mod. Phys. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008RvMP...80..633M. doi:10.1103/RevModPhys.80.633.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ ಇ. ನೊಥರ್ಸ್ ಡಿಸ್ಕವರಿ ಆಫ್ ದಿ ಡೀಪ್ ಕನೆಕ್ಷನ್ ಬಿಟ್ವೀನ್ ಸಿಮಿಟ್ರೀಸ್ ಅಂಡ್ ಕನ್ಸರ್ವೇಷನ್ ಲಾಡಸ್
- ↑ ಟೈಮ್ ಇನ್ವೇರಿಯನ್ಸ್
- ↑ ಈ ಉದಾಹರಣೆಗಳು ಕೇವಲ ಸ್ಪಷ್ಟನೆಗಾಗಿ, ಇದು ಓಟಗಾರನ ಕಾರ್ಯ ನಿರ್ವಾಹಣೆಯನ್ನು ಮಿತಗೊಳ್ಳಿಸಲು ದೊರಕುವ ಶಕ್ತಿಯಲ್ಲ ಬದಲಾಗಿ ಪೂರ್ಣವಾಗಿ ಓಡುವವನಿಂದ ಹೊಮ್ಮುವ ಸಾಮರ್ಥ್ಯ ಮತ್ತು ಭಾರ ಎತ್ತುವವನ ಬಲ. ಸೂಪರ್ ಮಾರ್ಕೆಟ್ನಲ್ಲಿ ನೌಕರನೊಬ್ಬ ಶೆಲ್ಫ್ ಮೇಲಿನ ಪದಾರ್ಥಗಳನ್ನು ಜೋಡಿಸುವ ಕಾರ್ಯವು (ಭೌತಿಕವಾಗಿ ಅರ್ಥದಲ್ಲಿ) ಒಬ್ಬ ಓಟಗಾರನ ಕಾರ್ಯಕ್ಕಿಂತ ಹೆಚ್ಚಿನದ್ದೇ ಆದರೆ ಅದು ತುಂಬಾ ನಿಧಾನಾಗಿರುತ್ತದೆ.
- ↑ ನಿಸರ್ಗದಲ್ಲಿ ದೊರೆಯುವ ಮತ್ತೊಂದು ಅತ್ಯಂತ ಶಿಸ್ತಾದ ವ್ಯವಸ್ಥೆಯ ಉದಾಹರಣೆ ಎಂದರೆ ಅದು ಸ್ಫಟಿಕಗಳು:ಈ ಶಿಸ್ತು ಕೂಡ ದೊಡ್ಡ ಮೊತ್ತದ [[ಸ್ಫಟಿಕ ಶಕ್ತಿಯ|ಸ್ಫಟಿಕ ಶಕ್ತಿಯ]] ಶಾಖವನ್ನು ಸುತ್ತ-ಮುತ್ತ ವರ್ಗಾಯಿಸುವುದರಿಂದ ಆಗಿದೆ.
- ↑ ಇಟೊ, ಅಕಿಹಿಟೊ; ಒಯಿಕಾವಾ, ತಾಕೆಹಿಸಾ (2004). "ಗ್ಲೋಬಲ್ ಮ್ಯಾಪಿಂಗ್ ಆಫ್ ಟೆರೆಸ್ಟ್ರಿಯಲ್ ಪ್ರೈಮೆರಿ ಪ್ರಾಡಕ್ಟಿವಿಟಿ ಅಂಡ್ ಲೈಟ್ ಯೂಸ್ ಎಫಿಷಿಯೆನ್ಸಿ ವಿತ್ ಎ ಪ್ರಾಸೆಸ್-ಬೇಸ್ಡ್ ಮಾಡಲ್. Archived 2006-10-02 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ." ಇನ್ ಷೊಯೊಮಿ, ಎಂ. ಮತ್ತಿತರರು. (ಸಂಪಾದಕರು.) ಗ್ಲೋಬಲ್ ಎನ್ವಿರಾನ್ಮೆಂಟಲ್ ಚೇಂಜ್ ಇನ್ ದಿ ಓಷೀನ್ ಅಂಡ್ ಆನ್ ಲ್ಯಾಂಡ್. ಪಿಪಿ. 343–58.
- ↑ ಮಿನ್ಯುಟ್ಸ್ ಈರ್ಸ್ಟ್ ಕಮೆರ್ ಡಿಬೆಟ್ "(ಪಾರ್ಟ್ a)[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ]", "ಪಾರ್ಟ್ b[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ]"
ಹೆಚ್ಚಿನ ಓದಿಗಾಗಿ[ಬದಲಾಯಿಸಿ]
- Alekseev, G. N. (1986). Energy and Entropy. Moscow: Mir Publishers.
- Walding, Richard, Rapkins, Greg, Rossiter, Glenn (1999-11-01). New Century Senior Physics. Melbourne, Australia: Oxford University Press. ISBN 0-19-551084-4.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Smil, Vaclav (2008). Energy in nature and society: general energetics of complex systems. Cambridge, USA: MIT Press. ISBN 987-0-262-19565-2.
{{cite book}}: Check|isbn=value: invalid prefix (help)
ಬಾಹ್ಯ ಕೊಂಡಿಗಳು[ಬದಲಾಯಿಸಿ]
| Find more about Energy at Wikipedia's sister projects | |
| Definitions and translations from Wiktionary | |
| Media from Commons | |
| Learning resources from Wikiversity | |
| Quotations from Wikiquote | |
| Source texts from Wikisource | |
| Textbooks from Wikibooks | |
- ಶಕ್ತಿಯ ಸಂರಕ್ಷಣೆ Archived 2010-04-16 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
- ಶಕ್ತಿ ಮತ್ತು ಜೀವನ
- ಶಕ್ತಿಯ ನೈಜ ಅರ್ಥವೇನು? Archived 2009-02-10 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.ಫಿಸಿಕ್ಸ್ವರ್ಲ್ಡ್ ಇಂದ Archived 2009-02-10 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
- Work, Power, Kinetic Energy PDF (399 KB)
- REDIRECT Template:Nature
- CS1 errors: unsupported parameter
- CS1 maint: multiple names: authors list
- ವೆಬ್ ಆರ್ಕೈವ್ ಟೆಂಪ್ಲೇಟಿನ ವೇಬ್ಯಾಕ್ ಕೊಂಡಿಗಳು
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಲೇಖನಗಳು from ಆಗಸ್ಟ್ 2021
- ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- Pages using ISBN magic links
- Pages with unresolved properties
- Articles containing Ancient Greek (to 1453)-language text
- CS1 errors: ISBN
- ಶಕ್ತಿ
- ಮೂಲಭೂತ ಭೌತವಿಜ್ಞಾನ ಪರಿಕಲ್ಪನೆಗಳು
- ಭೌತಶಾಸ್ತ್ರ
- ಆರಂಭಿಕ ಭೌತವಿಜ್ಞಾನ
- ಭೌತಿಕ ಪ್ರಮಾಣಗಳು
- ಗ್ರೀಕ್ ಎರವಲುಪದಗಳು











































