ದೃಗ್ವಿಜ್ಞಾನ
This article may be too long to read and navigate comfortably. (September 2009) |

ದೃಗ್ವಿಜ್ಞಾನ ಎನ್ನುವುದು ಬೆಳಕಿನ ವರ್ತನೆ ಮತ್ತು ಲಕ್ಷಣಗಳನ್ನು, ವಸ್ತುವಿನ ಜೊತೆಗೆ ಅದರ ಸಂವಹನ ಮತ್ತು ಅದನ್ನು ಬಳಸುವ ಅಥವಾ ಶೋಧಿಸುವ ಉಪಕರಣಗಳ ರಚನೆಯನ್ನು ಅಧ್ಯಯಿಸುವ ಭೌತಶಾಸ್ತ್ರದ ಒಂದು ಶಾಖೆ.[೧] ದೃಗ್ವಿಜ್ಞಾನವು ಸಾಮಾನ್ಯವಾಗಿ ದೃಷ್ಟಿಗೋಚರವಾದ, ಅತಿನೇರಳೆ, ಮತ್ತು ಅತಿಗೆಂಪು ಬೆಳಕಿನ ಬಗೆಗೆ ವಿವರಿಸುತ್ತದೆ. ಬೆಳಕು ವಿದ್ಯುದಯಸ್ಕಾಂತ ತರಂಗ ಆಗಿರುವುದರಿಂದ, ವಿದ್ಯುದಯಸ್ಕಾಂತ ವಿಕಿರಣದ ಇತರ ರೂಪಗಳು ಉದಾಹರಣೆಗೆ ಕ್ಷ-ಕಿರಣಗಳು, ಸೂಕ್ಷ್ಮತರಂಗಗಳು, ಮತ್ತು ರೇಡಿಯೋ ತರಂಗಗಳು ಇದೇ ರೀತಿಯ ಲಕ್ಷಣಗಳನ್ನು ತೋರುತ್ತದೆ.[೧]
ದೃಗ್ವಿಜ್ಞಾನದ ಅನೇಕ ಸ್ವರೂಪಗಳು ಬೆಳಕಿನ ಶಾಸ್ತ್ರೀಯ ವಿದ್ಯುದಯಸ್ಕಾಂತ ವಿವರಣೆಯನ್ನು ಬಳಸುವುದರಿಂದಲೇ ಆಗಿವೆ ಎನ್ನಬಹುದು. ಏನಾದರೂ, ಬೆಳಕಿನ ವಿದ್ಯುದಯಸ್ಕಾಂತ ವಿವರಣೆಗಳನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ಅನುಷ್ಠಾನಕ್ಕೆ ತರುವುದು ಅನೇಕ ವೇಳೆ ಕಷ್ಟಕರ. ಪ್ರಾಯೋಗಿಕ ದೃಗ್ವಿಜ್ಞಾನವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಸರಳೀಕರಿಸಿದ ಮಾದರಿಗಳೊಂದಿಗೆ ಸಾಧಿಸಲಾಗುತ್ತದೆ. ಇವುಗಳಲ್ಲಿ ಅತ್ಯಂತ ಸಾಮಾನ್ಯವಾದ, ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನವು ಬೆಳಕನ್ನು ಸರಳರೇಖೆಯಲ್ಲಿ ಚಲಿಸುವ ಮತ್ತು ಮೇಲ್ಮೈಗಳ ಮೂಲಕ ಹಾದುಹೋದಾಗ ಅಥವಾ ಅವುಗಳಿಂದ ಪ್ರತಿಫಲನಗೊಂಡಾಗ ಬಾಗುವ ಒಂದು ಕಿರಣಗಳ ಸಮೂಹ ಎಂದು. ಭೌತಿಕ ದೃಗ್ವಿಜ್ಞಾನವು ಹೆಚ್ಚು ಸಮಗ್ರವಾದ ಬೆಳಕಿನ ಮಾದರಿ. ಇದು ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನದಲ್ಲಿ ಕಂಡುಬರದ ತರಂಗ ಪರಿಣಾಮಗಳಾದ ಪಥಪಲ್ಲಟ ಮತ್ತು ಅಡ್ಡಬರುವಿಕೆಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಐತಿಹಾಸಿಕವಾಗಿ, ಕಿರಣ-ಆಧಾರಿತ ಬೆಳಕಿನ ಮಾದರಿಯನ್ನು ಮೊದಲು ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾಯಿತು, ತದನಂತರ ತರಂಗ-ಆಧಾರಿತ ಬೆಳಕಿನ ಮಾದರಿ. 19ನೇ ಶತಮಾನದಲ್ಲಾದ ವಿದ್ಯುದಯಸ್ಕಾಂತ ತತ್ತ್ವದ ಬೆಳವಣಿಗೆಯಿಂದ ಬೆಳಕಿನ ತರಂಗಗಳು ನಿಜದಲ್ಲಿ ವಿದ್ಯುದಯಸ್ಕಾಂತ ವಿಕಿರಣವೇ ಆಗಿರುತ್ತದೆ ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಲು ಸಾಧ್ಯವಾಯಿತು.ತರಂಗದಂತಹ ಮತ್ತು ಅಣುವಿನಂತಹ ಲಕ್ಷಣಗಳನ್ನು ಬೆಳಕು ಹೊಂದಿದೆ ಎಂಬ ಸತ್ಯದ ಮೇಲೆ ಕೆಲವು ಸ್ವರೂಪಗಳು ಅವಲಂಬಿತವಾಗಿವೆ. ಈ ಪರಿಣಾಮಗಳನ್ನು ವಿವರಿಸಲು ಪರಿಮಾಣ ಯಂತ್ರಶಾಸ್ತ್ರ ಬೇಕಾಗುತ್ತದೆ. ಬೆಳಕಿನ ಅಣುವಿನಂತಹ ಲಕ್ಷಣಗಳನ್ನು ಪರಿಗಣಿಸುವಾಗ, ಬೆಳಕನ್ನು "ಫೋಟಾನ್ಗಳು" ಎನ್ನುವ ಅಣುಗಳ ಸಮೂಹ ಎಂದು ಪರಿಭಾವಿಸಲಾಗುತ್ತದೆ. ಪರಿಮಾಣ ದೃಗ್ವಿಜ್ಞಾನವು ಆಪ್ಟಿಕಲ್ ವ್ಯವಸ್ಥೆಗಳಲ್ಲಿ ಪರಿಮಾಣ ಯಂತ್ರಶಾಸ್ತ್ರಗಳ ಉಪಯೋಗಗಳಿಗೆ ಸಂಬಂಧಿಸಿದುದಾಗಿದೆ.ಆಪ್ಟಿಕಲ್ ವಿಜ್ಞಾನವು ಖಗೋಳಶಾಸ್ತ್ರ, ವಿವಿಧ ಇಂಜಿನಿಯರಿಂಗ್ ಕ್ಷೇತ್ರಗಳು, ಛಾಯಾಗ್ರಹಣ, ಮತ್ತು ವೈದ್ಯಕೀಯ (ವಿಶೇಷವಾಗಿ ನೇತ್ರವಿಜ್ಞಾನ ಮತ್ತು ಆಪ್ಟೋಮೆಟ್ರಿ) ಕ್ಷೇತ್ರಗಳನ್ನು ಒಳಗೊಂಡಂತೆ ಅನೇಕ ಸಂಬಂಧಿತ ಶಿಸ್ತುಗಳಿಗೆ ಪ್ರಸ್ತುತವೆನಿಸುತ್ತದೆ ಮತ್ತು ಆ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ಇದರ ಅಧ್ಯಯನ ನಡೆಸಲಾಗುತ್ತದೆ. ಕನ್ನಡಿಗಳು, ಮಸೂರಗಳು, ದೂರದರ್ಶಕಗಳು, ಸೂಕ್ಷ್ಮದರ್ಶಕಗಳು, ಲೇಸರ್ಗಳು, ಮತ್ತು ಫೈಬರ್ ಆಪ್ಟಿಕ್ಸ್ ಒಳಗೊಂಡಂತೆ ವೈವಿಧ್ಯಮಯ ತಂತ್ರಜ್ಞಾನಗಳಲ್ಲಿ ಮತ್ತು ದಿನಬಳಕೆಯ ವಸ್ತುಗಳಲ್ಲಿ ದೃಗ್ವಿಜ್ಞಾನದ ಉಪಯೋಗಗಳನ್ನು ಕಾಣಬಹುದು.
ಇತಿಹಾಸ[ಬದಲಾಯಿಸಿ]

ಪ್ರಾಚೀನ ಈಜಿಪ್ಟರು ಮತ್ತು ಮೆಸಪಟೋಮಿಯನ್ನರು ಮಸೂರಗಳನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸುವುದರ ಜೊತೆಗೆ ದೃಗ್ವಿಜ್ಞಾನದ ಬೆಳವಣಿಗೆಯು ಪ್ರಾರಂಭವಾಯಿತು. ಅತ್ಯಂತ ಹಳೆಯ ಮಸೂರಗಳನ್ನು ಹೊಳಪು ಮಾಡಿದ ಹರಳಿನಿಂದ ಮಾಡಲಾಗಿದೆ, ಅನೇಕವೇಳೆ ಕ್ವಾರ್ಟ್ಸ್ನಿಂದ ಮಾಡಲಾಗಿದೆ, ಮತ್ತು ಅಸಿರಿಯಾದ ಮಸೂರಗಳಾದ ಲಾಯರ್ಡ್/ನಿಂಬೂರ್ಡ್ ಮಸೂರಗಳ ಕಾಲ ಕ್ರಿ.ಪೂ.700 ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ.[೨] ಪ್ರಾಚೀನ ರೋಮನ್ನರು ಮತ್ತು ಗ್ರೀಕರು ಗಾಜಿನ ಗೋಲಗಳಿಗೆ ನೀರನ್ನು ತುಂಬಿಸಿ ಮಸೂರಗಳನ್ನು ಮಾಡುತ್ತಿದ್ದರು. ಈ ಪ್ರಾಯೋಗಿಕ ಬೆಳವಣಿಗೆಗಳ ನಂತರ ಪ್ರಾಚೀನ ಗ್ರೀಕ್ ಮತ್ತು ಭಾರತೀಯ ತತ್ವಶಾಸ್ತ್ರಜ್ಞರು ಬೆಳಕು ಮತ್ತು ದೃಷ್ಟಿಯ ತತ್ವಗಳನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು, ಮತ್ತು ಗ್ರೀಕ್-ರೋಮನ್ ಪ್ರಪಂಚದಲ್ಲಿ ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನವು ಅಭಿವೃದ್ಧಿಗೊಂಡಿತು. ಇಂಗ್ಲಿಷಿನ ಆಪ್ಟಿಕ್ಸ್ ಎಂಬ ಪದ ಪ್ರಾಚೀನ ಗ್ರೀಕ್ ಪದದಿಂದ ಬಂದಿದೆ ὀπτική , ಅದರ ಅರ್ಥ ಕಾಣುವುದು ಅಥವಾ ನೋಟ .[೩] ಪ್ಲೇಟೊ ಮೊಟ್ಟಮೊದಲ ಬಾರಿಗೆ ತನ್ನ ಸೂಸುವಿಕೆ ತತ್ವವನ್ನು ಸ್ಪಷ್ಟಪಡಿಸಿದ, ಕಣ್ಣುಗಳು ಹೊರಹಾಕುವ ಬೆಳಕಿನ ಕಿರಣಗಳಿಂದ ದೃಷ್ಟಿ ಗ್ರಹಣವನ್ನು ಸಾಧಿಸಲಾಗುತ್ತದೆ ಎಂಬ ಅಭಿಪ್ರಾಯ ಅದಾಗಿತ್ತು ಮತ್ತು ತನ್ನ ಟೈಮಿಯಾಸ್ ನಲ್ಲಿ ಕನ್ನಡಿಗಳ ಸಮಾನ ಪರಾವರ್ತನದ ಬಗ್ಗೆ ಪ್ರಸ್ತಾಪಿಸಿದ.[೪] ಕೆಲವು ನೂರು ವರ್ಷಗಳ ನಂತರ, ಯೂಕ್ಲಿಡ್ ಎನ್ನುವವನು ಆಪ್ಟಿಕ್ಸ್ ಎನ್ನುವ ಗ್ರಂಥವನ್ನು ಬರೆದ, ಇದರಲ್ಲಿ ಆತನು ದೃಷ್ಟಿಯ ನಿಖರವಾದ ನಿಯಮಗಳನ್ನು ವಿವರಿಸುತ್ತಾನೆ ಮತ್ತು ವಕ್ರೀಭವನದ ಪರಿಣಾಮಗಳನ್ನು ಗುಣಾತ್ಮಕವಾಗಿ ವಿವರಿಸುತ್ತಾನೆ.[೫] ಟಾಲಮಿ ತನ್ನ ಆಪ್ಟಿಕ್ಸ್ ಗ್ರಂಥದಲ್ಲಿ, ಯೂಕ್ಲಿಡ್ನ ರೇಖಾಗಣಿತದ ಸಾರಾಂಶವನ್ನು ಹೇಳುತ್ತಾನೆ, ಮುಂದಕ್ಕೆ, ವಕ್ರೀಭವನ ಮತ್ತು ಅಧಿಪಾತಕೋನದ ನಡುವಿನ ಪ್ರಾಯೋಗಿಕ ಸಂಬಂಧವನ್ನು ಗುರುತಿಸುವುದರಲ್ಲಿ ವಿಫಲನಾದರೂ ಸಹ ವಕ್ರೀಭವನದ ಕೋನವನ್ನು ಅಳೆಯಲು ಒಂದು ವಿಧಾನವನ್ನು ವಿವರಿಸುತ್ತಾನೆ.[೬]ಇಸ್ಲಾಂ ಪ್ರಪಂಚದಲ್ಲಿ ದೃಗ್ವಿಜ್ಞಾನದ ಮೇಲೆ ಬರವಣಿಗೆ ಮಾಡಿದ ಮೊದಲಿಗರಲ್ಲಿ ಒಬ್ಬರು ಆಲ್-ಕಿಂಡಿ (ಸಿ. 801–73). ಡೇ ರೇಡಿಸ್ ಸ್ಟೆಲ್ಲಾರಮ್ ಎಂದು ಪರಿಚಿತವಾಗಿರುವ ಕೃತಿಯಲ್ಲಿ ಆಲ್-ಕಿಂಡಿ ಪ್ಲೇಟೋನ ಹೊರಸೂಸುವ ತತ್ತ್ವ[೭] ವನ್ನು ಪುನರುತ್ಥಾನಗೊಳಿಸಿದ, ಇದು ಆನಂತರ ರಾಬರ್ಟ್ ಗ್ರೊಸೆಟೆಸ್ಟ್ ಮತ್ತು ರಾಗರ್ ಬೆಕೋನ್ನಂತ ಪಾಶ್ಚಿಮಾತ್ಯ ವಿದ್ವಾಂಸರ ಮೇಲೆ ಪ್ರಭಾವ ಬೀರಿತು.[೮] 984ರಲ್ಲಿ, ಪರ್ಷಿಯನ್ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞನಾದ ಇಬ್ನ್ ಸಾಹ್ಲ್ ಎಂಬುವವನು "ಆನ್ ಬರ್ನಿಂಗ್ ಮಿರರ್ಸ್ ಅಂಡ್ ಲೆನ್ಸಸ್ (ಉರಿಯುವ ಕನ್ನಡಿಗಳು ಮತ್ತು ಮಸೂರಗಳ ಮೇಲೆ)" ಎಂಬ ಗ್ರಂಥವನ್ನು ಬರೆದ, ಇದರಲ್ಲಿ ವಕ್ರೀಭವನದ ತತ್ತ್ವವನ್ನು ಗಣಿತಾತ್ಮಕವಾಗಿ ಸ್ನೆಲ್ನ ತತ್ವಕ್ಕೆ ಸಮನಾಗಿ ಮತ್ತು ಸರಿಯಾಗಿ ವಿವರಿಸಿದ.[೯] ಈತನು, ಅಕ್ಷರೇಖೆಯ ಒಂದೇ ಬಿಂದುವಿನ ಮೇಲೆ ಬೆಳಕನ್ನು ಕೇಂದ್ರೀಕರಿಸುವ ಮಸೂರ ಮತ್ತು ಕನ್ನಡಿಗಳ ಆಕಾರವನ್ನು ಅಳೆಯಲು ವಕ್ರೀಭವನ ತತ್ವವನ್ನು ಬಳಸಿದ. 11ನೇ ಶತಮಾನದ ಪ್ರಾರಂಭದಲ್ಲಿ, ಅಲ್ಹಾಜೇನ್ (ಇಬ್ನ್ ಅಲ್-ಹೇದಮ್) ತನ್ನ ಬುಕ್ ಆಫ್ ಆಪ್ಟಿಕ್ಸ್ (ದೃಗ್ವಿಜ್ಞಾನದ ಪುಸ್ತಕ) ಅನ್ನು ಬರೆದ, ಈ ಪುಸ್ತಕವು ಆಗ್ಗೆ ಪ್ರಸ್ತುತವಾಗಿದ್ದ ’ದೃಗ್ವಿಜ್ಞಾನದ ಇಸ್ಲಾಮೀಯ ತಿಳುವಳಿಕೆ’ಯನ್ನು ವಿವರವಾಗಿ ದಾಖಲಿಸಿತು ಮತ್ತು ಆ ಕ್ಷೇತ್ರದಲ್ಲಿ ಕ್ರಾಂತಿ ಉಂಟುಮಾಡಿತು.[೧೦][೧೧][೧೨] ಇದು ಬಿಂದುರಂಧ್ರಗಳು ಮತ್ತು ನಿಮ್ನ ಮಸೂರಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ಆಪ್ಟಿಕಲ್ ಸ್ವರೂಪಗಳ ವಿವರಣೆಯನ್ನು ಹೊಂದಿದೆ,[೧೩][೧೪] ದೃಷ್ಟಿಯ ಬಗೆಗೆ ಮೊದಲ ಬಾರಿಗೆ ಸರಿಯಾದ ವಿವರಣೆಯನ್ನು ನೀಡಿತು, ಪ್ರಾಚೀನ ವೈಜ್ಞಾನಿಕ ವಿಧಾನವನ್ನು ಬಳಸಿಕೊಂಡು ವಿವಿಧ ಪ್ರಯೋಗಗಳನ್ನು ವಿವರಿಸಿತು,[೧೫] ಮತ್ತು ಆಧುನಿಕ ದೂರದರ್ಶಕದ ಅಭಿವೃದ್ಧಿಯ ಮೇಲೆ ಮಹತ್ವದ ಪ್ರಭಾವ ಬೀರಿತು.[೧೬] 13ನೇ ಶತಮಾನದಲ್ಲಿ, ಇಬ್ನ್ ಅಲ್-ಹೇದಮ್ನಿಂದ ಸ್ಫೂರ್ತಿಗೊಂಡ ರಾಗರ್ ಬೇಕೊನ್ ಎಂಬುವನು, ಗಾಜಿನ ಗೋಲಗಳ ಭಾಗಗಳನ್ನು ಭೂತಗನ್ನಡಿಗಳಾಗಿ ಬಳಸಿಕೊಂಡು, ಬೆಳಕು ವಸ್ತುಗಳಿಂದ ಬಿಡುಗಡೆಯಾಗುವುದಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿ ಅವುಗಳಿಂದ ಪ್ರತಿಫಲಿತವಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿದ. 1284ರ ಸುಮಾರಿನಲ್ಲಿ ಸಾಲ್ವಿನೊ ಡಿ'ಆರ್ಮೇಟ್ ಎಂಬುವನು ಮೊದಲ ಧರಿಸಬಹುದಾದ ಕನ್ನಡಕಗಳನ್ನು ತಯಾರಿಸಿದ.[೧೭] 1570 ಮತ್ತು 1580ರ ದಶಕಗಳಲ್ಲಿ ಮೊದಲ ಮೂಲರೂಪದ ದೂರದರ್ಶಕಗಳನ್ನು ಲಿಯೋನಾರ್ಡ್ ಡಿಗ್ಗೆಸ್,[೧೮] ಟಾಕಿ ಅಲ್-ದಿನ್[೧೯] ಮತ್ತು ಗಿಯಾಂಬಟ್ಟಿಸ್ಟ ಡೆಲ್ಲಾ ಪೋರ್ಟ ಎಂಬುವವರು ಕಂಡುಹಿಡಿದರು.[೨೦] ಪ್ರಾಚೀನ ದೂರದರ್ಶಕಗಳೆಂದರೆ ವಕ್ರೀಭವನದ ದೂರದರ್ಶಕಗಳು, ಇದು ದೊಡ್ಡದು ಮಾಡಿ ತೋರಿಸಲು ಸಂಪೂರ್ಣವಾಗಿ ಮಸೂರಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾಗುವ ವಿಧಾನ. 1608ರಲ್ಲಿ ನೆದರ್ಲ್ಯಾಂಡ್ಸ್ನಲ್ಲಿ ಮೂರು ವ್ಯಕ್ತಿಗಳು ಇದನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು: ಮಿಡಲ್ಬರ್ಗ್, ಹೋಲ್ಯಾಂಡ್ನಲ್ಲಿ ಕನ್ನಡಕಗಳ ತಯಾರಕರಾಗಿದ್ದ ಹ್ಯಾನ್ಸ್ ಲಿಪ್ಪರ್ಶೇ ಮತ್ತು ಜಾಚೇರಿಯಸ್ ಜಾನ್ಸೆನ್, ಮತ್ತು ಆಲ್ಕ್ಮಾರ್ನ ಜಾಕೋಬ್ ಮೆಟಿಯಸ್. ಮುಂದಿನ ವರ್ಷದಲ್ಲಿ, ಇಟಲಿಯಲ್ಲಿ, ಗೆಲಿಲಿಯೋ ಈ ವಿನ್ಯಾಸಗಳಿಗೆ ಬಹಳಷ್ಟು ಸುಧಾರಣೆಯನ್ನು ಮಾಡಿದ. 1668ರಲ್ಲಿ, ಐಸಾಕ್ ನ್ಯೂಟನ್ ಮೊದಲ ಪ್ರಾಯೋಗಿಕ ಪ್ರತಿಬಿಂಬಿಸುವ ದೂರದರ್ಶಕವನ್ನು ತಯಾರಿಸಿದ, ಅದಕ್ಕೆ ಆತನ ಹೆಸರೇ ಇದೆ ನ್ಯೂಟನ್ನನ ಪ್ರತಿಬಿಂಬಕ.[೨೧] 1595ರ ಸುಮಾರಿನಲ್ಲಿ ಮೊದಲ ಸೂಕ್ಷ್ಮದರ್ಶಕವನ್ನು ಮಾಡಲಾಯಿತು, ಮಿಡಲ್ಬರ್ಗ್ನಲ್ಲಿ.[೨೨] ಮೂರು ಜನ ಕನ್ನಡಕಗಳ ತಯಾರಕರಿಗೆ ಅದರ ಆವಿಷ್ಕಾರಕ್ಕಾಗಿ ಪ್ರಶಂಸಿಸಲಾಗಿದೆ: ಲಿಪರ್ಶೇ (ಮೊದಲ ನಿಜವಾದ ದೂರದರ್ಶಕವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದವ); ಜ್ಯಾನ್ಸೆನ್; ಮತ್ತು ಆತನ ತಂದೆ, ಹ್ಯಾನ್ಸ್. ಇಂಗ್ಲೀಷಿನ "ಮೈಕ್ರೋಸ್ಕೋಪ್" ಪದದ ಸೃಷ್ಟಿಯನ್ನು ಜಿಯೊವನ್ನಿ ಫೇಬರ್ ಮಾಡಿದ ಎನ್ನಲಾಗಿದೆ, ಗೆಲಿಲಿಯೋನ ಸೂಕ್ಷ್ಮದರ್ಶಕಕ್ಕೆ 1625ರಲ್ಲಿ ಹೆಸರು ಕೊಟ್ಟವನು ಈತನೇ.[೨೩] 17ನೇ ಶತಮಾನದಲ್ಲಿ ತತ್ವಜ್ಞಾನಿ ರೆನೆ ಡೆಸ್ಕಾರ್ಟ್ಸ್ ಬರೆದ ಟ್ರೀಟೈಸೆಸ್ನೊಂದಿಗೆ ದೃಗ್ವಿಜ್ಞಾನ ತತ್ವವು ಬೆಳೆಯಿತು. ಇದು ಬೆಳಕನ್ನು ಉಂಟುಮಾಡುವ ವಸ್ತುಗಳಿಂದಲೇ ಬೆಳಕು ಹೊರಸೂಸುತ್ತದೆ ಎಂದು ಭಾವಿಸಿಕೊಂಡು ಪ್ರತಿಬಿಂಬ ಮತ್ತು ವಕ್ರೀಭವನವನ್ನೊಳಗೊಂಡ ವೈವಿಧ್ಯ ದೃಗ್ವಿಜ್ಞಾನ ಸ್ವರೂಪಗಳನ್ನು ವಿವರಿಸಿತು.[೨೪] ಇದು, ಬೆಳಕು ಕಣ್ಣಿನಿಂದಲೇ ಹೊರಸೂಸುತ್ತದೆ ಎನ್ನುವ ಗ್ರೀಕ್ನ ಅಭಿಪ್ರಾಯಕ್ಕಿಂತ ಮೂಲಭೂತವಾಗಿ ಭಿನ್ನವಾಗಿತ್ತು. 1660ರ ದಶಕದ ಕಡೆಯಲ್ಲಿ ಮತ್ತು 1670ರ ದಶಕದ ಮೊದಲಲ್ಲಿ, ನ್ಯೂಟನ್ನನು ಡೆಸ್ಕಾರ್ಟೆಸ್ನ ಆಲೋಚನೆಗಳನ್ನು ಒಂದು ಬೆಳಕಿನ ಕಾರ್ಪುಸಲ್ ತತ್ವವನ್ನಾಗಿ ವಿಸ್ತರಿಸಿದ್ದ , ಪ್ರಖ್ಯಾತವಾಗಿ ಬಿಳಿಯ ಬೆಳಕು, ಒಂದು ಪ್ರತ್ಯೇಕ ಬಣ್ಣವಾಗಿರದೆ, ಲೋಲಕದ ಸಹಾಯದಿಂದ ವರ್ಣಪಂಕ್ತಿಗಳಿಗೆ ಬದಲಾಯಿಸಬಹುದಾದ ಬೇರೆ ಬೇರೆ ಬಣ್ಣಗಳಿಂದ ಕೂಡಿದೆ ಎಂಬುದನ್ನು ತೋರಿಸಿದ. 1664ರಲ್ಲಿ ರಾಬರ್ಟ್ ಹೂಕ್ ನೀಡಿದ್ದ ಸಲಹೆಗಳನ್ನಾಧರಿಸಿ, 1690ರಲ್ಲಿ, ಕ್ರಿಶ್ಚಿಯನ್ ಹೇಗೆನ್ಸ್ ಬೆಳಕಿಗೆ ತರಂಗ ತತ್ತ್ವವನ್ನು ಪ್ರಸ್ತಾಪಿಸಿದ. ಹೂಕ್ ತಾನೆ ಸಾರ್ವಜನಿಕವಾಗಿ ನ್ಯೂಟನ್ನನ ಬೆಳಕಿನ ತತ್ವಗಳನ್ನು ಟೀಕಿಸಿದ ಮತ್ತು ಇವರಿಬ್ಬರ ತಿಕ್ಕಾಟವು ಹೂಕ್ನ ಸಾವಿನವರೆಗೂ ಮುಂದುವರೆಯಿತು. 1704ರಲ್ಲಿ, ನ್ಯೂಟನ್ ಆಪ್ಟಿಕ್ಸ್ ಅನ್ನು ಪ್ರಕಟಿಸಿದ ಮತ್ತು ಆ ಸಮಯದಲ್ಲಿ ಭೌತಶಾಸ್ತ್ರದ ಇತರ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ಆತನು ಯಶಸ್ಸು ಗಳಿಸಿದ್ದ ಕಾರಣ, ಬೆಳಕಿನ ಸ್ವಭಾವದ ಬಗೆಗಿನ ಚರ್ಚೆಯಲ್ಲಿ ಆತನನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ವಿಜೇತನೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತಿತ್ತು.[೨೪]ಥಾಮಸ್ ಯಂಗ್ ಮತ್ತು ಅಗಸ್ಟಿನ್-ಜೀನ್ ಫ್ರೆಸ್ನೆಲ್ರವರುಬೆಳಕಿನ ತರಂಗ ಸ್ವಭಾವವನ್ನು ದೃಢಪಡಿಸಿದ, ಬೆಳಕಿನ ಹಸ್ತಕ್ಷೇಪದ ಮೇಲೆ ಪ್ರಯೋಗಗಳನ್ನು ಮಾಡುವವರೆಗೂ ಅಂದರೆ 19ನೇ ಶತಮಾನದ ಪ್ರಾರಂಭದವರೆಗೂ ನ್ಯೂಟನ್ನನ ದೃಗ್ವಿಜ್ಞಾನ ಮತ್ತು ಹೊರಸೂಸುವಿಕೆಯ ತತ್ವಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಒಪ್ಪಿಕೊಳ್ಳಲಾಗುತ್ತಿತ್ತು. ಯಂಗ್ನ ಪ್ರಸಿದ್ಧ ದ್ವಿಸೀಳು ಪ್ರಯೋಗವು ಬೆಳಕು ಸಾಮಾನ್ಯ ಕಣಗಳು ಪಾಲಿಸದ ತತ್ವವಾದ ಅತಿ ತತ್ವವನ್ನು ಪಾಲಿಸುತ್ತದೆ ಎಂಬುದನ್ನು ತೋರಿಸಿತು. ಈ ಕೆಲಸವು ಬೆಳಕಿನ ಕಿರಣ ವಕ್ರ ವಿಯೋಜನಕ್ಕೆ ಕಾರಣವಾಯಿತು ಮತ್ತು ಭೌತಿಕ ದೃಗ್ವಿಜ್ಞಾನದ ಹೊಸ ಅಧ್ಯಯನ ಶಾಖೆಯನ್ನೇ ತೆರೆಯಿತು.[೨೫] 1860ರ ದಶಕದಲ್ಲಿ ಜೇಮ್ಸ್ ಕ್ಲೆರ್ಕ್ ಮ್ಯಾಕ್ಸ್ವೆಲ್ ತರಂಗ ದೃಗ್ವಿಜ್ಞಾನವನ್ನು ವಿದ್ಯುದಯಸ್ಕಾಂತ ತತ್ವದ ಜೊತೆಗೆ ಯಶಸ್ವಿಯಾಗಿ ಒಗ್ಗೂಡಿಸಿದನು.[೨೬]
ಆಪ್ಟಿಕಲ್ ತತ್ವದ ಮುಂದಿನ ಬೆಳವಣಿಗೆ 1899ರಲ್ಲಿ ಬಂದಿತು, ಮ್ಯಾಕ್ಸ್ ಪ್ಲ್ಯಾಂಕ್ಅನು ಬೆಳಕು ಮತ್ತು ವಸ್ತುವಿನ ನಡುವಿನ ಶಕ್ತಿ ವಿನಿಮಯ, ತಾನು ಕ್ವಾಂಟ ಎಂದು ಕರೆದ, ಕೇವಲ ಅಖಂಡ, ಮೊತ್ತಗಳಲ್ಲಿ ಆಗುತ್ತದೆ ಎಂಬುದನ್ನು ತೋರಿಸಿದ. ಕಪ್ಪುದೇಹ ವಿಕಿರಣಶೀಲತೆಯಲ್ಲಿ ಇದರ ಸರಿಯಾದ ಮಾದರಿಯನ್ನು ಕಾಣಿಸಲಾಯಿತು.[೨೭][27][27][27][27][27]0[27][27][27][27][27][27] 1905ರಲ್ಲಿ, ಆಲ್ಬರ್ಟ್ ಐನ್ಸ್ಟೈನ್ ತೇಜೋವಿದ್ಯುತ್ ಪರಿಣಾಮದ ಬಗೆಗೆ ಒಂದು ತತ್ವವನ್ನು ಪ್ರಕಟಿಸಿದ, ಇದು ಬೆಳಕಿನದೇ ಪರಿಮಾಣೀಕರಣವನ್ನು ದೃಢವಾಗಿ ಸ್ಥಾಪಿಸಿತು.[೨೮][೨೯] 1913ರಲ್ಲಿ, ನೀಲ್ಸ್ ಬೋಹರನು ಕಣಗಳು ಕೇವಲ ಅಖಂಡ ಮೊತ್ತದ ಶಕ್ತಿಯನ್ನು ಹೊರಸೂಸಲು ಸಾಧ್ಯ ಎಂಬುದನ್ನು ತೋರಿಸಿದ, ಹಾಗಾಗಿ ಅವನು ಹೊರಸೂಸುವ ಮತ್ತು ಹೀರುವಿಕೆ ವರ್ಣಪಂಕ್ತಿಯಲ್ಲಿ ಕಾಣುವ ಅಖಂಡ ರೇಖೆಗಳನ್ನು ವಿವರಿಸಿದಂತಾಯ್ತು.[೩೦] ಈ ಬೆಳವಣಿಗೆಗಳ ನಂತರ ಬಂದ ಬೆಳಕು ಮತ್ತು ವಸ್ತುಗಳ ನಡುವಿನ ಸಂವಹನಗಳು ಪರಿಮಾಣ ದೃಗ್ವಿಜ್ಞಾನದ ಅಡಿಪಾಯವನ್ನು ರೂಪಿಸಿದ್ದಷ್ಟೇ ಅಲ್ಲ ಒಟ್ಟಾರೆಯಾಗಿ ಪರಿಮಾಣ ಯಂತ್ರಶಾಸ್ತ್ರದ ಬೆಳವಣಿಗೆಯಲ್ಲಿ ಮಹತ್ವದ ಪಾತ್ರವಹಿಸಿತು. ಅಂತಿಮವಾಗಿ ಪರಿಣಾಮ ವಿದ್ಯುದ್ಬಲ ವಿಜ್ಞಾನ ತತ್ವವು ರೂಪುಗೊಂಡಿತು, ಇದು ಎಲ್ಲ ದೃಗ್ವಿಜ್ಞಾನ ಮತ್ತು ವಿದ್ಯುದಯಸ್ಕಾಂತ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ನಿಜ ಮತ್ತು ತಾತ್ವಿಕ ಫೋಟೋನ್ಗಳ ವಿನಿಮಯದಿಂದ ಆಗುತ್ತದೆ ಎಂಬಂತೆ ವಿವರಿಸುತ್ತದೆ.[೩೧] 1953ರಲ್ಲಿ ಮೇಸರ್ನ ಅನ್ವೇಷಣೆ ಮತ್ತು 1960ರಲ್ಲಿ ಲೇಸರ್ನ ಅನ್ವೇಷಣೆಗಳೊಂದಿಗೆ ಪರಿಮಾಣ ದೃಗ್ವಿಜ್ಞಾನವು ಪ್ರಾಯೋಗಿಕ ಮಹತ್ತ್ವವನ್ನು ಪಡೆದುಕೊಂಡಿತು.[೩೨] 1950 ಮತ್ತು 1960ರ ದಶಕಗಳಲ್ಲಿ ಪರಿಮಾಣ ಕ್ಷೇತ್ರ ತತ್ವದಲ್ಲಿ ಪೌಲ್ ಡೈರಾಕ್ನ ಕೆಲಸಗಳ ನಂತರ ಜಾರ್ಜ್ ಸುದರ್ಶನ್, ರಾಯ್ ಜೆ. ಗ್ಲಾಬರ್, ಮತ್ತು ಲಿಯೋನಾರ್ಡ್ ಮ್ಯಾಂಡೆಲ್ ಎಂಬುವರು ತೇಜೋ ಪರಿಶೋಧನೆ ಮತ್ತು ಬೆಳಕಿನ ಅಂಕಿಅಂಶಗಳ ಬಗೆಗೆ ವಿವರವಾದ ತಿಳುವಳಿಕೆಯನ್ನು ಪಡೆಯಲು ಪರಿಮಾಣ ತತ್ವವನ್ನು ವಿದ್ಯುದಯಸ್ಕಾಂತ ಕ್ಷೇತ್ರಕ್ಕೆ ಉಪಯೋಗಿಸಿಕೊಂಡನು.
ಶಾಸ್ತ್ರೀಯ ದೃಗ್ವಿಜ್ಞಾನ[ಬದಲಾಯಿಸಿ]
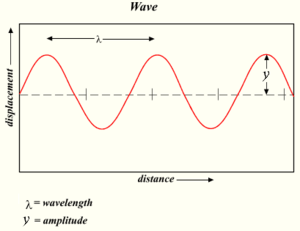
ಪೂರ್ವ-ಪರಿಮಾಣ-ಯಾಂತ್ರಿಕ ದೃಗ್ವಿಜ್ಞಾನದ ಪ್ರಕಾರ, ಬೆಳಕು ತೂಗಾಡುವ ವಿದ್ಯುತ್ ಮತ್ತು ಅಯಸ್ಕಾಂತ ಕ್ಷೇತ್ರಗಳನ್ನೊಳಗೊಂಡ ವಿದ್ಯುದಯಸ್ಕಾಂತ ತರಂಗ. ತರಂಗವು ಕಾಲದ ಮೂಲಕ ಮತ್ತು ಸಮಯದಲ್ಲಿ ತೂಗಾಡುವುದರಿಂದ ಈ ಕ್ಷೇತ್ರಗಳು ನಿರಂತರವಾಗಿ ಮತ್ತೊಂದನ್ನು ಸೃಷ್ಟಿಸುತ್ತಿರುತ್ತದೆ.[೩೩] ಬೆಳಕಿನ ತರಂಗದ ಪುನರಾವರ್ತನವನ್ನು ತೂಗಾಟದ ಕಾಲಾವಧಿಯ ಮೂಲಕ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ತರಂಗವು ವಿವಿಧ ಸಾಮಗ್ರಿ ("ಮಾಧ್ಯಮ")ಗಳ ಮೂಲಕ ಸಾಗುವುದರಿಂದ ಸಾಮಾನ್ಯವಾಗಿ ಪುನರಾವರ್ತನವು ಬದಲಾಗುವುದಿಲ್ಲ, ಆದರೆ ತರಂಗದ ವೇಗವು ಸಾಮಗ್ರಿಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ. ವೇಗ, ಪುನರಾವರ್ತನ, ಮತ್ತು ತರಂಗಾಯಾನುಗಳು ಈ ಸೂತ್ರದಂತೆ ಸಂಬಂಧಿತವಾಗಿರುತ್ತದೆ
ಇಲ್ಲಿ ವೇಗವಾದರೆ, ಎನ್ನುವುದು ತರಂಗಾಯಾನು ಮತ್ತು ಎನ್ನುವುದು ಪುನರಾವರ್ತನ. ಪುನರಾವರ್ತನವು ಸ್ಥಿರವಾಗಿರುವುದರಿಂದ, ತರಂಗದ ವೇಗದಲ್ಲಾಗುವ ಬದಲಾವಣೆಯು ತರಂಗಾಯಾನುವಿನಲ್ಲಿಯೂ ಬದಲಾವಣೆಯನ್ನು ಸೃಷ್ಟಿಸುತ್ತದೆ.[೩೪] ಒಂದು ಮಾಧ್ಯಮದಲ್ಲಿನ ಬೆಳಕಿನ ವೇಗವು ವಕ್ರೀಭವನದ ಸೂತ್ರದಿಂದ ಆಗಿರುತ್ತದೆ, , ಇದು ನಿರ್ವಾತದಲ್ಲಿ ಬೆಳಕಿನ ವೇಗ ಮತ್ತು ಮಾಧ್ಯಮದಲ್ಲಿನ ವೇಗದ ಅನುಪಾತ ಆಗಿರುತ್ತದೆ:
ನಿರ್ವಾತದಲ್ಲಿ ಬೆಳಕು ಅಚಲವಾಗಿರುತ್ತದೆ, ಇದು ಕರಾರುವಕ್ಕಾಗಿ ಪ್ರತಿ ಸೆಕೆಂಡಿಗೆ 299,792,458 ಮೀಟರುಗಳು.[೩೫] ಆದ್ದರಿಂದ, ತರಂಗಾಯಾನು ಹೊಂದಿದ ನಿರ್ವಾತದಲ್ಲಿರುವ ಬೆಳಕಿನ ಕಿರಣವು ವಕ್ರೀಭವನದ ಸೂತ್ರ n ಇರುವ ವಸ್ತುವಿನಲ್ಲಿ ತರಂಗಾಯಾನುವನ್ನು ಹೊಂದಿರುತ್ತದೆ.ಬೆಳಕಿನ ತರಂಗದ ವಿಸ್ತಾರವು ಬೆಳಕಿನ ತೀವ್ರತೆಗೆ ಸಂಬಂಧಿಸಿದುದಾಗಿರುತ್ತದೆ, ಇದು ತರಂಗದ ವಿದ್ಯುತ್ ಮತ್ತು ಅಯಸ್ಕಾಂತ ಕ್ಷೇತ್ರದಲ್ಲಿ ಶೇಖರವಾಗಿರುವ ಶಕ್ತಿಗೆ ಸಂಬಂಧಪಟ್ಟಿರುತ್ತದೆ.ಸಾಂಪ್ರದಾಯಿಕ ದೃಗ್ವಿಜ್ಞಾನವನ್ನು ಎರಡು ಪ್ರಮುಖ ಶಾಖೆಗಳನ್ನಾಗಿ ವಿಭಾಗಿಸಲಾಗಿದೆ: ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನ ಮತ್ತು ಭೌತಿಕ ದೃಗ್ವಿಜ್ಞಾನ.
ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನ[ಬದಲಾಯಿಸಿ]
This article should include a summary of another article. See Wikipedia:Summary style for information on how to incorporate it into this article's main text. (September 2009) |

ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನ , ಅಥವಾ ಕಿರಣ ದೃಗ್ವಿಜ್ಞಾನ ವು ಬೆಳಕಿನ ಪಸರಿಸುವಿಕೆಯನ್ನು "ಕಿರಣಗಳ" ಪದಗಳಲ್ಲಿ ವಿವರಿಸುತ್ತದೆ. ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನದಲ್ಲಿ "ಕಿರಣ"ವು ಅಬ್ಸ್ಟ್ರ್ಯಾಕ್ಷನ್, ಅಥವಾ "ಸಲಕರಣೆ", ಇದನ್ನು ಬೆಳಕಿನ ಪಥವನ್ನು ಊಹಿಸಲು ಬಳಸಬಹುದು. ಬೆಳಕಿನ ಕಿರಣವು ಬೆಳಕಿನ ತರಂಗಮುನ್ನೆಲೆಗೆ ನೇರಸಮಕೋನವಾದ (ಮತ್ತು ಆದ್ದರಿಂದ ತರಂಗ ವಾಹಕಕ್ಕೆ ಅನುರೇಖೀಯವಾದ) ಕಿರಣ. ಬೆಳಕಿನ ಕಿರಣಗಳು ಎರಡು ಬೇರೆ ಬೇರೆ ರೀತಿಯ ಮಾಧ್ಯಮಗಳ ನಡುವಿನ ಇಂಟರ್ಫೇಸ್ನಲ್ಲಿ ಬಾಗುತ್ತದೆ ಮತ್ತು ವಕ್ರೀಭವನದ ಸೂತ್ರ ಬದಲಾಗುವ ಮಾಧ್ಯಮದಲ್ಲಿ ವಕ್ರವಾಗಬಹುದು. ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನವು ಈ ಕಿರಣಗಳನ್ನು ಆಪ್ಟಿಕಲ್ ವ್ಯವಸ್ಥೆಯ ಮೂಲಕ ಪಸರಿಸಲು ನಿಯಮಗಳನ್ನು ಒದಗಿಸುತ್ತದೆ, ಇದು ನಿಜವಾದ ತರಂಗಮುನ್ನೆಲೆ ಹೇಗೆ ಪಸರಿಸುತ್ತದೆಂದು ಸೂಚಿಸುತ್ತದೆ. ಇದು ದೃಗ್ವಿಜ್ಞಾನದ ಗಣನೀಯ ಸಾಧಾರಣೀಕರಣ, ಇದು ಕಿರಣ ವಕ್ರ ವಿಯೋಜನ ಮತ್ತು ಧೃವೀಕರಣ ಮುಂತಾದ ಆಪ್ಟಿಕಲ್ ಪರಿಣಾಮಗಳಿಗೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ. ಇದು ಒಳ್ಳೆಯ ಸರಾಸರಿಯೇ, ಆದರೆ, ಬೆಳಕು ಸಂವಹನ ಮಾಡುವ ರಚನೆಗಳ ಗಾತ್ರಕ್ಕೆ ಹೋಲಿಸಿದಾಗ ತರಂಗಾಯಾನು ತುಂಬ ಸಣ್ಣದಿರುವಾಗ ಮಾತ್ರ. ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನವನ್ನು ದೃಗ್ವಿಜ್ಞಾನ ವಿಲಕ್ಷಣಗಳನ್ನೊಳಗೊಂಡಂತೆ ರೇಖಾಗಣಿತ ವಿಷಯಗಳಾದ ಇಮೇಜಿಂಗ್ ವಿಷಯಗಳಿಗೆ ಬಳಸಬಹುದು.ಇದಕ್ಕಿಂತ ಸ್ವಲ್ಪ ತೀಕ್ಷ್ಣವಾದ ವ್ಯಾಖ್ಯಾನವು ಫರ್ಮೆಟ್ನ ತತ್ವದಿಂದ ಸಿಗುತ್ತದೆ, ಇದು ಎರಡು ಬಿಂದುಗಳ ನಡುವೆ ಯಾವ ಪಥದಲ್ಲಿ ಕಿರಣವು ಸಾಗುತ್ತದೋ ಅದೇ ಅತ್ಯಂತ ಕಡಿಮೆ ಸಮಯದಲ್ಲಿ ಹಾದುಹೋಗಬಹುದಾದ ಪಥ [೩೬] ಎನ್ನುತ್ತದೆ.
ಸರಾಸರಿಗಳು[ಬದಲಾಯಿಸಿ]
ಪ್ಯಾರಾಕ್ಸಿಯಲ್ ಸರಾಸರಿ ಅಥವಾ "ಸಣ್ಣ ಕೋನ ಸರಾಸರಿ" ಮಾಡುವ ಮೂಲಕ ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನವನ್ನು ಸರಳಗೊಳಿಸಲಾಗುತ್ತದೆ. ಆನಂತರ ನಿಶ್ಚಿತವಾದ ಚರ್ಯೆ ಏಕಮುಖವಾಗುತ್ತದೆ, ಇದರಿಂದ ಆಪ್ಟಿಕಲ್ ಭಾಗಗಳನ್ನು ಮತ್ತು ವ್ಯವಸ್ಥೆಗಳನ್ನು ಸರಳ ಮಾತೃಕೆಗಳ ಮೂಲಕ ವಿವರಿಸಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ. ಇದು ಗಾಸಿಯಾನ್ ದೃಗ್ವಿಜ್ಞಾನ ತಂತ್ರಗಳಿಗೆ ಮತ್ತು ಪ್ಯಾರಾಕ್ಸಿಯಲ್ ಕಿರಣ ಶೋಧನೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ, ಇವುಗಳಿಂದ ಆಪ್ಟಿಕಲ್ ವ್ಯವಸ್ಥೆಗಳ ಮೂಲ ಗುಣಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ, ಉದಾಹರಣೆಗೆ ಸರಾಸರಿ ಇಮೇಜ್ ಮತ್ತು ವಸ್ತು-ಸ್ಥಾನಗಳು ಮತ್ತು ಪ್ರವರ್ಧನಗಳು.[೩೭]
ಪ್ರತಿಬಿಂಬಗಳು[ಬದಲಾಯಿಸಿ]

ಪ್ರತಿಬಿಂಬಗಳನ್ನು ಎರಡು ವಿಧಗಳನ್ನಾಗಿ ವಿಂಗಡಿಸಬಹುದು: ಕನ್ನಡಿಯಂತಹ ಪ್ರತಿಬಿಂಬ ಮತ್ತು ವಿಕೀರ್ಣ ಪ್ರತಿಬಿಂಬ. ಕನ್ನಡಿಯಂತಹ ಪ್ರತಿಬಿಂಬವು ಕನ್ನಡಿ ಮುಂತಾದ ಹೊಳೆಯುವ ಮೇಲ್ಮೈಗಳನ್ನು ವಿವರಿಸುತ್ತದೆ, ಇವು ಬೆಳಕನ್ನು ಸರಳವಾಗಿ, ಊಹಿಸಬಹುದಾದ ರೀತಿಯಲ್ಲಿ ಪ್ರತಿಬಿಂಬಿಸುತ್ತವೆ. ಇದರಿಂದ ಪ್ರತಿಬಿಂಬಿತವಾದ ಚಿತ್ರಗಳನ್ನು ಉತ್ಪತ್ತಿ ಮಾಡುವುದು ಸಾಧ್ಯವಾಗುತ್ತದೆ, ಇದನ್ನು ಪ್ರತ್ಯಕ್ಷ (ನಿಜವಾದ) ಅಥವಾ ಸಮಾನಾಂತರ ಅಂದಾಜು ಮಾಡಿದ (ತಾತ್ವಿಕ) ದೇಶದ ಸ್ಥಾನಕ್ಕೆ ಸಂಯೋಜಿಸಬಹುದು. ವಿಕೀರ್ಣ ಪ್ರತಿಬಿಂಬವು ಕಾಗದ ಅಥವಾ ಕಲ್ಲು ಮೊದಲಾದ ಬಿಂಬಾರೋಪಣ ಮುಸುಕು ಮೇಲ್ಮೈಗಳನ್ನು ವಿವರಿಸುತ್ತದೆ. ಈ ಮೇಲ್ಮೈಗಳ ಪ್ರತಿಬಿಂಬಗಳನ್ನು ಅಂಕಿಅಂಶಗಳಿಂದ ಮಾತ್ರ ವಿವರಿಸಲು ಸಾಧ್ಯ, ಪ್ರತಿಬಿಂಬಿತ ಬೆಳಕಿನ ನಿಖರ ಹಂಚಿಕೆಯು ಮೇಲ್ಮೈನ ಸೂಕ್ಷ್ಮಗ್ರಾಹೀಯ ರಚನೆಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ. ಅನೇಕ ವಿಕೀರ್ಣ ಪ್ರತಿಬಿಂಬಕಗಳನ್ನು ಲ್ಯಾಂಬರ್ಟ್ಸ್ ಕೋಸೈನ್ ಸೂತ್ರ ದಲ್ಲಿ ವಿವರಿಸಲಾಗಿದೆ ಅಥವಾ ಆ ಸೂತ್ರದಿಂದ ಅಂದಾಜು ಮಾಡಬಹುದು. ಯಾವ ಕೋನದಿಂದ ನೋಡಿದರೂ ಸಮನಾದ ಹೊಳಪಿರುವ ಮೇಲ್ಮೈಗಳನ್ನು ಈ ಸೂತ್ರವು ವಿವರಿಸುತ್ತದೆ.ಕನ್ನಡಿಯಂತಹ ಪ್ರತಿಬಿಂಬದಲ್ಲಿ, ಸಾಮಾನ್ಯ ಮೇಲ್ಮೈನೊಂದಿಗೆ ಪತನ ಕಿರಣವು ಯಾವ ಕೋನವನ್ನು ಮಾಡುತ್ತದೆ ಎಂಬುದರ ಮೇಲೆ ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣದ ದಿಕ್ಕನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ, ಸಾಮಾನ್ಯ ಮೇಲ್ಮೈ ಎಂಬುದು ಕಿರಣವು ಮೇಲ್ಮೈಯನ್ನು ಹೊಡೆಯುವ ಬಿಂದುವಿಗೆ ಲಂಬವಾಗಿರುವ ರೇಖೆ. ಪತನ ಮತ್ತು ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುತ್ತವೆ, ಮತ್ತು ಸಾಮಾನ್ಯ ಮೇಲ್ಮೈ ಮತ್ತು ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣದ ನಡುವಿನ ಕೋನ ಮತ್ತು ಸಾಮಾನ್ಯ ಮತ್ತು ಪತನ ಕಿರಣದ ನಡುವಿನ ಕೋನ ಎರಡೂ ಒಂದೇ ಆಗಿರುತ್ತದೆ.[೩೮] ಇದಕ್ಕೆ ಪ್ರತಿಬಿಂಬದ ಸೂತ್ರ ಎಂದು ಹೆಸರು.ಪ್ರತಿಬಿಂಬದ ಸೂತ್ರದ ಪ್ರಕಾರ ಸಮತಟ್ಟಾದ ಕನ್ನಡಿಗಳಿಗೆ, ವಸ್ತುಗಳ ಬಿಂಬಗಳು ನೇರವಾಗಿ ಇರುತ್ತವೆ ಮತ್ತು ಕನ್ನಡಿಯ ಮುಂದೆ ಎಷ್ಟು ಅಂತರವಿರುತ್ತದೆಯೋ ಕನ್ನಡಿಯ ಹಿಂದೆಯೂ ಅಷ್ಟೇ ಅಂತರ ಇರುತ್ತದೆ. ವಸ್ತುವಿನ ಗಾತ್ರ ಮತ್ತು ಚಿತ್ರದ ಗಾತ್ರ ಒಂದೇ ಅಗಿರುತ್ತದೆ. (ಒಂದು ಚಪ್ಪಟೆ ಕನ್ನಡಿಯ ವರ್ಧನೆಯು ಏಕತೆಯಾಗಿದೆ.) ಈ ಸೂತ್ರದ ಪ್ರಕಾರ ಕನ್ನಡಿಯ ಬಿಂಬಗಳು ಸಮಾನ ಪರಾವರ್ತನಗೊಂಡಿವೆ, ಇದನ್ನೇ ನಾವು ಬಲ-ಎಡ ತಿರುಗು ಮುರುಗು ಎಂದು ತಿಳಿದುಕೊಳ್ಳುತ್ತೇವೆ. ಎರಡು(ಅಥವಾ ಯಾವುದೇ ಸಮಸಂಖ್ಯೆಯ) ಕನ್ನಡಿಗಳಲ್ಲಾದ ಪ್ರತಿಬಿಂಬದಿಂದಾದ ಚಿತ್ರಗಳು ಸಮಾನ ಪರಾವರ್ತನಗಳಾಗಿರುವುದಿಲ್ಲ. ಮೂಲೆ ಪ್ರತಿಬಿಂಬಕಗಳು[೩೮] ಬೆಳಕನ್ನು ಹಿಂಪ್ರತಿಬಿಂಬಿಸುತ್ತವೆ, ಪತನ ರೇಖೆಗಳು ಬಂದ ದಿಕ್ಕಿನಲ್ಲಿ ವಾಪಾಸು ಹೋಗುವ ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣಗಳನ್ನು ಸೃಷ್ಟಿಸುತ್ತವೆ.ಕಿರಣ-ಶೋಧನೆಯ ಮೂಲಕ ಮತ್ತು ಮೇಲ್ಮೈನ ಪ್ರತಿಯೊಂದು ಬಿಂದುವಿನಲ್ಲಿ ಪ್ರತಿಬಿಂಬದ ಸೂತ್ರವನ್ನು ಬಳಸುವ ಮೂಲಕ ವಕ್ರ ಮೇಲ್ಮೈ ಇರುವ ಕನ್ನಡಿಗಳನ್ನು ನಿರ್ಮಿಸಬಹುದು. ಲಾಕ್ಷಣಿಕ ಮೇಲ್ಮೈಯುಳ್ಳ ಕನ್ನಡಿಗಳಲ್ಲಿ, ಕನ್ನಡಿಯ ಮೇಲೆ ಪತನವಾಗುವ ಕಿರಣಗಳು ಒಂದು ಸಾಮಾನ್ಯ ಕೇಂದ್ರದಲ್ಲಿ ಏಕಮುಖವಾಗುವ ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣಗಳನ್ನು ನಿರ್ಮಿಸುತ್ತದೆ. ಇತರ ವಕ್ರ ಮೇಲ್ಮೈಗಳು ಕೂಡ ಬೆಳಕನ್ನು ಕೇಂದ್ರೀಕರಿಸಬಹುದು, ಆದರೆ ಕೇಂದ್ರವು ಸ್ಥಳದಲ್ಲಿ ಸ್ವಲ್ಪ ಹರಡಿಕೊಳ್ಳುವಂತೆ ಮಾಡುವ ಚದುರುವಿಕೆ ಆಕಾರದಿಂದಾಗಿ ಸ್ವಲ್ಪ ವಿಲಕ್ಷಣಗಳೊಂದಿಗೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳಬೇಕೆಂದರೆ, ವರ್ತುಲ ಕನ್ನಡಿಗಳು ವರ್ತುಲ ವಿಲಕ್ಷಣವನ್ನು ತೋರುತ್ತದೆ. ವಕ್ರ ಕನ್ನಡಿಗಳು ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚಾದ ಇಲ್ಲವೆ ಒಂದಕ್ಕಿಂತ ಕಡಿಮೆಯಾದ ಪ್ರವರ್ಧನದಲ್ಲಿ ಬಿಂಬಗಳನ್ನು ರೂಪಿಸಬಲ್ಲುದು, ಮತ್ತು ಬಿಂಬವು ತಿರುಗುಮುರುಗು ಆಗಿದೆ ಎಂಬುದನ್ನು ಸೂಚಿಸುತ್ತ ಆ ಪ್ರವರ್ಧನವು ಋಣಾತ್ಮಕವೂ ಆಗಿರಬಹುದು. ಕನ್ನಡಿಯಲ್ಲಿ ಪ್ರತಿಬಿಂಬದಿಂದಾದ ನೇರ ಬಿಂಬವು ಯಾವಾಗಲೂ ತಾತ್ವಿಕವೇ ಆಗಿರುತ್ತದೆ, ಆದರೆ ತಿರುಗುಮುರುಗಾದ ಬಿಂಬವು ನಿಜವಾದದ್ದು ಮತ್ತು ಅದನ್ನು ಒಂದು ಪರದೆಯ ಮೇಲೆ ಪ್ರೊಜೆಕ್ಟ್ಮಾಡಬಹುದು.[೩೮]
ವಕ್ರೀಭವನಗಳು[ಬದಲಾಯಿಸಿ]

ವಕ್ರೀಭವನದ ಸೂತ್ರವು ಬದಲಾಗುವ ಸ್ಥಳದ ಮೂಲಕ ಬೆಳಕು ಹಾದುಹೋಗುವಾಗ ’ವಕ್ರೀಭವನ’ ಸಂಭವಿಸುತ್ತದೆ; ಇದು ಮಸೂರಗಳನ್ನು ಮಾಡಲು ಮತ್ತು ಬೆಳಕನ್ನು ಕೇಂದ್ರೀಕರಿಸಲು ಸಹಾಯ ಮಾಡುತ್ತದೆ. ವಕ್ರೀಭವನದ ಸೂತ್ರವನ್ನೊಳಗೊಂಡ ಒಂದು ಸಮಾನ ಮಾಧ್ಯಮ ಮತ್ತು ವಕ್ರೀಭವನದ ಸೂತ್ರವನ್ನೊಳಗೊಂಡ ಮತ್ತೊಂದು ಮಾಧ್ಯಮ ನ ನಡುವೆ ಇಂಟರ್ಫೇಸ್ ಇದ್ದಾಗ ಸರಳ ವಕ್ರೀಭವನ ಸಂಭವಿಸುತ್ತದೆ.. ಅಂತಹ ಸಂದರ್ಭಗಳಲ್ಲಿ ಉಂಟಾಗುವ ಬೆಳಕಿನ ಕಿರಣದ ಅಪಸರಣವನ್ನು ಸ್ನೆಲ್ನ ತತ್ವವು ವಿವರಿಸುತ್ತದೆ:
ಇಲ್ಲಿ ಮತ್ತು ಗಳು ಕ್ರಮವಾಗಿ ಸಾಮಾನ್ಯ (ಇಂಟರ್ಫೇಸ್ಗೆ) ಮತ್ತು ಪತನ ಮತ್ತು ವಕ್ರೀಭವನಗೊಂಡ ತರಂಗಗಳ ಕೋನಗಳು. ಮೇಲೆ ಕೊಟ್ಟಿರುವ ವಕ್ರೀಭವನದ ಸೂತ್ರದ ಪ್ರಕಾರ ಈ ಘಟನೆಯು ಬೆಳಕಿನ ಬದಲಾವಣೆಗೊಳ್ಳುವ ವೇಗದೊಂದಿಗೆಯೂ ಸಂಬಂಧಿಸಿದುದಾಗಿದೆ, ಇದರ ಅರ್ಥವೇನೆಂದರೆ :
ಇಲ್ಲಿ, ಅದರದರ ಮಾಧ್ಯಮಗಳ ಮೂಲಕ ಮತ್ತು ಗಳು ತರಂಗ ವೇಗಗಳು.[೩೮]
ಸ್ನೆಲ್ನ ತತ್ವದ ವಿವಿಧ ತತ್ಪರಿಣಾಮಗಳಲ್ಲಿ ಒಂದೆಂದರೆ, ಉಚ್ಚ ವಕ್ರೀಭವನ ಸೂತ್ರ ಹೊಂದಿದ ವಸ್ತುವಿನಿಂದ ಅಲ್ಪ ವಕ್ರೀಭವನದ ಸೂತ್ರ ಹೊಂದಿದ ವಸ್ತುವಿನ ಕಡೆಗೆ ಹೋಗುವ ಬೆಳಕಿನ ಕಿರಣಗಳಿಗೆ, ಇಂಟರ್ಫೇಸ್ನೊಂದಿಗಿನ ಪ್ರಭಾವ ಶೂನ್ಯ ಪ್ರಸಾರವೂ ಆಗಬಹುದು. ಈ ಘಟನೆಯನ್ನು ಪೂರ್ಣ ಆಂತರಿಕ ಪ್ರತಿಬಿಂಬ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಇದರಿಂದ ಫೈಬರ್ ಆಪ್ಟಿಕ್ಸ್ ತಂತ್ರಜ್ಞಾನವು ಸಾಧ್ಯವಾಗುತ್ತದೆ. ಬೆಳಕಿನ ಸಂಕೇತಗಳು ಫೈಬರ್ ಆಪ್ಟಿಕ್ ತಂತಿಯ ಮೂಲಕ ಸಾಗುತ್ತಿದ್ದಂತೆ ಪೂರ್ಣ ಆಂತರಿಕ ಪ್ರತಿಬಿಂಬಕ್ಕೆ ಒಳಗಾಗುತ್ತದೆ, ಇದರಿಂದ ತಂತಿಯ ಉದ್ದಕ್ಕೂ ಸ್ವಲ್ಪವೂ ಬೆಳಕು ನಷ್ಟವಾಗದಂತೆ ಮಾಡುವುದು ಸಾಧ್ಯವಾಗುತ್ತದೆ. ಪ್ರತಿಬಿಂಬ ಮತ್ತು ವಕ್ರೀಭವನದ ಒಂದು ರೀತಿಯ ಸಂಯೋಜನೆಯಿಂದ ಧೃವೀಕೃತ ಬೆಳಕಿನ ಕಿರಣಗಳನ್ನು ನಿರ್ಮಿಸುವುದು ಸಾಧ್ಯವಾಗುತ್ತದೆ: ವಕ್ರೀಭವನಗೊಂಡ ಕಿರಣ ಮತ್ತು ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣಗಳು ಲಂಬಕೋನವನ್ನು ರೂಪಿಸಿದಾಗ, ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣವು "ಸಮ ಧೃವೀಕರಣ"ದ ಗುಣವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಅಂತಹ ಘಟನೆಗೆ ಬೇಕಾದ ಅಧಿಪಾತಕೋನವನ್ನು ಬ್ರ್ಯೂಸ್ಟರ್ನ ಕೋನ ಎಂದು ಕರೆಯುತ್ತೇವೆ.[೩೮] ಬೆಳಕಿನ ಕಿರಣಗಳು "ಏಕ ಮಾಧ್ಯಮ"ದ ಮೂಲಕ ಸಾಗುತ್ತಿರುವಾಗ ಅವುಗಳ ಅಪಸರಣವನ್ನು ಊಹಿಸಲು ಸ್ನೆಲ್ನ ತತ್ವವನ್ನು ಬಳಸಬಹುದು, ವಕ್ರೀಭವನದ ಸೂತ್ರಗಳು ಮತ್ತು ಮಾಧ್ಯಮದ ರೇಖಾಗಣಿತವು ತಿಳಿದಿರುವವರೆಗೂ. ಉದಾಹರಣೆಗೆ, ಲೋಲಕದ ಮೂಲಕ ಬೆಳಕನ್ನು ಹೊರಸೂಸಿದರೆ, ಲೋಲಕದ ಆಕಾರ ಮತ್ತು ಅದು ಯಾವ ದಿಕ್ಕಿಗೆ ತಿರುಗಿದೆ ಎಂಬುದರ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿ ಬೆಳಕಿನ ಕಿರಣವು ಅಪಸರಣಗೊಳ್ಳುತ್ತದೆ. ಜೊತೆಗೆ, ಬಹುತೇಕ ವಸ್ತುಗಳಲ್ಲಿ ಬೆಳಕಿನ ವಿವಿಧ ಆವರ್ತನಗಳು ಸ್ವಲ್ಪ ವಿಭಿನ್ನವಾದ ವಕ್ರೀಭವನದ ಸೂತ್ರಗಳನ್ನು ಹೊಂದಿರುವುದರಿಂದ, ವಕ್ರೀಭವನವನ್ನು ಕಾಮನಬಿಲ್ಲಿನಂತೆ ಕಾಣುವ ವಿಕೀರ್ಣ ವರ್ಣಪಂಕ್ತಿಯನ್ನು ನಿರ್ಮಿಸಲು ಬಳಸಬಹುದು. ಲೋಲಕದ ಮೂಲಕ ಬೆಳಕು ಹಾದು ಹೋಗುವಾಗ ನಡೆಯುವ ಈ ಘಟನೆಯನ್ನು ಕಂಡುಹಿಡಿದವನು ಐಸಾಕ್ ನ್ಯೂಟನ್ ಎಂದೇ ಹೇಳಲಾಗುತ್ತದೆ.[೩೮] ಕೆಲವು ಮಾಧ್ಯಮಗಳು ಸ್ಥಾನದೊಂದಿಗೆ ಕ್ರಮೇಣ ಬದಲಾಗುವ ವಕ್ರೀಭವನ ಸೂತ್ರವನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ಆ ಮಾಧ್ಯಮಗಳಲ್ಲಿ ಬೆಳಕು ನೇರವಾಗಿ ಚಲಿಸುವ ಬದಲು ವಕ್ರವಾಗುತ್ತದೆ. ಬಿಸಿಲಿನ ದಿನಗಳಲ್ಲಿ ಉಂಟಾಗುವ ಮರೀಚಿಕೆಗಳಿಗೆ ಈ ಪರಿಣಾಮವೇ ಕಾರಣ, ಗಾಳಿಯಲ್ಲಿ ಬದಲಾಗುತ್ತಿರುವ ವಕ್ರೀಭವನದ ಸೂತ್ರವು ಬೆಳಕಿನ ಕಿರಣಗಳು ವಕ್ರವಾಗುವಂತೆ ಮಾಡುತ್ತವೆ. ಇದರಿಂದ ದೂರದಲ್ಲಿ ಕನ್ನಡಿಯಂತಹ ಪ್ರತಿಬಿಂಬಗಳು ಇರುವಂತೆ ಕಾಣುತ್ತವೆ (ನೀರಿನ ಕೊಳದ ಮೇಲ್ಮೈನ ಮೇಲಿರುವಂತೆ). ಬದಲಾಗುವ ವಕ್ರೀಭವನದ ಸೂತ್ರವನ್ನು ಹೊಂದಿರುವ ವಸ್ತುಗಳನ್ನು ಏರು-ಸೂತ್ರದ ವಸ್ತು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಇವು ಜೆರಾಕ್ಸ್ ಯಂತ್ರಗಳು ಮತ್ತು ಸ್ಕ್ಯಾನರ್ಗಳು ಸೇರಿದಂತೆ ಆಪ್ಟಿಕಲ್ ಸ್ಕ್ಯಾನಿಂಗ್ ತಂತ್ರಜ್ಞಾನಗಳಲ್ಲಿ ಉಪಯೋಗವಾಗುವ ಅನೇಕ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿರುತ್ತವೆ. ಈ ಘಟನೆಯನ್ನು ಏರು-ಸೂತ್ರದ ದೃಗ್ವಿಜ್ಞಾನ ಕ್ಷೇತ್ರದಲ್ಲಿ ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ.[೩೯]

ಏಕಮುಖವಾದ ಅಥವಾ ವಿಕೀರ್ಣ ಬೆಳಕಿನ ಕಿರಣಗಳನ್ನು ನಿರ್ಮಿಸುವ ಸಾಧನಕ್ಕೆ ಮಸೂರ ಎಂದು ಹೆಸರು. ತೆಳು ಮಸೂರಗಳು ಎರಡೂ ಕಡೆಗಳಲ್ಲಿ ತೇಜೋಕೇಂದ್ರಬಿಂದುಗಳನ್ನು ನಿರ್ಮಿಸುತ್ತವೆ, ಇದನ್ನು ಮಸೂರಮಾಡುವ ಸಮೀಕರಣದ ಮೂಲಕ ಉದಾಹರಿಸಬಹುದು.[೪೦] ಸಾಧಾರಣವಾಗಿ, ಎರಡು ರೀತಿಯ ಮಸೂರಗಳು ಇವೆ: ಪೀನ ಮಸೂರಗಳು, ಇದು ಸಮಾನಾಂತರ ಬೆಳಕಿನ ಕಿರಣಗಳನ್ನು ಏಕಮುಖವನ್ನಾಗಿ ಮಾಡುತ್ತವೆ, ಮತ್ತು ನಿಮ್ನ ಮಸೂರಗಳು, ಇವು ಸಮಾನಾಂತರ ಬೆಳಕಿನ ಕಿರಣಗಳನ್ನು ವಿಕೀರ್ಣ ಮಾಡುತ್ತವೆ. ವಕ್ರ ಕನ್ನಡಿಗಳಿಗೆ ಹೋಲುವ ಕಿರಣ-ಶೋಧನೆಯನ್ನು ಬಳಸಿಕೊಂಡು ಈ ಮಸೂರಗಳು ಹೇಗೆ ಬಿಂಬಗಳನ್ನು ಮೂಡಿಸುತ್ತವೆ ಎಂಬುದನ್ನು ವಿಶದವಾಗಿ ಊಹಿಸಬಹುದು. ವಕ್ರ ಕನ್ನಡಿಗಳ ಹಾಗೆಯೇ, ತೆಳು ಮಸೂರಗಳು ಒಂದು ಸರಳ ಸಮೀಕರಣವನ್ನು ಪಾಲಿಸುತ್ತದೆ, ಈ ಸಮೀಕರಣವು ಒಂದು ನಿರ್ದಿಷ್ಟ ಕೇಂದ್ರ ಉದ್ದ () ಮತ್ತು ವಸ್ತು ಅಂತರ () ಇದ್ದಾಗ ಬಿಂಬದ ಸ್ಥಾನವನ್ನು ಗುರುತಿಸುತ್ತದೆ:
ಇಲ್ಲಿ ಎಂಬುದು ಬಿಂಬಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಅಂತರ ಮತ್ತು ಸಂಪ್ರದಾಯದ ಪ್ರಕಾರ ಅದು ಮಸೂರದ ಪಕ್ಕಕ್ಕೇ ಇದ್ದರೆ ಅದನ್ನು ಋಣಾತ್ಮಕ ಎಂದೂ ಮತ್ತು ಮಸೂರದ ವಿರುದ್ಧಕ್ಕೆ ಇದ್ದರೆ ಗುಣಾತ್ಮಕ ಎಂದೂ ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ.[೪೦] ನಿಮ್ನ ಮಸೂರಗಳಿಗೆ ತೇಜೋಕೇಂದ್ರದ ಉದ್ದ f ಅನ್ನು ಋಣಾತ್ಮಕ ಎಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ.ಪೀನ ಮಸೂರವು ಒಳಬರುವ ಸಮಾನಾಂತರ ಕಿರಣಗಳನ್ನು, ಮಸೂರದ ಹಿಂದಿನ ಭಾಗದಲ್ಲಿ ಮಸೂರದ ಒಂದು ತೇಜಕೇಂದ್ರ ಅಳತೆಯಲ್ಲಿ ತಿರುಗು-ಮುರುಗು ನಿಜ ಬಿಂಬವನ್ನಾಗಿ ಕೇಂದ್ರಗೊಳಿಸುತ್ತದೆ. ಪರಿಮಿತ ಅಂತರದಲ್ಲಿರುವ ಒಂದು ವಸ್ತುವಿನಿಂದ ಬರುವ ಕಿರಣಗಳನ್ನು, ತೇಜಕೇಂದ್ರದ ಅಂತರಕ್ಕಿಂತ ದೂರವಾಗಿ ಮಸೂರದಲ್ಲಿ ಕೇಂದ್ರಮಾಡಲಾಗುತ್ತದೆ; ವಸ್ತುವು ಮಸೂರಕ್ಕೆ ಹತ್ತಿರವಿದ್ದಷ್ಟೂ, ಬಿಂಬವು ಮಸೂರದಿಂದ ದೂರ ಇರುತ್ತದೆ. ಪೀನ ಮಸೂರಗಳಲ್ಲಿ, ಒಳಬರುವ ಸಮಾನಾಂತರ ಕಿರಣಗಳು, ತಾವು ಸಮೀಪಿಸುತ್ತಿರುವ ಭಾಗದಲ್ಲಿಯೇ ಮಸೂರದ ಮೂಲಕ ಹಾದುಹೋದ ನಂತರ ವಿಕೀರ್ಣಗೊಳ್ಳುತ್ತವೆ, ಅವು ಮಸೂರದ ಒಂದು ತೇಜಕೇಂದ್ರ ಅಳತೆಯ ಒಂದು ನೇರ ತಾತ್ವಿಕ ಬಿಂಬದಲ್ಲಿ ಉತ್ಪತ್ತಿಯಾಗಿರುವಂತೆ ಕಾಣುತ್ತದೆ. ಪರಿಮಿತ ಅಂತರದಲ್ಲಿರುವ ಒಂದು ವಸ್ತುವಿನಿಂದ ಬರುವ ಕಿರಣಗಳು ತೇಜಕೇಂದ್ರದ ಅಳತೆಗಿಂತ ಹತ್ತಿರವಿರುವ ಮತ್ತು ವಸ್ತುವು ಮಸೂರದ ಯಾವ ಭಾಗದಲ್ಲಿ ಇದೆಯೋ ಅದೇ ಭಾಗದಲ್ಲಿ ಇರುವ ತಾತ್ವಿಕ ಬಿಂಬಗಳಿಗೆ ಸಂಬಂಧಿಸಿದುದಾಗಿದೆ. ವಸ್ತುವು ಮಸೂರಕ್ಕೆ ಹತ್ತಿರವಿದ್ದಷ್ಟೂ ತಾತ್ವಿಕ ಬಿಂಬವು ಮಸೂರಕ್ಕೆ ಹತ್ತಿರವಿರುತ್ತದೆ.ಹಾಗೆಯೇ, ಮಸೂರದಿಂದುಟಾಗುವ ಪ್ರವರ್ಧನವನ್ನು ಹೀಗೆ ಹೇಳಲಾಗುತ್ತದೆ -
ಇಲ್ಲಿ, ಸಾಧಾರಣವಾಗಿ, ಋಣಾತ್ಮಕ ಚಿಹ್ನೆಯನ್ನು ಕೊಡಲಾಗುತ್ತದೆ, ಇದು ನೇರ ವಸ್ತುಗಳು ಗುಣಾತ್ಮಕ ಮೌಲ್ಯಗಳನ್ನು ಮತ್ತು ತಿರುಗುಮುರುಗು ವಸ್ತುಗಳಿಗೆ ಋಣಾತ್ಮಕ ಮೌಲ್ಯಗಳನ್ನು ಕೊಡುವುದಕ್ಕಾಗಿ. ಕನ್ನಡಿಗಳ ಹಾಗೆಯೇ, ಏಕ ಮಸೂರಗಳಿಂದ ಉಂಟಾದ ನೇರ ಬಿಂಬಗಳು ತಾತ್ವಿಕವಾದವು ಆದರೆ ತಿರುಗು-ಮುರುಗು ಬಿಂಬಗಳು ನಿಜವಾದವು.[೩೮] ಬಿಂಬಗಳನ್ನು ಮತ್ತು ತೇಜಕೇಂದ್ರಬಿಂದುಗಳನ್ನು ಕೆಡಿಸುವ ವಿಲಕ್ಷಣಗಳಿಂದ ಮಸೂರಗಳು ತೊಂದರೆಗೀಡಾಗುತ್ತವೆ. ರೇಖಾಗಣಿತದ ಅಪರಿಪೂರ್ಣತೆಗಳು ಮತ್ತು ಬೇರೆ ಬೇರೆ ತರಂಗಾಯಾನುಗಳಿಗೆ ತಕ್ಕಂತೆ ಬದಲಾಗುವ ವಕ್ರೀಭವನದ ಸೂತ್ರ, ಎರಡೂ ಕಾರಣಗಳಿಗೆ ಹೀಗೆ ಆಗುತ್ತವೆ (ವರ್ಣಾತ್ಮಕ ವಿಲಕ್ಷಣ).[೩೮]
ಭೌತ ದೃಗ್ವಿಜ್ಞಾನ[ಬದಲಾಯಿಸಿ]
ಭೌತ ದೃಗ್ವಿಜ್ಞಾನ ಅಥವಾ ತರಂಗ ದೃಗ್ವಿಜ್ಞಾನವು, ಚಲಿಸುತ್ತಿರುವ ತರಂಗದಲ್ಲಿನ ಪ್ರತಿ ಬಿಂದುವೂ ಒಂದು ಹೊಸ ಕ್ಷೋಭೆಯ ಕೇಂದ್ರ ಎಂದು ಹೇಳುವ ಹೈಜೆನ್ನ ಸಿದ್ಧಾಂತದ ಆಧಾರಲ್ಲಿ ಬೆಳೆದಿದೆ. ಸುಪರ್ಪೊಸಿಶನ್ ಸಿದ್ಧಾಂತದೊಂದಿಗೆ ಸಂಯೋಜಿಸಿದಾಗ ಇದು, ಬೆಳಕಿನ ತರಂಗಾಂತರವನ್ನೇ ಹೋಲುವ ದೂರದಲ್ಲಿಟ್ಟ ಬಹು ವಿಧವಾದ ಆಕರಗಳು ಅಥವಾ ಅಡ್ಡಿಗಳು ಇದ್ದಾಗ ಹೇಗೆ ದೃಗ್ವಿಜ್ಞಾನದ ವಿದ್ಯಮಾನಗಳು ರೂಪುಗೊಳ್ಳುತ್ತವೆ ಎಂಬುದನ್ನು ವಿವರಿಸುತ್ತದೆ.[೪೧] ಭೌತ ದೃಗ್ವಿಜ್ಞಾನದ ಆಧಾರದಲ್ಲಿರುವ ಸಂಕೀರ್ಣ ಮಾದರಿಗಳು, ಅಲೆಯ ತರಂಗಾಂತರ, ಗಾತ್ರ ಹಾಗೂ ಬೆಳವಣಿಗೆಯ ಮಜಲುಗಳನ್ನು ಮುಂಚಿತವಾಗಿ ಹೇಳುವುದನ್ನೂ ಒಳಗೊಂಡಂತೆ ಒಂದು ದೃಗ್ವಿಜ್ಞಾನ ವ್ಯವಸ್ಥೆಯ ಮೂಲಕ ಒಂದೇರೀತಿಯ ಬೆಳವಣಿಗೆಯ ಮಜಲುಗಳನ್ನು ಹೊಂದಿರುವ ಬಿಂದುಪಥದ ಚಲನೆಗೆ ಹೊಣೆಯಾಗಬಲ್ಲವು.[೪೧] ಜೊತೆಗೆ, ಜ್ಯಾಮಿತಿ ದೃಗ್ವಿಜ್ಞಾನದಿಂದ ಬಂದ ಎಲ್ಲಾ ಫಲಿತಾಂಶಗಳನ್ನು, ಶಬ್ದಸಂಬಂಧಿ ತಂತ್ರಜ್ಞಾನ ಮತ್ತು ಸಂಕೇತ ಸಂಸ್ಕರಣೆಯಲ್ಲಿ ಬಳಸುವಂಥದ್ದೇ ಲೆಕ್ಕಶಾಸ್ತ್ರದ ಮತ್ತು ತರ್ಕಶಾಸ್ತ್ರದ ತಂತ್ರಗಳಿಗೆ ಅನ್ವಯವಾಗುವ ಫ್ಯೂರಿಯರ್ ದೃಗ್ವಿಜ್ಞಾನದ ತಂತ್ರಗಳ ಮೂಲಕ ಮರಳಿ ಪಡೆಯಬಹುದು. ಗಣಕಯಂತ್ರದಲ್ಲಿ ಸಂಖ್ಯಾತ್ಮಕ ಮಾದರಿಯನ್ನು ಬಳಸಿ, ದೃಗ್ವಿಜ್ಞಾನ ವಿಜ್ಞಾನಿಗಳು ಬೆಳಕಿನ ಚಲನೆಯನ್ನು ತೋರ್ಪಡಿಸಬಹುದು ಮತ್ತು ಹಲಾವಾರು ವ್ಯತಿಕರಣ, ಇಂಟರ್ಫರೆನ್ಸ್ ಮತ್ತು ಧ್ರುವೀಕರಣ ಪರಿಣಾಮಗಳಿಗೆ ವಿವರಣೆಯನ್ನು ನೀಡಬಹುದು. ಇಂಥ ವಿಡಂಬನೆಗಳು ಪ್ರಾತಿನಿಧಿಕವಾಗಿ ಈಗಲೂ ಅಂದಾಜಿನ ಲೆಕ್ಕಾಚಾರವನ್ನೇ ಅವಲಂಬಿಸಿವೆ, ಆದಾಗ್ಯೂ ಇದು ಬೆಳಕಿನ ಚಲನೆಯ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ಪೂರ್ಣ ಸಿದ್ಧಾಂತವಲ್ಲ. ಇಂಥ ಪೂರ್ಣ ಮಾದರಿ ಗಣಾನಾತ್ಮಕವಾಗಿ ಬೇಡಿಕೆಯುಳ್ಳದ್ದು ಮತ್ತು ಸಾಮಾನ್ಯವಾಗಿ ಅಸಾಮಾನ್ಯ ಖಚಿತತೆ ಅಗತ್ಯವಿರುವ ಸಣ್ಣಪ್ರಮಾಣದ ಸಮಸ್ಯೆಗಳನ್ನು ಬಗೆಹರಿಸಲು ಮಾತ್ರ ಬಳಸಲ್ಪಡುತ್ತದೆ.[೪೨] ಗಾಶಿಯನ್ ವಿಕಿರಣ ರಶ್ಮಿಯ ಪ್ರಸರಣವು ಲೇಸರ್ ಕಿರಣಗಳಂಥ ಸುಸಂಬದ್ಧ ಪ್ರಸರಣದ ಒಂದು ಸರಳ ಪಾರ್ಶ್ವಾಕ್ಷದ ಭೌತ ದೃಗ್ವಿಜ್ಞಾನದ ಮಾದರಿ. ಈ ತಂತ್ರವು, ಒಂದು ಲೇಸರ್ ಕಿರಣವು ದೂರದೊಂದಿಗೆ ವಿಸ್ತರಿಸುವ ದರ ಮತ್ತು ಕಿರಣವನ್ನು ಕೇಂದ್ರೀಕರಿಸಬಹುದಾದ ಅತಿ ಸಣ್ಣ ಗಾತ್ರ - ಇವುಗಳ ನಿಖರ ಲೆಕ್ಕಾಚಾರಕ್ಕೆ ಅನುವು ಮಾಡಿಕೊಟ್ಟು, ವ್ಯತಿಕರಣಕ್ಕೆ ಭಾಗಶಃ ಕಾರಣವಾಗುತ್ತದೆ. ಹಾಗಾಗಿ ಗಾಶಿಯನ್ ವಿಕಿರಣ ರಶ್ಮಿಯ ಪ್ರಸರಣವು ಜ್ಯಾಮಿತಿ ಮತ್ತು ಭೌತ ದೃಗ್ವಿಜ್ಞಾನದ ನಡುವಿನ ಅಂತರವನ್ನು ಒಂದಾಗಿಸುತ್ತದೆ.[೪೩]
ಒಂದರಮೇಲೊಂದು ಇರುವಿಕೆ ಮತ್ತು ಅಡ್ಡಬರುವಿಕೆ[ಬದಲಾಯಿಸಿ]
ರೇಖಾತ್ಮಕವಲ್ಲದ ಪರಿಣಾಮಗಳ ಗೈರುಹಾಜರಿಯಲ್ಲಿ, ಸೂಪರ್ಪೊಸಿಶನ್ ಸಿದ್ಧಾಂತವು, ಕ್ಷೋಭೆಯನ್ನು ಸರಳವಾಗಿ ಸೇರಿಸುವ ಮೂಲಕ ಪರಸ್ಪರ ಪ್ರತಿಕ್ರಿಯಿಸುವ ಅಲೆಗಳ ಆಕಾರವನ್ನು ಮುಂದಾಗಿ ಹೇಳಲು ಬಳಸಲ್ಪಡಬಹುದು.[೪೪] ಫಲಿತ ವಿನ್ಯಾಸವನ್ನು ಒದಗಿಸುವ ಈ ಅಲೆಗಳ ಹೊಂದಾಣಿಕೆಯು ಸಾಮಾನ್ಯವಾಗಿ "ಇಂಟರ್ಫರೆನ್ಸ್" ಎಂದು ಹೇಳಲ್ಪಡುತ್ತದೆ ಮತ್ತು ಇದು ವಿವಿಧ ಫಲಿತಾಂಶಗಳನ್ನು ನೀಡಬಲ್ಲುದು. ಒಂದೇ ತರಂಗಾಂತರ ಮತ್ತು ಆವರ್ತನವನ್ನು ಹೊಂದಿರುವ ಎರಡು ಅಲೆಗಳು ಒಂದೇ ತೆರನಾದ ಬೆಳವಣಿಗೆಯ ಮಜಲನ್ನು ಹೊಂದಿದ್ದರೆ, ಆ ಅಲೆಗಳ ತುದಿ ಮತ್ತು ಕುಳಿಗಳು ಸಾಲಾಗಿರುತ್ತವೆ. ಇದು ರಚನಾತ್ಮಕ ಇಂಟರ್ಫರೆನ್ಸ್ನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ ಮತ್ತು ಬೆಳಕಿಗೆ ಆ ಪ್ರದೇಶದಲ್ಲಿರುವ ಅಲೆಯ ಹೊಳೆಯುವಿಕೆಗೆ ಸಂಬಂಧಿಸಿದ, ಅಲೆಯ ಗಾತ್ರದಲ್ಲಿನ ಹೆಚ್ಚಳಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ. ಪರ್ಯಾಯವಾಗಿ, ಒಂದೇ ತರಂಗಾಂತರ ಮತ್ತು ಆವರ್ತನವನ್ನು ಹೊಂದಿದ ಎರಡು ಅಲೆಗಳು ಒಂದೇ ತೆರನಾದ ಬೆಳವಣಿಗೆಯ ಮಜಲನ್ನು ಹೊಂದಿರದಿದ್ದರೆ, ಆಗ ಅಲೆಗಳ ತುದಿಗಳು ಕುಳಿಗಳೊಂದಿಗೆ ಸೇರುತ್ತವೆ ಮತ್ತು ಪ್ರತಿಕ್ರಮ ಪರಿಣಾಮವುಂಟಾಗುತ್ತದೆ. ಇದು ವಿನಾಶಕಾರಕ ಇಂಟರ್ಫರೆನ್ಸ್ನ್ನು ಉಂಟುಮಾದುತ್ತದೆ ಮತ್ತು ಬೆಳಾಕಿಗೆ ಆ ಪ್ರದೇಶದಲ್ಲಿರುವ ಅಲೆಯ ಮಬ್ಬಾಗುವಿಕೆಗೆ ಸಂಬಂಧಿಸಿದ, ಅಲೆಯ ಗಾತ್ರದಲ್ಲಿ ಇಳಿಮುಖವಾಗುವಿಕೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ. ಈ ಪರಿಣಾಮದ ಸಚಿತ್ರ ವಿವರಣೆಯನ್ನು ಕೆಳಗೆ ಗಮನಿಸಿ.[೪೪]
| ಸಂಯೋಜಿತ ಅಲೆ |
 | |
| ಅಲೆ 1 | ||
| ಅಲೆ 2 | ||
| ಒಂದೇ ತೆರನಾದ ಬೆಳವಣಿಗೆಯ ಮಜಲಿನಲ್ಲಿರುವ ಎರಡು ಅಲೆಗಳು | ಎರಡು ಅಲೆಗಳು 180° ಯಷ್ಟು ಫೇಸ್ನ ಹೊರಗೆ | |

ಹೈಜೆನ್ನ ಸಿದ್ಧಾಂತವು, ಅಲೆಯಲ್ಲಿನ ಪ್ರತಿ ಬಿಂದುವೂ ಒಂದು ಹೊಸ ಕ್ಷೋಭೆಯನ್ನು ಉಂಟುಮಾಡುವಲ್ಲಿ ಒಡಗೂಡಿರುವುದು ಎಂದು ಹೇಳುವುದರಿಂದ, ಹೊಳೆಯುವ ಅಥವಾ ಕಪ್ಪುಛಾಯೆಯ ಅಂಚುಗಳನ್ನು ನಿಯತ ಅಥವಾ ನಿರೀಕ್ಷಿಸಬಹುದಾದ ವಿನ್ಯಾಸಗಳಲ್ಲಿ ಸೃಷ್ಟಿಸುತ್ತ ಒಂದು ಅಲೆಗೆ ರಚನಾತ್ಮಕವಾಗಿ ಅಥವಾ ವಿನಾಶಕಾರಿಯಾಗಿ ಅದರಷ್ಟಕ್ಕೇ ಮಧ್ಯಪ್ರವೇಶಿಸಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ.[೪೪] ಇಂಟರ್ಫರ್ಮೆಟ್ರಿಯು ಸಾಮಾನ್ಯವಾಗಿ ಅಂತರ ಅಥವಾ ಕೋನೀಯ ತಳಿದಗಳನ್ನು ಖಚಿತವಾಗಿ ಕಂಡುಹಿಡಿಯುವ ಮೂಲಕ ಈ ವಿನ್ಯಾಸಗಳನ್ನು ಅಳೆಯುವ ವಿಜ್ಞಾನವಾಗಿದೆ.[೪೫] ಮೈಕೆಲ್ಸನ್ ಇಂಟರ್ಫೆರೋಮೀಟರ್ ಬೆಳಕಿನ ವೇಗವನ್ನು ಖಚಿತವಾಗಿ ಅಳೆಯಲು ಇಂಟರ್ಫರೆನ್ಸ್ ಪರಿಣಾಮಗಳನ್ನು ಬಳಸಿದ ಒಂದು ಪ್ರಸಿದ್ಧ ಉಪಕರಣವಾಗಿತ್ತು.[೪೬] ತೆಳು ಛಾಯಾಚಿತ್ರ ಕಾಗದ ಮತ್ತು ಲೇಪನಗಳ ಆಗಮನವು ಇಂಟರ್ಫರೆನ್ಸ್ ಪರಿಣಾಮದಿಂದ ನೇರ ಪ್ರಭಾವ ಹೊಂದಿತ್ತು. ವಿರುದ್ಧಪ್ರತಿಫಲನ ಲೇಪನಗಳು ಅವು ಲೇಪಿಸಲ್ಪಡುವ ಮೇಲ್ಮೈಗಳ ಪ್ರತಿಫಲನವನ್ನು ಕಡಿಮೆಗೊಳಿಸಲು ವಿನಾಶಕಾರಕ ಇಂಟರ್ಫರೆನ್ಸ್ನ್ನು ಬಳಸುತ್ತವೆ ಮತ್ತು ಇವುಗಳನ್ನು ತೀಕ್ಷ್ಣಬೆಳಕು ಮತ್ತು ಅನಗತ್ಯ ಪ್ರತಿಫಲನಗಳನ್ನು ಕಡಿಮೆಮಾಡಲು ಬಳಸಬಹುದು. ಸರಳ ಸನ್ನಿವೇಶವೆಂದರೆ ಬಿದ್ದ ಬೆಳಕಿನ ತರಂಗಾಂತರದ ಕಾಲು ಭಾಗದಷ್ಟು ದಪ್ಪವಾಗಿರುವ ಒಂಟಿ ಪದರ. ಛಾಯಾಚಿತ್ರ ಕಾಗದದ ಮೇಲಿನಿಂದ ಪ್ರತಿಫಲಿತ ಅಲೆ ಮತ್ತು ಚಾಯಾಚಿತ್ರ ಕಾಗದ/ಮೂಲದ್ರವ್ಯಗಳ ಅಂತರ್ ಸಂಪರ್ಕದಿಂದ ಪ್ರತಿಫಲಿತ ಅಲೆಗಳು ನಿಖರವಾಗಿ ೧೮೦° ವ್ಯತಿರಿಕ್ತ ಬೆಳವಣಿಗೆಯ ಮಜಲಿನಲ್ಲಿರುತ್ತವೆ, ಮತ್ತು ಇದು ವಿನಾಶಕಾರಿ ಇಂಟರ್ಫರೆನ್ಸ್ನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ. ಸಾಮಾನ್ಯವಾಗಿ ಗೋಚರಿತ ವರ್ಣಪಂಕ್ತಿಯ ಮಧ್ಯಭಾಗದಲ್ಲಿ, ೫೫೦ ನ್ಯಾನೋಮೀಟರ್ನ ಆಸುಪಾಸಿನಲ್ಲಿ, ಇರುವ ಒಂದು ನಿರ್ದಿಷ್ಟ ತರಂಗಾಂತರಕ್ಕೆ ಮಾತ್ರ ಅಲೆಗಳು ವ್ಯತಿರಿಕ್ತ ಬೆಳವಣಿಗೆಯ ಮಜಲಿನಲ್ಲಿರುತ್ತವೆ. ಬಹು ವಿಧದ ಪದರಗಳನ್ನು ಬಳಸಿ ತಯಾರಿಸಿದ ಸಂಕೀರ್ಣ ವಿನ್ಯಾಸಗಳು ಅಗಲವಾದ ಪಟ್ಟಿಯಲ್ಲಿ ಕಡಿಮೆ ಪ್ರತಿಫಲನವನ್ನು, ಅಥವಾ ಒಂಟಿ ತರಂಗಾಂತರದಲ್ಲಿ ಅತ್ಯಂತ ಕಡಿಮೆ ಪ್ರತಿಫಲನವನ್ನು ನೀಡಬಲ್ಲವು. ರಚನಾತ್ಮಕ ಹಸ್ತಕ್ಷೇಪದ ತೆಳು ಪರದೆಯು ತರ೦ಗಾಂತರದ ವ್ಯಾಪ್ತಿಗಳಲ್ಲಿ ಬೆಳಕಿನ ಪ್ರಬಲ ಪ್ರತಿಫಲನವನ್ನು ಸೃಷ್ಟಿಸುತ್ತವೆ, ಅದು ಲೇಪನದ ನಕ್ಷೆಯ ಮೇಲೆ ಅವಲ೦ಬಿತವಾಗಿ ಕಿರಿದಾಗಿರಬಹುದು ಅಥವಾ ವಿಶಾಲವಾಗಿರಬಹುದು. ಈ ಫಲಕಗಳನ್ನು ದ್ವಿವಿದ್ಯುಜ್ಜನಕ ಪ್ರತಿಬಿಂಬಕಗಳು, ಹಸ್ತಕ್ಷೇಪ ಶೋಧಕಗಳು, ಶಾಖ ಪ್ರತಿಫಲಕಗಳು ಮತ್ತು ಬಣ್ಣ ದೂರದರ್ಶಕ ಕ್ಯಾಮರಾಗಳಲ್ಲಿ ಬಣ್ವವನ್ನು ಬೇರ್ಪಡಿಸುವ ಶೋಧಕಗಳಲ್ಲಿ ಬಳಸುವರು. ಈ ಹಸ್ತಕ್ಷೇಪ ಪರಿಣಾಮವು ತೈಲದ ನಯೆಯಲ್ಲಿ ಕಂಡುಬರುವ ವರ್ಣರ೦ಜಿತ ಕಾಮನಬಿಲ್ಲಿನ ನಮೂನೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ.[೪೪]
ಪಥಪಲ್ಲಟ ಮತ್ತು ದೃಗ್ವಿಜ್ಞಾನ ವಿಶ್ಲೇಷಣ[ಬದಲಾಯಿಸಿ]

ಪಥಪಲ್ಲಟ ಇದು ಸಾಮಾನ್ಯವಾಗಿ ಬೆಳಕಿನ ಹಸ್ತಕ್ಷೇಪವನ್ನು ಪರೀಕ್ಷಿಸುವ ಒಂದು ಪ್ರಕ್ರಿಯೆಯಾಗಿದೆ. ಈ ಪರಿಣಾಮವು ಪ್ರಥಮವಾಗಿ ೧೬೬೫ ರಲ್ಲಿ ಫ್ರಾನ್ಸಿಸ್ಕೊ ಮಾರಿಯಾ ಗ್ರಿಮಾಲ್ಡಿ ಯಿಂದ ವರ್ಣಿಸಲ್ಪಟ್ಟಿತು, ಅವರು ಲ್ಯಾಟಿನ್ ಶಬ್ದ ಡಿಫ್ರಿಂಜರ್ ಅನ್ನು ಕಂಡುಹಿಡಿದರು, ’ಚೂರುಗಳಾಗಿ ಬೇರ್ಪಡಿಸು’.[೪೭][೪೮] ಆ ಶತಮಾನದ ನಂತರ, ರಾಬರ್ಟ ಹೂಕ್ ಮತ್ತು ಐಸಾಕ್ ನ್ಯೂಟನ್ ಇವರುಗಳೂ ಕೂಡ ಈ ಘಟನೆಯನ್ನು ವರ್ಣಿಸಿದರು, ಅದು ಈಗ ಪಥಪಲ್ಲಟದಲ್ಲಿ ನ್ಯೂಟನ್ ನ ಮುದ್ರಿಕೆ[೪೯] ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ, ಅದೆ ಸಮಯದಲ್ಲಿ ಜೇಮ್ಸ್ ಗ್ರೆಗೊರಿ ಪಕ್ಷಿಯ ರೆಕ್ಕೆಗಳಿಂದ ಪಥಪಲ್ಲಟದ ನಮೂನೆಯ ಅವಲೋಕನಗಳನ್ನು (ಅಭಿಪ್ರಾಯಗಳನ್ನು)ನಮೂದಿಸಿದನು.[೫೦] ಹೈಜಿನ್ ನ ತತ್ವಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾದ ಪಥಪಲ್ಲಟದ ಪ್ರಥಮ ಭೌತಿಕ ದೃಗ್ವಿಜ್ಞಾನ ಮಾದರಿಯು ೧೮೦೩ ರಲ್ಲಿ ಥಾಮಸ್ ಯಂಗ್ ನಿಂದ, ಎರಡು ಸಮೀಪದಲ್ಲಿ ತೆರವಾದ ವಿದಳನ ಹಸ್ತಕ್ಷೇಪ ನಮೂನೆಯ ಅವನ ವಿವರಗಳಲ್ಲಿ ವಿಕಸಿಸಲ್ಪಟ್ಟಿತು. ಎರಡು ವಿದಳನಗಳು ಸೂಕ್ಷ್ಮಾಂಗಗಳಂತಲ್ಲದೆ ಎರಡು ಅನನ್ಯ ಮೂಲಗಳಂತೆ ಕಾರ್ಯನಿರ್ವಹಿಸಿದರೆ ಮಾತ್ರ ಅವನ ಫಲಿತಾಂಶಗಳನ್ನು ವರ್ಣಿಸಬಹುದು ಎಂದು ಯಂಗ್ ತೋರಿಸಿಕೊಟ್ಟನು.[೫೧] 1815 ಮತ್ತು 1818, ರಲ್ಲಿ, ಆಗಸ್ಟೀನ್-ಜೀನ್ ಫ್ರೆಸ್ನೆಲ್ ಹೇಗೆ ತರಂಗ ಹಸ್ತಕ್ಷೇಪವು ಪಥಪಲ್ಲಟಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಸ್ಥಿರವಾಗಿ ಪ್ರಮಾಣೀಕರಿಸಿದನು.[೪೦] ಪಥಪಲ್ಲಟದ ಸರಳ ಭೌತಿಕ ನಮೂನೆಗಳು ಬೆಳಕಿನ ಕೋನಗಳುಳ್ಳ ಪ್ರತ್ಯೇಕೀಕರಣ ಮತ್ತು ಬೆಳಕಿನ ನಿರ್ದಿಷ್ಟ ತರಂಗಾಂತರದಿಂದ ಉಂಟಾಗುವ ದಟ್ಟ ಅಂಚುಗಳನ್ನು ವರ್ಣಿಸುತ್ತವೆ (). ಸಾಮಾನ್ಯವಾಗಿ, ಸಮೀಕರಣವು ಈ ಬಗೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ
ಅಲ್ಲಿ ಎರಡು ತರ೦ಗಾಭಿಮುಖ ಮೂಲಗಳ ಪ್ರತ್ಯೇಕೀಕರಣವು 0/ ಆಗಿರುತ್ತದೆ ( ಯಂಗ್ ನ ಪ್ರಯೋಗಗಳಲ್ಲಿ, ಇದು ಎರಡು ವಿದಳನವಾಗಿತ್ತು), ಇದು ಕೇಂದ್ರದ ಅಂಚಿನ ನಡುವಣ ಕೋನಗಳುಳ್ಳ ಪ್ರತ್ಯೇಕೀಕರಣ ಮತ್ತು ನೇ ನಮೂನೆಯ ಅಂಚು, ಎಲ್ಲಿ ಕೇಂದ್ರದ ಗರಿಷ್ಠತೆತೆಯು ಆಗಿರುತ್ತದೆ.[೫೨] ವಿವಿಧ ಸನ್ನಿವೇಶಗಳನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಲು ಈ ಸಮೀಕರಣವನ್ನು ಸ್ವಲ್ಪ ಮಟ್ಟಿಗೆ ಮಾರ್ಪಡಿಸಲಾಯಿತು ಉದಾಹರಣೆಗೆ ಏಕೈಕ ತೆರಪಿನಲ್ಲಿ ಪಥಪಲ್ಲಟ, ಅಥವಾ ಸಮನಾದ ತೆರವನ್ನು ಹೊಂದಿರುವ ಬಹು ಸಂಖ್ಯೆಯ ವಿದಳನವನ್ನು ಒಳಗೊಂಡಿರುವ ಪಥಪಲ್ಲಟ ಜಾಲರಿಯ ಮೂಲಕ ಪಥಪಲ್ಲಟ.[೫೨] ಹೆಚ್ಚು ಕ್ಲಿಷ್ಟಕರವಾದ ಪಥಪಲ್ಲಟದ ನಮೂನೆಗಳು ಫ್ರೆಸ್ನೆಲ್ ಅಥವಾ ಫ್ರಾನ್ ಹೋಫರ್ ನ ಪಥಪಲ್ಲಟದ ಗಣಿತಶಾಸ್ತ್ರದ ಜೊತೆ ಕೆಲಸಮಾಡಬೇಕಾಗುತ್ತದೆ.[೪೧] ಎಕ್ಸ್-ರೇ ಪಥಪಲ್ಲಟವು ಹರಳಿನಲ್ಲಿರುವ ಕಣಗಳು ಒಂದು ನಿರ್ದಿಷ್ಟ ದೂರದಲ್ಲಿ ಒಂದು ಆಂಗ್ ಸ್ಟೋರ್ಮ್ ನ ಮೇಲೆ ಸಾಲಾಗಿರುವ ನಿಯತ ತೆರವಿನ ದೂರವನ್ನು ಬಳಸಿಕೊಳ್ಳುತ್ತವೆ. ಪಥಪಲ್ಲಟದ ನಮೂನೆಯನ್ನು ನೋಡಲು, ಹರಳಿನ ಮೂಲಕ ಹಾದುಹೋಗುವ ಸದೃಶ ತರಂಗಾಂತರದ ತೆರಪಿನ ಜೊತೆ ಎಕ್ಸ್-ರೇ ಗಳನ್ನು ಹಾಯಿಸಬೇಕು. ಆದ್ದರಿಂದ ಹರಳುಗಳು ಎರಡು-ಆಯಾಮದ ಜಾಲರಿಗಿಂತ ಹೆಚ್ಚಾಗಿ ಮೂರು-ಆಯಾಮದ ಭೌತಿಕ ವಸ್ತುಗಳಾಗಿರುತ್ತವೆ, ಅದಕ್ಕೆ ಸಂಬಂಧಿತ ಪಥಪಲ್ಲಟದ ನಮೂನೆಯು ಎರಡು ದಿಕ್ಕುಗಳಲ್ಲಿ ಬದಲಾಗುತ್ತದೆ, ಬ್ರಾಗ್ ನ ಪ್ರತಿಫಲನಕ್ಕೆ ಅನುಗುಣವಾಗಿ, ಅನನ್ಯ ನಮೂನೆಗಳಲ್ಲಿ ಕಂಡುಬರುವ ಕಾಂತಿಯುತ ಸ್ಥಳಗಳು ಮತ್ತು ಅಣುಗಳ ನಡುವೆ ದ್ವಿಗುಣ ತೆರಪುಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿರುತ್ತವೆ.[೫೨] ಪಥಪಲ್ಲಟದ ಪರಿಣಾಮಗಳು ದೃಗ್ವಿಜ್ಞಾನದಿಂದ ತೀರ್ಮಾನಿಸಿ ಬೇರ್ಪಡಿಸಿದ ಬೆಳಕಿನ ಮೂಲಗಳ ಬಳಿಗೆ ದೃಗ್ವಿಜ್ಞಾನ ಶೋಧಕದ ಸಾಮರ್ಥ್ಯವನ್ನು ಮೊಟಕುಗೊಳಿಸುತ್ತದೆ. ಸರ್ವೆಸಾಮಾನ್ಯವಾಗಿ, ದ್ಯುತಿರಂಧ್ರದ ಮೂಲಕ ಹಾದುಹೋಗುವ ಬೆಳಕು ಪಥಪಲ್ಲಟದ ಅನುಭವವನ್ನು ಪಡೆಯುತ್ತದೆ ಮತ್ತು ಸೃಷ್ಟಿಸಲ್ಪಡುವ ಅತ್ಯುತ್ಕೃಷ್ಟ ಚಿತ್ರಗಳು (ಪಥಪಲ್ಲಟ-ಸೀಮಿತ ದೃಗ್ವಿಜ್ಞಾನದಲ್ಲಿ ವರ್ಣಿಸಿದಂತೆ)ದಟ್ಟ ಶೂನ್ಯದಿಂದ ಬೆರ್ಪಡಿಸಲ್ಪಟ್ಟ ಕಾಂತಿಯುತ ಮುದ್ರಿಕೆಯಿಂದ ಸುತ್ತುವರೆಯಲ್ಪಟ್ಟ ಕೇಂದ್ರೀಯ ತಾಣದಂತೆ ಕಾಣಿಸುತ್ತದೆ: ಈ ನಮೂನೆಯು ಏಯರಿ ನಮೂನೆ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ, ಮತ್ತು ಕೇಂದ್ರೀಯ ಕಾಂತಿಯುತ ಪಟಲವು ಏಯರಿ ಡಿಸ್ಕ್ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ.[೪೦] ಆ ಮುದ್ರಿಕೆಯ ಗಾತ್ರವು ಈ ರೀತಿಯಾಗಿ ನೀಡಲ್ಪಡುತ್ತದೆ
ಅಲ್ಲಿ θ ಕೋನಗಳುಳ್ಳ ವಿಶ್ಲೇಷಣ, λ ಇದು ಬೆಳಕಿನ ತರ೦ಗಾಂತರ, ಮತ್ತು ಡಿ ಇದು ಮಸೂರ ದ್ಯುತಿರಂಧ್ರದ ವ್ಯಾಸವಾಗಿರುತ್ತದೆ. ಎರಡು ಬಿಂದುಗಳ ನಡುವಣ ಕೋನಗಳುಳ್ಳ ಪ್ರತ್ಯೇಕೀಕರಣವು ಏಯರಿ ಡಿಸ್ಕ್ ತ್ರಿಜ್ಯಕ್ಕಿಂತ ಗಮನಾರ್ಹವಾಗಿ ಕಮ್ಮಿಯಿದ್ದರೆ, ಆಗ ಆ ಎರಡು ಬಿಂದುಗಳು ಚಿತ್ರದಲ್ಲಿ ಸ್ಥಿರವಾಗಿರುವುದಿಲ್ಲ, ಆದರೆ ಅವುಗಳ ಕೋನಗಳುಳ್ಳ ಪ್ರತ್ಯೇಕೀಕರಣವು ಇದಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಎರಡು ಬಿಂದುಗಳ ಪ್ರತ್ಯೇಕ ಚಿತ್ರಗಳು ರಚನೆಯಾಗುತ್ತವೆ ಮತ್ತು ಅವು ಆದ್ದರಿಂದ ಸ್ಥಿರವಾಗಿರುತ್ತವೆ. ರೇಲಿಯು ತಕ್ಕಮಟ್ಟಿಗೆ "ರೇಲಿಯನ್ ಮಾನದಂಡ"ದಲ್ಲಿ ನಿರಂಕುಶವಾಗಿ ವರ್ಣಿಸಿದ್ದಾನೆ ಹೇಗೆಂದರೆ ಯಾವ ಎರಡು ಬಿಂದುಗಳ ಕೋನಗಳುಳ್ಳ ಪ್ರತ್ಯೇಕೀಕರಣವು ಏಯರಿ ಡಿಸ್ಕ್ನ ತ್ರಿಜ್ಯಕ್ಕೆ ಸಮವಾಗಿರುತ್ತದೆಯೋ (ಮೊದಲು ಶೂನ್ಯವಾಗಿ ಅಳತೆಮಾಡಲಾಗುತ್ತದೆ, ಅಂದರೆ ಅದು ಬೆಳಕು ಕಾಣದಿರುವ ಮೊದಲ ಸ್ಥಾನವಾಗುತ್ತದೆ)ಅದನ್ನು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಎಂದು ಪರಿಗಣಿಸಬಹುದು. ಮಸೂರ ಅಥವಾ ಅದರ ದ್ಯುತಿರಂಧ್ರದ ವ್ಯಾಸವು ಹೆಚ್ಚು ಇದ್ದಷ್ಟೂ ಚಿತ್ರದ ದೃಶ್ಯಸಾಂದ್ರತೆ ಹೆಚ್ಚು ಚೆನ್ನಾಗಿ ಬರುತ್ತದೆ ಎಂಬುದನ್ನು ಗುರುತಿಸಲಾಗಿದೆ.[೫೨] ಇಂಟರ್ಫೆರೋಮೆಟ್ರಿ, ಅತ್ಯಂತ ದೊಡ್ಡ ಬೇಸ್ಲೈನ್ ದ್ಯುತಿರಂಧ್ರಗಳನ್ನು ಅನುಕರಿಸುವ ತನ್ನ ಸಾಮರ್ಥ್ಯದಿಂದಾಗಿ ಅತ್ಯಂತ ಹೆಚ್ಚಿನ ಕೋನೀಯ ದೃಶ್ಯಸಾಂದ್ರತೆಯನ್ನು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ.[೪೫] ನಕ್ಷತ್ರಗಳನ್ನು ಹೊಳೆಯುವಂತೆ ಮಾಡುವ ವಾತಾವರಣದ ಹರಡಿರುವಿಕೆ ಮತ್ತು ಪ್ರಸರಣದ ಕಾರಣದಿಂದಾಗಿ ವಾತಾವರಣವು ಖಗೋಳಶಾಸ್ತ್ರದ ಕಾಣುವ ವರ್ಣಪಟಲದ ದೃಶ್ಯಚಿತ್ರೀಕರಣದಲ್ಲಿ ಅತ್ಯಂತ ಸೂಕ್ತ ದೃಶ್ಯಸಾಂದ್ರತೆಯನ್ನು ಹೊಂದುವುದರಿಂದ ತಡೆಯುತ್ತದೆ. ಖಗೋಳಶಾಸ್ತ್ರಜ್ಞರು ಈ ಪರಿಣಾಮವನ್ನು ಖಗೋಳಶಾಸ್ತ್ರೀಯ ನೋಟದ ಗುಣಮಟ್ಟ ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಚಿತ್ರಗಳನ್ನು ತೆಗೆಯುವಲ್ಲಿ ವಾತಾವರಣದಲ್ಲಿ ಉಂಟಾಗುವ ಇಂತಹ ಅಡಚಣೆಯನ್ನು ತೆಗೆಯಲು ಮತ್ತು ಪಥಪಲ್ಲಟ ಮಿತಿಯನ್ನು ಮುಟ್ಟುವ ಫಲಿತಾಂಶಗಳನ್ನು ಸಾಧಿಸಲು ಬಳಸುವ ತಂತ್ರಗಳನ್ನು ಸಂಯೋಜಿತ ದೃಗ್ವಿಜ್ಞಾನ ಎಂದು ಕರೆಯುತ್ತಾರೆ.[೫೩]
ಪ್ರಸರಣ ಮತ್ತು ಚೆದುರಿಕೆ[ಬದಲಾಯಿಸಿ]

ವಕ್ರೀಕಾರಕ ಪ್ರಕ್ರಿಯೆಯು ಭೌತಿಕ ದೃಗ್ವಿಜ್ಞಾನದ ಎಲ್ಲೆಯಲ್ಲಿ ನಡೆಯುತ್ತದೆ, ಅಲ್ಲಿ ಬೆಳಕಿನ ತರ೦ಗಾಂತರವು (ಅಥವಾ ತರ೦ಗ ದೂರವು) ಚದುರಿಕೆಯ ಒಂದು ವಿಧವಾಗಿ, ಉಳಿದ ಅಂತರಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಥೊಮ್ಸನ್ ಚದುರಿಕೆಯು ಒಂದು ಸರಳ ವಿಧವಾದ ಚದುರಿಕೆಯಾಗಿದೆ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರ೦ಗಗಳು ಏಕೈಕ ಕಣಗಳಿಂದ ಪಥತಪ್ಪಿಸಲ್ಪಟ್ಟಾಗ ಇದು ಸಂಭವಿಸುತ್ತದೆ. ಎಲ್ಲಿ ತರ೦ಗದ೦ಥ ಅಲೆಯನ್ನು ಹೋಲುವ ಪ್ರಕಾಶವು ನಿಚ್ಚಳವಾಗಿರುತ್ತದೆಯೋ, ಆ ಥೊಮ್ಸನ್ ಚದುರಿಕೆಯ ಎಲ್ಲೆಯಲ್ಲಿ ಆವರ್ತನದ ಅಧೀನದಲ್ಲಿದ ಬೆಳಕು ಚದುರುತ್ತದೆ, ಕೊಮ್ಪ್ಟನ್ ಚದುರಿಕೆಗೆ ವ್ಯತಿರಿಕ್ತವಾಗಿ ಯಾವುದು ಆವರ್ತನದ ಅಧೀನದಲ್ಲಿರುತ್ತದೆಯೊ ಮತ್ತು ಕರಾರುವಕ್ಕಾಗಿ ಒಂದು ಗೊತ್ತಾದ ಪರಿಮಾಣದ ಯಾಂತ್ರಿಕ ಪ್ರಕ್ರಿಯೆಯಾಗಿರುತ್ತದೆಯೊ ಅದು ಬೆಳಕಿನ ಸಹಜಗುಣವನ್ನು ಕಣಗಳಾಗಿ ಹೊಂದಿರುತ್ತದೆ. ಸಂಖ್ಯಾ ಶಾಸ್ತ್ರದ ಪ್ರಕಾರದಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಬೆಳಕಿನ ತರ೦ಗಾಂತರಕ್ಕಿಂತ ಬಹಳಷ್ಟು ಚಿಕ್ಕದಾಗಿರುವ ಬಹಳಷ್ಟು ಕಣಗಳಿಂದ ನಡೆಯುವ ಬೆಳಕಿನ ಸ್ಥಿತಿಸ್ಥಾಪಕ ಚದುರಿಕೆಯ ಪ್ರಕ್ರಿಯೆಯು ರೇಲಿ ಚದುರಿಕೆ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ ಹಾಗೆಯೇ ಅದೇ ರೀತಿಯ ಅಥವಾ ಅದಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿರುವ ತರ೦ಗಾಂತರವಿರುವ ಕಣಗಳ ಚದುರಿಕೆ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಮಿ ಚದುರಿಕೆ ಎನ್ನುವರು ಜೊತೆಗೆ ತಿಂದಾಲ್ ಪರಿಣಾಮವು ಸಾಮುದಾಯಿಕವಾಗಿ ಕಂಡುಬರುವ ಫಲಿತಾಂಶವಾಗಿರುತ್ತದೆ. ಆಟಮ್ ಅಥವಾ ಮೊಲಿಕ್ಯುಲ್ಸ್ ಗಳ ಚಿಕ್ಕ ಪ್ರಮಾಣದ ಬೆಳಕಿನ ಚದುರಿಕೆಯು ರಾಮನ್ ಚದುರಿಕೆಗೆ ಒಳಗಾಗಬಹುದು, ಅದರಲ್ಲಿ ಆಟಮ್ ಮತ್ತು ಮೊಲಿಕ್ಯುಲ್ಸ್ ಗಳ ಪ್ರಚೋದನೆಯಿಂದ ಆವರ್ತನವು ಬದಲಾಗುತ್ತದೆ. ಒಂದು ದಟ್ಟ(ಸಾಂದ್ರ)ಮೂಲವಸ್ತುವಿನ ಕಾಲ ಮತ್ತು ಚಲನೆಯ ಜೊತೆಗಿನ ಸ್ಥಳೀಯ ಬದಲಾವಣೆಯ ಕಾರಣದಿಂದಾಗಿ ಬೆಳಕಿನ ಆವರ್ತನವು ಬದಲಾದರೆ ಅದನ್ನು ಬ್ರಿಲ್ಲುಯಿನ್ ಚದುರಿಕೆ ಎನ್ನುವರು.[೫೪] ಮೂಲವಸ್ತುವಿನ ಸ್ವತ್ತು (ಮೂಲವಸ್ತುವಿನ ಪ್ರಸರಣ ) ಅಥವಾ ದೃಗ್ವಿಜ್ಞಾನದ ತರ೦ಗಮಾರ್ಗದರ್ಶಿ (ತರ೦ಗಮಾರ್ಗದರ್ಶಿ ಪ್ರಸರಣ ) ಗಳ ಕಾರಣದಿಂದಾಗಿ ಯಾವಾಗ ಭಿನ್ನರೀತಿಯ ಬೆಳಕಿನ ಆವರ್ತನಗಳು ಭಿನ್ನವಾದ ಮಜಲಿನ ವೇಗವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆಯೊ ಆವಾಗ ಪ್ರಸರಣವು ಸಂಭವಿಸುತ್ತದೆ. ಅತಿ ಹೆಚ್ಚು ಬಳಕೆಯ ಪ್ರಸರಣದ ಬಗೆಯೆಂದರೆ ತರ೦ಗಾಂತರವನ್ನು ವೃದ್ಧಿಗೊಳಿಸುವುದರ ಜೊತೆಗೆ ಸೂಚಿಯನ್ನು ತಗ್ಗಿಸುವುದು, ಇದು ಹೆಚ್ಚಾಗಿ ಅತಿ ಹೆಚ್ಚು ಪಾರದರ್ಶಕ ಮೂಲವಸ್ತುವಿನಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ. ಇದು "ಸಾಮಾನ್ಯ ಪ್ರಸರಣ" ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ. ಇದು ಎಲ್ಲಾ ದ್ವಿವಿದ್ಯುಜ್ಜನಕ ಮೂಲವಸ್ತುಗಳಲ್ಲಿ ಉಂಟಾಗುತ್ತದೆ, ಎಲ್ಲಿ ಮೂಲವಸ್ತುವು ಬೆಳಕನ್ನು ಹೀರಿಕೊಳ್ಳುವುದಿಲ್ಲವೋ ಆ ತರ೦ಗಾಂತರದ ಶ್ರೇಣಿಯಲ್ಲಿ ಉಂಟಾಗುತ್ತದೆ.[೫೫] ಎಲ್ಲಿ ಮಧ್ಯಂತರವು ತರ೦ಗಾಂತರದ ಶ್ರೇಣಿಗಳಲ್ಲಿ ಪ್ರಮುಖ ಮಗ್ನತೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆಯೊ, ಅಲ್ಲಿ ಸೂಚಿಯ ವಕ್ರೀಕರಣವು ತರ೦ಗಾಂತರಕ್ಕೆ ಅನುಗುಣವಾಗಿ ಹೆಚ್ಚಾಗುತ್ತದೆ. ಇದು "ಅಸ೦ಬದ್ಧ ಪ್ರಸರಣ" ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ.[೩೮][೫೫] ವರ್ಣಪಲ್ಲಟ ಕೊಳವೆಯ ಮುಖಾಂತರ ವರ್ಣವನ್ನು ಬೇರ್ಪಡಿಸುವುದು ಸಾಮಾನ್ಯ ಪ್ರಸರಣಕ್ಕೆ ಒಂದು ಉದಾಹರಣೆಯಾಗಿದೆ. ವರ್ಣಪಲ್ಲಟ ಕೊಳವೆಯ ಮೆಲ್ಮೈಯಲ್ಲಿ ಸ್ನೆಲ್ ನ ಕಟ್ಟಳೆಯು ಪ್ರತಿಪಾದಿಸುವುದೇನೆಂದರೆ ೮ ನೆ ಕೋನದ ಹತ್ತಿರದಿಂದ ಸಹಜಸ್ಥಿತಿಯವರೆಗೆ ಬೆಳಕಿನ ಪ್ರಾಸಂಗಿಕ ಘಟನೆಯು ಬಾಗಿದ ಕೋನದ೦ತೆ (ಸಿನ್(೮)/ಎನ್ ) ವಕ್ರೀಕಾರಕವಾಗಿರುತ್ತದೆ. ಹೀಗಾಗಿ, ಹೆಚ್ಚಿನ ವಕ್ರೀಕಾರಕ ಸೂಚಿಯನ್ನು ಹೊಂದಿರುವ ನೀಲಿ ಬೆಳಕು, ಕೆಂಪು ಬೆಳಕಿಗಿಂತ ಹೆಚ್ಚು ಬಲವಾಗಿ ಬಾಗಿರುತ್ತದೆ, ಮತ್ತು ಪ್ರಸಿದ್ಧ ಕಾಮನಬಿಲ್ಲಿನ ನಮೂನೆ ಸಂಭವಿಸುವಂತೆ ಮಾಡುತ್ತದೆ.[೩೮]

ಮೂಲವಸ್ತು ಪ್ರಸರಣವು ಸಾಮಾನ್ಯವಾಗಿ ಅಸ೦ಬದ್ಧ ಸಂಖ್ಯೆ ಎಂದು ವರ್ಣಿಸಲ್ಪಡುತ್ತದೆ, ಅದು ಮೂರು ನಿಶ್ಚಿತ ವಕ್ರೀಕಾರಕಗಳ ಸೂಚಿಗೆ ಅನುಗುಣವಾಗಿ ಪ್ರಸರಣದ ಒಂದು ಸುಲಭ ಮಾಪನವನ್ನು ನೀಡುತ್ತದೆ. ತರ೦ಗಮಾರ್ಗದರ್ಶಿ ಪ್ರಸರಣವು ಪ್ರಜನನ ಸ್ಥಿರಾಂಕದ ಮೇಲೆ ಅವಲ೦ಬಿತವಾಗಿದೆ.[೪೦] ಎರಡೂ ಬಗೆಯ ಪ್ರಸರಣಗಳು ತರ೦ಗದ ಗುಂಪು ಲಕ್ಷಣಗಳಲ್ಲಿ ಬದಲಾವಣೆಯನ್ನುಂಟುಮಾಡುತ್ತದೆ, ತರ೦ಗ ಪೊಟ್ಟಣಗಳ ಮುಖ್ಯಲಕ್ಷಣಗಳು ಅದೇ ರೀತಿಯ ಆವರ್ತನದೊಂದಿಗೆ ಬದಲಾಗುತ್ತವೆ ಹಾಗೆ ವಿದ್ಯುದ್ಕಾಂತೀಯ ತರ೦ಗಗಳ ವಿಸ್ತೀರ್ಣವೂ ಕೂಡ ಬದಲಾಗುತ್ತದೆ. "ಗುಂಪು ವೇಗ ಪ್ರಸರಣ"ವು ವಿಕಿರಣದ ಹೊದಿಕೆ ಸಂಕೇತವು ಹರಡಿ-ಹೊರಬೀಳುವುದನ್ನು ಸ್ಪಷ್ಟಪಡಿಸುತ್ತದೆ ಮತ್ತು ಅದನ್ನು ಗುಂಪು ಪ್ರಸರಣ ವಿಳಂಬ ಮಾನದ೦ಡದ ಜೊತೆ ಅಳತೆ ಮಾಡಬಹುದು:
ಅಲ್ಲಿ ಯು ಗುಂಪು ವೇಗವಾಗಿರುತ್ತದೆ.[೫೬] ಒಂದು ಏಕರೀತಿಯ ಮಧ್ಯಂತರದಲ್ಲಿ, ಗುಂಪು ವೇಗವು
ಅಲ್ಲಿ ಎನ್ ಎಂಬುದು ವಕ್ರೀಕರಣದ ಸೂಚಿಯಾಗಿರುತ್ತದೆ ಮತ್ತು ಸಿ ಎಂಬುದು ನಿರ್ವಾತ ಪ್ರದೇಶದಲ್ಲಿ ಬೆಳಕಿನ ವೇಗವಾಗಿರುತ್ತದೆ.[೫೭] ಇದು ಪ್ರಸರಣ ವಿಳಂಬ ಮಾನದ೦ಡಕ್ಕೆ ಒಂದು ಸುಲಭ ಬಗೆಯನ್ನು ನೀಡುತ್ತದೆ:
ಡಿ ಯು ಶೂನ್ಯಕ್ಕಿಂತ ಚಿಕ್ಕದಾಗಿದ್ದರೆ, ಮಧ್ಯಂತರವು ಧನಾತ್ಮಕ ಪ್ರಸರಣ ಅಥವಾ ಸಾಮಾನ್ಯ ಪ್ರಸರಣವನ್ನು ಹೊಂದಿರುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ. ಡಿ ಯು ಶೂನ್ಯಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿದ್ದರೆ, ಮಧ್ಯಂತರವು ಋಣಾತ್ಮಕ ಪ್ರಸರಣ ವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಒಂದು ಬೆಳಕಿನ ಕಿರಣವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಚದುರಿಸುವ ಮಧ್ಯಂತರದಲ್ಲಿ ಪ್ರಸಾರಿಸಿದರೆ, ಅದರ ಫಲಿತಾಂಶವು ತಗ್ಗಿದ ಆವರ್ತನ ಘಟಕಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿ ಉಚ್ಚ ಆವರ್ತನ ಘಟಕದ ನಿಧಾನ ಇಳಿಕೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ ಹಾಗಾಗಿ ಬೆಳಕಿನ ಕಿರಣವು, ಹೆಚ್ಚಾಗುತ್ತಿರುವ ಆವರ್ತನವು ಕಾಲದ ಜೊತೆಗೆ ಧನಾತ್ಮಕವಾಗಿ ಉಲಿ ಯುತ್ತದೆ ಅಥವಾ ಮೇಲ್ಮುಖವಾಗಿ ಉಲಿ ಯುತ್ತದೆ ಇದು ವರ್ಣಪಲ್ಲಟ ಕೊಳವೆಯಿಂದ ಹೊರಬರುವ ವರ್ಣಪ೦ಕ್ತಿಯು ಅತ್ಯಲ್ಪ ವಕ್ರೀಕಾರಕ ಕೆಂಪು ಬೆಳಕು ಮತ್ತು ಅತಿಹೆಚ್ಚು ವಕ್ರೀಕಾರಕ ನೀಲಿ/ನೇರಳೆ ಬೆಳಕುಗಳೊಂದಿಗೆ ಕಾಣಿಸಿಕೊಳ್ಳಲು ಕಾರಣವಾಗುತ್ತದೆ. ಇದಕ್ಕೆ ವಿಲೋಮವಾಗಿ, ಒಂದು ಕಿರಣವು ಅಸ೦ಬದ್ಧವಾಗಿ (ಋಣಾತ್ಮಕವಾಗಿ) ಚದುರಿಸುವ ಮಧ್ಯಂತರದ ಮೂಲಕ ಹಾದುಹೋದರೆ, ಉಚ್ಚ ಆವರ್ತನ ಘಟಕವು ತಗ್ಗಿದ ಆವರ್ತನಕ್ಕಿಂತ ಜೋರಾಗಿ ಚಲಿಸುತ್ತವೆ, ಮತ್ತು ಬೆಳಕಿನ ಕಿರಣವು ಋಣಾತ್ಮಕವಾಗಿ ಉಲಿ ಯುತ್ತವೆ, ಅಥವಾ ಕೆಳಮುಖವಾಗಿ-ಉಲಿ ಯುತ್ತವೆ, ಆವರ್ತನವು ಕಾಲದ ಜೊತೆಗೆ ಇಳಿಯುವುದಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ.[೫೮] ಗುಂಪು ವೇಗ ಪ್ರಸರಣದ ಫಲಿತಾಂಶವು, ಋಣತ್ಮಕವಾಗಿರಲಿ ಅಥವಾ ಧನಾತ್ಮಕವಾಗಿರಲಿ, ಕಟ್ಟಕಡೆಯದಾಗಿ ಬೆಳಕಿನ ಕಿರಣಗಳ ಮಾರ್ಪಡುವ ಹರಡುವಿಕೆಯಾಗಿರುತ್ತದೆ. ಇದು ಪ್ರಸರಣದ ಆಡಳಿತವನ್ನು ದೃಗ್ವಿಜ್ಞಾನ ಫೈಬರ್ ಗೆ ಸಂಬಂಧಿಸಿದ ದೃಗ್ವಿಜ್ಞಾನ ಸಂವಹನ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಅತ್ಯಂತ ಪ್ರಮುಖವಾಗಿಸುತ್ತದೆ, ತರುವಾಯ ಪ್ರಸರಣವು ತುಂಬಾ ಹೆಚ್ಚಿದ್ದರೆ, ಮಾಹಿತಿಯನ್ನು ಪ್ರತಿನಿಧಿಸುವ ಬೆಳಕಿನ ಕಿರಣಗಳ ಪ್ರತಿಯೊಂದು ಗುಂಪು ಕಾಲದ ಜೊತೆಗೆ ವಿಸ್ತರಿಸುತ್ತವೆ ಮತ್ತು ವಿಲೀನಗೊಳ್ಳುತ್ತವೆ, ಇದು ಸೂಚನೆಯನ್ನು ಹೊರತೆಗೆಯಲು ಆಗದ೦ತೆ ಮಾಡುತ್ತದೆ.[೫೬]
ಧ್ರುವೀಕರಣ[ಬದಲಾಯಿಸಿ]
ಧ್ರುವೀಕರಣವು ತರಂಗದ ಸರ್ವೆಸಾಮಾನ್ಯವಾದ ಸ್ವತ್ತಾಗಿದೆ ಮತ್ತು ಅದು ಆಂದೋಲನದ ದೃಷ್ಟಿಕೋನವನ್ನು (ನೆಲೆಯನ್ನು) ವರ್ಣಿಸುತ್ತದೆ. ವಿದ್ಯುದ್ಕಾಂತೀಯ ತರಂಗಗಳಂತಹ ವ್ಯತ್ಯಸ್ತ ತರಂಗಗಳಲ್ಲಿ, ಸಮತಲದಲ್ಲಿನ ಆಂದೋಲನದ ನೆಲೆಯು ತರಂಗದ ಸಂಚಾರ ಮಾರ್ಗಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ ಎಂಬುದನ್ನು ಇದು ವರ್ಣಿಸುತ್ತದೆ. ಈ ಆಂದೋಲನಗಳು ಏಕೈಕ ಮಾರ್ಗದಲ್ಲಿ (ರೇಖಾತ್ಮಕ ಧ್ರುವೀಕರಣ)ನೆಲೆಯಾಗಿರುತ್ತವೆ, ಅಥವಾ ಆಂದೋಲನದ ಮಾರ್ಗವು ತರಂಗವು ಚಲಿಸಿದಂತೆ(ವೃತ್ತಾಕಾರವಾಗಿ ಅಥವಾ ದೀರ್ಘವೃತ್ತಾಕಾರದ ಧ್ರುವೀಕರಣ) ಬದಲಾಗಬಹುದು (ತಿರುಗಬಹುದು). ವೃತ್ತಾಕಾರವಾಗಿ ಧ್ರುವೀಕರಣಗೊಂಡ ತರಂಗಗಳು ಚಲನೆಯ ಮಾರ್ಗದ ಬಲಮುಖವಾಗಿ ಅಥವಾ ಎಡಮಖವಾಗಿ ತಿರುಗಬಹುದು, ಮತ್ತು ತರಂಗದಲ್ಲಿ ಕಂಡುಬರುವ ಅವುಗಳ ಎರಡು ಪರಿಭ್ರಮಣವನ್ನು ತರಂಗದ ಅಸಮಮಿತತೆ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ.[೫೯] ಧ್ರುವೀಕರಣವನ್ನು ಪರಿಗಣಿಸುವ ವಿಶಿಷ್ಟ ವಿಧಾನವೆಂದರೆ ವಿದ್ಯುದ್ಕಾಂತೀಯ ತರಂಗವು ಪ್ರಸಾರಿಸಿದಂತೆ ಸದಿಶ ವಿದ್ಯುತ್ತಿನ ವ್ಯಾಪ್ತಿಯ ನೆಲೆಯ ಜಾಡನ್ನು ಇಟ್ಟುಕೊಳ್ಳುವುದು. ಸಮತಲ ತರಂಗದ ವಿದ್ಯುತ್ತಿನ ವ್ಯಾಪ್ತಿಯ ನೆಲೆಯು ಸಾಮಾನ್ಯವಾಗಿ ಎಕ್ಸ್ ಮತ್ತು ವೈ ಎಂದು ಹೆಸರಿಸಲ್ಪಡುವ ಎರಡು ಘಟಕಗಳಾಗಿ ವಿಂಗಡಿಸಲ್ಪಡುತ್ತದೆ (ಜೊತೆಗೆ ಝಡ್ ಇದು ಚಲನೆಯ ಮಾರ್ಗವನ್ನು ಸೂಚಿಸುತ್ತದೆ). ವಿದ್ಯುತ್ತಿನ ವ್ಯಾಪ್ತಿಯ ನೆಲೆಯಿಂದ ಎಕ್ಸ್-ವಾಯ್ ಸಮತಲದಲ್ಲಿ ಕಂಡುಹಿಡಿಯಲ್ಪಟ್ಟ ಆಕಾರವು ಲಿಸ್ಸಜೌಸ್ ಆಕೃತಿಯಾಗಿರುತ್ತದೆ, ಅದು ಧ್ರುವೀಕರಣ ಸ್ಥಿತಿ ಯನ್ನು ವರ್ಣಿಸುತ್ತದೆ.[೪೦] ಈ ಕೆಳಗಿನ ಆಕೃತಿಗಳು ಕಾಲದ ಜೊತೆಗೆ (ಲಂಬ ರೇಖೆ), ಒಂದು ನಿರ್ದಿಷ್ಟ ಸ್ಥಳದ ತುದಿಯಲ್ಲಿ, ಇದರ ಎಕ್ಸ್ ಮತ್ತು ವಾಯ್ ಘಟಕಗಳ ಜೊತೆ(ಕೆಂಪು/ಬಲಗಡೆ ಮತ್ತು ಹಸಿರು/ಎಡಗಡೆ), ಮತ್ತು ಸಮತಲದಲ್ಲಿ ನೆಲೆಯಿಂದ ಕಂಡುಹಿಡಿಯಲ್ಪಟ್ಟ(ನೇರಳೆ ಬಣ್ಣ)ಘಟಕಗಳಿಂದ ವಿದ್ಯುತ್ತಿನ ವ್ಯಾಪ್ತಿ ನೆಲೆ(ನೀಲಿ)ಯ ವಿಕಸನದ ಕೆಲವು ಉದಾಹರಣೆಯನ್ನು ತೋರಿಸುತ್ತದೆ: ವಿದ್ಯುತ್ತಿನ ಕ್ಷೇತ್ರದಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಮಯದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಸ್ಥಳದಲ್ಲಿನ ಬಿಂದುವನ್ನು ಪ್ರಜನನದ ದಿಕ್ಕಿಗೆ ವಿರುದ್ಧವಾಗಿ ಮುಂದುವರೆಯುವಾಗ ಅದೇ ರೀತಿಯ ವಿಕಸನವು ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ.
ಮೇಲೆ ಅತ್ಯಂತ ಎಡಗಡೆಯಿರುವ ಚಿತ್ರದಲ್ಲಿ, ಬೆಳಕಿನ ತರಂಗದ ಎಕ್ಸ್ ಮತ್ತು ವಾಯ್ ಘಟಕಗಳು ಮಜಲುಗಳಾಗಿವೆ. ಈ ನಿದರ್ಶನದಲ್ಲಿ, ಅವುಗಳ ಶಕ್ತಿಯ ಅನುಪಾತವು ಅಚಲವಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ವಿದ್ಯುತ್ ಪಥದ ಮಾರ್ಗವು ( ಈ ಎರಡು ಘಟಕಗಳ ಪಥದ ಮೊತ್ತ) ಅಚಲವಾಗಿರುತ್ತದೆ. ಅನಂತರ ಪಥದ ತುದಿಯು ಸಮತಲದಲ್ಲಿ ಏಕೈಕ ರೇಖೆಯನ್ನು ಕಂಡುಹಿಡಿಯುತ್ತದೆ, ಈ ವಿಶಿಷ್ಟವಾದ ದೃಷ್ಟಾಂತವು ರೇಖಾತ್ಮಕ ಧ್ರುವೀಕರಣ ಎಂದು ಕರೆಯಲ್ಪುತ್ತದೆ. ಈ ರೇಖೆಯ ಮಾರ್ಗವು ಎರಡು ಘಟಕಗಳ ಸಂಬಂಧ ಸೂಚಕ ವ್ಯಾಪ್ತಿಯ (ವಿಸ್ತೀರ್ಣ) ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ.[೫೯] ಮಧ್ಯದಲ್ಲಿರುವ ಚಿತ್ರದಲ್ಲಿ, ಅಸಂಬಂದಿತ ಘಟಕಗಳು ಒಂದೇ ರೀತಿಯ ವ್ಯಾಪ್ತಿ (ವಿಸ್ತೀರ್ಣ)ಯನ್ನು ಹೊಂದಿರುತ್ತವೆ ಮತ್ತು ಮಜಲಿನಿಂದ 90° ಹೊರಗಿರುತ್ತವೆ. ಈ ದೃಷ್ಟಾಂತದಲ್ಲಿ, ಯಾವಾಗ ಒಂದು ಘಟಕವು ಅದರ ಗರಿಷ್ಠ ಅಥವಾ ಕನಿಷ್ಠ ವ್ಯಾಪ್ತಿಯಲ್ಲಿರುತ್ತದೆಯೊ ಆಗ ಇನ್ನೊಂದು ಘಟಕವು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ. ಅಲ್ಲಿ ಎರಡು ಹಂತದ ಸಂಭವನೀಯ ಸಂಬಂಧಗಳಿವೆ ಅವು ಈ ಅವಶ್ಯಕತೆಯನ್ನು ಪೂರೈಸುತ್ತವೆ: ಎಕ್ಸ್ ಘಟಕವು 90° ಯಲ್ಲಿ ವಾಯ್ ಘಟಕಕ್ಕಿಂತ ಮುಂದಿರಬಹುದು ಅಥವಾ 90°ಯಲ್ಲಿ ವಾಯ್ ಘಟಕಕ್ಕಿಂತ ಹಿಂದಿರಬಹುದು. ಈ ವಿಶಿಷ್ಟಾದ ದೃಷ್ಟಾಂತದಲ್ಲಿ, ವಿದ್ಯುತ್ ಪಥವು ಸಮತಲದಲ್ಲಿ ಒಂದು ವರ್ತುಲವನ್ನು ನಿರೂಪಿಸುತ್ತದೆ, ಆದ್ದರಿಂದ ಈ ಧ್ರುವೀಕಣವು ವೃತ್ತಾಕಾರದ ಧ್ರುವೀಕರಣ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ. ವರ್ತುಲದಲ್ಲಿನ ಪರಿಭ್ರಮಣದ ಮಾರ್ಗವು ಅಸ್ತಿತ್ವದಲ್ಲಿರುವ ಎರಡು ಮಜಲುಗಳ ಸಂಬಂಧದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ ಮತ್ತು ಬಲಭಾಗದ ವರ್ತುಲ ಧ್ರುವೀಕರಣ ಮತ್ತು ಎಡಭಾಗದ ವರ್ತುಲ ಧ್ರುವೀಕರಣ ಕ್ಕೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.[೪೦] ಉಳಿದ ಇತರ ದೃಷ್ಟಾಂತಗಳಲ್ಲಿ, ಎಲ್ಲಿ ಎರಡು ಘಟಕಗಳು ಒಂದೇ ರೀತಿಯ ವಿಸ್ತೀರ್ಣವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲವೋ ಮತ್ತು/ಅಥವಾ ಅವುಗಳ ಮಜಲುಗಳ ಭಿನ್ನತೆಯು ಶೂನ್ಯವೂ ಆಗಿರುವುದಿಲ್ಲ ಅಥವಾ 90°ಯ ಗುಣಕಗಳೂ ಆಗಿರುವುದಿಲ್ಲ, ಈ ರೀತಿಯ ಧ್ರುವೀಕರಣವು ದೀರ್ಘವೃತ್ತಾಕಾರದ ಧ್ರುವೀಕರಣ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ ಏಕೆಂದರೆ ವಿದ್ಯುತ್ ಪಥವು ಸಮತಲದಲ್ಲಿ ದೀರ್ಘವೃತ್ತವನ್ನು ಸೃಷ್ಟಿಸುತ್ತದೆ ( ಧ್ರುವೀಕರಣ ದೀರ್ಘವೃತ್ತ ). ಮೇಲೆ ಬಲಗಡೆಯಿರುವ ಚಿತ್ರದಲ್ಲಿ ಇದನ್ನು ತೋರಿಸಲಾಗಿದೆ. ಧ್ರುವೀಕರಣದ ವಿವರವಾದ ಗಣಿತಶಾಸ್ತ್ರವು ಜೋನ್ಸ್ ಕಲನಶಾಸ್ತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಮಾಡಲಾಗುತ್ತದೆ ಮತ್ತು ಅದು ಗೀಟಿನ ಮಾನದಂಡದ ಮುಖಾಂತರ ನಿರೂಪಿಸಲ್ಪಡುತ್ತದೆ.[೪೦]---- ಭಿನ್ನ ಧ್ರುವೀಕರಣ ಬಗೆಗಳಿಗೆ ಭಿನ್ನ ಸೂಚಿಯನ್ನು ಹೊಂದಿರುವ ಮಾಧ್ಯಮಗಳನ್ನು ಜೋಡಿವಕ್ರೀಕರಣ ಗಳು ಎನ್ನುವರು.[೫೯] ಈ ಪರಿಣಾಮದ ಸುಪರಿಚಿತ ಸ್ಪಷ್ಟೀಕರಣವು ದೃಗ್ವಿಜ್ಞಾನ ತರಂಗ ಫಲಕ/ ವಿಳಂಬಕ (ರೇಖಾತ್ಮಕ ಬಗೆಗಳು) ಗಳಲ್ಲಿ ಕಂಡುಬರುತ್ತವೆ ಮತ್ತು ಫ್ಯಾರಡೆ ಭ್ರಮಣ/ದೃಗ್ವಿಜ್ಞಾನ ಭ್ರಮಣ (ವೃತ್ತಾಕಾರದ ಭ್ರಮಣ)ಗಳಲ್ಲಿ ಕಂಡುಬರುತ್ತದೆ.[೪೦] ಜೋಡಿವಕ್ರೀಕರಣ ಮಾದ್ಯಮದಲ್ಲಿ ಮಾರ್ಗದ ಉದ್ದವು ಸಾಕಷ್ಟಿದ್ದರೆ, ವಕ್ರೀಕರಣದ ಕಾರಣದಿಂದಾಗಿ ಗಮನಾರ್ಹವಾಗಿ ಭಿನ್ನ ಪ್ರಜನನ ದಿಕ್ಕಿನ ಜೊತೆ ಸಮತಲ ತರಂಗಗಳು ಮೂಲವಸ್ತುವನ್ನು ಹೊರಹಾಕುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಇದು ಬರಿಗಣ್ಣಿಗೆ ಕಾಣುವ ಕ್ಯಾಲ್ಸಿಯಂ ಕಾರ್ಬೋನೇಟ್ ಖನಿಜದ ಹರಳುಗಳ ನಿದರ್ಶನವಾಗಿದೆ, ಇದು ನೋಡುಗರಿಗೆ ಎರಡು ಪ್ರತಿಭಾರಗಳನ್ನು ಪ್ರಸ್ತುತಪಡಿಸುತ್ತದೆ, ಅವುಗಳ ಮೂಲಕ ಏನನ್ನೇ ನೋಡಿದರೂ ಅಸಂಬದ್ಧವಾಗಿ ವಕ್ರೀಕರಣಗೊಂಡ ಚಿತ್ರಗಳಂತೆ ಕಾಣುತ್ತವೆ. ಈ ಪರಿಣಾಮವು ಇರಾಮಸ್ ಬಾರ್ತೊಲಿನಸ್ ಗೆ ೧೬೬೯ ರಲ್ಲಿ ವಕ್ರೀಕರಣದ ಮೊದಲ ಸಂಶೋಧನೆಗೆ ಸಹಾಯವಾಯಿತು. ಇದರ ಜೊತೆಗೆ, ಮಜಲು ಸ್ಥಿತಿ, ಮತ್ತು ಹೀಗೆ ಧ್ರುವೀಕರಣ ಸ್ಥಿತಿಯ ಬದಲಾವಣೆಯು, ಸಾಮಾನ್ಯವಾಗಿ ಆವರ್ತನ ಆಧಾರಿತವಾಗಿರುತ್ತದೆ, ಅದು, ದ್ವಿವರ್ಣತ್ವದ ಸಂಯೋಗದೊಂದಿಗೆ, ಅನೇಕವೇಳೆ ಪ್ರಕಾಶಮಾನ ಬೆಳಕನ್ನು ಮತ್ತು ಕಾಮನಬಿಲ್ಲಿನ ತರದ ಪರಿಣಾಮವನ್ನು ಉಂಟುಮಾಡುತ್ತವೆ. ಖನಿಜ ಶಾಸ್ತ್ರದಲ್ಲಿ, ಬಹುವರ್ಣತ್ವ ಎಂದು ಕರೆಯಲ್ಪಡುವ ಆ ರೀತಿಯ ಸ್ವತ್ತುಗಳು, ಸಾಮಾನ್ಯವಾಗಿ ಸೂಕ್ಷ್ಮದರ್ಶಕ ಯಂತ್ರಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಖನಿಜಗಳನ್ನು ಗುರುತಿಸುವ ಉದ್ದೇಶಕ್ಕಾಗಿ ಬಳಸಿಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಜೊತೆಗೆ, ಜೋಡಿವಕ್ರೀಕಾರಕಗಳಲ್ಲದ ಹಲವು ಪ್ಲಾಸ್ಟಿಕ್ ಗಳು ಯಾಂತ್ರಿಕ ಒತ್ತಡದ ವಿಷಯದಲ್ಲಿ ಹಾಗಾಗುತ್ತವೆ, ಇದು ಪ್ರಕಾಶಸ್ಥಿತಿಸ್ಥಾಪಕತ್ವದ ತಳಹದಿಯ ಒಂದು ಅಪೂರ್ವ ಘಟನೆ.[೫೯]

ನಿರ್ದಿಷ್ಟ ವಕ್ರೀಕರಣ ಬಗೆಗಳ ವ್ಯಾಪ್ತಿಯನ್ನು ಕಡಿಮೆಗೊಳಿಸುವ ಮಾದ್ಯಮವು ದ್ವಿವರ್ಣಿ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ.ಎಲ್ಲಾ ನಿಕಟ ವಿಕಿರಣಗಳನ್ನು ಒಂದೇ ಬಗೆಯಲ್ಲಿ ತಡೆಗಟ್ಟಲು ಬಳಸುವ ಸಾಧನಗಳಿಗೆ ಧ್ರುವೀಕರಣ ಶೋಧಕ ಅಥವಾ ಸರಳವಾಗಿ "ಧ್ರುವೀಕಾರಕಗಳು" ಎನ್ನುವರು. ಮೆಲುಸ್ ನ ಸಂಹಿತೆ, ನಂತರ ಎಟಿಯನ್-ಲೂಯಿಸ್ ಮೆಲುಸ್ ಎಂದು ಹೆಸರಿಸಲ್ಪಟ್ಟ ಸಂಹಿತೆಯು ಹೇಳುವುದೇನೆಂದರೆ ಯಾವಾಗ ಒಂದು ನಿಖರವಾದ ಧ್ರುವೀಕರಣವು ರೇಖಾತ್ಮಕ ಧ್ರುವೀಕೃತ ಬೆಳಕಿನ ಕಿರಣದಲ್ಲಿ ಇರಿಸಲ್ಪಡುತ್ತದೆಯೋ, ಅಲ್ಲಿ ಹಾದುಹೋಗುವ ಬೆಳಕಿನ ತೀವ್ರತೆ, ಆಯ್ , ಈ ಕೆಳಗಿನಂತೆ ನೀಡಲ್ಪಡುತ್ತದೆ
ಇದರಲ್ಲಿ
- ಆಯ್ ಒ ಗಳು ಪ್ರಾಥಮಿಕ ತೀವ್ರತೆಗಳು,
- ಮತ್ತು ೮ ಆಯ್ ಗಳು ಬೆಳಕಿನ ಪ್ರಾಥಮಿಕ ಧ್ರುವೀಕರಣ ಮಾರ್ಗ ಮತ್ತು ಧ್ರುವೀಕರಣದ ಅಕ್ಷದ ನಡುವಿನ ಕೋನಗಳಾಗಿರುತ್ತವೆ.[೫೯]
ಅಧ್ರುವೀಕೃತ ಬೆಳಕಿನ ಕಿರಣವು ಎಲ್ಲಾ ಸಂಭವನೀಯ ಕೋನಗಳ ಏಕಪ್ರಕಾರದ ಮಿಶ್ರಣವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ ಎಂದು ಯೋಚಿಸಬಹುದು. ಆದುದರಿಂದ 1/2 ಸರಾಸರಿ ಮೌಲ್ಯ, ಪ್ರಸಾರಣಾ ಸಹಪ್ರಮಾಣವು ಹೀಗೆ ಸಂಭವಿಸುತ್ತದೆ
ರೂಢಿಯಲ್ಲಿ, ಧ್ರುವೀಕರಣದಲ್ಲಿ ಕೆಲವು ಬೆಳಕು ಕಾಣೆಯಾಗುತ್ತವೆ ಮತ್ತು ಅಧ್ರುವೀಕೃತ ಬೆಳಕಿನ ವಾಸ್ತವಿಕ ಪ್ರಸರಣವು ಇದಕ್ಕಿಂತ ಸ್ವಲ್ಪದರಲ್ಲಿ ಕಮ್ಮಿಯಾಗಿರುತ್ತದೆ, ಧ್ರುವೀಕಾರಕ-ವಿಧದ ಧ್ರುವೀಕರಣಗಳಲ್ಲಿ ಸುಮಾರಾಗಿ 38% ಇರುತ್ತದೆ ಆದರೆ ಕೆಲವು ಜೋಡಿವಕ್ರೀಕರಣ ವರ್ಣಪಲ್ಲಟ ಕೊಳವೆಯಲ್ಲಿ ಗಣನೀಯವಾಗಿ ಹೆಚ್ಚಾ(>49.9%) ಗಿರುತ್ತವೆ.[೪೦] ವ್ಯಾಪಿತ ಮಾಧ್ಯಮದಲ್ಲಿ ಜೋಡಿವಕ್ರೀಕರಣ ಮತ್ತು ದ್ವಿವರ್ಣತ್ವಗಳ ಜೊತೆಗೆ, ವಿಭಿನ್ನ ವಕ್ರೀಕಾರಕ ಸೂಚಿಯನ್ನು ಹೊಂದಿರುವ ಎರಡು ಮೂಲವಸ್ತುಗಳ (ಪ್ರತಿಫಲಿತ) ಅಂತರ ಸಂಪರ್ಕ ಸಾಧನಗಳ ನಡುವೆ ಧ್ರುವೀಕರಣದ ಪರಿಣಾಮಗಳೂ ಕೂಡ ಉಂಟಾಗಬಹುದು. ಈ ಪರಿಣಾಮಗಳು ಫ್ರೆಸ್ನೆಲ್ ಸಮೀಕರಣದಿಂದ ಪ್ರತಿಪಾದಿಸಲ್ಪಡುತ್ತವೆ. ಕಾರ್ಯದ ಪುನರಾವರ್ತನೆಯ ಕೋನ ಮತ್ತು ವಕ್ರೀಕರಣದ ಕೋನದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವ ಅನುಪಾತದ ಜೊತೆಗೆ, ತರಂಗದ ಒಂದು ಭಾಗವು ಪ್ರಸಾರಿಸಲ್ಪಡುತ್ತದೆ ಮತ್ತು ಒಂದು ಭಾಗವು ವಕ್ರೀಕರಿಸಲ್ಪಡುತ್ತದೆ ಈ ರೀತಿಯಲ್ಲಿ, ಭೌತಿಕ ದೃಗ್ವಿಜ್ಞಾನವು ಬ್ರೆವ್ಸ್ಟರ್ ನ ಕೋನದಿಂದ ಸ್ವಾಧೀನಪಡಿಸಿಕೊಳ್ಳುತ್ತದೆ.[೪೦]

ಹೆಚ್ಚಿನ ವಿದ್ಯುದ್ಕಾಂತೀಯ ವಿಕಿರಣಗಳ ಮೂಲಗಳು ಬೆಳಕನ್ನು ಹೊರಸೂಸುವ ಅತಿ ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಆಟಮ್ಸ್ ಮತ್ತು ಮೊಲಿಕ್ಯುಲ್ಸ್ ಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ವಿಸರ್ಜಕಗಳಿಂದ ಉತ್ಪಾದಿತಗೊಂಡ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಗುರಿಯು ಸಹಸಂಬಂಧಿತವಾಗಿರಬೇಕೆಂದೇನಿಲ್ಲ, ಆ ನಿದರ್ಶನದಲ್ಲಿ ಬೆಳಕು ಅಧ್ರುವೀಕೃತ ವಾಗಿರುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ. ಅಲ್ಲಿ ವಿಸರ್ಜಕಗಳ ನಡುವೆ ಭಾಗಶಃ (ಅಪೂರ್ಣ)ಸಹಸಂಬಂಧವಿದ್ದರೆ, ಬೆಳಕು ಭಾಗಶಃ ಧ್ರುವೀಕೃತವಾಗಿರುತ್ತದೆ . ಧ್ರುವೀಕರಣವು ವರ್ಣಪಂಕ್ತಿಯ ಮೂಲಕ್ಕೆ ಅಡ್ಡಲಾಗಿ ಸುಸಂಬದ್ಧವಾಗಿದ್ದರೆ, ಭಾಗಶಃ ಧ್ರುವೀಕೃತ ಬೆಳಕನ್ನು ವಿಶಿಷ್ಟಸ್ಥಾನದ ಸಮಗ್ರ ಅಧ್ರುವೀಕೃತ ಅಂಶ, ಮತ್ತು ಸಮಗ್ರ ಧ್ರುವೀಕೃತ ಭಾಗ ಎಂದು ವರ್ಣಿಸಬಹುದು. ಅವುಗಳಲ್ಲಿ ಒಂದು ಆಗ ಬೆಳಕನ್ನು ಧ್ರುವೀಕರಣದ ಮಟ್ಟದ ನಿಭಂದನೆಗಳ ಮತ್ತು ದೀರ್ಘವೃತ್ತದ ಮಾನದಂಡದ ಮೂಲಕ ವರ್ಣಿಸುತ್ತದೆ.[೪೦] ಮಿರುಗುವ ಪಾರದರ್ಶಕ ಮೂಲವಸ್ತುವಿನ ಮೂಲಕ ಪ್ರತಿಫಲಿಸಲ್ಪಟ್ಟ ಬೆಳಕು, ಬೆಳಕು ಸಮತಲಕ್ಕೆ ಸಾಮಾನ್ಯವಾಗಿರುವ (ಲಂಬವಾಗಿರುವ)ಸಮಯವನ್ನು ಹೊರತುಪಡಿಸಿ, ಭಾಗಶಃ ಅಥವಾ ಪೂರ್ತಿಯಾಗಿ ಧ್ರುವೀಕೃತವಾಗಿರುತ್ತದೆ. ಈ ಪರಿಣಾಮವು ಗಣಿತಶಾಸ್ತ್ರಜ್ಞ ಎಟಿಯನ್ ಲೂಯಿಸ್ ಮೆಲುಸ್ ಗೆ ಧ್ರುವೀಕೃತ ಬೆಳಕಿನ ಗಣಿತಶಾಸ್ತ್ರದ ಪ್ರಥಮ ನಮೂನೆಯ ವಿಕಾಸವನ್ನು ಮಾಪನ ಮಾಡಲು ಅವಕಾಶ ನೀಡಿತು ವಾತಾವರಣದಲ್ಲಿ ಬೆಳಕು ಚದುರಿದಾಗ ಧ್ರುವೀಕರಣವು ಉಂಟಾಗುತ್ತದೆ. ಚದುರಿದ ಬೆಳಕು ನಿರ್ಮಲ ಆಕಾಶದಲ್ಲಿ ಕಾಂತಿ ಮತ್ತು ಬಣ್ಣವನ್ನು ಉತ್ಪತ್ತಿಮಾಡುತ್ತದೆ. ಧ್ರುವೀಕಾರಕ ಶೋಧಕಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಛಾಯಾಚಿತ್ರದಲ್ಲಿ ಆಕಾಶವನ್ನು ಗಾಢವಾಗಿ ಮಾಡುವಲ್ಲಿ ಚದುರಿದ ಬೆಳಕಿನ ಈ ಭಾಗಶಃ ಧ್ರುವೀಕರಣದ ಉಪಯುಕ್ತತೆಯನ್ನು ಪಡೆದುಕೊಳ್ಳಹುದು. ವೃತ್ತಾಕಾರದ ದ್ವಿವರ್ಣತ್ವ ಮತ್ತು ದೃಗ್ವಿಜ್ಞಾನ ಭ್ರಮಣದ ಕಾರಣದಿಂದಾಗಿ ದೃಗ್ವಿಜ್ಞಾನ ಧ್ರುವೀಕರಣವು ರಸಾಯನ ಶಾಸ್ತ್ರದಲ್ಲಿ ಪ್ರಧಾನ ಮಹತ್ವವನ್ನು ಪಡೆದಿದೆ ( ದೃಷ್ಟಿಸಹಾಯಕ ಕ್ರಿಯಾಶೀಲ ಅಸಮಮಿತ ಮೊಲಿಕ್ಯುಲ್ಸಗಳಿಂದ ಪ್ರಕಟಪಡಿಸಲ್ಪಟ್ಟ ವೃತ್ತಾಕಾರದ ಜೋಡಿವಕ್ರೀಕರಣ ).[೪೦]
ಆಧುನಿಕ ದೃಗ್ವಿಜ್ಞಾನ[ಬದಲಾಯಿಸಿ]
ಬೆಳಕಿನ ಕುರಿತು ಅಧ್ಯಯನ ನಡೆಸುವ ಶಾಖೆಗಳನ್ನು ಹಾಗೂ ತಂತ್ರಗಾರಿಕೆಯನ್ನೂ ಒಳಗೊಂಡ ಆಧುನಿಕ ದೃಗ್ವಿಜ್ಞಾನ ಜನಪ್ರಿಯಗೊಂಡಿದ್ದು ೨೦ನೇ ಶತಮಾನದಲ್ಲಿ. ಈ ಎಲ್ಲಾ ದೃಗ್ವಿಜ್ಞಾನ ಶಾಖೆಗಳು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಥವಾ ಬೆಳಕಿನ ಮೊತ್ತಕ್ಕೆ ಸಂಬಂಧಿಸಿದ್ದಾದರೂ ಇನ್ನುಳಿದ ಸಂಗತಿಗಳನ್ನೂ ಅದು ಒಳಗೊಳ್ಳುತ್ತವೆ. ಆಧುನಿಕ ದೃಗ್ವಿಜ್ಞಾನದ ಅತ್ಯಂತ ಮಹತ್ವದ ಅಂಗವಾದ ಕ್ವಾಂಟಮ್ ದೃಗ್ವಿಜ್ಞಾನ ವಿಶೇಷವಾಗಿ ಬೆಳಕಿನ ವಿಕಿರಣ ಕಾರ್ಯವಿಧಾನಕ್ಕೆ ಸಂಬಂಧಿಸಿದ್ದು. ಕ್ವಾಂಟಮ್ ದೃಗ್ವಿಜ್ಞಾನ ಕೇವಲ ಸೈದ್ಧಾಂತಿಕ ಚೌಕಟ್ಟಿಗೆ ಮಾತ್ರ ಒಳಪಟ್ಟಿಲ್ಲ; ಪ್ರಾಯೋಗಿಕವಾಗಿಯೂ ಉಪಯುಕ್ತವಾಗಿರುವ ಇದರ ಸಹಾಯದಿಂದಲೇ ಲೇಸರ್ ರೀತಿಯ ಹಲವಾರು ಆಧುನಿಕ ಉಪಕರಣಗಳು ಕಾರ್ಯ ನಿರ್ವಹಿಸುತ್ತವೆ. ಫೋಟೋಮಲ್ಟಿಪ್ಲೈಯರ್ಗಳು ಹಾಗೂ ಚಾನೆಲ್ಟ್ರೋನ್ಗಳ ರೀತಿಯ ಬೆಳಕಿನ ಡಿಟೆಕ್ಟರ್ಗಳು ಕೂಡ ಪ್ರತ್ಯೇಕ ಫೋಟಾನ್ಗಳಿಗೆ ಅತ್ಯದ್ಭುತವಾಗಿ ಸ್ಪಂದಿಸುತ್ತವೆ. ಮಾತ್ರವಲ್ಲ, ಸಿಸಿಡಿರೀತಿಯ ವಿದ್ಯುನ್ಮಾನ ಇಮೇಜ್ ಸೆನ್ಸರ್ಗಳು ಪ್ರತ್ಯೇಕ ಫೋಟಾನ್ಗಳೊಂದಿಗೆ ಸಂವಾದಿಸಿ ಚಿಕ್ಕದಾಗಿ ಧ್ವನಿ ಹೊರಡಿಸುತ್ತವೆ ಹಾಗೆಯೇ,ಬೆಳಕಿನ ವಿಕಿರಣಗಳನ್ನು ಹೊರಹೊಮ್ಮಿಸುವ ಡಿಯೋಡ್ಗಳು ಹಾಗೂ ಫೋಟೋವೋಲ್ಟಾಯಿಕ್ ಸೆಲ್ಗಳನ್ನು ಕೂಡ ಕ್ವಾಂಟಮ್ ಕಾರ್ಯವಿಧಾನದಿಂದ ಹೊರತುಪಡಿಸಿ ಅರ್ಥ ಮಾಡಿಕೊಳ್ಳುವುದು ಅಸಂಭವ. ಈ ಎಲ್ಲಾ ಉಪಕರಣಗಳ ಅಧ್ಯಯನದ ಸಂದರ್ಭದಲ್ಲಿ ಕ್ವಾಂಟಮ್ ದೃಗ್ವಿಜ್ಞಾನ ಕೆಲವೊಮ್ಮೆ ಕ್ವಾಂಟಮ್ ವಿದ್ಯುನ್ಮಾನವನ್ನು ಅತಿಕ್ರಮಿಸುವ ಸಾಧ್ಯತೆಗಳು ಇಲ್ಲದಿಲ್ಲ.[೬೦] ಸ್ಪಟಿಕ ಹಾಗೂ ಮೆಟಾಮೆಟೀರಿಯಲ್ಗಳಿಗೆ ಬೆಳಕು ಹೇಗೆ ಪ್ರತಿಕ್ರಿಯಿಸುತ್ತದೆ ಎಂಬುದರ ಕುರಿತ ಅಧ್ಯಯನವನ್ನೂ ದೃಗ್ವಿಜ್ಞಾನ ಅಧ್ಯಯನದ ವಿಶೇಷ ಶಾಖೆಗಳು ಒಳಗೊಂಡಿವೆ. ಇನ್ನಿತರ ಅಧ್ಯಯನಗಳು ಓರೆಣಿಕೆಯ ದೃಗ್ವಿಜ್ಞಾನ, ಚಿತ್ರ ರಹಿತ ದೃಗ್ವಿಜ್ಞಾನ,ರೇಖಾತ್ಮಕವಲ್ಲದ ದೃಗ್ವಿಜ್ಞಾನ,ಅಂಕಿ-ಅಂಶ ಸಂಬಂಧಿ ದೃಗ್ವಿಜ್ಞಾನ ಹಾಗೂ ರೆಡಿಯೋಮೆಟ್ರಿಗಳ ರೀತಿಯಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ಕಾರ್ಯ ವಿಧಾನಗಳ ಮೇಲೆ ಬೆಳಕು ಚೆಲ್ಲುತ್ತವೆ. ಇದರ ಜೊತೆಗೆ, ಕಂಪ್ಯೂಟರ್ ಎಂಜಿನೀಯರ್ಗಳು ಇತ್ತೀಚೆಗೆ ಸಂಘಟಿತ ದೃಗ್ವಿಜ್ಞಾನ, ಯಾಂತ್ರಿಕ ದೃಷ್ಟಿ ಹಾಗೂ ಫೋಟೋನಿಕ್ ಕಂಪ್ಯೂಟಿಂಗ್ ಕುರಿತು ಆಸಕ್ತಿವಹಿಸಲಾರಂಭಿಸಿದ್ದು ಇವುಗಳನ್ನು ’ಭವಿಷ್ಯದ ಕಂಪ್ಯೂಟರ್’ಗಳ ಹೊಳವುಗಳೆಂದೇ ಪರಿಗಣಿಸಲಾಗುತ್ತಿದೆ.[೬೧] ಇಂದು, ಅನ್ವಯಿಕ ದೃಗ್ವಿಜ್ಞಾನದಿಂದ ಹೊರತುಪಡಿಸುವ ಉದ್ದೇಶದಿಂದ ಬೆಳಕಿನ ಅಧ್ಯಯನವನ್ನು ದೃಗ್ವಿಜ್ಞಾನೀಯ ಬೌತಶಾಸ್ತ್ರ ಅಥವಾ ದೃಗ್ವಿಜ್ಞಾನ ಎಂದು ಕರೆಯಲಾಗುತ್ತಿದೆ. ಅವುಗಳನ್ನು ದೃಗ್ವಿಜ್ಞಾನೀಯ ಎಂಜಿನೀಯರಿಂಗ್ ಎಂದೂ ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ. ಪ್ರಜ್ವಲನ ಎಂಜಿನೀಯರಿಂಗ್, ಫೋಟೋನಿಕ್ಸ್ ಹಾಗೂ ಆಪ್ಟೊಎಲೆಕ್ಟ್ರಾನಿಕ್ಸ್ಗಳನ್ನು ತನ್ನ ಪ್ರಮುಖ ಸಹ-ಕ್ಷೇತ್ರಗಳನ್ನಾಗಿಸಿಕೊಂಡಿರುವ ದೃಗ್ವಿಜ್ಞಾನೀಯ ಎಂಜನೀಯರಿಂಗ್, ಲೆನ್ಸ್ ವಿನ್ಯಾಸ,ದೃಷ್ಟಿ ಅನುಕೂಲಿ ಮಸೂರಗಳ ತಯಾರಿಕೆ ಹಾಗೂ ಪರೀಕ್ಷೆ, ಚಿತ್ರಗಳ ಪರಿಷ್ಕರಣೆಗಳಂಥ ಪ್ರಾಯೋಗಿಕ ಆಯಾಮಗಳನ್ನೂ ಒಳಗೊಂಡಿರುತ್ತದೆ. ಜಗತ್ತಿನ ಹಾಗೂ ಕೈಗಾರಿಕಾ ವಲಯದ ಹಲವೆಡೆ ಹಲವು ರೀತಿಯ ವಿಚಾರಗಳು ಚಾಲ್ತಿಯಲ್ಲಿದ್ದು ಅವುಗಳ ನಡುವಿನ ಅಂತರ ಅಸ್ಪಷ್ಟವಾಗಿರುವ ಕಾರಣ ಹತ್ತು ಹಲವು ಕ್ಷೇತ್ರಗಳ ಸಂಗತಿಗಳು ಒಂದಕ್ಕೊಂದು ತಳಿಕೆ ಹಾಕಿಕೊಂಡು ಗೋಜಲಾಗುವ ಸಂದರ್ಭಗಳು ಇಲ್ಲದಿಲ್ಲ.[೬೨] ಲೇಸರ್ ತಂತ್ರಜ್ಞಾನದ ಕ್ಷಿಪ್ರ ಬೆಳವಣಿಗೆಯಿಂದಾಗಿ ಕಳೆದ ಹಲವು ದಶಕಗಳಲ್ಲಿ ರೇಖಾತ್ಮಕವಲ್ಲದ ದೃಗ್ವಿಜ್ಞಾನ ಕ್ಷೇತ್ರದಲ್ಲಿನ ವೃತ್ತಿಪರ ಸಂಶೋಧಕರ ಸಂಖ್ಯೆ ಗಣನೀಯವಾಗಿ ಹೆಚ್ಚಿದೆ.[೬೩]
ಲೇಸರ್ಗಳು[ಬದಲಾಯಿಸಿ]

ಉತ್ತೇಜನಕಾರಿ ಹೊರಸೂಸುವಿಕೆ (ಸ್ಟಿಮ್ಯುಲೇಟೆಡ್ ಎಮಿಷನ್ ) ಎಂಬ ಕಾರ್ಯವಿಧಾನದ ಮೂಲಕ ಬೆಳಕನ್ನು (ವಿದ್ಯುತ್ ಕಾಂತೀಯ ವಿಕಿರಣ) ಹೊರಸೂಸುವ ಸಾಧನಕ್ಕೆ ಲೇಸರ್ ಎಂದು ಕರೆಯುತ್ತಾರೆ. Light Amplification by Stimulated Emission of Radiation ಎಂಬುದೇ ಲೇಸರ್ ನ (LASER) ವಿಸ್ತ್ರತ ರೂಪ.[೬೪][೬೪] ಲೇಸರ್ ಬೆಳಕಿನ ಕಿರಣಗಳು ಸಾಮಾನ್ಯವಾಗಿ ಪರಸ್ಪರ ಹೊಂದಾಣಿಕೆಯ ಗುಣಲಕ್ಷಣ ಪ್ರದರ್ಶಿಸುತ್ತವೆ. ಅವು ಕೆಲವೊಮ್ಮೆ ಕಿರಿದಾದ ಅಲ್ಪ ಅಪಸರಣ ಕಿರಣಗಳಾಗಿ ಹೊರಸೂಸುತ್ತವೆ, ಮತ್ತೆ ಕೆಲವೊಮ್ಮೆ ಅವುಗಳನ್ನು ಮಸೂರದಂತಹ ದೃಗ್ವಿಜ್ಞಾನ ಸಾಧನಗಳ ಮೂಲಕ ಏಕಕಿರಣವಾಗಿ ಪರಿವರ್ತಿಸಬಹುದು. ಸೂಕ್ಷ್ಮ ತರಂಗಗಳು ಸಹ ಲೇಸರ್ ಕಿರಣಗಳ ಸಮಾನ ಗುಣಗಳನ್ನು ಹೊರಗೆಡವಿದ ಹಿನ್ನೆಲೆಯಲ್ಲಿ, ಮೊದಲ ಬಾರಿಗೆ ಮೇಸರ್ ಸಾಧನವನ್ನು ಅಭಿವೃದ್ಢಿಪಡಿಸಲಾಯಿತು. ಸೂಕ್ಶ್ಮ ತರಂಗಗಳು ಮತ್ತು ರೇಡಿಯೊ ತರಂಗಗಳನ್ನು ಹೊರಸೂಸುವ ಸಾಧನವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಮೇಸರ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.[೬೫] ಕಾರ್ಯನಿರತ ಲೇಸರ್ ಸಾಧನವನ್ನು ಮೊಟ್ಟಮೊದಲ ಬಾರಿಗೆ 1960 ಮೇ 16 ರಂದು ಥಿಯೋಡರ್ ಮೇಮನ್ ನಲ್ಲಿರುವ ಹೂಗ್ಸ್ ಸಂಶೋಧನಾ ಪ್ರಯೋಗಾಲಯದಲ್ಲಿ ಪ್ರದರ್ಶಿಸಲಾಯಿತು.[೬೬] ಲೇಸರ್ ಸಾಧನ ಕಂದುಹಿಡಿದ ಸಂದರ್ಭದಲ್ಲಿ, ಸಂಶೋಧಕರು ಅದನ್ನು "ಸಮಸ್ಯೆಗೊಂದು ಪರಿಹಾರ ಹುಡುಕುತ್ತಿದ್ದೇವೆ" ಎಂದು ಕರೆದರು.[೬೭] ಆನಂತರದಲ್ಲಿ, ಲೇಸರ್ ವಿಶ್ವಾದ್ಯಂತ ಬಿಲಿಯನ್ ಡಾಲರ್ ಉದ್ದಿಮೆಯಾಗಿ ಬೆಳೆಯತೊಡಗಿತು. ಹಲವು ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ಅದರ ಅಗತ್ಯ ಮತ್ತು ಬಳಕೆ ಅನಿವಾರ್ಯವಾಗತೊಡಗಿತು. ದೈನಂದಿನ ಸಾಮಾನ್ಯ ಜೀವನಕ್ಕೆ ಅತ್ಯಗತ್ಯವಾಗಿ ಬೇಕು ಅನಿಸುವಷ್ಟರ ಮಟ್ಟಿಗೆ ಅನಿವಾರ್ಯತೆ ಸೃಷ್ಟಿಸಿದ ಲೇಸರನ್ನು ಮೊದಲ ಬಾರಿಗೆ 1974 ರಲ್ಲಿ ಸೂಪರ್ ಮಾರ್ಕೆಟ್ ಬಾರ್ ಕೋಡ್ ಸ್ಕ್ಯಾನರ್ ಆಗಿ ಪರಿಚಯಿಸಲಾಯಿತು.[೬೮] 1978 ರಲ್ಲಿ ಪರಿಚಯಿಸಲ್ಪಟ್ಟ ಲೇಸರ್ ಡಿಸ್ಕ್ ಪ್ಲೇಯರ್ ಮೊದಲ ಗ್ರಾಹಕ ಉತ್ಪನ್ನವಾಗಿ ಮಾರುಕಟ್ಟೆಯಲ್ಲಿ ಯಶಸ್ವಿಯಾಯಿತು.ಆದರೆ, ನಂತರ ಬಂದ ಲೇಸರ್ ಅಳವಡಿಕೆಯ ಕಾಂಪ್ಯಾಕ್ಟ್ ಡಿಸ್ಕ್ ಪ್ಲೇಯರ್ ಹೆಚ್ಚು ಜನಪ್ರಿಯಗೊಂಡಿತಲ್ಲದೆ, 1982 ರಲ್ಲಿ ಮನೆಮನೆಯ ನೆಚ್ಚಿನ ಸಂಗಾತಿಯಾಗಿಬಿಟ್ಟಿತು.[೬೯] ದ್ಯುತಿ ಸಂಗ್ರಹದ ಈ ಸಾಧನಗಳು ಸೆಮಿಕಂಡಕ್ಟರ್ ಲೇಸರ್ ಗಳನ್ನು ಬಳಸುತ್ತವೆ. ಕೇವಲ ಒಂದು ಮಿಲಿಮೀಟರ್ ಗಿಂತ ಕಡಿಮೆ ಅಗಲ ಹೊಂದಿರುವ ಈ ಲೇಸರ್ ಗಳು ಡಿಸ್ಕ್ ಮೇಲ್ಮೈನಿಂದ ಕ್ಷಣಾರ್ಧದಲ್ಲಿ ಮಾಹಿತಿಯನ್ನು ಶೋಧಿಸುತ್ತವೆ. ಬೃಹತ್ ಪ್ರಮಾಣದ ಮಾಹಿತಿಯನ್ನು ಬೆಳಕಿನ ವೇಗದಲ್ಲಿ ಪ್ರಸರಿಸಲು, ಫೈಬರ್ - ಆಪ್ಟಿಕ್ ಸಂವಹನವು ಸಂಪೂರ್ಣವಾಗಿ ಲೇಸರ್ ತಂತ್ರಜ್ಞಾನವನ್ನೇ ಅವಲಂಬಿಸಿದೆ. ಲೇಸರ್ ಪ್ರಿಂಟರ್ಸ್ ಮತ್ತು ಲೇಸರ್ ಪಾಯಿಂಟರ್ಸ್ ಗಳಲ್ಲಿ ಲೇಸರ್ ತಂತ್ರಜ್ಞಾನವನ್ನು ಬಳಸಲಾಗುತ್ತಿದೆ. ವೈದ್ಯಕೀಯ ರಂಗದಲ್ಲೂ ಲೇಸರ್ ತಂತ್ರಜ್ಞಾನದ ವಿಫುಲ ಬಳಕೆಯಾಗುತ್ತಿದೆ. ರಕ್ತರಹಿತ ಶಸ್ತ್ರಚಿಕಿತ್ಸೆ, ಕಣ್ಣಿನ ಶಸ್ತ್ರಚಿಕಿತ್ಸೆ, ಮೃತದೇಹಗಳ ಅಂಗಾಂಗ ಪರೀಕ್ಷೆ, ಸೇನಾಪಡೆಯಲ್ಲಿ ಕ್ಷಿಪಣಿ ರಕ್ಷಣಾ ವ್ಯವಸ್ಥೆ, ಎಲೆಕ್ಟ್ರೋ - ಆಪ್ಟಿಕಲ್ ಕೌಂಟರ್ ಮೆಷರ್ಸ್ (EOCM) ಮತ್ತು LIDAR ನಲ್ಲಿ ಲೇಸರ್ ಉಪಯೋಗಿಸಲಾಗುತ್ತಿದೆ. ಲೇಸರ್ ಅನ್ನು ಹಾಲೋಗ್ರಾಮ್, ಬಬಲ್ ಗ್ರಾಮ್ಸ್, ಲೇಸರ್ ಲೈಟ್ ಪ್ರದರ್ಶನ ಮತ್ತು ಕೂದಲು ತೆಗೆದು ಹಾಕಲು ಲೇಸರ್ ತಂತ್ರಜ್ಞಾನದ ವ್ಯಾಪಕ ಬಳಕೆಯಾಗುತ್ತಿದೆ.[೭೦]
ಉಪಯೋಗಗಳು[ಬದಲಾಯಿಸಿ]
ದೃಗ್ವಿಜ್ಞಾನವು ದೈನಂದಿನ ಜೀವನದ ಒಂದು ಭಾಗವಾಗಿದೆ. ಜೀವಶಾಸ್ತ್ರದ ಎಲ್ಲೆಡೆ ನಾವು ದೃಶ್ಯ ವ್ಯವಸ್ಠೆಯನ್ನು ಕಾಣುತ್ತೇವೆ. ಐದು ಇಂದ್ರಿಯ ಜ್ಞಾನಗಳಲ್ಲಿ ದೃಗ್ವಿಜ್ಞಾನವು ಪ್ರಮುಖ ವಿಜ್ಞಾನವಾಗಿ ಪಾತ್ರ ವಹಿಸುತ್ತದೆ ಎಂಬುದಕ್ಕೆ ಇದು ಸ್ಪಷ್ಟ ನಿದರ್ಶನ. ಹಲವಾರು ಜನರು ಕಣ್ಣಿಗೆ ಕನ್ನಡಕ ಮತ್ತು ಕಾಂಟ್ಯಾಕ್ಟ್ ಲೆನ್ಸ್ ಬಳಸುತ್ತಾರೆ. ಕ್ಯಾಮೆರಾ ಸೇರಿದಂತೆ ಹಲವಾರು ಗ್ರಾಹಕ ವಸ್ತುಗಳಿಗೆ ದೃಗ್ವಿಜ್ಞಾನವು ಅಪಾರ ಕೊದುಗೆ ನೀಡಿದೆ. ಕಾಮನಬಿಲ್ಲು ಮತ್ತು ಮರೀಚಿಕೆಗಳು ದೃಗ್ವಿಜ್ಞಾನದ ಕೆಲವು ಉದಾಹರಣೆಗಳು. ದೃಷ್ಟಿ ಅಥವಾ ಬೆಳಕಿನ ಸಂವಹನ ತತ್ವಗಳು ಅಂತರ್ಜಾಲ ಮತ್ತು ಆಧುನಿಕ ದೂರಸಂಪರ್ಕ ವ್ಯವಸ್ಥೆಯ ಆಧಾರಸ್ಥಂಭಗಳಾಗಿವೆ.
ಮಾನವನ ಕಣ್ಣು[ಬದಲಾಯಿಸಿ]

ಮಾನವನ ಕಣ್ಣಿನ ದೃಶ್ಯಗ್ರಾಹಿ ಜೀವಕೋಶಗಳು ಬೆಳಕಿನ ಕಿರಣಗಳನ್ನು ಗ್ರಹಿಸುತ್ತವೆ. ಈ ದೃಶ್ಯಗ್ರಾಹಿ ಜೀವಕೋಶಗಳ ಸಮೂಹಕ್ಕೆ ಅಕ್ಷಿಪಟಲ ಅಥವಾ ರೆಟಿನಾ ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಅಕ್ಷಿಪಟಲವು ಕಣ್ಣಿನ ಹಿಂಬದಿ ಇರುತ್ತದೆ. ಬೆಳಕಿನೆಡೆಗೆ ದೃಷ್ಟಿ ಕೇಂದ್ರೀಕರಿಸುವ ಕಣ್ಣಿನ ಈ ಪ್ರಕ್ರಿಯೆಯು ಹಲವು ಪಾರದರ್ಶಕ ಪದರಗಳ ಜೊತೆಗೂಡಿ ನಡೆಯುತ್ತದೆ. ಕಣ್ಣಿನೊಳಗೆ ಪ್ರವೇಶಿಸುವ ಬೆಳಕು, ಮೊಟ್ಟಮೊದಲು ಕಣ್ಣಿನ ಗುಡ್ಡೆಯ ಮುಂಭಾಗ ಕಾಣುವ ಪಾರದರ್ಶಕ ಪಟಲ ಅಥವಾ ಕಾರ್ನಿಯಾವನ್ನು ಪ್ರವೇಶಿಸುತ್ತದೆ. ಕಣ್ಣಿನ ಬಹುಪಾಲು ದೃಶ್ಯಶಕ್ತಿಯನ್ನು ಕಾರ್ನಿಯಾ ಒದಗಿಸುತ್ತದೆ. ಆನಂತರ, ಬೆಳಕು ಕಾರ್ನಿಯಾ ಹಿಂಭಾಗದಲ್ಲಿರುವ ಕಣ್ಣಿನ ದ್ರವರೂಪದ ಪದರ ಆಂಟಿರಿಯರ್ ಚೇಂಬರ್ ಸ್ಪರ್ಶಿಸಿ, ನಂತರ ಪ್ಯೂಪಿಲ್ ಪದರವನ್ನು ಪ್ರವೇಶಿಸುತ್ತದೆ. ಆಮೇಲೆ, ಬೆಳಕು ಕಣ್ಣಿನ ಮಸೂರವನ್ನು ಪ್ರವೇಶಿಸುತ್ತದೆ. ಮಸೂರವು ಬೆಳಕನ್ನು ದೃಷ್ಟಿಸಲು ಅಥವಾ ಹೊಂದಾಣಿಕೆ ಮಾಡಿಕೊಳ್ಳಲು ಸಹಕರಿಸುತ್ತದೆ. ಆನಂತರ, ಬೆಳಕು ಕಣ್ಣಿನ ಪ್ರಮುಖ ದ್ರವ ರೂಪದ ಗಾಜಿನ ಪದರ ಪ್ರವೇಶಿಸಿ, ಕೊನೆಗೆ ಅಕ್ಷಿಪಟಲ ತಲುಪುತ್ತದೆ. ದೃಷ್ಟಿನರವನ್ನು ಹೊರತುಪಡಿಸಿ ಕಣ್ಣಿನ ಹಿಂಬದಿಯನ್ನು ಅಕ್ಷಿಪಟಲದ ಜೀವಕೋಶಗಳು ಸುತ್ತುವರಿದಿರುತ್ತವೆ. ಇದರ ಪರಿಣಾಮವಾಗಿ ಕುರುಡುತನ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ. ದೃಶ್ಯಗ್ರಾಹಿ ಜೀವಕೋಶಗಳಲ್ಲಿ ಎರಡು ವಿಧ. ಅವುಗಳಿಗೆ ರಾಡ್ ಜೀವಕೋಶ ಮತ್ತು ಕೋನ್ ಜೀವಕೋಶ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ಕೋಶಗಳು ವಿವಿಧ ಪ್ರಖರತೆಯ ಬೆಳಕಿಗೆ ಸೂಕ್ಷ್ಮಗ್ರಾಹಿಗಳಾಗಿರುತ್ತವೆ.[೭೧] ವಿಸ್ತ್ರತ ತರಂಗಾಂತರಗಳಲ್ಲಿ, ಬೆಳಕಿನ ಸಾಂದ್ರತೆಗೆ ಸೂಕ್ಷ್ಮಗ್ರಾಹಿಗಳಾಗಿರುವ ರಾಡ್ ಜೀವಕೋಶಗಳೇ, ಕಪ್ಪು ಮತ್ತು ಬೆಳಕಿನ ದೃಶ್ಯ ಅಥವಾ ನೋಟಕ್ಕೆ ಕಾರಣೀಭೂತವಾಗುತ್ತವೆ. ರಾಡ್ ಕೋಶಗಳು ಅಕ್ಷಿಪಟಲ ಭಾಗದ ಫೋವಿಯಾ ಅಥವಾ ಕುಳಿಯಲ್ಲಿ ಇರುವುದಿಲ್ಲ, ಮತ್ತು ಅವು ಬೆಳಕಿನ ತಾತ್ಕಾಲಿಕ ಬದಲಾವಣೆ ಮತ್ತು ಜಾಗಗಳಿಗೆ ಕೋನ್ ಕೋಶಗಳಂತೆ ಸ್ಪಂದಿಸುವುದಿಲ್ಲ. ಆದಾಗ್ಯೂ, ಅಕ್ಷಿಪಟಲದಲ್ಲಿ ಕೋವ್ ಕೋಶಗಳಿಗಿಂತ ಇಪ್ಪತ್ತು ಪಟ್ಟು ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯಲ್ಲಿ ರಾಡ್ ಕೋಶಗಳಿಬೆ. ಕಣ್ಣಿನ ಬಹುಪಾಲು ಭಾಗದಲ್ಲಿ ರಾಡ್ ಕೋಶಗಳು ಇರುವುದೇ ಇದಕ್ಕೆ ಕಾರಣ. ಎಲ್ಲಾ ಭಾಗಗಳಲ್ಲೂ ಹರಡಿಕೊಂಡಿರುವ ರಾಡ್ ಕೋಶಗಳೇ ಬಾಹ್ಯ ದೃಷ್ಟಿಗೆ ಕಾರಣ.[೭೨]
ಆದರೆ, ಕೋನ್ ಕೋಶಗಳು ವ್ಯತಿರಿಕ್ತ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿವೆ. ಅವು ಒಟ್ಟಾರೆ ಬೆಳಕಿನ ಸಾಂದ್ರತೆಗೆ ಅಲ್ಪ ಸೂಕ್ಷ್ಮಗ್ರಾಹಿ ಪ್ರವೃತ್ತಿ ತೋರುತ್ತವೆ. ಆದರೆ ಅವು ಮೂರು ಬಗೆಯ ಸ್ವರೂಪಗಳಲ್ಲಿ ವಿವಿಧ ತರಂಗಾಂತರಗಳಲ್ಲಿ ಸೂಕ್ಷ್ಮಗ್ರಾಹಿ ಗುಣ ತೋರುತ್ತವೆ. ಹಾಗಾಗಿ, ಕೋನ್ ಕೋಶಗಳನ್ನು ಪ್ರಕಾಶಮಾನವಾದ ಹಾಗೂ ವರ್ಣಮಯ ದೃಷ್ಟಿ ಅಥವಾ ದೃಶ್ಯಗಳ ಗ್ರಹಿಕೆಗೆ ಬಳಸುತ್ತಾರೆ. ಫೋವಿಯಾದಲ್ಲಿ ಹೆಚ್ಚಾಗಿ ಕೇಂದ್ರೀಕೃತವಾಗಿರುವ ಕೋನ್ ಕೋಶಗಳು ಹೆಚ್ಚಿನ ಮಟ್ಟದ ದೃಷ್ಟಿ ತೀಕ್ಷ್ಣತೆ ಹೊಂದಿರುತ್ತವೆ. ಅಂದರೆ ಅವು ರಾಡ್ ಕೋಶಗಳಿಗಿಂತ ಉತ್ತಮ ರೆಸಲೂಷನ್ ಅಥವಾ ಅಭಿನಿವೇಶ ಹೊಂದಿವೆ ಎಂದರ್ಥ. ಕೋನ್ ಕೋಶಗಳು ಮಂಕು ಬೆಳಕಿಗೆ ಅಷ್ಟಾಗಿ ಸ್ಪಂದಿಸುವುದಿಲ್ಲ, ಆದರೆ ರಾಡ್ ಕೋಶಗಳು ಸೂಕ್ಷ್ಮಗ್ರಾಹಿಗಳಾಗಿರುತ್ತವೆ. ಹಾಗಾಗಿ, ಬಹುಪಾಲು ರಾತ್ರಿ ದೃಷ್ಟಿ ರಾಡ್ ಕೋಶಗಳಿಗೆ ಸೀಮಿತವಾಗಿರುತ್ತದೆ. ಕೋನ್ ಕೋಶಗಳು ಫೋವಿಯಾದಲ್ಲಿರುವುದರಿಂದ, ಪ್ರಮುಖ ಕಣ್ಣಿನ ನೋಟ ಅಥವಾ ವೀಕ್ಷಣೆಯು ಕೋನ್ ಕೋಶಗಳಿಂದಲೇ ನಡೆಯುತ್ತದೆ. ಪುಸ್ತಕಗಳ ಅಧ್ಯಯನ, ಹೊಲಿಗೆ, ವಿವಿಧ ವಸ್ತುಗಳ ಸೂಕ್ಷ್ಮ ಪರೀಕ್ಷೆ, ಕಸೂತಿಯಂತಹ ಸೂಕ್ಷ್ಮ ದೃಷ್ಟಿಯ ಕಾರ್ಯಗಳು ಕೋನ್ ಜೀವಕೋಶಗಳಿಂದಲೇ ನಡೆಯುತ್ತವೆ.[೭೨] ಕಣ್ಣಿನ ಮಸೂರದ ಸುತ್ತ ಇರುವ ಸಿಲಿಅರಿ ಸ್ನಾಯುಗಳು ದೃಷ್ಟಿ ಹಾಯಿಸಲು ನೆರವಾಗುತ್ತವೆ. ಈ ವಿಧಾನವನ್ನು ಅನುಕೂಲವರ್ತನೆ ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಕಣ್ಣಿನಿಂದ ಕಾಣುವ ಹತ್ತಿರದ ಮತ್ತು ದೂರದ ಅಂತರಗಳನ್ನು ಸಮೀಪ ದೃಷ್ಟಿ ಅಥವಾ ಬಿಂದು ಮತ್ತು ದೂರ ದೃಷ್ಟಿ ಅಥವಾ ಬಿಂದುಗಳಿಂದ ವ್ಯಾಖ್ಹ್ಯಾನಿಸಲಾಗುತ್ತದೆ. ಈ ಬಿಂದುಗಳಿಂದ ವಸ್ತುವಿನ ಮೇಲೆ ಸೂಕ್ಷ್ಮ ದೃಷ್ಟಿ ನೆಟ್ಟಲು ಸಾಧ್ಯ. ಸಾಮಾನ್ಯ ದೃಷ್ಟಿ ಹೊಂದಿರುವ ವ್ಯಕ್ತಿಗೆ, ದೂರ ಬಿಂದುವು ಅನಂತದಲ್ಲಿ ನೆಲೆಗೊಂಡಿರುತ್ತದೆ. ಕಣ್ಣಿನ ಮಸೂರ ಎಷ್ಟು ಪ್ರಮಾಣದಲ್ಲಿ ಬಾಗಲು ಅಥವಾ ಹೊರಳಾಡಲು ಸಿಲಿಅರಿ ಸ್ನಾಯುಗಳು ಸಹಕರಿಸುತ್ತವೆ ಎಂಬುದರ ಮೇಲೆ ಸಮೀಪ ದೃಷ್ಟಿಯ ನೆಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ. ಅಲ್ಲದೆ, ಇದು ಕಣ್ಣಿನ ಮಸೂರದ ಆಯಸ್ಸನ್ನೂ ಅವಲಂಬಿಸಿರುತ್ತದೆ. ದೃಷ್ಟಿಮಾಪನಕಾರರು, ನೇತ್ರ ವಿಜ್ಞಾನಿಗಳು ಮತ್ತು ನೇತ್ರತಜ್ಞರು ಸಾಮಾನ್ಯ ಓದುವ ಅಂತರಕ್ಕೆ ಸಮೀಪವಾದ (ಸುಮಾರು 25 ಸೆಂಮೀ ಅಂತರ) ದೂರವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಸಮೀಪ ದೃಷ್ಟಿ ಎಂದು ಪರಿಗಣಿಸುತ್ತಾರೆ.[೭೧] ದೃಗ್ವಿಜ್ಞಾನದ ತತ್ವಗಳ ಆಧಾರದ ಮೇಲೆ ದೃಷ್ಟಿ ನ್ಯೂನತೆಗಳನ್ನು ವಿವರಿಸಬಹುದು. ವಯಸ್ಸಾದಂತೆ, ಮನುಷ್ಯನ ಕಣ್ಣಿನ ಮಸೂರವು ತನ್ನ ಶಕ್ತಿಯನ್ನು ಕಳೆದುಕೊಳ್ಳುತ್ತದೆ, ಅಲ್ಲದೆ ಸಮೀಪ ದೃಷ್ಟಿಯು ಕ್ಷೀಣಿಸುತ್ತಾ ಸಾಗುತ್ತದೆ. ಕಣ್ಣಿನ ಈ ಸ್ಠಿತಿಗೆ ದೂರದೃಷ್ಟಿ ದೋಷ ಅಥವಾ ಪ್ರೆಬ್ಯೊಪಿಯಾ ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಅಂತೆಯೇ, ಸಮೀಪ ದೃಷ್ಟಿ ದೋಷ ಅಥವಾ ಹ್ಯೆಪೆರೋಪಿಯಾ ದೋಷದಿಂದ ಬಳಲುತ್ತಿರುವ ವ್ಯಕ್ತಿಗಳು ಸಮೀಪದ ವಸ್ತುಗಳನ್ನು ದೃಷ್ಟೀಕರಿಸಲು ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ. ಏಕೆಂದರೆ, ಅವರ ಕಣ್ಣಿನ ಮಸೂರದ ನಾಭಿದೂರವು (ಫೋಕಲ್ ಲೆಂಥ್) ಸಾಕಷ್ಟು ತಗ್ಗುವುದಿಲ್ಲ. ದೂರದ ವಸ್ತುಗಳ ಮೇಲೆ ದೃಷ್ಟಿ ನೆಡಲು ನೆರವಾಗುವಂತೆ ಕಣ್ಣಿನ ಮಸೂರದ ನಾಭಿದೂರವನ್ನು ಹೆಚ್ಚು ಮಾದಲು ಸಾಧ್ಯವಾಗದ ವ್ಯಕ್ತಿಗಳು ಸಮೀಪದೃಷ್ಟಿ ದೋಷ ಅಥವಾ ಮಯೋಪಿಯಾದಿಂದ ಬಳಲುತ್ತಾರೆ. ಅಂಥವರು ಅನಂತ ದೂರದವರೆಗಿನ ದೂರ ಬಿಂದು ಅಥವಾ ದೃಷ್ಟಿ ಹೊಂದಿರುತ್ತಾರೆ. ವರ್ತುಲಾಕಾರದಲ್ಲಿ ಇರಬೇಕಾದ ಅಕ್ಷಿಪಟಲವು ಹೆಚ್ಚಾಗಿ ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ ಬಾಗಿದಾಕಾರದಲ್ಲಿ ಇರುವ ಸ್ಠಿತಿಗೆ ಅಸಮ ದೃಷ್ಟಿದೋಷ ಅಥವಾ ಅಸ್ಟಿಗ್ಮ್ಯಾಟಿಸಂ ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಈ ಅಸಮ ದೃಷ್ಟಿದೋಷವು ಅಕ್ಷಿಪಟಲದ ವಿವಿಧ ಭಾಗಗಳ ಮೇಲೆ ಲಂಬಾಕೃತಿಯಲ್ಲಿ ಚಾಚಿರುವ ವಸ್ತುಗಳಿಗಿಂತ ಸಮತಲಾಕೃತಿಯಲ್ಲಿ ಚಾಚಿರುವ ವಸ್ತುಗಳನ್ನು ದೃಷ್ಟೀಕರಿಸುಂತೆ ಮಾಡುತ್ತದೆ. ಇದರ ಪರಿಣಾಮವಾಗಿ ಅಸ್ಪಷ್ಟ ಚಿತ್ರ ಅಥವಾ ಬಿಂಬಗಳು ಕಣ್ಣಿಗೆ ಮೂಡುತ್ತವೆ.[೭೧]ಸರಿಪಡಿಸಿದ ಮಸೂರ ಬಳಸುವುದರಿಂದ ಈ ಎಲ್ಲಾ ನ್ಯೂನತೆಗಳನ್ನು ಸರಿಪಡಿಸಬಹುದು. ದೂರದೃಷ್ಟಿ ದೋಷ ಅಥವಾ ಪ್ರೆಬ್ಯೊಪಿಯಾ ಇರುವವರು ಪರಿಚ್ಢಿನ್ನ ಮಸೂರ (ಕನ್ವರ್ಜೆಂಟ್ ಲೆನ್ಸ್)ಬಳಸುವುದರಿಂದ, ಅದು ಕಣ್ಣಿನ ಸಮೀಪ ದೃಷ್ಟಿಗೆ ನೆರವಾಗುವ ಹೆಚ್ಚಿನ ಬಾಗುವಿಕೆ ಅಥವಾ ವಕ್ರತೆಯನ್ನು ಒದಗಿಸುತ್ತದೆ. ಸಮೀಪದೃಷ್ಟಿ ದೋಷ ಅಥವಾ ಮಯೋಪಿಯಾ ಇರುವವರು ಅಪಸರಣ ಮಸೂರ (ಡೈವರ್ಜಿಂಗ್ ಲೆನ್ಸ್) ಬಳಸುವುದರಿಂದ, ದೂರದೃಷ್ಟಿಯನ್ನು ಅನಂತ ದೂರದವರೆಗೆ ಹಾಯಿಸಲು ಅಗತ್ಯವಾದ ವಕ್ರತೆ (ಕರ್ವೇಚರ್ ) ಅಥವಾ ಬಾಗುವಿಕೆಯನ್ನು ಅದು ಒದಗಿಸುತ್ತದೆ. ಅಸಮ ದೃಷ್ಟಿದೋಷವನ್ನು ವರ್ತುಲ ಸ್ತಂಭಾಕೃತಿ ಮೇಲ್ಮೈ ಹೊಂದಿರುವ ಮಸೂರ ಬಳಸುವುದರಿಂದ ಸರಿಪಡಿಸಬಹುದು. ಏಕೆಂದರೆ ಈ ಮಸೂರಗಳಲ್ಲಿನ ವಕ್ರತೆಗಳು ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ ಬಲಶಾಲಿಯಾಗಿರುತ್ತವೆ ಮತ್ತು ಸಮಸ್ಥಿತಿ ಹೊಂದಿರದ ಅಕ್ಷಿಪಟಲವನ್ನು ಸರಿದೂಗಿಸುತ್ತವೆ.[೭೩] ಸರಿಪಡಿಸಿದ ಮಸೂರಗಳ ದೃಶ್ಯಗ್ರಾಹಿ ಅಥವಾ ಬೆಳಕಿನ ಶಕ್ತಿಯನ್ನು ಡಯಾಪ್ಟರ್ ನಿಂದ ಅಳೆಯಲಾಗುತ್ತದೆ. ಡಯಾಪ್ಟರ್ ನ ಅಳತೆಯು ಮೀಟರ್ ನಲ್ಲಿ ಅಳೆಯಲಾದ ನಾಭಿದೂರಕ್ಕೆ (ಫೋಕಲ್ ಲೆಂಥ್) ಪರಸ್ಪರ ಸಮನಾಗಿರುತ್ತದೆ. ಜೊತೆಗೆ ಧನಾತ್ಮಕ ನಾಭಿದೂರವು ಪರಿಚ್ಢಿನ್ನ ಮಸೂರಕ್ಕೆ ಮತ್ತು ಋಣಾತ್ಮಕ ನಾಭಿದೂರವು ಅಪಸರಣ ಮಸೂರಕ್ಕೆ ಸರಿಸಮಾನವಾಗಿರುತ್ತದೆ. ಅಸಮ ದೃಷ್ಟಿದೋಷವನ್ನು ಸರಿಪಡಿಸುವ ಮಸೂರಗಳಿಗೆ ಮೂರು ಸಂಖ್ಯೆಗಳನ್ನು ಕೊಡಲಾಗಿರುತ್ತದೆ. ವರ್ತುಲಾಕಾರದ ದೃಷ್ಟಿ ಶಕ್ತಿ ಹೊಂದಿರುವ ಮಸೂರಗಳಿಗೆ ಒಂದು ಸಂಖ್ಯೆ, ವರ್ತುಲ ಸ್ತಂಭಾಕೃತಿಯ ದೃಷ್ಟಿ ಶಕ್ತಿಗೆ ಮತ್ತೊಂದು ಸಂಖ್ಯೆ ಹಾಗೂ ಅಸಮ ದೃಷ್ಟಿದೋಷ ನೆಲೆಗೊಂಡಿರುವ ಕೋನಕ್ಕೆ ಇನ್ನೊಂದು ಸಂಖ್ಯೆಯನ್ನು ಕೊಡಲಾಗುತ್ತದೆ.[೭೩]
ದೃಶ್ಯ ಪರಿಣಾಮಗಳು[ಬದಲಾಯಿಸಿ]

ಯಾವುದೇ ವಸ್ತುವಿನ ನೈಜತೆ ಅಥವಾ ವಾಸ್ತವಿಕತೆಗೆ ವ್ಯತಿರಿಕ್ತವಾಗಿ ಗ್ರಹಿಸುವ ದೃಶ್ಯಗಳಿಗೆ ದೃಷ್ಟಿ ಭ್ರಾಂತಿ ಅಥವಾ ದೃಶ್ಯ ಭ್ರಾಂತಿ ಎನ್ನಲಾಗುತ್ತದೆ. ಕಣ್ಣು ಕಲೆಹಾಕುವ ಮಾಹಿತಿಯನ್ನು ಮೆದುಳು ಸಂಸ್ಕರಿಸುತ್ತದೆ ಹಾಗೂ ವಸ್ತುವಿನ ದೃಶ್ಯವು ಬದಲಾಗಿದೆ ಎಂಬ ಗ್ರಹಿಕೆಯನ್ನು ನೀಡುತ್ತದೆ. ವಸ್ತುಗಳು ಮತ್ತು ಅವುಗಳಿಂದ ಬದಲಾದ ಚಿತ್ರಗಳು ಮತ್ತು ಅವುಗಳ ಮೇಲಿನ ಭೌತಿಕ ಪರಿಣಾಮ ಸೇರಿದಂತೆ ಬೆಳಕಿನ ಶಾಸ್ತ್ರದ ವಿವಿಧ ಸಂಗತಿಗಳಿಂದ ದೃಷ್ಟಿ ಭ್ರಾಂತಿ ಉಂಟಾಗುತ್ತದೆ. ಕಣ್ಣು ಮತ್ತು ಮೆದುಳಿನ ವಿಪರೀತ ಪ್ರಚೋದನೆಯಿಂದ ಉಂಟಾಗುವ ಶಾರೀರಿಕ ಪರಿಣಾಮಗಳಿಂದಲೂ (ಉದಾಹರಣೆಗೆ ಪ್ರಕಾಶಮಾನತೆ, ವಕ್ರತೆ, ಬಣ್ಣ, ಚಲನೆ) ದೃಷ್ಟಿ ಭ್ರಾಂತಿ ಉಂಟಾಗುತ್ತದೆ. ಅಲ್ಲದೆ, ಗ್ರಹಣ ಭ್ರಾಂತಿ (ಕಾಗ್ನಿಟಿವ್ ಇಲ್ಲೂಷನ್)ಯ ಪರಿಣಾಮವಾಗಿ ಕಣ್ಣು ಮತ್ತು ಮೆದುಳು ಪ್ರಜ್ಞಾಹೀನ ಸ್ಥಿತಿಯ ನಿಷ್ಪಲ ಅನುಭವಿಸುತ್ತವೆ.[೭೪] ದೃಗ್ವಿಜ್ಞಾನ ತತ್ವಗಳ ದುರುಪಯೋಗ ಹಾಗೂ ತಿಳಿವಳಿಕೆ ಕೊರತೆಯಿಂದಲೂ ಕೆಲವೊಮ್ಮೆ ಗ್ರಹಣ ಭ್ರಾಂತಿಯ ಪರಿಣಾಮಗಳು ಉಂಟಾಗುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಪರಿಚ್ಢಿನ್ನ ಮತ್ತು ಅಪಸರಣ ಮಸೂರಗಳನ್ನು ಉಪಯೋಗಿಸಿ ದೂರವನ್ನು ದೃಷ್ಟಿಸಬಹುದು ಎಂಬುದನ್ನು ಅಮೆಸ್ ರೂಮ್, ಹೆರಿಂಗ್, ಮುಲ್ಲೆರ್-ಲೈರ್, ಒರ್ಬಿಸನ್, ಪಾಂಜೊ, ಸಾಂಡರ್ ಮತ್ತು ವುಂಟ್ ನ ಭ್ರಾಂತಿ ಸಿದ್ಧಾಂತಗಳು ಪ್ರತಿಪಾದಿಸಿವೆ. ಅಲ್ಲದೆ, ಈ ಸಿದ್ಧಾಂತಗಳನ್ನೇ ಎಲ್ಲರೂ ಅವಲಂಬಿಸಿದ್ದಾರೆ. ಇದೇ ರೀತಿ, ಸಮಾನಂತರ ಬೆಳಕಿನ ಕಿರಣಗಳು (ಅಥವಾ ಸಮಾನಂತರ ರೇಖೆಗಳ ಗುಂಪು) ಅನಂತ ದೂರದ ಅದೃಷ್ಯ ಬಿಂದುವಿನಲ್ಲಿ ಒಂದುಗೂಡಿದಂತೆ ಕಾಣುತ್ತವೆ. ಈ ಕಿರಣಗಳು ಎರಡು ಪರಿಮಾಣಗಳಿಂದ ಕಲಾತ್ಮಕ ರೀತಿಯಲ್ಲಿ ಚಿತ್ರಗಳನ್ನು ಪ್ರತಿಯಾಗಿ ಕೊಡುತ್ತವೆ ಎಂಬ ಸಿದ್ಧಾಂತದ ಮೇಲೂ ಎಲ್ಲರೂ ಅವಲಂಬಿತವಾಗಿದ್ದಾರೆ.[೭೫] ಈ ಸಿದ್ಧಾಂತವು ಹೆಸರಾಂತ "ಚಂದ್ರ ಭ್ರಾಂತಿ"ಗೂ ಅನ್ವಯವಾಗಿದೆ. ಚಂದ್ರ ಅದೇ ಕೋನಾಕೃತಿ ಹೊಂದಿದ್ದರೂ, ಶಿಖರ ಅಥವಾ ತುತ್ತತುದಿಗಿಂತ ಕ್ಷಿತಿಜದ ಸಮೀಪ ವಿಸ್ತ್ರತವಾಗಿ ಅಥವಾ ಬಹುದೊಡ್ಡದಾಗಿ ಕಾಣುತ್ತದೆ.[೭೬] ಟೊಲೆಮಿ ಎಬಾತ ಈ ಭ್ರಾಂತಿ ಸಿದ್ಧಾಂತವನ್ನು ಹಾಳು ಮಾಡಿದ. ಇದು ವಾಯುಮಂಡಲದ ವಕ್ರೀಭವನ ಎಂದು ತಪ್ಪಾಗಿ ತನ್ನ ಪ್ರಬಂಧ ಮತ್ತು ದೃಷ್ಟಿಶಾಸ್ತ್ರ ದಲ್ಲಿ ಪ್ರತಿಪಾದಿಸಿದ.[೬] ಇನ್ನೊಂದು ವಿಧಧ ದೃಷ್ಟಿ ಭ್ರಾಂತಿಯು ಇಲ್ಲದಿರುವ ಹಲವು ವಿಫಲ ನಮೂನೆಗಳನ್ನು ಬಳಸಿ ಮನಸ್ಸಿನಲ್ಲಿ ಸಮಸೂತ್ರ ಅಥವಾ ಅಸಮಸೂತ್ರಗಳನ್ನು ಮೂಡಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಕೆಫೆ ವಾಲ್, ಇರೆನ್ ಸ್ಟೀನ್, ಫ್ರೆಸರ್ ಸ್ಪೈರಲ್, ಹಾಗೆನ್ ಡಾರ್ಫ್ ಮತ್ತು ಝೋಲ್ ನರ್ ದೃಷ್ಟಿ ಭ್ರಾಂತಿಗಳು ಅವುಗಳಲ್ಲಿ ಕೆಲವು. ಉದಾಹರಣೆಗೆ ಕೆಫೆ ವಾಲ್, ಎಹ್ರೆಸ್ಟೀನ್, ಫ್ರೇಸರ್ ಸ್ಪೈರಲ್, ಪೋಗೆಂಡಾರ್ಫ್ ಮತ್ತು ಝೋಲ್ನರ್ ಇಲ್ಲೂಶನ್ಸ್. ಸಂಬಂಧಿಸಿದ, ಆದರೆ ಕಟ್ಟುನಿಟ್ಟಲ್ಲದ ದೃಷ್ಟಿ ಭ್ರಾಂತಿಗಳು, ಒಂದರ ಮೇಲೊಂದು ನಿರ್ದಿಷ್ಟ ರಚನೆಗಳಾಗಿ ಸಂಭವಿಸಿದ ನಮೂನೆಗಳಾಗಿವೆ. ಉದಾಹರಣೆಗೆ, ಜಾಲರಿ ಸ್ವರೂಪದ ಪಾರದರ್ಶಕ ಪೊರೆಯು ಆಕರವನ್ನು ರೂಪಿಸುವ ವಿಧಾನಕ್ಕೆ ಮೊಯಿರ್ ನಮೂನೆ ಎಂದು ಕರೆಯುತ್ತಾರೆ, ಒಂದರ ಮೇಲೊಂದರಂತಿರುವ ನಿರ್ದಿಷ್ಟ ಪಾರದರ್ಶಕ ನಮೂನೆಗಳು ಒಳಗೊಂಡಿರುವ ಸಮಾನಂತರ ಅಪಾರದರ್ಶಕ ರೇಖೆ ಅಥವಾ ವಕ್ರತೆಗಳು ರೇಖೆ ಮೊಯಿರ್ ನಮೂನೆಗಳನ್ನು ತಯಾರು ಮಾಡುತ್ತವೆ.[೭೭]
ದೃಷ್ಟಿ ಉಪಕರಣಗಳು[ಬದಲಾಯಿಸಿ]
ಏಕಮಸೂರದಿಂದ ಹಲವಾರು ಉಪಯೋಗಗಳಿವೆ. ಅವುಗಳಲ್ಲಿ ಛಾಯಾಗ್ರಹಣ ಮಸೂರಗಳು, ಪರಿಶೋಧಿಸಿದ ಮಸೂರಗಳು ಮತ್ತು ಭೂತ ಮಸೂರಗಳು ಪ್ರಮುಖವಾದವು. ಏಕದರ್ಪಣ ಅಥವಾ ಕನ್ನಡಿಯನ್ನು ಅಲಂಕಾರಿಕ ಪ್ರತಿಫಲಕ ಮತ್ತು ಅಪರೂಪದ ದೃಷ್ಟಿ ದರ್ಪಣವಾಗಿ ವಾಹನಗಳಲ್ಲಿ ಬಳಸುತ್ತಾರೆ. ಹಲವು ದರ್ಪಣ, ಪ್ರಿಸಂ ಮತ್ತು ಮಸೂರಗಳನ್ನು ಸೇರಿಸಿ ಉತ್ಪಾದಿಸುವ ಸಂಯುಕ್ತ ದೃಷ್ಟಿ ಉಪಕರಣಗಳನ್ನು ವಾಣಿಜ್ಯ ಉದ್ದೇಶಗಳಿಗೆ ಹೆಚ್ಚಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಎರಡು ಸಮತಲದ ಮಸೂರ ಅಳವಡಿಸಿ, ತಯಾರಿಸಲಾದ ಪರಿದರ್ಶಕ ಅಥವಾ ಪೆರಿಸ್ಕೋಪ್ ಉಪಕರಣವನ್ನು ರಕ್ಷಣಾತ್ಮಕ ಉದ್ದೇಶಗಳಿಗಾಗಿ ಬಳಸುತ್ತಾರೆ. ವಿಜ್ಞಾನದ ಅತಿಮುಖ್ಯ ಸಂಕೀರ್ಣ ದೃಷ್ಟಿ ಉಪಕರಣಗಳಾದ ಅತಿಸೂಕ್ಷ್ಮದರ್ಶಕ (ಮೈಕ್ರೋಸ್ಕೋಪ್) ಹಾಗೂ ದೂರದರ್ಶಕ (ಟೆಲಿಸ್ಕೋಪ್) ವನ್ನು ಡಚ್ ವಿಜ್ಞಾನಿಗಳು 16ನೇ ಶತಮಾನದಲ್ಲಿ ಕಂಡು ಹಿಡಿದರು.[೭೮]ಬಾಹ್ಯ ವಸ್ತುವಿನ ಮಸೂರ ಮತ್ತು ನೇತ್ರಕವನ್ನು ಮಾತ್ರ ಅಳವಡಿಸಿ, ಅತಿಸೂಕ್ಷ್ಮದರ್ಶಕವನ್ನು ಮೊದಲು ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾಯಿತು. ಬಾಹ್ಯ ವಸ್ತುವಿನ ಮಸೂರವು ಮೂಲಭೂತವಾಗಿ ಭೂತಗಾಜು. ಇದನ್ನು ಅತಿಸಣ್ಣ ನಾಭಿದೂರದೊಂದಿಗೆ ವಿನ್ಯಾಸಪಡಿಸಲಾಗಿದೆ, ಆದರೆ ನೇತ್ರಕವು ಸಹಜವಾಗಿ ದೀರ್ಘ ನಾಭಿದೂರ ಹೊಂದಿರುತ್ತದೆ. ಸಮೀಪ ವಸ್ತುಗಳ ಭೂತ ಚಿತ್ರಗಳನ್ನು ಉತ್ಪಾದಿಸುವ ಪರಿಣಾಮಗಳನ್ನು ಇದು ಹೊಂದಿರುತ್ತದೆ. ಭೂತಚಿತ್ರಗಳು ಮಂಕಾಗಿರುವುದರಿಂದ ಸಾಮಾನ್ಯವಾಗಿ, ಬೆಳಕಿನ ಪ್ರಕಾಶಮಾನಕ್ಕೆ ಹೆಚ್ಚುವರಿ ಮೂಲವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ವಸ್ತುವಿನ ಮೇಲ್ಮೈನ ಬಹುಭಾಗದ ಮೇಲೆ ಬೆಳಕಿನ ಕಿರಣಗಳು ಹರಡಿಕೊಳ್ಳುವುದರಿಂದ ಹಾಗೂ ಬೆಳಕಿನ ಶಕ್ತಿಯ ಸಂರಕ್ಷಣೆಯಿಂದಾಗಿ ಭೂತಚಿತ್ರಗಳು ಮಂಕಾಗಿ ಕಾಣುತ್ತವೆ. ಸಂಯುಕ್ತ ಅತಿಸೂಕ್ಷ್ಮದರ್ಶಕ ಎಂದು ಕರೆಯಲಾಗುವ ಆಧುನಿಕ ಅತಿಸೂಕ್ಷ್ಮದರ್ಶಕವು ಹಲವು ಮಸೂರಗಳನ್ನು ಹೊಂದಿದೆ(ನಾಲ್ಕು ವಿಧದ ಮಸೂರ). ಈ ಮಸೂರಗಳು ಚಿತ್ರಗಳ ಗುಣಮಟ್ಟ ಸ್ಥಿರತೆ ಸೇರಿದಂತೆ ದೃಗ್ಗೋಚರದ ಎಲ್ಲಾ ಕಾರ್ಯಗಳನ್ನು ನೆರವೇರಿಸುತ್ತವೆ.[೭೮] ತುಸು ಭಿನ್ನವಾದ ತುಲನಾತ್ಮಕ ಅತಿಸೂಕ್ಷ್ಮದರ್ಶಕವು ಚಿತ್ರಗಳನ್ನು ಒಂದರ ಪಕ್ಕ ಒಂದರಂತೆ ನೋಡುತ್ತದೆ. ಅಲ್ಲದೆ, ಇದು ಸ್ಟೀರಿಯೋಸ್ಕೋಪಿಕ್ ಬೈನಾಕ್ಯುಲರ್ ಚಿತ್ರಗಳನ್ನು ಮೂರು ಪರಿಮಾಣಗಳಲ್ಲಿ ಕಾಣುವಂತೆ ಮಾದುತ್ತದೆ.[೭೯] ವಕ್ರೀಭವನ ದೂರದರ್ಶಕ ಎಂದು ಕರೆಯಲಾಗುವ ಮೊಟ್ಟಮೊದಲ ದೂರದರ್ಶಕ ಯಂತ್ರವನ್ನು ಒಂದು ಬಾಹ್ಯ ಮಸೂರ ಮತ್ತು ನೇತ್ರಕ ಅಳವಡಿಸಿ, ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾಯಿತು. ಅತಿಸೂಕ್ಷ್ಮದರ್ಶಕದ ಅಭಿವೃದ್ಧಿ ನಿಯಮಗಳಿಗೆ ವ್ಯತಿರಿಕ್ತ ಎಂಬಂತೆ, ದೂರದರ್ಶಕದ ಬಾಹ್ಯ ಮಸೂರವನ್ನು ದೀರ್ಘ ನಾಭಿದೂರ (ಫೋಕಲ್ ಲೆಂಥ್ )ದೊಂದಿಗೆ ವಿನ್ಯಾಸಗೊಳಿಸಲಾಗಿದೆ. ಬೆಳಕಿನ ಉನ್ಮಾದ ಅಥವಾ ಏರಿಳಿತಗಳನ್ನು ನಿವಾರಿಸಲು ಈ ರೀತಿ ಮಾಡಲಾಗಿದೆ. ದೂರದರ್ಶಕದ ಬಾಹ್ಯ ಮಸೂರವು ತನ್ನ ನಾಭಿ ಬಿಂದುವಿನಲ್ಲಿ ದೂರದ ವಸ್ತು ಅಥವಾ ಚಿತ್ರವನ್ನು ಕೇಂದ್ರೀಕರಿಸುತ್ತದೆ. ಸಣ್ಣ ನಾಭಿದೂರ ಹೊಂದಿರುವ ನೇತ್ರಕದ ನಾಭಿ ಬಿಂದು ಮತ್ತು ಬಾಹ್ಯ ಮಸೂರದ ನಾಭಿ ಬಿಂದುವನ್ನು ಸರಿಹೊಂದಿಸಲಾಗುತ್ತದೆ. ಬೆಳಕಿನ ವರ್ಧನೆಯೇ ದೂರದರ್ಶಕ ಯಂತ್ರದ ಮುಖ್ಯ ಗುರಿಯಲ್ಲ. ಆದರೆ, ಬಾಹ್ಯ ಮಸೂರದ ಮೂಲಕ ಬೆಳಕಿನ ಸಂಗ್ರಹ ಮಾಡುವುದೇ ಇದರ ಪ್ರಮುಖ ಉದ್ದೇಶ. ಹಾಗಾಗಿ, ಬಾಹ್ಯ ಮಸೂರಗಳು ಸೂಚಿಸುವ ಡಯಾಮೀಟರ್ ಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ದೂರದರ್ಶಕಗಳು ಪರಿಗಣಿಸುತ್ತವೆ. ಆದರೆ, ನೇತ್ರಕದ ಗುಂಡಿ ಒತ್ತಿದ ತಕ್ಷಣ ಬದಲಾಗುವ ಬೆಳಕಿನ ವರ್ಧನೆಯನ್ನು ಅದು ಅವಲಂಬಿಸುವುದಿಲ್ಲ. ಬಾಹ್ಯ ಮಸೂರದ ನಾಭಿದೂರವನ್ನು ನೇತ್ರಕದ ನಾಭಿದೂರದಿಂದ ವರ್ಗೀಕರಿಸಿದಾಗ ಬರುವ ಉಪಲಬ್ದವು ದೂರದರ್ಶಕದ ಬೆಳಕಿನ ವರ್ಧನೆಗೆ ಸಮನಾದ ಕಾರಣ, ಪುಟ್ಟ ನಾಭಿ ದೂರದ ನೇತ್ರಕವು ಹೆಚ್ಚಿನ ಬೆಳಕನ್ನು ವರ್ಧಿಸುತ್ತದೆ.[೭೮] ದೊಡ್ದ ಕನ್ನಡಿಗಳಿಗಿಂತ ದೊಡ್ಡ ಮಸೂರಗಳ ತಯಾರಿಕೆಯು ಕಷ್ಟಕರ. ಬಹುಪಾಲು ಆಧುನಿಕ ದೂರದರ್ಶಕಗಳು ಪ್ರತಿಫಲಕ ದೂರದರ್ಶಕ ಗಳಾಗಿವೆ. ಅಂದರೆ, ಈ ದೂರದರ್ಶಕಗಳು ಬಾಹ್ಯ ಮಸೂರಗಳಿಗಿಂತ ಪ್ರಾಥಮಿಕ ದರ್ಪಣಗಳನ್ನು ಬಳಸುತ್ತವೆ. ಒಂದೇ ರೀತಿಯ ಸಾಮಾನ್ಯ ದೃಗ್ವಿಜ್ಞಾನ ಪರಿಗಣನೆಗಳು ಪ್ರತಿಫಲನ ದೂರದರ್ಶಕ ಮತ್ತು ವಕ್ರೀಭವನ ದೂರದರ್ಶಕಗಳಿಗೆ ಅನ್ವಯಿಸುತ್ತದೆ. ಪ್ರಾಥಮಿಕ ಕನ್ನಡಿ ವಿಶಾಲವಿದ್ದಷ್ಟೂ, ಹೆಚ್ಚಿನ ಪ್ರಮಾಣದಲ್ಲಿ ಬೆಳಕು ಸಂಗ್ರಹವಾಗುತ್ತದೆ, ಮತ್ತು ಬೆಳಕಿನ ವರ್ಧನೆಯು ಪ್ರಾಥಮಿಕ ಕನ್ನಡಿಯ ನಾಭಿದೂರವನ್ನು ನೇತ್ರಕದ ನಾಭಿದೂರದಿಂದ ವರ್ಗೀಕರಿಸಿದಾಗ ಬರುವ ಉಪಲಬ್ದಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ. ವೃತ್ತಿಪರ ದೂರದರ್ಶಕಗಳು ಸಾಮಾನ್ಯವಾಗಿ ನೇತ್ರಕಗಳನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ. ಅದರ ಬದಲಿಗೆ ನಾಭಿ ಬಿಂದುವಿನಲ್ಲಿ ವಿದ್ಯುತ್ ಪೂರಣ ಉಪಕರಣವೊಂದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.[೭೮]
ಛಾಯಾಗ್ರಹಣ[ಬದಲಾಯಿಸಿ]


ಛಾಯಾಗ್ರಹಣ ದೃಗ್ವಿಜ್ಞಾನವು ಮಸೂರ ಮತ್ತು ಮಾಧ್ಯಮವನ್ನು ಒಳಗೊಂಡಿದೆ. ಅದರಲ್ಲಿ ವಿದ್ಯುತ್ ಕಾಂತೀಯ ವಿಕಿರಣಗಳನ್ನು ದಾಖಲಿಸಲಾಗುತ್ತದೆ. ಮಸೂರ ಮತ್ತು ಮಾಧ್ಯಮವು ಫಲಕ, ಪೊರೆ ಅಥವಾ ವಿದ್ಯುತ್ ಪೂರಣ ಸಾಧನವಾಗಿರಬಹುದು. ಛಾಯಾಗ್ರಾಹಕರು, ಕ್ಯಾಮೆರಾ ಮತ್ತು ಕ್ದ್ಲಿಕ್ಕಿಸಿದ ಚಿತ್ರದ ಪರಸ್ಪರ ಸಂಬದ್ಧತೆ ಪರಿಗಣಿಸಲು ಯಾವಾಗಲೂ ಈ ಕೆಳಗಿನ ಸಮ್ಮೀಕರಣವನ್ನು ಅರಿಯುವುದು ಸೂಕ್ತ.
- ತೆರೆತ (ಎಕ್ಸ್ ಪೋಷರ್) ∝ ದ್ಯುತಿರಂಧ್ರ (ಅಪರ್ಚರ್ ಏರಿಯಾ) ∝ ತೆರೆತ ಸಮಯ (ಎಕ್ಸ್ ಪೋಷರ್ ಟೈಂ) ∝ ದೃಶ್ಯ ಪ್ರಕಾಶಮಾನತೆ (ಸೀನ್ ಲೂಮಿನನ್ಚ್).[೮೦]
ಇದನ್ನೇ ಬೇರೆ ಮಾತುಗಳಲ್ಲಿ ಹೇಳುವುದಾದರೆ, (ಉತ್ತಮ ತೇಜಕೇಂದ್ರಧಾರಣ ನೀಡುವ) ರಂಧ್ರವು ಸಣ್ಣದಾದಷ್ಟೂ , ಕಡಿಮೆ ಬೆಳಕು ಒಳಗೆ ಬರುತ್ತದೆ, ಹಾಗಾಗಿ ಸಮಯದ ವ್ಯಾಪ್ತಿಯನ್ನು ಹೆಚ್ಚುಗೊಳಿಸಬೇಕು (ಇದರಿಂದ ಚಲನೆ ಉಂಟಾದರೆ ಮಂಜುಮಂಜಾಗಿ ಕಾಣುವುದಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ). ಪರಸ್ಪರ ಸಂಬದ್ಧತೆಯ ನಿಯಮದ ಉಪಯೋಗಕ್ಕೆ ಒಂದು ಉದಾಹರಣೆಯೆಂದರೆ ಸನ್ನಿ 16 ನಿಯಮ, ಇದು, ಬೆಳಗಿನ ಸಮಯದಲ್ಲಿ ಸರಿಯಾದ ಎಕ್ಸ್ಪೋಷರ್ (ಬೆಳಕೊಡ್ಡು ಸಮಯ)ಅನ್ನು ಅಂದಾಜು ಮಾಡಲು ಬೇಕಾದ ಸೆಟ್ಟಿಂಗ್ಗಳ ಒಂದು ಕರಡು ಅಂದಾಜನ್ನು ನೀಡುತ್ತದೆ.[೮೧]
ಒಂದು ಕ್ಯಾಮರಾದ ರಂಧ್ರವನ್ನು f-ಸಂಖ್ಯೆ ಅಥವಾ f-ಸ್ಟಾಪ್, ಎಂದು ಕರೆಯುವ f/#, ಸಾಮಾನ್ಯವಾಗಿ ಎಂದು ಗುರುತಿಸುವ ಘಟಕರಹಿತ ಸಂಖ್ಯೆಯಿಂದ ಅಳೆಯಲಾಗುತ್ತದೆ. ಅದನ್ನು ಹೀಗೆ ಕೊಡಲಾಗುತ್ತದೆ -
ಇಲ್ಲಿ ಎನ್ನುವುದು ತೇಜಕೇಂದ್ರ ವ್ಯಾಪ್ತಿ, ಮತ್ತು ಎನ್ನುವುದು ಪ್ರವೇಶ ಬಿಂದು (ಎಂಟ್ರೆನ್ಸ್ ಪ್ಯೂಪಿಲ್)ವಿನ ವ್ಯಾಸ. ರೂಢಿಯಿಂದ, "f/#" ಅನ್ನು ಏಕಚಿಹ್ನೆ ಎಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ, ಮತ್ತು , ಸಂಖ್ಯಾ ಚಿಹ್ನೆಯ ಜಾಗದಲ್ಲಿ f/#ನ ನಿರ್ದಿಷ್ಟ ಮೌಲ್ಯಗಳನ್ನು ಬರೆಯಲಾಗುತ್ತದೆ. f-ಸ್ಟಾಪ್ಅನ್ನು ದೊಡ್ಡದು ಮಾಡುವ ಎರಡು ವಿಧಾನಗಳೆಂದರೆ, ಒಂದು ಪ್ರವೇಶ ಬಿಂದುವಿನ ವ್ಯಾಸವನ್ನು ಚಿಕ್ಕದು ಮಾಡುವುದು ಅಥವಾ ದೊಡ್ಡ ತೇಜಕೇಂದ್ರ ವ್ಯಾಪ್ತಿಗೆ ಬದಲಾಯಿಸುವುದು (ಜೂಮ್ ಮಸೂರಗಳ ಸಂದರ್ಭದಲ್ಲಿ, ಕೇವಲ ಮಸೂರಗಳನ್ನು ಕ್ರಮಪಡಿಸುವುದರಿಂದ ಇದನ್ನು ಮಾಡಬಹುದು). ದೊಡ್ಡ f-ಸಂಖ್ಯೆಗಳು ದೊಡ್ಡ ದೃಶ್ಯಗಹನತೆಯನ್ನೂ ಹೊಂದಿರುತ್ತದೆ. ಏಕೆಂದರೆ , ಅಂತರ ಎಷ್ಟೇ ಇದ್ದರೂ ಎಲ್ಲಾ ಬಿಂಬಗಳನ್ನು ಸರಿಯಾಗಿ ಕೇಂದ್ರಮಾಡಬಲ್ಲ ಬಿಂದುರಂಧ್ರ ಕ್ಯಾಮರಾಕ್ಕೆ ಹತ್ತಿರವಾದ ಮಿತಿಯನ್ನು ಮಸೂರಗಳು ಮುಟ್ಟುತ್ತಿರುತ್ತದೆ. ಆದರೆ, ತುಂಬಾ ದೀರ್ಘವಾದ ಬೆಳಕೊಡ್ಡು ಸಮಯ ಬೇಕಾಗುತ್ತದೆ.[೮೨] ಸಾಮಾನ್ಯವಾಗಿ, ಮಸೂರಗಳನ್ನು ಆಯ್ಕೆ ಮಾಡುವ ಸಂದರ್ಭದಲ್ಲಿ, ಕ್ಯಾಮಾರಗಳ ನಿರ್ದಿಷ್ಟತೆಗಳಿಗನುಗುಣವಾಗಿ ಮಸೂರಗಳು ಎಷ್ಟು ದೃಶ್ಯವ್ಯಾಪ್ತಿಯನ್ನು ಕೊಡಬಹುದು ಎಂಬುದನ್ನು ಛಾಯಾಗ್ರಾಹಕರು ಪರಿಗಣಿಸುತ್ತಾರೆ. ಚಿತ್ರದ ಕರ್ಣೀಯ ಉದ್ದದಿಂದ ನಿರ್ಧಿಷ್ಟಪಡಿಸಿರುವ ಕೊಟ್ಟಿರುವ ಒಂದು ಫಿಲ್ಮ್ ಅಥವಾ ಗ್ರಾಹಕದ ಗಾತ್ರಕ್ಕೆ ಮಸೂರಗಳನ್ನು ಹೀಗೆ ವಿಂಗಡಿಸಬಹುದು
- ಸಾಮಾನ್ಯ ಮಸೂರಗಳು: ವ್ಯಾಸದ ನೋಟದ ಕೋನವು ಸುಮಾರು 50°, ತೇಜಕೇಂದ್ರ ವ್ಯಾಪ್ತಿಯು ಸರಾಸರಿ ವ್ಯಾಸಕ್ಕೆ ಸಮನಾಗಿದ್ದಾಗ ಈ ಕೋನವು ಉಂಟಾಗುತ್ತದೆ.[೮೩]
- ದೊಡ್ಡ ಮಸೂರಗಳು: ನೋಟದ ಕೋನವು 25°ಗಿಂತ ಕಡಿಮೆ ಮತ್ತು ತೇಜಕೇಂದ್ರ ವ್ಯಾಪ್ತಿಯು ಸಾಮಾನ್ಯಕ್ಕಿಂತ ದೊಡ್ಡದು. ಈ ಮಸೂರಗಳನ್ನು ಕ್ಲೋಸ್-ಅಪ್ಗಳಿಗೆ ಅಂದರೆ ವಸ್ತುವಿನಷ್ಟೇ ದೊಡ್ಡದಾದ ಬಿಂಬಗಳಿಗೆ ಉಪಯೋಗಿಸಲಾಗುತ್ತದೆ. ಇವು ಸಾಮಾನ್ಯವಾಗಿ ಚಪ್ಪಟೆಯಾದ ಕ್ಷೇತ್ರವನ್ನೂ ಹೊಂದಿರುತ್ತದೆ, ಅಂದರೆ ಅಧೀನದ ಪ್ಲೇನ್ ಫಿಲ್ಮ್ ಪ್ಲೇನ್ಗೆ ಸಮಾನಾಂತರವಾಗಿರುತ್ತದೆ.[೮೪]
- ವಿಶಾಲ-ಕೋನದ ಮಸೂರಗಳು: ನೋಟದ ಕೋನವು 60°ಗೂ ಕಡಿಮೆಯಿದೆ ಮತ್ತು ತೇಜಕೇಂದ್ರ ವ್ಯಾಪ್ತಿಯು ಸಾಮಾನ್ಯಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ.[೮೫]
- ಟೆಲಿಫೋಟೋ ಮಸೂರಗಳು ಅಥವಾ ಲಂಬ-ತೇಜಕೇಂದ್ರ ಮಸೂರಗಳು: ನೋಟದ ಕೋನವು ಕಿರಿದಾಗಿರುತ್ತದೆ ಮತ್ತು ತೇಜಕೇಂದ್ರದ ವ್ಯಾಪ್ತಿಯು ಸಾಮಾನ್ಯಕ್ಕಿಂತ ಉದ್ದವಿರುತ್ತದೆ. ಲಂಬ-ತೇಜಕೇಂದ್ರ ಮಸೂರಗಳು ಮತ್ತು ಒಂದು ನಿಜವಾದ ಟೆಲಿಫೋಟೋ ಮಸೂರಗಳ ನಡುವೆ ಕೆಲವು ಸಾರಿ ವ್ಯತ್ಯಾಸ ತೋರಿಸಲಾಗುತ್ತದೆ: ತನ್ನ ತೇಜಕೇಂದ್ರದ ವ್ಯಾಪ್ತಿಗಿಂತ ಭೌತಿಕವಾಗಿ ಚಿಕ್ಕದಾಗಿರುವುದಕ್ಕಾಗಿ ಟೆಲಿಫೋಟೋ ಮಸೂರಗಳು ಟೆಲಿಫೋಟೋ ಗುಂಪು ಗಳನ್ನು ಬಳಸುತ್ತದೆ.[೮೬] ಉಪಯೋಗಿಸುವ ಮಾಧ್ಯಮವು ಬೆಳಕಿಗೆ ಎಷ್ಟು ಶೀಘ್ರಗ್ರಾಹಿ ಆಗಿರುತ್ತದೆ ಎಂಬುದರ ಮೇಲೆ ಬೇಕಾದ ಬೆಳಕೊಡ್ಡುವ ಸಮಯದ ಸರಿಯಾದ ಮೌಲ್ಯವು ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ (ಫಿಲ್ಮ್ ವೇಗದಲ್ಲಿ ಅಳತೆಮಾಡಿದಂತೆ, ಅಥವಾ, ಡಿಜಿಟಲ್ ಮಾಧ್ಯಮಗಳಿಗೆ ಕ್ವಾಂಟಮ್ ಕಾರ್ಯಕ್ಷಮತೆಯ ಮೂಲಕ).[೮೭] ಪ್ರಾರಂಭಿಕ ಛಾಯಾಗ್ರಹಣದಲ್ಲಿ ಬೆಳಕಿಗೆ ಕಡಿಮೆ ಶೀಘ್ರಗ್ರಾಹಿಯಾಗಿದ್ದ ಮಾಧ್ಯಮಗಳನ್ನು ಬಳಸಲಾಗುತ್ತಿತ್ತು, ಆದ್ದರಿಂದ ಬಹಳ ಪ್ರಜ್ವಲ ಚಿತ್ರಗಳಿಗೂ ಕೂಡ ಬೆಳಕೊಡ್ಡುವ ಸಮಯವು ದೀರ್ಘವಾಗಿರಬೇಕಾಗಿತ್ತು. ತಂತ್ರಜ್ಞಾನ ಮುಂದುವರೆದ ಹಾಗೇ ಫಿಲ್ಮ್ ಕ್ಯಾಮೆರಾಗಳ ಮತ್ತು ಡಿಜಿಟಲ್ ಕ್ಯಾಮೆರಾಗಳ ಶೀಘ್ರಗ್ರಾಹಿತ್ವವೂ ಸುಧಾರಣೆಯಾಗಿದೆ.[೮೮] ಭೌತಿಕ ಮತ್ತು ರೇಖಾಗಣಿತದ ದೃಗ್ವಿಜ್ಞಾನದ ಇತರ ಫಲಿತಾಂಶಗಳು ಕ್ಯಾಮೆರಾ ದೃಗ್ವಿಜ್ಞಾನದ ಉಪಯೋಗಕ್ಕೆ ಬರುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ರೇಲ್ಹೈ ಮಾನದಂಡವು ಹೇಳುವಂತೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಕ್ಯಾಮೆರಾದ ಗರಿಷ್ಠ ರೆಸಲ್ಯೂಷನ್ ಸಾಮರ್ಥ್ಯವನ್ನು ಬಿಂದು ಗಾತ್ರಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಅಪಸರಣದ ಮಿತಿಯಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.[೮೯]
ವಾತಾವರಣೀಯ ದೃಗ್ವಿಜ್ಞಾನ[ಬದಲಾಯಿಸಿ]

ವಾತಾವರಣದ ಅನನ್ಯ ದೃಗ್ವಿಜ್ಞಾನ ಗುಣಗಳು ಹಲವು ಬಗೆಯ ಆಕರ್ಷಣೀಯ ಆಪ್ಟಿಕಲ್ ಘಟನೆಗಳಿಗೆ ಕಾರಣವಾಗುತ್ತದೆ. ಆಕಾಶದ ನೀಲಿ ಬಣ್ಣವು ರೇಲ್ಹೈ ವಿಕಿರಣದ ನೇರ ಫಲಿತಾಂಶ, ಅದು ಅಧಿಕ ಪುನಾರಾವರ್ತನವಿರುವ (ನೀಲಿ) ಬೆಳಕನ್ನು ವೀಕ್ಷಕನ ನೋಟದ ಕ್ಷೇತ್ರಕ್ಕೆ ವಾಪಾಸು ಕಳುಹಿಸುತ್ತದೆ. ಏಕೆಂದರೆ ನೀಲಿ ಬೆಳಕು ಕೆಂಪು ಬೆಳಕಿಗಿಂತ ಸುಲಭವಾಗಿ ವಿಕಿರಣಗೊಳ್ಳುತ್ತದೆ, ಸೂರ್ಯವು ದಪ್ಪ ವಾತಾವರಣದ ಮೂಲಕ ನೋಡಿದಾಗ ಕೆಂಪು ಬಣ್ಣ ಪಡೆದಿರುತ್ತದೆ, ಸೂರ್ಯೋದಯ ಅಥವಾ ಸೂರ್ಯಾಸ್ತದಲ್ಲಾಗುವಂತೆ. ಆಕಾಶದಲ್ಲಿರುವ ಇತರ ಕಣಗಳು ಬೇರೆ ಬೇರೆ ಕೋನಗಳಲ್ಲಿ ಬೇರೆ ಬೇರೆ ಬಣ್ಣಗಳನ್ನು ವಿಕಿರಣಗೊಳಿಸಬಹುದು, ಇದರಿಂದ ಅರುಣೋದಯ ಮತ್ತು ಮುಸ್ಸಂಜೆಯ ಸಮಯಗಳಲ್ಲಿ ಬಣ್ಣಬಣ್ಣದ ಹೊಳೆಯುವ ಆಕಾಶವು ಸೃಷ್ಟಿಯಾಗುತ್ತದೆ. ಮಂಜಿನ ಹರಳುಗಳು ಮತ್ತು ಇತರ ಕಣಗಳು ವಾತಾವರಣದಲ್ಲಿ ವಿಕಿರಣಗೊಳ್ಳುವುದರಿಂದ ಪ್ರಭಾವಳಿ, ಸಂಜೆಯ ಬೆಳಕು, ಕಿರೀಟಗಳು, ಸೂರ್ಯನ ಕಿರಣಗಳು, ಮತ್ತು ಮಿಥ್ಯಾ ಸೂರ್ಯಗಳು ಸಂಭವಿಸುತ್ತವೆ. ಈ ಘಟನೆಗಳಲ್ಲಿನ ವ್ಯತ್ಯಯಕ್ಕೆ ಕಾರಣವೆಂದರೆ ಕಣಗಳ ವಿವಿಧ ಗಾತ್ರ ಮತ್ತು ಜ್ಯಾಮಿತಿಗಳು.[೯೦] ಮರಿಚೀಕೆಗಳು ವಾತಾವರಣದ ಮೂಲಕ ಬೆಳಕಿನ ವಕ್ರೀಭವನದಿಂದ ಉಂಟಾಗುವ ಮತ್ತೊಂದು ರೀತಿಯ ಆಪ್ಟಿಕಲ್ ಘಟನೆ. ಇದಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಮತ್ತೊಂದು ಆಪ್ಟಿಕಲ್ ಘಟನೆಯು ನೊವಯ ಜೆಮ್ಲ್ಯ ಪರಿಣಾಮವನ್ನು ಒಳಗೊಂಡಿದೆ, ಇಲ್ಲಿ ಸೂರ್ಯನು ಊಹಿಸಿದ್ದಕ್ಕಿಂತ ಮೊದಲೇ ಕೊಂಕಾದ ಆಕಾರದಲ್ಲಿ ಹುಟ್ಟುತ್ತಿದ್ದಾನೇನೋ ಎನಿಸುತ್ತದೆ. ತಾಪಮಾನ ತಿರುಗು-ಮುರುಗಿನಿಂದ ಫ್ಯಾಟಾ ಮೋರ್ಗಾನಾ ಎಂದು ಕರೆಯಲಾಗುವ ಒಂದು ಆಕರ್ಷಕ ವಕ್ರೀಭವನ ಸಂಭವಿಸುತ್ತದೆ. ಆಗ ಕ್ಷಿತಿಜದಲ್ಲಿರುವ ಅಥವಾ ಕ್ಷಿತಿಜದ ಆಚೆಗೂ ಇರುವ ವಸ್ತುಗಳು ಉದಾಹರಣೆಗೆ ದ್ವೀಪಗಳು, ಕಮ್ಮರಿಗಳು, ಹಡಗುಗಳು ಅಥವಾ ಮಂಜುಗಡ್ಡೆಗಳು, ಉದ್ದವಾದಂತೆ ಮತ್ತು ಎತ್ತಿದಂತೆ ಕಾಣುತ್ತವೆ, "ಕಿನ್ನರ ಕತೆಯ ಕೋಟೆಗಳ" ತರಹ.[೯೧] ಕಾಮನಬಿಲ್ಲುಗಳು ಹಲವು ಆಪ್ಟಿಕಲ್ ಪರಿಣಾಮಗಳು ಜತೆಗೂಡಿ ಆಗುವ ಘಟನೆ: ಪೂರ್ಣ ಆಂತರಿಕ ವಕ್ರೀಭವನ ಮತ್ತು ಮಳೆಹನಿಗಳಾಗಿ ಬೆಳಕಿನ ಚದುರಿಕೆ. ಒಂದು ಮಳೆಹನಿಗಳ ವ್ಯೂಹದ ಹಿಂದೆ ಆಗುವ ಒಂದೇ ಒಂದು ಪ್ರತಿಬಿಂಬವು ಆಕಾಶದಲ್ಲಿ 40°ಯಿಂದ 42°ಕೋನ ಇರುವ, ಹೊರಭಾಗದಲ್ಲಿ ಕೆಂಪು ಇರುವ ಒಂದು ಸುಸಂಗತ ಕಾಮನಬಿಲ್ಲನ್ನು ನಿರ್ಮಿಸುತ್ತದೆ. 50.5°ನಿಂದ 54°ನ ಕೋನವಿರುವ ಎರಡು ಆಂತರಿಕ ಪ್ರತಿಬಿಂಬಗಳಾದರೆ ಹೊರಭಾಗದಲ್ಲಿ ನೇರಳೆ ಬಣ್ಣ ಇರುವ ಇಮ್ಮಡಿ ಕಾಮನಬಿಲ್ಲುಗಳು ಮೂಡುತ್ತವೆ. ಏಕೆಂದರೆ ಕಾಮನಬಿಲ್ಲುಗಳನ್ನು ಅವುಗಳ ಮಧ್ಯದಿಂದ 180° ದೂರದಲ್ಲಿ ಸೂರ್ಯನೊಂದಿಗೆ ನೋಡಬೇಕು, ಕ್ಷಿತಿಜಕ್ಕೆ ಸೂರ್ಯನು ಹತ್ತಿರವಾದಷ್ಟೂ ಕಾಮನಬಿಲ್ಲುಗಳು ಪ್ರಮುಖವಾಗಿ ಕಾಣಿಸುತ್ತವೆ.[೫೯]
ಇವನ್ನೂ ಗಮನಿಸಿ[ಬದಲಾಯಿಸಿ]
Page ಮಾಡ್ಯೂಲ್:Portal/styles.css has no content.
ಆಕರಗಳು[ಬದಲಾಯಿಸಿ]
- ↑ ೧.೦ ೧.೧ McGraw-Hill Encyclopedia of Science and Technology (5th ed.). McGraw-Hill. 1993.
- ↑ "World's oldest telescope?". BBC News. 1999-07-01. Retrieved 2010-01-03.
- ↑ T. F. Hoad (1996). The Concise Oxford Dictionary of English Etymology.
- ↑ T. L. Heath (2003). A manual of greek mathematics. Courier Dover Publications. pp. 181–182. ISBN 0486432319.
- ↑ Euclid (1999). Elaheh Kheirandish (ed.). The Arabic version of Euclid's optics = Kitāb Uqlīdis fī ikhtilāf al-manāẓir. New York: Springer. ISBN 0387985239.
- ↑ ೬.೦ ೬.೧ Ptolemy (1996). A. Mark Smith (ed.). Ptolemy's theory of visual perception: an English translation of the Optics with introduction and commentary. DIANE Publishing. ISBN 0871698625.
- ↑ ಡಿ. ಸಿ. ಲಿಂಡ್ಬರ್ಗ್, ಥೀಯರೀಸ್ ಆಫ್ ವರ್ಷನ್ ಫ್ರಾಮ್ ಆಲ್-ಕಿಂದಿ ಟು ಕೆಪ್ಲರ್ ನಲ್ಲಿ ಉಲ್ಲೇಖಿತ, (ಚಿಕಾಗೋ: ಚಿಕಾಗೋ ವಿಶ್ವವಿದ್ಯಾನಿಲಯ. Pr., 1976), ಪು. 19.
- ↑ D. C. Lindberg (1971). "Alkindi's Critique of Euclid's Theory of Vision". Isis. 62: 469. doi:10.1086/350790.
- ↑ R. Rashed (1990). "A Pioneer in Anaclastics: Ibn Sahl on Burning Mirrors and Lenses". Isis. 81: 464.
- ↑ A. I. Sabra and J. P. Hogendijk (2003). The Enterprise of Science in Islam: New Perspectives. MIT Press. pp. 85–118. ISBN 0262194821. OCLC 237875424 50252039.
{{cite book}}: Check|oclc=value (help) - ↑ G. Hatfield (1996). "Was the Scientific Revolution Really a Revolution in Science?". In F. J. Ragep, P. Sally, S. J. Livesey (ed.). Tradition, Transmission, Transformation: Proceedings of Two Conferences on Pre-modern Science held at the University of Oklahoma. Brill Publishers. p. 500. ISBN 9004091262. OCLC 19740432 234073624 234096934.
{{cite book}}: Check|oclc=value (help)CS1 maint: multiple names: editors list (link) - ↑ G. Simon (2006). "The Gaze in Ibn al-Haytham". The Medieval History Journal. 9: 89. doi:10.1177/097194580500900105.
- ↑ (Wade & Finger 2001)
- ↑ (Elliott, 1966 & Chapter 1)
- ↑ D. C. Lindberg (1968). "The Theory of Pinhole Images from Antiquity to the Thirteenth Century". Archive for History of the Exact Sciences. 5: 154.
- ↑ O. S. Marshall (1950). "Alhazen and the Telescope". Astronomical Society of the Pacific Leaflets. 6: 4.
- ↑ M. Bellis. "The History of Eye Glasses or Spectacles". About.com:Inventors. Retrieved 2007-09-01.[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ]
- ↑ A. van Helden. "Galileo's Telescope".
- ↑ H. G. Topdemir (1999). Takîyüddîn'in Optik Kitabi. Ankara: Ministry of Culture Press.
- ↑ Giambattista della Porta (Natural Magick). NuVision Publications, LLC. 2005. p. 339.
- ↑ Watson, Fred (2007). Stargazer: the life and times of the telescope. Allen & Unwin. pp. 125–30. ISBN 9781741753837.
- ↑ ಸೂಕ್ಷ್ಮದರ್ಶಕಗಳು: ಟೈಮ್ ಲೈನ್ , ನೋಬೆಲ್ ಫೌಂಡೇಶನ್, ಏಪ್ರಿಲ್ 3, 2009ರಲ್ಲಿ ಮರುಸಂಪಾದಿಸಲಾಗಿದೆ
- ↑ S. J. Gould&year=2000. The Lying Stones of Marrakech, ch.2 "The Sharp-Eyed Lynx, Outfoxed by Nature". London: Jonathon Cape. ISBN 0224050443.
{{cite book}}: CS1 maint: numeric names: authors list (link) - ↑ ೨೪.೦ ೨೪.೧ A. I. Sabra (1981). Theories of light, from Descartes to Newton. CUP Archive. ISBN 0521284368.
- ↑ W. F. Magie (1935). A Source Book in Physics. Harvard University Press. p. 309.
- ↑ J. C. Maxwell (1865). "A Dynamical Theory of the Electromagnetic Field". Philosophical Transactions of the Royal Society of London. 155: 459.
- ↑ ಕ್ವಾಂಟಮ್ ಕುರಿತ ಪ್ಲಾಂಕ್ಸ್ನ ಭೌದ್ಧಿಕ ಪ್ರಚೋದನೆಯ ಸಂಕೀರ್ಣತೆಯೆಡೆಗಿನ ದೃಢವಾದ ಹೆಜ್ಜೆಗಾಗಿ, ಮತ್ತು ಅವನು ಅದರ ಪರಿಣಾಮಗಳನ್ನು ಮನಸ್ಸಿಲ್ಲದೆ ಒಪ್ಪಿಕೊಳ್ಳುವುದನ್ನು ಅರಿಯಲು ನೋಡಿ ಎಚ್. ಕ್ರಗ್, ಮ್ಯಾಕ್ಸ್ ಪ್ಲಾಂಕ್ಸ್: ದ ರೆಲುಕ್ಟೆಂಟ್ ರೆವಲ್ಯೂಶನರಿ , ಫಿಜಿಕ್ಸ್ ವಲ್ಡ್ . ಡಿಸೆಂಬರ್ 1985
- ↑ Einstein, A. (1967). "On a heuristic viewpoint concerning the production and transformation of light". In Ter Haar, D. (ed.). The Old Quantum Theory (PDF). Pergamon. pp. 91–107.[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ] ಐನ್ಸ್ಟೀನ್ನ 1905ರ ಪೋಟೋಇಲೆಕ್ಟ್ರಾನಿಕ್ ಪ್ರಭಾವದ ಇಂಗ್ಲೀಷ್ ಭಾಷಾಂತರದ ಅಧ್ಯಾಯ
- ↑ Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt". Annalen der Physik (in German). 322 (6): 132–148. doi:10.1002/andp.19053220607.
{{cite journal}}: Unknown parameter|trans_title=ignored (help)CS1 maint: unrecognized language (link) - ↑ 1913. "ಆನ್ ದ ಕಾನ್ಸ್ಟಿಟ್ಯೂಷನ್ ಆಫ್ ಆಟಮ್ಸ್ ಆಯ್೦ಡ್ ಮೊಲಾಕ್ಯುಲೆಸ್ , Archived 2007-07-04 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ." ಫಿಲೋಸಾಫಿಕಲ್ ಮ್ಯಾಗಜೀನ್ 26 (ಸರಣಿ 6): 1–25. ಬೋರ್ನ ಪರಮಾಣು ಮಾದರಿ ಮತ್ತು ಮಾಲಿಕ್ಯೂಲಾರ್ ಬಾಂಡಿಂಗ್ ಕುರಿತು ಇರುವ ಅತ್ಯಂತ ಪ್ರಮುಖ ಮೈಲಿಗಲ್ಲಾದ ಪ್ರಬಂಧ.
- ↑ R. Feynman (1985). "Chapter 1". QED: The Strange Theory of Light and Matter. Princeton University Press. p. 6.
- ↑ N. Taylor (2000). LASER: The inventor, the Nobel laureate, and the thirty-year patent war. New York: Simon & Schuster. ISBN 0684835150.
- ↑ Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (pdf). Philosophical Transactions of the Royal Society of London. 155: 499. ಈ ಲೇಖನ ಡಿಸೆಂಬರ್ 8, 1864ರಂದು ಮ್ಯಾಕ್ಸ್ವೆಲ್ರಿಂದ ರಾಯಲ್ ಸೊಸೈಟಿಗೆ ಮಂಡನೆಯಾಯಿತು ಇದನ್ನೂ ನೋಡಿ ಕ್ರಿಯಾಶೀಲವಾದ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಸಿದ್ಧಾಂತ.
- ↑ T. Koupelis and K. F. Kuhn (2007). In Quest of the Universe. Jones & Bartlett Publishers. ISBN 0763743879.
- ↑ D. H. Delphenich (2006). "Nonlinear optical analogies in quantum electrodynamics". ArXiv preprint.
- ↑ ಆರ್ಥರ್ ಚ್ಯುಸ್ಟರ್, ಆಯ್ನ್ ಇಂಟ್ರಡಾಕ್ಷನ್ ಟು ದ ಥೀಯರಿ ಆಫ್ ಆಫ್ಟಿಕ್ಸ್ , ಲಂಡನ್: ಎಡ್ವರ್ಡ್ ಆರ್ನಾಲ್ಡ್, 1904 ಆನ್ಲೈನ್.
- ↑ J. E. Greivenkamp (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. pp. 19–20. ISBN 0819452947.
- ↑ ೩೮.೦೦ ೩೮.೦೧ ೩೮.೦೨ ೩೮.೦೩ ೩೮.೦೪ ೩೮.೦೫ ೩೮.೦೬ ೩೮.೦೭ ೩೮.೦೮ ೩೮.೦೯ H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.ಅಧ್ಯಾಯ 35
- ↑ ಇ. ಡಬ್ಲ್ಯೂ. ಮಾರ್ಚಂದ್, ಗ್ರೇಡಿಯೆಂಟ್ ಇಂಡೆಕ್ಸ್ ಆಪ್ಟಿಕ್ಸ್, ನ್ಯೂಯಾರ್ಕ್, ಎನ್ವೈ, ಆಕಾಡೆಮಿಕ್ ಪ್ರೆಸ್, 1978.
- ↑ ೪೦.೦೦ ೪೦.೦೧ ೪೦.೦೨ ೪೦.೦೩ ೪೦.೦೪ ೪೦.೦೫ ೪೦.೦೬ ೪೦.೦೭ ೪೦.೦೮ ೪೦.೦೯ ೪೦.೧೦ ೪೦.೧೧ ೪೦.೧೨ E. Hecht (1987). Optics (2nd ed.). Addison Wesley. ISBN 020111609X. ಅಧ್ಯಾಯಗಳು 5 & 6.
- ↑ ೪೧.೦ ೪೧.೧ ೪೧.೨ R. S. Longhurst (1968). Geometrical and Physical Optics, 2nd Edition. London: Longmans.
- ↑ J. Goodman (2005). Introduction to Fourier Optics (3rd ed, ed.). Roberts & Co Publishers. ISBN 0974707724.
{{cite book}}: CS1 maint: extra punctuation (link) - ↑ A. E. Siegman (1986). Lasers. University Science Books. ISBN 0935702113. ಅಧ್ಯಾಯ 16.
- ↑ ೪೪.೦ ೪೪.೧ ೪೪.೨ ೪೪.೩ H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.ಅಧ್ಯಾಯ 37
- ↑ ೪೫.೦ ೪೫.೧ P. Hariharan (2003). Optical Interferometry (PDF) (2nd ed.). San Diego, USA: Academic Press.
- ↑ E. R. Hoover (1977). Cradle of Greatness: National and World Achievements of Ohio's Western Reserve. Cleveland: Shaker Savings Association.
- ↑ D. Brewster (1831). A Treatise on Optics. London: Longman, Rees, Orme, Brown & Green and John Taylor. p. 95.
- ↑ J. L. Aubert (1760). Memoires pour l'histoire des sciences et des beaux arts. Paris: Impr. de S. A. S.; Chez E. Ganeau. p. 149.
- ↑ R. Hooke (1665). Micrographia: or, Some physiological descriptions of minute bodies made by magnifying glasses. London: J. Martyn and J. Allestry.
- ↑ H. W. Turnbull (1940–1941). "Early Scottish Relations with the Royal Society: I. James Gregory, F.R.S. (1638-1675)". Notes and Records of the Royal Society of London. 3: 22.
- ↑ T. Rothman (2003). Everything's Relative and Other Fables in Science and Technology. New Jersey: Wiley. ISBN 0471202576.
- ↑ ೫೨.೦ ೫೨.೧ ೫೨.೨ ೫೨.೩ H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.ಅಧ್ಯಾಯr 38
- ↑ ರಾಬರ್ಟ್ ನಿಗೆಲ್ ಟಬ್ಸ್ರಿಂದ ಲಕ್ಕಿ ಎಕ್ಸ್ಪೊಜರ್ಸ್: ಡಿಫ್ರಾಕ್ಷನ್ ಲಿಮಿಟೆಡ್ ಆಸ್ಟ್ರೊನಾಮಿಕಲ್ ಇಮೇಜಿಂಗ್ ಥ್ರೂ ದ ಅಟ್ಮೊಸ್ಪಿಯರ್
- ↑ C. F. Bohren and D. R. Huffman (1983). Absorption and Scattering of Light by Small Particles. Wiley. ISBN 0471293407.
- ↑ ೫೫.೦ ೫೫.೧ J. D. Jackson (1975). Classical Electrodynamics (2nd ed.). Wiley. p. 286. ISBN 047143132X.
- ↑ ೫೬.೦ ೫೬.೧ R. Ramaswami and K. N. Sivarajan (1998). Optical Networks: A Practical Perspective. London: Academic Press.
- ↑ ಬ್ರಿಲೊಂಟಿನ್, ಲಿಯೋನ್. ವೇವ್ ಪ್ರೊಪೊಗೆಷನ್ ಆಯ್೦ಡ್ ಗ್ರುಪ್ ವೆಲೊಸಿಟಿ . ಅಕಾಡೆಮಿಕ್ ಪ್ರೆಸ್ Inc., ನ್ಯೂಯಾರ್ಕ್ (1960)
- ↑ M. Born and E. Wolf (1999). Principle of Optics. Cambridge: Cambridge University Press. pp. 14–24. ISBN 0521642221.
- ↑ ೫೯.೦ ೫೯.೧ ೫೯.೨ ೫೯.೩ ೫೯.೪ ೫೯.೫ H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.ಅಧ್ಯಾಯ 34
- ↑ ಡಿ. ಎಫ್. ವಾಲ್ಸ್ ಮತ್ತು ಜಿ. ಜೆ. ಮಿಲ್ಬರ್ನ್ಕ್ವಾಂಟಮ್ ಆಪ್ಟಿಕ್ಸ್ (ಸ್ಪ್ರಿಂಗರ್ 1994)
- ↑ ಅಲಾಸ್ಟೇರ್ ಡಿ.ಮ್ಯಾಕ್ಅವುಲೆ ಯವರಿಂದ ಆಪ್ಟಿಕ್ ಕಂಪ್ಯೂಟರ್ ಆರ್ಕಿಟೆಕ್ಚರ್: ಮುಂದಿನ ಪೀಳಿಗೆಯ ಕಂಪ್ಯೂಟರಿನ ದೃಗ್ವಿಜ್ಞಾನ ಪರಿಕಲ್ಪನೆ , ಆಪ್ಟಿಕಲ್ ಕಂಪ್ಯೂಟರ್ ಆರ್ಕಿಟೆಕ್ಚರ್: ಮುಂದಿನ ಪೀಳಿಗೆಯ ಕಂಪ್ಯೂಟರಿನ ದೃಗ್ವಿಜ್ಞಾನ ಪರಿಕಲ್ಪನೆ ಪುಸ್ತಕ(1999)
- ↑ "SPIE society".
- ↑ Y. R. Shen (1984). The principles of nonlinear optics. New York, Wiley-Interscience.
- ↑ ೬೪.೦ ೬೪.೧ "laser". Reference.com. Retrieved 2008-05-15.
- ↑ "Charles H. Townes - Nobel Lecture" (PDF).
- ↑ C. H. Townes. "The first laser". University of Chicago. Retrieved 2008-05-15.
- ↑ C. H. Townes (2003). "The first laser". In Laura Garwin and Tim Lincoln (ed.). A Century of Nature: Twenty-One Discoveries that Changed Science and the World. University of Chicago Press. pp. 107–12. ISBN 0226284131.
- ↑ "Handheld barcode scanner technologies".
- ↑ "How the CD was developed". BBC News. 2007-08-17. Retrieved 2007-08-17.
- ↑ J. Wilson and J.F.B. Hawkes (1987). Lasers: Principles and Applications, Prentice Hall International Series in Optoelectronics. Prentice Hall. ISBN 0135236975.
- ↑ ೭೧.೦ ೭೧.೧ ೭೧.೨ D. Atchison and G. Smith (2000). Optics of the Human Eye. Elsevier. ISBN 0750637757.
- ↑ ೭೨.೦ ೭೨.೧ E. R. Kandel, J. H. Schwartz, T. M. Jessell (2000). Principles of Neural Science (4th ed.). New York: McGraw-Hill. pp. 507–513. ISBN 0838577016.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ ೭೩.೦ ೭೩.೧ D. Meister. "Ophthalmic Lens Design". OptiCampus.com. Retrieved November 12, 2008.
- ↑ J. Bryner (6-2-2008). "Key to All Optical Illusions Discovered". LiveScience.com.
{{cite web}}: Check date values in:|date=(help) - ↑ ಕನ್ವರ್ಜೆನ್ಸ್ದಲ್ಲಿಜೊಮೆಟ್ರಿ ಆಫ್ ದ ವಾಶಿಂಗ್ ಪಾಯಿಂಟ್
- ↑ "ದ ಮೂನ್ ಇಲ್ಲ್ಯೂಶನ್ ಎಕ್ಸ್ಪ್ಲೇನ್ಡ್" Archived 2015-12-04 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ., ಡಾನ್ ಮ್ಯಾಕ್ಕ್ರೇಡಿ ವಿಸ್ಕೊನ್ಸಿನ್ ವೈಟ್ವಾಟರ್ ವಿಶ್ವವಿದ್ಯಾನಿಲಯ
- ↑ A. K. Jain, M. Figueiredo, J. Zerubia (2001). Energy Minimization Methods in Computer Vision and Pattern Recognition. Springer.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ↑ ೭೮.೦ ೭೮.೧ ೭೮.೨ ೭೮.೩ H. D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.ಅಧ್ಯಾಯ 36
- ↑ P. E. Nothnagle, W. Chambers, M. W. Davidson. "Introduction to Stereomicroscopy". Nikon MicroscopyU.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ↑ Samuel Edward Sheppard and Charles Edward Kenneth Mees (1907). Investigations on the Theory of the Photographic Process. Longmans, Green and Co. p. 214.
- ↑ B. J. Suess (2003). Mastering Black-and-White Photography. Allworth Communications. ISBN 1581153066.
- ↑ M. J. Langford (2000). Basic Photography. Focal Press. ISBN 0240515927.
- ↑ Leslie D. Stroebel (1999). View Camera Technique. Focal Press. ISBN 0240803450.
- ↑ "Guide to macro photography". Photo.net. Archived from the original on 2011-04-18. Retrieved 2010-05-14.
- ↑ S. Simmons (1992). Using the View Camera. Amphoto Books. p. 35. ISBN 0817463534.
- ↑ New York Times Staff (2004). The New York Times Guide to Essential Knowledge. Macmillan. ISBN 9780312313678.
- ↑ R. R. Carlton, A. McKenna Adler (2000). Principles of Radiographic Imaging: An Art and a Science. Thomson Delmar Learning. ISBN 0766813002.
- ↑ W. Crawford (1979). The Keepers of Light: A History and Working Guide to Early Photographic Processes. Dobbs Ferry, New York: Morgan & Morgan. p. 20. ISBN 0871001586.
- ↑ J. M. Cowley (1975). Diffraction physics. Amsterdam: North-Holland. ISBN 0444107916.
- ↑ C. D. Ahrens (1994). Meteorology Today: an introduction to weather, climate, and the environment (5th ed.). West Publishing Company. pp. 88–89.
- ↑ A. Young. "An Introduction to Mirages".
- ಹೆಚ್ಚಿನ ಮಾಹಿತಿಗಾಗಿ
- M. Born and E.Wolf (1999). Principles of Optics (7th ed.). Pergamon Press.
- E. Hecht (2001). Optics (4th ed.). Pearson Education. ISBN 0805385665.
- R. A. Serway and J. W. Jewett (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0534408427.
- P. Tipler (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0716708108.
- S. G. Lipson (1995). Optical Physics (3rd ed.). Cambridge University Press. ISBN 0521436311.
- Fowles, Grant R. (1989). Introduction to Modern Optics. Dover Publications. ISBN 0-486-65957-7.
ಬಾಹ್ಯ ಕೊಂಡಿಗಳು[ಬದಲಾಯಿಸಿ]
- ಪಠ್ಯಪುಸ್ತಕಗಳು ಮತ್ತು ಟ್ಯೂಟೋರಿಯಲ್ಸ್
- ದೃಗ್ವಿಜ್ಞಾನ Archived 2005-06-22 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. – ಮುಕ್ತ-ಆಕರ ದೃಗ್ವಿಜ್ಞಾನ ಪಠ್ಯಪುಸ್ತಕ
- ದೃಗ್ವಿಜ್ಞಾನ 2001 – ದೃಗ್ವಿಜ್ಞಾನ ಗ್ರಂಥಾಲಯ ಮತ್ತು ಸಮುದಾಯ
- ಮೂಲಭೂತ ದೃಗ್ವಿಜ್ಞಾನ Archived 2013-09-22 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. - ಸಿವಿಐ ಮೆಲೆಸ್ ತಂತ್ರಿಕ ಮಾರ್ಗದರ್ಶಿ
- ವಿಕಿಬುಕ್ಸ್ ಮಾಡ್ಯುಲ್ಸ್
- ಸಮಾಜಗಳು
[[ವರ್ಗ:ಅನ್ವಯಿಕ ಮತ್ತು ಅಂತಶ್ಯಾಸ್ತ್ರೀಯ ಭೌತಶಾಸ್ತ್ರ]]
- Pages with TemplateStyles errors
- CS1 errors: OCLC
- CS1 maint: multiple names: editors list
- Harv and Sfn no-target errors
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಲೇಖನಗಳು from ಜನವರಿ 2023
- Articles with invalid date parameter in template
- ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- CS1 maint: numeric names: authors list
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಲೇಖನಗಳು from ಆಗಸ್ಟ್ 2021
- CS1 errors: unsupported parameter
- CS1 maint: unrecognized language
- ವೆಬ್ ಆರ್ಕೈವ್ ಟೆಂಪ್ಲೇಟಿನ ವೇಬ್ಯಾಕ್ ಕೊಂಡಿಗಳು
- CS1 maint: extra punctuation
- CS1 maint: multiple names: authors list
- CS1 errors: dates
- Articles that may be too long from September 2009
- Articles with hatnote templates targeting a nonexistent page
- Articles containing Ancient Greek (to 1453)-language text
- Portal templates with redlinked portals
- Pages with empty portal template
- Commons link is locally defined
- ದೃಗ್ವಿಜ್ಞಾನ
- ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ
- ಗ್ರೀಕ್ ನ ಸ್ವೀಕೃತ-ಪದ
- ಭೌತಶಾಸ್ತ್ರ
- ವಿಜ್ಞಾನ







































