ಸೊಲೆನಾಯ್ಡ್


ಸೊಲೆನಾಯ್ಡ್ / / ˈsoʊlənɔɪd / [ 1 ] [೧] ಎಂಬುದು ಒಂದು ರೀತಿಯ ವಿದ್ಯುತ್ಕಾಂತವಾಗಿದ್ದು, ತಂತಿಯ ಸುರುಳಿಯಿಂದ ರೂಪುಗೊಂಡಿದೆ, ಅದರ ಉದ್ದವು ಅದರ ವ್ಯಾಸಕ್ಕಿಂತ ಗಣನೀಯವಾಗಿ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ, [೨] ಇದು ನಿಯಂತ್ರಿತ ಕಾಂತಕ್ಷೇತ್ರವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ. ಸುರುಳಿಯಲ್ಲಿ ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಹಾಯುವಾಗ ಸುರುಳಿಯ ಒಳಭಾಗದಲ್ಲಿ ಏಕರೂಪದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ. ಸೊಲೆನಾಯ್ಡ್ ಎಂಬ ಪದವನ್ನು 1823 ರಲ್ಲಿ ಆಂಡ್ರೆ-ಮೇರಿ ಆಂಪಿಯರ್ ಅವರು ಸೃಷ್ಟಿಸಿದರು. [೩]
ಸೊಲೆನಾಯ್ಡ್ನ ತಂತಿಯ ಸುರುಳಿಯನ್ನು ನೇರ-ರೇಖೆಯ ಅಕ್ಷದ ಸುತ್ತ ಸುತ್ತುವ ಅಗತ್ಯವಿರುವುದಿಲ್ಲ; ಉದಾಹರಣೆಗೆ, 1824 ರ ವಿಲಿಯಂ ಸ್ಟರ್ಜನ್ನ ವಿದ್ಯುತ್ಕಾಂತವು ಕುದುರೆಗಾಲಿನ ಲಾಳದ ಆಕಾರಕ್ಕೆ ಬಾಗಿದ ಸೊಲೀನಾಯ್ಡ್ ಅನ್ನು ಒಳಗೊಂಡಿತ್ತು ( ಬಾಗಿದ ಸುರುಳಿಯ ಹಾಗಲ್ಲ).
ಸೊಲೆನಾಯ್ಡ್ಗಳು ನಿರ್ವಾತಗಳಲ್ಲಿ ಎಲೆಕ್ಟ್ರಾನ್ಗಳನ್ನು ಕಾಂತಕ್ಷೇತ್ರದ ಮೂಲಕ ನಿರ್ದೆಶಿಸುತ್ತವೆ. ವಿಶೇಷವಾಗಿ ದೂರದರ್ಶನ ಕ್ಯಾಮೆರಾ ಕೊಳವೆಯ ವಿಡಿಕಾನ್ಗಳು ಮತ್ತು ಇಮೇಜ್ ಆರ್ಥಿಕಾನ್ಗಳಲ್ಲಿ. ಎಲೆಕ್ಟ್ರಾನ್ಗಳು ಕಾಂತಕ್ಷೇತ್ರದೊಳಗೆ ಸುರುಳಿಯಾಕಾರದ ಪಥಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತವೆ. ಈ ಸೊಲೆನಾಯ್ಡ್ಗಳು, ನಾಭೀಕರಿಸಿದ ಸುರುಳಿಗಳು, ಕೊಳವೆಯ ಸಂಪೂರ್ಣ ಉದ್ದವನ್ನು ಸುತ್ತುವರೆದಿವೆ.
ಇಂಜಿನಿಯರಿಂಗ್ನಲ್ಲಿ " ಸೊಲೆನಾಯ್ಡ್ " ಎಂಬ ಪದವು ವಿದ್ಯುತ್ಕಾಂತಕ್ಕೆ ಮಾತ್ರವಲ್ಲದೆ ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಯಾಂತ್ರಿಕ ಶಕ್ತಿಯನ್ನಾಗಿ ಪರಿವರ್ತಿಸುವ ಒಂದು ಪ್ರಚೋದಕವನ್ನು ಒದಗಿಸುವ ಸಂಪೂರ್ಣ ಉಪಕರಣವನ್ನು ಸೂಚಿಸುತ್ತದೆ.
ಭೌತಶಾಸ್ತ್ರ
[ಬದಲಾಯಿಸಿ]ಅನಂತ ನಿರಂತರ ಸೊಲೆನಾಯ್ಡ್
[ಬದಲಾಯಿಸಿ]
ಒಂದು ಅನಂತ ಸೊಲೆನಾಯ್ಡ್ ಅನಂತ ಉದ್ದವನ್ನು ಹೊಂದಿದೆ ಆದರೆ ಸೀಮಿತ ವ್ಯಾಸವನ್ನು ಹೊಂದಿದೆ. "ನಿರಂತರ" ಎಂದರೆ ಸೊಲೆನಾಯ್ಡ್ ಪ್ರತ್ಯೇಕವಾದ ಸೀಮಿತ-ಅಗಲ ಸುರುಳಿಗಳಿಂದ ರಚನೆಯಾಗುವುದಿಲ್ಲ, ಆದರೆ ಸುರುಳಿಗಳ ನಡುವೆ ಯಾವುದೇ ಅಂತರವಿಲ್ಲದ, ಅನೇಕ ಅನಂತ ತೆಳುವಾದ ಸುರುಳಿಗಳಿಂದ ರೂಪುಗೊಳ್ಳುತ್ತದೆ; ಈ ಅಮೂರ್ತತೆಯಲ್ಲಿ, ಸೊಲೆನಾಯ್ಡ್ ಅನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ವಾಹಕ ವಸ್ತುಗಳ ಸಿಲಿಂಡರಾಕಾರದ ಹಾಳೆಯಾಗಿ ನೋಡಲಾಗುತ್ತದೆ.
ಅನಂತ ಉದ್ದದ ಸೊಲೆನಾಯ್ಡ್ನೊಳಗಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಏಕರೂಪವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅದರ ಕಾಂತ ಶಕ್ತಿಯು ಅಕ್ಷದಿಂದ ಇರುವ ದೂರವನ್ನು ಅಥವಾ ಸೊಲೆನಾಯ್ಡ್ನ ಅಡ್ಡ-ವಿಭಾಗದ ಪ್ರದೇಶದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ.
ಇದು ಸೊಲೆನಾಯ್ಡ್ ಸುತ್ತಲಿನ ಕಾಂತೀಯ ಅಭಿವಾಹದ ಸಾಂದ್ರತೆಯ ವ್ಯುತ್ಪನ್ನವಾಗಿದೆ, ಇದು ಸಾಕಷ್ಟು ಉದ್ದವಾಗಿದೆ ಆದ್ದರಿಂದ ಫ್ರಿಂಜ್ ಪರಿಣಾಮಗಳನ್ನು ನಿರ್ಲಕ್ಷಿಸಬಹುದು. ಚಿತ್ರ 1 ರಲ್ಲಿ, ಕಾಂತೀಯ ಹರಿವಿನ ಸಾಂದ್ರತೆಯ ಸದಿಶವು ಸೊಲೆನಾಯ್ಡ್ನ ಒಳಗಿನ ಧನಾತ್ಮಕ z ದಿಕ್ಕಿನಲ್ಲಿ ಮತ್ತು ಸೊಲೆನಾಯ್ಡ್ನ ಹೊರಗೆ ಋಣಾತ್ಮಕ z ದಿಕ್ಕಿನಲ್ಲಿ ಬಿಂದುಗಳನ್ನು ತೋರಿಸುತ್ತದೆ ಎಂದು ನಮಗೆ ತಕ್ಷಣ ತಿಳಿಸುತ್ತವೆ. ತಂತಿಯ ಸುತ್ತಲಿನ ಕ್ಷೇತ್ರಕ್ಕೆ ಬಲಗೈ ಹಿಡಿತದ ನಿಯಮವನ್ನು ಅನ್ವಯಿಸುವ ಮೂಲಕ ನಾವು ಇದನ್ನು ಖಚಿತಪಡಿಸುತ್ತೇವೆ. ನಮ್ಮ ಬಲಗೈಯಲ್ಲಿ ತಂತಿಯನ್ನು ಹಿಡಿದು, ಹೆಬ್ಬೆರಳು ಪ್ರವಾಹದ ದಿಕ್ಕನ್ನು ಸೂಚಿಸಿದರೆ, ಸುತ್ತಿದ ಬೆರಳುಗಳ ಸುರುಳಿಯು ಕಾಂತ ಕ್ಷೇತ್ರವನ್ನು ಸೂಚಿಸುತ್ತದೆ ಎಂಬುದನ್ನು ತೋರಿಸುತ್ತದೆ. ನಾವು ದೀರ್ಘವಾದ ಸೊಲೀನಾಯ್ಡ್ನೊಂದಿಗೆ ವ್ಯವಹರಿಸುತ್ತಿರುವುದರಿಂದ, ಮೇಲ್ಮುಖವಾಗಿ ತೋರಿಸದ ಕಾಂತಕ್ಷೇತ್ರದ ಎಲ್ಲಾ ಘಟಕಗಳು ಸಮ್ಮಿತಿಯಿಂದ ರದ್ದುಗೊಳ್ಳುತ್ತವೆ. ಹೊರಗೆ, ಇದೇ ರೀತಿಯ ರದ್ದತಿ ಸಂಭವಿಸುತ್ತದೆ, ಮತ್ತು ಕ್ಷೇತ್ರವು ಕೇವಲ ಕೆಳಮುಖವಾಗಿದೆ.
ಈಗ ಸೊಲೆನಾಯ್ಡ್ ಒಳಗೆ ಇರುವ ಕಾಲ್ಪನಿಕ ಕುಣಿಕೆ c ಅನ್ನು ಪರಿಗಣಿಸಿ. ಆಂಪಿಯರ್ನ ನಿಯಮದ ಪ್ರಕಾರ, ಈ ಕುಣಿಕೆಯ ಸುತ್ತ B ಯ ಲೈನ್ ಇಂಟಗ್ರಲ್ (ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಡೆನ್ಸಿಟಿ ವೆಕ್ಟರ್) ಶೂನ್ಯ ಎಂದು ನಮಗೆ ತಿಳಿದಿದೆ, ಏಕೆಂದರೆ ಇದು ಯಾವುದೇ ವಿದ್ಯುತ್ ಪ್ರವಾಹಗಳನ್ನು ಸುತ್ತುವರೆದಿಲ್ಲ (ಕುಣಿಕೆ ಮೂಲಕ ಹಾದುಹೋಗುವ ಸರ್ಕ್ಯೂಟ್ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ಅಂತಹ ಸಂದರ್ಭದಲ್ಲಿ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಎಂದು ಸಹ ಊಹಿಸಬಹುದು. ಅಥವಾ: ಸೊಲೆನಾಯ್ಡ್ ಮೂಲಕ ಸ್ಥಿರ ಅಥವಾ ನಿರಂತರವಾಗಿ ಬದಲಾಗುತ್ತಿರುವ ಪ್ರವಾಹ). ಕ್ಷೇತ್ರವು ಸೊಲೆನಾಯ್ಡ್ನೊಳಗೆ ಮೇಲ್ಮುಖವಾಗಿದೆ ಎಂದು ನಾವು ಮೇಲೆ ತೋರಿಸಿದ್ದೇವೆ, ಆದ್ದರಿಂದ ಕುಣಿಕೆ c ನ ಸಮತಲ ಭಾಗಗಳು ಇಂಟಗ್ರಲ್ಗೆ ಏನನ್ನೂ ನೀಡುವುದಿಲ್ಲ. ಹೀಗಾಗಿ ಮೇಲ್ಮುಖ 1 ರ ಇಂಟಗ್ರಲ್ ಕೆಳಮುಖ 2 ರ ಇಂಟಗ್ರಲ್ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ನಾವು ಕುಣಿಕೆಯ ಆಯಾಮಗಳನ್ನು ನಿರಂಕುಶವಾಗಿ ಬದಲಾಯಿಸಬಹುದು ಮತ್ತು ಅದೇ ಫಲಿತಾಂಶವನ್ನು ಪಡೆಯಬಹುದು, ಕೇವಲ ಭೌತಿಕ ವಿವರಣೆಯೆಂದರೆ ಇಂಟಿಗ್ರ್ಯಾಂಡ್ಸ್ ವಾಸ್ತವವಾಗಿ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ, ಸೊಲೆನಾಯ್ಡ್ನೊಳಗಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ತ್ರಿಜ್ಯದ ದಿಕ್ಕಿನಲ್ಲಿರುವ (ರೇಡಿಯಲ್ ) ಏಕರೂಪವಾಗಿರುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಕಾಂತ ಕ್ಷೇತ್ರವು ಅನುಲಂಬವಾಗಿ ಬದಲಾಗುವುದನ್ನು ಯಾವುದೂ ತಡೆಯುವುದಿಲ್ಲ ಮತ್ತು ಅದು ವಾಸ್ತವವಾಗಿ ಬದಲಾಗುತಿರುತ್ತದೆ ಎಂಬುದನ್ನು ನಾವು ಗಮನಿಸಬಹುದು.
ಸೊಲೆನಾಯ್ಡ್ನ ಹೊರಗಿನ ಕ್ಷೇತ್ರವು ತ್ರಿಜ್ಯೀಯ ಏಕರೂಪ ಅಥವಾ ಸ್ಥಿರವಾಗಿದೆ ಎಂದು ತೀರ್ಮಾನಿಸಲು ಲೂಪ್ a ಗೆ ಇದೇ ರೀತಿಯ ವಾದವನ್ನು ಅನ್ವಯಿಸಬಹುದು. ಕ್ಷೇತ್ರ ರೇಖೆಗಳು ಅದರ ಉದ್ದಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿರುವ ಸೊಲೆನಾಯ್ಡ್ನ ಮಧ್ಯಭಾಗದಲ್ಲಿ ಮಾತ್ರ ಅನ್ವಯವಾಗುವ ಈ ಕೊನೆಯ ಫಲಿತಾಂಶವು ಮುಖ್ಯವಾಗಿದೆ, ಏಕೆಂದರೆ ಸೊಲೆನಾಯ್ಡ್ನ ಹೊರಗಿನ ಕ್ಷೇತ್ರದ ತ್ರಿಜ್ಯಗಳು ಒಲವು ತೋರುವುದರಿಂದ ಹೊರಗಿನ ಫ್ಲಕ್ಸ್ ಸಾಂದ್ರತೆಯು ಪ್ರಾಯೋಗಿಕವಾಗಿ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ ಎಂದು ತೋರಿಸುತ್ತದೆ. ಅನಂತ. ಸೊಲೆನಾಯ್ಡ್ನ ಹೊರಗಿನ ಫ್ಲಕ್ಸ್ ಸಾಂದ್ರತೆಯು ವಾಸ್ತವವಾಗಿ ಶೂನ್ಯವಾಗಿದೆ ಎಂದು ತೋರಿಸಲು ತಾರ್ಕಿಕ ವಾದವನ್ನು ಸಹ ಬಳಸಬಹುದು. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್ ಲೈನ್ಗಳು ಲೂಪ್ಗಳಾಗಿ ಮಾತ್ರ ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ, ಅವು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರ ರೇಖೆಗಳಂತೆ ಒಂದು ಬಿಂದುವಿನಿಂದ ಬೇರೆಯಾಗುವುದಿಲ್ಲ ಅಥವಾ ಒಮ್ಮುಖವಾಗುವುದಿಲ್ಲ( ಕಾಂತೀಯತೆಗಾಗಿ ಗಾಸ್ ನಿಯಮವನ್ನು ನೋಡಿ).ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳು ಸೊಲೆನಾಯ್ಡ್ನ ಉದ್ದದ ಮಾರ್ಗವನ್ನು ಅನುಸರಿಸುತ್ತವೆ, ಆದ್ದರಿಂದ ಅವು ಸೊಲೆನಾಯ್ಡ್ನ ಹೊರಗೆ ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಹೋಗಬೇಕು ಇದರಿಂದ ರೇಖೆಗಳು ಕುಣಿಕೆಗಳನ್ನು ರೂಪಾಂತರವಾಗುತ್ತವೆ. ಆದಾಗ್ಯೂ, ಸೊಲೆನಾಯ್ಡ್ನ ಹೊರಗಿನ ಪರಿಮಾಣವು ಒಳಗಿನ ಪರಿಮಾಣಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ಹೊರಗಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳ ಸಾಂದ್ರತೆಯು ಬಹಳವಾಗಿ ಕಡಿಮೆಯಾಗುತ್ತದೆ. ಹೊರಗಿನ ಕ್ಷೇತ್ರವು ಸ್ಥಿರವಾಗಿದೆ ಎಂದು ಈಗ ನೆನಪಿಸಿಕೊಳ್ಳಿ. ಒಟ್ಟು ಸಂಖ್ಯೆಯ ಕ್ಷೇತ್ರ ರೇಖೆಗಳನ್ನು ಸಂರಕ್ಷಿಸಲು, ಸೊಲೆನಾಯ್ಡ್ ಉದ್ದವಾಗುವುದರಿಂದ ಹೊರಗಿನ ಕ್ಷೇತ್ರವು ಶೂನ್ಯಕ್ಕೆ ಹೋಗಬೇಕು. ಸಹಜವಾಗಿ, ಸೊಲೆನಾಯ್ಡ್ ಅನ್ನು ತಂತಿಯ ಸುರುಳಿಯಾಗಿ ನಿರ್ಮಿಸಿದರೆ (ಆಚರಣೆಯಲ್ಲಿ ಸಾಮಾನ್ಯವಾಗಿ ಮಾಡಲಾಗುತ್ತದೆ), ನಂತರ ಇದು ಸೊಲೆನಾಯ್ಡ್ನ ಉದ್ದಕ್ಕೂ ಒಟ್ಟಾರೆಯಾಗಿ ಹರಿಯುವ ಪ್ರವಾಹದಿಂದಾಗಿ ಒಂದೇ ತಂತಿಯಂತೆಯೇ ಹೊರಗಿನ ಕ್ಷೇತ್ರವನ್ನು ಹೊರಹೊಮ್ಮಿಸುತ್ತದೆ.
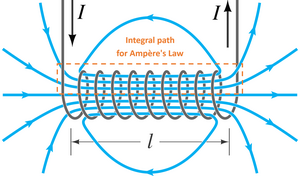
ಆಂಪಿಯರ್ನ ಸರ್ಕ್ಯೂಟ್ ನಿಯಮವನ್ನು ಸೊಲೆನಾಯ್ಡ್ಗೆ ಅನ್ವಯಿಸುವುದು (ಬಲಭಾಗದಲ್ಲಿರುವ ಚಿತ್ರ ನೋಡಿ) ನಮಗೆ ಕೆಳಗಿನ ಸಮೀಕರಣ ಸಿಗುತ್ತದೆ
ಇಲ್ಲಿ ಕಾಂತೀಯ ಅಭಿವಾಹ ಸಾಂದ್ರತೆ, ಸೊಲೆನಾಯ್ಡ್ನ ಉದ್ದ , ಕಾಂತೀಯ ಸ್ಥಿರಾಂಕವಾಗಿದೆ, ಸುರುಳಿಯ ತಿರುವುಗಳ ಸಂಖ್ಯೆ, ಮತ್ತು ವಿದುತ್ಪ್ರವಾಹ. ಇದರಿಂದ ನಾವು ಈ ಕೆಳಗಿನ ಸಮೀಕರಣ ಪಡೆಯುತ್ತೇವೆ
ವ್ಯಾಪತೆ (ಪೆರ್ಮಿಯೆಬಿಲಿಟಿ) ಯು ಈ ಸಮೀಕರಣವು ಮುಕ್ತ ಜಾಗ (ನಿರ್ವಾತ) ದಲ್ಲಿ ಸೊಲೆನಾಯ್ಡ್ಗೆ ಮಾನ್ಯವಾಗಿದೆ, ಅಂದರೆ ಕಾಂತೀಯ ಮಾರ್ಗದ ಮುಕ್ತ ಜಾಗದ ವ್ಯಾಪತೆಯಂತೆಯೇ ಇರುತ್ತದೆ, μ 0 .
ಸಾಪೇಕ್ಷ ವ್ಯಾಪತೆಯನ್ನು μr, ಹೊಂದಿರುವ ವಸ್ತುವಿನಲ್ಲಿ ಸೊಲೀನಾಯ್ಡ್ ಸುತ್ತುವರಿಯಲ್ಪಟ್ಟರೆ, ನಂತರ ಕ್ಷೇತ್ರವು ಆ ಪ್ರಮಾಣದಲ್ಲಿ ಹೆಚ್ಚಾಗುತ್ತದೆ:
ಹೆಚ್ಚಿನ ಸೊಲೆನಾಯ್ಡ್ಗಳಲ್ಲಿ, ಸೊಲೆನಾಯ್ಡ್ ಹೆಚ್ಚಿನ ವ್ಯಾಪತೆಯಿರುವ ವಸ್ತುವಿನಿಂದ ಸುತ್ತುವರಿಯಲ್ಪಟ್ಟಿರುವುದಿಲ್ಲ. ಆದರೆ ಸೊಲೆನಾಯ್ಡ್ ಸುತ್ತಲಿನ ಜಾಗದ ಕೆಲವು ಭಾಗವು ಹೆಚ್ಚಿನ ವ್ಯಾಪತೆಯಿರುವ ವಸ್ತುವನ್ನು ಹೊಂದಿರುತ್ತದೆ ಮತ್ತು ಕೆಲವು ಪ್ರದೇಶಗಳಲ್ಲಿ ಕೇವಲ ಗಾಳಿಯಿರಿತ್ತದೆ. (ಇದು ಮುಕ್ತ ಸ್ಥಳದಂತೆ ವರ್ತಿಸುತ್ತದೆ). ಆ ಸನ್ನಿವೇಶದಲ್ಲಿ, ಹೆಚ್ಚಿನ ವ್ಯಾಪತೆಯಿರುವ ವಸ್ತುವಿನ ಸಂಪೂರ್ಣ ಪರಿಣಾಮವು ಕಂಡುಬರುವುದಿಲ್ಲ, ಆದರೆ ಪರಿಣಾಮಕಾರಿ (ಅಥವಾ ಸ್ಪಷ್ಟವಾದ) ವ್ಯಾಪತೆ ಇರುತ್ತದೆ μeff ಅಂದರೆ 1 ≤ μ ಎಫ್ಎಫ್ ≤ μr _
ಕಬ್ಬಿಣದಂತಹ ಫ಼ೆರೋಕಾಂತೀಯ (ಫೆರೋಮ್ಯಾಗ್ನೆಟಿಕ್ ) ವಸ್ತುವನ್ನು ಸುರುಳಿಯ ಒಳಗೆ (ಕೋರ್) ಸೇರ್ಪಡೆಯು ಸೊಲೆನಾಯ್ಡ್ನಲ್ಲಿನ ಕಾಂತೀಯ ಹರಿವಿನ ಸಾಂದ್ರತೆಯ ಪ್ರಮಾಣವನ್ನು ಹೆಚ್ಚಿಸುತ್ತದೆ ಮತ್ತು ಕಾಂತೀಯ ಮಾರ್ಗದ ಪರಿಣಾಮಕಾರಿ ಪ್ರವೇಶಸಾಧ್ಯತೆಯನ್ನು ಹೆಚ್ಚಿಸುತ್ತದೆ. ಇದನ್ನು ಸೂತ್ರದಿಂದ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ
ಅಲ್ಲಿ μ eff ಕೋರ್ನ ಪರಿಣಾಮಕಾರಿ ಅಥವಾ ಸ್ಪಷ್ಟವಾದ ವ್ಯಾಪತೆಯಾಗಿದೆ. ಪರಿಣಾಮಕಾರಿ ವ್ಯಾಪತೆಯು ಕೋರ್ ನ ಜ್ಯಾಮಿತಿಯ ಗುಣಲಕ್ಷಣಗಳು ಮತ್ತು ಅದರ ಸಾಪೇಕ್ಷ ವ್ಯಾಪತೆ ಕ್ರಿಯೆಯಾಗಿದೆ. ಸಾಪೇಕ್ಷ ವ್ಯಾಪತೆಯು (ಕೇವಲ ವಸ್ತುವಿನ ದ್ರವ್ಯ) ಮತ್ತು ಪರಿಣಾಮಕಾರಿ ವ್ಯಾಪತೆಯು (ವಸ್ತುವಿನ ಇಡೀ ರಚನೆಯ ದ್ರವ್ಯ) ಪದಗಳು ಸಾಮಾನ್ಯವಾಗಿ ನಮ್ಮನ್ನು ಗೊಂದಲಕ್ಕೊಳಗಾಗುವಂತೆ ಮಾಡುತ್ತವೆ; ಅವು ಅನೇಕ ಪ್ರಮಾಣದ ಕ್ರಮಗಳಿಂದ ಭಿನ್ನವಾಗಿರಬಹುದು.
ತೆರೆದ ಕಾಂತೀಯ ರಚನೆಗಾಗಿ, ಪರಿಣಾಮಕಾರಿ ವ್ಯಾಪತೆ ಮತ್ತು ಸಾಪೇಕ್ಷ ವ್ಯಾಪತೆಯ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ನೀಡಲಾಗಿದೆ:
ಇಲ್ಲಿ k ಎಂಬುದು ಕೋರ್ ನ ವಿಕಾಂತೀಕರಣದ ಅಂಶವಾಗಿದೆ. [೪]
ಸೀಮಿತ ನಿರಂತರ ಸೊಲೆನಾಯ್ಡ್
[ಬದಲಾಯಿಸಿ]
ಪರಿಮಿತ ಸೊಲೆನಾಯ್ಡ್ ಎಂಬುದು ಸೀಮಿತ ಉದ್ದವನ್ನು ಹೊಂದಿರುವ ಸೊಲೆನಾಯ್ಡ್ ಆಗಿದೆ. ನಿರಂತರ ಎಂದರೆ ಸೊಲೆನಾಯ್ಡ್ ಪ್ರತ್ಯೇಕ ಸುರುಳಿಗಳಿಂದ ರೂಪುಗೊಳ್ಳುವುದಿಲ್ಲ ಆದರೆ ವಾಹಕ ವಸ್ತುಗಳ ಹಾಳೆಯಿಂದ ರೂಪುಗೊಳ್ಳುತ್ತದೆ. ಪ್ರಸ್ತುತವು ಸೊಲೆನಾಯ್ಡ್ನ ಮೇಲ್ಮೈಯಲ್ಲಿ ಏಕರೂಪವಾಗಿ ಹಂಚಲ್ಪಟ್ಟಿದೆ ಎಂದು ನಾವು ಊಹಿಸುತ್ತೇವೆ, ಮೇಲ್ಮೈ ಪ್ರವಾಹ ಸಾಂದ್ರತೆ K ; ಕೊಳವೆಯಾಕಾರದ ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿ :ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಸದಿಶ ವಿಭವವನ್ನು ಬಳಸಿಕೊಂಡು ಕಂಡುಹಿಡಿಯಬಹುದು, ಇದು ಕೊಳವೆಯಾಕಾರದ ನಿರ್ದೇಶಾಂಕ (ಸಿಲಿಂಡ್ರಿಕಲ್ ಕೊರ್ಡಿನತಟ್ಸ್) R ತ್ರಿಜ್ಯ ಮತ್ತು ಉದ್ದ l ಹೊಂದಿರುವ ಸೀಮಿತ ಸೊಲೆನಾಯ್ಡ್ಗೆ [೫] [೬] ಆಗಿದೆ,ಎಲ್ಲಿ:
ಇಲ್ಲಿ, , , ಮತ್ತು ಮೊದಲ, ಎರಡನೆಯ ಮತ್ತು ಮೂರನೇ ವಿಧದ ಸಂಪೂರ್ಣ ದೀರ್ಘವ್ರುತಾಕಾರದ ಅನುಕಲ(ಎಲಿಫ್ಟಿಕಲ್ ಇಂಟೆಗ್ರಲ್).
ಬಳಸಿ:ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಸಾಂದ್ರತೆಯನ್ನು [೭] [೮] [೯] ಎಂದು ಪಡೆಯಲಾಗುತ್ತದೆಸಮ್ಮಿತಿಯ ಅಕ್ಷದ ಮೇಲೆ, ತ್ರಿಜ್ಯೀಯ ಘಟಕವು ಮರೆಯಾಗುತ್ತದೆ ಮತ್ತು ಅಕ್ಷೀಯ ಕ್ಷೇತ್ರದ ಘಟಕವುಸೊಲೆನಾಯ್ಡ್ ಒಳಗೆ, ತುದಿಗಳಿಂದ ದೂರದಲ್ಲಿ ( ), ಇದು ಸ್ಥಿರ ಮೌಲ್ಯದ ಕಡೆಗೆ ತೋರುತ್ತದೆ .
ಸೀಮಿತ ನಿರಂತರವಲ್ಲದ ಸೊಲೆನಾಯ್ಡ್
[ಬದಲಾಯಿಸಿ]
ತ್ರಿಜ್ಯವು ಸೊಲೆನಾಯ್ಡ್ನ ಉದ್ದಕ್ಕಿಂತ ಹೆಚ್ಚು ದೊಡ್ಡದಾಗಿದ್ದರೆ, ಸೊಲೆನಾಯ್ಡ್ನ ಮಧ್ಯಭಾಗದ ಮೂಲಕ ಕಾಂತೀಯ ಅಭಿವಾಹದ ಸಾಂದ್ರತೆಯು ( z ದಿಕ್ಕಿನಲ್ಲಿ, ಸೊಲೆನಾಯ್ಡ್ನ ಉದ್ದಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿರುತ್ತದೆ, ಅಲ್ಲಿ ಸುರುಳಿಯು z =0 ನಲ್ಲಿ ಕೇಂದ್ರೀಕೃತವಾಗಿರುತ್ತದೆ) ಒಂದೇ ವೃತ್ತಾಕಾರದ ವಾಹಕ ಕುಣಿಕೆಯ ಸಾಂದ್ರತೆ ಎಂದು ಅಂದಾಜಿಸಬಹುದು:
ಉದ್ದಕ್ಕೆ ಹೋಲಿಸಿದರೆ ತ್ರಿಜ್ಯವು ದೊಡ್ಡದಾಗಿರದ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಈ ಅಂದಾಜನ್ನು z ನ ಉದ್ದಕ್ಕೂ ವಿವಿಧ ಸ್ಥಾನಗಳಲ್ಲಿ ತಂತಿ ತಿರುವುಗಳು/ಸುರುಳಿಗಳ N ಸಂಖ್ಯೆಯ ಮೇಲೆ ಸಂಕ್ಷೇಪಿಸುವ ಮೂಲಕ ಮತ್ತಷ್ಟು ಪರಿಷ್ಕರಿಸಬಹುದು.
ಅನಿಯಮಿತ ಸೊಲೆನಾಯ್ಡ್ಗಳು
[ಬದಲಾಯಿಸಿ]ವಿದ್ಯುತ್ ಪರಿಮಿತ ಸೊಲೆನಾಯ್ಡ್ಗಳ ವರ್ಗದಲ್ಲಿ, ಒಂದೇ ಪಿಚ್ನೊಂದಿಗೆ ವಿರಳವಾಗಿ ಸುತ್ತಲ್ಪಟ್ಟು, ವಿಭಿನ್ನ ಪಿಚ್ಗಳೊಂದಿಗೆ ವಿರಳವಾಗಿ ಸುತ್ತಲ್ಪಟ್ಟಿವೆ (ವಿವಿಧ-ಪಿಚ್ ಸೊಲೆನಾಯ್ಡ್), ಅಥವಾ ವಿಭಿನ್ನ ಕುಣಿಕೆಗಳಿಗಾಗಿ ವಿಭಿನ್ನ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುವವುಗಳು (ಸಿಲಿಂಡರಾಕಾರದ ಸೊಲೆನಾಯ್ಡ್ಗಳು ಅಲ್ಲ). ಅವುಗಳನ್ನು ಅನಿಯಮಿತ ಸೊಲೆನಾಯ್ಡ್ಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.ನಿಸ್ತಂತು ವಿದ್ಯುತ್ ವರ್ಗಾವಣೆಗಾಗಿ ವಿರಳವಾದ ಸುರುಳಿಗಳ ಸೊಲೆನಾಯ್ಡ್ಗಳು, [೧೦] [೧೧] ಮ್ಯಾಗ್ನೆಟಿಕ್ ರೆಸೋನೆನ್ಸ್ ಇಮೇಜಿಂಗ್ (MRI), [೧೨] ಮತ್ತು ಇತರ ವೈದ್ಯಕೀಯ ಸಾಧನಗಳಿಗೆ ಸಿಲಿಂಡರಾಕಾರದಲ್ಲದ ಸೊಲೀನಾಯ್ಡ್ಗಳಿಗಾಗಿ ವಿವಿಧ-ಪಿಚ್ ಸೊಲೀನಾಯ್ಡ್ಗಳಂತಹ ವಿವಿಧ ಉದ್ದೇಶಗಳಿಗೆ ಅವನ್ನು ಬಲಸುತ್ತಾರೆ.[೧೩]
ಸಾಂಪ್ರದಾಯಿಕ ಸೊಲೆನಾಯ್ಡ್ಗಳಿಗೆ ಅಂದರೆ ಬಿಗಿಯಾಗಿ ಸುತ್ತಲ್ಪಟ್ಟ ಸುರುಳಿಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಮಾಡಿದ ಸೊಲೆನಾಯ್ಡ್ಗಳಿಗೆ ಆಂತರಿಕ ಪ್ರೇರಕತೆ ಮತ್ತು ಧಾರಕತೆಯ ಲೆಕ್ಕಾಚಾರವನ್ನು ಮಾಡಲಾಗುವುದಿಲ್ಲ. ಅಂತರ್ಗತ ಪ್ರೇರಕತೆ [೧೪] (ಸಂಕೇತಗಳು [೧೫] ನಲ್ಲಿ ಲಭ್ಯವಿದೆ) ಮತ್ತು ಧಾರಣಶಕ್ತಿಯ ಲೆಕ್ಕಾಚಾರಕ್ಕಾಗಿ ಹೊಸ ಲೆಕ್ಕಾಚಾರದ ವಿಧಾನಗಳನ್ನು ಪ್ರಸ್ತಾಪಿಸಲಾಗಿದೆ. [೧೬] (ಸಂಕೇತಗಳು [೧೭] ನಲ್ಲಿ ಲಭ್ಯವಿದೆ)
ಇಂಡಕ್ಟನ್ಸ್
[ಬದಲಾಯಿಸಿ]ಮೇಲೆ ತೋರಿಸಿರುವಂತೆ, ಕಾಂತೀಯ ಅಭಿವಾಹ ಸಾಂದ್ರತೆ ಸುರುಳಿಯೊಳಗೆ ಪ್ರಾಯೋಗಿಕವಾಗಿ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅದನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಪಡೆಯಲಾಗುತ್ತದೆ
ಅಲ್ಲಿ μ0 ಕಾಂತೀಯ ಸ್ಥಿರಾಂಕವಾಗಿದೆ, ತಿರುವುಗಳ ಸಂಖ್ಯೆ, ವಿದ್ಯುತ್ಪ್ರವಾಹ ಮತ್ತು ಸುರುಳಿಯ ಉದ್ದ. ಸುರುಳಿಯ ಕೊನೆಯ ತುದಿಗಳ ಪರಿಣಾಮಗಳನ್ನು ನಿರ್ಲಕ್ಷಿಸಿ, ಸುರುಳಿಯ ಮೂಲಕ ಒಟ್ಟು ಕಾಂತೀಯ ಅಭಿವಾಹ ಅನ್ನು ಅಭಿವಾಹ ಸಾಂದ್ರತೆ ಯನ್ನು ಅಡ್ಡ-ವಿಭಾಗದ ವಿಸ್ತೀರ್ಣ ಗೆ ಗುಣಿಸುವ ಮೂಲಕ ಪಡೆಯಲಾಗುತ್ತದೆ:
ಪ್ರೇರಕತೆ ವ್ಯಾಖ್ಯಾನದೊಂದಿಗೆ ಇದನ್ನು ಸಂಯೋಜಿಸುವುದರ ಮೂಲಕ
ಸೊಲೆನಾಯ್ಡ್ನ ಪ್ರೇರಕತೆ ಈ ರೀತಿ ಇರುತ್ತದೆ
ವಿವಿಧ ವ್ಯಾಸದಿಂದ ಉದ್ದದ ಅನುಪಾತಗಳ ಸಣ್ಣ ಸೊಲೆನಾಯ್ಡ್ಗಳಿಗೆ ಪ್ರೇರಕತೆ ಕೋಷ್ಟಕವನ್ನು ಡೆಲ್ಲಿಂಗರ್, ವಿಟ್ಮೋರ್ ಮತ್ತು ಔಲ್ಡ್ ಅವರ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ. [೧೮]
ಇದು ಮತ್ತು ಹೆಚ್ಚು ಸಂಕೀರ್ಣವಾದ ಆಕಾರಗಳ ಪ್ರೇರಕತೆಯನ್ನು ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ಸಮೀಕರಣಗಳಿಂದ ಪಡೆಯಬಹುದು. ಗಟ್ಟಿಯದ ಸುರುಳಿಯಿಂದ ಮಾಡಲ್ಪಟ್ಟ ( ಕೋರ್ ಗಳಿಲ್ಲದ), ಸುರುಳಿಗಳಿಗೆ ಪ್ರೇರಕತೆ ಯು ಸುರುಳಿಯ ಜ್ಯಾಮಿತಿ ಮತ್ತು ತಿರುವುಗಳ ಸಂಖ್ಯೆಯನ್ನು ಅವಲಂಬಿಸಿದೆ ಮತ್ತು ವಿದ್ಯುತ್ಪ್ರವಾಹವನ್ನು ಅವಲಂಬಿಸಿರುದಿಲ್ಲ.
ಇದೇ ರೀತಿಯ ವಿಶ್ಲೇಷಣೆಯು ಕಾಂತೀಯ ಕೋರ್ ಹೊಂದಿರುವ ಸೊಲೆನಾಯ್ಡ್ಗೆ ಅನ್ವಯಿಸುತ್ತದೆ, ಆದರೆ ಕಾಂತೀಯ ಕೋರ್ ಮತ್ತು ವ್ಯಾಸದ ಸಾಪೇಕ್ಷ ವ್ಯಾಪತೆಯ ಗಣಲಬ್ದಕಿಂತ ಸುರುಳಿಯ ಉದ್ದವು ಹೆಚ್ಚು ಹೆಚ್ಚಿದ್ದರೆ ಮಾತ್ರ. ಅದು ಸರಳವಾದ ವಿಶ್ಲೇಷಣೆಯನ್ನು ಕಡಿಮೆ-ವ್ಯಾಪತೆಯ ಕೋರ್ಗಳಿಗೆ ಅಥವಾ ಅತ್ಯಂತ ಉದ್ದವಾದ ತೆಳುವಾದ ಸೊಲೀನಾಯ್ಡ್ಗಳಿಗೆ ಸೀಮಿತಗೊಳಿಸುತ್ತದೆ. ಕಾಂತೀಯ ಸ್ಥಿರಾಂಕದ μ0 ಅನ್ನು μ ಅಥವಾ μ 0 μr ನೊಂದಿಗೆ ಬದಲಾಯಿಸುವ ಮೂಲಕ ಮೇಲಿನ ಸಮೀಕರಣಗಳಲ್ಲಿ ಕೋರ್ ನ ಉಪಸ್ಥಿತಿಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬಹುದು, ಅಲ್ಲಿ μ ವ್ಯಾಪತೆ ಮತ್ತು μr ಸಾಪೇಕ್ಷ ವ್ಯಾಪತೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಕಾಂತೀಯ ಅಭಿವಾಹದೊಂದಿಗೆ ಫೆರೋಕಾಂತೀಯ ವಸ್ತುಗಳ ವಾಪತೆಯು ಬದಲಾಗುವುದರಿಂದ, ಫೆರೋಕಾಂತೀಯ ಕೋರ್ ಹೊಂದಿರುವ ಸುರುಳಿಯ ಪ್ರೇರಕತೆಯು ಸಾಮಾನ್ಯವಾಗಿ ವಿದ್ತುತ್ಪ್ರವಾಹದೊಂದಿಗೆ ಬದಲಾಗುತ್ತದೆ.
ಸಹ ನೋಡಿ
[ಬದಲಾಯಿಸಿ]- ಹೆಲ್ಮ್ಹೋಲ್ಟ್ಜ್ ಸುರುಳಿ
- ಪ್ರೇರಕ
- ಸೊಲೆನಾಯ್ಡ್ (ಎಂಜಿನಿಯರಿಂಗ್)
ಉಲ್ಲೇಖಗಳು
[ಬದಲಾಯಿಸಿ]- ↑ "solenoid: Meaning in the Cambridge English Dictionary". dictionary.cambridge.org. Archived from the original on 16 January 2017. Retrieved 16 January 2017.
- ↑ or equivalently, the diameter of the coil is assumed to be infinitesimally small (Ampère 1823, p. 267: "des courants électriques formants de très-petits circuits autour de cette ligne, dans des plans infiniment rapprochés qui lui soient perpendiculaires").
- ↑ Session of the Académie des sciences of 22 December 1823, published in print in: Ampère, "Mémoire sur la théorie mathématique des phénomènes électro-dynamiques", Mémoires de l'Académie royale des sciences de l'Institut de France 6 (1827), Paris, F. Didot, pp. 267ff. (and figs. 29–33). "l'assemblage de tous les circuits qui l'entourent [viz. l'arc], assemblage auquel j'ai donné le nom de solénoïde électro-dynamique, du mot grec σωληνοειδὴς, dont la signification exprime précisement ce qui a la forme d'un canal, c'est-à-dire la surface de cette forme sur laquelle se trouvent tous les circuits." (p. 267).
- ↑ Jiles, David. Introduction to magnetism and magnetic materials. CRC press, p. 48, 2015.
- ↑ "Archived copy" (PDF). Archived from the original (PDF) on 10 April 2014. Retrieved 28 March 2013.
{{cite web}}: CS1 maint: archived copy as title (link) - ↑ "Archived copy" (PDF). Archived from the original (PDF) on 19 July 2021. Retrieved 10 July 2021.
{{cite web}}: CS1 maint: archived copy as title (link) - ↑ Müller, Karl Friedrich (1 May 1926). "Berechnung der Induktivität von Spulen". Archiv für Elektrotechnik (in ಜರ್ಮನ್). 17 (3): 336–353. doi:10.1007/BF01655986. ISSN 1432-0487.
{{cite journal}}: Unknown parameter|trans_title=ignored (help) - ↑ Callaghan, Edmund E.; Maslen, Stephen H. (1 October 1960). "The magnetic field of a finite solenoid". NASA Technical Reports (in ಇಂಗ್ಲಿಷ್). NASA-TN-D-465 (E-900).
- ↑ Caciagli, Alessio; Baars, Roel J.; Philipse, Albert P.; Kuipers, Bonny W.M. (2018). "Exact expression for the magnetic field of a finite cylinder with arbitrary uniform magnetization". Journal of Magnetism and Magnetic Materials. 456: 423–432. Bibcode:2018JMMM..456..423C. doi:10.1016/j.jmmm.2018.02.003. ISSN 0304-8853.
- ↑ Kurs, André; Karalis, Aristeidis; Moffatt, Robert; Joannopoulos, J. D.; Fisher, Peter; Soljačić, Marin (6 July 2007). "Wireless Power Transfer via Strongly Coupled Magnetic Resonances". Science. 317 (5834): 83–86. Bibcode:2007Sci...317...83K. doi:10.1126/science.1143254. PMID 17556549.
- ↑ Zhou, Wenshen; Huang, Shao Ying (28 September 2017). "Novel coil design for wideband wireless power transfer". 2017 International Applied Computational Electromagnetics Society Symposium (ACES): 1–2.
- ↑ Ren, Zhi Hua; Huang, Shao Ying (August 2018). "The design of a short solenoid with homogeneous B1 for a low-field portable MRI scanner using genetic algorithm". Proc. 26th ISMRM: 1720.[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ]
- ↑ Jian, L.; Shi, Y.; Liang, J.; Liu, C.; Xu, G. (June 2013). "A Novel Targeted Magnetic Fluid Hyperthermia System Using HTS Coil Array for Tumor Treatment". IEEE Transactions on Applied Superconductivity. 23 (3): 4400104. Bibcode:2013ITAS...23Q0104J. doi:10.1109/TASC.2012.2230051.
- ↑ Zhou, Wenshen; Huang, Shao Ying (July 2019). "An Accurate Model for Fast Calculating the Resonant Frequency of an Irregular Solenoid". IEEE Transactions on Microwave Theory and Techniques. 67 (7): 2663–2673. Bibcode:2019ITMTT..67.2663Z. doi:10.1109/TMTT.2019.2915514.
- ↑ Zhou, Wenshen; Huang, Shao Ying (12 April 2021). "the code for accurate model for fast calculating the resonant frequency of an irregular solenoid".
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Zhou, Wenshen; Huang, Shao Ying (October 2020). "Modeling the Self-Capacitance of an Irregular Solenoid". IEEE Transactions on Electromagnetic Compatibility. 63 (3): 783–791. doi:10.1109/TEMC.2020.3031075. ISSN 0018-9375.
- ↑ Zhou, Wenshen; Huang, Shao Ying (12 April 2021). "the code for accurate model for self-capacitance of irregular solenoids".
{{cite journal}}: Cite journal requires|journal=(help) - ↑ D. Howard Dellinger; L. E. Whittmore; R. S. Ould (1924). Radio Instruments and Measurements. Vol. C74. ISBN 9780849302527. Retrieved 7 September 2009.
{{cite book}}:|work=ignored (help)
ಬಾಹ್ಯ ಕೊಂಡಿಗಳು
[ಬದಲಾಯಿಸಿ]- ಇಂಟರಾಕ್ಟಿವ್ ಜಾವಾ ಟ್ಯುಟೋರಿಯಲ್: ಸೊಲೆನಾಯ್ಡ್ನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್, ನ್ಯಾಷನಲ್ ಹೈ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್ ಲ್ಯಾಬೋರೇಟರಿ
- ಹೈಪರ್ಫಿಸಿಕ್ಸ್ನಲ್ಲಿ ಸೊಲೆನಾಯ್ಡ್ಗಳ ಚರ್ಚೆ
- CS1 maint: archived copy as title
- CS1 errors: unsupported parameter
- CS1 ಜರ್ಮನ್-language sources (de)
- CS1: long volume value
- CS1 ಇಂಗ್ಲಿಷ್-language sources (en)
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಲೇಖನಗಳು from ಅಕ್ಟೋಬರ್ 2022
- Articles with invalid date parameter in template
- ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- CS1 errors: missing periodical
- CS1 errors: periodical ignored













![{\displaystyle A_{\phi }={\frac {\mu _{0}I}{2\pi }}{\frac {1}{l}}{\sqrt {\frac {R}{\rho }}}\left[\zeta k\left({\frac {k^{2}+h^{2}-h^{2}k^{2}}{h^{2}k^{2}}}K(k^{2})-{\frac {1}{k^{2}}}E(k^{2})+{\frac {h^{2}-1}{h^{2}}}\Pi (h^{2},k^{2})\right)\right]_{\zeta _{-}}^{\zeta _{+}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b65c9d85a95a4c38f9ede2134c8707871660e929)










![{\displaystyle B_{\rho }={\frac {\mu _{0}I}{4\pi }}{\frac {2}{l}}{\sqrt {\frac {R}{\rho }}}\left[{\frac {k^{2}-2}{k}}K(k^{2})+{\frac {2}{k}}E(k^{2})\right]_{\zeta _{-}}^{\zeta _{+}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e75c1d786d2b4a354e8ce72f0ccf5c93f1db62)
![{\displaystyle B_{z}={\frac {\mu _{0}I}{4\pi }}{\frac {1}{l}}{\frac {1}{\sqrt {R\rho }}}\left[\zeta k\left(K(k^{2})+{\frac {R-\rho }{R+\rho }}\Pi (h^{2},k^{2})\right)\right]_{\zeta _{-}}^{\zeta _{+}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53f497b1a0756653b4c2b4cddd5d64fcd055043d)








