ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ

ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಯು ಒಂದು ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಯಾಗಿದ್ದು,ಕೇವಲ ೧ ಮತ್ತು ಅದೇ ಸಂಖ್ಯೆ ಮಾತ್ರವೇ ಇದರ ಅಪವರ್ತನಗಳಾಗಿರುತ್ತವೆ :ಮೊದಲ ಇಪ್ಪತ್ತೈದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಇಂತಿವೆ:
ಕ್ರಿಸ್ತ ಪೂರ್ವ ೩೦೦ರ ಆಸುಪಾಸಿನಲ್ಲಿ ಯೂಕ್ಲಿಡ್ನಿಂದ ಪ್ರಮಾಣೀಕರಿಸಿದ ಹಾಗೆ [೨] ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಒಂದು ಅಪರಿಮಿತತೆ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ.[೨] ಸಂಖ್ಯೆ ೧ ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯಲ್ಲ. ಅಂಕಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯವು ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಅವಿಭಾಜ್ಯಗಳ ಪ್ರಧಾನ ಪಾತ್ರವನ್ನು ಸ್ಥಾಪಿಸುತ್ತದೆ: ಯಾವುದೇ ಶೂನ್ಯವಲ್ಲದ ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆ n ಅವಿಭಾಜ್ಯಗಳಾಗಿ ಪ್ರತಿನಿಧಿಸಲು ಸಾಧ್ಯ, ಅದನ್ನು ಅವಿಭಾಜ್ಯಗಳ ಫಲಿತಾಂಶ ಅಥವಾ ಅವಿಭಾಜ್ಯಗಳ ಘಾತ ಎಂದು ಬರೆಯಲಾಗುತ್ತದೆ (ಸಂಖ್ಯೆ ೧ಕ್ಕೆ ಅಪವರ್ತನದ ಖಾಲಿ ಫಲಿತಾಂಶವನ್ನು ಒಳಗೊಂಡಿದೆ). ಅದಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿ, ಅಪವರ್ತನಗಳ ಪುನಃಕ್ರಮಗೊಳಿಸುವ ಒಂದು ಸಂಭವನೀಯತೆಗೆ ಹೊರತಾಗಿ ಈ ಅಪವರ್ತನೀಕರಣ ವಿಶಿಷ್ಟವಾಗಿದೆ. ಅವಿಭಾಜ್ಯವಾಗುವ ವಿಶೇಷ ಗುಣವನ್ನು ಅವಿಭಾಜ್ಯತೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಒಂದು ನೀಡಿದ ಸಂಖ್ಯೆ n ನ ಅವಿಭಾಜ್ಯತೆಯ ಪರಿಶೀಲನೆಯನ್ನು ಅನುಸರಣೆ ವಿತರಣೆಯ ಮೂಲಕ ಮಾಡಬಹುದು, ಹಾಗೆಂದರೆ n ನ್ನು ಕ್ಕಿಂತ ಚಿಕ್ಕದಾಗಿರುವ ಎಲ್ಲಾ ಪೂರ್ಣಸಂಖ್ಯೆಯಿಂದ ಭಾಗಿಸುವುದು, ನಂತರ n m ನ ಗುಣಿತ ಹೌದೋ ಅಲ್ಲವೋ ಎಂದು, ಮತ್ತು ಆದ್ದರಿಂದ ಅವಿಭಾಜ್ಯ ಅಲ್ಲ ಆದರೆ ಒಂದು ಸಂಯುಕ್ತ ಎಂದು ಪರೀಕ್ಷಿಸುವುದು. ದೊಡ್ಡ ಅವಿಭಾಜ್ಯಗಳಿಗೆ, ಅವುಗಳು ರಚಿಸಿರುವ ಆ ತಂತ್ರಾಂಶಕ್ಕಿಂತ ವೇಗವಾಗಿರುವ, ಹೆಚ್ಚು ಸಂಕೀರ್ಣವಾಗುತ್ತಿರುವ ಕ್ರಮಾವಳಿಗಳನ್ನು ನಿರ್ಮಿಸಲಾಗಿದೆ. ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಮತ್ತು ಸಂಯುಕ್ತಗಳಿಲ್ಲದ ಫಲಿತಾಂಶವನ್ನು ನೀಡುವ ಯಾವುದೇ ಪರಿಚಿತ ಸೂತ್ರವಿಲ್ಲ. ಆದ್ಯಾಗಿಯೂ, ಅವಿಭಾಜ್ಯಗಳ ಹಂಚಿಕೆ, ಅಂದರೆ ಭಾರಿ ಪ್ರಮಾಣದಲ್ಲಿ ಅವಿಭಾಜ್ಯಗಳ ಸಂಖ್ಯಾ ಶಾಸ್ತ್ರದ ವರ್ತನೆಯನ್ನು ವಿನ್ಯಾಸಗೊಳಿಸಲು ಸಾಧ್ಯ. ಆ ದಿಕ್ಕಿನಲ್ಲಿ ಮೊದಲ ಫಲಿತಾಂಶ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಪ್ರಮೇಯವಾಗಿದ್ದು, ಇದು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆರಿಸಲ್ಪಟ್ಟ ಒಂದು n ಸಂಖ್ಯೆಯು ಅವಿಭಾಜ್ಯವಾಗಿದ್ದಲ್ಲಿ, ಅದು ಅದರ ಅಂಕೆಗಳ ಸಂಖ್ಯೆಗಳಿಗೆ ವಿಲೋಮಾನುಪಾತವಾಗಿರುತ್ತದೆ, ಅಥವಾ n ನ ವಿಘಾತವಾಗಿರುತ್ತದೆ ಎಂಬ ಸಂಭವನೀಯತೆಯನ್ನು ಹೇಳುತ್ತದೆ. ೧೯ನೇ ಶತಮಾನದ ಕೊನೆಯಿಂದ ಈ ಹೇಳಿಕೆಯನ್ನು ಸಾಬೀತು ಪಡಿಸಲಾಗುತ್ತಿದೆ. ೧೮೫೯ರ ಸಾಬೀತು ಪಡಿಸಲಾಗದ ರೀಮನ್ ಕಲ್ಪಿತ ಸಿದ್ಧಾಂತ ಅವಿಭಾಜ್ಯಗಳ ಹಂಚಿಕೆಗೆ ಸಂಬಂಧಿಸಿದ ಒಂದು ಸಂಸ್ಕರಿಸಿದ ಹೇಳಿಕೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ. ತೀವ್ರ/ಆಳವಾಗಿ ಆಧ್ಯಯನ ಮಾಡಿದರೂ ಸಹ, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಸುತ್ತಲಿನ ಹಲವು ಮೂಲಭೂತ ಪ್ರಶ್ನೆಗಳು ಅನಿಶ್ಚಿತವಾಗಿದೆ/ನಿರ್ಧಾರವಾಗದೆ ಇದೆ. ಉದಾಹರಣೆಗೆ, ಗೋಲ್ಡ್ಬಾಚ್ನ ಅಭಿಪ್ರಾಯದ ಪ್ರಕಾರ, ಎರಡಕ್ಕಿಂತ ದೊಡ್ಡದಾದ ಯಾವುದೇ ಸರಿ ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಯು ಎರಡು ಅವಿಭಾಜ್ಯಗಳ ಮೊತ್ತವಾಗಿದೆ, ಅಥವಾ ಅವಳಿ ಅವಿಭಾಜ್ಯ ಅಭಿಪ್ರಾಯದ ಪ್ರಕಾರ ಕೊನೆಯಿಲ್ಲದ ಹಲವು ಅವಳಿ ಅವಿಭಾಜ್ಯಗಳು (ಅವಿಭಾಜ್ಯಗಳ ಜೋಡಿಗಳು ಅವುಗಳ ಅಂತರ ಎರಡು) ಇವೆ. ಅವರ ಈ ಹೇಳಿಕೆಗಳ ಸರಳತೆಯ ಹೊರತಾಗಿಯೂ ಒಂದು ಶತಮಾನಕ್ಕಿಂತ ಹೆಚ್ಚು ಸಮಯದಿಂದ ಅವುಗಳನ್ನು ಬಗೆಹರಿಸಲಾಗಿಲ್ಲ. ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಇತರೆ ಗಣಿತಶಾಸ್ತ್ರ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ವಿಭಿನ್ನ ಸಾಮಾನ್ಯೀಕರಣಗಳಿಗೆ ದಾರಿ ಮಾಡಿತು, ಪ್ರಮುಖವಾಗಿ ಬೀಜಗಣಿತದ, ಅವಿಭಾಜ್ಯ ಮಾದರಿಗಳ ಕಲ್ಪನೆ ವಿಶೇಷವಾದದ್ದು. ಅವಿಭಾಜ್ಯಗಳನ್ನು ಮಾಹಿತಿ ತಂತ್ರಜ್ಞಾನದಲ್ಲಿನ ಹಲವು ನಿಯತಕಾರ್ಯಗಳಲ್ಲಿ ಅನ್ವಯಿಸಲಾಗಿದೆ, ಉದಾಹರಣೆಗೆ ಸಾರ್ವಜನಿಕ-ಕೀಲಿ ಗುಪ್ತಲಿಪಿಶಾಸ್ತ್ರ, ಅವುಗಳ ಅವಿಭಾಜ್ಯ ಅಂಶಗಳ ಒಳಗೆ ದೊಡ್ಡ ಸಂಖ್ಯೆಗಳ ಅಪವರ್ತನಮಾಡುವ ಸಮಸ್ಯೆಯನ್ನು ಇದು ಉಪಯೋಗ ಮಾಡಿಕೊಳ್ಳುತ್ತದೆ. ದೊಡ್ಡ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಹುಡುಕಲು ವಿತರಿಸಿದ ಗಣನೆಯನ್ನು ಪದೇ ಪದೇ ಬಳಸಿರುವುದು, ಅವಿಭಾಜ್ಯಗಳ ವಿಶೇಷ ವಿಧಗಳ ಆಧ್ಯಯನವನ್ನು ಮಾಡಲು ಉತ್ತೇಜಿಸಿದೆ, ಅದರಲ್ಲಿಯೂ ಮುಖ್ಯವಾಗಿ ಮರ್ಸಿನೆ ಅವಿಭಾಜ್ಯಗಳನ್ನು. ಏಕೆಂದರೆ ಇದರ ಅವಿಭಾಜ್ಯತೆಯನ್ನು ನಿರ್ಧರಿಸುವುದು ತುಲನಾತ್ಮಕವಾಗಿ ಸುಲಭದ್ದಾಗಿದೆ. ೨೦೧೦ರಂತೆ, ಗೊತ್ತಿರುವ ಅತಿ ದೊಡ್ಡ ಅವಿಭಾಜ್ಯ ಸುಮಾರು ೧೩ ಮಿಲಿಯನ್ ದಶಾಂಶ ಅಂಕೆಗಳನ್ನು ಹೊಂದಿದೆ.[೩] ೨೦೧೦ರ ಹೊತ್ತಿಗೆ ಕಂಡುಹಿಡಿಯಲ್ಪಟ್ಟ ಅತ್ಯಂತ ದೊಡ್ಡ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯು ಸುಮಾರು ೧೩ ಮಿಲಿಯನ್ ದಶಮಾಂಶ ಅಂಕೆಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಮತ್ತು ಅಂಕಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯ[ಬದಲಾಯಿಸಿ]
ಒಂದು ಸ್ವಾಭಾವಿಕವಾದ ಸಂಖ್ಯೆಯು ಖಚಿತವಾಗಿ ಎರಡು ವಿಭಿನ್ನ ಸ್ವಾಭಾವಿಕವಾದ ಸಂಖ್ಯೆ ಭಾಜಕಗಳನ್ನು ಹೊಂದಿದ್ದಲ್ಲಿ, ಅದನ್ನು ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಅಥವಾ ಕೇವಲ ಅವಿಭಾಜ್ಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ೧ಕ್ಕಿಂತ ದೊಡ್ಡದಾದ ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಗಳು ಅವಿಭಾಜ್ಯಗಳಲ್ಲವಾದರೆ ಅವುಗಳನ್ನು ಸಂಯುಕ್ತ ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಆದ್ದರಿಂದ, ೧ ಒಂದೇ ಒಂದು ಭಾಜಕವನ್ನು ಹೊಂದಿರುವುದರಿಂದ, ಅದು ಅವಿಭಾಜ್ಯವಲ್ಲ. ಅದರ ಭಾಜಕ ೧. ಆದರೂ, ೨ ಮತ್ತು ೩ ಅವಿಭಾಜ್ಯಗಳು, ಅವುಗಳು ಕರಾರುವಾಕ್ಕಾಗಿ ಎರಡು ಭಾಜಕಗಳನ್ನು ಹೊಂದಿರುವುದರಿಂದ, ಅವುಗಳು ಅನುಕ್ರಮವಾಗಿ ೧ ಮತ್ತು ೨, ಮತ್ತು ೧ ಮತ್ತು ೩. ನಂತರ, ೪, ಸಂಯುಕ್ತವಾಗಿದ್ದು, ೩ ಭಾಜಕಗಳನ್ನು ಹೊಂದಿದೆ: ೧, ೨, ಮತ್ತು ೪. ಚಿಹ್ನೆಗಳನ್ನು ಉಪಯೋಗಿಸಿ, ಒಂದು ಸಂಖ್ಯೆ n > ೧ ಇದೊಂದು ಅವಿಭಾಜ್ಯ ಎಂದು ಬರೆಯುವುದಾದರೆ, ಇದು ೧ಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿರುವ a ಮತ್ತು b ಎಂಬ ಎರಡು ಅಪವರ್ತನಗಳ ಒಂದು ಗುಣಕವಾಗಿರಬಾರದು:
- n = a · b .
ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತಕ್ಕೆ ಮತ್ತು ಗಣಿತಕ್ಕೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ನಿರ್ಣಾಯಕ ಮಹತ್ವ ಅಂಕಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯ ದಿಂದ ಬಂದಿದ್ದು, ೧ಕ್ಕಿಂತ ದೊಡ್ಡದಾದ ಧನಾತ್ಮಕ ಪೂರ್ಣಸಂಖ್ಯೆಯೊಂದನ್ನು ಒಂದು ಅಥವಾ ಹೆಚ್ಚು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ದವಾಗಿ ವಿಶೇಷವಾಗಿ ಬರೆಯಬಹುದಾಗಿದೆ. ಆದರೆ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನಗಳ ಕ್ರಮವು ಇದಕ್ಕೆ ಅಪವಾದವಾಗಿದೆ. ಹಾಗೇ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಗಳ "ಪ್ರಮುಖ ನಿರ್ಮಾಣದ ಇಟ್ಟಿಗೆಗಳು" ಎಂದು ಪರಿಗಣಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ, ನಾವು ಹೀಗೆ ಬರೆಯಲು ಸಾಧ್ಯವಿದೆ:
| ೨೩೨೪೪ | = ೨ · ೨ · ೩ · ೧೩ · ೧೪೯ |
| = ೨೨/sup> · ೩ · ೧೩ · ೧೪೯. (೨೨ ಇದನ್ನು ೨ರ ಚದರ ಅಥವಾ ಎರಡನೇ ಘಾತ ಎಂದು ಗುರುತಿಸಲಾಗುತ್ತದೆ.) |
ಈ ಉದಾಹರಣೆಯಲ್ಲಿರುವ ಹಾಗೆ, ಒಂದೇ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನ ಅನೇಕ ಬಾರಿ ಉಂಟಾಗಬಹುದು. ಒಂದು ವಿಭಜನೆ
- n = p ೧ · p ೨ · ... · p t
n ಸಂಖ್ಯೆಯ (ನಿಯಮಿತವಾಗಿ ಅನೇಕ) ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನಗಳು p ೧, p ೨, ... to p t ನ್ನು n ನ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನೀಕರಣ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅಪವರ್ತನದ ಕ್ರಮಗಳಿಗೆ ಹೊರತಾಗಿ ಅವಿಭಾಜ್ಯಗಳ ಒಳಗೆ ಯಾವುದೇ ಅಪವರ್ತನೀಕರಣ ಅನನ್ಯವಾಗಿರುತ್ತದೆ ಎಂದು ಹೇಳಲು ಅಂಕಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯವನ್ನು ಹೊಸ ರೀತಿಯಲ್ಲಿ ಬರೆಯಬಹುದಾಗಿದೆ. ಆದ್ದರಿಂದ, ಅದಾಗ್ಯೂ ಇದನ್ನು ದೊಡ್ಡ ಸಂಖ್ಯೆಗಳಿಗೆ ಅನುಷ್ಠಾನಗೊಳಿಸಲು ಹಲವು ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನೀಕರಣ ಕ್ರಮಾವಳಿಗಳಿವೆ, ಅವು ಎಲ್ಲವು ಒಂದೇ ಫಲಿತಾಂಶವನ್ನು ನೀಡಬೇಕು. ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯಗಳ ಗುಂಪನ್ನು ಹೆಚ್ಚಾಗಿ P ಮೂಲಕ ಸೂಚಿಸಲಾಗುತ್ತದೆ.
ಉದಾಹರಣೆಗಳು ಮತ್ತು ಮೊದಲ ಲಕ್ಷಣಗಳು[ಬದಲಾಯಿಸಿ]
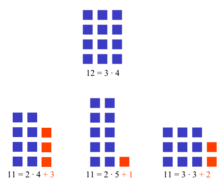
ಏಕೈಕ ಸರಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ೨ ಆಗಿದೆ, ಏಕೆಂದರೆ ಯಾವುದೇ ದೊಡ್ಡ ಸರಿ ಸಂಖ್ಯೆ ೨ರಿಂದ ಭಾಗವಾಗಬಲ್ಲದು. ಆದ್ದರಿಂದ, ಬೆಸ ಅವಿಭಾಜ್ಯ ಪದವು ೨ಕ್ಕಿಂತ ದೊಡ್ಡದಾದ ಯಾವುದೇ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಬಲ ಭಾಗಗಲ್ಲಿರುವ ಚಿತ್ರ ೧೨ ಅವಿಭಾಜ್ಯವಲ್ಲ ಎಂದು ತೋರಿಸುವ ರೇಖಾಚಿತ್ರದ ವಿಧಾನ. ಹೆಚ್ಚು ಸಾಮಾನ್ಯವಾಗಿ, ೨ ಮತ್ತು ೫ನ್ನು ಬಿಟ್ಟು ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು, ಸಾಧಾರಣ ದಶಾಂಶ ಪದ್ಧತಿಯಲ್ಲಿ ಬರೆಯಲಾಗುತ್ತದೆ, ೧, ೩, ೭ ಅಥವಾ 9 ಅಲ್ಲಿ ಕೊನೆ, ಹಾಗಾಗಿ ೦, ೨, ೪, ೬ ಅಥವಾ ೮ ಕೊನೆಗೊಳ್ಳುವ ಸಂಖ್ಯೆಗಳು ೨ರ ಗುಣಕಗಳು ಮತ್ತು 0 ಅಥವಾ ೫ ರಿಂದ ಕೊನೆಗೊಳ್ಳುವ ಸಂಖ್ಯೆಗಳು ೫ ರ ಗುಣಕಗಳು. ಹಾಗೆಯೇ, ೩ಕ್ಕಿಂತ ಮೇಲ್ಪಟ್ಟ ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ೬n − ೧ ಅಥವಾ ೬n + ೧ ನ ರೂಪವಾಗಿದೆ, ಏಕೆಂದರೆ ಎಲ್ಲಾ ಇತರೆ ಸಂಖ್ಯೆಗಳು ೨ ಅಥವಾ ೩ರಿಂದ ಭಾಗವಾಗಬಲ್ಲವು. ಇದನ್ನು ಸಾಮಾನ್ಯೀಕರಿಸಿದ್ದಾಗ, q ನ ಮೇಲ್ಪಟ್ಟ ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು q #·n + m ನ ರೂಪ, ಆದರೆ 0 < m < q , ಮತ್ತು m ≤ q ಅವಿಭಾಜ್ಯ ಅಂಶವನ್ನು ಹೊಂದಿಲ್ಲ. p ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯಾದರೆ ಮತ್ತು p ಪೂರ್ಣಸಂಖ್ಯೆಯ ಒಂದು ಫಲಿತಾಂಶ ab ಯನ್ನು ಭಾಗಿಸುತ್ತದೆಯಾದರೆ, p ಯು a ಯನ್ನು ಅಥವಾ ಭಾಗಿಸುತ್ತದೆ p ಯು b ಯನ್ನು ಭಾಗಿಸುತ್ತದೆ. ಈ ಪ್ರತಿಪಾದನೆಯು ಯೂಕ್ಲಿಡ್ನ ಲೆಮ್ಮಾ ಎಂದು ಪ್ರಚಲಿತವಾಗಿದೆ. ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನೀಕರಣಗಳ ವಿಶಿಷ್ಟತೆಯ ಕೆಲವು ಸಾಕ್ಷಿಗಳಲ್ಲಿ ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
ಸಂಖ್ಯೆ ಒಂದರ ಅವಿಭಾಜ್ಯತೆ[ಬದಲಾಯಿಸಿ]
ಈ ಸಿದ್ಧಾಂತದ ಪ್ರಾಮುಖ್ಯತೆಯು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಗುಂಪಿನಿಂದ ೧ ಅನ್ನು ಹೊರತುಪಡಿಸುವುದಕ್ಕೆ ಮುಖ್ಯ ಕಾರಣಗಳಲ್ಲಿ ಒಂದು ಆಗಿದೆ. ೧ ಅನ್ನು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಎಂದು ಒಪ್ಪಿಕೊಂಡಿದ್ದರೆ, ಈ ಸಿದ್ಧಾಂತದ ನಿಖರವಾದ ಹೇಳಿಕೆಗೆ ಇನ್ನಷ್ಟು ಮಾರ್ಪಾಡುಗಳ ಅಗತ್ಯ ಬೀಳಬಹುದಾಗಿತ್ತು, ಏಕೆಂದರೆ ೩ ಅನ್ನು ಹಲವು ರೀತಿಗಳಲ್ಲಿ ವಿಂಗಡಿಸಬಹುದಾಗಿದೆ:
- ೩ = ೧ · ೩ ಹಾಗೂ ೩ = ೧ · ೧ · ೧ · ೩ = ೧೩ · ೩.
೧೯ನೇ ಶತಮಾನದವರೆಗೆ, ಹಲವು ಗಣಿತಜ್ಞರು ೧ ಅನ್ನು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಎಂದು ಪರಿಗಣಿಸಿದ್ದರು, ಕಾರಣ ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಕೇವಲ ಒಂದು ಅಥವಾ ಅದೇ ಸಂಖ್ಯೆಯೊಂದಿಗೆ ಭಾಗ ಮಾಡಲಾಗುತ್ತದೆ, ಆದರೆ ಇದಕ್ಕೆ ನಿರ್ಧಿಷ್ಟ ಸಂಖ್ಯೆಯ ವಿಶಿಷ್ಟ ಭಾಜಕಗಳಿರುವುದಿಲ್ಲ. ೧ ಅನ್ನು ಅವಿಭಾಜ್ಯ ಎಂದು ಹೇಳಲಾದರೂ ಸಹ ಅನೇಕ ಗಣಿತ ಪುಸ್ತಕಗಳ ಒಂದು ದೊಡ್ಡ ಭಾಗ ಕಾರ್ಯಸಮ್ಮತವಾಗಿ ಉಳಿದಿದೆ, ಉದಾಹರಣೆಗೆ ಸ್ಟರ್ನ್ ಹಾಗೂ ಜಿಸಲ್ ಅವರುಗಳ ಗ್ರಂಥಗಳು. ಡೆರಿಕ್ ನೊರ್ಮೆನ್ ಲೆಹ್ಮರ್ರವರ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಪಟ್ಟಿಯಲ್ಲಿ ೧ ಮೊದಲ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯಿಂದ ಹಿಡಿದು ೧೦,೦೦೬,೭೨೧ ರವರೆಗೆ ಇದ್ದು,[೪] ಇದನ್ನು ೧೯೫೬ರಲ್ಲಿ ಮರು ಮುದ್ರಣಿಸಲಾಗಿತ್ತು.[೫] ಹೆನ್ರಿ ಲಿಬೆಸ್ಗೂರವರು ೧ ಅನ್ನು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಎಂದು ಕರೆದ ಕೊನೆಯ ವೃತ್ತಿ ನಿರತ ಗಣಿತಜ್ಞರು ಎಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ.[ಸಾಕ್ಷ್ಯಾಧಾರ ಬೇಕಾಗಿದೆ] ಅಂಕಗಣಿತದ ಮೂಲ ಸಿದ್ಧಾಂತ "ಪ್ರತಿ ಸಂಖ್ಯೆಗೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ತನ್ನ ವಿಶಿಷ್ಟವಾದ ಅಪವರ್ತನೀಕರಣ ಇರುತ್ತದೆ" ಎಂಬುದನ್ನು ಸಮಂಜಸವಾಗಿಸಲು ಶೀರ್ಷಿಕೆಯ ಬದಲಾವಣೆ ಉಂಟಾಯಿತು.[೬][೭] ಮುಂದುವರೆದು, ಸಂಖ್ಯೆ ೧ರಲ್ಲಿ ಇಲ್ಲದಿರುವ ಹಲವು ಗುಣಗಳು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳಲ್ಲಿರುತ್ತದೆ, ಉದಾಹರಣೆಗೆ ಯೂಲರ್ನ ಟೊಟಿನೆಂಟ್ ಕ್ರಿಯೆ ಅಥವಾ ಭಾಜಕಗಳ ಮೊತ್ತದ ಕ್ರಿಯೆಯಲ್ಲಿನ ಒಂದು ಸಂಖ್ಯೆಯ ತನ್ನ ಸರಿಹೊಂದುವ ಮೌಲ್ಯದ ಜೊತೆಗಿನ ಸಂಬಂಧ.[೮]
ಇತಿಹಾಸ[ಬದಲಾಯಿಸಿ]

ಪುರಾತನ ಈಜಿಪ್ಟರ ಉಳಿದ ದಾಖಲೆಗಳಿಂದ ಸುಳಿವು ಸಿಕ್ಕಿದ ಅನುಸಾರ, ಅವರಿಗೂ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಸ್ವಲ್ಪ ಜ್ಞಾನವಿತ್ತು ಎಂದು ತಿಳಿದು ಬರುತ್ತದೆ: ಉದಾಹರಣೆಗೆ ರಿಂಡ್ ಪ್ಯಾಪಿರಸ್ನ ಈಜಿಪ್ಟಿನ ಭಿನ್ನಾಂಕ ವಿಸ್ತರಣೆಗಳಲ್ಲಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಹಾಗೂ ಸಂಯುಕ್ತ ಸಂಖ್ಯೆಗಳ ಹಲವು ರೂಪಗಳಿವೆ. ಹೇಗಿದ್ದರೂ, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ದೊರೆತಿರುವ ಸ್ಪಷ್ಟ ಅಧ್ಯಯನಗಳ ಅತ್ಯಂತ ಪ್ರಾಚೀನವಾದ ದಾಖಲೆಗಳು ಪುರಾತನ ಗ್ರೀಕರಿಂದ ಬಂದಿವೆ. ಯೂಕ್ಲಿಡ್ನ ಅಂಶಗಳಲ್ಲಿ (ಸುಮಾರು ೩೦೦ BC) ಅವಿಭಾಜ್ಯತೆಗಳ ಅಪರಿಮಿತತೆ ಹಾಗೂ ಅಂಕಗಣಿತದ ಮೂಲ ಸಿದ್ಧಾಂತ ಸೇರಿ ಅವಿಭಾಜ್ಯಗಳ ಹಲವು ಮುಖ್ಯ ಸಿದ್ಧಾಂತಗಳಿವೆ. ಮರ್ಸಿನೆ ಸಂಖ್ಯೆಯಿಂದ ಪರಿಪೂರ್ಣ ಸಂಖ್ಯೆಯನ್ನು ಹೇಗೆ ನಿರ್ಮಿಸುವುದು ಎಂದು ಕೂಡ ಯೂಕ್ಲಿಡ್ ತೋರಿಸಿಕೊಟ್ಟರು. ಎರೆಟೊಸ್ತೆನೀಜ್ಗೆ ರಚಿಸಿದನೆಂದು ಹೇಳಲಾದ ಎರೆಟೊಸ್ತೆನೀಜ್ನ ಶೋಧನೆಯು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಗಣನಿಸುವ ಒಂದು ಸುಲಭ ಪದ್ಧತಿಯಾಗಿದೆ. ಆದಾಗ್ಯೂ ಕಂಪ್ಯೂಟರ್ಗಳಿಂದ ಉತ್ಪತ್ತಿಯಾದ ದೊಡ್ಡ ಅವಿಭಾಜ್ಯಗಳ ಶೋಧನೆಗೆ ಈ ಪದ್ಧತಿಯನ್ನು ಬಳಸುವುದಿಲ್ಲ. ಗ್ರೀಕರ ನಂತರ, ೧೭ನೇಯ ಶತಮಾನದವರಗೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಅಧ್ಯಯನ ಬಹಳ ಕಡಿಮೆಯಾಯಿತು. ೧೬೪೦ರಲ್ಲಿ ಪಿಯೆರ್ ಡಿ ಫೆರ್ಮಾಟ್ ಫೆರ್ಮಾಟ್ನ ಸಣ್ಣ ಸಿದ್ಧಾಂತವನ್ನು ಸ್ಥಾಪಿಸಿದನು (ರುಜುವಾತು ಇಲ್ಲದೆ). (ನಂತರ ಇದರ ರುಜುವಾತನ್ನು ಲೈಬ್ನಿಜ್ ಹಾಗೂ ಯೂಲರ್ ನೀಡಿದರು). ಫೆರ್ಮಾಟ್ನ ಈ ಸಿದ್ಧಾಂತದ ಒಂದು ವಿಶೇಷ ಸನ್ನಿವೇಶ ಬಹಳ ಮುಂಚೆಯೇ ಚೀನಾದ ಜನರಲ್ಲಿ ಪ್ರಚಲಿತದಲ್ಲಿತ್ತು. ಫೆರ್ಮಾಟ್ ಅವರು ಎಲ್ಲಾ ೨೨n + ೧ ರೂಪದ ಸಂಖ್ಯೆಗಳು ಅವಿಭಾಜ್ಯ ಎಂದು ಅನುಮಾನಿಸಿದರು (ಅವುಗಳನ್ನು ಫೆರ್ಮಾಟ್ ಸಂಖ್ಯೆಗಳು ಎಂದು ಕರೆಯಲಾಗಿತ್ತು) ಹಾಗೂ ಅವರು ಇದನ್ನು n = ೪ (ಅಥವಾ ೨೧೬ + ೧) ತನಕ ಪರಿಶೀಲಿಸಿದರು. ಹೇಗಿದ್ದರೂ, ಇದರ ಮುಂದಿನ ಫೆರ್ಮಾಟ್ ಸಂಖ್ಯೆಯಾದ ೨೩೨ + ೧ ಸಂಯುಕ್ತ ಸಂಖ್ಯೆಯಾಗಿದೆ (ಇದರ ಒಂದು ಅವಿಭಾಜ್ಯ ಭಾಜ್ಯ ೬೪೧). ಯೂಲರ್ನ ನಂತರದ ಸಂಶೋಧನೆಯ ಪ್ರಕಾರ, ಮತ್ತು ವಾಸ್ತವದಲ್ಲಿ ಇದರ ಮುಂದೆ ಯಾವುದೇ ಫೆರ್ಮಾಟ್ ಸಂಖ್ಯೆಗಳನ್ನು ಅವಿಭಾಜ್ಯ ಎಂದು ಪರಿಗಣಿಸಲಾಗುವುದಿಲ್ಲ. ಫ್ರೆಂಚ್ ಸನ್ಯಾಸಿ ಮಾರಿನ್ ಮರ್ಸಿನೆ ೨p − ೧ ರೂಪದಲ್ಲಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು p ಅವಿಭಾಜ್ಯದ ಮೂಲಕ ವೀಕ್ಷಿಸಿದ. ಇವುಗಳನ್ನು ಅವರ ಗೌರವದಲ್ಲಿ ಮರ್ಸಿನೆ ಅವಿಭಾಜ್ಯಗಳೆಂದು ಕರೆಯಲಾಗಿತು. ಯೂಲರ್ನ ಸಂಖ್ಯೆ ಸಿದ್ಧಾಂತಗಳ ಕೆಲಸಗಳಲ್ಲಿ ಅವಿಭಾಜ್ಯಗಳ ಬಗ್ಗೆ ಹಲವು ಫಲಿತಾಂಶಗಳು ಸೇರಿದ್ದವು. ಅಸಂಖ್ಯಾತ ಸರಣಿಯು[[೧/೨ + ೧/೩ + ೧/೫ + ೧/೭ + ೧/೧೧ + …]] ಬೇರೆಯಾಗುತ್ತಾ ಹೋಗುವ ಗುಣವನ್ನು ಹೊಂದಿದೆ ಎಂದು ಅವರು ತೋರಿಸಿದರು. ೧೭೪೭ರಲ್ಲಿ, ಸಮ ಪರಿಪೂರ್ಣ ಸಂಖ್ಯೆಗಳು ನಿರ್ಧಿಷ್ಟವಾಗಿ ೨p −೧(೨p − ೧) ರೂಪದ ಪೂರ್ಣಾಂಕಗಳಾಗಿರುತ್ತದೆ ಹಾಗೂ ಎರಡನೇಯ ಅಪವರ್ತನ ಮರ್ಸಿನೆ ಅವಿಭಾಜ್ಯವಾಗಿರುತ್ತದೆ ಎಂದು ಅವರು ತೋರಿಸಿದರು. ೧೯ನೇಯ ಶತಮಾನದ ಆರಂಭದಲ್ಲಿ, x ಅನಂತತೆಯೆಡೆಗೆ ಸಾಗುವಾಗ x ವರೆಗಿನ ಅವಿಭಾಜ್ಯಗಳ ಸಂಖ್ಯೆ x /ln(x )ಕ್ಕೆ ಅಸಿಂಪ್ಟೊಟಿಕ್ ಆಗಿರುತ್ತದೆ ಹಾಗೂ ln(x )ಯು x ರ ಸ್ವಾಭಾವಿಕ ಲಘುಗಣಕ ಎಂದು ಲೆಜೆಂಡ್ರೆ ಹಾಗೂ ಗಾಸ್ ಸ್ವತಂತ್ರವಾಗಿ ಶೋಧಿಸಿದರು. ರಿಮಾನ್ನನ ಅವರ ೧೮೫೯ರ ಜೀಟಾ-ಕಾರ್ಯದ ಪ್ರಬಂಧದಲ್ಲಿದ್ದ ಆಲೋಚನೆಗಳು ಒಂದು ಪ್ರೋಗ್ರಾಮ್ ಅನ್ನು ಚಿತ್ರಿಸಿತು. ಇದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯ ಸಿದ್ಧಾಂತದ ಒಂದು ರುಜುವಾತಿಗೆ ದಾರಿ ಮಾಡಿತು. ಈ ರೂಪರೇಖೆಯನ್ನು ಹೆಡಮಾರ್ಡ್ ಹಾಗೂ ಡಿ ಲಾ ವಾಲೆ ಪೂಸಿನ್ರು ಪೂರ್ಣಗೊಳಿಸಿದರು, ಇವರು ಸ್ವತಂತ್ರವಾಗಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಸಿದ್ಧಾಂತವನ್ನು ೧೮೯೬ರಲ್ಲಿ ರುಜುವಾತುಪಡಿಸಿದರು. ಟ್ರಿವಿಯಲ್ ಭಾಗಾಕಾರದ ಪದ್ಧತಿಯಲ್ಲಿ ಒಂದು ಸಂಖ್ಯೆಯನ್ನು ಅವಿಭಾಜ್ಯ ಎಂದು ರುಜುವಾತು ಮಾಡಲು (ದೊಡ್ಡ ಸಂಖ್ಯೆಗಳಿಗೆ) ಆಗುವುದಿಲ್ಲ. ಹಲವು ಗಣಿತಜ್ಞರು ದೊಡ್ಡ ಸಂಖ್ಯೆಗಳ ಮೇಲೆ ಅವಿಭಾಜ್ಯತೆಯ ಪ್ರಯೋಗಗಳ ಕೆಲಸ ಮಾಡಿದ್ದಾರೆ, ಆದರೆ ಇವು ಸಾಮಾನ್ಯವಾಗಿ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆ ರೂಪಗಳಿಗೆ ಸೀಮಿತವಿರುತ್ತದೆ. ಇದರಲ್ಲಿ ಫೆರ್ಮಾಟ್ ಸಂಖ್ಯೆಗಳಿಗೆ(೧೮೭೭) ಪೆಪಿನ್ನ ಪ್ರಯೋಗ, ಪ್ರೊಥ್ನ ಸಿದ್ಧಾಂತ (ಸುಮಾರು ೧೮೭೮), ಲುಕಾಸ್-ಲೆಹ್ಮರ್ ಅವಿಭಾಜ್ಯತೆಯ ಪ್ರಯೋಗ (1856ರಲ್ಲಿ ಆರಂಭಗೊಂಡಿತು) ಹಾಗೂ ಸಾಮಾನ್ಯೀಕರಿಸಿದ ಲುಕಾಸ್ ಅವಿಭಾಜ್ಯತೆಯ ಪ್ರಯೋಗಗಳು ಸೇರಿವೆ. ಇನ್ನು ಇತ್ತೀಚಿನ APRT-CL, ECPP ಹಾಗೂ AKS ಅಂತಹ ಗಣನ ಪದ್ಧತಿಗಳು ಕ್ರಮವಿಲ್ಲದ ಸಂಖ್ಯೆಗಳ ಮೇಲೆ ಕೆಲಸ ನಡೆಸುತ್ತವೆ, ಆದರೆ ಅವು ಬಹಳ ನಿಧಾನವಾಗಿವೆ. ಬಹಳ ಸಮಯದವರೆಗೆ, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಬಳಕೆ ಶುದ್ಧ ಗಣಿತಶಾಸ್ತ್ರವನ್ನು ಹೊರತು ಪಡಿಸಿ ಅತಿ ಸಿಮಿತವೆಂದು ಪರಿಗಣಿಸಲಾಗಿತ್ತು;[ಸಾಕ್ಷ್ಯಾಧಾರ ಬೇಕಾಗಿದೆ] ಇದು ೧೯೭೦ರಲ್ಲಿ ಹೊಸ ಪಬ್ಲಿಕ್-ಕೀ ಕ್ರಿಪ್ಟೋಗ್ರಫಿ ಪರಿಕಲ್ಪನೆಯ ಆವಿಷ್ಕಾರದ ನಂತರ ಬದಲಾಯಿತು. ಅದರಲ್ಲಿ RSA ಕ್ರಿಪ್ಟೊಸಿಸ್ಟಂ ಕ್ರಮಾವಳಿಯಂತಹ ಮೊದಲ ಗಣನ ಪದ್ಧತಿಗಳಿಗೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಆಧಾರವಾದವು. ೧೯೫೧ೞರಿಂದ ಎಲ್ಲಾ ಪರಿಚಿತ ದೊಡ್ಡ ಅವಿಭಾಜ್ಯಗಳು ಕಂಪ್ಯೂಟರ್ಗಳ ಮೂಲಕ ಕಂಡು ಹಿಡಿಯಲಾಗಿದೆ. ಇನ್ನು ದೊಡ್ಡ ಅವಿಭಾಜ್ಯಗಳ ಶೋಧನೆ ಗಣಿತ ಶಾಸ್ತ್ರವನ್ನು ಹೊರೆತ ವೃತ್ತಗಳಲ್ಲಿ ಕುತುಹಲ ಸೃಷ್ಟಿಸಿದೆ. ದ ಗ್ರೇಟ್ ಇಂಟರ್ನೆಟ್ ಮರ್ಸಿನೆ ಪ್ರೈಮ್ ಸೀರ್ಚ್ ಹಾಗೂ ಇತರ ಡಿಸ್ಟ್ರಿಬ್ಯೂಟಡ್ ಕಂಪ್ಯೂಟಿಂಗ್ ಯೋಜನೆಗಳು ಕಳೆದ ಹತ್ತರಿಂದ ಹದಿನೈದು ವರ್ಷಗಳಲ್ಲಿ ದೊಡ್ಡ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಕಂಡು ಹಿಡಿಯಲು ಜನಪ್ರಿಯವಾಗಿವೆ, ಆದರೆ ಅದೇ ಸಮಯದಲ್ಲಿ ಗಣಿತಜ್ಞರು ಅವಿಭಾಜ್ಯತೆಯ ಸಿದ್ಧಾಂತಗಳ ಜೊತೆಗೆ ತಮ್ಮ ಹೋರಾಟ ಮುಂದುವರಿಸುತ್ತಿದ್ದಾರೆ.
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಸಂಖ್ಯೆ[ಬದಲಾಯಿಸಿ]
ಹಲವು ಅಸಂಖ್ಯಾತವಾದ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳಿವೆ. ಈ ಹೇಳಿಕೆಗೆ ಪರಿಚಿತ ಪುರಾತನ ರುಜುವಾತು ಯೂಕ್ಲಿಡ್ನ ಸಿದ್ಧಾಂತ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ, ಗ್ರೀಕ ಗಣಿತಜ್ಞ ಯೂಕ್ಲಿಡ್ನ ಕಾರಣ. ಯೂಕ್ಲಿಡ್ರ ಫಲಿತಾಂಶದ ಪ್ರಕಾರ "ಯಾವುದೇ [ಸೀಮಿತ] ಕೊಟ್ಟ ಸಂಖ್ಯೆಯನ್ನು ಮೀರಿ ಅವಿಭಾಜ್ಯಗಳು ಇವೆ" ಮತ್ತು ಅವರ ಅಗತ್ಯವಾದ ರುಜುವಾತು ಈ ರೀತಿ ಇದೆ:
ಯಾವುದೇ ಸೀಮಿತ ಅವಿಭಾಜ್ಯಗಳ ಗುಂಪನ್ನು ಪರಿಗಣಿಸಿ. ಎಲ್ಲವನ್ನು ಒಟ್ಟಿಗೆ ಗುಣಿಸಿ ಮತ್ತು ೧ ಅನ್ನು ಕೂಡಿರಿ (ಯೂಕ್ಲಿಡ್ ಸಂಖ್ಯೆ ನೋಡಿ). ಫಲಿತಾಂಶವಾಗಿ ಬರುವ ಸಂಖ್ಯೆ ನಾವು ಪರಿಗಣಿಸಿದ ಸೀಮಿತ ಗುಂಪಿನ ಯಾವುದೇ ಅವಿಭಾಜ್ಯಗಳಿಂದ ಭಾಜ್ಯವಾಗುವುದಿಲ್ಲ, ಏಕೆಂದರೆ ಇವುಗಳಲ್ಲಿ ಯಾವುದಾದರಿಂದಲೂ ಭಾಗಿಸಿದಾಗ ಶೇಷ ೧ ಕೊಡುತ್ತದೆ. ಏಕೆಂದರೆ ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯವಲ್ಲದ ಸಂಖ್ಯೆಗಳನ್ನು ಅವುಗಳ ಆಧಾರವಾದ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಗುಣಿಸಿ ವಿಂಗಡಿಸಬಹುದು, ಅವಾಗ ಈ ಪರಿಣಾಮಕ ಸಂಖ್ಯೆಯೇ ಅವಿಭಾಜ್ಯವಿರಬಹುದು ಅಥವಾ ಇದರಲ್ಲಿ ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯಿರಬಹುದು ಅಥವಾ ಇವು ಪರಿಣಾಮಕ ಸಂಖ್ಯೆಯನ್ನು ವಿಂಗಡಿಸಬಲ್ಲದ ಆದರೆ ಆರಂಭದ ಸೀಮಿತ ಅವಿಭಾಜ್ಯಗಳ ಗುಂಪಿನಲ್ಲಿಲ್ಲದ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳಿರಬಹುದು. ಈ ಯಾವುದೇ ರೀತಿಯಲ್ಲಿಯಾದರೂ, ಇದರಲ್ಲಿ ನಾವು ಆರಂಭಿಸಿದ ಸೀಮಿತ ಗುಂಪಿನಲ್ಲಿಲ್ಲದ ಕನಿಷ್ಟ ಇನ್ನೊಂದು ಅವಿಭಾಜ್ಯವಿದೆ. ನಾವು ಯಾವುದೇ ಸೀಮಿತ ಗುಂಪನ್ನು ಆರಂಭಿಸಿದರೂ ಈ ವಾದ ಅನ್ವಯಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ ಇದರಲ್ಲಿ ಕೊಟ್ಟಿರುವ ಸೀಮಿತ ಸಂಖ್ಯೆಗಳಿಗಿಂತ ಹೆಚ್ಚು ಅವಿಭಾಜ್ಯಗಳಿವೆ. (ಯೂಕ್ಲಿಡ್, ಎಲಿಮೆಂಟ್ಸ್ : ಪುಸ್ತಕ IX, ಪ್ರತಿಪಾದನೆ ೨೦)
ಯಾಕೆ ಸೀಮಿತ ಹಲವು ಅವಿಭಾಜ್ಯಗಳ ಗುಣಿಸಿದ ಫಲಿತಾಂಶ P ಅನ್ನು ೧ರಿಂದ ಕೂಡಿಸಿ ಯಾವುದೇ ಅವಿಭಾಜ್ಯದಿಂದ (ಪ್ರಾಯಶಃ ಅದರಿಂದಲೇ) ಸೀಮಿತವಾಗಿರುವ ಹಲವು ಅವಿಭಾಜ್ಯಗಳು ಅಲ್ಲದೆ ಭಾಜಿಸಬಲ್ಲದಾಗಿರಬೇಕು ಎಂದು ಈ ಹಿಂದಿನ ವಾದ ವಿವರಿಸುತ್ತದೆ. ಈ ರುಜುವಾತನ್ನು ಕೆಲವು ಸಲ ಅಭಿವ್ಯಕ್ತಿಸಿದ ರೀತಿಯು ಓದುಗರು ತಪ್ಪಾಗಿ ಆಲೋಚಿಸಲು ದಾರಿ ಮಾಡಿಕೊಡುತ್ತದೆ, ಓದುಗರು P + ೧ ಯೇ ಅವಿಭಾಜ್ಯ ಎಂದು ಆಲೋಚಿಸುತ್ತಾರೆ ಹಾಗೂ ಯೂಕ್ಲಿಡ್ನ ಅವಿಭಾಜ್ಯ ಫಲಿತಾಂಶಕ್ಕೆ ೧ ಅನ್ನು ಕೂಡಿಸಿದರೆ ಅದು ಅವಿಭಾಜ್ಯವಾಗುತ್ತದೆ ಎಂದು ಆಲೋಚಿಸುತ್ತಾರೆ. ಈ ಗೊಂದಲವು ನಿರಾಕರಣೆಯನ್ನು ಬಳಸಿ ರುಜುವಾತನ್ನು ನೀಡಿದ ಮೇಲೆ ಹುಟ್ಟುತ್ತದೆ ಹಾಗೂ P ಯನ್ನು ಎಲ್ಲ ಅವಿಭಾಜ್ಯಗಳನ್ನೊಳಗೊಂಡ ಸೀಮಿತ ಗುಂಪಿನ ಗುಣಾಕಾರ ಎಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ. P + ೧ಅದೆ ಗುಂಪಿನ ಯಾವುದೇ ಸದಸ್ಯರಿಂದ ಭಾಜ್ಯವಾಗದಿದ್ದರೆ ಅದು ಯಾವ ಅವಿಭಾಜ್ಯದಿಂದಲೂ ಭಾಜ್ಯವಾಗುವುದಿಲ್ಲ ಮತ್ತು "ಈ ಕಾರಣದಿಂದ ಅದೇ ಅವಿಭಾಜ್ಯ" ಎಂದು ಆಮೇಲೆ ಪ್ರತಿಪಾದಿಸಿದರು (G.H. ಹಾರ್ಡಿ[೯] ಹೇಳಿಕೆ). ಇದು ಕೆಲವು ಸಲ ಓದುಗರಿಗೆ ತಪ್ಪು ತೀರ್ಮಾನದತ್ತ ದಾರಿ ತೋರುತ್ತದೆ, ಅದು ಏನೆಂದರೆ P ಮೊದಲ n ಅವಿಭಾಜ್ಯಗಳ ಗುಣಾಕಾರವಿದ್ದರೆ P + ೧ ಅವಿಭಾಜ್ಯ. ಆ ತೀರ್ಮಾನವು ನಂತರದಲ್ಲಿ ತಪ್ಪು ಎಂದು ರುಜುವಾತಾದ ಒಂದು ಪ್ರತಿಪಾದನೆಯ ಮೇಲೆ ಆಧಾರವಾಗಿದೆ ಹಾಗಾಗಿ ಇದು ರುಜುವಾತಾಗಿದೆ ಎಂದು ಪರಿಗಣಿಸಲಾಗುವುದಿಲ್ಲ. ಸಮ್ಮಿಶ್ರ ಸಂಖ್ಯೆಯP + ೧ ಒಂದು ವಿರುದ್ಧ ಉದಾಹರಣೆಯೆಂದರೆ
- (೨ × ೩ × ೫ × ೭ × ೧ × ೧೩) + ೧ = ೩೦,೦೩೧ = ೫೯ × ೫೦೯ (ಎರಡೂ ಅವಿಭಾಜ್ಯಗಳು).
ಅವಿಭಾಜ್ಯಗಳ ಅಪರಿಮಿತತೆಯ ಕುರಿತು ಇನ್ನೂ ಹಲವು ರುಜುವಾತುಗಳು ತಿಳಿದಿವೆ. ಎಲ್ಲ ಅವಿಭಾಜ್ಯಗಳ ಬದಲಿಗಳನ್ನು ಒಟ್ಟಾಗಿ ಕೂಡಿದಾಗ ಬರುವ ಫಲಿತಾಂಶ ಬೇರೆಯಾಗುತ್ತಾ ಹೋಗುವ ಅಪರಿಮಿತ ಸರಣಿ:
ಆ ಹೇಳಿಕೆಯ ರುಜುವಾತಿಗೆ ಕಾರಣ ಯೂಲರ್ ಆಗಿದ್ದಾನೆ. ಇನ್ನು ನಿರ್ಧಿಷ್ಟವಾಗಿ ಹೇಳುವುದಾದರೆ, S (x ) ಎಲ್ಲ p ಅವಿಭಾಜ್ಯಗಳ ಅನುಗುಣಗಳನ್ನು ಒಟ್ಟಾಗಿ ಕೂಡಿದಾಗ ಬರುವ ಫಲಿತಾಂಶವೆಂದು ಪರಿಗಣಿಸಿದರೆ p ≤ x ಜೊತೆಗೆ, ಅವಾಗ
- S (x ) = ln ln x + O(೧) for x → ∞.
ಇನ್ನೊಂದು ರುಜುವಾತನ್ನು ಫೆರ್ಮಾಟ್ ಸಂಖ್ಯೆಗಳ ಆಧಾರದ ಮೇಲೆ ಗೊಲ್ಡ್ಬಾಕ್ರವರು ನೀಡಿದರು.[೧೦] ಕುಮ್ಮರ್ನ ರುಜುವಾತು ನಿರ್ಧಿಷ್ಟವಾಗಿ ನಾಜೂಕಾಗಿದ್ದು,[೧೧] ಹ್ಯಾರಿ ಫರ್ಸ್ಟೆಬರ್ಗ್ ಸಾಮಾನ್ಯ ತಂತಿಜಾಲವನ್ನು ಬಳಸಿ ಒಂದು ರುಜುವಾತನ್ನು ನೀಡಿದ್ದಾರೆ.[೧೨] ಬರೀ ಅಪರಿಮಿತವಾಗಿ ಹಲವು ಅವಿಭಾಜ್ಯಗಳು ಇರದೆ, ಡಿರಿಕ್ಲೆಟ್ನ ಅಂಕಗಣಿತದ ಸರಣಿಗಳ ಸಿದ್ಧಾಂತ ಇದನ್ನು ಕೂಡ ಪ್ರತಿಪಾದಿಸುತ್ತದೆ. ಪ್ರತಿ ಅಂಕಗಣಿತದ ಸರಣಿ a , a + q, a + ೨q, a + ೩q, … ಇಲ್ಲಿ ಸೊನ್ನೆಗಿಂತ ಹೆಚ್ಚಾದ ಪೂರ್ಣಾಂಕಗಳು a ಹಾಗೂ q ಸಹಅವಿಭಾಜ್ಯವಾಗಿರುತ್ತವೆ ಹಾಗೂ ಅಪರಿಮಿತವಾಗಿ ಹಲವು ಅವಿಭಾಜ್ಯಗಳಿರುತ್ತವೆ. ಅವಿಭಾಜ್ಯಗಳನ್ನು ಹೊಂದಿದ ಕ್ರಮವಿಲ್ಲದ ಉದ್ದ ಸರಣಿಗಳಿವೆ ಎಂದು ಇತ್ತೀಚಿನ ಗ್ರೀನ್-ಟಾವ್ ಸಿದ್ಧಾಂತ ತೋರಿಸುತ್ತದೆ.[೧೩]
ಅವಿಭಾಜ್ಯತೆಯ ಪರಿಶೀಲನೆ[ಬದಲಾಯಿಸಿ]
ಅವಿಭಾಜ್ಯಗಳನ್ನು ಬಳಸಲು ಮೊದಲು ಕೊಟ್ಟಿರುವ ಸಂಖ್ಯೆ n ಅವಿಭಾಜ್ಯವೋ ಅಲ್ಲವೋ ಎಂದು ಪರಿಶೀಲಿಸುವುದು ಅಗತ್ಯ. ಇದನ್ನು ಪಡೆಯಲು ಹಲವು ದಾರಿಗಳಿವೆ. ಕೊಟ್ಟಿರುವ ಮಿತಿಯವರೆಗಿನ ಎಲ್ಲ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಸೀವ್ ಗಣನ ಪದ್ಧತಿಯ ಮೂಲಕ ಪಡೆಯಬಹುದು. ಇಂತಹ ಒಂದು ಪುರಾತನ ಸೀವ್ ಎಂದರೆ ಸೀವ್ ಆಫ್ ಎರಟೊಸ್ಥೆನೀಸ್ (ಮೇಲೆ ನೋಡಿ). ಇದು ತುಲನಾತ್ಮಕವಾಗಿ ಚಿಕ್ಕ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಉಪಯುಕ್ತವಾಗಿದೆ. ಆಧುನಿಕ ಸೀವ್ ಆಫ್ ಅಟ್ಕಿನ್ ಹೆಚ್ಚು ಜಟಿಲವಾಗಿದ್ದು ಸರಿಯಾಗಿ ಅತ್ಯುತ್ತಮವಾಗಿಸಿದರೆ ಇದು ಬಹಳ ವೇಗವಾಗಿ ಕಾರ್ಯ ಎಸಗುತ್ತದೆ. ಕಂಪ್ಯೂಟರ್ಗಳ ಆಗಮನದ ಮುಂಚೆ, ೧೦೭ ವರೆಗಿನ ಮಿತಿಯ ಅವಿಭಾಜ್ಯಗಳ ಪಟ್ಟಿಗಳನ್ನು ಕೂಡ ಬಳಸುತ್ತಿದ್ದರು.[೧೪] ರೂಢಿಯಲ್ಲಿರುವಂತೆ, ಮೇಲೆ ಹೇಳಲಾದ ಎರಡು ಸೀವ್ ಗಣನ ಪದ್ಧತಿಗಳು ಅವಿಭಾಜ್ಯಗಳ ಪಟ್ಟಿಯನ್ನು ಉತ್ಪತ್ತಿ ಮಾಡಿದ ಹಾಗೆ ಮಾಡುವ ಬದಲು ಕೊಟ್ಟಿರುವ ಸಂಖ್ಯೆ ಅವಿಭಾಜ್ಯವೋ ಅಲ್ಲವೋ ಎಂದು ಪರಿಶೀಲಿಸಬಹುದು. ಇದನ್ನು ಮಾಡಲು ಬಹಳ ಪ್ರಾಥಮಿಕ ಪದ್ಧತಿ ಟ್ರಿವಿಯಲ್ ಭಾಜ್ಯ ಎಂಬುದನ್ನು ಬಳಸುತ್ತಿದ್ದು, ಇದು ಈ ರೀತಿ ಕಾರ್ಯ ನಿರ್ವಹಿಸುತ್ತದೆ: ಕೊಟ್ಟಿರುವ ಒಂದು ಸಂಖ್ಯೆ n ಆಗಿದ್ದು, n ಅನ್ನು ಎಲ್ಲ m ಸಂಖ್ಯೆಗಳಿಂದ ಭಾಜಿಸುವುದು. ಇದರಲ್ಲಿ m ಸಂಖ್ಯೆಯು ಕೊಟ್ಟಿರುವ ಸಂಖ್ಯೆಯ ವರ್ಗಮೂಲಕ್ಕಿಂತ ಕಡಿಮೆ ಅಥವಾ ಸಮವಾಗಿರುತ್ತದೆ. ಯಾವುದಾದರು ಭಾಜನೆಗಳು ಪೂರ್ಣಾಂಕವಾಗಿ ಹೊರ ಬಂದರೆ ಆರಂಭದ ಸಂಖ್ಯೆಯು ಅವಿಭಾಜ್ಯವಾಗಿರುವುದಿಲ್ಲ. ಇಲ್ಲವಾದರೆ ಅದು ಒಂದು ಅವಿಭಾಜ್ಯ. ವಾಸ್ತವದಲ್ಲಿ ಈ ಟ್ರಿವಿಯಲ್ ಭಾಜನೆಗಳನ್ನು m ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಮಾಡುವುದು ಸಾಕು. ಆದರೆ ಒಂದು ಸುಲಭ ಗಣನ ಪದ್ಧತಿಯ ಮೂಲಕ, ದೊಡ್ಡ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಪರಿಶೀಲಿಸುವುದು ಕಾರ್ಯರೂಪದಲ್ಲಿ ಆಗುವುದಿಲ್ಲ ಏಕೆಂದರೆ ಪರಿಶೀಲಿಸುವ ಸಂಖ್ಯೆ ದೊಡ್ಡದಾದ ಹಾಗೆ ಸಂಭಾವನೀಯ ಭಾಜ್ಯಗಳ ಸಂಖ್ಯೆ ಕೂಡ ಹೆಚ್ಚಾಗುತ್ತದೆ: ಕೆಳಗೆ ವಿಸ್ತರಿಸಿದ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಸಿದ್ಧಾಂತದ ಅನುಸಾರ, ಅವಿಭಾಜ್ಯಗಳ ಸಂಖ್ಯೆ n ಗಿಂತ ಕಡಿಮೆ ಇದ್ದರೆ ಅದು n / (ln (n ) − ೧)ರ ಹತ್ತಿರ ಇರುತ್ತದೆ. ಹೀಗಾಗಿ, n ನ ಅವಿಭಾಜ್ಯತೆಯನ್ನು ಪರಿಶೀಲಿಸಲು ಅತಿ ದೊಡ್ಡ ಬೇಕಾದ ಅವಿಭಾಜ್ಯ ಭಾಜಕವು ಕೇವಲ ಗಿಂತ ಚಿಕ್ಕದಾಗಿರುತ್ತದೆ ಮತ್ತು ಹೀಗೆ ಇಂತಹ ಅವಿಭಾಜ್ಯ ಭಾಜಕ ಪರೀಕ್ಷಾರ್ಥಗಳ ಸಂಖ್ಯೆ ಗೆ ಹತ್ತಿರ ಇರುತ್ತದೆ. ಇದು ನಿಧಾನವಾಗಿ n ದೊಡ್ಡದಾದ ಹಾಗೆ ಹೆಚ್ಚಾಗುತ್ತಾ ಹೋಗುತ್ತದೆ, ಆದರೆ n ನ ದೊಡ್ಡ ಮೌಲ್ಯಗಳ ಮೇಲೆ ಆಸಕ್ತಿ ಇರುವುದರಿಂದ, ಗಣನೆ ಕೂಡ ದೊಡ್ಡದಾಗಿರುತ್ತದೆ: n = ೧೦ ೨೦ಗೆ ಇದು ೪೫೦ ಮಿಲಿಯನ್ ಇರುತ್ತದೆ. ಆಧುನಿಕ ಅವಿಭಾಜ್ಯತೆ ಪರೀಕ್ಷೆಯು ಗಣನ ಪದ್ಧತಿಗಳನ್ನು ಎರಡು ಮುಖ್ಯ ವಿಭಾಗಗಳಲ್ಲಿ ವಿಂಗಡಿಸಬಹುದು, ಕಂಡುಹಿಡಿಯುವಿಕೆ ಹಾಗೂ ಸಂಭಾವನೀಯಕತೆ (ಅಥವಾ "ಮಾಂಟೆ ಕಾರ್ಲೊ") ಗಣನ ಪದ್ಧತಿಗಳು. ಸಂಭಾವನೀಯ ಗಣನ ಪದ್ಧತಿಗಳು ಒಂದು ಸಮ್ಮಿಶ್ರ ಸಂಖ್ಯೆಯನ್ನು ಅವಿಭಾಜ್ಯ ಎಂದು ವರದಿ ಮಾಡಬಹುದು, ಆದರೆ ನಿಶ್ಚಿತವಾಗಿ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಸಮ್ಮಿಶ್ರ ಸಂಖ್ಯೆಗಳೆಂದು ಗುರುತಿಸುವುದಿಲ್ಲ; ಇನ್ನೊಂದೆಡೆ ಕಂಡುಹಿಡಿಯುವಿಕೆಯ ಗಣನ ಪದ್ಧತಿಗಳು ಈ ತರಹದ ತಪ್ಪುಗಳನ್ನು ಮಾಡುವುದಿಲ್ಲ. ಹಲವು ಸಲ ಸಂಭಾವನೀಯಕತೆಯ ಗಣನ ಪದ್ಧತಿ ಕಂಡುಹಿಡಿಯುವಿಕೆಯ ಗಣನ ಪದ್ಧತಿಗಿಂತ ವೇಗವಾಗಿ ಕಾರ್ಯ ಎಸಗುತ್ತವೆ ಎಂಬ ಕಾರಣಕ್ಕಾಗಿ ಅದು ಆಸಕ್ತಿಕರವಾಗಿದೆ; ಇದಲ್ಲದೆ ಈ ತರಹದ ಹಲವು ಗಣನ ಪದ್ಧತಿಗಳು ಸಮ್ಮಿಶ್ರ ಸಂಖ್ಯೆಯನ್ನು ಅವಿಭಾಜ್ಯ ಎಂದು ತಪ್ಪಾಗಿ ಗುರುತಿಸುವ ಸಂಭಾವನೀಯತೆ ಹೆಚ್ಚು. ಅವುಗಳು ವಿಶಿಷ್ಟವಾಗಿ ಒಂದು ಸ್ವೇಚ್ಛೆಯಾದ ಸಂಖ್ಯೆ a ಯನ್ನು "ಸಾಕ್ಷಿ"ಯಾಗಿ ಆರಿಸುತ್ತವೆ ಮತ್ತು ಸಾಕ್ಷಿಯನ್ನು ಒಳಗೊಂಡ ಒಂದು ಸೂತ್ರವನ್ನು ಹಾಗೂ ಸಂಭಾವ್ಯ ಅವಿಭಾಜ್ಯ n ಅನ್ನು ಪರೀಕ್ಷಿಸುತ್ತದೆ. ಹಲವು ಪುನರಾವೃತ್ತಿಗಳ ನಂತರ, ಅವುಗಳು n ಅನ್ನು "ನಿಶ್ಚಿತವಾಗಿ ಸಮ್ಮಿಶ್ರ ಸಂಖ್ಯೆ" ಅಥವಾ "ಸಂಭಾವ್ಯ ಅವಿಭಾಜ್ಯ" ಎಂದು ಘೋಷಿಸುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಫೆರ್ಮಾಟ್ನ ಅವಿಭಾಜ್ಯತೆಯ ಪರೀಕ್ಷೆ ಫೆರ್ಮಾಟ್ನ ಚಿಕ್ಕ ಸಿದ್ಧಾಂತದ ಮೇಲೆ ಆಧಾರಿತವಿದೆ (ಮೇಲೆ ನೋಡಿ). ಹೀಗಾಗಿ, ಒಂದುವೇಳೆ
- a p − ೧ (mod p )
೧ಗೆ ಸಮಾನವಾಗದಿದ್ದರೆ, p ಯು ಖಚಿತವಾಗಿ ಸಮ್ಮಿಶ್ರವಾಗಿರುತ್ತದೆ. ಹೇಗಾದರೂ, a p − ೧ = ೧ (mod p ) ಇದ್ದರು ಸಹ p ಸಮ್ಮಿಶ್ರವಾಗಿರಬಹುದು ಎಲ್ಲ a ಸಾಕ್ಷಿಗಳಿಗೆ, p ಒಂದು ಕಾರಮೈಕಲ್ ಸಂಖ್ಯೆ ಇದೆ ಎಂದು ಹೆಸರಿಸಿದಾಗ. ಸಾಮಾನ್ಯವಾಗಿ, ಯಾವ ಸಾಕ್ಷಿಗಳನ್ನು ಆರಿಸಲಾಗಿದೆ ಎಂದು ಸಂಬಂಧಿಸದೆ ಸಮ್ಮಿಶ್ರ ಸಂಖ್ಯೆಗಳನ್ನು ಸಂಭಾವಿಕ ಅವಿಭಾಜ್ಯ ಎಂದು ಘೋಷಿಸಲಾದವುಗಳನ್ನು ತುಲನಾತ್ಮಕ ಪರೀಕ್ಷೆಯ ಅನುಗುಣವಾಗಿ ಸೂಡೊಪ್ರೈಮ್ಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಹೇಗಿದ್ದರೂ, ಅತಿ ಜನಪ್ರಿಯವಾದ ಸಂಭಾವನಾತ್ಮಕ ಪರೀಕ್ಷೆಗಳು ಈ ಹಿಂಜರಿಕೆಯನ್ನು ಅನುಭವಿಸುವುದಿಲ್ಲ. ಕೆಳಗಿರುವ ಮಂಡನೆ ಕೆಲವು ಅವಿಭಾಜ್ಯತೆಯ ಪರೀಕ್ಷೆಗಳ ಹೋಲಿಕೆಯನ್ನು ತೋರಿಸುತ್ತದೆ. ಚಾಲನೆಯ ಸಮಯ n ನ್ನು ಶಬ್ದದಲ್ಲಿ ಕೊಡಲಾಗಿದೆ, ಪರೀಕ್ಷಿಸುವ ಸಂಖ್ಯೆ ಹಾಗೂ ಸಂಭಾವಿಕಾತ್ಮಕ ಗಣನ ಪದ್ಧತಿಗಳಿಗೆ k ಸಂಖ್ಯೆಯಷ್ಟು ಪರೀಕ್ಷೆಗಳನ್ನು ನಡೆಸಲಾಗುತ್ತದೆ.
| ಪರೀಕ್ಷೆ | ಆಭಿವೃದ್ಧಿಗೊಳಿಸಿದ ಸಮಯ | ನಿರ್ಣಯಕ | ಚಾಲನೆಯ ಸಮಯ | ಟಿಪ್ಪಣಿಗಳು |
|---|---|---|---|---|
| AKS ಅವಿಭಾಜ್ಯತೆಯ ಪರಿಕ್ಷೆ | ೨೦೦೨ | ಹೌದು | O(log೬+ε(n )) | |
| ಫೆರ್ಮಾಟ್ ಅವಿಭಾಜ್ಯತೆಯ ಪರೀಕ್ಷೆ | ಇಲ್ಲ | O(k · log೨n · log log n · log log log n ) | ಕಾರಮಿಕೈಲ್ ಸಂಖ್ಯೆಗಳಲ್ಲಿ ಅಸಫಲವಾಗುತ್ತದೆ. | |
| ಲುಕಾಸ್ ಅವಿಭಾಜ್ಯತೆ ಪರೀಕ್ಷೆ | ಹೌದು | n − ೧ ರ ಭಾಜಕತೆ ಅವಶ್ಯಕವಾಗಿರುತ್ತದೆ | ||
| ಸೊಲೊವೆ-ಸ್ಟ್ರಾಸ್ಸೆನ್ ಅವಿಭಾಜ್ಯತೆ ಪರೀಕ್ಷೆ | ೧೯೭೭ | ಇಲ್ಲ, ದೋಷ ಸಂಭಾವನೆ ೨−k | O(k ·log೩ n ) | |
| ಮಿಲ್ಲರ್-ರಾಬಿನ್ ಅವಿಭಾಜ್ಯತೆ ಪರೀಕ್ಷೆ | ೧೯೮೦ | ಇಲ್ಲ, ದೋಷ ಸಂಭಾವನೆ ೪−k | O(k · log೨ n · log log n · log log log n ) | |
| ಎಲಿಪ್ಟಿಕ್ ಕರ್ವ್ ಅವಿಭಾಜ್ಯತೆ ರುಜುವಾತು ನಡೆಸುವುದು | ೧೯೭೭ | ಇಲ್ಲ | O(log೫+ε(n )) | ಹ್ಯುರಿಸ್ಟಿಕ್ ಚಾಲನೆಯ ಸಮಯ |
ವಿಶೇಷ ರೀತಿಯ ಅವಿಭಾಜ್ಯಗಳು[ಬದಲಾಯಿಸಿ]

ಅವಿಭಾಜ್ಯಗಳ ಹಲವು ವಿಶಿಷ್ಟ ವಿಧಗಳಿವೆ, ಉದಾಹರಣೆಗೆ ವಿಭಿನ್ನ ಸೂತ್ರ ಮೂಲಕ ಅಥವಾ ಇದರ ದಶಾಂಶ ಅಂಕೆಗಳನ್ನು ಪರಿಗಣಿಸುವುದರ ಮೂಲಕ ಅರ್ಹತೆ ಪಡೆದಿರುವಂತಹವು. ೨p − ೧ ರಚನೆಯ ಅವಿಭಾಜ್ಯಗಳಲ್ಲಿ, p ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ, ಅವುಗಳು ಮರ್ಸಿನ್ನೆ ಅವಿಭಾಜ್ಯಗಳು ಎಂದು ಪರಿಚಿತ. ಮರ್ಸಿನೆ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಪೂರ್ಣಸಂಖ್ಯೆಗಳನ್ನು ಪರೀಕ್ಷಿಸುವಲ್ಲಿ ಇನ್ನೂ ವೇಗವಾದ ಕ್ರಮಾವಳಿ ಪರೀಕ್ಷೆಯಿವೆ ಎಂಬ ವಿಷಯಕ್ಕಾಗಿ ಅವುಗಳು ಮಹತ್ವ ಪಡೆದಿವೆ.
೨೨n + ೧ ರಚನೆಯ ಅವಿಭಾಜ್ಯಗಳು ಫೆರ್ಮ್ಯಾಟ್ ಅವಿಭಾಜ್ಯಗಳು ಎಂದು ಪರಿಚಿತವಾಗಿವೆ; ಒಂದು ವ್ಯವಸ್ಥಿತ n -gon ನ್ನು ಗೆರೆಕೋಲು ಮತ್ತು ಕಂಪಾಸ್ ಬಳಸಿ ರಚಿಸಬೇಕಾದರೆ, ಕೇವಲ, ಮತ್ತು ಕೇವಲ
- n = ೨i · m
ಆಗಿರಬೇಕು, ಮತ್ತು ಅದರಲ್ಲಿ m ಭಿನ್ನವಾದ ಫೆರ್ಮ್ಯಾಟ್ ಅವಿಭಾಜ್ಯಗಳ ಯಾವುದೇ ಸಂಖ್ಯೆಯ ಮತ್ತು i ಯು, ಸೊನ್ನೆಯು ಒಳಗೊಂಡು, ಯಾವುದೇ ಒಂದು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಯ ಗುಣಕವಾಗಿದೆ. ಕೇವಲ ಐದು ಫೆರ್ಮ್ಯಾಟ್ ಅವಿಭಾಜ್ಯಗಳು ಪರಿಚಿತವಾಗಿದ್ದು, ಅವು: ೩, ೫, ೧೭, ೨೫೭, ಮತ್ತು ೬೫,೫೩೭. ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು p ಯಾಗಿದ್ದು ೨p + ೧ ಸಹ ಅವಿಭಾಜ್ಯವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅವುಗಳನ್ನು ಸೋಫೀ ಜರ್ಮನ್ ಅವಿಭಾಜ್ಯಗಳು ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಒಂದು ಅವಿಭಾಜ್ಯ p ಯನ್ನು ಅದು ಕೆಳಗಿನ ರಚನೆಯನ್ನು ಹೊಂದಿದ್ದರೆ ಪ್ರಿಮೋರಿಯಲ್ ಅಥವಾ ಪ್ರೈಮ್-ಫ್ಯಾಕ್ಟೋರಿಯಲ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ:
- p = n # ± 1
ಇದರಲ್ಲಿ, n ಎಂಬ ಒಂದು ಸಂಖ್ಯೆಗೆ, ಇದರಲ್ಲಿ n # ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯಗಳ ಗುಣಕ೨ · ೩ · ೫ · ೭ · …ವಾಗಿರುತ್ತದೆ ≤ n. ಒಂದು ಅವಿಭಾಜ್ಯವು ರಚನೆಯಲ್ಲಿದರೇ ಅದನ್ನು ಕ್ರಮಗಣಿತ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆn! ± ೧. ಕೊನೆಯಿಲ್ಲದಷ್ಟು ಪ್ರಿಮೋರಿಯಲ್ ಅಥವಾ ಕ್ರಮಗಣಿತ ಅವಿಭಾಜ್ಯಗಳು ಇದೆಯೋ ಇಲ್ಲವೋ ಎಂಬುದನ್ನು ಇನ್ನೂ ಕಂಡುಹಿಡಿಯಲಾಗಿಲ್ಲ.
ಪರಿಚಿತ ಅತಿ ದೊಡ್ದ ಅವಿಭಾಜ್ಯದ ನೆಲೆ[ಬದಲಾಯಿಸಿ]
ಇಲೆಕ್ಟ್ರಾನಿಕ್ ಕಂಪ್ಯೂಟರ್ನ ಹುಟ್ಟಿನಿಂದ ಪರಿಚಿತ ದೊಡ್ಡ ಅವಿಭಾಜ್ಯವು ಮರ್ಸೆನ್ನೆ ಅವಿಭಾಜ್ಯ ಆಗಿದೆ, ಏಕೆಂದರೆ ಅಲ್ಲಿ ಈ ರಚನೆಯ ಸಂಖ್ಯೆಗಳಿಗೆ ಒಂದು ವಿಶಿಷ್ಟವಾಗಿ ವೇಗದ ಪ್ರೈಮ್ಯಾಲಿಟಿ ಪರೀಕ್ಷೆ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ. ಅದು ಲ್ಯೂಕಾಸ್–ಲೆಹ್ಮರ್ ಪ್ರೈಮ್ಯಾಲಿಟಿ ಪರೀಕ್ಷೆ. ಕೆಳಗೆ ಕಾಣುವ ಕೋಷ್ಟಕವು ಈ ಉಲ್ಲೇಖಿಸಿದ ವಿಧಗಳ ದೊಡ್ಡ ಪರಿಚಿತ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಒದಗಿಸುತ್ತದೆ.
| ೧೪೨,೮೯೧ | factorial prime | ೨೦೦೨ | Marchal, Carmody and Kuosa [೧೬] | |
| ೬೫೫೧೬೪೬೮೩೫೫ × ೨೩೩೩೩೩೩ ± ೧ | ೧೦೦,೩೫೫ | twin primes | ೨೦೦೯ | Twin prime search[೧೭] |
ಯಾವುದೇ ನಿರ್ದಿಷ್ಟವಾದ ರಚನೆಯಿಲ್ಲದ (ಮರ್ಸಿನೆ ಅವಿಭಾಜ್ಯಗಳ ಹಾಗೆ ಯಾವುದೇ ಸರಳವಾದ ಸೂತ್ರವಿಲ್ಲದ) ಕೆಲವು ದೊಡ್ಡ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಅರೆ-ಯಾದೃಚ್ಛಿಕವಾದ ಜೋಡಿ ಡಾಟಾದ ಒಂದು ಅಂಶವನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಮೂಲಕ ಪತ್ತೆ ಮಾಡಲಾಗಿದ್ದು, ಅದನ್ನು n ಸಂಖ್ಯೆಗೆ ಪರಿವರ್ತಿಸಿ, ಒಂದು ಧನಾತ್ಮಕ ಪೂರ್ಣಸಂಖ್ಯೆ kಯನ್ನು ತೆಗೆದುಕೊಂಡು, 256kರಿಂದ ಗುಣಿಸಿ, [೨೫೬k n + ೧, ೨೫೬k (n + ೧) − ೧] ಈ ಅಂತರದಲ್ಲಿ ಸಾಧ್ಯವಿರುವ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳಿಗಾಗಿ ಹುಡುಕುವ ಮೂಲಕ ಕಂಡುಕೊಳ್ಳಲಾಗಿದೆ. ಕನಿಷ್ಟ ೧೦ ಮಿಲಿಯನ್ ಅಂಕೆಗಳ ಒಂದು ಅವಿಭಾಜ್ಯವನ್ನು ಮೊದಲು ಕಂಡುಹಿಡಿದವರಿಗೆ ಇಲೆಕ್ಟ್ರಾನಿಕ್ ಫ್ರೊನ್ಟಿಯರ್ ಫೌಂಡೇಷನ್ US$೧೦೦,೦೦೦ ಬಹುಮಾನವನ್ನು ಘೋಷಿಸಿತ್ತು. ಅಕ್ಟೋಬರ್ ೨೨, ೨೦೦೯ರಂದು, ಈ ಬಹುಮಾನವನ್ನು ಗ್ರೇಟ್ ಇಂಟರ್ನೆಟ್ ಮರ್ಸಿನೆ ಅವಿಭಾಜ್ಯ ಹುಡುಕಾಟಕ್ಕೆ (GIMPS) ೪೫ನೇ ಪರಿಚಿತ ಮರ್ಸಿನ್ನೆ ಅವಿಭಾಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿದ ಕಾರಣಕ್ಕಾಗಿ ನೀಡಲಾಯಿತು, ಅದು ೨೪೩,೧೧೨,೬೦೯ − ೧. ಇದನ್ನು ಕಂಡು ಹಿಡಿಯಲು ಬಳಸಿದ ಕಂಪ್ಯೂಟರ್ UCLA ಗಣಿತಶಾಸ್ತ್ರ ಇಲಾಖೆ ಮಾಲೀಕತ್ವದ್ದು ಮತ್ತು ಬಹುಮಾನ ಮೊತ್ತದ ಅರ್ಧ ಹಣವನ್ನು ಪಡೆಯಿತು, ಮತ್ತು ಉಳಿದದ್ದನ್ನು ಧರ್ಮಾರ್ಥಕ್ಕೆ ಮತ್ತು ಭವಿಷ್ಯದ ಸಂಶೋಧನೆಗಾಗಿ ನೀಡಲಾಯಿತು.[೧೮] EFF ಸಹ ೧೦೦ ಮಿಲಿಯನ್ ಅಂಕೆಗಳಿಗೆ ಮತ್ತು ೧ ಬಿಲಿಯನ್ ಅಂಕೆಗಳಿಗೆ ಕ್ರಮವಾಗಿ $೧೫೦,೦೦೦ ಮತ್ತು $೨೫೦,೦೦೦ ಬಹುಮಾನ ಘೋಷಿಸಿದೆ.[೧೯]
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ರಚಿಸುವುದು[ಬದಲಾಯಿಸಿ]
ಅವಿಭಾಜ್ಯಗಳನ್ನು ಪತ್ತೆಹಚ್ಚುವಲ್ಲಿ ಮೇಲೆ ಉಲ್ಲೇಖಿಸಿರುವ ವಿಧಾನಗಳಿಗಿಂತ ಹೆಚ್ಚು ಸಮರ್ಥವಾದ ಪರಿಚಿತ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಸೂತ್ರವಿಲ್ಲ. ಕೆಳಗಿನ ಲಕ್ಷಣದೊಂದಿಗೆ ೯ ಛಲಪರಿಮಾಣಗಳು ಮತ್ತು ಒಂದು ಗಣಿತದ ಸ್ಥಿರ ರಾಶಿ/ಮಾನದಂಡಗಳಲ್ಲಿ ಡಯೋಫ್ಯಾಂಟೈನ್ ಸಮೀಕರಣಗಳ ಒಂದು ಗುಂಪು ಇದೆ: ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಗಳ ಮೇಲೆ ಸಂಭವಿಸುವ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆ ಒಂದು ಪರಿಹಾರವನ್ನು ಹೊಂದಿದಲ್ಲಿ ಮಾತ್ರ ಒಂದು ಗಣಿತದ ಸ್ಥಿರ ರಾಶಿ/ಮಾನದಂಡ ಅವಿಭಾಜ್ಯವಾಗುತ್ತದೆ. ಎಲ್ಲಾ ಲಕ್ಷಣಗಳು ಸೊನ್ನೆಗಿಂತ ಹೆಚ್ಚಾದ ಮೌಲ್ಯಗಳು ಅವಿಭಾಜ್ಯ ಹೊಂದಿರುವ ಒಂದು ಸೂತ್ರವನ್ನು ಪಡೆಯಲು ಇದನ್ನು ಉಪಯೋಗಿಸಲು ಸಾಧ್ಯ. ಕೇವಲ ಅವಿಭಾಜ್ಯ ಮೌಲ್ಯಗಳನ್ನು ಮಾತ್ರ ತೆಗೆದುಕೊಳ್ಳುವ, ಹಲವು ಛಲಪರಿಮಾಣಗಳಲ್ಲಿ ಸಹ ಪಾಲಿನಾಮಿಯಲ್ ಇಲ್ಲ. ಆದ್ಯಾಗಿಯೂ, ಸೊನ್ನೆಗಿಂತ ಹೆಚ್ಚಾದ ಮೌಲ್ಯಗಳು (ಎಲ್ಲ ಬದಲಾಗುವ ಸಂಖ್ಯೆಗಳು ಧನಾತ್ಮಕ ಪೂರ್ಣ ಸಂಖ್ಯೆ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುವುದರಿಂದ) ಖಚಿತವಾಗಿ ಅವಿಭಾಜ್ಯಗಳಾಗಿರುವ ಹಲವು ಛಲಪರಿಮಾಣಗಳಲ್ಲಿ ಪಾಲಿನಾಮಿಯಲ್ಗಳಿವೆ (ಉದಾಹರಣೆಗೆ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಸೂತ್ರ ನೋಡಿ). ಇನ್ನೊಂದು ಸೂತ್ರ ಮೇಲೆ ಉಲ್ಲೇಖಿಸಿರುವ ವಿಲ್ಸನ್ನ ಪ್ರಮೇಯದ ಮೇಲೆ ಆಧಾರವಾಗಿದೆ, ಮತ್ತು ಸಂಖ್ಯೆ ೨ನ್ನು ಹಲವು ಬಾರಿ ಉತ್ಪಾದಿಸುತ್ತದೆ ಮತ್ತು ಇತರೆ ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಖಚಿತವಾಗಿ ಒಂದು ಬಾರಿ. ಅವಿಭಾಜ್ಯಗಳನ್ನು ಉತ್ಪಾದಿಸುವ ಇದನ್ನು ಹೋಲುವ ಇತರೆ ಸೂತ್ರಗಳು ಇವೆ.
ಹಂಚಿಕೆ-ವಿತರಣೆ[ಬದಲಾಯಿಸಿ]

ಕೊಟ್ಟಿರುವ ವಾಸ್ತವದ ಅನುಸಾರ ಅವಿಭಾಜ್ಯಗಳ ಅಪರಿಮಿತತೆ ಇದ್ದರೆ, ಅವಿಭಾಜ್ಯಗಳ ಹಂಚಿಕೆಯಲ್ಲಿ ವಿನ್ಯಾಸ ಅಥವಾ ಅಸಹಜತೆಯನ್ನು ಹುಡುಕುವುದು ಸಹಜ. ಸಂಖ್ಯೆ ಸಿದ್ಧಾಂತಿಗಳಿಗೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಹಂಚಿಕೆ ಮಾದರಿಯನ್ನು ರೂಪುಗೊಳಿಸುವುದು ಒಂದು ಜನಪ್ರಿಯ ತಪಾಸಣೆಯ ವಿಷಯವಾಗಿದೆ. ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಬಹುತೇಕ ಹಂಚಿಕೆಗಳ ಉಸ್ತುವಾರಿ ನಿರ್ವಹಿಸಲು ಕಾನೂನುಗಳಿದ್ದರೂ (ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಸಿದ್ಧಾಂತ ಹಾಗೂ ಬರ್ಟೆಂಡ್ನ ಸಮರ್ಥನೆಯಂತಹವು) ಕೂಡಾ ವೈಯಕ್ತಿಕ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ನೈಜ ಸಂಖ್ಯೆಗಳಲ್ಲಿ ಇರುವುದು (ಈವರೆಗೆ) ಅನಿರೀಕ್ಷಿತವಾಗಿದೆ. ಲಿಯೊನ್ಹಾರ್ಡ್ ಯೂಲರ್ ಹೀಗೆ ಹೇಳಿದ್ದಾರೆ:
ಗಣಿತಜ್ಞರು ಇವತ್ತಿನವರೆಗೂ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಅನುಕ್ರಮದಲ್ಲಿ ಕೆಲವು ನಿರ್ಧಿಷ್ಟ ರೀತಿಯನ್ನು ಕಂಡು ಹಿಡಿಯಲು ವ್ಯರ್ಥವಾಗಿ ಪ್ರಯತ್ನಿಸಿದ್ದಾರೆ ಮತ್ತು ಇದು ಮನಸ್ಸು ಎಂದಿಗೂ ಭೇದಿಸಲಾಗದ ನಿಗೂಢತೆ ಎಂದು ನಂಬಲು ನಮ್ಮ ಬಳಿ ಕಾರಣವಿದೆ.[೨೦]
೧೯೭೫ರ ಒಂದು ಉಪನ್ಯಾಸದಲ್ಲಿ ಡೊನ್ ಜಾಗಿರ್ ಹೀಗೆ ಪ್ರತಿಕ್ರಿಯಿಸಿದರು:
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಹಂಚಿಕೆಯ ಬಗ್ಗೆ ಎರಡು ವಾಸ್ತವಿಕತೆಗಳಿವೆ, ಇದರಿಂದ ಅವುಗಳು ನಿಮ್ಮ ಹೃದಯದ ಮೇಲೆ ಶಾಶ್ವತವಾದ ಮನದಟ್ಟಾಗುವಂತೆ ಮಾಡುತ್ತೇನೆ ಎಂಬ ಅಗಾಧವಾದ ಆಸೆಯನ್ನಿಟ್ಟು ಕೊಂಡಿದ್ದೇನೆ. ಮೊದಲನೆಯದು, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ತಮ್ಮ ಕುರಿತ ಸಾಧಾರಣ ವ್ಯಾಖ್ಯಾನದಿಂದ ಹಾಗೂ ನೈಜ ಸಂಖ್ಯೆಗಳ ನಿರ್ಮಾಣದಲ್ಲಿ ಘಟಕಗಳ ಪಾತ್ರ ವಹಿಸಿದರೂ ಸಹ ಅವು ನೈಜ ಸಂಖ್ಯೆಗಳೊಳಗೆ ಕಳೆಗಳಂತೆ ಬೆಳೆಯುತ್ತವೆ. ಇವು ಸಾಧ್ಯತೆಯ ಹೊರತಾಗಿ ಯಾವ ನಿಯಮವನ್ನೂ ಪಾಲಿಸುವುದಿಲ್ಲ, ಹಾಗೂ ಯಾರೂ ಕೂಡ ಮುಂದಿನ ಸಂಖ್ಯೆ ಎಲ್ಲಿ ಮೊಳಕೆ ಯೊಡೆದು ಹೊರಗೆ ಬರುತ್ತದೆ ಎಂದು ಹೇಳಲಾರರು. ಎರಡನೆಯ ವಾಸ್ತವಿಕತೆ ಇನ್ನಷ್ಟು ಆಶ್ಚರ್ಯ ಮೂಡಿಸುತ್ತದೆ. ಏಕೆಂದರೆ ಇದು ವಿರುದ್ಧವಾದ ಹೇಳಿಕೆ ನೀಡುತ್ತದೆ: ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಕ್ರಮವತ್ತತೆ ದಿಗ್ಭ್ರಮೆ ಮೂಡಿಸುತ್ತದೆ, ಈ ವರ್ತನೆಯ ಹಿನ್ನೆಲೆಯಲ್ಲಿ ನಿಯಮಗಳಿವೆ ಮತ್ತು ಈ ನಿಯಮಗಳನ್ನು ಅವುಗಳು ಸೈನ್ಯದ ನಿಖರತೆಯಂತೆ ಪಾಲಿಸುತ್ತವೆ.[೨೧]
ಯೂಲರ್ ಈ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಗಮನಿಸಿದರು:
- n ೨ + n +೪೧
ಇದು n < ೪೦ ಗೆ (ಆದರೆ ಅಷ್ಟು ದೊಡ್ಡ n ಅಗತ್ಯವಿಲ್ಲ) ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಕೊಡುತ್ತದೆ. ಇದರಿಂದಾಗಿ ಒಂದು ಆಳವಾದ ಬೀಜಗಣಿತ ಸಂಖ್ಯೆ ಸಿದ್ಧಾಂತಕ್ಕೆ ದಾರಿ ಮಾಡಿಕೊಡುತ್ತದೆ, ಅದರಲ್ಲೂ ಹೆಚ್ಚು ನಿಖರವಾಗಿ ಹೀಗ್ನರ್ ಸಂಖ್ಯೆಗಳ ಕುರಿತು. ಉಲಮ್ ಸ್ಪೈರಲ್ ಎಲ್ಲ ನೈಜ ಸಂಖ್ಯೆಗಳನ್ನು ಸುರುಳಿಯ ಹಾಗೆ ತೋರಿಸುತ್ತದೆ. ಆಶ್ಚರ್ಯಕರವಾಗಿ, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಕೆಲವು ನಿರ್ಧಿಷ್ಟ ಓರೆಯಾದವುಗಳ ಮೇಲೆ ಗುಂಪಾಗಿ-ಸೇರುತ್ತವೆ ಹಾಗೂ ಇತರರಲ್ಲಿ ಹೀಗೆ ಆಗುವುದಿಲ್ಲ.
ಒಂದು ನೀಡಿದ ಸಂಖ್ಯೆಯ ಕೆಳಗೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಸಂಖ್ಯೆ[ಬದಲಾಯಿಸಿ]

ಅವಿಭಾಜ್ಯ-ಎಣಿಕೆಯ ಕಾರ್ಯ π(n )ನ್ನು n ವರೆಗೆ ಅವಿಭಾಜ್ಯಗಳ ಸಂಖ್ಯೆ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ಉದಾಹರಣೆಗೆ π(೧೧) = ೫, ೧೧ಕ್ಕಿಂತ ಕಡಿಮೆ ಅಥವಾ ಸಮನಾದ ಐದು ಅವಿಭಾಜ್ಯಗಳಿವೆ. n ವರೆಗಿನ ಪ್ರತಿ ಅವಿಭಾಜ್ಯವನ್ನು ಗಣನೆಮಾಡಲು ಸಾಧ್ಯವಾಗುವುದಕ್ಕಿಂತ ಶೀಘ್ರವಾಗಿ π(n )ನ ಖಚಿತ ಮೌಲ್ಯವನ್ನು ಗಣನೆಮಾಡಲು ಪರಿಚಿತ ಕ್ರಮಾವಳಿಗಳಿವೆ. π(೧೦೨೦)ರಷ್ಟು ದೊಡ್ದದಾದ ಮೌಲ್ಯಗಳನ್ನು ಅಧುನಿಕ ಕಂಪ್ಯೂಟರ್ಗಳಿಂದ ಕ್ಷೀಪ್ರವಾಗಿ ಮತ್ತು ಖಚಿತವಾಗಿ ಎಣಿಸಲು ಸಾಧ್ಯ. ಅಧುನಿಕ ಉಪಕರಣದ ಮಿತಿಯ ಹೊರಗಿನ,n ನ ದೊಡ್ಡದಾದ ಮೌಲ್ಯಗಳಿಗೆ, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯಾ ಪ್ರಮೇಯ ಒಂದು ಅಳತೆಯನ್ನು ಒದಗಿಸುತ್ತದೆ: π(n ) ಸುಮಾರು n /ln(n ಆಗಿದೆ). ಇನ್ನೊಂದು ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, n ದೊಡ್ಡದಾದ ಹಾಗೆ, n ಗಿಂತ ಚಿಕ್ಕದಾದ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯು n ನಲ್ಲಿನ ಸಂಖ್ಯೆಗಳಿಗೆ ವಿಲೋಮಾನುಪಾತವಾಗಿರುತ್ತದೆ. ಇನ್ನೂ ಉತ್ತಮ ಅಂದಾಜುಗಳು ಪರಿಚಿತವಾಗಿವೆ; ಉದಾಹರಣೆಗೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯಾ ಪ್ರಮೇಯ#ವಿಘಾತದ ಸಮಗ್ರ ನಿಯಮಗಳಲ್ಲಿ ಅವಿಭಾಜ್ಯ-ಎಣಿಕೆಯ ಕಾರ್ಯ. ಒಂದುವೇಳೆ n ೧ಕ್ಕಿಂತ ದೊಡ್ಡದಾದ ಒಂದು ಖಚಿತ ಪೂರ್ಣಸಂಖ್ಯೆಯಾದರೆ, ಯಾವಾಗಲೂ ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ p ಇದ್ದು, ಅದು n < p < ೨n ಆಗಿರುತ್ತದೆ (ಬರ್ಟ್ರಾಂಡ್ನ ಮೂಲಭೂತ ನಿಯಮ).
ಆವಿಭಾಜ್ಯಗಳ ನಡುವೆ ಅಂತರ[ಬದಲಾಯಿಸಿ]
ನಿರಂತರ ಪೂರ್ಣಸಂಖ್ಯೆಗಳ ಒಂದು ಅನುಕ್ರಮದಲ್ಲಿ ಯಾವುದೂ ಅವಿಭಾಜ್ಯವಾದದ್ದು ಇಲ್ಲವಾದರೆ, ಅದು ಒಂದು ಅವಿಭಾಜ್ಯ ಅಂತರ ವನ್ನು ನಿರ್ಮಾಣಮಾಡುತ್ತದೆ. ಕ್ರಮವಿಲ್ಲದ ಉದ್ದವಾದ ಅವಿಭಾಜ್ಯ ಅಂತರಗಳಿವೆ : ೧ಗಿಂತ ದೊಡ್ಡದಾದ ಯಾವುದೇ ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆ n ಗೆ, ಅನುಕ್ರಮ (ಅಂಕನ ಪದ್ಧತಿ n !ಗೆ ಸಂಕೇತನ ಓದಿ)
- n
! + ೨, n ! + ೩, …, n ! + n ಇದೊಂದು n − ೧ ನಿರಂತರ ಸಂಯುಕ್ತ ಪೂರ್ಣಸಂಖ್ಯೆಗಳ ಒಂದು ಅನುಕ್ರಮವಾಗಿದೆ, ಆದ್ದರಿಂದ
- n
! + m = m · (n !/m + ೧) = m · [(೧ · ೨ · … · (m − ೧) · (m + ೧) … n ) + ೧] ಯಾವುದೇ ೨ ≤ m ≤ n ಗೆ ಸಂಯುಕ್ತ. ಇದಲ್ಲದೇ, ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಅಂತರಗಳು ಅನುಪಾತದಲ್ಲಿ ಕ್ರಮವಿಲ್ಲದೆ ಚಿಕ್ಕದಾಗುತ್ತದೆ: ಭಾಗಲಬ್ಧವು
- (p i + ೧ − p i ) / p i ,
ಇಲ್ಲಿ p i i ನೇ ಅವಿಭಾಜ್ಯವನ್ನು ಸೂಚಿಸುತ್ತದೆ (ಉದಾ., p ೧ = ೨, p ೨ = ೩, ಇತ್ಯಾದಿ.), ಮತ್ತು i ಅನಂತವನ್ನು ತಲುಪುತ್ತಿರುವಂತೆಯೇ ಅದು ಸೊನ್ನೆಯನ್ನು ತಲುಪುತ್ತದೆ.
ಅನಿಶ್ಚಿತ ಪ್ರಶ್ನೆಗಳು[ಬದಲಾಯಿಸಿ]
ರೀಮನ್ ಸಿದ್ಧಾಂತ[ಬದಲಾಯಿಸಿ]
ರೀಮನ್ ಕಲ್ಪನೆ ಯು ಒಂದು ತುಂಬ ಪುರಾತನವಾದದ್ದು, ೨೦೧೦ರಲ್ಲಿಯೂ ಬಿಡಿಸಲಾಗದ ಗಣಿತದ ಊಹೆಗಳನ್ನು ಹೊಂದಿದ್ದು, ಅದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ರೀಮನ್ ಜೀಟಾ ಕಾರ್ಯವನ್ನು ಅರ್ಥೈಸಿಕೊಳ್ಳುವುದು ಅವಶ್ಯಕವಾಗಿದೆ (s ಒಂದು ಸಂಯುಕ್ತ ಸಂಖ್ಯೆಯಾಗಿದ್ದು ಅದರ ನೈಜ ಭಾಗವು ೧ಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿರುತ್ತದೆ).
ಅಂಕಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯದ ಫಲಿತಾಂಶ ಎರಡನೇಯ ಗುಣವಾಗಿದ್ದು, ಜೀಟಾ ಕಾರ್ಯವು ಅಳವಾಗಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಜೊತೆ ಆಳವಾಗಿ ಸಂಪರ್ಕ ಹೊಂದಿದೆ ಎಂದು ತೋರಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಅಸಂಖ್ಯಾತವಾಗಿ ಹಲವು ಅವಿಭಾಜ್ಯಗಳಿವೆ ಎಂಬ ವಸ್ತುಸ್ಥಿತಿಯನ್ನು (ಮೇಲೆ ನೋಡಿ), ಅವುಗಳನ್ನು ಸಂಗತ ಸರಣಿಗಳ ಚದುರುವಿಕೆಯಿಂದ ಓದಲು ಸಾಧ್ಯ:
ಜೀಟಾ ಕಾರ್ಯದ ಸಮೃದ್ಧಿಗೆ ಮತ್ತು ಅಧುನಿಕ ಬೀಜಗಣಿತದ ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತದ ಒಂದು ಮಿನುಗು ನೋಟಕ್ಕೆ ಮತ್ತೊಂದು ಉದಾಹರಣೆ ಎಂದರೆ ಯೂಲರ್ ನ ಕಾರಣದಿಂದ ಉಂಟಾದ ಈ ಮುಂದಿನ ಗುರುತು(ಬ್ಯಾಸೆಲ್ ಸಮಸ್ಯೆ):
ರೀಮನ್ನ ಕಲ್ಪನೆ ζ-ಕಾರ್ಯದ ಸೊನ್ನೆಗಳೊದಿಗೆ ಸಂಬಂಧಪಟ್ಟಿದೆ (ಉದಾ., s ಹೇಗಿದೆಯೆಂದರೆ ζ(s ) = 0). ಅವಿಭಾಜ್ಯಗಳು ಎಷ್ಟೂ ಸಾಧ್ಯವೋ ಅಷ್ಟು ಕ್ರಮವಾಗಿ ವಿತರಿಸಲಾಗಿದೆ ಎಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಸಂಪರ್ಕ ಮೂಲಭೂತವಾಗಿ ಹೇಳುತ್ತದೆ. ಒಂದು ಭೌತಿಕ ದೃಷ್ಟಿಕೋನದಿಂದ, ಈ ಕಲ್ಪನೆಯು, ಕ್ರಮವಿಲ್ಲದಿರುವಿಕೆಯಲ್ಲಿ ಅವಿಭಾಜ್ಯಗಳ ಹಂಚಿಕೆಯು ಸ್ವೇಚ್ಛೆಯಾದ ಶಬ್ದದಿಂದ ಮಾತ್ರ ಬರುತ್ತದೆ ಸ್ಥೂಲವಾಗಿ ಹೇಳುತ್ತದೆ. ಗಣಿತಶಾಸ್ತ್ರದ ದೃಷ್ಟಿಕೋನದಿಂದ, ಈ ಕಲ್ಪನೆ ಸ್ಥೂಲವಾಗಿ ಹೀಗೆ ಹೇಳುತ್ತದೆ, ಅವಿಭಾಜ್ಯಗಳ ಏಸಿಂಪ್ಟೋಟಿಕ್ ಹಂಚಿಕೆ (೧/ log x ರಷ್ಟು) x ನ ವರ್ಗಮೂಲದ ಬಗ್ಗೆ ಉದ್ದದ ಅತಿ ಕಡಿಮೆ ಮಧ್ಯಾಂತರಗಳಿಗೆ ಸಹ ಅನ್ವಯಿಸುತ್ತದೆ (ಸುಮಾರು x ಮಧ್ಯಾಂತರಗಳಿಗೆ). ಈ ಕಲ್ಪನೆಯನ್ನು ವ್ಯಾಪಕವಾಗಿ/ಬಹುಮಟ್ಟಿಗೆ ಸರಿಯೆಂದು ನಂಬಲಾಗಿದೆ. ವಿಶೇಷವಾಗಿ, ಸರಳ ಊಹೆ ಎಂದರೆ ಅವಿಭಾಜ್ಯಗಳು ಸಕಾರಣವಿಲ್ಲದೆ ಅರ್ಥಪೂರ್ಣವಾದ ಕ್ರಮವಿಲ್ಲದಿರುವಿಕೆಗಳನ್ನು ಹೊಂದಿರುವ ಹಾಗಿಲ್ಲ.
ಇತರೆ ಅಭಿಪ್ರಾಯಗಳು[ಬದಲಾಯಿಸಿ]
ರೀಮನ್ ಕಲ್ಪನೆಯ ಹೊರತಾಗಿ, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಕುರಿತು ಹಲವು ಅಭಿಪ್ರಾಯಗಳಿವೆ, ಅದರಲ್ಲಿ ಹೆಚ್ಚಿನವು ಹಳೆಯದು: ಉದಾಹರಣೆಗೆ, ಎಲ್ಲಾ ನಾಲ್ಕು ಲ್ಯಾಂಡೌನ ಸಮಸ್ಯೆಗಳು ೧೯೧೨ರಿಂದ (ಗೋಲ್ಡ್ಬ್ಯಾಚ್, ಅವಳಿ ಅವಿಭಾಜ್ಯ, ಲೆಂಜೆಂಡ್ರ್ ಅಭಿಪ್ರಾಯ ಮತ್ತು n ೨+೧ ಅವಿಭಾಜ್ಯಗಳ ಬಗ್ಗೆ ಅಭಿಪ್ರಾಯ) ಇನ್ನೂ ಬಗೆಹರಿಯದೆ ಉಳಿದಿವೆ. ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಒಂದು ಅನಂತತೆ ಕೆಲವು ನಿಯಮಗಳಿಗೆ ಗುರಿಯಾಗಿ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆಯೇ ಎಂಬ ಪ್ರಶ್ನೆಯೊಂದಿಗೆ ಹೆಚ್ಚಿನ ಊಹೆಗಳು ವ್ಯವಹರಿಸುತ್ತವೆ. ಅನಂತವಾದ ಫಿಬೊನಾಚಿ ಅವಿಭಾಜ್ಯಗಳು[೨೨] ಮತ್ತು ಅನಂತವಾದ ಮರ್ಸಿನೆ ಅವಿಭಾಜ್ಯಗಳು ಇವೆ, ಆದರೆ ಅಸಂಖ್ಯಾತ ಫರ್ಮ್ಯಾಟ್ ಅವಿಭಾಜ್ಯಗಳಿಲ್ಲ ಎಂಬ ಊಹೆಯಿದೆ.[೨೩] ಒಂದು ಅನಂತ ಸಂಖ್ಯೆಯ ಅವಿಭಾಜ್ಯ ಯೂಕ್ಲಿಡ್ ಸಂಖ್ಯೆಗಳು ಇವೆಯೇ ಇಲ್ಲವೇ ಎಂಬುದು ತಿಳಿದಿಲ್ಲ. ಅವಿಭಾಜ್ಯಗಳ ವಿತರಣೆ ಪ್ರಕಲ್ಪನೆಯ ಕುರಿತಾಗಿ ಹಲವು ಊಹೆಗಳಿವೆ. ಅನಂತವಾದ ಅವಳಿ ಅವಿಭಾಜ್ಯಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ ಎಂಬ ಊಹೆಯಿದ್ದು, ಅವು ೨ ಅಂತರ ಹೊಂದಿರುವ ಅವಿಭಾಜ್ಯಗಳ ಜೋಡಿಗಳಾಗಿವೆ.(ಅವಳಿ ಅವಿಭಾಜ್ಯ ಊಹೆ). ಪೋಲಿನ್ಯಾಕ್ನ ಊಹೆ ಆ ಊಹೆಯನ್ನು ಬೆಂಬಲಿಸುತ್ತದೆ. ಇದರ ಪ್ರಕಾರ, ಪ್ರತಿ ಪೂರ್ಣಸಂಖ್ಯೆ n ಗೆ, ಅನಂತವಾದ ಅವಿಭಾಜ್ಯಗಳ ಕ್ರಮಬದ್ಧವಾದ ಜೋಡಿಗಳಿವೆ, ಮತ್ತು ಅವುಗಳ ನಡುವೆ ೨n ನ ಅಂತರವಿರುತ್ತದೆ. n ೨ + ೧.[೨೪] ರಚನೆಯ/ವಿಧದ ಕೊನೆಯಿಲ್ಲದ ಹಲವು ಅವಿಭಾಜ್ಯಗಳಿವೆ ಎಂಬ ಊಹೆಯಿದೆ. ಈ ಊಹೆಗಳು ವಿಸ್ತಾರವಾದ ಶಿಂಜೆಲ್ನ ಸಿದ್ಧಾಂತ Hನ ವಿಶೇಷ ಸನ್ನಿವೇಶಗಳಾಗಿವೆ.[ಸಾಕ್ಷ್ಯಾಧಾರ ಬೇಕಾಗಿದೆ] ಬ್ರೊಕಾರ್ಡ್ನ ಊಹೆಯ ಪ್ರಕಾರ, 2ಕ್ಕಿಂತ ದೊಡ್ಡದಾದ ಕ್ರಮಬದ್ಧವಾದ ಅವಿಭಾಜ್ಯಗಳ ವರ್ಗಗಳ ನಡುವೆ ಯಾವಾಗಲೂ ಕನಿಷ್ಟ ನಾಲ್ಕು ಅವಿಭಾಜ್ಯಗಳಿರುತ್ತವೆ. ಲೆಜೆಂಡ್ರೆಯ ಊಹೆಯು n ೨ ಮತ್ತು (n + ೧)೨ ನಡುವೆ ಪ್ರತಿ ಸೊನ್ನೆಗಿಂತ ಹೆಚ್ಚಾದ ಪೂರ್ಣಸಂಖ್ಯೆ n ಗೆ ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯಿದೆ ಎಂದು ಹೇಳುತ್ತದೆ. ದೃಢವಾದ ಕ್ರ್ಯಾಮರ್ನ ಊಹೆಯದ ಮೂಲಕ ಇದು ವ್ಯಕ್ತವಾಗಿದೆ. ಇತರೆ ಅಭಿಪ್ರಾಯಗಳು ಸಂಖ್ಯೆಗಳ ಅಧಿಕ ಆಕಾರಗಳನ್ನು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಜೊತೆ ನಿರೂಪಿಸುತ್ತವೆ:ಗೋಲ್ಡ್ಬ್ಯಾಚ್ ಅಭಿಪ್ರಾಯ ಹೀಗೆ ಪ್ರತಿಪಾದಿಸುತ್ತದೆ, ೨ಕ್ಕಿಂತ ಹೆಚ್ಚಾದ ಪ್ರತಿ ಸರಿ ಪೂರ್ಣಸಂಖ್ಯೆಯನ್ನು ಎರಡು ಅವಿಭಾಜ್ಯಗಳ ಒಂದು ಮೊತ್ತ ಎಂದು ಬರೆಯಲು ಸಾಧ್ಯ, ಹಾಗೇ ೫ಕ್ಕಿಂತ ಹೆಚ್ಚಾದ ಪ್ರತಿ ಬೆಸ ಪೂರ್ಣಸಂಖ್ಯೆಯನ್ನು ಮೂರು ಅವಿಭಾಜ್ಯಗಳ ಒಂದು ಮೊತ್ತ ಎಂದು ಬರೆಯಲು ಸಾಧ್ಯ ಎಂದು ಅನಿಶ್ಚಿತ ಆವೃತ್ತಿ ಹೇಳುತ್ತದೆ.
ಅಳವಡಿಕೆಗಳು[ಬದಲಾಯಿಸಿ]
ಒಂದು ದೀರ್ಘ ಸಮಯದವರೆಗೆ, ಸ್ಥೂಲವಾಗಿ ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತ ಮತ್ತು ಪ್ರತ್ಯೇಕವಾಗಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಅಧ್ಯಯನವು ವಿಷಯದ ಅಧ್ಯಯನದ ಸ್ವಹಿತದೃಷ್ಟಿಯ ಬಾಹ್ಯ ಅಳವಡಿಕೆಗಳಿಲ್ಲದೆ, ಶುದ್ಧ ಗಣಿತಶಾಸ್ತ್ರದ ಅಧಿಕೃತ/ಅಂಗೀಕೃತ ಉದಾಹರಣೆಯಾಗಿ ಕಂಡುಬಂದಿದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳುವುದಾದರೆ, ಸಂಖ್ಯಾ ಸಿದ್ದಾಂತಿಗಳಾದ ಬ್ರಿಟಿಷ್ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞ ಜಿ.ಎಚ್. ಹಾರ್ಡಿ ಸಂಪೂರ್ಣವಾಗಿ ಯಾವುದೇ ಮಿಲಟರಿ ಮಹತ್ವವನ್ನು ಹೊಂದಿರದ ಕೆಲಸ ಮಾಡಿರುವುದಕ್ಕಾಗಿ ಅವರ ಬಗ್ಗೆ ಅವರೇ ಅಭಿಮಾನ ಪಡುತ್ತಾರೆ.[೨೫] ಆದರೆ,ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಸಾರ್ವಜನಿಕ ಕೀ ಗುಪ್ತ ಲಿಪಿಶಾಸ್ತ್ರ ಕ್ರಮಾವಳಿಯ ರಚನೆಗೆ ಆಧಾರದಂತೆ ಬಳಸಬಹುದು ಎಂದು ೧೯೭೦ರಲ್ಲಿ ಸಾರ್ವಜನಿಕವಾಗಿ ಘೋಷಿಸಿದಾಗ, ಈ ದೃಷ್ಟಿಕೋನವು ಛಿದ್ರವಾಯಿತು. ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಹ್ಯಾಶ್ ಕೋಷ್ಟಕಗಳು ಮತ್ತು ನಕಲಿ-ಯಾದೃಚ್ಛಿಕ ಸಂಖ್ಯೆ ಉತ್ಪಾದಕಗಳಿಗಾಗಿ ಸಹ ಬಳಸುತ್ತಾರೆ. ಕೆಲವು ತಿರುಗೋಲು ಯಂತ್ರಗಳನ್ನು ಪ್ರತಿ ತಿರುಗೋಲು ಮೇಲೆ ಒಂದು ವಿಭಿನ್ನ ಪಿನ್ನುಗಳ ಸಂಖ್ಯೆಯಿಂದ ವಿನ್ಯಾಸ ಮಾಡಲಾಯಿತು, ಯಾವುದೇ ಒಂದು ತಿರುಗೋಲಿನ ಮೇಲಿನ ಪಿನ್ನುಗಳ ಸಂಖ್ಯೆ ಯಾವುದೇ ಇನ್ನೊಂದು ತಿರುಗೋಲಿನ ಮೇಲಿನ ಪಿನ್ನುಗಳ ಸಂಖ್ಯೆಗೆ ಅವಿಭಾಜ್ಯ ಅಥವಾ ಸಹಅವಿಭಾಜ್ಯವಾಗಿರುತ್ತದೆ. ಯಾವುದೇ ಸ್ಥಾನವನ್ನು ಪುನರಾವರ್ತಿಸುವ ಮೊದಲು ಪೂರ್ಣ ಚಕ್ರ ತಿರುಗೋಲು ಸಂಭವನೀಯ ಸ್ಥಾನಗಳ ಉತ್ಪಾದನೆಗೆ ಇದು ಸಹಾಯಕವಾಯಿತು. ಅಂತರಾಷ್ಟ್ರೀಯ ದರ್ಜೆಯ ಪುಸ್ತಕ ಸಂಖ್ಯೆಗಳು ಒಂದು ಅಂಕದ ಜೊತೆ ಕೆಲಸ ಮಾಡುತ್ತವೆ, ಅದು ೧೧ ಒಂದು ಅವಿಭಾಜ್ಯ ಎಂಬ ಸಂಗತಿಯನ್ನು ಬಳಸಿಕೊಳ್ಳುತ್ತದೆ.
ಅಂಕಗಣಿತದ ಪ್ರಮಾಣ ಒಂದು ಅವಿಭಾಜ್ಯ p[ಬದಲಾಯಿಸಿ]
ಪ್ರಮಾಣ ಅಂಕಗಣಿತ ಬಳಕೆಯಲ್ಲಿರುವ ಅಂಕಗಣಿತದ ಒಂದು ಮಾರ್ಪಾಡಾಗಿದ್ದು, "ಪ್ರಮಾಣ" ಒಂದು ನಿರ್ಧಿಷ್ಟ ಸಂಖ್ಯೆಯಾದ n ಬಳಸಿ ಎಲ್ಲಾ ಎಣಿಕೆಗಳನ್ನು ಮಾಡುವುದಾಗಿದೆ. ಪ್ರಮಾಣ ಅಂಕಗಣಿತದ ಎಲ್ಲಾ ಲೆಕ್ಕಾಚಾರಗಳು ಸೀಮಿತ ಶ್ರೇಣಿಯಲ್ಲಿ ನೆಡೆಯುತ್ತದೆ.
- {೦, ೧, ೨, ..., n − ೧}.
ಪ್ರಮಾಣ n ಅನ್ನು ಎಣಿಕೆ ಮಾಡುವುದರಲ್ಲಿ ಕೂಡಿಸುವ, ಕಳೆಯುವ ಮತ್ತು ಗುಣಕಗಳನ್ನು ಎಣಿಸುವುದನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಮಾಡಲಾಗುತ್ತದೆ, ಆದರೆ ಅನಂತರ ಮಾತ್ರ n ನಿಂದ ಭಾಗಿಸಿದ ನಂತರದ ಶೇಷವನ್ನು ಪರಿಗಣಿಸಲಾಗುವುದು. ಉದಾಹರಣೆಗೆ, n = ೭ ಆಗಿರಲಿ. ನಂತರ, ಪ್ರಮಾಣ ಅಂಕಗಣಿತದಲ್ಲಿ ಪ್ರಮಾಣ ೭, ೩ + ೫ರ ಮೊತ್ತ 8ರ ಬದಲಾಗಿ ೧, ಏಕೆಂದರೆ ೭ರಿಂದ ೮ಅನ್ನು ಭಾಗಿಸಿದಾಗ ೧ ಶೇಷ ಉಳಿಯುತ್ತದೆ. ಹಾಗೆಯೇ, ೬ + ೧ = ೦ ಪ್ರಮಾಣ ೭, ೨ − ೫ = ೪ ಪ್ರಮಾಣ ೭ ( −೩ + ೭ = ೪ ಆಗಿರುವುದರಿಂದ) ಮತ್ತು ೩·೪ = ೫ ಪ್ರಮಾಣ ೭ (೧೨ ಎಂಬ ಸಂಖ್ಯೆಯು ೫ ಶೇಷವನ್ನು ಹೊಂದಿದೆ). ಸಂಕಲನ ಮತ್ತು ವ್ಯವಕಲನದ ಗುಟಮಟ್ಟದ ಲಕ್ಷಣಗಳು ಪೂರ್ಣಸಂಖ್ಯೆಗಳ ಅಥವಾ ತರ್ಕಾಧಾರಿತ ಸಂಖ್ಯೆಗಳ ಸಂಖ್ಯಾ ವ್ಯವಸ್ಥೆಯಿಂದ ಪರಿಚಿತ ಊರ್ಜಿತವಾಗಿ ಉಳಿಯುತ್ತವೆ, ಉದಾಹರಣೆಗೆ
- (a + b ) · c = a · c + b · c (ವಿತರಣಶೀಲತೆಯ ನಿಯಮ).
ಆದರೆ, ಸಾಮಾನ್ಯವಾಗಿ ಇದನ್ನು ಈ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಭಾಗಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ. ಉದಾಹರಣೆಗೆ, n = ೬ಗೆ, ಸಮೀಕರಣ
- ೩ · x = ೨ (ಪ್ರಮಾಣ ೬),
೨/೩ಗೆ ಸಮಾನಾಂತರವಾದ x ನ ಒಂದು ಪರಿಹಾರವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಸಾಧ್ಯವಿಲ್ಲ. ಇದನ್ನು ೩ · ೦, ..., ೩ · ೫ ಪ್ರಮಾಣ ೬ ನ್ನು ಎಣಿಕೆ ಮಾಡುವುದರ ಮೂಲಕ ಅರ್ಥಮಾಡಿಕೊಳ್ಳಬಹುದಾಗಿದೆ. ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ವಿಶಿಷ್ಟ ಲಕ್ಷಣಗಳು ಹೀಗಿವೆ: n ಒಂದು ಅವಿಭಾಜ್ಯವಾಗಿದ್ದಲ್ಲಿ ಮಾತ್ರ ಪ್ರಮಾಣ ಅಂಕಗಣಿತದಲ್ಲಿ ಭಾಗಕಾರ ಸಾಧ್ಯವಿದೆ. n = ೭ಗೆ, ಸಮೀಕರಣ
- ೩ · x = ೩ (ಪ್ರಮಾಣ ೭)
ಇದೊಂದು ಒಂದು ವಿಶಿಷ್ಟ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ: x = ೩. ಇದಕ್ಕೆ ಸಮನಾಗಿ, m ೩ ≤ m ≤ n − ೧ ನೆರವೇರಿಸುವ ಎಲ್ಲಾ ಪೂರ್ಣಸಂಖ್ಯೆಗಳು n ಗೆ ಸಹಅವಿಭಾಜ್ಯ ವಾದರೆ ಮಾತ್ರ n ಅವಿಭಾಜ್ಯವಾಗುತ್ತದೆ, ಅಂದರೆ, 1 ಅವುಗಳ ದೊಡ್ಡ ಸಾಮಾನ್ಯ ಭಾಜಕವಾಗುತ್ತದೆ. ಯೂಲರ್ನ ಟೋಟಿಯೆಂಟ್ ಫಂಕ್ಶನ್ φ ಬಳಸಿದಾಗ n ಎಂಬುದು ಅವಿಭಾಜ್ಯವಾಗಬೇಕಾದರೆ φ(n ) = n − ೧. ಆಗಿರಲೇಬೇಕಾಗುತ್ತದೆ. ಎಲ್ಲಾ n ಗೆ ಸಂಕಲನ ಮತ್ತು ವ್ಯವಕಲನ ಹೊಂದಿದ {೦, ೧, ೨, ..., n − ೧}, ಗುಂಪು Z /n Z ಸೂಚಿಸುತ್ತದೆ. ಅಮೂರ್ತವಾದ ಬೀಜಗಣಿತದ ಮಾತಿನ ವಿಧಾನದಲ್ಲಿ, ಯಾವುದೇ n ಗೆ ಇದು ಒಂದು ವರ್ತುಲ, ಆದರೆ n ಅವಿಭಾಜ್ಯವಾದರೆ ಮಾತ್ರ ಅದು ಒಂದು ಪರಿಮಿತ ಕ್ಷೇತ್ರವಾಗುತ್ತದೆ. ಒಂದು ಅಮೂರ್ತವಾದ ಮಾರ್ಗದಲ್ಲಿ Z /p Z ಯನ್ನು ಪರಿಶೀಲಿಸುವುದರಿಂದ ಹಲವು ಪ್ರಮೇಯಗಳನ್ನು ಪಡೆಯಲು ಸಾಧ್ಯ. ಉದಾಹರಣೆಗೆ, ಫೆರ್ಮ್ಯಾಟ್ನ ಸಣ್ಣ ಪ್ರಮೇಯ ಹೀಗೆ ಹೇಳುತ್ತದೆ, ಯಾವುದೇ ಪೂರ್ಣಸಂಖ್ಯೆ a ಗೆ p ಯಿಂದ a p − a ಯನ್ನು ಭಾಗಿಸಬಲ್ಲದು, ಈ ಕಲ್ಪನೆಗಳನ್ನು ಬಳಸಿ ಸಾಬೀತುಮಾಡಬಹುದು. ಕೆಳಗಿನದು ಇದರ ಒಂದು ಪರಿಣಾಮವಾಗಿದೆ: 2 ಮತ್ತು 5ನ್ನು ಹೊರತು ಪಡಿಸಿ p ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯಾದರೆ, ೧/p ಯಾವಾಗಲೂ ಒಂದು ಪುನರಾವರ್ತಕ ದಶಮಾಂಶ ಆಗಿರುತ್ತದೆ, ಅದರ ಕಾಲ p − ೧ ಅಥವಾ p − ೧ರ ಒಂದು ಭಾಜಕವಾಗಿದೆ. p q ನ ಒಂದು ಅವಿಭಾಜ್ಯ ಫಲಿತಾಂಶವಾಗದ್ದಿದಲ್ಲಿ ಮೂಲದಲ್ಲಿನ q ನಲ್ಲಿ ನಿರೂಪಿಸಿದ ದಶಮಾಂಶ ೧/p ವು (ತಳ ೧೦ರ ಬದಲು) ಅದೇ ರೀತಿಯ ಪರಿಣಾಮವನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ. ವೀಲ್ಸನ್ನ ಪ್ರಮೇಯ ಹೀಗೆ ಹೇಳುತ್ತದೆ, ಒಂದು ಪೂರ್ಣಸಂಖ್ಯೆ p > ೧ ಅವಿಭಾಜ್ಯ ಕ್ರಮಗುಣಿತದ (p − ೧)! + ೧ is p ಯಿಂದ ಭಾಗಿಸಲು ಸಾಧ್ಯವಾದರೆ ಮಾತ್ರ. ಹೆಚ್ಚಾಗಿ, ಒಂದು ಪೂರ್ಣಸಂಖ್ಯೆ n > ೪ ಯು (n − ೧) n ಯಿಂದ ಭಾಗಿಸಲು ಸಾಧ್ಯವಾದರೆ ಮಾತ್ರ ಒಂದು ಸಂಯುಕ್ತವಾಗುತ್ತದೆ!.
ಅವಿಭಾಜ್ಯದ ಇತರೆ ಗಣಿತಶಾಸ್ತ್ರದ ಸಂಗತಿಗಳು[ಬದಲಾಯಿಸಿ]
ಹಲವು ಗಣಿತಶಾಸ್ತ್ರದ ಕ್ಷೇತ್ರಗಳು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ವ್ಯಾಪಕವಾಗಿ ಬಳಸಿಕೊಳ್ಳುತ್ತವೆ. ಸೈಲೋ ಪ್ರಮೇಯಗಳು ಪರಿಮಿತ ಗುಂಪುಗಳ ಸಿದ್ಧಾಂತದಿಂದ ಒಂದು ಉದಾಹರಣೆಯಾಗಿದೆ: G ಒಂದು ಪರಿಮಿತ ಗುಂಪಾದರೆ ಮತ್ತು p n ಇದು G ನ ಕ್ರಮವನ್ನು ಭಾಗಿಸುವ p ಅವಿಭಾಜ್ಯದ ಅತ್ಯುನ್ನತವಾದ ಘಾತವಾಗಿದ್ದರೆ, ಆಗ G p n ಕ್ರಮದ ಒಂದು ಉಪಗುಂಪನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಹಾಗೆಯೇ, ಅವಿಭಾಜ್ಯ ಕ್ರಮದ ಯಾವುದೇ ಗುಂಪು ಆವರ್ತ (ಲ್ಯಾಗ್ರೇಂಜ್ನ ಪ್ರಮೇಯ) ಆಗಿರುತ್ತದೆ.
ಸಾರ್ವಜನಿಕ-ಕೀ ಗುಪ್ತ ಲಿಪಿ ಶಾಸ್ತ್ರ[ಬದಲಾಯಿಸಿ]
RSA ಮತ್ತು ಡಿಫೀ-ಹೆಲ್ಮನ್ ಕೀ ಬದಲಾವಣೆಗಳಂತಹ ಹಲವು ಸಾರ್ವಜನಿಕ-ಕೀ ಗುಪ್ತ ಲಿಪಿಶಾಸ್ತ್ರ ಕ್ರಮಾವಳಿಗಳು ದೊಡ್ಡ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಮೇಲೆ ಆಧಾರವಾಗಿವೆ(ಉದಾಹರಣೆಗೆ ೫೧೨ bitಗಳ ಜೊತೆ). x ಮತ್ತು y ಎಂಬ ಎರಡು (ದೊಡ್ಡ) ಸಂಖ್ಯೆಗಳನ್ನು ಗುಣಿಸುವ ಕಾರ್ಯ ಮಾಡುವುದು x ಮತ್ತು y (ಸಹಅವಿಭಾಜ್ಯ ಎಂದುಕೊಂಡಂತಹವು)ಗಳನ್ನು ಅವುಗಳ ಮೊತ್ತವಾದ xy ನ ಬೆಲೆ ಗೊತ್ತಿರುವಾಗ ಲೆಕ್ಕ ಮಾಡುವುದಕ್ಕಿಂತ ಹೆಚ್ಚು ಸುಲಭ (ಅಂದರೆ.. ಹೆಚ್ಚು ಫಲಕಾರಿ) ಎಂಬ ಆಲೋಚನೆಯ ಮೇಲೆ ಅವರು ಅವಲಂಬಿತರಾಗಿರುತ್ತಾರೆ.
ಪರಿಸರದಲ್ಲಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು[ಬದಲಾಯಿಸಿ]
ಅನಿವಾರ್ಯವಾಗಿ, ಪರಿಸರದಲ್ಲಿ ಇರುವ ಕೆಲವು ಸಂಖ್ಯೆಗಳು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳಾಗಿವೆ. ಹೇಗಿದ್ದರೂ, ಅವುಗಳು ಹೆಚ್ಚು ಕಡಿಮೆ ಪರಿಸರದಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳುವ ಸಂಖ್ಯೆ ಬಹಳ ಕಡಿಮೆ, ಏಕೆಂದರೆ ಅವುಗಳು ಅವಿಭಾಜ್ಯ ಅಂಕೆಗಳು. ಪರಿಸರದಲ್ಲಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಉಪಯೋಗದ ಒಂದು ಉದಾಹರಣೆ ಎಂದರೆ Magicicada ವರ್ಗದ ಸಿಕಾಡಾಗಳು ಉಪಯೋಗಿಸುವ ವಿಕಸನತೆಯ ತಂತ್ರ.[೨೬] ಈ ಕೀಟಗಳು ಅವುಗಳ ಜೀವನದ ಹೆಚ್ಚಿನ ಸಮಯವನ್ನು ರಹಸ್ಯ/ ಭೂವಿಯೊಳಗಿನ ಲಾರ್ವಾಗಳ ರೀತಿಯಲ್ಲಿ ಕಳೆಯುತ್ತವೆ. ಅವುಗಳು ಗೂಡುಹುಳುಗಳಾಗಿ ಮಾತ್ರ ಇರುತ್ತವೆ ಮತ್ತು ೧೩ ಅಥವಾ ೧೭ ವರ್ಷಗಳ ನಂತರ ಅವುಗಳ ಬಿಲದಿಂದ ಹೊರ ಬರುತ್ತವೆ, ಆ ಸಮಯದಲ್ಲಿ ಸ್ವಲ್ಪ ಹಾರುತ್ತವೆ, ಸಂತಾನೋತ್ಪತ್ತಿ ಮಾಡುತ್ತವೆ ಮತ್ತು ಅಮೇಲೆ ಹೆಚ್ಚೆಂದರೆ ಕೆಲವು ವಾರಗಳ ನಂತರ ಸಾಯುತ್ತವೆ. ಇದರಲ್ಲಿರುವ ನಂಬಿದಂತಹ ತರ್ಕವೆಂದರೆ, ಅವು ಹೊರಬರುವ ಸಮಯದ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯ ನಡುವಣ ಅವಧಿಯು ಇವುಗಳನ್ನು ತಿನ್ನುವಂತಹ ಜೀವಿಗಳಿಗೆ Magicicadas ಗಳನ್ನು ಹುಡುಕಿ ತಿನ್ನಲು ಸಾಧ್ಯವಾಗುವ ವೈಶಿಷ್ಟ್ಯತೆಗಳನ್ನು ಪಡೆದುಕೊಳ್ಳುವುದು ಅತ್ಯಂತ ಕಷ್ಟವಾಗುತ್ತದೆ.[೨೭] ಒಂದು ವೇಳೆ Magicicadas ಒಂದು ಅವಿಭಾಜ್ಯವಲ್ಲದ ಸಂಖ್ಯೆಯ ಮಧ್ಯಂತರದಲ್ಲಿ ಕಾಣಿಸಿಕೊಂಡರೆ, ಅಂದರೆ ಪ್ರತಿ ೧೨ ವರ್ಷಗಳಿಗೆ ಕಾಣಿಸಿಕೊಂಡರೆ, ಆಗ ಪ್ರತಿ ೨, ೩, ೪, ೬, ಅಥವಾ ೧೨ ವರ್ಷಗಳಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳುವ ಪರಭಕ್ಷಕಗಳಿಗೆ ಖಚಿತವಾಗಿ ಅವುಗಳು ದೊರಕಿಬಿಡುತ್ತವೆ. ಸುಮಾರು ೨೦೦-ವರ್ಷಗಳ ಸಮಯದಲ್ಲಿ, ಈ ೧೪ ಮತ್ತು ೧೫-ವರ್ಷಗಳ ಕಲ್ಪಿತ ಸಿಕಾಡಾಗಳ ಹೊರಬರುವ ಸಮಯದಲ್ಲಿ ಕಾಣಿಸಿಕೊಂಡ ಪರಭಕ್ಷಕಗಳ ಸರಾಸರಿ ಸಂಖ್ಯೆಯು ೧೩ ಮತ್ತು ೧೭-ವರ್ಷಗಳ ಸಿಕಾಡಾಗಳ ಹೊರಬರುವ ಸಮಯದಲ್ಲಿ ಕಾಣಿಸಿಕೊಂಡ ಪರಭಕ್ಷಕಗಳ ಸರಾಸರಿ ಸಂಖ್ಯೆಗಿಂತ ೨%ರಷ್ಟು ಹೆಚ್ಚಾಗಿರುತ್ತದೆ.[೨೮] ಈ ವ್ಯತ್ಯಾಸವು ಸಣ್ಣದಾದರೂ, ಈ ಕೀಟಗಳಿಗೆ ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯ ಕಾಲಮಾನದ ಜೀವನ ಚಕ್ರವನ್ನು ಅವಲಂಬಿಸುವ ಪ್ರಾಕೃತಿಕ ಆಯ್ಕೆಯನ್ನು ಸಾಧ್ಯವಾಗಿಸಿದೆ. ಜೀಟಾ ಕಾರ್ಯದ ಸೊನ್ನೆಗಳು ಸಂಯುಕ್ತ ಪರಿಮಾಣ ವ್ಯವಸ್ಥೆಗಳ ಸಾಮರ್ಥ್ಯದ ಮಟ್ಟಗಳಿಗೆ ಜೋಡಿಸಲ್ಪಟ್ಟಿವೆ ಎಂಬ ಚಿಂತನೆಯೊಂದು ಇದೆ.[೨೯]
ಸಾಮಾನ್ಯೀಕರಣಗಳು[ಬದಲಾಯಿಸಿ]
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಪರಿಕಲ್ಪನೆ ಎಷ್ಟು ಮಹತ್ವವಾಗಿದೆ ಎಂದರೆ ಇದನ್ನು ಗಣಿತ ಶಾಸ್ತ್ರದ ವಿಭಿನ್ನ ಶಾಖೆಗಳಲ್ಲಿ ಬೇರೆ ಬೇರೆ ವಿಧದಲ್ಲಿ ಸಾಮಾನ್ಯೀಕರಣಗೊಳ್ಳಿಸಲಾಗಿದೆ. ಸಾಮಾನ್ಯವಾಗಿ, ಸರಿಯಾದ ಅರ್ಥದಲ್ಲಿ "ಅವಿಭಾಜ್ಯ" ಅತಿ ಸಣ್ಣದಾಗಿರುವಿಕೆ ಅಥವಾ ವಿಂಗಡಿಸಲಾಗದಿರುವಿಕೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಅವಿಭಾಜ್ಯ ಕ್ಷೇತ್ರವು ೦ ಮತ್ತು ೧ ಎರಡನ್ನೂ ಹೊಂದಿರುವ F ಕ್ಷೇತ್ರದ ಅತಿ ಸಣ್ಣ ಉಪಕ್ಷೇತ್ರವಾಗಿದೆ. ಇದು Q ಅಥವಾ p ಅಂಶಗಳನ್ನು ಹೊಂದಿದ ಪರಿಮಿತ ಕ್ಷೇತ್ರ ಆಗಿದೆ, ಹೆಸರಿನ ಮೂಲದ ಮೇಲೆ. ಕೆಲವೊಮ್ಮೆ ಹೆಚ್ಚಿನ ಅರ್ಥವನ್ನೂ ಸಹಾ ಈ ಶಬ್ದ ಅವಿಭಾಜ್ಯದಿಂದ ಊಹಿಸಬಹುದಾಗಿದೆ, ಅಂದರೆ ಯಾವುದೇ ವಸ್ತುವನ್ನೂ ಅತ್ಯಂತ ಅನನ್ಯವಾಗಿ ಅದರ ಅವಿಭಾಜ್ಯ ಅಂಗಗಳನ್ನಾಗಿ ವಿಂಗಡಿಸಬಹುದಾಗಿದೆ. ಉದಾಹರಣೆಗೆ, ನಾಟ್ ಸಿದ್ಧಾಂತದಲ್ಲಿ, ಒಂದು ಅವಿಭಾಜ್ಯ ನಾಟ್ ಒಂದು ವಿಂಗಡಿಸಲಾಗದ ನಾಟ್ ಆಗಿದೆ. ಅಂದರೆ, ಇದು ಎರಡು ಸಾಮಾನ್ಯವಲ್ಲದ ನಾಟ್ಗಳ ನಾಟ್ ಮೊತ್ತ ಎಂದು ಬರೆಯಲು ಸಾಧ್ಯವಿಲ್ಲ ಎಂದು ಅರ್ಥ. ಯಾವುದೇ ನಾಟ್ನ್ನು ಅವಿಭಾಜ್ಯ ನಾಟ್ಗಳ ಒಂದು ಜೋಡಿಸಿದ ಮೊತ್ತ ಎಂದು ವಿಶಿಷ್ಟವಾಗಿ ಸೂಚಿಸಲು ಸಾಧ್ಯ.[೩೦] ಅವಿಭಾಜ್ಯ ಮಾದರಿಗಳು ಮತ್ತು ಅವಿಭಾಜ್ಯ 3-ಬಹುವಿಧಗಳು ಈ ವಿಧಕ್ಕೆ ಇತರೆ ಉದಾಹರಣೆಗಳು.
ವರ್ತುಲಗಳಲ್ಲಿ ಅವಿಭಾಜ್ಯ ಅಂಶಗಳು[ಬದಲಾಯಿಸಿ]
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಇನ್ನೂ ಎರಡು ಸಾಮಾನ್ಯ ಪರಿಕಲ್ಪನೆಗಳನ್ನು ಹುಟ್ಟುಹಾಕಿವೆ. ಅವು ಯಾವುದೇ ವರ್ತುಲ R ನ ಅಂಶಗಳಿಗೆ ಅನ್ವಯಿಸುತ್ತಿದ್ದು, R ಒಂದು ಬೀಜಗಣಿತದ ರಚನೆಯಾಗಿದ್ದು, ಸಂಕಲನ, ವ್ಯವಕಲನ ಮತ್ತು ಗುಣಾಕಾರಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತದೆ: ಅವುಗಳು ಅವಿಭಾಜ್ಯ ಅಂಶಗಳು ಮತ್ತು ಅಪರಿವರ್ತನೀಯ ಅಂಶಗಳು . ಒಂದು ಅಂಶವು ಏಕಮಾನ ಆಗಿರದಿದ್ದಲ್ಲಿ (ಅಂದರೆ, ಒಂದು ಗುಣಾಕಾರದ ವಿಲೋಮವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲವಾದರೆ) ಮತ್ತು ಮುಂದೆ ಹೇಳುವ ಲಕ್ಷಣವನ್ನು ಹೊಂದಿರದ್ದಿದರೆ R ನ p ಅಂಶವನ್ನು ಅವಿಭಾಜ್ಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ: R ನಲ್ಲಿ ನೀಡಿದ x ಮತ್ತು y ಹಾಗೆ p ಫಲಿತಾಂಶವನ್ನು ಭಾಗಿಸುತ್ತದೆ, ನಂತರ p ಕನಿಷ್ಟ ಒಂದು ಅಪವರ್ತನವನ್ನು ಭಾಗಿಸುತ್ತದೆ. ಘಟಕಗಳಲ್ಲದವುಗಳನ್ನು ಎರಡು ವರ್ತುಲದ ಅಂಶಗಳ ಒಂದು ಫಲಿತಾಂಶ ಎಂದು ಬರೆಯಲು ಅಸಾಧ್ಯವಾಗಿರುವವೇ ಅಪರಿವರ್ತನೀಯ ಅಂಶಗಳು. ಸಾಮಾನ್ಯವಾಗಿ ಹೇಳುವುದಾದರೆ, ಇದು ಒಂದು ಅನಿಶ್ಚಿತವಾದ ಪರಿಸ್ಥಿತಿ, ಪೂರ್ಣಸಂಖ್ಯೆಗಳ ವರ್ತುಲ Z ನಂತಹ ಯಾವುದೇ ವಿಶಿಷ್ಟವಾದ ಅಪವರ್ತನೀಕರಣ ಕ್ಷೇತ್ರಕ್ಕೆ, ಅವಿಭಾಜ್ಯ ಅಂಶಗಳ ಗುಂಪು ಅಪರಿವರ್ತನೀಯ ಅಂಶಗಳ ಗುಂಪಿಗೆ ಸಮವಾಗುತ್ತದೆ, ಅದು Z ಗೆ:
- {…, −೧೧, −೭, −೫, −೩, −೨, ೨, ೩, ೫, ೭, ೧೧, …}.
Z [i ] ಗಾಸಿಯನ್ ಪೂರ್ಣಸಂಖ್ಯೆಗಳಿಗೆ ಒಂದು ಸಾಮಾನ್ಯ ಉದಾಹರಣೆಯಾಗಿದೆ, ಅಂದರೆ, Z ನಲ್ಲಿ a + bi ಜೊತೆಗೆ a ಮತ್ತು b ರಚನೆಯ ಸಂಯುಕ್ತ ಸಂಖ್ಯೆಗಳ ಗುಂಪು. ಇದು ಒಂದು ಗಣಿತದ ಸಮಗ್ರ ಕ್ಷೇತ್ರವಾಗಿದ್ದು, ಇದರ ಅವಿಭಾಜ್ಯ ಅಂಶಗಳು ಗಾಸಿಯನ್ ಅವಿಭಾಜ್ಯಗಳು ಎಂದು ಪರಿಚಿತವಾಗಿವೆ. ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯಗಳೂ (Z ನಲ್ಲಿನ) ಒಂದು ಗಾಸಿಯನ್ ಅವಿಭಾಜ್ಯ ಅಲ್ಲ: ದೊಡ್ಡದಾದ Z [i ] ವರ್ತುಲದಲ್ಲಿ, ಅವಿಭಾಜ್ಯಗಳ ಫಲಿತಾಂಶ (೧ + i )ಮತ್ತು (೧ − i )ರ ಒಳಗೆ ೨ ಅಪವರ್ತನಗಳು. ೪k + ೩ ನ ಸ್ವರೂಪದ ತರ್ಕಾಧಾರಿತ ಅವಿಭಾಜ್ಯಗಳು (ಉದಾಹರಣೆ Z ನಲ್ಲಿ ಅವಿಭಾಜ್ಯ ಅಂಶಗಳು) ಗಾಸಿಯನ್ ಅವಿಭಾಜ್ಯಗಳಾಗಿವೆ, ಆದರೆ ೪k + ೧ ಸ್ವರೂಪದ ತರ್ಕಾಧಾರಿತ ಅವಿಭಾಜ್ಯಗಳು ಅಲ್ಲ. ಗಾಸಿಯನ್ ಅವಿಭಾಜ್ಯಗಳನ್ನು ವರ್ಗ ಸಮೀಕರಣ ಪರಸ್ಪರ ಸಂಬದ್ಧತೆಯನ್ನು ನಿರೂಪಿಸುವಾಗ ಬಳಸಬಹುದಾಗಿದೆ. ಹಾಗೆಯೇ ಐನ್ಸ್ಟೀನ್ ಅವಿಭಾಜ್ಯಗಳು ಘನಾಕೃತಿಯ ಪರಸ್ಪರ ಸಂಬದ್ಧತೆಗೆ ಸಮಾನ ರೂಪದ ಪಾತ್ರವಹಿಸುತ್ತದೆ.
ಅವಿಭಾಜ್ಯ ಪರಿಪೂರ್ಣಗಳು[ಬದಲಾಯಿಸಿ]
ವರ್ತುಲ ಸಿದ್ಧಾಂತದಲ್ಲಿ, ಸಂಖ್ಯೆಯ ಕಲ್ಪನೆ ಸಾಧಾರಣವಾಗಿ ಪರಿಪೂರ್ಣದೊಂದಿಗೆ ಬದಲಾಯಿಸಲಾಗುತ್ತದೆ. ಅವಿಭಾಜ್ಯ ಪರಿಪೂರ್ಣಗಳು , ಅವಿಭಾಜ್ಯ ಅಂಶಗಳನ್ನು ಸಾಮಾನ್ಯೀಕರಿಸುತ್ತದೆ, ಅಂದರೆ ಒಂದು ಅವಿಭಾಜ್ಯ ಅಂಶದಿಂದ ಸೃಷ್ಟಿಸಿದ ಪ್ರಮುಖ ಪರಿಪೂರ್ಣ ಒಂದು ಅವಿಭಾಜ್ಯ ಪರಿಪೂರ್ಣವಾಗಿರುತ್ತದೆ, ಅವುಗಳು ಕಮ್ಯೂಟೇಟಿವ್ ಬೀಜಗಣಿತ, ಬೀಜಗಣಿತದ ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತ ಮತ್ತು ಬೀಜಗಣಿತದ ರೇಖಾಗಣಿತಗಳ ಅಧ್ಯಯನದಲ್ಲಿ ಒಂದು ಮುಖ್ಯ ಸಾಧನ ಮತ್ತು ಉದ್ದೇಶ/ವಿಷಯವಾಗಿದೆ. ವರ್ತುಲ ಪೂರ್ಣಸಂಖ್ಯೆಗಳ ಅವಿಭಾಜ್ಯ ಪರಿಪೂರ್ಣಗಳು (೦), (೨), (೩), (೫), (೭), (೧೧), … ಅಂಕಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯ ಲಾಸ್ಕರ್-ನೋಥರ್ ಪ್ರಮೇಯಕ್ಕೆ ಸಾಮಾನ್ಯೀಕರಿಸುತ್ತದೆ. ಈ ಪ್ರಮೇಯವು ಒಂದು ನೋಥೇರಿಯನ್ ಕಮ್ಯೂಟೇಟಿವ್ ವರ್ತುಲದಲ್ಲಿನ ಯಾವುದೇ ಪರಿಪೂರ್ಣವನ್ನು ಪ್ರಾಥಮಿಕ ಪರಿಪೂರ್ಣಗಳ ಛೇದನ ಎಂದು ಸೂಚಿಸುತ್ತದೆ. ಅವುಗಳು ಅವಿಭಾಜ್ಯ ವರ್ಗಗಳ ಸೂಕ್ತ ಸಾಮಾನ್ಯೀಕರಣಗಳಾಗಿರುತ್ತವೆ.[೩೧] ಅವಿಭಾಜ್ಯ ಪರಿಪೂರ್ಣಗಳು ಒಂದು ವರ್ತುಲದ ವೈವಿಧ್ಯದ ಕಲ್ಪನೆ ಮೂಲಕ ಬೀಜಗಣಿತ-ರೇಖಾಗಣಿತದ ವಿಷಯಗಳ ಲಕ್ಷಣಗಳಾಗಿವೆ. ಅಂಕಗಣಿತದ ರೇಖಾಗಣಿತ ಸಹ ಈ ಕಲ್ಪನೆಯಿಂದ ಲಾಭ ಪಡೆಯುತ್ತದೆ, ಮತ್ತು ರೇಖಾಗಣಿತ ಮತ್ತು ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತ ಎರಡರಲ್ಲೂ ಹಲವು ಪರಿಕಲ್ಪನೆಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ. ಉದಾಹರಣೆಗೆ, ಅವರ್ತನೀಕರಣ ಅಥವಾ ಅವಿಭಾಜ್ಯ ಪರಿಪೂರ್ಣಗಳ ಶಾಖೆಗಳು ವಿಸ್ತರಣೆ ಕ್ಷೇತ್ರಕ್ಕೆ ಎತ್ತಿಹಿಡಿದಾಗ, ಬೀಜಗಣಿತದ ಮೂಲಭೂತ ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತದ ಒಂದು ಸಮಸ್ಯೆ ರೇಖಾಗಣಿತದಲ್ಲಿನ ಶಾಖೆಗಳ ಜೊತೆ ಕೆಲವು ಹೋಲಿಕೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆ.
ಮೌಲ್ಯಮಾಪನ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಅವಿಭಾಜ್ಯಗಳು[ಬದಲಾಯಿಸಿ]
ಬೀಜಗಣಿತದ ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತದಲ್ಲಿ, ಮತ್ತೊಂದು ಸಾಮಾನ್ಯೀಕರಣವನ್ನು ಉಪಯೋಗಿಸಲಾಗಿದೆ. ಮೌಲ್ಯಮಾಪನ ಸಿದ್ಧಾಂತಕ್ಕೆ p -adic ಮೌಲ್ಯಮಾಪನಗಳು ಒಂದು ಆರಂಭದ ಬಿಂದುವಾಗಿದ್ದು, ಇಲ್ಲಿ p ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯಾಗಿರುತ್ತದೆ. ಇದು ಯಾವುದು ಉನ್ನತ ವರ್ಗ p ನೀಡಿದ ಸಂಖ್ಯೆ n ಅನ್ನು ಭಾಗಿಸುತ್ತದೆ ಎಂದು ತಿಳಿಸುತ್ತದೆ. ಅದನ್ನು ಬಳಸಿ, p -adic ಮಟ್ಟವನ್ನು ರಚಿಸಲಾಗಿದೆ. ಇದು ಬಳಕೆಯ ಖಚಿತ ಮೌಲ್ಯಕ್ಕೆ ವಿರುದ್ಧವಾಗಿದೆ, p ಯಿಂದ ಒಂದು ಸಂಖ್ಯೆಯನ್ನು ಗುಣಿಸಿದಾಗ ಸಣ್ಣ ಸಂಖ್ಯೆಯನ್ನು ಪಡೆಯುತ್ತದೆ. ಈ ಮಾಪನ ಮಟ್ಟಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ Q ನ ಮುಕ್ತಾಯವು ಅಸಲಿಗಳಾದ R ಗೆ ವಿರುದ್ಧವಾಗಿ (ತರ್ಕಧಾರಿತ ಸಂಖ್ಯೆಗಳ ಕ್ಷೇತ್ರ) p -adic ಸಂಖ್ಯೆಗಳ ಕ್ಷೇತ್ರವಾದ Q p ಗೆ ದಾರಿ ಮಾಡುತ್ತದೆ. ಇಲ್ಲಿ R ಸಂಪೂರ್ಣವಾದ ಮೌಲ್ಯಕ್ಕೆ ಸಂಬಂಧಿಸಿ ಮುಕ್ತಾಯವಾಗಿರುತ್ತವೆ. ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಇರುವ ಸಂಪರ್ಕವನ್ನು ಎತ್ತಿತೋರಿಸಲು, ಖಚಿತ ಮೌಲ್ಯವನ್ನು ಅನಂತ ಅವಿಭಾಜ್ಯ ಎಂದು ಆಗಾಗ ಕರೆಯಲಾಗುತ್ತದೆ. ಇವುಗಳು ಆಸ್ಟ್ರೋವ್ಸ್ಕಿಯ ಪ್ರಮೇಯದ ಪ್ರಕಾರ ಇವೆಲ್ಲವೂ Q ಅನ್ನು ಪೂರ್ಣಗೊಳಿಸಲು ಅಗತ್ಯವಾದ ಸಂಭವನೀಯ ಮಾರ್ಗಗಳಾಗಿವೆ. ಒಂದು ಕ್ರಮವಿಲ್ಲದ ಕ್ಷೇತ್ರ K ಯಲ್ಲಿ, K ದಿಂದ ಯಾವುದೇ ಸಹಜ ಸಂಖ್ಯೆ R ವರೆಗಿನ ಕೆಲವು ಕ್ರಿಯೆಗಳ ಮೂಲಕ K ನ ಮೇಲಿನ ಮೌಲ್ಯಮಾಪನಗಳನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬಹುದು. ಇಂತಹ ಪ್ರತಿಯೊಂದು ಮೌಲ್ಯಮಾಪನವೂ K ಯಲ್ಲಿನ ಟೋಪಾಲಜಿಯನ್ನು ಉತ್ಪನ್ನವಾಗಿ ನೀಡುತ್ತದೆ, ಮತ್ತು ಎರಡು ಮೌಲ್ಯಮಾಪನಗಳು ಒಂದೇ ಟೋಪಾಲಜಿಯನ್ನು ನೀಡಿದರೆ ಅವುಗಳನ್ನು ಸಮಾನವೆಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಒಂದು Kನ ಅವಿಭಾಜ್ಯ (ಕೆಲವು ಬಾರಿ ಒಂದು Kನ ಸ್ಥಳ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ) ಮೌಲ್ಯಮಾಪನಗಳ ಒಂದು ಸಮಾನಸ್ಥಿತಿ ವರ್ಗ ಆಗಿರುತ್ತದೆ. ವಿಶ್ವವ್ಯಾಪಿ ಕ್ಷೇತ್ರಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ಪ್ರಶ್ನೆಗಳಾದ Q ಬಹುಶಃ, ಕೆಲವು ಪ್ರಸಂಗಗಳಲ್ಲಿ, ಪೂರ್ಣವಾದ ಕ್ಷೇತ್ರಗಳಿಗೆ (ಸ್ಥಳೀಯ ಕ್ಷೇತ್ರಗಳು ಎಂದು ಪರಿಚಿತ) ಹಿಂದಕ್ಕೆ ಮತ್ತು ಮುಂದಕ್ಕೆ ವರ್ಗಾಯಿಸಬಹುದು, ಈ ಪರಿಕಲ್ಪನೆ ಸ್ಥಳೀಯ-ವಿಶ್ವವ್ಯಾಪಿ ನಿಯಮ ಎಂದು ಪರಿಚಿತ. ಇದು ಮತ್ತೊಮ್ಮೆ ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತಕ್ಕೆ ಅವಿಭಾಜ್ಯಗಳ ಮಹತ್ವವನ್ನು ಪ್ರಮುಖವಾಗಿ ಪರಿಗಣಿಸುತ್ತದೆ.
ಕಲೆ ಮತ್ತು ಸಾಹಿತ್ಯದಲ್ಲಿ[ಬದಲಾಯಿಸಿ]
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಹಲವು ಕಲಾವಿದರು ಮತ್ತು ಬರಹಗಾರರ ಮೇಲೆ ಪ್ರಭಾವ ಬೀರಿವೆ. ಪ್ರೆಂಚ್ ರಚನಾಕಾರ ಓಲಿವಿಯರ್ ಮೆಸ್ಸಿಯನ್ "ಸ್ವಾಭಾವಿಕ ವಿದ್ಯಮಾನ"ದ ಮೂಲಕ ಅಂಕಗಣಿದ ಸಂಗೀತವನ್ನು ಸೃಷ್ಟಿಸಲು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಬಳಸಿದರು. La Nativité du Seigneur ಮತ್ತು Quatre études de rythme (೧೯೪೯-೫೦) ಕೃತಿಗಳಲ್ಲಿ, ಊಹಿಸಲಾಗದ ಸ್ವರತರಂಗಗಳನ್ನು ಸೃಷ್ಟಿಸಲು ಅವರು ಏಕಕಾಲದಲ್ಲಿ ಸಂಗೀತಗಳ ಜೊತೆ ವಿಭಿನ್ನ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ನೀಡಿದ ಉದ್ದಗಳನ್ನು ಉಪಯೋಗಿಸುತ್ತಾರೆ: ಅಧ್ಯಯನ ಒಂದರಲ್ಲಿ ೪೧, ೪೩, ೪೭ ಮತ್ತು ೫೩ ಅವಿಭಾಜ್ಯಗಳು ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತವೆ. ಮೆಸ್ಸಿಯನ್ ಪ್ರಕಾರ ಈ ರೀತಿಯ ರಚನೆಯು "ಪರಿಸರದ ಚಲನೆಗಳು, ಸ್ವತಂತ್ರವಾದ ಚಲನೆಗಳು ಮತ್ತು ಅಸಮಾನವಾದ ಸಮಯಗಳಿಂದ ಪ್ರಭಾವಗೊಂಡಿದೆ".[೩೨] ಅವನ ವಿಜ್ಞಾನದ ಕಲ್ಪಿತ ಕಾದಂಬರಿ ಕಾಂಟ್ಯಾಕ್ಟ್ ಯನ್ನು, ನಂತರ ಅದೇ ಹೆಸರಿನ ಚಲನಚಿತ್ರವಾಗಿ ಮಾಡಲಾಯಿತು, ಅದರಲ್ಲಿ ನಾಸಾ ವಿಜ್ಞಾನಿ ಕಾರ್ಲ್ ಸಾಗನ್ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಅನ್ಯಲೋಕ ಜೀವಿಗಳ ಜೊತೆ ಸಂಪರ್ಕಿಸಲು ಒಂದು ವಿಧಾನವಾಗಿ ಬಳಸಲು ಸಾಧ್ಯ ಎಂಬುದನ್ನು ಸೂಚಿಸುತ್ತಾರೆ. ಅವರು ಮೊದಲಿಗೆ ೧೯೭೫ರಲ್ಲಿ ಅಮೆರಿಕದ ಖಗೋಳವಿಜ್ಞಾನಿ ಫ್ರಾಂಕ್ ಡ್ರಾಕ್ ಜೊತೆ ಸೇರಿ ಅನೌಪಚಾರಿಕವಾಗಿ ಈ ವಿಚಾರವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದ್ದರು.[೩೩] [೩೪] ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ರಹಸ್ಯಗಳು ಮತ್ತು ಗುಪ್ತಲಿಪಿ ಶಾಸ್ತ್ರದ ಜೊತೆಗಿನ ಒಂದು ಜನಪ್ರಿಯ ಸೆಳೆತ/ಮೋಡಿಯನ್ನು ಹಲವು ಚಲನಚಿತ್ರಗಳು ಪ್ರತಿಬಿಂಬಿಸುತ್ತವೆ: ಆ ಚಲನಚಿತ್ರಗಳು ಕ್ಯೂಬ್ , ಸ್ನೀಕರ್ಸ್ , ದಿ ಮಿರರ್ ಹ್ಯಾಸ್ ಟು ಫೇಸ್ಸ್ ಮತ್ತು ಎ ಬ್ಯೂಟಿಫೂಲ್ ಮೈಂಡ್ , ಕೊನೆಯದು ಸೈಲ್ವಿಯಾ ನಾಸರ್ ಬರೆದ ಗಣಿತಶಾಸ್ತ್ರಜ್ಞ ಮತ್ತು ನೊಬೆಲ್ ಪ್ರಶಸ್ತಿ ವಿಜೇತ ಜಾನ್ ಫೊರ್ಬ್ಸ್ ನ್ಯಾಶ್ನ ಜೀವನ ಚರಿತ್ರೆಯನ್ನು ಆಧಾರಿಸಿದೆ.[೩೪] ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಒಂಟಿತನ ಮತ್ತು ಪ್ರತ್ಯೇಕೀಕರಣಕ್ಕೆ ಒಂದು ರೂಪಕಾಲಂಕಾರವಾಗಿ ಪಾವ್ಲೋ ಜಿಯಾರ್ಡಾನೋನ ಕಾದಂಬರಿ ದಿ ಸಾಲಿಟ್ಯೂಡ್ ಅಫ್ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಗಳಲ್ಲಿ ಉಪಯೋಗಿಸಲಾಗಿದೆ.[೩೫]
ಇವನ್ನೂ ಗಮನಿಸಿ[ಬದಲಾಯಿಸಿ]
- ಬೋನ್ಸ್ರ ಅಸಮತೆ
- ಬ್ರೂನ್ರ ಸ್ಥಿರತೆ
- ಬರ್ನ್ಸೈಡ್ ಸಿದ್ದಾಂತ
- ಚೆಬೊಟರ್ವ್ನ ಸಾಂದ್ರತೆ ಸಿದ್ದಾಂತ
- ಚೆನ್ನ ಸಿದ್ದಾಂತ
- ಚೀನಿಯರ ಶೇಷ ಸಿದ್ದಾಂತ
- ಸೀಮಿತ ಸರಳ ಗುಂಪುಗಳ ವರ್ಗೀಕರಣ
- ಕೊಪ್ಲ್ಯಾಂಡ್-ಎರ್ಡೊಸ್ ಸ್ಥಿರಾಂಕ
- ಐಸೆನ್ಸ್ಟೈನ್ರ ಮಾನದಂಡ
- ಅಕ್ರಮ ಅವಿಭಾಜ್ಯ
- ಪೂರ್ಣಾಂಕದ ಅಪವರ್ತನೀಕರಣ
- ಲಾರ್ಜ್ ಸೀವ್
- ಮಧ್ಯಯುಗದ ಇಸ್ಲಾಂನ ಗಣಿತಶಾಸ್ತ್ರ
- ಗುಣಾತ್ಮಕ ಕಾರ್ಯ
- ಗುಣಾತ್ಮಕ ಸಂಖ್ಯಾ ಸಿದ್ದಾಂತ
- ಪೈಲಿಯಾರ್ ಕ್ರಿಪ್ಟೊಸಿಸ್ಟಮ್
- ಅವಿಭಾಜ್ಯ ಬಲ
- ಪ್ರಿಮನ್ ಅನಿಲ
- ಕ್ವಾಡ್ರಾಟಿಕ್ ರೆಸಿಡ್ಯುಯೊಸಿಟಿ ಸಮಸ್ಯೆ
- ರಾಮಾನುಜನ್-ಪೀಟರ್ಸನ್ ಅಭಿಪ್ರಾಯ
- ಕ್ರಮಬದ್ಧ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ
ಹಂಚಲ್ಪಟ್ಟ ಅವಿಭಜಕಗಳನ್ನು ಹುಡುಕುವ ಗಣನೆ ಯೋಜನೆಗಳು[ಬದಲಾಯಿಸಿ]
- ಪ್ರೈಮ್ಗ್ರಿಡ್ ಬೃಹತ್ ಅವಿಭಾಜ್ಯಕಗಳನ್ನು ಹುಡುಕುತ್ತದೆ.
- Wieferich@Home ವೈಫೆರಿಚ್ ಅವಿಭಾಜ್ಯಕಗಳನ್ನು ಹುಡುಕುತ್ತದೆ.
- GIMPS ಮಾರ್ಸೆನ್ ಅವಿಭಾಜ್ಯಕಗಳನ್ನು ಹುಡುಕುತ್ತದೆ.
ಟಿಪ್ಪಣಿಗಳು[ಬದಲಾಯಿಸಿ]
- ↑ 2.1%
- ↑ ೨.೦ ೨.೧ http://primes.utm.edu/notes/proofs/infinite/euclids.html
- ↑ GIMPS Home; http://www.mersenne.org/
- ↑ [7] ^ [6]
- ↑ Conway & Guy 1996, pp. 129–130.
- ↑ Gowers 2002, p. 118 "ಅವಿಭಾಜ್ಯದ ವ್ಯಾಖ್ಯಾನದಲ್ಲಿ ಬಾಹ್ಯರೂಪವಾಗಿ ಕ್ರಮವಿಲ್ಲದ ೧ ಅನ್ನು ಸೇರಿಸಿರುವುದಿಲ್ಲ… ಆ ಸಂಖ್ಯೆಗಳ ಬಗ್ಗೆ ಆಳವಾಗಿ ಸ್ಪಷ್ಟಪಡಿಸುವುದಿಲ್ಲ: ಇದು ಉಪಯೋಗಾರ್ಹ ರೀತಿನೀತಿಯಾಗಿ ನಡೆಯುತ್ತದೆ, ಅಳವಡಿಸಲಾಗಿರುವುದರಿಂದ ಇದು ಅವಿಭಾಜ್ಯಗಳಲ್ಲಿ ಯಾವುದಾದರೊಂದು ಕೊಟ್ಟಿರುವ ಸಂಖ್ಯೆಯನ್ನು ಅಪವರ್ತನೀಕರಿಸುವ ಒಂದು ಮಾರ್ಗ ಮಾತ್ರವಾಗಿದೆ."
- ↑ ""ವೈ ಈಸ್ ದ ನಂಬರ್ ಒನ್ ನಾಟ್ ಪ್ರೈಮ್?"". ೨೦೦೭-೧೦-೦೨ರಲ್ಲಿ ಪುನರ್ ಸ್ಥಾಪಿಸಲಾಗಿದೆ.
- ↑ ""ಆರ್ಗ್ಯುಮೆಂಟ್ಸ್ ಫಾರ್ ಆಯ್೦ಡ್ ಆಗೈನೆಸ್ಟ್ ದ ಪ್ರಿಮಾಲಿಟಿ ಆಫ್ 1".
- ↑ Hardy 1908, pp. 122–123.
- ↑ ಜುಲೈ ೧೭೩೦, ಲ್ಯಾಟಿನ್ನಲ್ಲಿ ಗೋಲ್ಡ್ಬ್ಯಾಚ್ ಟು ಯೂಲರ್ನ ಲೆಟರ್.
- ↑ Ribenboim 2004, p. 4.
- ↑ Furstenberg ೧೯೫೫.
- ↑ (Ben Green & Terence Tao ೨೦೦೮).
- ↑ [36] ^ [35]
- ↑ The Top Twenty: Primorial
- ↑ ದ ಟಾಪ್ ಟ್ವೆಂಟಿ:ಫ್ಯಾಕ್ಟೊರಿಯಲ್
- ↑ ದ ಟಾಪ್ ಟ್ವೆಂಟಿ: ಟ್ವಿನ್ ಪ್ರೈಮ್ ಸರ್ಚ್
- ↑ "Record ೧೨-Million-Digit Prime Number Nets $೧೦೦,೦೦೦ Prize". Electronic Frontier Foundation. October ೧೪, ೨೦೦೯. Retrieved ೨೦೧೦-೦೧-೦೪.
{{cite web}}: Check date values in:|accessdate=and|date=(help) - ↑ "EFF Cooperative Computing Awards". Electronic Frontier Foundation. Retrieved ೨೦೧೦-೦೧-೦೪.
{{cite web}}: Check date values in:|accessdate=(help) - ↑ Havil ೨೦೦೩, p. ೧೬೩.
- ↑ Havil ೨೦೦೩, p. ೧೭೧.
- ↑ ದ ಪ್ರೈಮ್ ಪೇಜಸ್ನಲ್ಲಿ ಕಾಡ್ವೆಲ್, ಚೆರೀಸ್, ದ ಟಾಪ್ ಟ್ವೆಂಟಿ: ಲುಕಾಸ್ ನಂಬರ್ .
- ↑ ಉದಾ.ನೋಡಿGuy ೧೯೮೧, problem A3, pp. 7–8.
- ↑ Weisstein, Eric W., "Landau's Problems", MathWorld.
- ↑ Hardy ೧೯೪೦ "ಸಂಖ್ಯೆಗಳ ಸಿದ್ದಾಂತ ಅಥವಾ ಸಾಪೇಕ್ಷತೆಯಿಂದ ಯಾರೊಬ್ಬರೂ ಯಾವುದೇ ಯುದ್ದೋಚಿತ ಉದ್ದೇಶಕ್ಕಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸಲು ಕಾಣುವುದಿಲ್ಲ.ಯಾರಾದರೂ ಸುಮಾರು ವರ್ಷಗಳವರೆಗೆ ಅನೀರಿಕ್ಷಿತವಾಗಿ ಇದನ್ನು ನೋಡಬಹುದು."
- ↑ ಗೊಲ್ಸ್,ಇ., ಶುಲ್ಜ್, ಒ. ಆಯ್೦ಡ್ ಎಮ್. ಮಾರ್ಕಸ್(೨೦೦೧). "ಪ್ರೈಮ್ ನಂಬರ್ ಸೆಲೆಕ್ಷನ್ ಆಫ್ ಸೈಕಲ್ಸ್ ಇನ್ ಅ ಪ್ರೀಡೇಟರ್-ಪ್ರೇ ಮಾಡೆಲ್", ಕಾಂಪ್ಲೆಕ್ಸಿಟಿ ೬(೪): ೩೩-೩೮
- ↑ Paulo R. A. Campos, Viviane M. de Oliveira, Ronaldo Giro, and Douglas S. Galvão. (೨೦೦೪). "Emergence of Prime Numbers as the Result of Evolutionary Strategy". Phys. Rev. Lett. ೯೩: ೦೯೮೧೦೭. doi:10.1103/PhysRevLett.93.098107. Retrieved 2006-11-26.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ "Invasion of the Brood". The Economist. May 6, 2004. Retrieved 2006-11-26.
- ↑ Ivars Peterson (June 28, 1999). "The Return of Zeta". MAA Online. Retrieved 2008-03-14.
- ↑ ಶುಬರ್ಟ್, ಹೆಚ್. "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten". ಎಸ್.-ಬಿ ಹೈಡೆಲ್ಬರ್ಗರ್ ಅಕಾಡ್. ವಿಸ್. ಮ್ಯಾತ್.-ನಾಟ್. ಕೆಎಲ್. ೧೯೪೯ (1949), ೫೭–೧೦೪.
- ↑ Eisenbud 1995, section 3.3.
- ↑ Hill, ed. ೧೯೯೫.
- ↑ ಕಾರ್ಲ್ ಪೊಮರ್ಯಾನ್ಸ್, ಪ್ರೈಮ್ ನಂಬರ್ಸ್ ಆಯ್೦ಡ್ ದ ಸರ್ಚ್ ಫಾರ್ ಎಕ್ಸ್ಟ್ರಾಟೆರೆಸ್ಟ್ರಿಯಲ್ ಇಂಟಲಿಜೆನ್ಸ್, ಡಿಸೆಂಬರ್ ೨೨, ೨೦೦೭ರಂದು ಮರು ಸಂಪಾದಿಸಲಾಗಿದೆ.
- ↑ ೩೪.೦ ೩೪.೧ ಸ ಮ್ಯೂಸಿಕ್ ಆಫ್ ಪ್ರೈಮ್ಸ್ Archived 2015-10-09 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ., ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಚಿತ್ರಿಸಿರುವ ಮರ್ಕಸ್ ಡು ಸೌಟಾಯ್'ರ ಚಿತ್ರಗಳ ಆಯ್ಕೆ.
- ↑ "Introducing Paolo Giordano". Books Quarterly.[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ]
ಆಕರಗಳು[ಬದಲಾಯಿಸಿ]
- Conway, John Horton; Guy, Richard K. (1996), The Book of Numbers, New York: Copernicus, ISBN 978-0-387-97993-9
- Crandall, Richard; Pomerance, Carl (2005), Prime Numbers: A Computational Perspective (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-25282-7
- Derbyshire, John (2003), Prime obsession, Joseph Henry Press, Washington, DC, ISBN 978-0-309-08549-6, MR 1968857
- Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, vol. 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1, MR 1322960
- Furstenberg, Harry (1955), "On the infinitude of primes", The American Mathematical Monthly, 62: 353, doi:10.2307/2307043, ISSN 0002-9890
- Green, Ben; Tao, Terence (2008), "The primes contain arbitrarily long arithmetic progressions", Annals of Mathematics, 167: 481–547, arXiv:math.NT/0404188
- Gowers, Timothy (2002), Mathematics: A Very Short Introduction, Oxford University Press, ISBN 978-0-19-285361-5
- Guy, Richard K. (1981), Unsolved Problems in Number Theory, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90593-8
- Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5
- Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, Cambridge University Press, ISBN 978-0-521-09227-2
- Hardy, Godfrey Harold (1940), A Mathematician's Apology, Cambridge University Press, ISBN 978-0-521-42706-7
- Lehmer, D. H. (1909), Factor table for the first ten millions containing the smallest factor of every number not divisible by 2, 3, 5, or 7 between the limits 0 and 10017000, Washington, D.C.: Carnegie Institution of Washington
- Narkiewicz, Wladyslaw (2000), The development of prime number theory: from Euclid to Hardy and Littlewood, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-66289-1
- Ribenboim, Paulo (2004), The little book of bigger primes, Berlin, New York: Springer-Verlag, ISBN 978-0-387-20169-6
- Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9
- Sabbagh, Karl (2003), The Riemann hypothesis, Farrar, Straus and Giroux, New York, ISBN 978-0-374-25007-2, MR 1979664
- du Sautoy, Marcus (2003), The music of the primes, HarperCollins Publishers, ISBN 978-0-06-621070-4, MR 2060134, archived from The Music of Primes website the original on 2015-09-07, retrieved 2010-02-10
{{citation}}: Check|url=value (help)
ಹೆಚ್ಚಿನ ಓದಿಗೆ[ಬದಲಾಯಿಸಿ]
- Hill, Peter Jensen, ed. (1995), The Messiaen companion, Portland, Or: Amadeus Press, ISBN 978-0-931340-95-6
- Kelly, Katherine E., ed. (2001), The Cambridge companion to Tom Stoppard, Cambridge University Press, ISBN 978-0-521-64592-8
- Stoppard, Tom (1993), Arcadia, London: Faber and Faber, ISBN 978-0-571-16934-4
ಹೊರಗಿನ ಕೊಂಡಿಗಳು[ಬದಲಾಯಿಸಿ]
- ಕಾಡ್ವೆಲ್, ಕ್ರಿಸ್,primes.utm.edu ನಲ್ಲಿ ದ ಪ್ರೈಮ್ ಪೇಜಸ್.
- ಮ್ಯಾಥ್ವರ್ಲ್ಡ್ನಲ್ಲಿ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು
- ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಮ್ಯಾಕ್ಟುಟರ್ ಇತಿಹಾಸ
- ಅವಿಭಾಜ್ಯಗಳ ಸಮಸ್ಯೆಗಳು
- ಎಕ್ಲಿಡ್ನ ಆಂಗ್ಲ ಭಾಷಾಂತರ ಕರಡುಪ್ರತಿಯಲ್ಲಿ ಅನಂತ ಅನೇಕ ಅವಿಭಾಜ್ಯಗಳಿವೆ
- ಅವಭಾಜ್ಯ ಮಾದರಿಯ ಸಂಖ್ಯಾ ಸುರುಳಿ
- ಐಲಾನ್ ವರ್ದಿ ಮತ್ತು ಸಿರಿಲ್ ಬಂಡೆರಿಯರ್ ಅವರ ಆಯ್ನ್ ಇಂಟ್ರುಡಕ್ಷನ್ ಟು ಅನಾಲಿಟಿಕ್ ನಂಬರ್ ಥಿಯರಿ Archived 2006-09-25 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
- EFF ಕೊಅಪರೇಟಿವ್ ಕಂಪ್ಯೂಟಿಂಗ್ ಅವಾರ್ಡ್ಸ್ Archived 2008-12-05 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
- ಎನ್ರಿಕ್ಯು ಜೆಲೆನಿಯ, ವೊಲ್ಫ್ರಾಮ್ ಡೆಮಾನ್ಸ್ಟ್ರೇಷನ್ಸ್ ಪ್ರಾಜೆಕ್ಟ್ನಿಂದ ವೈ ಎ ನಂಬರ್ ಈಸ್ ಪ್ರೈಮ್ .
- ಯೂನಿವರ್ಸಿಟಿ ಆಫ್ ಕೇಂಬ್ರಿಡ್ಜ್ನಲ್ಲಿನ ಮಿಲೇನಿಯಂ ಮ್ಯಾಥ್ಮೆಟಿಕ್ಸ್ ಪ್ರಾಜೆಕ್ಟ್ನ ಉಚಿತ ಆನ್ಲೈನ್ ಗಣಿತಶಾಸ್ತ್ರ ನಿಯತಕಾಲಿಕೆಯಾದ ಪ್ಲಸ್ನಿಂದ ಪ್ಲಸ್ ಟೀರ್ ಆಯ್೦ಡ್ ಸ್ಟುಡೆಂಟ್ ಪ್ಯಾಕೇಜ್: ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು
- ಲೂಯಿಸ್ ಮ್ಯಾಟೊಸ್ ಅವರ ಪ್ರೈಮ್ ನಂಬರ್ಸ್ ಸ್ಪೈರಲ್ಸ್ ಆಯ್೦ಡ್ ವಿಷ್ಯುವಲ್ ಪ್ಯಾಟರ್ನ್ಸ್ Archived 2009-11-28 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಯ ಉತ್ಪಾದಕರು ಮತ್ತು ಕೋಷ್ಟಕಗಳು[ಬದಲಾಯಿಸಿ]
- ಆನ್ಲೈನ್ ಪ್ರೈಮ್ ನಂಬರ್ ಜೆನೆರೇಟರ್ ಆಯ್೦ಡ್ ಚೆಕ್ಕರ್ - 128 ಅಂಕಿಗಳವರೆಗೆ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಕೂಡಲೇ ತಪಾಸಿಸುವುದು ಮತ್ತು ಹುಡುಕುವುದು (ಜಾವಾ ಅಥವಾ ಜಾವಾಸ್ಕ್ರಿಪ್ಟ್ ಅಗತ್ಯವಿರುವುದಿಲ್ಲ)
- ಫಾಸ್ಟ್ ಆನ್ಲೈನ್ ಪ್ರೈಮಲಿಟಿ ಟೆಸ್ಟ್- ಡರಿಯೊ ಆಲ್ಪರ್ನ್’ಸ್ ಪರ್ಸನಲ್ ಸೈಟ್ – ಎಲಿಪ್ಟಿಕ್ ಕರ್ವೆ ಮೆಥೆಡ್ ಬಳಕೆಯನ್ನು ಮಾಡಲಾಗಿದೆ(ಸಾವಿರ ಅಂಕಿಗಳ ಸಂಖ್ಯೆಗಳವರೆಗೆ ತಪಾಸಿಸಲಾಗುತ್ತದೆ
!, ಇದಕ್ಕೆ ಜಾವಾ ಅಗತ್ಯವಿದೆ)
- ಪ್ರೈಮ್ ನಂಬರ್ ಜೆನರೇಟರ್ Archived 2009-08-14 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. — ಕೊಟ್ಟಿರುವ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳನ್ನು ಕೊಟ್ಟಿರುವ ಆರಂಭದ ಸಂಖ್ಯೆಗಿಂತ ಹೆಚ್ಚಾಗಿ ಸೃಷ್ಠಿಸಲಾಗುತ್ತದೆ.
- ಆನ್ಲೈನ್ ಪ್ರೈಮ್ ಜನರೇಟಾರ್ ಆದ WIMSನಿಂದ ಪ್ರೈಮ್ಸ್.
- ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಬಹಳ ದೊಡ್ಡ ಡೇಟಾಬೇಸ್
- ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು 10,000,000,000ರ ಕೆಳಗಿರುತ್ತವೆ.
- CS1 errors: dates
- CS1 maint: multiple names: authors list
- ವೆಬ್ ಆರ್ಕೈವ್ ಟೆಂಪ್ಲೇಟಿನ ವೇಬ್ಯಾಕ್ ಕೊಂಡಿಗಳು
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಲೇಖನಗಳು from ಜನವರಿ 2024
- Articles with invalid date parameter in template
- ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- ಉಲ್ಲೇಖಗಳ ಅಗತ್ಯ ಇರುವ ಲೇಖನಗಳು
- Articles with hatnote templates targeting a nonexistent page
- CS1 errors: URL
- ಪೂರ್ಣಸಂಖ್ಯೆ ಪರಿವಿಡಿಗಳು
- ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು
- ಲೇಖನಗಳು ಕರಡುಪ್ರತಿಯನ್ನು ಒಳಗೊಂಡಿವೆ
- ಗಣಿತ








