ಕಾನ್ಫಿಡೆನ್ಸ್‌ ಇಂಟರ್‌ವಲ್ (ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ‌)

ಸಂಖ್ಯಾಶಾಸ್ತ್ರದಲ್ಲಿ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಎನ್ನುವುದು ಜನಸಂಖ್ಯಾ ನಿಯತಾಂಕದ ಒಂದು ವಿಶಿಷ್ಟ ರೀತಿಯ ಅಂದಾಜು ಮಾಡಿದ ಮಧ್ಯಂತರ. ನಿಯತಾಂಕವನ್ನು ಒಂದೇ ಮೌಲ್ಯದ ಮೇಲೆ ಅಂದಾಜು ಮಾಡುವ ಬದಲು, ನಿಯಾತಾಂಕವನ್ನು ಒಳಗೊಳ್ಳಬಹುದಾದಂತಹ ಮಧ್ಯಂತರವನ್ನು ಅಂದಾಜು ಮಾಡಲಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವು ಒಂದು ಅಂದಾಜಿನ ವಿಶ್ವಾಸಾರ್ಹತೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಮಧ್ಯಂತರವು ನಿಯತಾಂಕವನ್ನು ಹೊಂದಿರುವ ಸಂಭವನೀಯತೆಯನ್ನು ವಿಶ್ವಾಸ ಹಂತ ಅಥವಾ ವಿಶ್ವಾಸ ಗುಣಾಂಕದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ವಿಶ್ವಾಸ ಹಂತವನ್ನು ಹೆಚ್ಚಿಸುವುದರಿಂದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವು ವಿಸ್ತೃತವಾಗುತ್ತದೆ.

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಯಾವಾಗಲೂ ಒಂದು ಪ್ರತ್ಯೇಕ ವಿಶ್ವಾಸ ಹಂತ ದಿಂದ ಅರ್ಹಗೊಳಿಸಲಾಗುತ್ತದೆ, ಸಾಮಾನ್ಯವಾಗಿ ಶೇಕಡಗಳಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ; ಆದ್ದರಿಂದ "95% ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ" ಎಂಬುದನ್ನು ಕೇಳಬಹುದು. ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರದ ತುದಿಗಳನ್ನು ವಿಶ್ವಾಸಾರ್ಹ ಮಿತಿಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಕೊಟ್ಟಿರುವ ಸಂದರ್ಭದಲ್ಲಿ, ಕೊಟ್ಟಿರುವ ಅಂದಾಜು ಪ್ರಕ್ರಿಯೆಗೆ, ವಿಶ್ವಾಸ ಹಂತವು ಹೆಚ್ಚಾಗಿದ್ದಷ್ಟೂ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವು ವಿಸ್ತೃತವಾಗಿರುತ್ತದೆ.

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಕಂಡುಹಿಡಿಯುವಾಗ ಸಾಮಾನ್ಯವಾಗಿ ಅಂದಾಜು ಪ್ರಕ್ರಿಯೆಯ ಸ್ವಭಾವದ ಬಗ್ಗೆ ಊಹೆಗಳನ್ನು ಮಾಡಬೇಕಾಗುತ್ತದೆ – ಅದು ಮೂಲತಃ ನಿಯತಾಂಕಿಕ ವಿಧಾನ – ಉದಾಹರೆಣೆಗೆ, ಅದು ಸ್ಯಾಂಪಲ್‌ಅನ್ನು ತೆಗೆದುಕೊಂಡ ಜನಸಂಖ್ಯಾ ಹರಹು ಸಾಮಾನ್ಯವಾದುದು ಎಂಬ ಊಹೆಯ ಮೇಲೆ ಅವಲಂಬಿಸಿರಬಹುದು. ಕೆಳಗೆ ಚರ್ಚಿಸಿದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ತಮ್ಮಷ್ಟಕ್ಕೆ ತಾವೇ ಸಕ್ರಿಯ ಸಂಖ್ಯಾಶಾಸ್ತ್ರಗಳಲ್ಲ, ಆದರೂ ಸಕ್ರಿಯತೆಯನ್ನು ಸೇರಿಸಲು ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡಬಹುದು – ಸಕ್ರಿಯ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನೋಡಿ.

[[ನೇಮನ್‌–ಪಿಯರ್‌ಸನ್‌ (ಫ್ರೀಕ್ವೆಂಟಿಸ್ಟ್‌) ಸಂಖ್ಯಾಶಾಸ್ತ್ರದ ಮಿತಿಯೊಳಗೇ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಬಳಸಲಾಗುತ್ತದೆ; ಬೇಸಿಯಾನ್‌ ಸಂಖ್ಯಾಶಾಸ್ತ್ರದಲ್ಲಿ ನಂಬಲರ್ಹ ಮಧ್ಯಂತರ (ಕ್ರೆಡಿಬಲ್‌ ಇಂಟರ್‌ವಲ್‌)|ನೇಮನ್‌–ಪಿಯರ್‌ಸನ್‌ (ಫ್ರೀಕ್ವೆಂಟಿಸ್ಟ್‌) ಸಂಖ್ಯಾಶಾಸ್ತ್ರದ ಮಿತಿಯೊಳಗೇ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಬಳಸಲಾಗುತ್ತದೆ; ಬೇಸಿಯಾನ್‌ ಸಂಖ್ಯಾಶಾಸ್ತ್ರದಲ್ಲಿ ನಂಬಲರ್ಹ ಮಧ್ಯಂತರ (ಕ್ರೆಡಿಬಲ್‌ ಇಂಟರ್‌ವಲ್‌)]]ವು ಇಂಥದ್ದೇ ಪತ್ರವನ್ನು ವಹಿಸುತ್ತದೆ, ಆದರೆ ನಂಬಲರ್ಹ ಮಧ್ಯಂತರ ಮತ್ತು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಬೇರೆ ಬೇರೆ ಪರಿಕಲ್ಪನೆಗಳ ತಳಹದಿಯನ್ನು ಹೊಂದಿದ್ದು ಸಾಮಾನ್ಯವಾಗಿ ಬೇರೆ ಬೇರೆ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಫ್ರೀಕ್ವೆಂಟಿಸಮ್‌ ಮತ್ತು ಬೇಸಿಯಾನ್‌ ನಡುವಿನ ಸಾಧಾರಣ ಚರ್ಚೆಯ ಭಾಗವಾಗಿ, ಈ ಸಂಖ್ಯಾಶಾಸ್ತ್ರಗಳಲ್ಲಿ ಯಾವುದು ಹೆಚ್ಚು ಉಪಯುಕ್ತ ಮತ್ತು ಅನ್ವರ್ಥ ಎಂಬ ಬಗ್ಗೆ ಭಿನ್ನಾಭಿಪ್ರಾಯವಿದೆ, ಆಲ್ಟರ್‌ನೇಟಿವ್ಸ್‌ ಮತ್ತು ಕ್ರಿಟಿಕ್ಸ್‌ನಲ್ಲಿ ಚರ್ಚಿಸಿದಂತೆ.

ಪರಿಕಲ್ಪನಾತ್ಮಕ ಆಧಾರ

ಈ ಬಾರ್ ನಕ್ಷೆಯಲ್ಲಿ, ಬಾರ್‌ಗಳ ಮೇಲಿನ ತುದಿಗಳು ವೀಕ್ಷಣೆ ಬಗೆಗಳನ್ನು ಮತ್ತು ಕೆಂಪು ಸಾಲಿನ ಖಂಡಗಳು ಅವುಗಳ ಸುತ್ತಲಿನ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಸೂಚಿಸುತ್ತವೆ.

ಮಧ್ಯಂತರಗಳನ್ನು ಕೆಲವೊಮ್ಮೆ ಬಿಂದು ಅಂದಾಜುಗಳ ಜೊತೆಗೆ ಹೋಲಿಸಬಹುದು. ಬಿಂದು ಅಂದಾಜು ಎಂಬುದು ಆಸಕ್ತಿಯ ವಿಷಯದಲ್ಲಿನ ಜನಸಂಖ್ಯಾ ನಿಯತಾಂಕದ ಅಂದಾಜು ಎಂದು ನೀಡಲಾಗುವ ಒಂದೇ ಒಂದು ಮೌಲ್ಯ, ಉದಾಹರಣೆಗೆ ಯಾವುದಾದರೂ ಒಂದು ಪರಿಮಾಣದ ಮಧ್ಯಕ. ಆದರೆ, ಮಧ್ಯಂತರ ಅಂದಾಜು ನಿಯತಾಂಕವು ಇರಬಹುದಾದ ಒಂದು ರೇಂಜ್‌ಅನ್ನು ಸೂಚಿಸುತ್ತದೆ. ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಅದೇ ನಿಯಾಂತಕದ ಬಿಂದು ಅಂದಾಜುಗಳ ಗುಂಟ ಟೇಬಲ್‌ಗಳಲ್ಲಿ ಅಥವಾ ನಕ್ಷೆಗಳಲ್ಲಿ ವರದಿಮಾಡಲಾಗುತ್ತದೆ, ಅಂದಾಜುಗಳ ವಿಶ್ವಾಸಾರ್ಹತೆಯನ್ನು ತೋರಿಸಲು.

ಉದಾಹರಣೆಗೆ, ಒಂದು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಸಮೀಕ್ಷೆಯ ಫಲಿತಾಂಶಗಳು ಎಷ್ಟು ವಿಶ್ವಾಸಾರ್ಹ ಎಂದು ವಿವರಿಸಲು ಬಳಸಬಹುದು. ಒಂದು ಚುನಾವಣೆಯ ಮತದಾನ ಮಾಡುವ-ಇರಾದೆಯ ಸಂಗ್ರಹದಲ್ಲಿ, ಫಲಿತಾಂಶವು ಹೀಗೆ ಬರಬಹುದು - ಪ್ರತಿಕ್ರಿಯಿಸಿದವರಲ್ಲಿ 40%ರಷ್ಟು ಜನ ಒಂದು ಪಕ್ಷಕ್ಕೆ ಮತ ಹಾಕುತ್ತಾರೆ. 90% ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವಿದ್ದಲ್ಲಿ, ಪೂರ್ಣ ಜನಸಂಖ್ಯೆಯಲ್ಲಿ ಈ ಅನುಪಾತಕ್ಕೆ ಅದೇ ಸಮೀಕ್ಷೆಯ ದಿನದಂದು ಅದೇ ಇರಾದೆ ಇರುವ ಅನುಪಾತ 38% ರಿಂದ 42% ಆಗುತ್ತದೆ. ಅದೇ ಡೇಟಾದಿಂದ ಮತ್ತೊಬ್ಬರು 95% ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಕಂದುಹಿಡಿಯಬಹುದು, ಆಗ ಅನುಪಾತವು 36%ದಿಂದ 44%ಶೇಕಡಾ ಆಗುತ್ತದೆ. ಒಂದು ಕೊಟ್ಟಿರುವ ವಿಶ್ವಾಸಾರ್ಹ ಹಂತದಲ್ಲಿ, ಮತ್ತು ಬೇರೆಲ್ಲವೂ ಸಮನಾಗಿರುವ ಪಕ್ಷದಲ್ಲಿ, ದೊಡ್ಡ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಇರುವ ಫಲಿತಾಂಶಕ್ಕಿಂತ ಚಿಕ್ಕ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಇರುವ ಫಲಿತಾಂಶವು ಹೆಚ್ಚು ವಿಶ್ವಾಸಾರ್ಹ. ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ನಿರ್ಧರಿಸುವ ಪ್ರಮುಖ ಅಂಶವೆಂದರೆ ಅಂದಾಜು ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಉಪಯೋಗಿಸುವ ಸ್ಯಾಂಪಲ್‌ನ ಗಾತ್ರ, ಉದಾಹರಣೆಗೆ ಸಮೀಕ್ಷೆಯಲ್ಲಿ ಭಾಗವಹಿಸುವ ಜನರ ಸಂಖ್ಯೆ.

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಮಹತ್ತ್ವ ಪರೀಕ್ಷೆಗಳಿಗೆ ಬಹಳ ಹತ್ತಿರದಿಂದ ಸಂಬಂಧಪಟ್ಟಿವೆ. ಹಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ, ಒಂದು ನಿಯತಾಂಕದ ಅಂದಾಜು X ಆಗಿದ್ದರೆ, ವಿಶ್ವಾಸಾರ್ಹ ಹಂತ P ನಲ್ಲಿ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು [a ,b ] ಆಗಿದ್ದರೆ, [a ,b ] ಮಧ್ಯಂತರದ ಆಚೆಗಿನ ಯಾವುದೇ ಮೌಲ್ಯವು ಮಹತ್ವ ಹಂತ α = 1 − Pರಲ್ಲಿ X ಗಿಂತ ಸಾಕಷ್ಟು ಬೇರೆಯಾಗಿರುತ್ತದೆ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಮಾಡಿದ ಅದೇ ಹರಹಿನ ಊಹೆಗಳಿಗೆ. ಅಂದರೆ, ಎರಡನೇ ನಿಯತಾಂಕವನ್ನು ಅಂದಾಜಿಸುವಾಗ a ಗಿಂತ ಕಡಿಮೆಯಾದ ಅಥವಾ b ಗಿಂತ ದೊಡ್ಡದಾದ ಮೌಲ್ಯವನ್ನು ಗಮನಿಸಿದಲ್ಲಿ, α ಮಹತ್ತ್ವದ ಹಂತದಲ್ಲಿ, ಈ ನಿಯತಾಂಕದ ಮೌಲ್ಯವು X ಗೆ ಸಮನಾಗಿರುತ್ತದೆ ಎನ್ನುವ ಶೂನ್ಯ ಊಹೆಯನ್ನು ತಿರಸ್ಕರಿಸಬಹುದು, ಅದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ, ಎರಡನೇ ನಿಯತಾಂಕವನ್ನು ಅಂದಾಜಿಸುವಾಗ [a ,b ] ಮಧ್ಯಂತರದಲ್ಲೇ ಇದ್ದರೆ, ನಿಯತಾಂಕವು X ಗೆ ಸಮನಾಗಿರುತ್ತದೆ ಎನ್ನುವ ಕಲ್ಪನೆಯನ್ನು ತಿರಸ್ಕರಿಸಲು ಆಗುವುದಿಲ್ಲ. ಇದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ, ಎರಡು ನಿಯತಾಂಕಗಳ ಅಂದಾಜುಗಳು (ಉದಾಹರಣೆಗೆ, ಎರಡು ಸ್ವತಂತ್ರ ಗುಂಪುಗಳಲ್ಲಿ ಒಂದು ವ್ಯತ್ಯಯದ ಮಧ್ಯಕ ಮೌಲ್ಯ), ಕೊಟ್ಟಿರುವ P ಮೌಲ್ಯದಲ್ಲಿ ಮೇಲ್ಚಾಚಾಗದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಸಂವಾದಿ ಮೌಲ್ಯ αದಲ್ಲಿ ಈ ಎರಡು ಮೌಲ್ಯಗಳು ಬೇರೆಬೇರೆಯಾಗಿರುವುದು ಹೆಚ್ಚು ಸಂಭವನೀಯ. ಆದಾಗ್ಯೂ, ಇದು ಅಕ್ಷರಶಃ ಸತ್ಯವಲ್ಲ. ಏಕೆಂದರೆ ಎರಡು ಮಧ್ಯಕಗಳ ವ್ಯತ್ಯಾಸದ ಮಹತ್ತ್ವ ಪರೀಕ್ಷೆಯು, ಆ ವ್ಯತ್ಯಾಸದ ಸ್ಯಾಂಪಲ್‌ ಹರಹಿನ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ. ಆದರೆ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಎರಡು ನಿರಪೇಕ್ಷ ಮೌಲ್ಯಗಳ ಸ್ಯಾಂಪಲ್‌ ಹರಹಿನ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ.

ವಿಶ್ವಾಸಾರ್ಹ ಪ್ರದೇಶಗಳು ಬಹು-ಪರಿಮಾಣಗಳೊಂದಿಗೆ ವ್ಯವಹರಿಸುವುದಕ್ಕಾಗಿ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಪರಿಕಲ್ಪನೆಯನ್ನು ಸಾಮಾನ್ಯೀಕರಣಗೊಳಿಸುತ್ತದೆ. ಈ ಪ್ರದೇಶಗಳು ಸಂಭವನೀಯ ಊಹಾತ್ಮಕ ದೋಷಗಳನ್ನು ಸೂಚಿಸಬಹುದು ಆದರೆ (ಉದಾಹರಣೆಗೆ) ಇದು ಒಂದು ಪರಿಮಾಣದ ಅಂದಾಜು ವಿಶ್ವಾಸಾರ್ಹವಾಗಿಲ್ಲದಿದ್ದರೆ ಮತ್ತೊಂದು ಪರಿಮಾಣದ ಅಂದಾಜು ಕೂಡ ವಿಶ್ವಾಸಾರ್ಹವಾಗದೇ ಹೋಗುವ ಸಂದರ್ಭವೇ ಎಂಬುದನ್ನೂ ಸೂಚಿಸುತ್ತದೆ. ವಿಶ್ವಾಸಾರ್ಹ ಗುಂಪುಗಳನ್ನು ನೋಡಿ.

ರೂಢಿಯಲ್ಲಿ, ಸಾಮಾನ್ಯವಾಗಿ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು 95% ವಿಶ್ವಾಸಾರ್ಹ ಹಂತದಲ್ಲಿ ಹೇಳಲಾಗುತ್ತದೆ. ಆದರೆ, ನಕ್ಷೆಯಲ್ಲಿ ತೋರಿಸುವಾಗ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಹಲವು ವಿಶ್ವಾಸಾರ್ಹ ಹಂತಗಳಲ್ಲಿ ತೋರಿಸಬಹುದು ಉದಾಹರಣೆಗೆ 50%, 95% ಮತ್ತು 99%.

ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಸಿದ್ಧಾಂತ

ವ್ಯಾಖ್ಯಾನ

ಯಾದೃಚ್ಛಿಕ ಮಧ್ಯಂತರಗಳಾಗಿ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು

ಕೊಟ್ಟಿರುವ ಡೇಟಾಸೆಟ್‌ನ ಆಧಾರದ ಮೇಲೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನಿರ್ಮಿಸಲಾಗುತ್ತದೆ: x ಎನ್ನುವುದು ಡೇಟಾಸೆಟ್‌ನಲ್ಲಿರುವ ಅಭಿಪ್ರಾಯಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ, ಮತ್ತು ಅದೇ ಜನಸಂಖ್ಯೆಯಿಂದ ಗಮನಿಸಿರಬಹುದಾದ ಫಲಿತಾಂಶವನ್ನು ಪರಿಗಣಿಸುವಾಗ X ಅನ್ನು ಬಳಸಲಾಗುತ್ತದೆ, ಇಲ್ಲಿ X ಅನ್ನು ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯ ಎಂಬಂತೆ ಬಳಸಲಾಗುತ್ತದೆ, ಇದರ ಫಲಿತಾಂಶವು X  = x . ಒಂದು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು u (.) ಮತ್ತು v (.) ಎಂಬ ಎರಡು ಉತ್ಪನ್ನವಾಕ್ಯಗಳಿಂದ ವಿವರಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಕೊಟ್ಟಿರುವ ಡೇಟಾಸೆಟ್‌ನ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು (u (x ), v (x )) ಮಧ್ಯಂತರ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುತ್ತದೆ. ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರದ ವ್ಯಾಖ್ಯಾನವನ್ನು ಪೂರ್ತಿ ಮಾಡಬೇಕೆಂದರೆ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವು ಯಾವುದಕ್ಕೆ ಮಧ್ಯಂತರ ಅಂದಾಜನ್ನು ಕೊಡುತ್ತದೆಯೋ ಅದರ ಪರಿಮಾಣದ ಬಗೆಗೆ ಸಷ್ಟವಾದ ಅರಿವು ಇರಬೇಕು. ಈ ಪರಿಮಾಣವು w ಆಗಿದ್ದರೆ. (u (x ), v (x )) ಅನ್ನು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಇರಬಹುದಾದ w ಗೆ ಅತ್ಯಂತ ಸಮೀಪ ತರುವ u (.) ಮತ್ತು v (.) ನಿಯಮದ ಗುಣಲಕ್ಷಣವು, (u (X ), v (X ))ನಿಂದ ಕೊಡಲಾದ ಯಾದೃಚ್ಛಿಕ ಮಧ್ಯಂತರಗಳ ಸೆಟ್‌ನ ಗುಣಲಕ್ಷಣಗಳಿಗೆ ಸಂಬಂಧಿಸಿರುತ್ತದೆ: ಅಂದರೆ ತುದಿ-ಬಿಂದುಗಳನ್ನು ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯಗಳೆಂದು ಪರಿಗಣಿಸುತ್ತದೆ. ಈ ಗುಣಲಕ್ಷಣವೇ coverage ಸಂಭವನೀಯತೆ ಅಥವಾ ಯಾದೃಚ್ಛಿಕ ಮಧ್ಯಂತರ w ಅನ್ನು ಒಳಗೊಂಡ ಸಂಭವನೀಯತೆ ಸಿ .

$c=\Pr(u(X)$

ಇಲ್ಲಿ ತುದಿಬಿಂದುಗಳಾದ U  = u (X ) ಮತ್ತು V  = v (X )ಗಳು ಅಂಕಿಅಂಶಗಳು (ಅಂದರೆ ಡೇಟಾಸೆಟ್‌ನಲ್ಲಿರುವ ಮೌಲ್ಯಗಳಿಂದ ನಿಷ್ಪನ್ನ ಮಾಡಿದ ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯಗಳು). ಯಾದೃಚ್ಛಿಕ ಮಧ್ಯಂತರ (U , V ).

ಸಿದ್ಧಾಂತಕ್ಕೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು

ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಸಿದ್ಧಾಂತಕ್ಕೆ ಇದು ವ್ಯಾವಹಾರಿಕ ಮಧ್ಯಕವನ್ನು ಕೊಡಬೇಕಾದರೆ, ಮುಂದುವರಿದ ಕೆಲವು ಆವಶ್ಯಕತೆಗಳಿವೆ: X ಹೊರಹರಿವಿನ ಸಂಭವನೀಯತೆಯ ಹರಹು ಮತ್ತು ಅಂದಾಜು ಮಾಡಿದ ಪ್ರಮಾಣದ ನಡುವೆ ಒಂದು ಸಮಾನತೆ ಇರಬೇಕು. ಈ ಸಂಭವನೀಯತೆಯ ಹರಹು, ಅಂದಾಜು ಮಾಡಬೇಕಾದ ಪ್ರಮಾಣವಾದ - ಕಾಣಲಾಗದ ಸ್ಥಿರರಾಶಿ θ ದಿಂದ ಮತ್ತು ತಕ್ಷಣಕ್ಕೆ ಬೇಡವಾದ ಕಾಣಲಾಗದ ಇತರೆ ಸ್ಥಿರರಾಶಿಗಳು φ ನಿಂದ ಕೂಡಿದ್ದರೆ, ತಕ್ಷಣಕ್ಕೆ ಬೇಡವಾದ ಇತರ ಪ್ರಮಾಣಗಳಾದ φಗಳನ್ನು ರಗಳೆ ಸ್ಥಿರರಾಶಿಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಸಿದ್ಧಾಂತವು ಇವುಗಳ ಜೊತೆಗೆ ಕೆಲಸಮಾಡಲು ಇನ್ನೂ ದಾರಿಗಳನ್ನು ಹುಡುಕಿಕೊಳ್ಳಬೇಕಾಗಿದೆ.

0 ಮತ್ತು 1ರ ನಡುವಿನ ಯಾವುದೇ ಸಂಖ್ಯೆ αದ θದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರದ ವ್ಯಾಖ್ಯಾನವೆಂದರೆ, ಅದೊಂದು

$(u(X),v(X))\,$

ಮಧ್ಯಂತರ, ಇದಕ್ಕೆ

${\Pr }_{\theta ,\varphi }(u(X)$

ಮತ್ತು u (X ) ಮತ್ತು v (X )ಗಳು ಕಾಣುವ ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯಗಳು, ಅಂದರೆ u (X ) ಮತ್ತು v (X )ಗಳ ಮೌಲ್ಯವನ್ನು ತಿಳಿದುಕೊಳ್ಳಲು ಕಾಣದ ಪ್ರಮಾಣಗಳಾದ θ , φ ಗಳ ಮೌಲ್ಯವನ್ನು ತಿಳಿದುಕೊಳ್ಳುವ ಆವಶ್ಯಕಥೆಯಿಲ್ಲ.

ಸಂಖ್ಯೆ 1 − α (ಕೆಲವೊಮ್ಮೆ ಶೇಕಾಡಾಂಶದಲ್ಲಿ ವರದಿಮಾಡಲಾಗುತ್ತದೆ 100%·(1 − α )) ಎನ್ನುವುದು ವಿಶ್ವಾಸ ಹಂತ , ಕೆಲವೊಮ್ಮೆ ವಿಶ್ವಾಸ ಗುಣಾಂಕ ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ. ಹಲವಾರು ಪುಸ್ತಕಗಳು ಇದೇ ಸಂಪ್ರದಾಯವನ್ನು ಅಳವಡಿಸಿಕೊಂಡಿವೆ, ಇಲ್ಲಿ α ಸಣ್ಣ ಸಂಖ್ಯೆಯಾಗಿರುತ್ತದೆ. ಇಲ್ಲಿ ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯ X (θ , φ )ಅನ್ನು ಒಳಗೊಂಡ ಹರಹನ್ನು ಹೊಂದಿರುವಾಗ, ಸಂಭವನೀಯತೆಯನ್ನು ಸೂಚಿಸಲು Pr_{θ ,φ} ಅನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಈ ವಿವರಣೆಯಲ್ಲಿ ಅತ್ಯಂತ ಪ್ರಮುಖ ಭಾಗವೆಂದರೆ, ಯಾದೃಚ್ಛಿಕ ಮಧ್ಯಂತರ (U , V )ಗಳು ಗೊತ್ತಿಲ್ಲದ ಮೌಲ್ಯ θವನ್ನೂ ಅತ್ಯಧಿಕ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ ಒಳಗೊಂಡಿರುತ್ತದೆ, θರ ನಿಜವಾದ ಮೌಲ್ಯ ಏನಿದೆ ಎಂಬುದನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳದೆ.

ಇಲ್ಲಿ Pr_{θ ,φ} ಎಂಬುದು ಪರಿಸ್ಫುಟವಾಗಿ ಕೊಟ್ಟ ಸ್ಥಿರರಾಶೀಕೃತ ಹರಹಿನ ಕುಟುಂಬದ ಕಡೆಗೆ ನಿರ್ದೇಶಿಸಬೇಕೆಂದೇನೂ ಇಲ್ಲ, ಅನೇಕವೇಳೆ ಅದು ಹಾಗೆ ಮಾಡಿದರೂ ಸಹ. ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯ X ವು, ಅದೇ ಜನಸಂಖ್ಯೆಯಿಂದ ಅಥವಾ ವಾಸ್ತವದ ಅದೇ ಆವೃತ್ತಿಯಿಂದ ಸಾಧ್ಯವಾಗುಬಹುದಾದ x ನ ವಾಸ್ತವಾಂಶಗಳಿಗೆ ಕಾಲ್ಪನಿಕವಾಗಿ ಸಂವಾದಿಯಾಗುವ ಹಾಗೆ, (θ , φ ) ಸ್ಥಿರರಾಶಿಗಳು X ನ ಹರಹು ವಿವಿಧ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿರುವ ಸಂದರ್ಭದಲ್ಲಿ, ನಾವು ವಾಸ್ತವದ ಇತರ ಆವೃತ್ತಿಗಳನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕೆಂದು ಸೂಚಿಸುತ್ತದೆ.

ಯಾದೃಚ್ಛಿಕ ಹೊರಹರಿವಿಗೆ ಮಧ್ಯಂತರಗಳು

ಮೇಲಿನಂತೆ, ಯಾದೃಚ್ಛಿಕ ಪ್ರಮಾಣಗಳಿಗೆ ಹಾಗೆಯೇ ಸ್ಥಿರ ಪ್ರಮಾಣಗಳಿಗೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು. ಮಧ್ಯಂತರವನ್ನೂ ನೋಡಿ. ಇದಕ್ಕೆ, ಒಂದು ಹೆಚ್ಚಿವರಿ ಏಕ-ಮೌಲ್ಯ ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯ Y ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ, ಇದು ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯವಾಗಿ X ನ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರಬಹುದು ಅಥವಾ ಅವಲಂಬಿತವಾಗದೆಯೂ ಇರಬಹುದು. ಆಮೇಲೆ, u (x ), v (x )) ಮಧ್ಯಂತರವನ್ನು ನಿರ್ಮಿಸುವ ನಿಯಮವು, ಇನ್ನೂ ಕಾಣಬೇಕಾದ Y ನ y ಮೌಲ್ಯಕ್ಕೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಒದಗಿಸುತ್ತದೆ. ಆದರೆ

${\Pr }_{\theta ,\varphi }(u(X)$

ಆಗಿರಬೇಕು. ಇಲ್ಲಿ Pr_{θ ,φ} ಯನ್ನು ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯಗಳಾದ (X , Y )ಗಳು (θ , φ ) ಸ್ಥಿರರಾಶಿಗಳನ್ನು ಒಳಗೊಂಡಿದ್ದಾಗ ಜಂಟಿ ಹರಹಿನ ಸಂಭವನೀಯತೆಯನ್ನು ಸೂಚಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ.

ಸರಿಸುಮಾರು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು

ಘನವಲ್ಲದ ಉಪಯೋಗಗಳಿಗೆ, ಬೇಕಾದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿರುವ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನಿರ್ಮಿಸುವ ನಿಯಮಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಕೆಲವು ಸಾರಿ ಕಷ್ಟವಾಗುತ್ತದೆ. ಆದರೂ ಪ್ರಾಯೋಗಿಕವಾಗಿ ಉಪಯೋಗವಾಗುವ ಮಧ್ಯಂತರಗಳನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು. ಯಾದೃಚ್ಛಿಕ ಮಧ್ಯಂತರದ ಕವರೇಜ್‌ ಸಂಭವನೀಯತೆ c (θ , φ )ಯನ್ನು

${\Pr }_{\theta ,\phi }(u(X)$

ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಮಧ್ಯಂತರವನ್ನು ನಿರ್ಮಿಸುವ ನಿಯಮವನ್ನು,

$c(\theta ,\phi )\approxeq 1-\alpha {\text{ for all }}(\theta ,\phi )\,$

ಒಪ್ಪಬಹುದಾದ ಸರಿಸುಮಾರು ಹಂತದಲ್ಲಿದ್ದರೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಕೊಡುತ್ತದೆ ಎಂದು ಒಪ್ಪಬಹುದು.

ಬೇಸಿಯಾನ್‌ ಮಧ್ಯಂತರ ಅಂದಾಜುಗಳ ಜೊತೆ ಹೋಲಿಕೆ

ಬೇಸಿಯಾನ್‌ ಮಧ್ಯಂತರ ಅಂದಾಜನ್ನು ನಂಬಲರ್ಹ ಮಧ್ಯಂತರ ಅಂದಾಜು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಮೇಲಿನಂತೆಯೇ ಸಂಖ್ಯಾಲೇಖನಗಳನ್ನು ಬಳಸಿಕೊಂಡು, ಒಂದು ಕೊಟ್ಟಿರುವ ಮೌಲ್ಯ α ಗೊತ್ತಿಲ್ಲದ θ ದ ಮೌಲ್ಯದ ಒಂದು ನಂಬಲರ್ಹ ಮಧ್ಯಂತರದ ವ್ಯಾಖ್ಯಾನವು ಹೀಗಿದೆ -

$\Pr(u(x)$

ಇಲ್ಲಿ, ಮೌಲ್ಯ ಗೊತ್ತಿಲ್ಲದ θ ವನ್ನು ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯವೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಒತ್ತಿಹೇಳುವುದಕ್ಕೋಸ್ಕರ Θಅನ್ನು ಬಳಸಲಾಗಿದೆ. ಈ ಎರಡು ವಿಧದ ಮಧ್ಯಂತರಗಳ ವ್ಯಾಖ್ಯಾನಗಳನ್ನು ಹೀಗೆ ಹೋಲಿಸಬಹುದು.

• ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರದ ವ್ಯಾಖ್ಯಾನವು, ಕೊಟ್ಟಿರುವ (θ , φ )ಗಳಿಗೆ X ನ ಹರಹಿನಿಂದ ಕಂಡುಹಿಡಿದುಕೊಂಡ ಸಂಭವನೀಯತೆಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ, (ಅಥವಾ ಈ ಮೌಲ್ಯಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ) ಮತ್ತು ಆ ಷರತ್ತುಗಳು (θ , φ )ಗಳ ಎಲ್ಲ ಮೌಲ್ಯಗಳಿಗೂ ಅನ್ವಯಿಸುತ್ತದೆ.
• ನಂಬಲರ್ಹ ಮಧ್ಯಂತರದ ವ್ಯಾಖ್ಯಾನವು X = x ಗಳ ಕಾಣುವ ಮೌಲ್ಯಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾದ Θನ ಹರಹಿನಿಂದ ಕಂಡುಹಿಡಿದ ಸಂಭವನೀಯತೆಗಳನ್ನು ಮತ್ತು Φನ ಮೌಲ್ಯಗಳ ಮೇಲೆ ಅಮುಖ್ಯಗೊಳಿಸಿದ (ಅಥವಾ ಸರಾಸರಿ ಮಾಡಿದ) ಸಂಭವನೀಯತೆಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ಇಲ್ಲಿ Φ ಪ್ರಮಾಣವು φ ನಲ್ಲಿರುವ ರಗಳೆ ಸ್ಥಿರರಾಶಿಗಳ ಅಸ್ಥಿರತೆಗೆ ಸಂವಾದಿಯಾದ ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯ.

ಮೇಲೆ ಹೇಳಿರುವ ರಗಳೆ ಸ್ಥಿರರಾಶಿಗಳ ಪರಿಗಣನೆಯನ್ನು ವಿಶ್ವಾಸಾರ್ಹ ಮತ್ತು ನಂಬಲರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಹೋಲಿಸುವ ಚರ್ಚೆಗಳಿಂದ ಕೈಬಿಡಲಾಗುತ್ತದೆ ಆದರೆ ಅದು ಈ ಎರಡು ಸಂದರ್ಭಗಳಲ್ಲಿ ಎದ್ದು ಕಾಣುವಷ್ಟು ವ್ಯತ್ಯಾಸವನ್ನು ತಾಳುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ.

ಕೆಲವು ಸರಳ-ಸ್ಥಿರ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಒಂದೇ ಡೇಟಾದಿಂದ ನಿರ್ಮಿಸಿದ ವಿಶ್ವಾಸಾರ್ಹ ಮತ್ತು ನಂಬಲರ್ಹ ಮಧ್ಯಂತರಗಳು ಒಂದೇ ಆಗಿರಬಹುದು. ಬೇಸಿಯಾನ್‌ ವಿಶ್ಲೇಷಣೆಯಲ್ಲಿ ಮಧ್ಯಮ ಅಥವಾ ಪ್ರಬಲ ಪೂರ್ವ ಮಾಹಿತಿಯನ್ನು ಸೇರಿಸಿದರೆ ಅವೆರಡೂ ಯಾವಾಗಲೂ ಬಹಳ ಬೇರೆಬೇರೆಯಾಗಿರುತ್ತದೆ.

ಅಪೇಕ್ಷಣೀಯ ಗುಣಲಕ್ಷಣಗಳು

ಸ್ಥಿರ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ಯಾವಾಗ ಉಪಯೋಗಿಸಿದರೂ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನಿರ್ಮಿಸುವ ಸ್ಥಿರರೀತಿಗಳು ಇದ್ದೇ ಇರುತ್ತವೆ. ಇವುಗಳನ್ನು ಕೆಲವು ಅಪೇಕ್ಷಣೀಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಮುಟ್ಟುವುದಕ್ಕಾಗಿಯೇ ರೂಪಿಸಲಾಗಿರುತ್ತದೆ, ಪ್ರಕ್ರಿಯೆಯು ಅವಲಂಬಿತವಾಗಿರುವ ಊಹೆಗಳು ನಿಜವಾದಲ್ಲಿ ಇದು ಅನ್ವಯವಾಗುತ್ತದೆ. ಈ ಅಪೇಕ್ಷಣಿಯ ಗುಣಗಳೆಂದರೆ: ಸಾಕ್ಷ್ಯ, ಅತ್ಯುತ್ತಮಿಕೆ ಮತ್ತು ನಿರ್ವೈಷಮ್ಯ. ಇವುಗಳಲ್ಲಿ "ಸಾಕ್ಷ್ಯ" ಬಹಳ ಮುಖ್ಯ, ಇದರ ಹಿಂದೆಯೇ ಬರುವುದು "ಅತ್ಯುತ್ತಮಿಕೆ". "ನಿರ್ವೈಷಮ್ಯ"ವನ್ನು ಮಧ್ಯಂತರವನ್ನು ನಿರ್ಮಿಸುವ ನಿಯಮ ಎಂಬುದಕ್ಕಿಂತಲೂ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ನಿಷ್ಪತ್ತಿ ಮಾಡುವ ವಿಧಾನದ ಒಂದು ಗುಣಲಕ್ಷಣ ಎನ್ನಬಹುದು. ಅಸ್ಥಿರ ಉಪಯೋಗಗಳಲ್ಲಿ, ಈ ಅಪೇಕ್ಷಣೀಯ ಗುಣಲಕ್ಷಣಗಳನ್ನೇ ಬಯಸಬಹುದು.

• ಸಾಕ್ಷ್ಯ. ಅತ್ಯಲ್ಪ ಕವರೇಜ್‌ ಸಂಭವನೀಯತೆಯ (ವಿಶ್ವಾಸ ಹಂತ) ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವು ಸರಿಯಾಗಿ ಇಲ್ಲವೇ ಉತ್ತಮ ಸರಿಸುಮಾರಾಗಿ ಅನ್ವಯಿಸಬೇಕೆಂದು ಇದರ ಅರ್ಥ.
• ಅತ್ಯುತ್ತಮಿಕೆ. ಎಂದರೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ನಿರ್ಮಿಸುವ ನಿಯಮವು, ಡೇಟಾ-ಸೆಟ್‌ನಲ್ಲಿರುವ ಮಾಹಿತಿಯನ್ನು ಎಷ್ಟು ಸಾಧ್ಯವೋ ಅಷ್ಟು ಬಳಸಿಕೊಳ್ಳಬೇಕು. ಡೇಟಾಸೆಟ್‌ನ ಅರ್ಧದಷ್ಟನ್ನು ಹೊರಹಾಕಿದರೂ ಸಹ ಒಂದು ಮಾನ್ಯ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದೆಂಬುದನ್ನು ನೆನಪಿಡಿ. ಅತ್ಯುತ್ತಮಿಕೆಯನ್ನು ಪರೀಕ್ಷೆ ಮಾಡುವ ಒಂದು ವಿಧವೆಂದರೆ, ಮಧ್ಯಂತರದ ವಿಸ್ತಾರದಿಂದ, ಸಾಮಾನ್ಯವಾಗಿ ಕಡಿಮೆ ವಿಸ್ತಾರಗಳಿಗೆ ಎಡೆಮಾಡಿಕೊಡುವ ಇತರ ಮಧ್ಯಂತರಗಳಿಗೆ ಎದುರಾಗಿ ಒಂದು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಸರಿಯಾಗಿ ವಿಮರ್ಶಿಸುವುದು ಸಾಧ್ಯವಾಗಲಿ ಎಂದು.
• ನಿರ್ವೈಷಮ್ಯ. ಹಲವು ಉಪಯೋಗಗಳಲ್ಲಿ, ಅಂದಾಜು ಮಾಡಲಾದ ಪ್ರಮಾಣವನ್ನು ಅಷ್ಟೇನೂ ಕರಾರುವಕ್ಕಾಗಿ ವ್ಯಾಖ್ಯಾನ ಮಾಡಿರುವುದಿಲ್ಲ. ಉದಾಹರಣೆಗೆ, ಒಂದು ಸಮೀಕ್ಷೆಯು ಜನಸಂಖ್ಯೆಯ ಮಧ್ಯರೇಖೆ ಆದಾಯದ ಅಂದಾಜಿನಲ್ಲಿ ಪರಿಣಮಿಸಬಹುದು, ಆದರೆ ಅದನ್ನು ಮಧ್ಯರೇಖೆ ಆದಾಯದ ಪ್ರತಿಘಾತವನ್ನು ಒದಗಿಸಲೂ ಬಳಸಬಹುದು, ನಕ್ಷಾ ಫಲಿತಾಂಶಗಳನ್ನು ಕೊಡಲು ಇದೊಂದು ಸಮಾನ ಮಾನದಂಡವಾಗಿದ್ದ ಪಕ್ಷದಲ್ಲಿ. ಮಧ್ಯರೇಖೆ ಗಳಿಕೆಗೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ರಚಿಸಲು ಬಳಸುವ ವಿಧಾನವು ಮಧ್ಯರೇಖೆ ಗಳಿಕೆಯ ಪ್ರತಿಘಾತಕ್ಕೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ರಚಿಸಲು ಬಳಸಿದಾಗಲೂ ಅದೇ ರೀತಿಯ ಫಲಿತಾಂಶಗಳನ್ನು ಕೊಡುವುದು ಅಪೇಕ್ಷಣೀಯ: ಪ್ರತ್ಯೇಕವಾಗಿ ಪೂರ್ವ ಮಧ್ಯಂತರದ ತುದಿಗಳಲ್ಲಿರುವ ಮೌಲ್ಯಗಳಿಗೆ ಉತ್ತರ ಮಧ್ಯಂತರಗಳ ತುದಿಯಲ್ಲಿರುವ ಮೌಲ್ಯಗಳು ಪ್ರತಿಘಾತಗಳಾಗಿರುತ್ತವೆ.

ನಿಷ್ಪನ್ನ ಮಾಡುವ ವಿಧಾನಗಳು

ಅಸ್ಥಿರ ಉಪಯೋಗಗಳಿಗೆ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನಿರ್ಮಿಸುವ ನಿಯಮಗಳನ್ನು ನಿಷ್ಪನ್ನ ಮಾಡಲು ಅನೇಕ ಮಾರ್ಗಗಳಿವೆ. ಸ್ಥಿರ ಪ್ರಕ್ರಿಯೆಗಳಿಗೆ ಸ್ಥಾಪಿಸಲಾದ ನಿಯಮಗಳನ್ನು ಈ ಮಾರ್ಗಗಳ ಮೂಲಕ ಸಮರ್ಥಿಸಬಹುದು ಅಥವಾ ವಿವರಿಸಬಹುದು. ಸಾಧಾರಣವಾಗಿ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನಿರ್ಮಿಸುವ ನಿಯಮಗಳು, ಪರಿಗಣಿಸಿರುವ ಪ್ರಮಾಣದ ಬಿಂದು ಅಂದಾಜನ್ನು ಕಂಡುಹಿಡಿಯುವ ಒಂದು ಪ್ರತ್ಯೇಕ ರೀತಿಗೆ ಬಹುತೇಕ ಸಮನಾಗಿರುತ್ತದೆ.

ಸಂಖ್ಯಾಶಾಸ್ತ್ರ

ಇದು ಅಂದಾಜು ಮಾಡುವ ಕ್ಷಣಗಳ ವಿಧಾನಕ್ಕೆ ಬಹಳ ಹತ್ತಿರವಾದದ್ದು. ಇದಕ್ಕೆ ಸರಳವಾದ ಉದಾಹರಣೆಯೆಂದರೆ, ಅಂದಾಜು ಮಾಡಬೇಕಾಗಿರುವ ಪ್ರಮಾಣವು ಮಧ್ಯಕ, ಈ ಸಂದರ್ಭದಲ್ಲಿ ಸ್ವಾಭಾವಿಕ ಅಂದಾಜು ಸ್ಯಾಂಪಲ್‌ ಮಧ್ಯಕವಾಗುತ್ತದೆ. ಸಾಮಾನ್ಯವಾದ ವಾದಗಳು ಸ್ಯಾಂಪಲ್‌ ವೈಷಮ್ಯವನ್ನು, ಸ್ಯಾಂಪಲ್‌ ಮಧ್ಯಕದ ವೈಷಮಯವನ್ನು ಅಂದಾಜು ಮಾಡಲು ಬಳಸಬಹುದೆಂದು ಸೂಚಿಸುತ್ತದೆ. ನಿಜವಾದ ಮಧ್ಯಕಕ್ಕೆ ಒಂದು ಸರಳ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಸ್ಯಾಂಪಲ್‌ ಮಧ್ಯಕದ ಮೇಲೆ ಕೇಂದ್ರೀಕೃತ ಮಾಡಿ ನಿರ್ಮಿಸಬಹುದು, ಮಧ್ಯಕದ ಗಾತ್ರವು a ಸ್ಯಾಂಪಲ್‌ ವೈಷಮ್ಯದ ವರ್ಗಮೂಲದ ಅಪವರ್ತ್ಯ.

ಸಾಧ್ಯತೆ ಸಿದ್ಧಾಂತ

ಇಲ್ಲಿ ಅಂದಾಜುಗಳನ್ನು ಗರಿಷ್ಠ ಸಾಧ್ಯತೆ ಸಿದ್ಧಾಂತವನ್ನು ಬಳಸಿಕೊಂಡು ನಿರ್ಮಿಸಲಾಗುತ್ತದೆ, ಈ ಸಿದ್ಧಾಂತವು ಅಂದಾಜುಗಳಿಗೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಅಥವಾ ವಿಶ್ವಾಸ ಪ್ರದೇಶಗಳನ್ನು ನಿರ್ಮಿಸಲು ಎರಡು ವಿಧಗಳನ್ನು ಒದಗಿಸುತ್ತದೆ.

ಸಮೀಕರಣಗಳನ್ನು ಅಂದಾಜು ಮಾಡುವುದು

ಈ ಅಂದಾಜು ಮಾಡುವ ವಿಧಾನವು ಕ್ಷಣಗಳ ವಿಧಾನದ ಸಾಮಾನ್ಯೀಕರಣ ಮತ್ತು ಗರಿಷ್ಠ ಸಾಧ್ಯತೆ ಸಿದ್ಧಾಂತದ ಸಾಮಾನ್ಯೀಕರಣ ಎಂದು ಭಾವಿಸಬಹುದು. ಗರಿಷ್ಠ ಸಾಧ್ಯತೆ ಸಿದ್ಧಾಂತದ ಫಲಿತಾಂಶಗಳ ಸಂವಾದಿ ಸಾಮಾನ್ಯೀಕರಿಸಣವೂ ಇದೆ, ಇವು ಸಮೀಕರಣಗಳನ್ನು ಅಂದಾಜು ಮಾಡುವುದರಿಂದ ನಿಷ್ಪನ್ನವಾದ ಅಂದಾಜುಗಳ ಆಧಾರದ ಮೇಲೆ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನಿರ್ಮಿಸಲು ಅನುವು ಮಾಡಿಕೊಡುತ್ತದೆ.

ಪ್ರಾಮುಖ್ಯ ಪರೀಕ್ಷೆಯ ಮೂಲಕ

ಒಂದು ಸ್ಥಿರರಾಶಿಯ ಸಾಮಾನ್ಯ ಮೌಲ್ಯಗಳಿಗೆ ಪ್ರಾಮುಖ್ಯತೆ ಪರೀಕ್ಷೆಗಳು ಒದಗುವುದಾದರೆ, "ಕೊಟ್ಟಿರುವ ಮೌಲ್ಯವೇ ನಿಜವಾದ ಮೌಲ್ಯ ಮತ್ತು ಪ್ರಮುಖ ಹಂತ (1-p)ನಲ್ಲಿ ಅದನ್ನು ತಿರಸ್ಕರಿಸಲಾಗುವುದಿಲ್ಲ" ಎಂಬ ಶೂನ್ಯ ಊಹೆಯನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಬಿಂದುಗಳನ್ನು 100p%ನಲ್ಲಿ ವಿಶ್ವಾಸ ವಲಯದಲ್ಲಿ ಸೇರಿಸುವ ಮೂಲಕ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು/ಪ್ರದೇಶಗಳನ್ನು ನಿರ್ಮಿಸಬಹುದು.

ಉದಾಹರಣೆಗಳು

ಪ್ರಾಯೋಗಿಕ ಉದಾಹರಣೆಗಳು

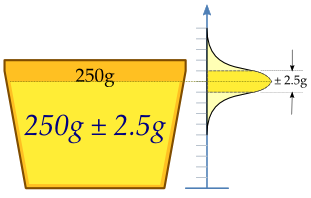
ಒಂದು ಯಂತ್ರವು ಕಪ್‌ಗಳನ್ನು ಕೃತಕ ಬೆಣ್ಣೆಯಿಂದ ತುಂಬುತ್ತದೆ ಮತ್ತು ಅದು ಕಪ್‌ಗಳಲ್ಲಿ 250ಗ್ರಾಂ‌ ಕೃತಕ ಬೆಣ್ಣೆಯಿರುವಂತೆ ಸರಿಹೊಂದಿಸಬೇಕು. ಯಂತ್ರವು ಪ್ರತಿಯೊಂದು ಕಪ್‌ಅನ್ನೂ ಸರಿಯಾಗಿ 250 ಗ್ರಾಂನಿಂದಲೇ ತುಂಬಲು ಸಾದ್ಯವಿಲ್ಲವಾದ್ದರಿಂದ ಸ್ವಲ್ಪ ವ್ಯತ್ಯಯವಾಗುತ್ತದೆ, ಮತ್ತು ಆ ವ್ಯತ್ಯಯವನ್ನು ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯ X ಎಂದು ಪರಿಗಣಿಸೋಣ. ಈ ವ್ಯತ್ಯಯವು ಅಪೇಕ್ಷಿತ ಸರಾಸರಿ 250 ಗ್ರಾಂ‌ನ ಸುತ್ತ, ಮಾನಕ ವಿಚಲನೆ 2.5 ಗ್ರಾಂ‌ನೊಂದಿಗೆ ಸಾಮಾನ್ಯವಾಗಿ ಹರಹಿದೆ ಎಂದು ಊಹಿಸಿಕೊಳ್ಳೋಣ. ಯಂತ್ರವು ಸರಿಯಾದ ಸಾಮರ್ಥ್ಯವನ್ನು ಪಡೆದುಕೊಂಡಿದೆಯೇ ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಲು, n  = 25 ಕೃತಕ ಬೆಣ್ಣೆ ಕಪ್‌ಗಳು ಎಂಬ ಯಾದೃಚ್ಛಿಕ ಉದಾಹರಣೆಯನ್ನು ತೆಗೆದುಕೊಂಡು ಕಪ್‌ಗಳನ್ನು ತೂಕಮಾಡಲಾಗುತ್ತದೆ. X ₁, ..., X ₂₅ಗಳು ಕಪ್‌ಗಳ ತೂಕಗಳು, ಇದು X ನಿಂದ ತೆಗೆದುಕೊಂಡ ಒಂದು ಯಾದೃಚ್ಛಿಕ ಸ್ಯಾಂಪಲ್‌.

μ ನಿರೀಕ್ಷಣೆಯ ಆವೃತ್ತಿಯನ್ನು ಪಡೆಯಲು, ಒಂದು ಅಂದಾಜನ್ನು ಕೊಟ್ಟರೆ ಸಾಕು. ಸರಿಯಾದ ಅಂದಾಜು ಕಟ್ಟುವಸಾಧನವೆಂದರೆ ಸ್ಯಾಂಪಲ್‌ ಮಧ್ಯಕ:

${\hat {\mu }}={\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}.$

ಸ್ಯಾಂಪಲ್‌ ನಿಜವಾದ ತೂಕಗಳಾದx ₁, ..., x ₂₅ಗಳನ್ನು ಮಧ್ಯಕದೊಂದಿಗೆ ತೋರಿಸುತ್ತದೆ:

${\bar {x}}={\frac {1}{25}}\sum _{i=1}^{25}x_{i}=250.2\,{\text{grams}}.$

ನಾವು 25 ಕಪ್‌ಗಳ ಮತ್ತೊಂದು ಸ್ಯಾಂಪಲ್‌ಅನ್ನು ತೆಗೆದುಕೊಂಡರೆ, 250.4 ಗ್ರಾಂ ಅಥವಾ 251.1 ಗ್ರಾಂ‌ನಂತಹ ಮೌಲ್ಯಗಳನ್ನು ಸುಲಭವಾಗಿ ನಿರೀಕ್ಷಿಸಬಹುದು. ಕಪ್‍ಗಳ ತೂಕದ ಮಧ್ಯಕವು ನಿಜವಾಗಿಯೂ 250 ಗ್ರಾಂ‌ ಆಗಿದ್ದರೆ, 280 ಗ್ರಾಂನ ಒಂದು ಸ್ಯಾಂಪಲ್‌ ಮಧ್ಯಕ ಮೌಲ್ಯ ಅತ್ಯಂತ ವಿರಳವಾಗುತ್ತದೆ. ಪರಿಗಣಿಸಿದ ಮೌಲ್ಯ 250.2ರ ಸುತ್ತ ಪೂರ್ಣ ಮಧ್ಯಂತರವೇ ಇದೆ, ಪೂರ್ತಿ ಜನಸಂಖ್ಯೆಯ ಮಧ್ಯಕವು ಈ ರೇಂಜ್‌ನಲ್ಲೇ ಒಂದು ಮೌಲ್ಯವನ್ನು ತೆಗೆದುಕೊಂಡರೆ ಪರಿಗಣಿಸಿದ ಡೇಟಾವನ್ನು ಅಸ್ವಾಭಾವಿಕ ಎಂದು ಭಾವಿಸುವುದಿಲ್ಲ. ಅಂತಹ ಮಧ್ಯಂತರವನ್ನು μ ಸ್ಥಿರರಾಶಿಯ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅಂತಹ ಮಧ್ಯಂತರವನ್ನು ಲೆಕ್ಕ ಮಾಡುವುದು ಹೇಗೆ? ಮಧ್ಯಂತರದ ತುದಿಬಿಂದುಗಳನ್ನು ಸ್ಯಾಂಪಲ್‌ನಿಂದ ಲೆಕ್ಕ ಮಾಡಬೇಕು, ಅವು X ₁, ..., X ₂₅ನ ಅಂಕಿಅಂಶಗಳು ಮತ್ತು ನಿಷ್ಪನ್ನವಾಕ್ಯಗಳಾಗುತ್ತವೆ, ಆದ್ದರಿಂದ ಅವೇ ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯಗಳೂ ಆಗುತ್ತವೆ.

ನಮ್ಮ ವಿಷಯದಲ್ಲಿ, ಸಾಮಾನ್ಯ ಹರಹಿನ ಸ್ಯಾಂಪಲ್‌ನ ಸ್ಯಾಂಪಲ್‌ ಮಧ್ಯಕ Xವೂ ಕೂಡ ಸಾಮಾನ್ಯ ಹರಹನ್ನು ಹೊಂದಿರುತ್ತದೆ ಎಂದು ಪರಿಗಣಿಸಿ ತುದಿಬಿಂದುಗಳನ್ನು ನಿರ್ಧರಿಸಬಹುದು, ಅದೇ μ ನ ನಿರೀಕ್ಷೆಯಲ್ಲಿ, ಆದರೆ ಸ್ಥಿರದೋಷ σ /√n  = 0.5 (ಗ್ರಾಂ‌)ನೊಂದಿಗೆ. ಸ್ಥೀರಿಕರಿಸುವುದರಿಂದ ನಾವು ಯಾದೃಚ್ಛಿಕ ವ್ಯತ್ಯಯ

$Z={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}={\frac {{\bar {X}}-\mu }{0.5}}$

ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಇದು ಅಂದಾಜು ಮಾಡಬೇಕಾಗಿರುವ ಸ್ಥಿರರಾಶಿ μನ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ, ಆದರೆ μ ಸ್ಥಿರರಾಶಿಯಿಂದ ಸ್ವತಂತ್ರವಾದ ಸ್ಥಿರ ಸಾಮಾನ್ಯ ಹರಹಿನ ಜೊತೆಗೆ. ಆದ್ದರಿಂದ μ ನಿಂದ ಸ್ವತಂತ್ರವಾಗಿ z ಮತ್ತು z ಸಂಖ್ಯೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಸಾಧ್ಯವಾಗುತ್ತದೆ, ಇಲ್ಲಿ 1 − α ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ Z ಮಧ್ಯದಲ್ಲಿ ಬೀಳುತ್ತದೆ, ನಾವು ಎಷ್ಟು ’ವಿಶ್ವಸನೀಯ’ವಾಗಿರಬೇಕಾಗುತ್ತೇವೆಂಬುದರ . ನಾವು 1 − α = 0.95 ಎಂದು ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ. ಆದ್ದರಿಂದ:

$P(-z\leq Z\leq z)=1-\alpha =0.95.\,$

ಸಂಖ್ಯೆ z follows from the cumulative distribution ಉತ್ಪನ್ನವಾಕ್ಯದ:

${\begin{aligned}\Phi (z)&=P(Z\leq z)=1-{\tfrac {\alpha }{2}}=0.975,\\[6pt]z&=\Phi ^{-1}(\Phi (z))=\Phi ^{-1}(0.975)=1.96,\end{aligned}}$

ಅದರಿಂದ

${\begin{aligned}0.95&=1-\alpha =P(-z\leq Z\leq z)=P\left(-1.96\leq {\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}\leq 1.96\right)\\[6pt]&=P\left({\bar {X}}-1.96{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\bar {X}}+1.96{\frac {\sigma }{\sqrt {n}}}\right)\\[6pt]&=P\left({\bar {X}}-1.96\times 0.5\leq \mu \leq {\bar {X}}+1.96\times 0.5\right)\\[6pt]&=P\left({\bar {X}}-0.98\leq \mu \leq {\bar {X}}+0.98\right).\end{aligned}}$

ಬರುತ್ತದೆ. ಇದನ್ನು ಹೀಗೆ ಅರ್ಥೈಸಬಹುದು: 0.95 ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ, ಸ್ಟೊಖ್ಯಾಸ್ಟಿಕ್‌ ತುದಿಬಿಂದುಗಳ ನಡುವೆ μ ಸ್ಥಿರರಾಶಿಯನ್ನು ಮುಟ್ಟುವ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಪಡೆಯುತ್ತೇವೆ.

${\bar {X}}-0{.}98\,$

ಮತ್ತು

${\bar {X}}+0.98.\,$

ಅಂದರೆ ಲೆಕ್ಕ ಮಾಡಿದ ಮಧ್ಯಂತರದಲ್ಲಿ μ ಸ್ಥಿರರಾಶಿಯನ್ನು ಮುಟ್ಟುವ ಸಂಭವನೀಯತೆ 0.95 ಎಂದು ಅರ್ಥವಲ್ಲ. ಪ್ರತಿಸಾರಿ ಮಾಪನವನ್ನು ಮಾಡಿದಾಗಲೂ, ಸ್ಯಾಂಪಲ್‌ನ ಮಧ್ಯಕಕ್ಕೆ X ಮತ್ತೊಂದು ಮೌಲ್ಯ ಇರುತ್ತದೆ. 95% ಸಂದರ್ಭಗಳಲ್ಲಿ, ಈ ಮಧ್ಯಕದಿಂದ ಲೆಕ್ಕ ಮಾಡಿದ ತುದಿಬಿಂದುಗಳ ನಡುವೆ μ ಇರುತ್ತದೆ, ಆದರೆ 5% ಸಂದರ್ಭಗಳಲ್ಲಿ ಅವು ಇರುವುದಿಲ್ಲ. ನಿಜವಾದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಉತ್ಪನ್ನವಾಕ್ಯದಲ್ಲಿ ಅಳತೆಮಾಡಿದ ತೂಕಗಳನ್ನು ನಮೂದಿಸುವ ಮೂಲಕ ಕಂಡುಹಿಡಿಯಲಾಗುತ್ತದೆ. ನಮ್ಮ 0.95 ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವು

$({\bar {x}}-0.98;{\bar {x}}+0.98)=(250.2-0.98;250.2+0.98)=(249.22;251.18).\,$

μ ನ ಅಪೇಕ್ಷಿತ ಮೌಲ್ಯ 250 ಪರಿಣಮಿಸಿದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವಾಗಿರುವುದರಿಂದ, ಯಂತ್ರವು ತಪ್ಪಾದ ಸಾಮರ್ಥ್ಯವನ್ನೊಳಗೊಂಡಿದೆ ಎಂದು ನಂಬಲು ಯಾವ ಕಾರಣವೂ ಇಲ್ಲ.

ಲೆಕ್ಕ ಮಾಡಿದ ಮಧ್ಯಂತರಗಳಿಗೆ ಸ್ಥಿರ ತುದಿಬಿಂದುಗಳಿವೆ, ಇಲ್ಲಿ μ ಮಧ್ಯದಲ್ಲಿ ಇರಬಹುದು (ಅಥವಾ ಇರದೆಯೇ ಇರಬಹುದು). ಆದ್ದರಿಂದ ಈ ಘಟನೆಯು 0 ಅಥವಾ 1ರ ಸಂಭವನೀಯತೆಯನ್ನು ಹೊಂದಿದೆ. "(1 − α)ರ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ μ ಸ್ಥಿರರಾಶಿಯು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯತಂತರದಲ್ಲಿ ಬೀಳುತ್ತದೆ" ಎಂದು ನಾವು ಹೇಳಲು ಆಗುವುದಿಲ್ಲ . 100(1 − α) % ಸಂದರ್ಭಗಳಲ್ಲಿ ಪುನರಾವರ್ತನೆಯಾಗುವುದರಿಂದ μ ಲೆಕ್ಕ ಮಾಡಿದ ಮಧ್ಯಂತರದಲ್ಲೇ ಇರುತ್ತದೆ ಎಂದಷ್ಟೇ ನಮಗೆ ತಿಳಿದಿರುವುದು. ಆದರೆ ಅದು 100α % ಸಂದರ್ಭಗಳಲ್ಲಿ ಆಗುವುದಿಲ್ಲ. ಮತ್ತು ದುರದೃಷ್ಟವಶಾತ್‌ ಇದು ಯಾವ ಸಂದರ್ಭಗಳಲ್ಲಿ ಆಗುತ್ತದೆಂದು ನಮಗೆ ತಿಳಿದಿಲ್ಲ. ಆದ್ದರಿಂದ "ವಿಶ್ವಾಸ ಹಂತ 100(1 − α) %ನೊಂದಿಗೆ, μ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರದಲ್ಲಿ ಬೀಳುತ್ತದೆ."

ಬಲದಲ್ಲಿರುವ ಚಿತ್ರವು, ಕೊಟ್ಟಿರುವ μ ಮಧ್ಯಕದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರದ 50 ಸಾಧನಗಳನ್ನು ತೊರಿಸುತ್ತದೆ. ನಾವು ಯಾದೃಚ್ಛಿಕವಗಿ ಒಂದು ಸಾಧನವನ್ನು ಆಯ್ಕೆ ಮಾಡಿಕೊಂಡರೆ, ನಾವು ಸ್ಥಿರರಾಶಿ ಇರುವ ಮಧ್ಯಂತರವನ್ನು ಆಯ್ಕೆಮಾಡಿಕೊಳ್ಳುವ ಸಂಭವನೀಯತೆ 95% ಇರುತ್ತದೆ; ಆದರೆ ನಾವು ದುರಾದೃಷ್ಟರಾಗಿ ತಪ್ಪಾದ್ದನ್ನೂ ಅಯ್ಕೆಮಾಡಿಕೊಂಡಿರಬಹುದು. ನಮಗೆ ಎಂದಿಗೂ ತಿಳಿಯುವುದಿಲ್ಲ; ನಾವು ನಮ್ಮ ಮಧ್ಯಂತರದಲ್ಲಿ ಸಿಕ್ಕಿಕೊಂಡುಬಿಟ್ಟಿರುತ್ತೇವೆ.

ಸೈದ್ಧಾಂತಿಕ ಉದಾಹರಣೆ

X ₁, ..., X _n ಎನ್ನುವುದು (ಸ್ಥಿರರಾಶಿಗಳು) ಮಧ್ಯಕ μ ಮತ್ತು ವೈಷಮ್ಯ σ²ಗಳನ್ನೊಳಗೊಂಡ ಸಾಮಾನ್ಯ ಹರಹಿನ ಜನಸಂಖ್ಯೆಯ ಸ್ವತಂತ್ರ ಸ್ಯಾಂಪಲ್‌ ಎಂದುಕೊಳ್ಳೋಣ.

${\overline {X}}=(X_{1}+\cdots +X_{n})/n\,,$

$S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}\left(X_{i}-{\overline {X}}\,\right)^{2}.$

ಎಂಬುದು ಸಾಮಾನ್ಯವಾಗಿ ಗೊತ್ತಿರುವ ಅಂಕಿಅಂಶಗಳು, ಸ್ಯಾಂಪಲ್‌ ಮಧ್ಯಕ ಮತ್ತು ಸ್ಯಾಂಪಲ್‌ ವೈಷಮ್ಯಗಳಾಗಲಿ.

ಆಗ

$T={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}$

ಎಂಬುದು ವಿದ್ಯಾರ್ಥಿಯ ಟಿ-ಹರಹನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ, n − 1 ಸ್ವಾತಂತ್ರ್ಯದ . ಟಿ ನ ಹರಹು ಕಾಣದ ಸ್ಥಿರರಾಶಿಗಳಾದ μ ಮತ್ತು σ ²ಗಳ ಮೌಲ್ಯದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ ಎಂಬುದನ್ನು ಗಮನಿಸಿ; ಅಂದರೆ ಅದೊಂದು ಪರಿವರ್ತಿಸಬಲ್ಲ ಪ್ರಮಾಣ. ನಾವು μ ಗೆ 90% ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕೆಂದುಕೊಳ್ಳೋಣ. ಆಗ, c ಯನ್ನು ಈ ಹರಹಿನ 95ನೇ ಶೇಕಡಾ ಎಂದು Denote ಮಾಡಬೇಕು.

$\Pr(-c$

(ಸೂಚನೆ: ಹಿಂದಿನ ಸಾಲಿನಲ್ಲಿರುವ "95ನೇ" ಮತ್ತು "0.9"ಗಳು ಸರಿಯಾಗಿವೆ. ಟಿ −c ಗಿಂತ ಕಡಿಮೆಯಿರುವ ಸಂಭವನೀಯತೆ 5% ಮತ್ತು +c ಗಿಂತ ಹೆಚ್ಚಿರುವ ಸಂಭವನೀಯತೆ 5%. ಆದ್ದರಿಂದ, ಟಿ ಯು −c ಮತ್ತು +c ಗಳ ನಡುವೆ ಇರುವ ಸಂಭಾವ್ಯತೆಯು ಶೇಕಡಾ 90%.)

ಆದ್ದರಿಂದ

$\Pr({\overline {X}}-{\frac {cS}{\sqrt {n}}}$

ಮತ್ತು ನಾವು μ ಗೆ ಸೈದ್ಧಾಂತಿಕವಾಗಿ (stochastic) 90% ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಹೊಂದಿದ್ದೇವೆ.

ಸ್ಯಾಂಪಲ್‌ಅನ್ನು ಗಮನಿಸಿದ ಮೇಲೆ ನಾವು Xಗೆ x ಮತ್ತು S ಗೆ s ಮೌಲ್ಯಗಳನ್ನು ಕಂಡುಹಿಡಿಯುತ್ತೇವೆ, ಇದರಿಂದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ಲೆಕ್ಕ ಹಾಕುತ್ತೇವೆ.

$\left[{\overline {x}}-{\frac {cs}{\sqrt {n}}},{\overline {x}}+{\frac {cs}{\sqrt {n}}}\right],\,$

ಈ ಮಧ್ಯಂತರವು ತುದಿಬಿಂದುಗಳಲ್ಲಿ ಸ್ಥಿರ ಸಂಖ್ಯೆಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಇದು μ ಸ್ಥಿರರಾಶಿಯನ್ನು ನಿಸ್ಸಂಶಯ ಹೊಂದಿರುತ್ತದೆ ಎಂದು ನಾವು ಖಂಡಿತವಾಗಿ ಹೇಳಲಾಗುವುದಿಲ್ಲ. μ ಈ ಮಧ್ಯಂತರದಲ್ಲಿ ಇದೆಯೇ ಇಲ್ಲವೇ ಎಂದು.

ಊಹಾ ಪರೀಕ್ಷೆಗೆ ಸಂಬಂಧ

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಮತ್ತು ಸಂಖ್ಯಾಶಾಸ್ತ್ರ ಊಹಾ ಪರೀಕ್ಷೆ ಗಳು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳ ಉದ್ದೇಶಗಳನ್ನು ರೂಪಿಸುವಾಗ ಭಿನ್ನವಾಗಿದ್ದರೂ, ಅವೆರಡೂ ಕೆಲವೊಂದು ವಿಚಾರಗಳಲ್ಲಿ ಸಂಬಂಧಿಸಿವೆ ಮತ್ತು ಒಂದು ಹಂತದವರೆಗೆ ಪೂರಕವಾಗಿವೆ. ಎಲ್ಲಾ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಹೀಗೇ ನಿರ್ಮಿಸುವುದಿಲ್ಲವಾದರೂ, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ನಿರ್ಮಿಸುವಾಗ ಬಳಸುವ ಒಂದು ಸಾಮಾನ್ಯ ಮಾರ್ಗವೆಂದರೆ - ಪ್ರಾಮುಖ್ಯ ಹಂತ 100α%ದಲ್ಲಿ θ=θ₀ಅನ್ನು ತಿರಸ್ಕರಿಸಲಾಗುವುದಿಲ್ಲ ಎನ್ನುವ ಊಹಾಪರೀಕ್ಷೆಯನ್ನೊಳಗೊಂಡ θ₀ನ ಎಲ್ಲಾ ಮೌಲ್ಯಗಳನ್ನು ಒಳಗೊಂಡ 100(1−α)% ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವುದು. ಸರಿಯಾದ ಪ್ರಾಮುಖ್ಯ ಪರೀಕ್ಷೆಯ ಲಭ್ಯತೆಯನ್ನು ಊಹೆ ಮಾಡುವುದರಿಂದ ಈ ವಿಧಾನವು ಸದಾಕಾಲ ಉಪಯೋಗಕ್ಕೆ ಬರುತ್ತದೆಂದು ಹೇಳಲಾಗುವುದಿಲ್ಲ. ಸ್ವಾಭಾವಿಕವಾಗಿ, ಪ್ರಾಮುಖ್ಯ ಪರೀಕ್ಷೆಗೆ ಬೇಕಾಗುವ ಕಲ್ಪನೆಗಳೆಲ್ಲವೂ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳಿಗೆ ರವಾನೆಯಾಗುತ್ತದೆ.

ಒಂದು ಸಾಮಾನ್ಯ ಸಂವಾದಿಯನ್ನು ಮಾಡುವುದು ಸುಲಭವಾಗಬಹುದು, ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರದ ಒಳಗಿನ ಸ್ಥಿರರಾಶಿ ಮೌಲ್ಯಗಳು ಊಹೆ ಪರೀಕ್ಷೆಯಲ್ಲಿ ತಿರಸ್ಕೃತವಾಗದ ಮೌಲ್ಯಗಳಿಗೆ ಸಮವಾಗಿರುತ್ತದೆ ಎಂದು, ಆದರೆ ಇದು ಅಪಾಯಕಾರಿ. ಹಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ ಹೇಳಲಾದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಕೇವಲ ಸರಿಸುಮಾರು ಮಾನ್ಯವಾಗಿರುತ್ತದೆ, ಬಹುಶಃ "ಹೆಚ್ಚು ಕಡಿಮೆ ಸ್ಥಿರ ದೋಷದ ದುಪ್ಪಟ್ಟು" ಎಂಬ ಆಧಾರದ ಮೇಲೆ ನಿಷ್ಪನ್ನಮಾಡಿರಬಹುದು, ಆದರೆ ಸಂವಾದಿ ಎನ್ನಲಾಗುವ ಊಹಾ ಪರೀಕ್ಷೆಗಳ ಮೇಲೆ ಇದರ ಪರಿಣಾಮಗಳೇನು ಎಂಬುದು ತಿಳಿದಿರುವುದಿಲ್ಲ.

ಅರ್ಥ ಮತ್ತು ವ್ಯಾಖ್ಯಾನ

ಪುನರಾವರ್ತನೆ ಕ್ರಮದ ಬಳಕೆದಾರರಿಗೆ, ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್‌ನ ಹಲವು ರೀತಿಯ ಅರ್ಥವಿವರಣೆಯನ್ನು ನೀಡಲಾಗುವುದು.

• "ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್‌ನ್ನು ಮಾದರಿಯ ರೂಪದಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಲಾಗುವುದು (ಅಥವಾ ಪುನರಾವರ್ತನೆ ಮಾದರಿಗಳು): "ಬಹು ವಿಧದ ಮಾದರಿಗಳಲ್ಲಿ ಈ ಕ್ರಮವು ಪುನರಾವರ್ತನೆಯಾಗುವುದು, ಲೆಕ್ಕ ಹಾಕಿದ ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್ (ಯಾವುದು ಪ್ರತಿ ಮಾದರಿಯಲ್ಲೂ ಬದಲಾಗುವುದು) 90% ರಷ್ಟು ವೇಳೆ ಕರಾರುವಕ್ಕಾದ ಜನಸಂಖ್ಯೆಯ ಪರಿಮಾಣವನ್ನು ಒಳಗೊಂಡಿರುವುದು." ಗಮನಿಸಿ ಏನೆಂದರೆ ಇದು ಅದೇ ಜನಸಂಖ್ಯೆಯ ಪುನರಾವರ್ತನೆ ಮಾದರಿಯಲ್ಲ, ಕೇವಲ ಪುನರಾವರ್ತನೆಯ ಮಾದರಿ.
• ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್‌ನ ವಿವರಣೆಯು ಸ್ವಲ್ಪ ಮಟ್ಟಿಗೆ ಇದನ್ನು ಹೊಂದುವುದು: "ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್ ಜನಸಂಖ್ಯೆಯ ಪರಿಮಾಣದ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ ಎಲ್ಲಿ ಪರಿಮಾಣ ಮತ್ತು ಗಮನಿಸಲ್ಪಟ್ಟ ಎಣಿಕೆಯ ವ್ಯತ್ಯಾಸವು ೧೦% ಮಟ್ಟದಲ್ಲಿ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯವಾಗಿ ಮಹತ್ವವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ ". ವಾಸ್ತವವಾಗಿ, ಇದು ಒಂದು ನಿರ್ದಿಷ್ಟ ಮಾರ್ಗವನ್ನು ಎಲ್ಲಿ ಒಂದು ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್ ರಚಿಸಲ್ಪಡುವುದು ಅದನ್ನು ಸಂಬಂಧಿಸುವುದು.
• ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್‌ನಲ್ಲಿ ಸಹಕರಿಸಲ್ಪಟ್ಟ ಸಂಭವನೀಯತೆಯು ಪೂರ್ವ ಪ್ರಾಯೋಗಿಕ ಪರೀಕ್ಷೆಯ ದೃಷ್ಟಿಯಿಂದ ಕೂಡ ಪರಿಗಣಿಸಲ್ಪಡಬಹುದು, ಅದೇ ಪ್ರಸಂಗದಲ್ಲಿ ಎಲ್ಲಿ ಯಾದೃಚ್ಛಿಕ ವಿಂಗಡನೆಗೆ ವಿಷಯದ ಅಭ್ಯಾಸ ಕೈಗೊಂಡಿರುವುದು ಚರ್ಚಿಸಲ್ಪಡುವುದು. ಇಲ್ಲಿ ಪ್ರಯೋಗಾರ್ಥಿಗಳು ನಿಜವಾದ ಪ್ರಯೋಗ ನಡೆಸುವ ಮೊದಲು ಅವರು, ಒಂದು ಮಾರ್ಗವನ್ನು ನಿಗದಿಪಡಿಸುವರು ಎಲ್ಲಿ ಅವರು ಒಂದು ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್‌ನ್ನು ಲೆಕ್ಕಿಸುವ ಉದ್ದೇಶವನ್ನು ಹೊಂದಿರುವರು ಮತ್ತು ತಿಳಿದಿರುವರು, ಅಂದರೆ ಅವರು ಊಹಿಸಲ್ಪಟ್ಟು ಕೊನೆಗಾಣಿಸುವ ಇಂಟರ್ವಲ್‌ ಸ್ವಲ್ಪ ಪ್ರಮಾಣದ ನಿಜವನ್ನು ಆದರೆ ತಿಳಿಯದ ಮೌಲ್ಯವನ್ನು ಒಳಗೊಳ್ಳುವುದು. ಇದು ಮೇಲಿನ ವ್ಯಾಖ್ಯಾನ "ಪುನರಾವರ್ತನೆ ಮಾದರಿಗೆ" ಬಹಳ ಸದೃಶವಾಗಿರುವುದು, ಹೊರತಾಗಿ ಇದು ಮಾದರಿ ಕ್ರಮದಲ್ಲಿ ಯಾವುದೇ ಅರ್ಥಪೂರ್ಣವಾದ ಅಭಿಪ್ರಾಯದಲ್ಲಿ ಪುನರಾವರ್ತನೆಯಾಗದಂಥಹ ಊಹೆಮಾಡಿದ ಪುನರಾವರ್ತನೆಯ ಅವಲಂಬನೆಯನ್ನು ನಿವಾರಿಸುತ್ತದೆ. ನೇಮನ್ ರಚನೆ ನೋಡಿ.

ಮೇಲಿನ ಪ್ರತಿಯೊಂದೂ, ಇವುಗಳನ್ನು ಅನ್ವಯಿಸುವುದು: ಒಂದು ವೇಳೆ ಪರಿಮಾಣದ ನಿಜ ಮೌಲ್ಯವು ಒಮ್ಮೆ ಗಣಿಸಲ್ಪಟ್ಟ ನಂತರ ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್‌ನ ೯೦% ಕ್ಕಿಂತ ಹೊರಗೆ ಇದ್ದರೆ, ನಂತರ ಒಂದು ಸಂದರ್ಭ ೧೦% (ಅಥವಾ ಕಡಿಮೆ) ಉಂಟಾಗುವ ಸಾಧ್ಯತೆ ಕೇವಲ ಅನಿರೀಕ್ಷಿತ ವೇಳೆ.

"ಕಾನ್ಫಿಡೆನ್ಸ್" ಪದದ ಅರ್ಥ

ಜನಸಾಮಾನ್ಯರಿಗೆ ಬಹಳ ಸಲ ಗೊಂದಲ ಮಾಡುವ, ಸಾಮಾನ್ಯ ಬಳಕೆಯ "ಕಾನ್ಫಿಡೆನ್ಸ್" ಶಬ್ದಕ್ಕೂ ಹಾಗೂ ಅದರ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಬಳಕೆಯ ಅರ್ಥಕ್ಕೂ ವ್ಯತ್ಯಾಸವಿದೆ, ಮತ್ತು ಇದು ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್ವಲ್ಸ್ ನ ವಿಮರ್ಶಕಗಳಲ್ಲಿ ಒಂದು, ಹೆಸರಿಸುವಂತೆ ಸಂಖ್ಯಾಶಾಸ್ತ್ರದವರಲ್ಲದವರಿಂದ ಕಾನ್ಫಿಡೆನ್ಸ್ ಪದ ಬಳಸುವಿಕೆ, ತಪ್ಪು ಅಭಿಪ್ರಾಯವನ್ನುಂಟುಮಾಡುತ್ತಿದೆ.

ಸಾಮಾನ್ಯ ಬಳಕೆಯಲ್ಲಿ, ಯಾವುದರಲ್ಲಾದರೂ ಶೇಖಡ 95% ಕಾನ್ಫಿಡೆನ್ಸ್‌ನ ಹಕ್ಕು ಸಾಧಿಸಿದರೆ ಅದು ಸಾಧಾರಣವಾಗಿ ನಿರ್ಧಿಷ್ಟತೆಯನ್ನು ತೋರಿಸುತ್ತದೆ. ಸಂಖ್ಯಾಶಾಸ್ತ್ರದಲ್ಲಿ, ಶೇಖಡ 95% ಕಾನ್ಫಿಡೆನ್ಸ್‌ನ ಹಕ್ಕು ಸಾಧಿಸಿದರೆ ಅದರ ಅರ್ಥ ಅನ್ವೇಶಕ ಇಪ್ಪತ್ತು ಅಥವಾ ಇನ್ನು ಕಡಿಮೆ ಬಾರಿಯಲ್ಲಿ ಒಂದು ಸಲ ಸಂಭವಿಸುವುದು ಎಂಬುದು ಅಷ್ಟೆ. ಯಾರಾದರು ಎರಡು ಪಗಡೆಗಳನ್ನು ಉರುಳಿಸಿ ಎರಡು ಆರುಗಳನ್ನು ಪಡೆಯುವುದಾದರೆ (ಇದು 1/36ನೇಯ ಸಮಯದಲ್ಲಿ ಸಾಧ್ಯ, ಅಥವಾ 3%), ಕೆಲವರು ಪಗಡೆಗಳು ನಿಗದಿತವಾಗಿವೆ ಎಂದು ಹಕ್ಕು ಸಾಧಿಸಿದರೂ ಸಹ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯವಾಗಿ ಮಾತನಾಡುವುದಾದರೆ ನಾವು ಅದರ ಇರುವಿಕೆಯನ್ನು 97% ಕಾನ್ಫಿಡೆನ್ಸ್‌ ಇಡಬಹುದು. ಅದೇ ತರಹ, ವಸ್ತುಗಳ ಮಧ್ಯೆ ನಿಜವಾದ ಸಂಪರ್ಕವಿದೆ ಎಂಬ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಕೊಂಡಿಯ ಶೋಧನೆಯು 95% ಕಾನ್ಫಿಡೆನ್ಸ್ ರುಜುವಾತು ಅಲ್ಲ ಹಾಗೂ ಇದು ಒಳ್ಳೆಯ ಸೂಚನೆಯು ಅಲ್ಲ.

ಒಂದು ಅಧ್ಯಯನ ಹಲವು ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಪರೀಕ್ಷೆಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತೆ, ಸಾಮನರು ವೈಯುಕ್ತಿಕ ಪ್ರಯೋಗಗಳ ಜೊತೆ ಸಂಭಂದಿಸಿದ ಕಾನ್ಫಿಡೆನ್ಸ್ ಅದರ ಅಧ್ಯಯನಗಳ ಫಲಿತಾಂಶದ ಮೇಲೂ ಅದೇ ಕಾನ್ಫಿಡೆನ್ಸ್ ಇರುತ್ತದೆ ಎಂದು ಕಲ್ಪಿಸಿಕೊಂಡಿದ್ದಾರೆ. ವಾಸ್ತವದಲ್ಲಿ, ಒಂದು ಅಧ್ಯಯನದ ಸಮಯದಲ್ಲಿ ಮಾಡಿದ ಎಲ್ಲ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಪ್ರಯೋಗಗಳ ಫಲಿತಾಂಶಗಳನ್ನು ಒಟ್ಟಿಗೆ ಒಂದಾಗಿಸಿ ನಿರ್ನಯಿಸ ಬೇಕು ಹಾಗೂ ಅದು ಉತ್ಪಾದಿಸುವ ಸಕಾರಾತ್ಮಕ ಕೊಂಡಿಗಳಲ್ಲಿ ಒಬ್ಬರು ಏಷ್ಟು ಕಾನ್ಫಿಡೆನ್ಸ್ ಅನ್ನು ಗುರುತಿಸುವಲ್ಲಿ ಸಹಾಯವಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, 40 ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಪ್ರಯೋಗಗಳನ್ನೊಳಗೊಂಡ ಒಂದು ಅಧ್ಯಯನವನ್ನು 95% ಕಾನ್ಫಿಡೆನ್ಸ್‌ನಲ್ಲಿ ನಡೆಸಲಾದರೆ ಹಾಗೂ ಅದು 3 ಸಕಾರಾತ್ಮಕ ಫಲಿತಾಂಶಗಳನ್ನು ಉತ್ಪತ್ತಿಸಿದರೆ. ಪ್ರತಿಯೊಂದು ಪ್ರಯೋಗ ತಪ್ಪು ಸಕಾರಾತ್ಮಕ ಫಲಿತಾಂಶವನ್ನು ಉತ್ಪಾದಿಸಲು 5% ಅವಕಾಶವಿದೆ ಎಂದು, ಹೀಗಾಗಿ ಒಂದು ಅಧ್ಯಯನ ಮೂರರಲ್ಲಿ ಎರಡು ಸಲ 3 ತಪ್ಪು ಸಕಾರಾತ್ಮಕ ಫಲಿತಾಂಶಗಳನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ. ಹೀಗೆ ಯಾವುದೇ ಅಧ್ಯಯನದ ಸಕಾರಾತ್ಮಕ ತೀರ್ಮಾನಗಳು ಸರಿಯಿರಲು ಒಬ್ಬರಿಗೆ 32% ಅಷ್ಟು ಕಾನ್ಫಿಡೆನ್ಸ್ ಇರಬಹುದು, 95%ಗಂತ ಕಡಿಮೆಯಿದ್ದರೆ ಅನ್ವೇಶಕರು ಸ್ವೀಕರಣೆಯ ಗುಣಮಟ್ಟ ಎಂದು ನಿಗದಿಪಡಿಸಿದ್ದಾರೆ.

ಪರ್ಯಾಯಗಳು ಮತ್ತು ವಿಮರ್ಶಾತ್ಮಕ-ಲೇಖನಗಳು

Main articles: Credible interval and Prediction interval

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಮಧ್ಯಂತರ ಅಭಿಪ್ರಾಯದ ಒಂದು ಕ್ರಮವಾಗಿದೆ, ಮತ್ತು ಆವರ್ತನಕ ಅಂಕಿಅಂಶಗಳಲ್ಲಿ ಹೆಚ್ಚು ವಿಸ್ತಾರವಾಗಿ ಬಳಸಲಾಗಿದೆ. 

ಒಂದು ಸದೃಶ ಪರಿಕಲ್ಪನೆಯು ಬೆಯೆಸ್‌ರ ಅಂಕಿಅಂಶಗಳಲ್ಲಿ ನಂಬಲರ್ಹ ಮಧ್ಯಂತರಗಳು,

ಹಾಗೇ ಒಂದು ಪರ್ಯಾಯ ಆವರ್ತನಕ ಕ್ರಮವು ಭವಿಷ್ಯದ ಮಧ್ಯಂತರವಾಗಿದೆ, ಅದು  ವ್ಯಾಪ್ತಿ ನಿರ್ಣಯ ಗಳನ್ನು ನಿರ್ಣಯಿಸುವ ಬದಲು, ಮುಂದೆ ನಡೆಯುವ  ಮಾದರಿಗಳ ಫಲಿತಾಂಶವನ್ನು ನಿರ್ಣಯಿಸುತ್ತದೆ.

ಈ ಕ್ರಮಗಳಲ್ಲಿ ಯಾವುದು ಹೆಚ್ಚು ಉಪಯುಕ್ತ ಫಲಿತಾಂಶಗಳನ್ನು ಉತ್ಪಾದಿಸುತ್ತವೆ ಎಂಬುದರ ಬಗ್ಗೆ ವ್ಯತ್ಯಾಸವಿದೆ: ಎಣಿಕೆಗಳ ಗಣಿತಶಾಸ್ತ್ರಗಳು ಅಪರೂಪವಾಗಿ ಪ್ರಶ್ನೆಮಾಡುಲಾಗುತ್ತವೆ- ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಮಾದರಿ ನೋಡುವ ವಿತರಣೆಗಳ ಮೇಲೆ ಆಧಾರವಾಗಿವೆ, ನಂಬಲರ್ಹ ಮಧ್ಯಂತರಗಳು ಬೆಯಸ್‌ರ ಸಿದ್ಧಾಂತದ ಮೇಲೆ ಅವಲಂಬಿಸಿದೆ - ಆದರೆ ಈ ಕ್ರಮಗಳ ಅನ್ವಯಿಸುವಿಕೆ, ಉತ್ಪಾದಿಸಿದ ಅಂಕಿಅಂಶಗಳ ಉಪಯುಕ್ತತೆ ಮತ್ತು  ವ್ಯಾಖ್ಯಾನವನ್ನು ಚರ್ಚಿಸಲಾಗಿದೆ/ಪರಿಶೀಲಿಸಲಾಗಿದೆ.

ಬೆಯಸ್‌ರ ಕ್ರಮವನ್ನು ಬಳಸುವವರು, ಒಂದು ಮಧ್ಯಂತರ ಅಬಿಪ್ರಾಯವನ್ನು ಸೃಷ್ಟಿಸಿದರೆ, ಅದು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳಿಗೆ ವಿರುದ್ಧವಾಗಿರುತ್ತದೆ, ಹೇಳಬಯಸುತ್ತಾರೆ, "ನನ್ನ ವಿಶ್ವಾಸದ ದರ್ಜೆಯೆಂದರೆ ಈ ಮಧ್ಯಂತರದಲ್ಲಿ ಈ ಪ್ಯಾರಾಮೀಟರ್ 90% ಆಗಿರುತ್ತದೆ, " ಹಾಗೆ ಭವಿಷ್ಯ ಮಧ್ಯಂತರಗಳನ್ನು ಬಳಸುವವರು ಬದಲಾಗಿ "ಈ ಮಧ್ಯಂತರದಲ್ಲಿ ಮುಂದಿನ ಮಾದರಿ ಯು ಸಮಯದ 90%ರಷ್ಟು ಸಂಭವಿಸುತ್ತದೆ ಎಂದು ನಾನು ಭವಿಷ್ಯ ನುಡಿ ಯುತ್ತೇನೆ" ಎಂದು ಹೇಳುತ್ತಾರೆ.

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳು ಸಂಭವನೀಯತೆಯ ಒಂದು ಭಾವ ಮತ್ತು ಸಂಭವನೀಯತೆಯ ಸಾಮಾನ್ಯ ಕಾನೂನುಗಳಿಗೆ ಒಳಪಟ್ಟಿವೆ.  ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳ ಜೊತೆ ಹಲವು ಅಂಕಿಅಂಶಗಳನ್ನು ಪರಿಚಯಿಸಿದರೆ, ಪ್ರತಿಯೊಂದು ಸ್ವಾತಂತ್ರದ ಊಹೆಯ ಮೇಲೆ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ, ಆ ಊಹೆಯನ್ನು ಗೌರವಿಸಬೇಕು ಅಥವಾ ಲೆಕ್ಕಾಚಾರಗಳು  ಅಸಿಂಧು ಎಂದು ಪ್ರತಿಯಾಗಿ ಕೊಡಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಅತಿ ಸಣ್ಣ ಮಧ್ಯಂತರದ ಜೊತೆಗೆ ಅಂಕಿಅಂಶಗಳನ್ನು ಗಮನಕ್ಕೆ ಆರಿಸಿದರೆ, ಆ ಮಧ್ಯಂತರವು ಆ ಅಂಕಿಅಂಶಕ್ಕೆ ಇನ್ನೂ ಮುಂದೆ ಸರಿಯಾದ/ನಿಜವಾದ ಮಧ್ಯಂತರವಾಗಿರುವುದಿಲ್ಲ. ಆಯ್ಕೆಯ ಕ್ರಿಯೆ ಸಂಭವನೀಯತೆಯನ್ನು ಬದಲಿಸುತ್ತದೆ ಮತ್ತು ಈ ಸನ್ನಿವೇಶದಲ್ಲಿ  ಮಧ್ಯಂತರವನ್ನು ವಿಸ್ತರಿಸುತ್ತದೆ.

ಇದು ಪ್ರಮುಖವಾಗಿ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯ ಪರೀಕ್ಷೆಗಳನ್ನು ನಿರ್ವಹಿಸಲು ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಗಳನ್ನು ಸೃಷ್ಟಿಸಿದ್ದಾಗ ಮುಖ್ಯವಾಗುತ್ತದೆ. ವಿವಿಧ ಪರೀಕ್ಷೆಗಳನ್ನು ನಡೆಸಿದರೆ ಮತ್ತು ಅವುಗಳಲ್ಲಿ ಯಾವುವು ಧನಾತ್ಮಕ ಫಲಿತಾಂಶವನ್ನು ನೀಡುತ್ತವೆಯೋ ಅವುಗಳನ್ನು ಆಯ್ಕೆ ಮಾಡಿದರೆ, ಪರೀಕ್ಷೆಯನ್ನು ಏರ್ಪಡಿಸಲು ಉಪಯೋಗಿಸಿದ ಮಧ್ಯಂತರವು ಬದಲಾಗುತ್ತದೆ, ಮತ್ತು ಹೆಚ್ಚಿನ ಸನ್ನಿವೇಶಗಳಲ್ಲಿ ಪರೀಕ್ಷೆಗಳು ಅಸಿಂಧು ಎಂದು ಪ್ರತಿಕೊಡಲಾಗುತ್ತದೆ.

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಕ್ಕೆ ಸರಿಯಾದ ಪ್ರಮಾಣಗಳು ಮತ್ತು ಸಂಬಂಧಿತ ಮೊತ್ತಗಳು

ಇದನ್ನೂ ನೋಡಿ: Margin of error and Binomial proportion confidence interval

ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರಕ್ಕೆ ಜನಸಂಖ್ಯೆಯ ಅಂದಾಜಿನ ಅರ್ಥವೆನೇಂದರ‍ೇ ರಚಿಸಬಹುದಾದ ಯಾದೃಚ್ಛಿಕ ಛಲಪರಿಮಾಣಗಳು ಜನಸಂಖ್ಯೆಯಲ್ಲಿ ಸಾಮಾನ್ಯವಾಗಿ ಹಂಚಿಕೆಯಾಗುವುದಿಲ್ಲ,ಕೇಂದ್ರೀಯ ಮಿತಿಯ ಸಿದ್ಧಾಂತದಲ್ಲಿ ನಂಬಿಕೆ ಇಡಬಹುದು, ಮಾದರಿ ಗಾತ್ರಗಳು ಮತ್ತು ಎಣಿಕೆಗೆ ಅಗತ್ಯವಾದಷ್ಟು ಇದ್ದರೆ ಸಾಕು. ಮೇಲಿನ ಸನ್ನಿವೇಶಕ್ಕೆ ತದ್ರೂಪವಾದ ಸೂತ್ರ(ಇಲ್ಲಿ ಮಾದರಿಯ ಅರ್ಥವೆಂದರೆ ಕ್ರಮಬದ್ಧವಾಗಿ ವಸ್ತುನಿಷ್ಠವಾಗಿ ಜನಸಂಖ್ಯೆಯ ಅರ್ಥದ ಬಗ್ಗೆ ಹಂಚುವಿಕೆ ). ಒಂದು ವೇಳೆ ಯಾದೃಚ್ಛಿಕ ಛಲಪರಿಮಾಣದ ಸಂಭವನೀಯತೆ ಹಂಚಿಕೆ ಸಾಮಾನ್ಯ ಹಂಚಿಕೆಗಿಂತ ತುಂಬಾ ಬೇರೆಯಾಗಿರದಿದ್ದಾಗ ಕೆಲವು ಡಜನ್‌ ವೀಕ್ಷಣೆಗಳಲ್ಲಿ ನೋಡಿದಾಗ ಮಾತ್ರ ಅಂದಾಜು ಉತ್ತಮವಾಗಿ ಬರುತ್ತದೆ.(ಉದಾಹರಣೆಗೆ, ಅದರ ಒಟ್ಟು ಹಂಚಿಕೆ ಕಾರ್ಯದಲ್ಲಿ ಯಾವುದೇ ಮಧ್ಯ ನಿಲ್ಲುವಿಕೆ ಉಂಟಾಗುವುದಿಲ್ಲ ಮತ್ತು ಅದರ ಓರೆತನ ಮಧ್ಯಮ ಹಂತದಲ್ಲಿರುತ್ತದೆ).

ಒಂದು ತರಹದ ಮಾದರಿ ಸರಾಸರಿ ಎಂದರೆ ದಾಖಲೆ ಸೂಚಕ ಛಲಪರಿಮಾಣದ ಸರಾಸರಿ, ಇದು ಸರಿಯಿದ್ದಲ್ಲಿ ಮೌಲ್ಯ 1 ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ ಹಾಗೂ ತಪ್ಪಿದಲ್ಲಿ ಮೌಲ್ಯ 0 ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಇಂತಹ ಛಲಪರಿಮಾಣದ ಸರಾಸರಿ ಒಂದು ಛಲಿಪರಿಮಾಣವಿರುವ ಅನುಪಾತಕ್ಕೆ ಸಮವಾಗಿರುತ್ತದೆ (ಗುಂಪು ಹಾಗೂ ಮಾದರಿಯಲ್ಲಿ). ಇದು ದಾಖಲೆ ಸೂಚಕ ಛಲಿಪರಿಣಾಮಗಳ ಉಪಯುಕ್ತ ಗುಣಲಕ್ಷಣ, ವಿಶೇಷವಾಗಿ ಊಹಾಪೋಹ ಪ್ರಯೋಗಗಳಿಗೆ. ಕೇಂದ್ರ ಸಿಮತತೆಯ ಸಿದ್ಧಾಂತವನ್ನು ಅನ್ವಯಸಲು ಒಬ್ಬರು ಅತಿ ದೊಡ್ಡ ಮಾದರಿಯನ್ನು ಬಳಸಬೇಕು. ಒಂದು ಹೆಬ್ಬೆರಳ ಕರಡು ನಿಯಮವೆಂದರೆ ಒಬ್ಬರು ದಾಖಲೆ ಸಚಕ 1 ಇರುವುದನ್ನು ಕನಿಷ್ಟ 5 ಪ್ರಸಂಗಗಳಲ್ಲಿ ನೋಡಬೇಕು ಹಾಗೂ ದಾಖಲೆ ಸೂಚಕ 0 ಇರುವುದನ್ನು ಕನಿಷ್ಟ 5 ಸಲ ನೋಡಬೇಕು. ಮೇಲಿನ ನಿಯಮಗಳನ್ನು ಬಳಸಿ ನಿರ್ಮಿಸಿದ ಕಾನ್ಫಿಡೆನ್ಸ್ ಮಧ್ಯಂತರಗಳು ಘನಸಂಖ್ಯೆ ಅಥವಾ 1 ಗಿಂತ ದೊಡ್ಡ ಸಂಖ್ಯೆಗಳನ್ನು ಒಳಗೊಳ್ಳಬಹುದು, ಆದರೆ ಅನುಪಾತಗಳು ನಿರ್ಧಷ್ಟವಾಗಿ ಘನ ಅಥವಾ 1 ಅನ್ನು ಮೀರಿದವು ಇರುವುದಿಲ್ಲ. ಅಲ್ಲದೇ, ಮಾದರಿ ಅನುಪಾತಗಳು ಬರಿ ನಿರ್ಧಿಷ್ಟ ಸಂಖ್ಯೆಯ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು, ಆದ್ದರಿಂದ ಕೇಂದ್ರಿಯ ಸಿಮಿತತೆಯ ಸಿದ್ಧಾಂತ ಹಾಗೂ ಸಾಧಾರಣ ವಿತರಣೆಯು ಕಾನ್ಫಿಡೆನ್ಸ್ ಮಧ್ಯಂತರವನ್ನು ನಿರ್ಮಿಸಲು ಉತ್ತಮ ಸಕರಣೆಗಳಲ್ಲ. ಈ ಸಂದರ್ಭಕ್ಕೆ ನಿರ್ದಿಷ್ಟವಾಗಿ ಸಂಬಂಧಿಸಿದ ಇನ್ನೂ ಉತ್ತಮ ಪದ್ಧತಿಗಳಿಗಾಗಿ "ಬೈನಾಮಿಯಲ್ ಅನುಪಾತದ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ"ವನ್ನು ನೋಡಿ.

ಇವನ್ನೂ ಗಮನಿಸಿ

• p-ವ್ಯಾಲ್ಯೂ
• ಕಾನ್ಫಿಡೆನ್ಸ್ ರೀಜನ್‌
• ಎರರ್‌ ಬಾರ್‌
• ಪ್ರಿಡಿಕ್ಷನ್‌ ಇಂಟರ್‌ವಲ್‌
• ಟಾಲೆರೆನ್ಸ್ ಇಂಟರ್‌ವಲ್‌
• ಬೂಟ್‌ಸ್ಟ್ರ್ಯಾಪಿಂಗ್‌(ಸಂಖ್ಯಾಶಾಸ್ತ್ರ)
• ಬೈನಾಮಿನಲ್‌ ಪ್ರಪೋರ್ಶನ್ ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್‌
• ರೋಬಸ್ಟ್‌ ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್‌
• [[ಚೆಬಿಶೇವ್‌ನ ಅಸಮಾನತೆ

]]

• ಇಂಟರ್‌ನಲ್‌ ಫೈನೈಟ್‌ ಇಲೆಮೆಂಟ್

ಅಂತರ್‌ಜಾಲ ಗಣಕಯಂತ್ರ

• ಟಾಮು ಅವರ ಕಾನ್ಫಿಡೆನ್‌ ಇಂಟರ್‌ವಲ್ ಗಣಕಯಂತ್ರ Archived 2010-06-15 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
• GraphPad QuickCalcs

ಆಕರಗಳು

• ಫಿಶರ್, ಆರ್.ಎ. 1956) ಸ್ಟಾಟಿಸ್ಟಿಕಲ್ ಮೆಥಡ್ಸ್ ಆ‍ಯ್‌೦ಡ್ ಸೈಂಟಿಫಿಕ್ ಇನ್ಫೆರೆನ್ಸ್. ಆಲಿವರ್ ಆ‍ಯ್‌೦ಡ್ ಬೊಯ್ಡ್ ಎಡಿನ್‌ಬರ್ಗ್. (See ಪು. 32.)
• ಫ್ರೆಂಡ್, ಜೆ.ಇ. (1962) ಮ್ಯಾಥಮ್ಯಾಟಿಕಲ್ ಸ್ಟಾಟಿಸ್ಟಿಕ್ಸ್ ಪ್ರೆಂಟಿಸ್ ಹಾಲ್, ಇಗಲ್‌ವುಡ್ ಕ್ಲಿಪ್ಸ್ ಎನ್‌ಜೆ. (See ಪು. 227–228.)
• ಹಾಕಿಂಗ್, ಐ. (1965) ಲಾಜಿಕ್ ಆಫ್ ಸ್ಟಾಟಿಸ್ಟಿಕಲ್ ಇನ್ಫರನ್ಸ್‌. ೦.೨ ಕ್ಯಾಂಬ್ರಿಜ್ ಯುನಿವರ್ಸಿಟಿ ಪ್ರೆಸ್, ಕ್ಯಾಂಬ್ರಿಜ್.
• ಕೀಪಿಂಗ್, ಇ.ಎಸ್. (1962) ಇಂಟ್ರಡಕ್ಷನ್ ಸ್ಟಾಟಿಸ್ಟಿಕಲ್ ಇನ್ಫರನ್ಸ್‌. ಡಿ. ವ್ಯಾನ್ ನೊಸ್ಟ್ರಾಂಡ್ ಪ್ರಿನ್ಸ್‌ಟನ್, ಎನ್‌ಜೆ.
• ಕಿಯೆಫರ್, ಜೆ. (1977) "ಕಂಡಿಶನಲ್ ಕಾನ್ಫಿಡೆನ್ಸ್ ಸ್ಟೆಟ್‌ಮೆಂಟ್ಸ್ ಆ‍ಯ್‌೦ಡ್ ಕಾನ್ಫಿಡೆನ್ಸ್ ಎಸ್ಟೀಮೇಟರ್ಸ್ (ವಿತ್ ಡಿಸ್ಕಶನ್)" ಜರ್ನಲ್ ಆಫ್ ದ ಅಮೆರಿಕನ್ ಸ್ಟಾಟಿಸ್ಟಿಕಲ್ ಅಸೊಸಿಯೇಶನ್, 72, 789–827.
• ನೀಮನ್, ಜೆ. (1937) "ಔಟ್‌ಲೈನ್ ಆಫ್ ಎ ಥೇರಿ ಆಫ್ ಸ್ಟಾಟಿಸ್ಟಿಕಲ್ ಎಸ್ಟಿಮೇಶನ್ ಬೇಸ್ಡ್ ಆನ್ ಥೇರಿ ಆಫ್ ಪ್ರೊಬಾಬಿಲಿಟಿ " ಫಿಲೊಸೊಫಿಕಲ್ ಟ್ರಾನ್ಸಾಕ್ಷನ್ಸ್ ಆಪ್ ದ ರಾಯಲ್ ಸೊಸೈಟಿ ಆಫ್ ಲಂಡನ್ ಎ, 236, 333–380. (ಸೆಮಿನಲ್ ವರ್ಕ್.)
• ರಾಬಿನ್‌ಸನ್, ಜಿ.ಕೆ. (1975) "ಸಮ್ ಕೌಂಟರ್‌‌ಎಕ್ಸಾಂಪಲ್ಸ್ ಟು ದ ಥೇರಿ ಆಪ್ ಕಾಸ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್ಸ್." ಬಯೋಮೆಟ್ರಿಕಾ, 62, 155–161.
• Reiczigel ಜೆ. (2003) ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್ಸ್ ಫಾರ್ ದ ಬಿನೊಮಿಯಲ್ ಪ್ಯಾರಾಮೀಟರ್: ಸಮ್ ನ್ಯೂ ಕಂಸಿಡರೇಶನ್ಸ್. ಸ್ಟಾಟಿಸ್ಟಿಕ್ಸ್ ಇನ್ ಮೆಡಿಸಿನ್, 22, 611–621.
• ರೆಕ್ಜಿಗೆಲ್ ಜೆ., ಅಬೋನಿ-ಟಾತ್ ಜಡ್., & ಸಿಂಗರ್ ಜೆ. (2008) ಆನ್ ಎಕ್ಸಾಕ್ಟ್ ಕಾನ್ಫಿಡೆನ್ಸ್ ಸೆಟ್ ಫಾರ್ ಟು ಬಿನೊಮಿಯಲ್ ಪ್ರೊಪೊರ್ಶನ್ಸ್ ಆ‍ಯ್‌೦ಡ್ ಎಕ್ಸಾಕ್ಟ್ ಅನ್‌ಕಂಡಿಶನಲ್ ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್ಸ್ ಫಾರ‍್ ದ ಡಿಫರೆನ್ಸ್ ಆ‍ಯ್‌೦ಡ್ ರೆಶಿಯೊ ಆಫ್ ಪ್ರೊಪೊರ್ಶನ್ಸ್. ಕಾಂಪ್ಯುಟೇಶನಲ್ ಸ್ಟೆಟಿಸ್ಟಿಕ್ಸ್ & ಡಾಟಾ ಅನಾಲಿಸೀಸ್, 52, 5046–5053.
• ಸ್ಮಿತ್‌ಸನ್, ಎಮ್. (2003) ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್ಸ್ . ಕ್ವಾಂಟಿಟೇಟಿವ್ ಅಪ್ಲೀಕೇಶನ್ಸ್ ಇನ್ ದ ಸೋಶಿಯಲ್ ಸೈನ್ಸ್‌ಸ್ ಸೀರೀಸ್ , ನಂ. 140. ಬೆಲ್ಮೌಂಟ್, ಸಿಎ: ಎಸ್‌ಎ‌ಜಿಇ ಪಬ್ಲೀಕೆಶನ್ಸ್. ISBN 9780761924999.

ಹೊರಗಿನ ಕೊಂಡಿಗಳು

• ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್ಸ್ ಪರಿಶೋಧನೆಗೆ ಸಂಬಂಧಿಸಿದ ಭೋದನೆಯ ಪ್ರೊಗ್ರಾಮ್‌ಗಳು ಎಕ್ಸೆಲ್‌ನಲ್ಲಿ ಇರುತ್ತವೆ. Archived 2011-11-22 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.
• ಆರ್-ಸ್ಕ್ವಾರ್ಸ್ Archived 2009-07-03 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ., ರಿಗ್ರೆಶನ್ ಕೋಎಫಿಶಿಯಂಟ್ Archived 2009-08-06 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ., ಮತ್ತು ರಿಗ್ರೆಶನ್ ಇಂಟರ್ಸೆಪ್ಟ್ಸ್ Archived 2009-04-04 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. ಗಾಗಿ ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಕ್ಯಾಲ್ಕ್ಯುಲೇಟರ್.
• Weisstein, Eric W., "Confidence Interval", MathWorld.
• CAUSEweb.org ವಿಶ್ವಾಸಾರ್ಹ ಮಧ್ಯಂತರ ಒಳಗೊಂಡಂತೆ ಸಂಖ್ಯಾಶಾಸ್ತ್ರ ಕಲಿಕೆಗೆ ಹಲವು ಮಾರ್ಗಗಳು
• ಅ‍ಯ್‌ನ್ ಇಂಟರ್ಯಾಕ್ಟಿವ್ ಇಂಟರ್‌ಡಕ್ಷನ್ ಟು ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್ಸ್
• ಕಾನ್ಫಿಡೆನ್ಸ್ ಇಂಟರ್‌ವಲ್ಸ್: ಕಾನ್ಫಿಡೆನ್ಸ್ ಲೆವೆಲ್, ಸ್ಯಾಂಪಲ್ ಸೈಜ್, ಅ‍ಯ್‌೦ಡ್ ಮಾರ್ಜಿನ್ ಆಫ್ ಎರರ್ ಎರಿಕ್ ಶುಲ್ಜ್‌ರಿಂದ, ದ ವೋಲ್ಫ್ರಾಮ್ ಡೆಮಾನ್‌ಸ್ಟ್ರೇಶನ್ ಪ್ರೊಜೆಕ್ಟ್.