ಮೇಜ್ ಜೆನರೇಷನ್ ಅಲ್ಗಾರಿದಮ್

ಗ್ರಾಫ್ ಥಿಯರಿ ಆಧಾರಿತ ವಿಧಾನಗಳು[ಬದಲಾಯಿಸಿ]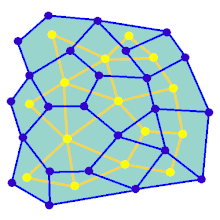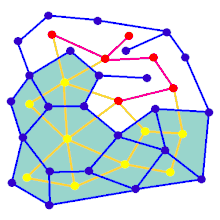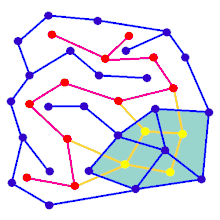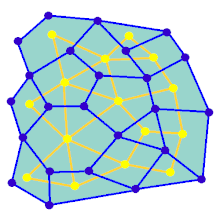

ಸೆಲ್ ಗಳ ಪೂರ್ವನಿರ್ಧರಿತ ವ್ಯವಸ್ಥೆಯೊಂದಿಗೆ (ಸಾಮಾನ್ಯವಾಗಿ ಆಯತಾಕಾರದ ಗ್ರಿಡ್ ಆದರೆ ಇತರ ವ್ಯವಸ್ಥೆಗಳು ಸಾಧ್ಯವಾಗಬಹುದು) ಅವುಗಳ ನಡುವೆ ಗೋಡೆಯ ಸೈಟ್‌ಗಳೊಂದಿಗೆ ಪ್ರಾರಂಭಿಸುವ ಮೂಲಕ ಮೇಜ್ ಅನ್ನು ರಚಿಸಬಹುದು. ಈ ಪೂರ್ವನಿರ್ಧರಿತ ವ್ಯವಸ್ಥೆಯನ್ನು ಸಂಭವನೀಯ ಗೋಡೆಯ ಸೈಟ್‌ಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ಎಡ್ಜ್ ಗಳು ಮತ್ತು ಸೆಲ್ ಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ನೋಡ್‌ಗಳೊಂದಿಗೆ ಸಂಪರ್ಕಿತ ಗ್ರಾಫ್ ಎಂದು ಪರಿಗಣಿಸಬಹುದು. ಮೇಜ್ ಜೆನೆರೇಷನ್ ಅಲ್ಗಾರಿದಮ್‌ನ ಉದ್ದೇಶವು ಎರಡು ನಿರ್ದಿಷ್ಟ ನೋಡ್‌ಗಳ ನಡುವಿನ ಮಾರ್ಗವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಸವಾಲಿನ ಸಬ್‌ಗ್ರಾಫ್ ಅನ್ನು ತಯಾರಿಸುತ್ತಿದೆ ಎಂದು ಪರಿಗಣಿಸಬಹುದು.

ಸಬ್‌ಗ್ರಾಫ್ ಸಂಪರ್ಕ ಹೊಂದಿಲ್ಲದಿದ್ದರೆ, ಗ್ರಾಫ್‌ನ ಪ್ರದೇಶಗಳು ವ್ಯರ್ಥವಾಗುತ್ತವೆ. ಏಕೆಂದರೆ ಅವು ಹುಡುಕಾಟದ ಜಾಗಕ್ಕೆ ಕೊಡುಗೆ ನೀಡುವುದಿಲ್ಲ. ಗ್ರಾಫ್ ಲೂಪ್‌ಗಳನ್ನು ಹೊಂದಿದ್ದರೆ, ಆಯ್ಕೆ ಮಾಡಲಾದ ನೋಡ್‌ಗಳ ನಡುವೆ ಅನೇಕ ಮಾರ್ಗಗಳು ಇರಬಹುದು. ಈ ಕಾರಣದಿಂದಾಗಿ, ಮೇಜ್ ಜೆನೆರೇಷನ್ ಅನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಸ್ಪ್ಯಾನಿಂಗ್ ಟ್ರೀ ಉತ್ಪಾದಿಸುವಂತೆ ಸಂಪರ್ಕಿಸಲಾಗುತ್ತದೆ. ನಿಷ್ಕಪಟ ಮೇಜ್ ಪರಿಹಾರಕಗಳನ್ನು ಗೊಂದಲಗೊಳಿಸಬಹುದಾದ ಲೂಪ್‌ಗಳನ್ನು ಅಲ್ಗಾರಿದಮ್‌ನ ಅವಧಿಯಲ್ಲಿ ಫಲಿತಾಂಶಕ್ಕೆ ಯಾದೃಚ್ಛಿಕ ಎಡ್ಜ್ ಗಳನ್ನು ಸೇರಿಸುವ ಮೂಲಕ ಪರಿಚಯಿಸಬಹುದು.

ಆಯತಾಕಾರದ ಗ್ರಿಡ್‌ನಲ್ಲಿಲ್ಲದ ಗ್ರಾಫ್‌ಗಾಗಿ ಮೇಜ್ ರಚನೆಯ ಹಂತಗಳನ್ನು ಅನಿಮೇಷನ್ ತೋರಿಸುತ್ತದೆ. ಮೊದಲಿಗೆ, ಕಂಪ್ಯೂಟರ್ ನೀಲಿ ಬಣ್ಣದಲ್ಲಿ ತೋರಿಸಿರುವ ಯಾದೃಚ್ಛಿಕ ಪ್ಲ್ಯಾನರ್ ಗ್ರಾಫ್ G ಅನ್ನು ರಚಿಸುತ್ತದೆ ಮತ್ತು ಅದರ ಡ್ಯುಯಲ್ F ಅನ್ನು ಹಳದಿ ಬಣ್ಣದಲ್ಲಿ ತೋರಿಸಲಾಗುತ್ತದೆ. ಎರಡನೆಯದಾಗಿ, ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟದಂತಹ ಆಯ್ಕೆ ಮಾಡಿದ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ಎಫ್ ಅನ್ನು ಕಂಪ್ಯೂಟರ್ ಹಾದುಹೋಗುತ್ತದೆ. ಈ ಮಾರ್ಗವನ್ನು ಕೆಂಪು ಬಣ್ಣ ತಿಳಿಸುತ್ತದೆ. ಪ್ರಯಾಣದ ಸಮಯದಲ್ಲಿ, ನೀಲಿ ಅಂಚಿನ ಮೇಲೆ ಕೆಂಪು ಅಂಚು ದಾಟಿದಾಗ, ನೀಲಿ ಅಂಚನ್ನು ತೆಗೆದುಹಾಕಲಾಗುತ್ತದೆ. ಅಂತಿಮವಾಗಿ, F ನ ಎಲ್ಲಾ ವರ್ಟಿಸಿಸ್ ಗಳನ್ನು ಭೇಟಿ ಮಾಡಿದಾಗ, F ಅನ್ನು ಅಳಿಸಲಾಗುತ್ತದೆ ಮತ್ತು G ನಿಂದ ಎರಡು ಎಡ್ಜ್ ಗಳನ್ನು ತೆಗೆದುಹಾಕಲಾಗುತ್ತದೆ, ಒಂದು ಪ್ರವೇಶಕ್ಕಾಗಿ ಮತ್ತು ಒಂದು ನಿರ್ಗಮನಕ್ಕಾಗಿ.

ಯಾದೃಚ್ಛಿಕ ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ (ಆಳ-ಮೊದಲ) ಹುಡುಕಾಟ[ಬದಲಾಯಿಸಿ]

ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟವನ್ನು ಬಳಸಿಕೊಂಡು ಜನರೇಟರ್‌ನ ಅನಿಮೇಷನ್

ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟವನ್ನು ಬಳಸಿಕೊಂಡು ಜನರೇಟರ್‌ನ ವಿಭಿನ್ನ ಅನಿಮೇಷನ್

"ರಿಕರ್ಸಿವ್ ಬ್ಯಾಕ್‌ಟ್ರ್ಯಾಕರ್" ಅಲ್ಗಾರಿದಮ್ ಎಂದೂ ಕರೆಯಲ್ಪಡುವ ಈ ಅಲ್ಗಾರಿದಮ್ ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟ ಅಲ್ಗಾರಿದಮ್‌ನ ಯಾದೃಚ್ಛಿಕ ಆವೃತ್ತಿಯಾಗಿದೆ.

ಸ್ಟಾಕ್‌ನೊಂದಿಗೆ ಆಗಾಗ್ಗೆ ಕಾರ್ಯಗತಗೊಳಿಸಲಾಗುತ್ತದೆ, ಈ ವಿಧಾನವು ಕಂಪ್ಯೂಟರ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ಮೇಜ್ ಅನ್ನು ರಚಿಸುವ ಸರಳ ವಿಧಾನಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ. ಒಂದು ಮೇಜ್ ಸ್ಥಳವನ್ನು ಸೆಲ್ ಗಳ ದೊಡ್ಡ ಗ್ರಿಡ್ ಎಂದು ಪರಿಗಣಿಸಿ (ದೊಡ್ಡ ಚೆಸ್ ಬೋರ್ಡ್‌ನಂತೆ), ಪ್ರತಿ ಸೆಲ್ ನಾಲ್ಕು ಗೋಡೆಗಳಿಂದ ಪ್ರಾರಂಭವಾಗುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕ ಸೆಲ್ ನಿಂದ ಪ್ರಾರಂಭಿಸಿ, ಕಂಪ್ಯೂಟರ್ ನಂತರ ಇನ್ನೂ ಭೇಟಿ ನೀಡದ ಯಾದೃಚ್ಛಿಕ ನೆರೆಯ ಸೆಲ್ ಅನ್ನು ಆಯ್ಕೆ ಮಾಡುತ್ತದೆ. ಕಂಪ್ಯೂಟರ್ ಎರಡು ಸೆಲ್ ಗಳ ನಡುವಿನ ಗೋಡೆಯನ್ನು ತೆಗೆದುಹಾಕುತ್ತದೆ ಮತ್ತು ಹೊಸ ಸೆಲ್ ಅನ್ನು ಭೇಟಿ ಮಾಡಿದಂತೆ ಗುರುತಿಸುತ್ತದೆ ಮತ್ತು ಬ್ಯಾಕ್‌ಟ್ರ್ಯಾಕಿಂಗ್‌ಗೆ ಅನುಕೂಲವಾಗುವಂತೆ ಅದನ್ನು ಸ್ಟಾಕ್‌ಗೆ ಸೇರಿಸುತ್ತದೆ. ಕಂಪ್ಯೂಟರ್ ಈ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಮುಂದುವರೆಸುತ್ತದೆ, ಯಾವುದೇ ಭೇಟಿ ನೀಡದ ನೆರೆಹೊರೆಯವರಿಲ್ಲದ ಸೆಲ್ ಅನ್ನು ಡೆಡ್-ಎಂಡ್ ಎಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ. ಕೊನೆಯ ಹಂತದಲ್ಲಿ ಅದು ಭೇಟಿ ನೀಡದ ನೆರೆಹೊರೆಯವರೊಂದಿಗೆ ಸೆಲ್ ಅನ್ನು ತಲುಪುವವರೆಗೆ ಮಾರ್ಗದ ಮೂಲಕ ಹಿಮ್ಮೆಟ್ಟಿಸುತ್ತದೆ. ಈ ಹೊಸ, ಭೇಟಿಯಾಗದ ಸೆಲ್ ಗೆ (ಹೊಸ ಜಂಕ್ಷನ್ ಅನ್ನು ರಚಿಸುವ) ಭೇಟಿ ನೀಡುವ ಮೂಲಕ ಮಾರ್ಗ ರಚನೆಯನ್ನು ಮುಂದುವರಿಸುತ್ತದೆ. ಪ್ರತಿ ಸೆಲ್ ಗೆ ಭೇಟಿ ನೀಡುವವರೆಗೆ ಈ ಪ್ರಕ್ರಿಯೆಯು ಮುಂದುವರಿಯುತ್ತದೆ. ಇದರಿಂದಾಗಿ ಕಂಪ್ಯೂಟರ್ ಪ್ರಾರಂಭದ ಸೆಲ್ ಗೆ ಹಿಂತಿರುಗುತ್ತದೆ. ಪ್ರತಿ ಸೆಲ್ ಗೆ ಭೇಟಿ ನೀಡಲಾಗಿದೆ ಎಂದು ನಾವು ಖಚಿತವಾಗಿ ಹೇಳಬಹುದು.

ಮೇಲೆ ನೀಡಿರುವಂತೆ ಈ ಅಲ್ಗಾರಿದಮ್ ಆಳವಾದ ಪುನರಾವರ್ತನೆಯನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ಇದು ಕೆಲವು ಕಂಪ್ಯೂಟರ್ ಆರ್ಕಿಟೆಕ್ಚರ್‌ಗಳಲ್ಲಿ ಸ್ಟಾಕ್ ಓವರ್‌ಫ್ಲೋ ಸಮಸ್ಯೆಗಳನ್ನು ಉಂಟುಮಾಡಬಹುದು. ಮೇಜ್ ನಲ್ಲಿಯೇ ಬ್ಯಾಕ್‌ಟ್ರ್ಯಾಕಿಂಗ್ ಮಾಹಿತಿಯನ್ನು ಸಂಗ್ರಹಿಸುವ ಮೂಲಕ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಲೂಪ್‌ಗೆ ಮರುಹೊಂದಿಸಬಹುದು. ಇದು ಯಾವುದೇ ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಪ್ರಾರಂಭಿಸಿ ಮತ್ತು ಪ್ರಾರಂಭಕ್ಕೆ ಬ್ಯಾಕ್‌ಟ್ರ್ಯಾಕ್ ಮಾಡುವ ಮೂಲಕ ಪರಿಹಾರವನ್ನು ಪ್ರದರ್ಶಿಸಲು ತ್ವರಿತ ಮಾರ್ಗವನ್ನು ಒದಗಿಸುತ್ತದೆ.

ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟದೊಂದಿಗೆ ರಚಿಸಲಾದ ಮೇಜ್‌ಗಳು ಕಡಿಮೆ ಕವಲೊಡೆಯುವ ಅಂಶವನ್ನು ಹೊಂದಿರುತ್ತವೆ ಮತ್ತು ಅನೇಕ ಉದ್ದದ ಕಾರಿಡಾರ್‌ಗಳನ್ನು ಹೊಂದಿರುತ್ತವೆ. ಏಕೆಂದರೆ ಅಲ್ಗಾರಿದಮ್ ಬ್ಯಾಕ್‌ಟ್ರ್ಯಾಕ್ ಮಾಡುವ ಮೊದಲು ಪ್ರತಿ ಶಾಖೆಯ ಉದ್ದಕ್ಕೂ ಸಾಧ್ಯವಾದಷ್ಟು ಪರಿಶೋಧಿಸುತ್ತದೆ.

ಪುನರಾವರ್ತಿತ ಅನುಷ್ಠಾನ[ಬದಲಾಯಿಸಿ]

ಷಡ್ಭುಜೀಯ ಗ್ರಿಡ್‌ನಲ್ಲಿ ಯಾದೃಚ್ಛಿಕ ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟ

ಮೇಜ್ ಜೆನೆರೇಷನ್ ಯ ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಬ್ಯಾಕ್‌ಟ್ರ್ಯಾಕಿಂಗ್ ಬಳಸಿಕೊಂಡು ಆಗಾಗ್ಗೆ ಅಳವಡಿಸಲಾಗಿದೆ. ಇದನ್ನು ಈ ಕೆಳಗಿನ ರಿಕರ್ಸೀವ್ ರೂಟೀನ್ ನೊಂದಿಗೆ ವಿವರಿಸಬಹುದು:

ಪ್ರಸ್ತುತ ಸೆಲ್ ಅನ್ನು ನಿಯತಾಂಕವಾಗಿ ನೀಡಲಾಗಿದೆ
ಪ್ರಸ್ತುತ ಸೆಲ್ ಅನ್ನು ಭೇಟಿ ಮಾಡಿದಂತೆ ಗುರುತಿಸಿ
ಪ್ರಸ್ತುತ ಸೆಲ್ ಯಾವುದೇ ಭೇಟಿ ನೀಡದ ನೆರೆಯ ಸೆಲ್ ಗಳನ್ನು ಹೊಂದಿದೆ
1. ಭೇಟಿ ನೀಡದ ನೆರೆಹೊರೆಯವರಲ್ಲಿ ಒಬ್ಬರನ್ನು ಆರಿಸಿ.
2. ಪ್ರಸ್ತುತ ಸೆಲ್ ಮತ್ತು ಆಯ್ಕೆಮಾಡಿದ ಸೆಲ್ ನ ನಡುವಿನ ಗೋಡೆಯನ್ನು ತೆಗೆದುಹಾಕಿ
3. ಆಯ್ಕೆಮಾಡಿದ ಸೆಲ್‌ಗೆ ರಿಕರ್ಸೀವ್ ಆಗಿ ರೂಟೀನ್ ಅನ್ನು ಆಹ್ವಾನಿಸಿ.

ಪ್ರದೇಶದಲ್ಲಿನ ಯಾವುದೇ ಆರಂಭಿಕ ಸೆಲ್ ಗೆ ಒಮ್ಮೆ ಇನ್ವೋಕ್ ಮಾಡಲಾಗುತ್ತದೆ.

ಪುನರಾವರ್ತಿತ ಅನುಷ್ಠಾನ (ಸ್ಟಾಕ್‌ನೊಂದಿಗೆ)[ಬದಲಾಯಿಸಿ]

ಮೊದಲ ವಿಧಾನದ ಅನನುಕೂಲವೆಂದರೆ ರಿಕರ್ಸೀವ್ ದೊಡ್ಡ ಆಳವಾಗಿ ಕರೆಯಲಾಗುತ್ತದೆ - ಕನಿಷ್ಠ ಸಂದರ್ಭದಲ್ಲಿ, ಪ್ರಕ್ರಿಯೆಗೊಳಿಸುತ್ತಿರುವ ಪ್ರದೇಶದ ಪ್ರತಿಯೊಂದು ಸೆಲ್ ನಲ್ಲಿ ರೂಟೀನ್ ನಲ್ಲಿ ಮರುಕಳಿಸಬೇಕಾಗಬಹುದು. ಇದು ಅನೇಕ ಪರಿಸರಗಳಲ್ಲಿ ಗರಿಷ್ಠ ರಿಕರ್ಶನ್ ಸ್ಟಾಕ್ ಆಳವನ್ನು ಮೀರಬಹುದು. ಪರಿಹಾರವಾಗಿ, ಅದೇ ಬ್ಯಾಕ್‌ಟ್ರ್ಯಾಕಿಂಗ್ ವಿಧಾನವನ್ನು ಸ್ಪಷ್ಟವಾದ ಸ್ಟಾಕ್‌ನೊಂದಿಗೆ ಕಾರ್ಯಗತಗೊಳಿಸಬಹುದು. ಇದು ಸಾಮಾನ್ಯವಾಗಿ ಯಾವುದೇ ಹಾನಿಯಾಗದಂತೆ ಹೆಚ್ಚು ದೊಡ್ಡದಾಗಿ ಬೆಳೆಯಲು ಅವಕಾಶ ನೀಡುತ್ತದೆ.

ಆರಂಭಿಕ ಸೆಲ್ ಅನ್ನು ಆರಿಸಿ, ಭೇಟಿ ನೀಡಿದಂತೆ ಗುರುತಿಸಿ ಮತ್ತು ಅದನ್ನು ಸ್ಟಾಕ್‌ಗೆ ತಳ್ಳಿರಿ.
ಸ್ಟಾಕ್ ಖಾಲಿಯಾಗಿಲ್ಲದಿದ್ದರೂ
1. ಸ್ಟಾಕ್‌ನಿಂದ ಸೆಲ್ ಅನ್ನು ಪಾಪ್ ಮಾಡಿ ಮತ್ತು ಅದನ್ನು ಪ್ರಸ್ತುತ ಸೆಲ್ ಅನ್ನಾಗಿ ಮಾಡಿ.
2. ಪ್ರಸ್ತುತ ಸೆಲ್ ಯಾವುದೇ ನೆರೆಹೊರೆಯಾಗಿದ್ದರೆ ಅದನ್ನು ಭೇಟಿ ಮಾಡಿಲ್ಲ.
  1. ಪ್ರಸ್ತುತ ಸೆಲ್ ಅನ್ನು ಸ್ಟಾಕ್‌ಗೆ ತಳ್ಳಿರಿ.
  2. ಭೇಟಿ ನೀಡದ ನೆರೆಹೊರೆಯಲ್ಲಿ ಒಂದನ್ನು ಆರಿಸಿ.
  3. ಪ್ರಸ್ತುತ ಸೆಲ್ ಮತ್ತು ಆಯ್ಕೆಮಾಡಿದ ಸೆಲ್ ನ ನಡುವಿನ ಗೋಡೆಯನ್ನು ತೆಗೆದುಹಾಕಿ.
  4. ಆಯ್ಕೆಮಾಡಿದ ಸೆಲ್ ಅನ್ನು ಭೇಟಿ ಮಾಡಿದಂತೆ ಗುರುತಿಸಿ ಮತ್ತು ಅದನ್ನು ಸ್ಟಾಕ್‌ಗೆ ತಳ್ಳಿರಿ.

ಪುನರಾವರ್ತಿತ ಯಾದೃಚ್ಛಿಕ ಕ್ರುಸ್ಕಲ್ ಅಲ್ಗಾರಿದಮ್ (ಸೆಟ್‌ಗಳೊಂದಿಗೆ)[ಬದಲಾಯಿಸಿ]

ಕ್ರುಸ್ಕಲ್ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು 30 ರಿಂದ 20 ಮೇಜ್ ಅನ್ನು ಉತ್ಪಾದಿಸುವ ಅನಿಮೇಷನ್.

ಈ ಅಲ್ಗಾರಿದಮ್ ಕ್ರುಸ್ಕಲ್ ಅಲ್ಗಾರಿದಮ್‌ನ ಯಾದೃಚ್ಛಿಕ ಆವೃತ್ತಿಯಾಗಿದೆ.

ಎಲ್ಲಾ ಗೋಡೆಗಳ ಪಟ್ಟಿಯನ್ನು ರಚಿಸಿ ಮತ್ತು ಪ್ರತಿ ಸೆಲ್ ಗೆ ಒಂದು ಸೆಟ್ ಅನ್ನು ರಚಿಸಿ, ಪ್ರತಿಯೊಂದೂ ಕೇವಲ ಒಂದು ಸೆಲ್ ಅನ್ನು ಹೊಂದಿರುತ್ತದೆ.
ಪ್ರತಿ ಗೋಡೆಗೆ, ಕೆಲವು ಯಾದೃಚ್ಛಿಕ ಕ್ರಮದಲ್ಲಿ:
1. ಈ ಗೋಡೆಯಿಂದ ಭಾಗಿಸಿದ ಸೆಲ್ ಗಳು ವಿಭಿನ್ನ ಸೆಟ್‌ಗಳಿಗೆ ಸೇರಿದ್ದರೆ:
  1. ಪ್ರಸ್ತುತ ಗೋಡೆಯನ್ನು ತೆಗೆದುಹಾಕಿ.
  2. ಹಿಂದೆ ವಿಭಜಿಸಲಾದ ಸೆಲ್ ಗಳ ಸೆಟ್‌ಗಳನ್ನು ಸೇರಿ.

ಸೆಲ್ ಗಳ ಸೆಟ್‌ಗಳನ್ನು ಮಾಡೆಲ್ ಮಾಡಲು ಹಲವಾರು ಡೇಟಾ ರಚನೆಗಳನ್ನು ಬಳಸಬಹುದು. ಡಿಸ್ಜಾಯಿಂಟ್-ಸೆಟ್ ಡೇಟಾ ರಚನೆಯನ್ನು ಬಳಸಿಕೊಂಡು ಸಮರ್ಥ ಅನುಷ್ಠಾನವು ಪ್ರತಿ ಒಕ್ಕೂಟವನ್ನು ನಿರ್ವಹಿಸುತ್ತದೆ ಮತ್ತು ಸುಮಾರು ಸ್ಥಿರವಾದ ಅಮೋರ್ಟೈಸ್ಡ್ ಸಮಯದಲ್ಲಿ ಎರಡು ಸೆಟ್‌ಗಳಲ್ಲಿ ಕಾರ್ಯಾಚರಣೆಯನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು (ನಿರ್ದಿಷ್ಟವಾಗಿ, $O(\alpha (V))$ ಸಮಯ; $\alpha (x)<5$ ಯಾವುದೇ ತೋರಿಕೆಯ ಮೌಲ್ಯಕ್ಕಾಗಿ $x$ ), ಆದ್ದರಿಂದ ಈ ಅಲ್ಗಾರಿದಮ್‌ನ ಚಾಲನೆಯಲ್ಲಿರುವ ಸಮಯವು ಮೂಲಭೂತವಾಗಿ ಜಟಿಲಕ್ಕೆ ಲಭ್ಯವಿರುವ ಗೋಡೆಗಳ ಸಂಖ್ಯೆಗೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.

ಗೋಡೆಗಳ ಪಟ್ಟಿ (ಲಿಸ್ಟ್)ಯನ್ನು ಆರಂಭದಲ್ಲಿ ಯಾದೃಚ್ಛಿಕಗೊಳಿಸಲಾಗಿದೆಯೇ ಅಥವಾ ಯಾದೃಚ್ಛಿಕವಲ್ಲದ ಪಟ್ಟಿಯಿಂದ ಗೋಡೆಯನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆಮಾಡಿದರೆ, ಎರಡೂ ರೀತಿಯಲ್ಲಿ ಕೋಡ್ ಮಾಡಲು ಸುಲಭವಾಗಿದೆ.

ಈ ಅಲ್ಗಾರಿದಮ್‌ನ ಪರಿಣಾಮವು ಸಮಾನ ತೂಕದ ಎಡ್ಜ್ ಗಳೊಂದಿಗೆ ಗ್ರಾಫ್‌ನಿಂದ ಕನಿಷ್ಠ ಸ್ಪ್ಯಾನಿಂಗ್ ಟ್ರೀ ಯನ್ನು ರಚನೆ ಮಾಡುತ್ತದೆ. ಇದು ಪರಿಹರಿಸಲು ಸಾಕಷ್ಟು ಸುಲಭವಾದ ನಿಯಮಿತ ಮಾದರಿಗಳನ್ನು ರಚನೆ ಮಾಡುತ್ತದೆ.

ಪುನರಾವರ್ತಿತ ಯಾದೃಚ್ಛಿಕ ಪ್ರೈಮ್ ಅಲ್ಗಾರಿದಮ್ (ಸ್ಟಾಕ್ ಇಲ್ಲದೆ, ಸೆಟ್‌ಗಳಿಲ್ಲದೆ)[ಬದಲಾಯಿಸಿ]

ಪ್ರಿಮ್ಸ್ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು 30 ಬೈ 20 ಮೇಜ್ ರಚನೆಯ ಅನಿಮೇಷನ್.

ಈ ಅಲ್ಗಾರಿದಮ್ ಪ್ರಿಮ್‌ನ ಅಲ್ಗಾರಿದಮ್‌ನ ಯಾದೃಚ್ಛಿಕ ಆವೃತ್ತಿಯಾಗಿದೆ.

ಗೋಡೆಗಳ ಪೂರ್ಣ ಗ್ರಿಡ್ನೊಂದಿಗೆ ಪ್ರಾರಂಭಿಸಿ.
ಸೆಲ್ ಅನ್ನು ಆರಿಸಿ, ಅದನ್ನು ಮೇಜ್ ಭಾಗವಾಗಿ ಗುರುತಿಸಿ. ಗೋಡೆಯ ಪಟ್ಟಿಗೆ ಸೆಲ್ ನ ಗೋಡೆಗಳನ್ನು ಸೇರಿಸಿ.
ಪಟ್ಟಿಯಲ್ಲಿ ಗೋಡೆಗಳಿದ್ದರೂ:
1. ಪಟ್ಟಿಯಿಂದ ಯಾದೃಚ್ಛಿಕ ಗೋಡೆಯನ್ನು ಆರಿಸಿ. ಗೋಡೆಯು ವಿಭಜಿಸುವ ಸೆಲ್ ಗಳಲ್ಲಿ ಒಂದನ್ನು ಮಾತ್ರ ಭೇಟಿ ಮಾಡಿದರೆ, ನಂತರ:
  1. ಗೋಡೆಯನ್ನು ಹಾದಿಯನ್ನಾಗಿ ಮಾಡಿ ಮತ್ತು ಭೇಟಿಯಾಗದ ಸೆಲ್ ಅನ್ನು ಮೇಜ್ ಭಾಗವಾಗಿ ಗುರುತಿಸಿ.
  2. ಗೋಡೆಯ ಪಟ್ಟಿಗೆ ಸೆಲ್ ನ ನೆರೆಯ ಗೋಡೆಗಳನ್ನು ಸೇರಿಸಿ.
2. ಪಟ್ಟಿಯಿಂದ ಗೋಡೆಯನ್ನು ತೆಗೆದುಹಾಕಿ.

ಯಾದೃಚ್ಛಿಕ ಅಂಚಿನ ತೂಕದೊಂದಿಗೆ ಗ್ರಾಫ್‌ನಲ್ಲಿ ಕ್ಲಾಸಿಕಲ್ ಪ್ರಿಮ್‌ಗಳನ್ನು ಸರಳವಾಗಿ ಚಾಲನೆ ಮಾಡುವುದರಿಂದ ಕ್ರುಸ್ಕಲ್‌ಗೆ ಸ್ಟೈಲಿಸ್ಟಿಕಲ್ ಆಗಿ ಒಂದೇ ರೀತಿಯ ಮೇಜ್ ಗಳನ್ನು ರಚಿಸುತ್ತದೆ. ಏಕೆಂದರೆ ಅವೆರಡೂ ಕನಿಷ್ಠ ವ್ಯಾಪಿಸಿರುವ ಟ್ರೀನ (ಮಿನಿಮಮ್ ಸ್ಪ್ಯಾನಿಂಗ್ ಟ್ರೀ) ಕ್ರಮಾವಳಿಗಳಾಗಿವೆ. ಬದಲಾಗಿ, ಈ ಅಲ್ಗಾರಿದಮ್ ಶೈಲಿಯ ವ್ಯತ್ಯಾಸವನ್ನು ಪರಿಚಯಿಸುತ್ತದೆ. ಏಕೆಂದರೆ ಆರಂಭಿಕ ಹಂತಕ್ಕೆ ಹತ್ತಿರವಿರುವ ಎಡ್ಜ್ ಗಳು ಕಡಿಮೆ ಪರಿಣಾಮಕಾರಿ ತೂಕವನ್ನು ಹೊಂದಿರುತ್ತವೆ.

ಮಾರ್ಪಡಿಸಿದ ಆವೃತ್ತಿ[ಬದಲಾಯಿಸಿ]

ಕ್ಲಾಸಿಕಲ್ ಪ್ರಿಮ್‌ನ ಅಲ್ಗಾರಿದಮ್ ಎಡ್ಜ್ ಗಳ ಪಟ್ಟಿಯನ್ನು ಇರಿಸುತ್ತದೆಯಾದರೂ, ಮೇಜ್ ಉತ್ಪಾದನೆಗಾಗಿ ನಾವು ಪಕ್ಕದ ಸೆಲ್ ಗಳ ಪಟ್ಟಿಯನ್ನು ನಿರ್ವಹಿಸಬಹುದು. ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆಮಾಡಿದ ಸೆಲ್ ಅಸ್ತಿತ್ವದಲ್ಲಿರುವ ಸೆಲ್ ಗೆ ಸಂಪರ್ಕಿಸುವ ಬಹು ಎಡ್ಜ್ ಗಳನ್ನು ಹೊಂದಿದ್ದರೆ, ಈ ಎಡ್ಜ್ ಗಳಲ್ಲಿ ಒಂದನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆಮಾಡಿ. ಇದು ಮೇಲಿನ ಎಡ್ಜ್-ಆಧಾರಿತ ಆವೃತ್ತಿಗಿಂತ ಸ್ವಲ್ಪ ಹೆಚ್ಚು ಕವಲೊಡೆಯುತ್ತದೆ.

ಸರಳೀಕೃತ ಆವೃತ್ತಿ[ಬದಲಾಯಿಸಿ]

ಎಲ್ಲಾ ಸೆಲ್ ಗಳು ಅಥವಾ ಎಡ್ಜ್ ಗಳ ತೂಕದ ಮೇಲೆ ನಿಗಾ ಇಡುವ ಬದಲು ಈಗಾಗಲೇ ಭೇಟಿ ನೀಡಿದ ಸೆಲ್ ಗಳ ನೆರೆಯ ಸೆಲ್ ಗಳನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಆಯ್ಕೆ ಮಾಡುವ ಮೂಲಕ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಇನ್ನಷ್ಟು ಸರಳಗೊಳಿಸಬಹುದು.

ಪ್ರಾರಂಭದ ಸೆಲ್ ಗೆ ದಾರಿಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಸಾಮಾನ್ಯವಾಗಿ ತುಲನಾತ್ಮಕವಾಗಿ ಸುಲಭವಾಗಿರುತ್ತದೆ. ಆದರೆ ಬೇರೆಲ್ಲಿಯಾದರೂ ಮಾರ್ಗವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಕಷ್ಟ.

ವಿಲ್ಸನ್ ಅಲ್ಗಾರಿದಮ್[ಬದಲಾಯಿಸಿ]

ವಿಲ್ಸನ್ ಅವರ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ಮೇಜ್ ಜನರೇಷನ್ ಅನಿಮೇಷನ್ (ಬೂದು ನಡೆಯುತ್ತಿರುವ ಯಾದೃಚ್ಛಿಕ ನಡಿಗೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ). ಒಮ್ಮೆ ನಿರ್ಮಿಸಿದ ನಂತರ ಮೇಜ್ ಅನ್ನು ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟವನ್ನು ಬಳಸಿ ಪರಿಹರಿಸಲಾಗುತ್ತದೆ

ಮೇಲಿನ ಎಲ್ಲಾ ಅಲ್ಗಾರಿದಮ್‌ಗಳು ವಿವಿಧ ರೀತಿಯ ಪಕ್ಷಪಾತಗಳನ್ನು ಹೊಂದಿವೆ: ಡೆಪ್ತ್-ಫರ್ಸ್ಟ್ ಹುಡುಕಾಟವು ದೀರ್ಘ ಕಾರಿಡಾರ್‌ಗಳ ಕಡೆಗೆ ಪಕ್ಷಪಾತವನ್ನು ಹೊಂದಿದೆ. ಆದರೆ ಕ್ರುಸ್ಕಾಲ್‌ನ/ಪ್ರಿಮ್‌ನ ಅಲ್ಗಾರಿದಮ್‌ಗಳು ಅನೇಕ ಶಾರ್ಟ್ ಡೆಡ್ ಎಂಡ್‌ಗಳ ಕಡೆಗೆ ಪಕ್ಷಪಾತವನ್ನು ಹೊಂದಿವೆ. ವಿಲ್ಸನ್ನ ಅಲ್ಗಾರಿದಮ್, ^[೧] ಮತ್ತೊಂದೆಡೆ, ಲೂಪ್-ಅಳಿಸಿದ ಯಾದೃಚ್ಛಿಕ ನಡಿಗೆಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಎಲ್ಲಾ ಮೇಜ್‌ಗಳ ಮೇಲೆ ಏಕರೂಪದ ವಿತರಣೆಯಿಂದ ಪಕ್ಷಪಾತವಿಲ್ಲದ ಮಾದರಿಯನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ.

ಅನಿಯಂತ್ರಿತವಾಗಿ ಆಯ್ಕೆ ಮಾಡಿದ ಒಂದು ಸೆಲ್ ನೊಂದಿಗೆ ಮೇಜ್ ಅನ್ನು ಪ್ರಾರಂಭಿಸುವ ಮೂಲಕ ನಾವು ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಪ್ರಾರಂಭಿಸುತ್ತೇವೆ. ನಂತರ ನಾವು ನಿರಂಕುಶವಾಗಿ ಆಯ್ಕೆ ಮಾಡಿದ ಹೊಸ ಸೆಲ್ ನಿಂದ ಪ್ರಾರಂಭಿಸುತ್ತೇವೆ ಮತ್ತು ನಾವು ಈಗಾಗಲೇ ಮೇಜ್ ನಲ್ಲಿರುವ ಸೆಲ್ ಅನ್ನು ತಲುಪುವವರೆಗೆ ಯಾದೃಚ್ಛಿಕ ನಡಿಗೆಯನ್ನು ಮಾಡುತ್ತೇವೆ. ಆದಾಗ್ಯೂ, ಯಾವುದೇ ಹಂತದಲ್ಲಿ ಯಾದೃಚ್ಛಿಕ ನಡಿಗೆ ತನ್ನದೇ ಆದ ಮಾರ್ಗವನ್ನು ತಲುಪಿದರೆ, ಲೂಪ್ ಅನ್ನು ರೂಪಿಸಿದರೆ, ನಾವು ಮಾರ್ಗದಿಂದ ಲೂಪ್ ಅನ್ನು ಅಳಿಸುತ್ತೇವೆ. ಮುಂದುವರೆಯುವ ಮೊದಲು. ಮಾರ್ಗವು ಮೇಜ್ ಅನ್ನು ತಲುಪಿದಾಗ, ನಾವು ಅದನ್ನು ಮೇಜ್ ಗೆ ಸೇರಿಸುತ್ತೇವೆ. ನಂತರ ನಾವು ಮತ್ತೊಂದು ಅನಿಯಂತ್ರಿತ ಆರಂಭಿಕ ಸೆಲ್ ನಿಂದ ಮತ್ತೊಂದು ಲೂಪ್-ಅಳಿಸಿದ ಯಾದೃಚ್ಛಿಕ ನಡಿಗೆಯನ್ನು ನಿರ್ವಹಿಸುತ್ತೇವೆ. ಇದನ್ನು ಎಲ್ಲಾ ಸೆಲ್ ಗಳು ಭೇಟಿ ಮಾಡುವವರೆಗೆ ಪುನರಾವರ್ತಿಸುತ್ತೇವೆ.

ಆರಂಭಿಕ ಸೆಲ್ ಗಳನ್ನು ಅನಿಯಂತ್ರಿತವಾಗಿ ಆಯ್ಕೆ ಮಾಡಲು ನಾವು ಯಾವ ವಿಧಾನವನ್ನು ಬಳಸಿದರೂ ಈ ಕಾರ್ಯವಿಧಾನವು ನಿಷ್ಪಕ್ಷಪಾತವಾಗಿ ಉಳಿಯುತ್ತದೆ. ಆದ್ದರಿಂದ ನಾವು ಯಾವಾಗಲೂ ಸರಳತೆಗಾಗಿ ಎಡದಿಂದ ಬಲಕ್ಕೆ, ಮೇಲಿನಿಂದ ಕೆಳಗಿನ ಕ್ರಮದಲ್ಲಿ (ಹೇಳಲು) ಮೊದಲ ಭರ್ತಿ ಮಾಡದ ಸೆಲ್ ಅನ್ನು ಆಯ್ಕೆ ಮಾಡಬಹುದು.

ಆಲ್ಡಸ್-ಬ್ರೋಡರ್ ಅಲ್ಗಾರಿದಮ್[ಬದಲಾಯಿಸಿ]

ಆಲ್ಡಸ್-ಬ್ರೋಡರ್ ಅಲ್ಗಾರಿದಮ್ ಏಕರೂಪದ ಸ್ಪ್ಯಾನಿಂಗ್ ಟ್ರೀ ಸಹ ರಚನೆ ಮಾಡುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಇದು ಕಡಿಮೆ ಪರಿಣಾಮಕಾರಿ ಮೇಜ್ ಅಲ್ಗಾರಿದಮ್‌ಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ. ^[೨]

ಪ್ರಸ್ತುತ ಸೆಲ್ ಆಗಿ ಯಾದೃಚ್ಛಿಕ ಸೆಲ್ ಅನ್ನು ಆರಿಸಿ ಮತ್ತು ಭೇಟಿ ನೀಡಿದಂತೆ ಗುರುತಿಸಿ.
ಭೇಟಿ ನೀಡದ ಸೆಲ್ ಗಳು ಇರುವಾಗ:
1. ಯಾದೃಚ್ಛಿಕ ನೆರೆಹೊರೆಯ ಸೆಲ್ ಗಳನ್ನು ಆರಿಸಿ.
2. ಆಯ್ಕೆಮಾಡಿದ ನೆರೆಯ ಸೆಲ್ ಗಳನ್ನು ಭೇಟಿ ಮಾಡದಿದ್ದರೆ:
  1. ಪ್ರಸ್ತುತ ಸೆಲ್ ಮತ್ತು ಆಯ್ಕೆಮಾಡಿದ ನೆರೆಹೊರೆಯವರ ನಡುವಿನ ಗೋಡೆಯನ್ನು ತೆಗೆದುಹಾಕಿ.
  2. ಆಯ್ಕೆಮಾಡಿದ ನೆರೆಯವರನ್ನು ಭೇಟಿ ಮಾಡಿದಂತೆ ಗುರುತಿಸಿ.
3. ಆಯ್ಕೆಮಾಡಿದ ನೆರೆಯವರನ್ನು ಪ್ರಸ್ತುತ ಸೆಲ್ ಅನ್ನಾಗಿ ಮಾಡಿ.

ಪುನರಾವರ್ತಿತ ವಿಭಾಗ ವಿಧಾನ[ಬದಲಾಯಿಸಿ]

**ರಿಕರ್ಸಿವ್ ವಿಭಾಗದ ವಿವರಣೆ**
ಮೂಲ ಚೇಂಬರ್	ಎರಡು ಗೋಡೆಗಳಿಂದ ವಿಭಜನೆ	ಗೋಡೆಗಳಲ್ಲಿ ರಂಧ್ರಗಳು	ಉಪವಿಭಾಗವನ್ನು ಮುಂದುವರಿಸಿ...	ಪೂರ್ಣಗೊಂಡಿದೆ
ಹಂತ 1	ಹಂತ 2	ಹಂತ 3	ಹಂತ 4	ಹಂತ 5

ರಿಕರ್ಸೀವ್ ಡಿವಿಸನ್ ನೊಂದಿಗೆ ಮೇಜ್ ಗಳನ್ನು ರಚಿಸಬಹುದು. ಇದು ಈ ಕೆಳಗಿನಂತೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಅಲ್ಗಾರಿದಮ್: ಗೋಡೆಗಳಿಲ್ಲದ ಮೇಜ್ ಜಾಗದಿಂದ ಪ್ರಾರಂಭಿಸಿ. ಇದನ್ನು ಚೇಂಬರ್ ಎಂದು ಕರೆಯಿರಿ. ಯಾದೃಚ್ಛಿಕವಾಗಿ ಸ್ಥಾನದಲ್ಲಿರುವ ಗೋಡೆಯೊಂದಿಗೆ (ಅಥವಾ ಬಹು ಗೋಡೆಗಳು) ಚೇಂಬರ್ ಅನ್ನು ವಿಭಜಿಸಿ, ಅಲ್ಲಿ ಪ್ರತಿ ಗೋಡೆಯು ಅದರೊಳಗೆ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಸ್ಥಾನದಲ್ಲಿರುವ ಪ್ಯಾಸೇಜ್ ತೆರೆಯುವಿಕೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆ. ನಂತರ ಎಲ್ಲಾ ಕೋಣೆಗಳು ಕನಿಷ್ಠ ಗಾತ್ರದವರೆಗೆ ಉಪಚೇಂಬರ್‌ಗಳಲ್ಲಿ ಪ್ರಕ್ರಿಯೆಯನ್ನು ರಿಕರ್ಸೀವ್ ಆಗಿ ಪುನರಾವರ್ತಿಸಿ. ಈ ವಿಧಾನವು ಉದ್ದನೆಯ ನೇರವಾದ ಗೋಡೆಗಳನ್ನು ಹೊಂದಿರುವ ಮೇಜ್ ಗಳನ್ನು ಅವುಗಳ ಜಾಗವನ್ನು ದಾಟಲು ಕಾರಣವಾಗುತ್ತದೆ, ಇದು ಯಾವ ಪ್ರದೇಶಗಳನ್ನು ತಪ್ಪಿಸಬೇಕೆಂದು ನೋಡಲು ಸುಲಭವಾಗುತ್ತದೆ.

ಉದಾಹರಣೆಗೆ, ಆಯತಾಕಾರದ ಮೇಜ್ ನಲ್ಲಿ, ಯಾದೃಚ್ಛಿಕ ಬಿಂದುಗಳಲ್ಲಿ ಪರಸ್ಪರ ಲಂಬವಾಗಿರುವ ಎರಡು ಗೋಡೆಗಳನ್ನು ನಿರ್ಮಿಸಿ. ಈ ಎರಡು ಗೋಡೆಗಳು ದೊಡ್ಡ ಕೋಣೆಯನ್ನು ನಾಲ್ಕು ಗೋಡೆಗಳಿಂದ ಬೇರ್ಪಡಿಸಿದ ನಾಲ್ಕು ಸಣ್ಣ ಕೋಣೆಗಳಾಗಿ ವಿಭಜಿಸುತ್ತವೆ. ಯಾದೃಚ್ಛಿಕವಾಗಿ ನಾಲ್ಕು ಗೋಡೆಗಳಲ್ಲಿ ಮೂರನ್ನು ಆಯ್ಕೆಮಾಡಿ, ಮತ್ತು ಪ್ರತಿಯೊಂದರಲ್ಲೂ ಯಾದೃಚ್ಛಿಕ ಬಿಂದುವಿನಲ್ಲಿ ಒಂದು ಸೆಲ್ ನ ಅಗಲದ ರಂಧ್ರವನ್ನು ತೆರೆಯಿರಿ. ಈ ರೀತಿಯಲ್ಲಿ ಪುನರಾವರ್ತಿತವಾಗಿ ಮುಂದುವರಿಯಿರಿ, ಪ್ರತಿ ಚೇಂಬರ್ ಎರಡು ದಿಕ್ಕುಗಳಲ್ಲಿ ಒಂದು ಸೆಲ್ ನ ಅಗಲವನ್ನು ಹೊಂದಿರುತ್ತದೆ.

ಟೆಸ್ಸಲೇಷನ್ ಅಲ್ಗಾರಿದಮ್[ಬದಲಾಯಿಸಿ]

ಮೇಜ್ ಅನ್ನು ರಚಿಸಲು ಇದು ಸರಳ ಮತ್ತು ವೇಗವಾದ ಮಾರ್ಗವಾಗಿದೆ. ^[೩]

ಪ್ರತಿ ಪುನರಾವರ್ತನೆಯಲ್ಲಿ, ಈ ಅಲ್ಗಾರಿದಮ್ ಸ್ವತಃ 3 ಬಾರಿ ನಕಲಿಸುವ ಮೂಲಕ ಎರಡು ಪಟ್ಟು ಗಾತ್ರದ ಮೇಜ್ ಅನ್ನು ರಚಿಸುತ್ತದೆ. ಪ್ರತಿ ಪುನರಾವರ್ತನೆಯ ಕೊನೆಯಲ್ಲಿ, 4 ಸಣ್ಣ ಮೇಜ್ ಗಳ ನಡುವೆ 3 ಮಾರ್ಗಗಳನ್ನು ತೆರೆಯಲಾಗುತ್ತದೆ.

ಈ ವಿಧಾನದ ಪ್ರಯೋಜನವೆಂದರೆ ಅದು ತುಂಬಾ ವೇಗವಾಗಿರುತ್ತದೆ. ಅನಾನುಕೂಲವೆಂದರೆ ಆಯ್ಕೆಮಾಡಿದ ಗಾತ್ರದ ಮೇಜ್ ಅನ್ನು ಪಡೆಯಲು ಸಾಧ್ಯವಿಲ್ಲ - ಆದರೆ ಈ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸಲು ವಿವಿಧ ತಂತ್ರಗಳನ್ನು ಬಳಸಬಹುದು.

ಸರಳ ಅಲ್ಗಾರಿದಮ್ ಗಳು[ಬದಲಾಯಿಸಿ]

2D ಮೇಜ್ ನ ಒಂದು ಸಾಲು ಅಥವಾ 3D ಮೇಜ್ ನ ಒಂದು ಪ್ಲೇನ್ ಅನ್ನು ಸಂಗ್ರಹಿಸಲು ಸಾಕಷ್ಟು ಮೆಮೊರಿ ಅಗತ್ಯವಿರುವ ಇತರ ಅಲ್ಗಾರಿದಮ್‌ಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ. ಎಲ್ಲರ್‌ನ ಅಲ್ಗಾರಿದಮ್ ಪ್ರಸ್ತುತ ಸಾಲಿನಲ್ಲಿ ಯಾವ ಸೆಲ್ ಗಳನ್ನು ಹಿಂದಿನ ಸಾಲುಗಳಲ್ಲಿನ ಸೆಲ್ ಗಳ ಮೂಲಕ ಸಂಪರ್ಕಿಸಲಾಗಿದೆ ಎಂಬುದನ್ನು ಸಂಗ್ರಹಿಸುವ ಮೂಲಕ ಲೂಪ್‌ಗಳನ್ನು ತಡೆಯುತ್ತದೆ ಮತ್ತು ಈಗಾಗಲೇ ಸಂಪರ್ಕಗೊಂಡಿರುವ ಯಾವುದೇ ಎರಡು ಸೆಲ್ ಗಳ ನಡುವಿನ ಗೋಡೆಗಳನ್ನು ಎಂದಿಗೂ ತೆಗೆದುಹಾಕುವುದಿಲ್ಲ. ^[೪] ಸೈಡ್‌ವಿಂಡರ್ ಅಲ್ಗಾರಿದಮ್ ಸಂಪೂರ್ಣ ಮೇಲಿನ ಸಾಲಿನ ಉದ್ದಕ್ಕೂ ತೆರೆದ ಹಾದಿಯೊಂದಿಗೆ ಪ್ರಾರಂಭವಾಗುತ್ತದೆ, ಮತ್ತು ನಂತರದ ಸಾಲುಗಳು ಮೇಲಿನ ಮಾರ್ಗಕ್ಕೆ ಒಂದು ಸಂಪರ್ಕದೊಂದಿಗೆ ಕಡಿಮೆ ಸಮತಲ ಹಾದಿಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತವೆ. ಸೈಡ್‌ವಿಂಡರ್ ಅಲ್ಗಾರಿದಮ್ ಕೆಳಗಿನಿಂದ ಮೇಲಕ್ಕೆ ಪರಿಹರಿಸಲು ಕ್ಷುಲ್ಲಕವಾಗಿದೆ ಏಕೆಂದರೆ ಅದು ಮೇಲ್ಮುಖವಾಗಿ ಡೆಡ್ ಎಂಡ್ ಗಳನ್ನು ಹೊಂದಿಲ್ಲ. ^[೫] ಆರಂಭಿಕ ಅಗಲವನ್ನು ನೀಡಿದರೆ, ಎರಡೂ ಅಲ್ಗಾರಿದಮ್‌ಗಳು ಅನಿಯಮಿತ ಎತ್ತರದ ಪರಿಪೂರ್ಣ ಮೇಜ್ ಗಳನ್ನು ರಚಿಸುತ್ತವೆ.

ಹೆಚ್ಚಿನ ಮೇಜ್ ಜೆನರೇಷನ್ ಅಲ್ಗಾರಿದಮ್‌ಗಳು ಫಲಿತಾಂಶವು ಪರಿಹರಿಸಬಹುದಾದುದನ್ನು ಖಚಿತಪಡಿಸಿಕೊಳ್ಳಲು ಅದರೊಳಗಿನ ಸೆಲ್ ಗಳ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ನಿರ್ವಹಿಸುವ ಅಗತ್ಯವಿರುತ್ತದೆ. . ಮಾನ್ಯವಾದ ಸರಳವಾಗಿ ಸಂಪರ್ಕಗೊಂಡಿರುವ ಮೇಜ್ ಗಳನ್ನು ಸ್ವತಂತ್ರವಾಗಿ ಪ್ರತಿ ಸೆಲ್ ನ ಮೇಲೆ ಕೇಂದ್ರೀಕರಿಸುವ ಮೂಲಕ ರಚಿಸಬಹುದು. ಬೈನರಿ ಟ್ರೀ ಮೇಜ್ ಪ್ರಮಾಣಿತ ಆರ್ಥೋಗೋನಲ್ ಮೇಜ್ ಆಗಿದ್ದು, ಪ್ರತಿ ಸೆಲ್ ಯಾವಾಗಲೂ ಮೇಲಕ್ಕೆ ಅಥವಾ ಎಡಕ್ಕೆ ಮುನ್ನಡೆಯುವ ಹಾದಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಆದರೆ ಎರಡೂ ಎಂದಿಗೂ. ಬೈನರಿ ಟ್ರೀ ಮೇಜ್ ನಲ್ಲಿ, ಪ್ರತಿ ಸೆಲ್ ಗೆ ಒಂದು ನಾಣ್ಯವನ್ನು ಫ್ಲಿಪ್ ಮಾಡಿ, ಮುಂದಕ್ಕೆ ಹೋಗುವ ಅಥವಾ ಎಡಕ್ಕೆ ಹೋಗುವ ಮಾರ್ಗವನ್ನು ಸೇರಿಸಬೇಕೆ ಎಂದು ನಿರ್ಧರಿಸಿ ಮೇಜ್ ಅನ್ನು ರಚಿಸಬಹುದು. ಗಡಿಯಲ್ಲಿರುವ ಸೆಲ್ ಗಳಿಗೆ ಯಾವಾಗಲೂ ಒಂದೇ ದಿಕ್ಕನ್ನು ಆರಿಸಿ, ಮತ್ತು ಫಲಿತಾಂಶವು ಬೈನರಿ ಟ್ರೀಯಂತೆ ಕಾಣುವ ಮಾನ್ಯವಾದ ಸರಳ ಸಂಪರ್ಕಿತ ಮೇಜ್ ಆಗಿರುತ್ತದೆ. ಮೇಲಿನ ಎಡ ಮೂಲೆಯಲ್ಲಿ ಅದರ ಮೂಲ ಇರುತ್ತದೆ. ಸೈಡ್‌ವಿಂಡರ್‌ನಂತೆ, ಬೈನರಿ ಟ್ರೀ ಮೇಜ್ ಪಕ್ಷಪಾತದ ದಿಕ್ಕುಗಳಲ್ಲಿ ಯಾವುದೇ ಡೆಡ್ ಎಂಡ್‌ಗಳನ್ನು ಹೊಂದಿಲ್ಲ.

ಪ್ರತಿ ಸೆಲ್ ಗೆ ನಾಣ್ಯವನ್ನು ಫ್ಲಿಪ್ ಮಾಡುವಂತೆ ಫಾರ್ವರ್ಡ್ ಸ್ಲ್ಯಾಶ್ ಅಥವಾ ಬ್ಯಾಕ್ ಸ್ಲ್ಯಾಶ್ ಅಕ್ಷರಗಳನ್ನು ರ್ಯಂಡಮ್ ಆಗಿ ಬಳಸಿ ಚಿತ್ರಗಳನ್ನು ರಚಿಸಬಹುದು. ಇದು ಸುಮ್ಮನೆ ಸರಿಯಾದ ಮೇಜ್ ಅನ್ನು ಮಾತ್ರ ರಚಿಸುವುದಿಲ್ಲ ಬದಲಿಗೆ, ಕ್ಲೋಸ್ಡ್ ಲೂಪ್ ಗಳು ಮತ್ತು ಯುನಿಕರ್ಸಲ್ ಪ್ಯಾಸೇಜ್ ಗಳನ್ನು ಆರಿಸುತ್ತದೆ. ಕಮೋಡರ್ ೬೪ ರ ಮ್ಯಾನುಯಲ್ ನಲ್ಲಿ ಈ ಅಲ್ಗೋರಿದಮ್ ಅನ್ನು ಬೇಸಿಕ್ ಪ್ರೋಗ್ರಾಮ್ ಬಳಸಿ ರಚಿಸಲಾಗಿದೆ. ಇದನ್ನು ಬಳಸಿಕೊಂಡು ನವಿರಾದ ಗ್ರಾಫಿಕ್ ತೋರುವಿಕೆ ಬಳಸದೆ PETSCII ವಕ್ರ ರೇಖೆಯ ಗ್ರಾಫಿಕ್ ಅಕ್ಷರಗಳನ್ನು ಬಳಸಲಾಗಿದೆ.

ಸೆಲ್ಯೂಲರ್ ಅಟೋಮೇಷನ್ ಅಲ್ಗೋರಿದಮ್ ಗಳು[ಬದಲಾಯಿಸಿ]

ಇವನ್ನು ನೋಡಿ[ಬದಲಾಯಿಸಿ]

ಮೇಜ್ ಪರಿಹಾರಕ ಅಲ್ಗೋರಿದಮ್
ಸ್ವಯಂ ತಪ್ಪಿಸುವಿಕೆ ವಾಕ್
ಬ್ರೂಟ್ ಫೋರ್ಸ್ ಹುಡುಕಾಟ

ಉಲ್ಲೇಖಗಳು[ಬದಲಾಯಿಸಿ]

ಬಾಹ್ಯ ಲಿಂಕ್ ಗಳು[ಬದಲಾಯಿಸಿ]

↑ . Philadelphia. May 22–24, 1996. pp. 296–303. {{cite conference}}: Missing or empty |title= (help)
↑ Jamis Buck (17 January 2011). "Maze Generation: Aldous-Broder algorithm".
↑ Ze Oliveira (18 June 2023). "Maze Walls".
↑ Jamis Buck (29 December 2010). "Maze Generation: Eller's Algorithm".
↑ Jamis Buck (3 February 2011). "Maze Generation: Sidewinder Algorithm".

[1] . Philadelphia. May 22–24, 1996. pp. 296–303. {{cite conference}}: Missing or empty |title= (help)

[2] Jamis Buck (17 January 2011). "Maze Generation: Aldous-Broder algorithm".

[3] Ze Oliveira (18 June 2023). "Maze Walls".

[4] Jamis Buck (29 December 2010). "Maze Generation: Eller's Algorithm".

[5] Jamis Buck (3 February 2011). "Maze Generation: Sidewinder Algorithm".

[೧]

[೨]

[೩]

[೪]

[೫]