ಬೈನರಿ ಸರ್ಚ್ ಆಲಗೋರಿತಮ್
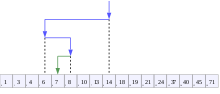 ಸಂಖ್ಯೆ ೭ ಅನ್ನು ಹುಡುಕುವ ದೃಶ್ಯೀಕರಣ | |
| ಕ್ಲಾಸ್ | ಹುಡುಕುವ ಆಲಗೋರಿತಮ್ |
|---|---|
| ಡೇಟಾ ರಚನೆ | ಅರ್ರೆ |
| ಪ್ರತಿಕೂಲ ಸ್ಥಿತಿ ವಿಶ್ಲೇಷಣೆ | O(log n) |
| ಆಪ್ಟಿಮಲ್ ಷರತ್ತು ವಿಶ್ಲೇಷಣೆ | O(1) |
| ಸರಾಸರಿ ಸಾಧನೆ | O(log n) |
| ಕೆಟ್ಟ-ಸ್ಥಳದ ಸಂಕೀರ್ಣತೆ | O(1) |
ಕಂಪ್ಯೂಟರ್ ವಿಜ್ಞಾನದಲ್ಲಿ, ಬೈನರಿ ಹುಡುಕಾಟವನ್ನು ಅರ್ಧ-ಮಧ್ಯಂತರ ಹುಡುಕಾಟ, [೧] ಲಾಗರಿಥಮಿಕ್ ಹುಡುಕಾಟ, ಅಥವಾ ಬೈನರಿ ಚಾಪ್, ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಇದು ವಿಂಗಡಿಸಲಾದ ರಚನೆಯೊಳಗೆ ಗುರಿ ಮೌಲ್ಯದ ಸ್ಥಾನವನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತದೆ. ಬೈನರಿ ಹುಡುಕಾಟವು ಗುರಿ ಮೌಲ್ಯವನ್ನು ಅರ್ರೆಯ ಮಧ್ಯದ ಅಂಶಕ್ಕೆ ಹೋಲಿಸುತ್ತದೆ. ಅವು ಸಮಾನವಾಗಿಲ್ಲದಿದ್ದರೆ, ಗುರಿಯು ಅರ್ಧದ ಅಂಶದಲ್ಲಿ ಇರಲು ಸಾಧ್ಯವಿಲ್ಲ. ಉಳಿದ ಅರ್ಧಭಾಗದಲ್ಲಿ ಹುಡುಕಾಟ ಮುಂದುವರಿಯುತ್ತದೆ, ಮತ್ತೆ ಮಧ್ಯದ ಅಂಶವನ್ನು ಗುರಿ ಮೌಲ್ಯಕ್ಕೆ ಹೋಲಿಸಲು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಗುರಿ ಮೌಲ್ಯವು ಕಂಡುಬರುವವರೆಗೆ ಇದನ್ನು ಪುನರಾವರ್ತಿಸುತ್ತದೆ. ಉಳಿದ ಅರ್ಧ ಖಾಲಿಯಾಗಿರುವುದರಿಂದ ಹುಡುಕಾಟ ಕೊನೆಗೊಂಡರೆ, ಗುರಿ ಶ್ರೇಣಿಯಲ್ಲಿಲ್ಲ.
ಬೈನರಿ ಹುಡುಕಾಟವು ಕೆಟ್ಟ ಸಂದರ್ಭದಲ್ಲಿ ಲಾಗರಿಥಮಿಕ್ ಸಮಯದಲ್ಲಿ ಚಲಿಸುತ್ತದೆ ಮತ್ತು ಹೋಲಿಕೆಗಳನ್ನು ಮಾಡುತ್ತದೆ, ಇಲ್ಲಿ ಎಂಬುದು ಶ್ರೇಣಿಯಲ್ಲಿನ ಅಂಶಗಳ ಸಂಖ್ಯೆ ಮತ್ತು ಎಂಬುದು ಲಾಗರಿಥಮ್ ಆಗಿದೆ. [೨] ಸಣ್ಣ ಸರಣಿಗಳನ್ನು ಹೊರತುಪಡಿಸಿ ಬೈನರಿ ಹುಡುಕಾಟ ರೇಖೀಯ ಹುಡುಕಾಟಕ್ಕಿಂತ ವೇಗವಾಗಿರುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಬೈನರಿ ಹುಡುಕಾಟವನ್ನು ಅನ್ವಯಿಸಲು ಶ್ರೇಣಿಯನ್ನು ಮೊದಲು ವಿಂಗಡಿಸಬೇಕು. ವೇಗದ ಹುಡುಕಾಟಕ್ಕಾಗಿ ವಿನ್ಯಾಸಗೊಳಿಸಲಾದ ವಿಶೇಷ ದತ್ತಾಂಶ ರಚನೆಗಳಿವೆ, ಉದಾಹರಣೆಗೆ ಹ್ಯಾಶ್ ಕೋಷ್ಟಕಗಳು, ಬೈನರಿ ಹುಡುಕಾಟಕ್ಕಿಂತ ಹೆಚ್ಚು ಪರಿಣಾಮಕಾರಿಯಾಗಿ ಹುಡುಕಬಹುದು. ಬೈನರಿ ಹುಡುಕಾಟವನ್ನು ವ್ಯಾಪಕ ಶ್ರೇಣಿಯ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ಬಳಸಬಹುದು.
ಬೈನರಿ ಹುಡುಕಾಟದ ಹಲವಾರು ಮಾರ್ಪಾಡುಗಳಿವೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳುವುದಾದರೆ, ಭಾಗಶಃ ಕ್ಯಾಸ್ಕೇಡಿಂಗ್ ಅನೇಕ ಸರಣಿಗಳಲ್ಲಿ ಒಂದೇ ಮೌಲ್ಯಕ್ಕಾಗಿ ಬೈನರಿ ಹುಡುಕಾಟಗಳನ್ನು ವೇಗಗೊಳಿಸುತ್ತದೆ. ಫ್ರ್ಯಾಕ್ಷನಲ್ ಕ್ಯಾಸ್ಕೇಡಿಂಗ್ ಕಂಪ್ಯೂಟೇಶನಲ್ ಜ್ಯಾಮಿತಿಯಲ್ಲಿ ಮತ್ತು ಹಲವಾರು ಇತರ ಕ್ಷೇತ್ರಗಳಲ್ಲಿನ ಹಲವಾರು ಹುಡುಕಾಟ ಸಮಸ್ಯೆಗಳನ್ನು ಸಮರ್ಥವಾಗಿ ಪರಿಹರಿಸುತ್ತದೆ. ಘಾತೀಯ ಹುಡುಕಾಟವು ಬೈನರಿ ಹುಡುಕಾಟವನ್ನು ಮಿತಿಯಿಲ್ಲದ ಪಟ್ಟಿಗಳಿಗೆ ವಿಸ್ತರಿಸುತ್ತದೆ. ಬೈನರಿ ಸರ್ಚ್ ಟ್ರೀ ಮತ್ತು ಬಿ-ಟ್ರೀ ಡೇಟಾ ರಚನೆಗಳು ಬೈನರಿ ಹುಡುಕಾಟವನ್ನು ಆಧರಿಸಿವೆ.
ಆಲಗೋರಿತಮ್
[ಬದಲಾಯಿಸಿ]ಬೈನರಿ ಹುಡುಕಾಟ ವಿಂಗಡಿಸಲಾದ ಅರ್ರೆಗಳಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ. ರಚನೆಯ ಮಧ್ಯದಲ್ಲಿರುವ ಒಂದು ಅಂಶವನ್ನು ಗುರಿ ಮೌಲ್ಯದೊಂದಿಗೆ ಹೋಲಿಸುವ ಮೂಲಕ ಬೈನರಿ ಹುಡುಕಾಟ ಪ್ರಾರಂಭವಾಗುತ್ತದೆ. ಗುರಿ ಮೌಲ್ಯವು ಅಂಶಕ್ಕೆ ಹೊಂದಿಕೆಯಾದರೆ, ರಚನೆಯಲ್ಲಿ ಅದರ ಸ್ಥಾನವನ್ನು ಹಿಂತಿರುಗಿಸಲಾಗುತ್ತದೆ. ಗುರಿ ಮೌಲ್ಯವು ಅಂಶಕ್ಕಿಂತ ಕಡಿಮೆಯಿದ್ದರೆ, ಹುಡುಕಾಟವು ರಚನೆಯ ಕೆಳಗಿನ ಅರ್ಧಭಾಗದಲ್ಲಿ ಮುಂದುವರಿಯುತ್ತದೆ. ಗುರಿ ಮೌಲ್ಯವು ಅಂಶಕ್ಕಿಂತ ಹೆಚ್ಚಿದ್ದರೆ, ರಚನೆಯ ಮೇಲಿನ ಅರ್ಧಭಾಗದಲ್ಲಿ ಹುಡುಕಾಟ ಮುಂದುವರಿಯುತ್ತದೆ. ಇದನ್ನು ಮಾಡುವುದರ ಮೂಲಕ, ಅಲ್ಗಾರಿದಮ್ ಪ್ರತಿ ಪುನರಾವರ್ತನೆಯಲ್ಲೂ ಗುರಿ ಮೌಲ್ಯವು ಸುಳ್ಳಾಗದ ಅರ್ಧವನ್ನು ತೆಗೆದುಹಾಕುತ್ತದೆ.[೩]
ಕಾರ್ಯವಿಧಾನ
[ಬದಲಾಯಿಸಿ]ಮೌಲ್ಯಗಳು ಅಥವಾ ದಾಖಲೆಗಳನ್ನು ಹೊಂದಿರುವ ಅರ್ರೆಯು ಎನ್ನುವ ದಾಖಲೆಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಇದನ್ನು ರಂತೆ ವಿಂಗಡಿಸಲಾಗುತ್ತದೆ. ಎಂಬುದು ಗುರಿ ಮೌಲ್ಯ. ಕೆಳಗೆ ಆರ್ರೆ ನಲ್ಲಿ ಗುರಿ ಮೌಲ್ಯ ಯ ಸೂಚ್ಯಂಕವನ್ನು ಕಂಡುಹಿಡಿಯುವ ವಿಧಾನವನ್ನು ತಿಳಿಸಲಾಗಿದೆ.[೩]
- ಅನ್ನು ಮತ್ತು ಅನ್ನು ಗೆ ಹೊಂದಿಸಿ.
- ಆಗಿದ್ದಲ್ಲಿ, ಹುಡುಕಾಟ ವಿಫಲವಾಗಿ ಅಲ್ಲೇ ಅಂತ್ಯಗೊಳ್ಳುತ್ತದೆ.
- (ಮಧ್ಯದ ಅಂಶದ ಸ್ಥಾನ) ಅನ್ನು ರ ಫ್ಲೋರಿಗೆ ಹೊಂದಿಸಿ. ಇದು ಕ್ಕಿಂತ ಕಡಿಮೆ ಅಥವಾ ಸಮನಾದ ದೊಡ್ಡ ಪೂರ್ಣಾಂಕವಾಗಿರುತ್ತದೆ .
- ಆಗಿದ್ದಲ್ಲಿ, ಅನ್ನು ಹೊಂದಿಸಿ ಮತ್ತು ಎರಡನೇ ಸ್ಟೆಪ್ಗೆ ಹಿಂದಿರುಗಿ.
- ಆಗಿದ್ದಲ್ಲಿ, ಅನ್ನು ಹೊಂದಿಸಿ ಮತ್ತು ಎರಡನೇ ಸ್ಟೆಪ್ಗೆ ಹಿಂದಿರುಗಿ.
- ಈಗ ಆಗಿದಲ್ಲಿ, ಹುಡುಕಾಟ ಯಶಸ್ವಿಯಾಗಿ ಮುಕ್ತಾಯವಾಗಿದೆ; ಅನ್ನು ಹಿಂಪಡೆಯಿರಿ.
ಈ ಮರುಕಳಿಸುವ ವಿಧಾನವು ಹುಡುಕಾಟ ಗಡಿಗಳು ಮತ್ತು ವೇರಿಯಬಲ್ ಗಳಾದ and ಅನ್ನು ಟ್ರ್ಯಾಕ್ ಮಾಡುತ್ತದೆ. ಸ್ಯುಡೋ ಕೋಡ್ ನಲ್ಲಿ ಈ ವಿಧಾನವನ್ನು ವ್ಯಕ್ತಪಡಿಸಬಹುದು. ವೇರಿಯಬಲ್ ನ ಹೆಸರುಗಳು ಮೇಲಿನಂತಯೇ ಇರುತ್ತವೆ. floor ಎಂಬುದು ಫ್ಲೋರ್ ಫಂಕ್ಷನ್, ಮತ್ತು unsuccessful ಎಂಬುದು ನಿರ್ದಿಷ್ಟ ಮೌಲ್ಯವನ್ನು ಬಿಂಬಿಸುತ್ತದೆ ಮತ್ತು ಹುಡುಕಾಟದ ವಿಫಲತೆಯನ್ನು ಸ್ಪಷ್ಟಪಡಿಸುತ್ತದೆ.[೩]
function binary_search(A, n, T):
L := 0
R := n − 1
while L <= R:
m := floor((L + R) / 2)
if A[m] < T:
L := m + 1
else if A[m] > T:
R := m - 1
else:
return m
return unsuccessful
ಇತಿಹಾಸ
[ಬದಲಾಯಿಸಿ]ವೇಗವಾಗಿ ಹುಡುಕಲು ಅನುಮತಿಸುವ ಐಟಂಗಳ ಪಟ್ಟಿಯನ್ನು ವಿಂಗಡಿಸುವ ಕಲ್ಪನೆಯು ಪ್ರಾಚೀನ ಕಾಲಕ್ಕೆ ಸೇರಿದೆ. ಮೊಟ್ಟಮೊದಲ ಉದಾಹರಣೆಯೆಂದರೆ ಬ್ಯಾಬಿಲೋನ್ನಿಂದ ಇನಕಿಬಿಟ್-ಅನು ಟ್ಯಾಬ್ಲೆಟ್ ಕ್ರಿ.ಪೂ. ೨೦೦ ಕ್ಕೆ ಹೋಗುತ್ತದೆ. ಟ್ಯಾಬ್ಲೆಟ್ ಸುಮಾರು ೫೦೦ ಸೆಕ್ಸಾಗೆಸಿಮಲ್ ಸಂಖ್ಯೆಗಳನ್ನು ಮತ್ತು ಅವುಗಳ ಪರಸ್ಪರಗಳನ್ನು ಲೆಕ್ಸಿಕೋಗ್ರಾಫಿಕಲ್ ಕ್ರಮದಲ್ಲಿ ವಿಂಗಡಿಸಿದ್ದರು. ಇದು ನಿರ್ದಿಷ್ಟ ಪ್ರವೇಶವನ್ನು ಹುಡುಕುವುದನ್ನು ಸುಲಭಗೊಳಿಸಿತು. ಇದರ ಜೊತೆಯಲ್ಲಿ, ಅವರ ಮೊದಲ ಅಕ್ಷರದಿಂದ ವಿಂಗಡಿಸಲಾದ ಹಲವಾರು ಹೆಸರುಗಳ ಪಟ್ಟಿಗಳನ್ನು ಏಜಿಯನ್ ದ್ವೀಪಗಳಲ್ಲಿ ಕಂಡುಹಿಡಿಯಲಾಯಿತು. ಕ್ರಿ.ಶ ೧೨೮೯ ರಲ್ಲಿ ಬಂದ ಲ್ಯಾಟಿನ್ ನಿಘಂಟು ಕ್ಯಾಥೊಲಿಕ್, ಮೊದಲ ಕೆಲವು ಅಕ್ಷರಗಳಿಗೆ ವಿರುದ್ಧವಾಗಿ ಪದಗಳನ್ನು ವರ್ಣಮಾಲೆಯಂತೆ ವಿಂಗಡಿಸುವ ನಿಯಮಗಳನ್ನು ವಿವರಿಸಿದ ಮೊದಲ ಕೃತಿ. [೪]
೧೯೪೬ ರಲ್ಲಿ, ಜಾನ್ ಮೌಚ್ಲಿ ಬೈನರಿ ಹುಡುಕಾಟದ ಬಗ್ಗೆ ಮೂರ್ ಸ್ಕೂಲ್ ಲೆಕ್ಚರ್ಸ್ನ ಭಾಗವಾಗಿ ಪ್ರಸ್ತಾಪಿಸಿದರು. ಇದು ಕಂಪ್ಯೂಟಿಂಗ್ನಲ್ಲಿ ಒಂದು ಮೂಲ ಮತ್ತು ಅಡಿಪಾಯ ಕಾಲೇಜು ಕೋರ್ಸ್. [೪] ೧೯೫೭ ರಲ್ಲಿ, ವಿಲಿಯಂ ವೆಸ್ಲಿ ಪೀಟರ್ಸನ್ ಇಂಟರ್ಪೋಲೇಷನ್ ಹುಡುಕಾಟಕ್ಕಾಗಿ ಮೊದಲ ವಿಧಾನವನ್ನು ಪ್ರಕಟಿಸಿದರು. [೪][೫] ಪ್ರತಿ ಪ್ರಕಟಿತ ಬೈನರಿ ಸರ್ಚ್ ಅಲ್ಗಾರಿದಮ್ ೧೯೬೦ ರಲ್ಲಿ ಡೆರಿಕ್ ಹೆನ್ರಿ ಲೆಹ್ಮರ್ ಬೈನರಿ ಸರ್ಚ್ ಅಲ್ಗಾರಿದಮ್ ಅನ್ನು ಪ್ರಕಟಿಸುವವರೆಗೆ ಎರಡು ದೈಮೆಂಶನ್ ಗಿಂತ ಕಡಿಮೆ ಇರುವ ಅರೇಗಳಿಗೆ ಮಾತ್ರ ಕೆಲಸ ಮಾಡುತ್ತಿತ್ತು. [೬] ೧೯೬೨ ರಲ್ಲಿ, ಹರ್ಮನ್ ಬಾಟನ್ಬ್ರಚ್ ಬೈನರಿ ಹುಡುಕಾಟದ ALGOL 60 ಅನುಷ್ಠಾನವನ್ನು ಪ್ರಸ್ತುತಪಡಿಸಿದರು. ಅದು ಸಮಾನತೆಯ ಹೋಲಿಕೆಯನ್ನು ಕೊನೆಯಲ್ಲಿ ಇರಿಸಿತು. ಸರಾಸರಿ ಪುನರಾವರ್ತನೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ಒಂದರಿಂದ ಹೆಚ್ಚಿಸಿತು. ಆದರೆ ಪ್ರತಿ ಪುನರಾವರ್ತನೆಯ ಹೋಲಿಕೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ಒಂದಕ್ಕೆ ಇಳಿಸಿತು. ಏಕರೂಪದ ಬೈನರಿ ಹುಡುಕಾಟವನ್ನು ೧೯೭೧ ರಲ್ಲಿ ಸ್ಟ್ಯಾನ್ಫೋರ್ಡ್ ವಿಶ್ವವಿದ್ಯಾಲಯದ ಎ. ಕೆ. ಚಂದ್ರ ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು. [೪] 1986 ರಲ್ಲಿ, ಬರ್ನಾರ್ಡ್ ಚೆಝೆಲ್ ಮತ್ತು ಲಿಯೊನಿಡಾಸ್ ಜೆ. ಗುಯಿಬಾಸ್ ಕಂಪ್ಯೂಟೇಶನಲ್ ಜ್ಯಾಮಿತಿಯಲ್ಲಿ ಹಲವಾರು ಹುಡುಕಾಟ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವ ವಿಧಾನವಾಗಿ ಭಾಗಶಃ ಕ್ಯಾಸ್ಕೇಡಿಂಗ್ ಅನ್ನು ಪರಿಚಯಿಸಿದರು.[೭][೮]
ಲೈಬ್ರರಿ ಸಹಾಯ
[ಬದಲಾಯಿಸಿ]ಹಲವು ಕಂಪ್ಯೂಟರ್ ಭಾಷೆಗಳು ಬೈನರಿ ಸರ್ಚ್ ಮಾಡಲು ಸಹಾಯವನ್ನು ಮಾಡುತ್ತವೆ:
- C ಪ್ರೋಗ್ರಾಮಿಂಗ್ ಭಾಷೆಯು
bsearch()ಎಂಬ ಫಂಕ್ಷನ್ ಅನ್ನು ತನ್ನ ಸ್ಟ್ಯಾಂಡರ್ಡ್ ಲೈಬ್ರರಿಯಲ್ಲಿ ಒದಗಿಸುತ್ತದೆ.[೯] - C++ ಪ್ರೋಗ್ರಾಮಿಂಗ್ ಭಾಷೆಯು
binary_search(),lower_bound(),upper_bound()ಮತ್ತುequal_range()ಗಳನ್ನು ತನ್ನ ಸ್ಟ್ಯಾಂಡರ್ಡ್ ಟೆಂಪ್ಲೆಟ್ ಲೈಬ್ರರಿಯಲ್ಲಿ ಹೊಂದಿದೆ.[೧೦] - COBOL ಬಾಷೆಯು
SEARCH ALLಎಂಬ ಪದವನ್ನು COBOL ವಿಂಗಡಿತ ಟೇಬಲ್ ಗಳಲ್ಲಿ ಬಳಿಸಲು ಅನುಮತಿಸುತ್ತದೆ.[೧೧] - Go ಭಾಷೆಯ
sortಸ್ಟ್ಯಾಂಡರ್ಡ್ ಲೈಬ್ರರಿಯಲ್ಲಿSearch,SearchInts,SearchFloat64s, ಮತ್ತುSearchStringsಎಂಬ ಕೋಡ್ಗಳು ಲಭ್ಯವಿದೆ.[೧೨] - Java ಫಂಕ್ಷನ್ ಓವರಲೋಡಿಂಗ್ ನಲ್ಲಿ
binarySearch()ಎಂಬ ಸ್ಥಿರ ಕೋಡ್ ಅನ್ನುjava.utilನಲ್ಲಿ ಹೊಂದಿರುತ್ತದೆ.[೧೩][೧೪] - ಮೈಕ್ರೋಸಾಫ್ಟ್ ನ .NET Framework 2.0 ನಲ್ಲಿ
System.Arrayಯ ವಿಧಾನದಲ್ಲಿBinarySearch<T>(T[] array, T value)ಎಂಬ ಕೋಡ್ಗಳು ಲಭ್ಯವಿದೆ.[೧೫]
ಉಲ್ಲೇಖಗಳು
[ಬದಲಾಯಿಸಿ]- ↑ Williams, Jr., Louis F. (22 ಏಪ್ರಿಲ್ 1976). A modification to the half-interval search (binary search) method. Proceedings of the 14th ACM Southeast Conference. ACM. pp. 95–101. doi:10.1145/503561.503582. Archived from the original on 12 ಮಾರ್ಚ್ 2017. Retrieved 29 ಜೂನ್ 2018.
- ↑ Flores, Ivan; Madpis, George (1 September 1971). "Average binary search length for dense ordered lists". ಕಮ್ಯುನಿಕೇಶನ್ಸ್ ಆಫ್ ಎಸಿಎಂ. 14 (9): 602–603. Bibcode:1985CACM...28...22S. doi:10.1145/362663.362752. ISSN 0001-0782.
- ↑ ೩.೦ ೩.೧ ೩.೨ Knuth 1998, §6.2.1 ("Searching an ordered table"), subsection "Algorithm B".
- ↑ ೪.೦ ೪.೧ ೪.೨ ೪.೩ Knuth 1998, §6.2.1 ("Searching an ordered table"), subsection "History and bibliography".
- ↑ Peterson, William Wesley (1957). "Addressing for random-access storage". IBM Journal of Research and Development. 1 (2): 130–146. doi:10.1147/rd.12.0130.
- ↑ Lehmer, Derrick (1960). Teaching combinatorial tricks to a computer. Proceedings of Symposia in Applied Mathematics. Vol. 10. pp. 180–181. doi:10.1090/psapm/010.
- ↑ Chazelle, Bernard; Guibas, Leonidas J. (1986). "Fractional cascading: I. A data structuring technique" (PDF). Algorithmica. 1 (1–4): 133–162. CiteSeerX 10.1.1.117.8349. doi:10.1007/BF01840440.
- ↑ Chazelle, Bernard; Guibas, Leonidas J. (1986), "Fractional cascading: II. Applications" (PDF), Algorithmica, 1 (1–4): 163–191, doi:10.1007/BF01840441
- ↑ "bsearch – binary search a sorted table". The Open Group Base Specifications (7th ed.). The Open Group. 2013. Archived from the original on 21 ಮಾರ್ಚ್ 2016. Retrieved 28 ಮಾರ್ಚ್ 2016.
- ↑ Stroustrup 2013, p. 945.
- ↑ Unisys (2012), COBOL ANSI-85 programming reference manual, vol. 1, pp. 598–601
- ↑ "Package sort". The Go Programming Language. Archived from the original on 25 ಏಪ್ರಿಲ್ 2016. Retrieved 28 ಏಪ್ರಿಲ್ 2016.
- ↑ "java.util.Arrays". Java Platform Standard Edition 8 Documentation. Oracle Corporation. Archived from the original on 29 ಏಪ್ರಿಲ್ 2016. Retrieved 1 ಮೇ 2016.
- ↑ "java.util.Collections". Java Platform Standard Edition 8 Documentation. Oracle Corporation. Archived from the original on 23 ಏಪ್ರಿಲ್ 2016. Retrieved 1 ಮೇ 2016.
- ↑ "List<T>.BinarySearch method (T)". Microsoft Developer Network. Archived from the original on 7 ಮೇ 2016. Retrieved 10 ಏಪ್ರಿಲ್ 2016.




















