ಪುಶ್‌ ಡೌನ್ ಆಟೊಮೆಟಾ

ಟೆಂಪ್ಲೇಟು:Automata theory ಕಂಪ್ಯೂಟೇಶನ್ ಥಿಯರಿಯಲ್ಲಿ, ಥಿಯರೇಟಿಕ್ ಕಂಪ್ಯೂಟರ್ ವಿಜ್ಞಾನದ ಒಂದು ಶಾಖೆ, ಪುಶ್‌ ಡೌನ್ ಆಟೊಮೆಟಾ ( ಪಿಡಿಎ ) ಎಂಬುದು ಒಂದು ರೀತಿಯ ಆಟೋಮೆಟಾ ಆಗಿದ್ದು ಅದು ಸ್ಟಾಕ್ ಅನ್ನು ಬಳಸಿಕೊಳ್ಳುತ್ತದೆ.

ಪುಶ್‌ ಡೌನ್ ಆಟೊಮೆಟಾವನ್ನು ಯಂತ್ರಗಳಿಂದ ಕಂಪ್ಯೂಟ್ ಮಾಡಬಹುದಾದ ಸಿದ್ಧಾಂತಗಳಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ. ಅವು ಫೈನೈಟ್-ಸ್ಟೇಟ್ ನ ಮೆಷಿನ್ ಗಳಿಗಿಂತ ಹೆಚ್ಚು ಸಾಮರ್ಥ್ಯ ಹೊಂದಿವೆ. ಆದರೆ ಟ್ಯೂರಿಂಗ್ ಮೆಷಿನ್ ಗಳಿಗಿಂತ ಕಡಿಮೆ ಸಾಮರ್ಥ್ಯ ಹೊಂದಿವೆ ( ಕೆಳಗೆ ನೋಡಿ). ಡಿಟರ್ಮಿನಿಸ್ಟಿಕ್ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಎಲ್ಲಾ ನಿರ್ಣಾಯಕ ಸಂದರ್ಭ-ಮುಕ್ತ ಭಾಷೆಗಳನ್ನು ಗುರುತಿಸಬಹುದು ಆದರೆ ಅನಿರ್ದಿಷ್ಟವಾದವುಗಳು ಎಲ್ಲಾ ಸಂದರ್ಭ-ಮುಕ್ತ ಭಾಷೆಗಳನ್ನು ಗುರುತಿಸಬಹುದು, ಮೊದಲನೆಯದನ್ನು ಪಾರ್ಸರ್ ವಿನ್ಯಾಸದಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ.

"ಪುಶ್‌ಡೌನ್" ಎಂಬ ಪದವು ಕೆಫೆಟೇರಿಯಾದಲ್ಲಿ ಟ್ರೇ ಡಿಸ್ಪೆನ್ಸರ್‌ನಂತೆ ಸ್ಟಾಕ್ ಅನ್ನು "ಕೆಳಗೆ ತಳ್ಳಲಾಗಿದೆ" ಎಂದು ಪರಿಗಣಿಸಬಹುದು. ಏಕೆಂದರೆ ಕಾರ್ಯಾಚರಣೆಗಳು ಉನ್ನತ ಎಲಿಮೆಂಟ್ ಅನ್ನು ಹೊರತುಪಡಿಸಿ ಇತರ ಎಲಿಮೆಂಟ್ ಗಳ ಮೇಲೆ ಎಂದಿಗೂ ಕಾರ್ಯನಿರ್ವಹಿಸುವುದಿಲ್ಲ. ಸ್ಟಾಕ್ ಆಟೊಮೆಟಾ. ಇದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ, ಆಳವಾದ ಎಲಿಮೆಂಟ್ ಗಳಿಗೆ ಪ್ರವೇಶ ಮತ್ತು ಕಾರ್ಯಾಚರಣೆಗಳನ್ನು ಅನುಮತಿಸುತ್ತದೆ. ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾಕ್ಕಿಂತ ಕಟ್ಟುನಿಟ್ಟಾಗಿ ದೊಡ್ಡದಾದ ಭಾಷೆಗಳನ್ನು ಸ್ಟಾಕ್ ಆಟೊಮೆಟಾ ಗುರುತಿಸಬಹುದು. ^[೧] ನೆಸ್ಟೆಡ್ ಸ್ಟಾಕ್ ಆಟೊಮ್ಯಾಟನ್ ಪೂರ್ಣ ಪ್ರವೇಶವನ್ನು ಅನುಮತಿಸುತ್ತದೆ, ಮತ್ತು ಸ್ಟ್ಯಾಕ್ ಮಾಡಲಾದ ಮೌಲ್ಯಗಳು ಕೇವಲ ಒಂದೇ ಸೀಮಿತ ಚಿಹ್ನೆಗಳಿಗಿಂತ ಸಂಪೂರ್ಣ ಉಪ-ಸ್ಟ್ಯಾಕ್‌ಗಳಾಗಿರಲು ಅನುಮತಿಸುತ್ತದೆ.

 <a href="./ಫಿನೈಟ್-ಸ್ಟೇಟ್_ಯಂತ್ರ" rel="mw:WikiLink" data-linkid="15" data-cx="{&quot;adapted&quot;:false,&quot;sourceTitle&quot;:{&quot;title&quot;:&quot;Finite-state machine&quot;,&quot;thumbnail&quot;:{&quot;source&quot;:&quot;https://upload.wikimedia.org/wikipedia/commons/thumb/a/a2/Automata_theory.svg/80px-Automata_theory.svg.png&quot;,&quot;width&quot;:80,&quot;height&quot;:60},&quot;description&quot;:&quot;Mathematical model of computation&quot;,&quot;pageprops&quot;:{&quot;wikibase_item&quot;:&quot;Q176452&quot;},&quot;pagelanguage&quot;:&quot;en&quot;},&quot;targetFrom&quot;:&quot;mt&quot;,&quot;targetTitle&quot;:{&quot;title&quot;:&quot;Finite-state machine&quot;,&quot;pagelanguage&quot;:&quot;kn&quot;,&quot;sourceLanguage&quot;:&quot;en&quot;,&quot;missing&quot;:true,&quot;description&quot;:&quot;This page does not exist yet&quot;}}" class="cx-link" id="mwGQ" title="ಫಿನೈಟ್-ಸ್ಟೇಟ್ ಯಂತ್ರ">ಫೈನೈಟ್-ಸ್ಟೇಟ್ ನ  ಮೆಷಿನ್</a>  ಇನ್‌ಪುಟ್ ಸಿಗ್ನಲ್ ಮತ್ತು ಪ್ರಸ್ತುತ ಸ್ಟೇಟ್ ಅನ್ನು ನೋಡುತ್ತದೆ: ಇದು ಕೆಲಸ ಮಾಡಲು ಯಾವುದೇ ಸ್ಟಾಕ್ ಅನ್ನು ಹೊಂದಿಲ್ಲ ಮತ್ತು ಆದ್ದರಿಂದ ಇನ್‌ಪುಟ್‌ನ ಹಿಂದಿನ ಮೌಲ್ಯಗಳನ್ನು ತಿಳಿಯಲು ಅಥವಾ ಅವುಗಳನ್ನು ಉಳಿಸಲು ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ. ಇದು ಇನ್ಪುಟ್ ನ ಆಧಾರದ ಮೇಲೆ ಕೇವಲ ಹೊಸ ಸ್ಟೇಟ್ ಅನ್ನು ಆಯ್ಕೆ ಮಾಡಬಹುದು. ಇನ್ಪುಟ್ ನ ಆಧಾರದ ಮೇಲೆ ಸ್ಟೇಟ್ ಬದಲಾಗುವುದನ್ನು ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಎಂದು ಕರೆಯುತ್ತಾರೆ. ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ (ಪಿಡಿಎ) ಫೈನೈಟ್-ಸ್ಟೇಟ್ ನ  ಮೆಷಿನ್  ನಿಂದ ಎರಡು ರೀತಿಯಲ್ಲಿ ಭಿನ್ನವಾಗಿದೆ:

ಯಾವ ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳಬೇಕೆಂದು ನಿರ್ಧರಿಸಲು ಇದು ಸ್ಟಾಕ್‌ನ ಮೇಲ್ಭಾಗವನ್ನು ಬಳಸಬಹುದು.
ಇದು ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಅನ್ನು ನಿರ್ವಹಿಸುವ ಭಾಗವಾಗಿ ಸ್ಟಾಕ್ ಅನ್ನು ಕುಶಲತೆಯಿಂದ ನಿರ್ವಹಿಸಬಹುದು.

ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಕೊಟ್ಟಿರುವ ಇನ್‌ಪುಟ್ ಸ್ಟ್ರಿಂಗ್ ಅನ್ನು ಎಡದಿಂದ ಬಲಕ್ಕೆ ಓದುತ್ತದೆ. ಪ್ರತಿ ಹಂತದಲ್ಲಿ, ಇನ್‌ಪುಟ್ ಚಿಹ್ನೆ, ಪ್ರಸ್ತುತ ಸ್ಟೇಟ್ ಮತ್ತು ಸ್ಟಾಕ್‌ನ ಮೇಲ್ಭಾಗದಲ್ಲಿರುವ ಚಿಹ್ನೆಯಿಂದ ಟೇಬಲ್ ಅನ್ನು ಇಂಡೆಕ್ಸ್ ಮಾಡುವ ಮೂಲಕ ಇದು ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಅನ್ನು ಆಯ್ಕೆ ಮಾಡುತ್ತದೆ. ಒಂದು ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಅನ್ನು ನಿರ್ವಹಿಸುವ ಭಾಗವಾಗಿ ಸ್ಟಾಕ್ ಅನ್ನು ಕುಶಲತೆಯಿಂದ ನಿರ್ವಹಿಸಬಹುದು. ಕುಶಲತೆಯು ನಿರ್ದಿಷ್ಟ ಚಿಹ್ನೆಯನ್ನು ಸ್ಟಾಕ್‌ನ ಮೇಲ್ಭಾಗಕ್ಕೆ ಪುಷ್ ಮಾಡುತ್ತದೆ ಅಥವಾ ಸ್ಟಾಕ್‌ನ ಮೇಲ್ಭಾಗದಲ್ಲಿರುವ ಚಿಹ್ನೆಯನ್ನು ಪಾಪ್ ಮಾಡುತ್ತದೆ. ಆಟೊಮೆಟಾ ಪರ್ಯಾಯವಾಗಿ ಸ್ಟಾಕ್ ಅನ್ನು ನಿರ್ಲಕ್ಷಿಸಬಹುದು ಮತ್ತು ಅದನ್ನು ಹಾಗೆಯೇ ಬಿಡಬಹುದು.

ಒಟ್ಟುಗೂಡಿಸಿ: ಇನ್‌ಪುಟ್ ಚಿಹ್ನೆ, ಪ್ರಸ್ತುತ ಸ್ಟೇಟ್ ಮತ್ತು ಸ್ಟಾಕ್ ಚಿಹ್ನೆಯನ್ನು ನೀಡಿದರೆ, ಆಟೊಮೆಟಾ ಮತ್ತೊಂದು ಸ್ಟೇಟ್ ಗೆ ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಆಗಬಹುದು ಮತ್ತು ಐಚ್ಛಿಕವಾಗಿ ಸ್ಟಾಕ್ ಅನ್ನು ಕುಶಲತೆಯಿಂದ (ಪುಶ್ ಅಥವಾ ಪಾಪ್) ಮಾಡಬಹುದು.

ಪ್ರತಿಯೊಂದು ಸಂದರ್ಭದಲ್ಲೂ, ಅಂತಹ ಒಂದು ಟ್ರ್ಯಾನ್ಸಿಷನ್ ನ ಕ್ರಿಯೆಯು ಸಾಧ್ಯವಾದರೆ, ಆಟೊಮೆಟಾವನ್ನು ಡಿಟರ್ಮಿನಿಸ್ಟಿಕ್ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ (DPDA) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಸಾಮಾನ್ಯವಾಗಿ, ಹಲವಾರು ಕ್ರಿಯೆಗಳು ಸಾಧ್ಯವಾದರೆ, ಆಟೊಮೆಟಾ ಅನ್ನು ಸಾಮಾನ್ಯ ಅಥವಾ ಅನಿರ್ದಿಷ್ಟ, PDA ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ನೀಡಿದ ಇನ್‌ಪುಟ್ ಸ್ಟ್ರಿಂಗ್ ಹಲವಾರು ಕಾನ್ಫಿಗರೇಶನ್ ಅನುಕ್ರಮಗಳಲ್ಲಿ ಒಂದಕ್ಕೆ ಅನಿರ್ದಿಷ್ಟವಾದ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಅನ್ನು ಚಾಲನೆ ಮಾಡಬಹುದು; ಅವುಗಳಲ್ಲಿ ಒಂದು ಸಂಪೂರ್ಣ ಇನ್‌ಪುಟ್ ಸ್ಟ್ರಿಂಗ್ ಅನ್ನು ಓದಿದ ನಂತರ ಸ್ವೀಕರಿಸುವ ಕಾನ್ಫಿಗರೇಶನ್‌ಗೆ ಕಾರಣವಾದರೆ, ಎರಡನೆಯದು ಆಟೊಮೆಟಾ ಇಂದ ಸ್ವೀಕರಿಸಲ್ಪಟ್ಟ ಭಾಷೆಗೆ ಸೇರಿದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ.

ಔಪಚಾರಿಕ ವ್ಯಾಖ್ಯಾನ[ಬದಲಾಯಿಸಿ]

ನಾವು ಪ್ರಮಾಣಿತ ಔಪಚಾರಿಕ ಭಾಷಾ ಸಂಕೇತವನ್ನು ಬಳಸುತ್ತೇವೆ: $\Gamma ^{*}$ ವರ್ಣಮಾಲೆಯ ಮೇಲೆ ಸೀಮಿತ-ಉದ್ದದ ಸ್ಟ್ರಿಂಗ್ ಗಳ ಗುಂಪನ್ನು ಸೂಚಿಸುತ್ತದೆ $\Gamma$ ಮತ್ತು $\varepsilon$ ಖಾಲಿ ಸ್ಟ್ರಿಂಗ್ ಅನ್ನು ಸೂಚಿಸುತ್ತದೆ.

PDA ಅನ್ನು ಔಪಚಾರಿಕವಾಗಿ 7-tuple ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

$M=(Q,\Sigma ,\Gamma ,\delta ,q_{0},Z,F)$ ಇದರಲ್ಲಿ

$Q$ ಸ್ಟೇಟ್ ಗಳ ಸೀಮಿತ ಗುಂಪಾಗಿದೆ
$\Sigma$ ಇನ್‌ಪುಟ್ ಆಲ್ಫಾಬೆಟ್ ಎಂದು ಕರೆಯಲ್ಪಡುವ ಸೀಮಿತ ಸೆಟ್ ಆಗಿದೆ
$\Gamma$ ಸ್ಟಾಕ್ ಆಲ್ಫಾಬೆಟ್ ಎಂದು ಕರೆಯಲ್ಪಡುವ ಒಂದು ಸೀಮಿತ ಸೆಟ್ ಆಗಿದೆ
$\delta$ ನ ಸೀಮಿತ ಉಪವಿಭಾಗವಾಗಿದೆ $Q\times (\Sigma \cup \{\varepsilon \})\times \Gamma \times Q\times \Gamma ^{*}$ , ಟ್ರ್ಯಾನ್ಸಿಷನ್ ನ ಸಂಬಂಧ
$q_{0}\in Q$ ಪ್ರಾರಂಭದ ಸ್ಟೇಟ್ ಆಗಿದೆ
$Z\in \Gamma$ ಆರಂಭಿಕ ಸ್ಟಾಕ್ ಸಂಕೇತವಾಗಿದೆ
$F\subseteq Q$ ಸ್ವೀಕರಿಸುವ ಸ್ಟೇಟ್ ಗಳ ಗುಂಪಾಗಿದೆ

ಒಂದು ಎಲಿಮೆಂಟ್ $(p,a,A,q,\alpha )\in \delta$ , $M$ ನ ಒಂದು ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಆಗಿದೆ . ಇದು ಉದ್ದೇಶಿತ ಅರ್ಥವೇನೆಂದರೆ $M$ ಎನ್ನುವ ಅಟೊಮೆಟಾದ ಸ್ಟೇಟ್ ನಲ್ಲಿ $p\in Q$ , ಇನ್ಪುಟ್ನಲ್ಲಿ $a\in \Sigma \cup \{\varepsilon \}$ ಮತ್ತು ಜೊತೆಗೆ $A\in \Gamma$ ಮೇಲ್ಭಾಗದ ಸ್ಟಾಕ್ ಚಿಹ್ನೆಯಾಗಿ, ಓದಬಹುದು $a$ , ಗೆ ಸ್ಟೇಟ್ ಅನ್ನು ಬದಲಾಯಿಸಿ $q$ , $A$ ಅನ್ನು ಪಾಪ್ ಮಾಡಿ , $\alpha \in \Gamma ^{*}$ ಅನ್ನುತಳ್ಳುವ ಮೂಲಕ ಅದನ್ನು ಬದಲಾಯಿಸುವುದು. $(\Sigma \cup \{\varepsilon \})$ PDA ಇನ್‌ಪುಟ್‌ನಿಂದ ಅಕ್ಷರವನ್ನು ಓದಬಹುದು ಅಥವಾ ಇನ್‌ಪುಟ್ ಅನ್ನು ಸ್ಪರ್ಶಿಸದೆಯೇ ಮುಂದುವರಿಸಬಹುದು ಎಂಬುದನ್ನು ಔಪಚಾರಿಕಗೊಳಿಸಲು ಟ್ರ್ಯಾನ್ಸಿಷನ್ ನ ಸಂಬಂಧದ ಘಟಕವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.^{[ಸಾಕ್ಷ್ಯಾಧಾರ ಬೇಕಾಗಿದೆ]}</link>^{[ ಉಲ್ಲೇಖದ ಅಗತ್ಯವಿದೆ ]}

ಅನೇಕ ಪಠ್ಯಗಳಲ್ಲಿ ^[೨] ^: 110ಟ್ರ್ಯಾನ್ಸಿಷನ್ ನ ಸಂಬಂಧವನ್ನು (ಸಮಾನ) ಔಪಚಾರಿಕೀಕರಣದಿಂದ ಬದಲಾಯಿಸಲಾಗುತ್ತದೆ, ಅದರಲ್ಲಿ

$\delta$ ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಫಂಕ್ಷನ್ ಆಗಿದೆ, ಇದನ್ನು $Q\times (\Sigma \cup \{\varepsilon \})\times \Gamma$ ಗಿ $Q\times \Gamma ^{*}$ ಇದರ ಜೊತೆ ಸೀಮಿತ ಉಪಸೆಟ್ ಗಳಲ್ಲಿ ಮ್ಯಾಪಿಂಗ್ ಮಾಡಲಾಗಿದೆ.

ಇಲ್ಲಿ $\delta (p,a,A)$ $p$ ಸ್ಟೇಟ್ ನಲ್ಲಿ $A$ ಚಿಹ್ನೆ ಸ್ಟಾಕ್ ಮೇಲೆ ಓದುವಾಗ $a$ ಇನ್ಪುಟ್ನಲ್ಲಿ ಸಾಧ್ಯವಿರುವ ಎಲ್ಲಾ ಫಂಕ್ಷನ್ ಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಉದಾಹರಣೆಗೆ $\delta (p,a,A)=\{(q,BA)\}$ ನಿಖರವಾಗಿ ಯಾವಾಗ $(q,BA)\in \{(q,BA)\},(q,BA)\in \delta (p,a,A),$ ಏಕೆಂದರೆ $((p,a,A),\{(q,BA)\})\in \delta$ . ಈ ವ್ಯಾಖ್ಯಾನದಲ್ಲಿ ಫೈನೈಟ್ ಅತ್ಯಗತ್ಯ ಎಂಬುದನ್ನು ಗಮನಿಸಿ.

ಲೆಕ್ಕಾಚಾರಗಳು

ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾದ ಶಬ್ದಾರ್ಥವನ್ನು ಔಪಚಾರಿಕಗೊಳಿಸಲು ಪ್ರಸ್ತುತ ಸ್ಟೇಟ್ ನ ವಿವರಣೆಯನ್ನು ಪರಿಚಯಿಸಲಾಗಿದೆ. ಯಾವುದೇ 3-ಟುಪಲ್ $(p,w,\beta )\in Q\times \Sigma ^{*}\times \Gamma ^{*}$ ಅನ್ನು $M$ ನ ತತ್ ಕ್ಷಣದ ವಿವರಣೆ ಅಥವಾ ಇನ್ಸ್ಟಾಟೇನಿಯಸ್ ಡಿಸ್ಕ್ರಿಪ್ಶನ್ (ID) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಇದು ಪ್ರಸ್ತುತ ಸ್ಥಿತಿ, ಓದದಿರುವ ಇನ್‌ಪುಟ್ ಟೇಪ್‌ನ ಭಾಗ ಮತ್ತು ಸ್ಟಾಕ್‌ನ ವಿಷಯಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ (ಮೊದಲು ಬರೆಯಲಾದ ಮೇಲಿನ ಚಿಹ್ನೆ). ಟ್ರ್ಯಾನ್ಸಿಷನ್ ನ ಸಂಬಂಧ $\delta$ ಹಂತ-ಸಂಬಂಧವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತದೆ $\vdash _{M}$ ನ $M$ ತತ್ ಕ್ಷಣದ ವಿವರಣೆಗಳ ಮೇಲೆ. ಸೂಚನೆಗಾಗಿ $(p,a,A,q,\alpha )\in \delta$ ಒಂದು ಹಂತ ಇದೆ $(p,ax,A\gamma )\vdash _{M}(q,x,\alpha \gamma )$ ಇದು, ಪ್ರತಿಯೊಂದಕ್ಕೂ $x\in \Sigma ^{*}$ ಮತ್ತು ಪ್ರತಿ $\gamma \in \Gamma ^{*}$ ಆಗಿದೆ.

ಸಾಮಾನ್ಯವಾಗಿ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾದಲ್ಲಿ ಎಂಬುದು ಅನಿರ್ದಿಷ್ಟವಾದ ಅರ್ಥವಾಗಿದ್ದು, ನೀಡಿದ ತತ್‌ಕ್ಷಣದ ವಿವರಣೆಯಲ್ಲಿ $(p,w,\beta )$ ಹಲವಾರು ಸಂಭವನೀಯ ಹಂತಗಳು ಇರಬಹುದು. ಈ ಯಾವುದೇ ಹಂತಗಳನ್ನು ಗಣನೆಯಲ್ಲಿ ಆಯ್ಕೆ ಮಾಡಬಹುದು. ಪ್ರತಿ ಹಂತದಲ್ಲೂ ಮೇಲಿನ ವ್ಯಾಖ್ಯಾನದೊಂದಿಗೆ ಯಾವಾಗಲೂ ಒಂದೇ ಚಿಹ್ನೆಯನ್ನು (ಸ್ಟಾಕ್‌ನ ಮೇಲ್ಭಾಗ) ಪಾಪ್ ಮಾಡಲಾಗುತ್ತದೆ, ಮತ್ತು ಅದನ್ನು ಅಗತ್ಯವಿರುವಷ್ಟು ಚಿಹ್ನೆಗಳೊಂದಿಗೆ ಬದಲಾಯಿಸಲಾಗುತ್ತದೆ. ಪರಿಣಾಮವಾಗಿ ಸ್ಟಾಕ್ ಖಾಲಿಯಾಗಿರುವಾಗ ಯಾವುದೇ ಹಂತವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುವುದಿಲ್ಲ.

ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾದ ಲೆಕ್ಕಾಚಾರಗಳು ಹಂತಗಳ ಅನುಕ್ರಮಗಳಾಗಿವೆ. ಲೆಕ್ಕಾಚಾರವು ಆರಂಭಿಕ ಸ್ಟೇಟ್ ನಲ್ಲಿ ಪ್ರಾರಂಭವಾಗುತ್ತದೆ $q_{0}$ ಆರಂಭಿಕ ಸ್ಟಾಕ್ ಚಿಹ್ನೆಯೊಂದಿಗೆ $Z$ ಸ್ಟಾಕ್ ಮೇಲೆ, ಮತ್ತು ಸ್ಟ್ರಿಂಗ್ $w$ ಇನ್ಪುಟ್ ಟೇಪ್ನಲ್ಲಿ, ಹೀಗೆ ಆರಂಭಿಕ ವಿವರಣೆಯೊಂದಿಗೆ $(q_{0},w,Z)$ ಕಾಣುತ್ತದೆ. ಇದನ್ನು ಸ್ವೀಕರಿಸಲು ಎರಡು ವಿಧಾನಗಳಿವೆ. ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಅಂತಿಮ ಸ್ಟೇಟ್ ಅನ್ನು ಸ್ವೀಕರಿಸುತ್ತದೆ, ಅಂದರೆ ಅದರ ಇನ್‌ಪುಟ್ ಅನ್ನು ಓದಿದ ನಂತರ ಆಟೊಮೆಟಾ ಸ್ವೀಕರಿಸುವ ಸ್ಟೇಟ್ ಅನ್ನು ತಲುಪುತ್ತದೆ (ಇನ್ $F$ ), ಅಥವಾ ಇದು ಖಾಲಿ ಸ್ಟಾಕ್ ಮೂಲಕ ಸ್ವೀಕರಿಸುತ್ತದೆ ( $\varepsilon$ ), ಅಂದರೆ ಅದರ ಇನ್ಪುಟ್ ಅನ್ನು ಓದಿದ ನಂತರ ಆಟೊಮೆಟಾ ಅದರ ಸ್ಟಾಕ್ ಅನ್ನು ಖಾಲಿ ಮಾಡುತ್ತದೆ. ಮೊದಲ ಸ್ವೀಕಾರ ಕ್ರಮವು ಆಂತರಿಕ ಮೆಮೊರಿ (ಸ್ಟೇಟ್), ಎರಡನೆಯದು ಬಾಹ್ಯ ಮೆಮೊರಿ (ಸ್ಟಾಕ್) ಅನ್ನು ಬಳಸುತ್ತದೆ.

ಔಪಚಾರಿಕವಾಗಿ ಹೀಗೆ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು

$L(M)=\{w\in \Sigma ^{*}|(q_{0},w,Z)\vdash _{M}^{*}(f,\varepsilon ,\gamma )$ ಜೊತೆಗೆ $f\in F$ ಮತ್ತು $\gamma \in \Gamma ^{*}\}$ (ಅಂತಿಮ ಸ್ಟೇಟ್)
$N(M)=\{w\in \Sigma ^{*}|(q_{0},w,Z)\vdash _{M}^{*}(q,\varepsilon ,\varepsilon )$ ಜೊತೆಗೆ $q\in Q\}$ (ಖಾಲಿ ಸ್ಟಾಕ್)

ಇಲ್ಲಿ $\vdash _{M}^{*}$ ಹಂತದ ಸಂಬಂಧದ ಪ್ರತಿಫಲಿತ ಮತ್ತು ಟ್ರಾನ್ಸಿಟಿವ್ ಮುಚ್ಚುವಿಕೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ $\vdash _{M}$ ಅಂದರೆ ಯಾವುದೇ ಸಂಖ್ಯೆಯ ಸತತ ಹಂತಗಳು (ಶೂನ್ಯ, ಒಂದು ಅಥವಾ ಹೆಚ್ಚು).

ಪ್ರತಿಯೊಂದು ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾಗೆ ಈ ಎರಡು ಭಾಷೆಗಳಿಗೆ ಯಾವುದೇ ಸಂಬಂಧವಿಲ್ಲ: ಅವು ಸಮಾನವಾಗಿರಬಹುದು ಆದರೆ ಸಾಮಾನ್ಯವಾಗಿ ಇದು ಹಾಗಿರುವುದಿಲ್ಲ. ಆಟೊಮೆಟಾದ ನಿರ್ದಿಷ್ಟತೆಯು ಸ್ವೀಕಾರದ ಉದ್ದೇಶಿತ ವಿಧಾನವನ್ನು ಸಹ ಒಳಗೊಂಡಿರಬೇಕು. ಎಲ್ಲಾ ಪುಶ್‌ಡೌನ್ ಆಟೋಮೆಟಾವನ್ನು ತೆಗೆದುಕೊಂಡರೆ ಎರಡೂ ಅಕ್ಸೆಪ್ಟಿಂಗ್ ಸ್ಟೇಟ್ ಗಳು ಒಂದೇ ಕುಟುಂಬದ ಭಾಷೆಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತವೆ.

ಪ್ರಮೇಯ. ಪ್ರತಿ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ $M$ ಗೆ ಒಬ್ಬರು ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ $M'$ ಅನ್ನು ನಿರ್ಮಿಸಬಹುದು. ಅಂದರೆ $L(M)=N(M')$ , ಮತ್ತು ಪ್ರತಿ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ $M$ ಗೆ ಪ್ರತಿಯಾಗಿ ಒಂದು ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ $M'$ ಅನ್ನು ನಿರ್ಮಿಸಬಹುದು ಅಂದರೆ $N(M)=L(M')$ .

ಉದಾಹರಣೆ[ಬದಲಾಯಿಸಿ]

ಕೆಳಗಿನವುಗಳು ಭಾಷೆಯನ್ನು ಗುರುತಿಸುವ PDA ನ ಔಪಚಾರಿಕ ವಿವರಣೆಯು ಅಕ್ಸೆಪ್ಟಿಂಗ್ ಸ್ಟೇಟ್ ಮೂಲಕ ಆಗಿದೆ $\{0^{n}1^{n}\mid n\geq 0\}$ :

ಗಾಗಿ PDA $\{0^{n}1^{n}\mid n\geq 0\}$

</br> (ಅಕ್ಸೆಪ್ಟಿಂಗ್ ಸ್ಟೇಟ್ ಯಿಂದ)

$M=(Q,\ \Sigma ,\ \Gamma ,\ \delta ,\ q_{0},\ Z,\ F)$ , ಎಂಬುದರಲ್ಲಿ

ಸ್ಟೇಟ್ ಗಳು: $Q=\{p,q,r\}$
ಇನ್ಪುಟ್ ವರ್ಣಮಾಲೆ: $\Sigma =\{0,1\}$
ಸ್ಟಾಕ್ ವರ್ಣಮಾಲೆ: $\Gamma =\{A,Z\}$
ಪ್ರಾರಂಭ ಸ್ಥಿತಿ: $q_{0}=p$
ಸ್ಟಾರ್ಟ್ ಸ್ಟಾಕ್ ಚಿಹ್ನೆ: Z
ಅಕ್ಸೆಪ್ಟಿಂಗ್ ಸ್ಟೇಟ್ ಗಳು: $F=\{r\}$

ಟ್ರ್ಯಾನ್ಸಿಶನ್ ನ ಸಂಬಂಧ $\delta$ ಕೆಳಗಿನ ಆರು ಸೂಚನೆಗಳನ್ನು ಒಳಗೊಂಡಿದೆ:

(p,0,Z,p,AZ)

,

(p,0,A,p,AA)

,

(p,\epsilon ,Z,q,Z)

,

(p,\epsilon ,A,q,A)

,

(q,1,A,q,\epsilon )

, ಮತ್ತು

(q,\epsilon ,Z,r,Z)

.

ವಿವರಣೆಗಾಗಿ, ಮೊದಲ ಎರಡು ಸೂಚನೆಗಳು p ಸ್ಟೇಟ್ ಯಾವುದೇ ಸಮಯದಲ್ಲಿ 0 ಚಿಹ್ನೆಯನ್ನು ಓದಿದಾಗ, ಒಂದು A ಸ್ಟಾಕ್‌ಗೆ ಪುಷ್ ಮಾಡಲಾಗುತ್ತದೆ ಎಂದು ಹೇಳುತ್ತದೆ. ಮತ್ತೊಂದು A ಮೇಲೆ ಚಿಹ್ನೆ A A AA ಯಿಂದ ಬದಲಾಯಿಸುವಂತೆ ಔಪಚಾರಿಕಗೊಳಿಸಲಾಗುತ್ತದೆ (ಮತ್ತು Z ನ ಮೇಲೆ A ಚಿಹ್ನೆಯನ್ನು ತಳ್ಳಲು).

ಮೂರನೇ ಮತ್ತು ನಾಲ್ಕನೇ ಸೂಚನೆಗಳು, ಯಾವುದೇ ಕ್ಷಣದಲ್ಲಿ ಆಟೊಮೆಟಾದ ಸ್ಥಿತಿ p ನಿಂದ ರಾಜ್ಯ q ಗೆ ಚಲಿಸಬಹುದು ಎಂದು ಹೇಳುತ್ತದೆ.

ಐದನೇ ಸೂಚನೆಯು ಸ್ಟೇಟ್ ನಲ್ಲಿ q ನಲ್ಲಿ ಪ್ರತಿ ಚಿಹ್ನೆ 1 ಓದಲು, ಒಂದು A ಪಾಪ್ ಮಾಡಲಾಗಿದೆ ಎಂದು ಹೇಳುತ್ತದೆ.

ಅಂತಿಮವಾಗಿ, ಆರನೇ ಸೂಚನೆಯು ಸ್ಟಾಕ್ ಒಂದೇ Z ಅನ್ನು ಒಳಗೊಂಡಿರುವಾಗ ಮಾತ್ರ ಯಂತ್ರವು ಸ್ಥಿತಿ q ನಿಂದ ಸ್ಟೇಟ್ r ಸ್ವೀಕರಿಸಲು ಚಲಿಸಬಹುದು ಎಂದು ಹೇಳುತ್ತದೆ.

PDA ಗಾಗಿ ಸಾಮಾನ್ಯವಾಗಿ ಬಳಸಲಾದ ಪ್ರಾತಿನಿಧ್ಯವಿಲ್ಲ ಎಂದು ತೋರುತ್ತಿದೆ. ಇಲ್ಲಿ ನಾವು ಸೂಚನೆಯನ್ನು ಚಿತ್ರಿಸಿದ್ದೇವೆ $(p,a,A,q,\alpha )$ p ನಿಂದ ಸ್ಟೇಟ್ q ಗೆ ಒಂದು ಎಡ್ಜ್ ನಿಂದ ಲೇಬಲ್ ಮಾಡಲಾಗಿದೆ $a;A/\alpha$ ( a ಓದಿ; A ಅನ್ನು ಬದಲಿಸಿ $\alpha$ )

ವಿವರಣೆ[ಬದಲಾಯಿಸಿ]

0011 ಗಾಗಿ ಲೆಕ್ಕಾಚಾರವನ್ನು ಸ್ವೀಕರಿಸಲಾಗುತ್ತಿದೆ

ಮೇಲಿನ PDA ವಿವಿಧ ಇನ್‌ಪುಟ್ ಸ್ಟ್ರಿಂಗ್‌ಗಳ ಮೇಲೆ ಹೇಗೆ ಲೆಕ್ಕಾಚಾರ ಮಾಡುತ್ತದೆ ಎಂಬುದನ್ನು ಕೆಳಗಿನವು ವಿವರಿಸುತ್ತದೆ. ಹೆಜ್ಜೆ ಚಿಹ್ನೆಯಿಂದ ಸಬ್‌ಸ್ಕ್ರಿಪ್ಟ್ M $\vdash$ ಇಲ್ಲಿ ಬಿಟ್ಟುಬಿಡಲಾಗಿದೆ.

Input string = 0011. There are various computations, depending on the moment the move from state p to state q is made. Only one of these is accepting.
1. $(p,0011,Z)\vdash (q,0011,Z)\vdash (r,0011,Z)$
  The final state is accepting, but the input is not accepted this way as it has not been read.
2. $(p,0011,Z)\vdash (p,011,AZ)\vdash (q,011,AZ)$
  No further steps possible.
3. $(p,0011,Z)\vdash (p,011,AZ)\vdash (p,11,AAZ)\vdash (q,11,AAZ)\vdash (q,1,AZ)\vdash (q,\epsilon ,Z)\vdash (r,\epsilon ,Z)$
  Accepting computation: ends in accepting state, while complete input has been read.
Input string = 00111. Again there are various computations. None of these is accepting.
1. $(p,00111,Z)\vdash (q,00111,Z)\vdash (r,00111,Z)$
  The final state is accepting, but the input is not accepted this way as it has not been read.
2. $(p,00111,Z)\vdash (p,0111,AZ)\vdash (q,0111,AZ)$
  No further steps possible.
3. $(p,00111,Z)\vdash (p,0111,AZ)\vdash (p,111,AAZ)\vdash (q,111,AAZ)\vdash (q,11,AZ)\vdash (q,1,Z)\vdash (r,1,Z)$
  The final state is accepting, but the input is not accepted this way as it has not been (completely) read.

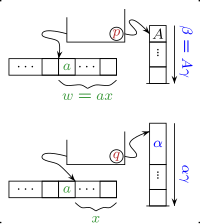
ಸಂದರ್ಭ-ಮುಕ್ತ ಭಾಷೆಗಳು[ಬದಲಾಯಿಸಿ]

ಪ್ರತಿಯೊಂದು ಸಂದರ್ಭ-ಮುಕ್ತ ವ್ಯಾಕರಣವನ್ನು ಸಮಾನ ಅನಿರ್ದಿಷ್ಟ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಆಗಿ ಪರಿವರ್ತಿಸಬಹುದು. ವ್ಯಾಕರಣದ ವ್ಯುತ್ಪನ್ನ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಎಡಭಾಗದ ರೀತಿಯಲ್ಲಿ ಅನುಕರಿಸಲಾಗಿದೆ. ವ್ಯಾಕರಣವು ನಾನ್ ಟರ್ಮಿನಲ್ ಅನ್ನು ಪುನಃ ಬರೆಯುವಾಗ, PDA ತನ್ನ ಸ್ಟಾಕ್‌ನಿಂದ ಅಗ್ರ ನಾನ್ ಟರ್ಮಿನಲ್ ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಅದನ್ನು ವ್ಯಾಕರಣ ನಿಯಮದ ಬಲಭಾಗದ ಭಾಗದಿಂದ ಬದಲಾಯಿಸುತ್ತದೆ ( ವಿಸ್ತರಿಸುವುದು ). ವ್ಯಾಕರಣವು ಟರ್ಮಿನಲ್ ಚಿಹ್ನೆಯನ್ನು ರಚಿಸಿದರೆ, PDA ಸ್ಟಾಕ್‌ನಲ್ಲಿ ( ಹೊಂದಾಣಿಕೆ ) ಮೇಲಿನ ಚಿಹ್ನೆಯಾಗಿರುವಾಗ ಇನ್‌ಪುಟ್‌ನಿಂದ ಚಿಹ್ನೆಯನ್ನು ಓದುತ್ತದೆ. ಒಂದು ಅರ್ಥದಲ್ಲಿ PDA ಯ ಸ್ಟಾಕ್ ವ್ಯಾಕರಣದ ಸಂಸ್ಕರಿಸದ ಡೇಟಾವನ್ನು ಹೊಂದಿದೆ. ಇದು ವ್ಯುತ್ಪನ್ನ ಟ್ರೀ ದ ಪ್ರೀ-ಆರ್ಡರ್ ಟ್ರ್ಯಾವರ್ಸಲ್ ಗೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.

ತಾಂತ್ರಿಕವಾಗಿ, ಸಂದರ್ಭ-ಮುಕ್ತ ವ್ಯಾಕರಣವನ್ನು ನೀಡಿದರೆ, PDA ಒಂದೇ ಸ್ಟೇಟ್ ಅನ್ನು ಹೊಂದಿದೆ, 1, ಮತ್ತು ಅದರ ಟ್ರ್ಯಾನ್ಸಿಶನ್ ಸಂಬಂಧವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ನಿರ್ಮಿಸಲಾಗಿದೆ.

$(1,\varepsilon ,A,1,\alpha )$ ಪ್ರತಿ ನಿಯಮಕ್ಕೆ $A\to \alpha$ ( ವಿಸ್ತರಿಸಲು )
$(1,a,a,1,\varepsilon )$ ಪ್ರತಿ ಟರ್ಮಿನಲ್ ಚಿಹ್ನೆಗೆ $a$ ( ಹೋಲಿಕೆಯಾದಾಗ )

PDA ಖಾಲಿ ಸ್ಟಾಕ್ ಮೂಲಕ ಸ್ವೀಕರಿಸುತ್ತದೆ. ಇದರ ಆರಂಭಿಕ ಸ್ಟಾಕ್ ಚಿಹ್ನೆಯು ವ್ಯಾಕರಣದ ಪ್ರಾರಂಭದ ಸಂಕೇತವಾಗಿದೆ.^{[ಸಾಕ್ಷ್ಯಾಧಾರ ಬೇಕಾಗಿದೆ]}</link>^{[ ಉಲ್ಲೇಖದ ಅಗತ್ಯವಿದೆ ]}

Greibach ಸಾಮಾನ್ಯ ರೂಪದಲ್ಲಿ ಸಂದರ್ಭ-ಮುಕ್ತ ವ್ಯಾಕರಣಕ್ಕಾಗಿ, ಪ್ರತಿ ವ್ಯಾಕರಣ ನಿಯಮಕ್ಕೆ (1,γ) ∈ δ(1, a, A ) ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವುದು A → aγ ಸಹ ಸಮಾನವಾದ ಅನಿರ್ದಿಷ್ಟ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಅನ್ನು ನೀಡುತ್ತದೆ. ^[೨] ^: 115

ಕೊಟ್ಟಿರುವ PDA ಗಾಗಿ ವ್ಯಾಕರಣವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಅಷ್ಟು ಸುಲಭವಲ್ಲ. PDA ಯ ಎರಡು ಸ್ಟೇಟ್ ಗಳನ್ನು ವ್ಯಾಕರಣದ ನಾನ್ ಟರ್ಮಿನಲ್ ಗಳಿಗೆ ಕೋಡ್ ಮಾಡುವುದು ಉಪಾಯವಾಗಿದೆ.

ಪ್ರಮೇಯ. ಪ್ರತಿ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ $M$ ಗೆ ಒಂದು ಸಂದರ್ಭ-ಮುಕ್ತ ವ್ಯಾಕರಣವನ್ನು ನಿರ್ಮಿಸಬಹುದು $G$ ಅಂದರೆ $N(M)=L(G)$ . ^[೨] ^: 116

ಡಿಟರ್ಮಿನಿಸ್ಟಿಕ್ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ (ಡಿಪಿಡಿಎ) ಸ್ವೀಕರಿಸಿದ ಸ್ಟ್ರಿಂಗ್ ಗಳ ಭಾಷೆಯನ್ನು ನಿರ್ಣಾಯಕ ಸಂದರ್ಭ-ಮುಕ್ತ ಭಾಷೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಎಲ್ಲಾ ಸಂದರ್ಭ-ಮುಕ್ತ ಭಾಷೆಗಳು ನಿರ್ಣಾಯಕವಲ್ಲ. [note 1] ಪರಿಣಾಮವಾಗಿ, DPDA ಯು PDA ಯ ಕಟ್ಟುನಿಟ್ಟಾಗಿ ದುರ್ಬಲ ರೂಪಾಂತರವಾಗಿದೆ. ಸಾಮಾನ್ಯ (ರೆಗ್ಯೂಲರ್) ಭಾಷೆಗಳಿಗೆ ಸಹ, ಗಾತ್ರದ ಸ್ಫೋಟದ ಸಮಸ್ಯೆ ಇದೆ: ಯಾವುದೇ ಪುನರಾವರ್ತಿತ ಕಾರ್ಯ (ರಿಕರ್ಸೀವ್ ಫಂಕ್ಷನ್) ಕ್ಕಾಗಿ $f$ ಗಾಗಿ ಮತ್ತು ನಿರಂಕುಶವಾಗಿ ದೊಡ್ಡ ಪೂರ್ಣಾಂಕಗಳಿಗೆ $n$ , ಗಾತ್ರದ PDA ಇದೆ $n$ ಕನಿಷ್ಠ $f(n)$ ಸ್ಟೇಟ್ ಗಳನ್ನು DPDA ಹೊಂದಿರುವ ಸಾಮಾನ್ಯ ಭಾಷೆಯನ್ನು ವಿವರಿಸುತ್ತದೆ . ಅನೇಕ ನಿಯಮಿತವಲ್ಲದ PDA ಗಳಿಗೆ, ಯಾವುದೇ ಸಮಾನ DPDA ಗೆ ಅನಿಯಮಿತ ಸಂಖ್ಯೆಯ ಸ್ಟೇಟ್ ಗಳ ಅಗತ್ಯವಿರುತ್ತದೆ.

ಎರಡು ಸ್ಟ್ಯಾಕ್‌ಗಳಿಗೆ ಪ್ರವೇಶವನ್ನು ಹೊಂದಿರುವ ಫೈನೈಟ್ ಅಟೊಮೆಟಾ ಹೆಚ್ಚು ಶಕ್ತಿಯುತ ಸಾಧನವಾಗಿದೆ. ಇದು ಟ್ಯೂರಿಂಗ್ ಮೆಷೀನ್ ಗೆ ಸಮಾನವಾದ ಶಕ್ತಿಯಾಗಿದೆ. ^[೨] ^: 171ಲೀನಿಯರ್ ಬೌಂಡೆಡ್ ಆಟೊಮೆಟಾ ಎನ್ನುವುದು ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾಗಿಂತ ಹೆಚ್ಚು ಶಕ್ತಿಶಾಲಿ ಆದರೆ ಟ್ಯೂರಿಂಗ್ ಮೆಷೀನ್ ಗಿಂತ ಕಡಿಮೆ ಶಕ್ತಿ ಇರುವ ಸಾಧನವಾಗಿದೆ. [note 2]

ಟ್ಯೂರಿಂಗ್ ಮಷೀನ್ ಗಳು[ಬದಲಾಯಿಸಿ]

ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಗಣಕೀಯವಾಗಿ ಎರಡು ಟೇಪ್‌ಗಳನ್ನು ಹೊಂದಿರುವ 'ನಿರ್ಬಂಧಿತ' ಟ್ಯೂರಿಂಗ್ ಮೆಷೀನ್ ಗೆ (TM) ಸಮನಾಗಿರುತ್ತದೆ. ಇದನ್ನು ಈ ಕೆಳಗಿನ ರೀತಿಯಲ್ಲಿ ನಿರ್ಬಂಧಿಸಲಾಗಿದೆ- ಮೊದಲ ಟೇಪ್‌ನಲ್ಲಿ, TM ಕೇವಲ ಇನ್‌ಪುಟ್ ಅನ್ನು ಓದಬಹುದು ಮತ್ತು ಎಡದಿಂದ ಬಲಕ್ಕೆ ಚಲಿಸಬಹುದು (ಇದು ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡಲು ಸಾಧ್ಯವಿಲ್ಲ ) ಎರಡನೇ ಟೇಪ್‌ನಲ್ಲಿ, ಇದು ಡೇಟಾವನ್ನು 'ಪುಶ್' ಮತ್ತು 'ಪಾಪ್' ಮಾತ್ರ ಮಾಡಬಹುದು. ಅಥವಾ ಸಮಾನವಾಗಿ, ಅದು ಪ್ರತಿ ಹಂತದಲ್ಲೂ ನಿರ್ವಹಿಸಬಹುದಾದ ಏಕೈಕ ಕ್ರಿಯೆಯೆಂದರೆ ಸ್ಟ್ರಿಂಗ್‌ನಲ್ಲಿ (ಪಾಪ್) ಎಡಭಾಗದಲ್ಲಿರುವ ಅಕ್ಷರವನ್ನು ಅಳಿಸುವುದು ಅಥವಾ ಎಡಕ್ಕೆ ಹೆಚ್ಚುವರಿ ಅಕ್ಷರವನ್ನು ಸೇರಿಸುವುದು ಎಂಬ ನಿರ್ಬಂಧದೊಂದಿಗೆ ಅದು ಓದಬಹುದು, ಬರೆಯಬಹುದು ಮತ್ತು ಸ್ಟ್ರಿಂಗ್‌ನಲ್ಲಿನ ಹೆಚ್ಚಿನ ಅಕ್ಷರ (ಪುಶ್) ಎಡಕ್ಕೆ ಮತ್ತು ಬಲಕ್ಕೆ ಚಲಿಸಬಹುದು. .

ಒಂದು TM ಗಿಂತ PDA ದುರ್ಬಲವಾಗಿದೆ ಎಂದರೆ 'ಪಾಪ್' ಕಾರ್ಯವಿಧಾನವು ಕೆಲವು ಡೇಟಾವನ್ನು ಅಳಿಸುತ್ತದೆ ಎಂಬ ಅಂಶಕ್ಕೆ ತರಬಹುದು. PDA ಅನ್ನು TM ನಂತೆ ಬಲವಾಗಿ ಮಾಡಲು, ನಾವು 'ಪಾಪ್' ಮೂಲಕ ಕಳೆದುಹೋದ ಡೇಟಾವನ್ನು ಎಲ್ಲೋ ಉಳಿಸಬೇಕಾಗಿದೆ. ಎರಡನೇ ಸ್ಟಾಕ್ ಅನ್ನು ಪರಿಚಯಿಸುವ ಮೂಲಕ ನಾವು ಇದನ್ನು ಸಾಧಿಸಬಹುದು. ಕೊನೆಯ ಪ್ಯಾರಾಗ್ರಾಫ್‌ನ PDA ನ TM ಮಾದರಿಯಲ್ಲಿ, ಇದು 3 ಟೇಪ್‌ಗಳನ್ನು ಹೊಂದಿರುವ TM ಗೆ ಸಮನಾಗಿರುತ್ತದೆ. ಅಲ್ಲಿ ಮೊದಲ ಟೇಪ್ ಓದಲು-ಮಾತ್ರ ಇರುವ ಇನ್‌ಪುಟ್ ಟೇಪ್ ಆಗಿದೆ ಮತ್ತು 2 ನೇ ಮತ್ತು 3 ನೇ ಟೇಪ್ 'ಪುಶ್ ಮತ್ತು ಪಾಪ್' (ಸ್ಟಾಕ್) ಟೇಪ್‌ಗಳಾಗಿವೆ. ಅಂತಹ PDA ಯಾವುದೇ TM ಅನ್ನು ಅನುಕರಿಸಲು, ನಾವು PDA ಯ ಇನ್‌ಪುಟ್ ಅನ್ನು ಮೊದಲ ಟೇಪ್‌ಗೆ ನೀಡುತ್ತೇವೆ, ಆದರೆ ಎರಡೂ ಸ್ಟಾಕ್‌ಗಳನ್ನು ಖಾಲಿ ಇಡುತ್ತೇವೆ. ಇದು ನಂತರ ಇನ್‌ಪುಟ್ ಟೇಪ್‌ನಿಂದ ಎಲ್ಲಾ ಇನ್‌ಪುಟ್ ಅನ್ನು ಮೊದಲ ಸ್ಟಾಕ್‌ಗೆ ಪುಷ್ ಮಾಡಲು ಶುರು ಮಾಡುತ್ತದೆ. ಸಂಪೂರ್ಣ ಇನ್‌ಪುಟ್ ಅನ್ನು 1 ನೇ ಸ್ಟಾಕ್‌ಗೆ ವರ್ಗಾಯಿಸಿದಾಗ, ಈಗ ನಾವು ಸಾಮಾನ್ಯ TM ನಂತೆ ಮುಂದುವರಿಯುತ್ತೇವೆ, ಅಲ್ಲಿ ಟೇಪ್‌ನಲ್ಲಿ ಬಲಕ್ಕೆ ಚಲಿಸುವುದು 1 ನೇ ಸ್ಟಾಕ್‌ನಿಂದ ಚಿಹ್ನೆಯನ್ನು ಪಾಪ್ ಮಾಡುವುದು ಮತ್ತು ಎರಡನೇ ಸ್ಟಾಕ್‌ಗೆ (ಬಹುಶಃ ನವೀಕರಿಸಿದ) ಚಿಹ್ನೆಯನ್ನು ಪುಷ್ ಮಾಡುವುದು ಮತ್ತು ಎಡಕ್ಕೆ ಚಲಿಸುವುದು 2 ನೇ ಸ್ಟಾಕ್‌ನಿಂದ ಚಿಹ್ನೆಯನ್ನು ಪಾಪ್ ಮಾಡಲು ಮತ್ತು ಮೊದಲ ಸ್ಟಾಕ್‌ಗೆ (ಬಹುಶಃ ನವೀಕರಿಸಿದ) ಚಿಹ್ನೆಯನ್ನು ಪುಷ್ ಮಾಡಲು ಅನುರೂಪವಾಗಿದೆ. ಆದ್ದರಿಂದ ನಾವು ಯಾವುದೇ TM ಅನ್ನು ಅನುಕರಿಸುವ 2 ಸ್ಟ್ಯಾಕ್‌ಗಳೊಂದಿಗೆ PDA ಅನ್ನು ಹೊಂದಿದ್ದೇವೆ.

ಸಾಮಾನ್ಯೀಕರಣ[ಬದಲಾಯಿಸಿ]

ಸಾಮಾನ್ಯೀಕರಿಸಿದ (ಜನರಲೈಸ್ಡ್) ಪುಶ್‌ ಡೌನ್ ಆಟೊಮೆಟಾ (ಜಿಪಿಡಿಎ) ಎಂಬುದು ಪಿಡಿಎ ಆಗಿದ್ದು ಅದು ಕೆಲವು ತಿಳಿದಿರುವ ಉದ್ದದ ಸಂಪೂರ್ಣ ಸ್ಟ್ರಿಂಗ್ ಅನ್ನು ಸ್ಟಾಕ್‌ಗೆ ಬರೆಯುತ್ತದೆ ಅಥವಾ ಒಂದು ಹಂತದಲ್ಲಿ ಸ್ಟಾಕ್‌ನಿಂದ ಸಂಪೂರ್ಣ ಸ್ಟ್ರಿಂಗ್ ಅನ್ನು ತೆಗೆದುಹಾಕುತ್ತದೆ.

GPDA ಅನ್ನು ಔಪಚಾರಿಕವಾಗಿ 6-tuple ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

M=(Q,\ \Sigma ,\ \Gamma ,\ \delta ,\ q_{0},\ F)

ಇದರಲ್ಲಿ $Q,\Sigma \,,\Gamma \,,q_{0}$ , ಮತ್ತು F

{\displaystyle F}

PDA ಯ ರೀತಿಯಲ್ಲಿಯೇ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.

\,\delta

:

Q\times \Sigma _{\epsilon }\times \Gamma ^{*}\longrightarrow P(Q\times \Gamma ^{*})

ಎಂಬುದು ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಫಂಕ್ಷನ್ ಆಗಿದೆ.

GPDA ಗಾಗಿ ಗಣನೆಯ ನಿಯಮಗಳು PDA ಯಂತೆಯೇ ಇರುತ್ತವೆ. ಅದನ್ನು ಹೊರತುಪಡಿಸಿ $a_{i+1}$ ' ಮತ್ತು $b_{i+1}$ ಗಳು ಈಗ ಚಿಹ್ನೆಗಳ ಬದಲಿಗೆ ಸ್ಟ್ರಿಂಗ್ ಗಳಾಗಿವೆ.

GPDA ಗಳು ಮತ್ತು PDA ಗಳು ಸಮಾನವಾಗಿರುತ್ತದೆ. ಒಂದು ಭಾಷೆ PDA ಯಿಂದ ಗುರುತಿಸಲ್ಪಟ್ಟರೆ, ಅದನ್ನು GPDA ಯಿಂದ ಗುರುತಿಸಲಾಗುತ್ತದೆ. ಅಂತೆಯೇ ಪ್ರತಿಯಾಗಿಯೂ ಈ ಮಾತು ಒಪ್ಪುತ್ತದೆ.

ಕೆಳಗಿನ ಸಿಮ್ಯುಲೇಶನ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು GPDA ಮತ್ತು PDA ಗಳ ಸಮಾನತೆಗೆ ವಿಶ್ಲೇಷಣಾತ್ಮಕ ಪುರಾವೆಯನ್ನು ರೂಪಿಸಬಹುದಾಗಿದೆ. ಇದರಿಂದ ನಮಗೆ ಹೆಚ್ಚಿನ ಮಾಹಿತಿ ಸಿಗುತ್ತದೆ.

$\delta (q_{1},w,x_{1}x_{2}\cdot x_{m})\longrightarrow (q_{2},y_{1}y_{2}...y_{n})$ ಎಂಬುದು GPDA ಯ ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಆಗಿರಲಿ.

ಅದರಲ್ಲಿ $q_{1},q_{2}\in Q,w\in \Sigma _{\epsilon },x_{1},x_{2},\ldots ,x_{m}\in \Gamma ^{*},m\geq 0,y_{1},y_{2},\ldots ,y_{n}\in \Gamma ^{*},n\geq 0$ .

PDA ಗಾಗಿ ಕೆಳಗಿನ ಟ್ರ್ಯಾನ್ಸಿಷನ್ ಗಳನ್ನು ರಚಿಸಿ:

{\begin{array}{lcl}\delta '(q_{1},w,x_{1})&\longrightarrow &(p_{1},\epsilon )\\\delta '(p_{1},\epsilon ,x_{2})&\longrightarrow &(p_{2},\epsilon )\\&\vdots &\\\delta '(p_{m-1},\epsilon ,x_{m})&\longrightarrow &(p_{m},\epsilon )\\\delta '(p_{m},\epsilon ,\epsilon )&\longrightarrow &(p_{m+1},y_{n})\\\delta '(p_{m+1},\epsilon ,\epsilon )&\longrightarrow &(p_{m+2},y_{n-1})\\&\vdots &\\\delta '(p_{m+n-1},\epsilon ,\epsilon )&\longrightarrow &(q_{2},y_{1}).\end{array}}

ಸ್ಟಾಕ್ ಆಟೋಮೆಟಾ[ಬದಲಾಯಿಸಿ]

ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾದ ಸಾಮಾನ್ಯೀಕರಣವಾಗಿ, ಗಿನ್ಸ್‌ಬರ್ಗ್, ಗ್ರೀಬಾಚ್ ಮತ್ತು ಹ್ಯಾರಿಸನ್ (1967) ಸ್ಟಾಕ್ ಆಟೋಮೆಟಾವನ್ನು ಮತ್ತಷ್ಟು ಸಂಶೋಧನೆಗೆ ಒಳ ಪಡಿಸಿದರು. ಇದು ಹೆಚ್ಚುವರಿಯಾಗಿ ಇನ್‌ಪುಟ್ ಸ್ಟ್ರಿಂಗ್‌ನಲ್ಲಿ ಎಡ ಅಥವಾ ಬಲಕ್ಕೆ ಹೆಜ್ಜೆ ಹಾಕಬಹುದು (ಜಾರುವುದನ್ನು ತಡೆಯಲು ವಿಶೇಷ ಎಂಡ್‌ಮಾರ್ಕರ್ ಚಿಹ್ನೆಗಳಿಂದ ಸುತ್ತುವರೆದಿದೆ), ಮತ್ತು ಸ್ಟೆಪ್ ಅಪ್ ಅಥವಾ ಡೌನ್ ಓದಲು-ಮಾತ್ರ ಕ್ರಮದಲ್ಲಿ ಸ್ಟ್ಯಾಕ್ ನಂತೆ ಮಾಡಿದ್ದಾರೆ. ^[೩] ^[೪] ಸ್ಟಾಕ್ ಆಟೊಮೆಟಾವನ್ನು ಎಂದಿಗೂ ಸ್ಟಾಕ್‌ನಿಂದ ಪಾಪ್ ಆಗದಿದ್ದರೆ ಅದನ್ನು ನಾನ್‌ರೇಸಿಂಗ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅನಿರ್ದಿಷ್ಟ, ಅಳಿಸದ ಸ್ಟಾಕ್ ಆಟೋಮೆಟಾದಿಂದ ಸ್ವೀಕರಿಸಲ್ಪಟ್ಟ ಭಾಷೆಗಳ ವರ್ಗವು NSPACE ( n ² ), ಇದು ಸಂದರ್ಭ-ಸೂಕ್ಷ್ಮ ಭಾಷೆಗಳ ಸೂಪರ್‌ಸೆಟ್ ಆಗಿದೆ. ^[೧] ನಿರ್ಣಾಯಕ, ಅಳಿಸದ ಸ್ಟಾಕ್ ಆಟೋಮೆಟಾದಿಂದ ಸ್ವೀಕರಿಸಲ್ಪಟ್ಟ ಭಾಷೆಗಳ ವರ್ಗವು DSPACE ( n ⋅log( n )) ಆಗಿದೆ. ^[೧]

ಪರ್ಯಾಯ ಪುಶ್‌ಡೌನ್ ಆಟೋಮೆಟಾ[ಬದಲಾಯಿಸಿ]

ಪರ್ಯಾಯ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ (ಎಪಿಡಿಎ) ಎನ್ನುವುದು ಸ್ಟೇಟ್ ಸೆಟ್‌ನೊಂದಿಗೆ ಪುಶ್‌ಡೌನ್ ಆಟೊಮೆಟಾ ಆಗಿದೆ.

$Q=Q_{\exists }\cup Q_{\forall }$ ಎಲ್ಲಿ $Q_{\exists }\cap Q_{\forall }=\emptyset$ .

ಸ್ಟೇಟ್ ಗಳಲ್ಲಿ ಸಾರ್ವತ್ರಿಕವಾಗಿ $Q_{\exists }$ ಮತ್ತು $Q_{\forall }$ ಅಸ್ತಿತ್ವವಾದದ ರೆಸ್ಪ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅಸ್ತಿತ್ವವಾದದ ಸ್ಟೇಟ್ ನಲ್ಲಿ ಎಪಿಡಿಎ ಅನಿರ್ದಿಷ್ಟವಾಗಿ ಮುಂದಿನ ಸ್ಟೇಟ್ ಅನ್ನು ಆಯ್ಕೆ ಮಾಡುತ್ತದೆ ಮತ್ತು ಫಲಿತಾಂಶದ ಲೆಕ್ಕಾಚಾರಗಳಲ್ಲಿ ಕನಿಷ್ಠ ಒಂದನ್ನು ಸ್ವೀಕರಿಸಿದರೆ ಸ್ವೀಕರಿಸುತ್ತದೆ. ಸಾರ್ವತ್ರಿಕ ಸ್ಟೇಟ್ ನಲ್ಲಿ APDA ಎಲ್ಲಾ ಮುಂದಿನ ಸ್ಟೇಟ್ ಗಳಿಗೆ ಚಲಿಸುತ್ತದೆ ಮತ್ತು ಎಲ್ಲಾ ಫಲಿತಾಂಶದ ಲೆಕ್ಕಾಚಾರಗಳು ಒಪ್ಪಿಕೊಂಡರೆ ಸ್ವೀಕರಿಸುತ್ತದೆ.

ಈ ಮಾದರಿಯನ್ನು ಚಂದ್ರ, ಕೊಜೆನ್ ಮತ್ತು ಸ್ಟಾಕ್‌ಮೇಯರ್ ಪರಿಚಯಿಸಿದರು . ^[೫] ಲ್ಯಾಡ್ನರ್, ಲಿಪ್ಟನ್ ಮತ್ತು ಸ್ಟಾಕ್‌ಮೇಯರ್ ^[೬] ಈ ಮಾದರಿಯು ಎಕ್ಸ್‌ಪಿಟೈಮ್‌ಗೆ ಸಮನಾಗಿದೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಿದರು. ಅಂದರೆ ಕೆಲವು ಎಪಿಡಿಎ ಒಂದು ಭಾಷೆಯನ್ನು ಸ್ವೀಕರಿಸಿದರೆ , ಮತ್ತು ಎಕ್ಸ್ ಪೊನೆಂನ್ಶಿಯಲ್ -ಸಮಯದ ಅಲ್ಗಾರಿದಮ್‌ನಿಂದ ಮಾತ್ರ ಅದನ್ನು ನಿರ್ಧರಿಸಬಹುದು.

Aizikowitz ಮತ್ತು Kaminski ^[೭] ಅವರು ಸಿಂಕ್ರೊನೈಸ್ಡ್ ಆಲ್ಟರ್ನೇಟಿಂಗ್ ಪುಶ್‌ಡೌನ್ ಆಟೋಮೆಟಾ (SAPDA)ವನ್ನು ಪರಿಚಯಿಸಿದರು. ಅದು ಸಂಯೋಜಕ ವ್ಯಾಕರಣಗಳಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ. ಅದೇ ರೀತಿಯಲ್ಲಿ ಅನಿರ್ದಿಷ್ಟ PDA ಸಂದರ್ಭ-ಮುಕ್ತ ವ್ಯಾಕರಣಗಳಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ.

ಸಹ ನೋಡಿ[ಬದಲಾಯಿಸಿ]

ಟಿಪ್ಪಣಿಗಳು[ಬದಲಾಯಿಸಿ]

.mw-parser-output .reflist{font-size:90%;margin-bottom:0.5em;list-style-type:decimal}.mw-parser-output .reflist .references{font-size:100%;margin-bottom:0;list-style-type:inherit}.mw-parser-output .reflist-columns-2{column-width:30em}.mw-parser-output .reflist-columns-3{column-width:25em}.mw-parser-output .reflist-columns{margin-top:0.3em}.mw-parser-output .reflist-columns ol{margin-top:0}.mw-parser-output .reflist-columns li{page-break-inside:avoid;break-inside:avoid-column}.mw-parser-output .reflist-upper-alpha{list-style-type:upper-alpha}.mw-parser-output .reflist-upper-roman{list-style-type:upper-roman}.mw-parser-output .reflist-lower-alpha{list-style-type:lower-alpha}.mw-parser-output .reflist-lower-greek{list-style-type:lower-greek}.mw-parser-output .reflist-lower-roman{list-style-type:lower-roman}

ಉಲ್ಲೇಖಗಳು[ಬದಲಾಯಿಸಿ]

↑ ^೧.೦ ^೧.೧ ^೧.೨ John E. Hopcroft; Jeffrey D. Ullman (1967). "Nonerasing Stack Automata". Journal of Computer and System Sciences. 1: 166–186. doi:10.1016/s0022-0000(67)80013-8.
↑ ^೨.೦ ^೨.೧ ^೨.೨ ^೨.೩ John E. Hopcroft and Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Reading/MA: Addison-Wesley. ISBN 0-201-02988-X.
↑ Seymour Ginsburg, Sheila A. Greibach and Michael A. Harrison (1967). "Stack Automata and Compiling". J. ACM. 14: 172–201. doi:10.1145/321371.321385.
↑ Seymour Ginsburg, Sheila A. Greibach and Michael A. Harrison (1967). "One-Way Stack Automata". J. ACM. 14: 389–418. doi:10.1145/321386.321403.
↑ Chandra, Ashok K.; Kozen, Dexter C.; Stockmeyer, Larry J. (1981). "Alternation". Journal of the ACM. 28 (1): 114–133. doi:10.1145/322234.322243. ISSN 0004-5411.
↑ Ladner, Richard E.; Lipton, Richard J.; Stockmeyer, Larry J. (1984). "Alternating Pushdown and Stack Automata". SIAM Journal on Computing. 13 (1): 135–155. doi:10.1137/0213010. ISSN 0097-5397.
↑ Aizikowitz, Tamar; Kaminski, Michael (2011). "LR(0) Conjunctive Grammars and Deterministic Synchronized Alternating Pushdown Automata". Computer Science – Theory and Applications. Lecture Notes in Computer Science. Vol. 6651. pp. 345–358. doi:10.1007/978-3-642-20712-9_27. ISBN 978-3-642-20711-2. ISSN 0302-9743.

Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Section 2.2: Pushdown Automata, pp. 101–114.
Jean-Michel Autebert, Jean Berstel, Luc Boasson, Context-Free Languages and Push-Down Automata, in: G. Rozenberg, A. Salomaa (eds.), Handbook of Formal Languages, Vol. 1, Springer-Verlag, 1997, 111–174.

ಬಾಹ್ಯ ಕೊಂಡಿಗಳು[ಬದಲಾಯಿಸಿ]

JFLAP, ಅನಿರ್ದಿಷ್ಟ ಪುಶ್‌ಡೌನ್ ಆಟೋಮ್ಯಾಟಾ ಸೇರಿದಂತೆ ಹಲವಾರು ರೀತಿಯ ಆಟೋಮ್ಯಾಟಾಗಳಿಗೆ ಸಿಮ್ಯುಲೇಟರ್
CoAn Archived 2023-04-11 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ., ಅನಿರ್ದಿಷ್ಟ ಪುಶ್‌ಡೌನ್ ಆಟೋಮ್ಯಾಟಾ (C++, ವಿಂಡೋಸ್, ಲಿನಕ್ಸ್, MacOS) ಸೇರಿದಂತೆ ಹಲವಾರು ಯಂತ್ರ ಪ್ರಕಾರಗಳಿಗೆ ಮತ್ತೊಂದು ಸಿಮ್ಯುಲೇಟರ್

[Hopcroft.Ullman.1967-1] ೧.೦ ^೧.೧ ^೧.೨ John E. Hopcroft; Jeffrey D. Ullman (1967). "Nonerasing Stack Automata". Journal of Computer and System Sciences. 1: 166–186. doi:10.1016/s0022-0000(67)80013-8.

[Hopcroft.Ullman.1979-2] ೨.೦ ^೨.೧ ^೨.೨ ^೨.೩ John E. Hopcroft and Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Reading/MA: Addison-Wesley. ISBN 0-201-02988-X.

[3] Seymour Ginsburg, Sheila A. Greibach and Michael A. Harrison (1967). "Stack Automata and Compiling". J. ACM. 14: 172–201. doi:10.1145/321371.321385.

[4] Seymour Ginsburg, Sheila A. Greibach and Michael A. Harrison (1967). "One-Way Stack Automata". J. ACM. 14: 389–418. doi:10.1145/321386.321403.

[ChandraKozen1981-5] Chandra, Ashok K.; Kozen, Dexter C.; Stockmeyer, Larry J. (1981). "Alternation". Journal of the ACM. 28 (1): 114–133. doi:10.1145/322234.322243. ISSN 0004-5411.

[LadnerLipton1984-6] Ladner, Richard E.; Lipton, Richard J.; Stockmeyer, Larry J. (1984). "Alternating Pushdown and Stack Automata". SIAM Journal on Computing. 13 (1): 135–155. doi:10.1137/0213010. ISSN 0097-5397.

[AizikowitzKaminski2011-7] Aizikowitz, Tamar; Kaminski, Michael (2011). "LR(0) Conjunctive Grammars and Deterministic Synchronized Alternating Pushdown Automata". Computer Science – Theory and Applications. Lecture Notes in Computer Science. Vol. 6651. pp. 345–358. doi:10.1007/978-3-642-20712-9_27. ISBN 978-3-642-20711-2. ISSN 0302-9743.

[೧]

[೨]

[೩]

[೪]

[೫]

[೬]

[೭]