ಟೆಂಪ್ಲೇಟು:Function

Template documentation[view] [edit] [history] [purge]

{{Function
|name =
|image =

|heading1 = 1
|parity =
|domain =
|codomain =
|period =

|heading2 = 1
|zero =
|plusinf =
|minusinf =
|max =
|min =
|vr1 =
|f1 =
|vr2 =
|f2 =
|vr3 =
|f3 =
|vr4 =
|f4 =
|vr5 =
|f5 =

|heading3 = 1
|asymptote =
|root =
|critical =
|inflection =
|fixed = 

|notes =
}}

Explanation:

Pairs VR1-f1, f1-VR2, etc. are used for labeling specific value functions. Suppose a function at the point e has a value of 2e and that this point is because of something specific. In this case you should put that as VR1 = eand f1 = 2e. For the next point is used a couple of VR2-f2, etc. If you run out of points (five currently available), ask for more.
Variables heading1, heading2, heading3 define whether some of the headlines basic properties, specific values, etc. be displayed. If you do not want a title to be displayed, simply delete the variable from the template. Set the value of the variable to 0 or anything will not prevent the display title.
Variables plusinf and minusinf indicate the value function at + ∞ and - ∞.
root is the x-intercept, critical is the critical point(s), inflection is inflection point(s)
fixed is fixed point(s)

For example, the below produces the box to the right:

Sine

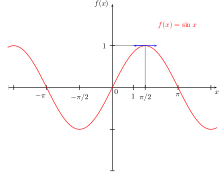Basic features
Parity	odd
Domain	(-∞,∞)
Codomain	[-1,1]
Period	2π
Specific values
At zero	0
Maxima	((2k+½)π,1)
Minima	((2k-½)π,-1)
Specific features
Root	kπ
Critical point	kπ-π/2
Inflection point	kπ
Fixed point	0
Variable k is an integer.

{{Function
|name = Sine
|image = Sinus.svg
|heading1 = 1
|parity = odd
|domain =  (-∞,∞)
|codomain = [-1,1]
|period = 2π
|heading2 = 1
|zero = 0
|plusinf =
|minusinf =
|max = ((2k+½)π,1)
|min = ((2k-½)π,-1)
|vr1 =
|f1 =
|vr2 =
|f2 =
|vr3 =
|f3 =
|vr4 =
|f4 =
|vr5 =
|f5 =
|heading3 = 1
|asymptote =
|root = kπ
|critical = kπ-π/2
|inflection = kπ
|fixed = 0
|notes =Variable k is an [[integer]].
}}

See also