ಪೇಜ್ರ್ಯಾಂಕ್
ಪೇಜ್ರ್ಯಾಂಕ್ ಎಂಬುದು ಸಂಪರ್ಕ ವಿಶ್ಲೇಷಣೆಯ ಕ್ರಮಾವಳಿ, ಲಾರ್ರಿ ಪೇಜ್ನ ನಂತರ ಹೆಸರಿಸಲಾಯಿತು.[೧] ಗೂಗಲ್ ಇಂಟರ್ ನೆಟ್ ಸರ್ಚ್ ಎಂಜಿನ್ನ ಮೂಲಕ ಉಪಯೋಗಿಸಲ್ಪಡುವ ಇದು ವರ್ಲ್ಡ್ ವೈಡ್ ವೆಬ್ನಂತಹ ಹೈಪರ್ ಲಿಂಕ್ ಇರುವ ಡಾಕ್ಯುಮೆಂಟ್ಗಳ ಗುಂಪಿನ ಪ್ರತಿ ಘಟಕಗಳಿಗೆ ಸಂಖ್ಯಾತ್ಮಕ ಅಧಿಕಾನುಕೂಲವನ್ನು ನಿಗದಿಮಾಡುತ್ತದೆ. ಗುಂಪಿನಲ್ಲಿ ಇವುಗಳ ತುಲನಾತ್ಮಕ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು "ಅಳೆಯುವುದು" ಇದರ ಉದ್ದೇಶ.[೧] ಪರಸ್ಪರ ಉಲ್ಲೇಖನಗಳು ಮತ್ತು ಪರಾಮರ್ಶೆಗಳ ಜೊತೆ ಯಾವುದೇ ಘಟಕಗಳ ಗುಂಪಿಗೆ ಕ್ರಮಾವಳಿಯನ್ನು ಅಳವಡಿಸಬಹುದು. ಇದು ಯಾವುದೇ ಕೊಟ್ಟ E ಘಟಕಕ್ಕೆ ನಿಗದಿಪಡಿಸುವ ಸಂಖ್ಯಾತ್ಮಕ ಬೆಲೆಯನ್ನು E ಯ ಪೇಜ್ರ್ಯಾಂಕ್ ಎನ್ನುವರು ಮತ್ತು PR(E) ಎಂದು ನಮೂದಿಸಲಾಗುತ್ತದೆ. "ಪೇಜ್ರ್ಯಾಂಕ್" ಹೆಸರು ಗೂಗಲ್ನ ಟ್ರೇಡ್ ಮಾರ್ಕ್ ಆಗಿದೆ, ಮತ್ತು ಪೇಜ್ರ್ಯಾಂಕ್ನ ಕಾರ್ಯನಿರ್ವಹಣೆಯನ್ನು ಪೇಟೆಂಟ್ ಮಾಡಲಾಗಿದೆ.ಯು.ಎಸ್ ಪೇಟೆಂಟ್ ೬೨,೮೫,೯೯೯ ಆದಾಗ್ಯೂ, ಪೇಟೆಂಟನ್ನು ಸ್ಟೆನ್ಫೋರ್ಡ್ ಯುನಿವರ್ಸಿಟಿಗೆ ಕೊಡಲಾಗಿತ್ತು ಮತ್ತು ಗೂಗಲ್ಗೆ ಇಲ್ಲ. ಸ್ಟೆನ್ಫೋರ್ಡ್ ಯುನಿವರ್ಸಿಟಿಯಿಂದ ಪೇಟೆಂಟ್ನ ಮೇಲೆ ಗೂಗಲ್ಗೆ ಮಾತ್ರ ಸೀಮಿತವಾದ ಒಪ್ಪಿಗೆ ಹಕ್ಕುಗಳನ್ನು ಗೂಗಲ್ ಹೊಂದಿದೆ. ಪೇಟೆಂಟ್ನ ಬಳಕೆಯ ಬದಲಾಗಿ ಯುನಿವರ್ಸಿಟಿ ಗೂಗಲ್ನ 1.8 ಮಿಲಿಯನ್ ಷೇರುಗಳನ್ನು ಪಡೆದಿದೆ; 2005ರಲ್ಲಿ ಷೇರುಗಳು $336 ಮಿಲಿಯನ್ಗೆ ಮಾರಾಟವಾಯಿತು.[೨][೩]
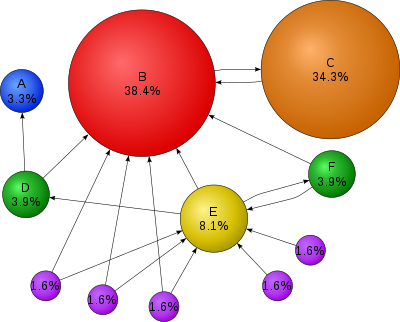
ಚಿತ್ರಣ[ಬದಲಾಯಿಸಿ]
ಗೂಗಲ್ ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ವಿವರಿಸುತ್ತದೆ:[೪]
| “ | PageRank relies on the uniquely democratic nature of the web by using its vast link structure as an indicator of an individual page's value. In essence, Google interprets a link from page A to page B as a vote, by page A, for page B. But, Google looks at more than the sheer volume of votes, or links a page receives; it also analyzes the page that casts the vote. Votes cast by pages that are themselves "important" weigh more heavily and help to make other pages "important". | ” |
ಬೇರೆ ಪದಗಳಲ್ಲಿ, ವರ್ಲ್ಡ್ ವೈಡ್ ವೆಬ್ನ ಮೇಲೆ ಪುಟದ ಪ್ರಾಮುಖ್ಯತೆಯ ಬಗ್ಗೆ ಉಳಿದ ಎಲ್ಲಾ ಪುಟಗಳ ನಡುವೆ "ಮತದಾನ"ದಿಂದ ಪೇಜ್ರ್ಯಾಂಕ್ ಪರಿಣಾಮಕಾರಿಯಾಗಿದೆ. ಪುಟದ ಹೈಪರ್ಲಿಂಕ್ ಅನ್ನು ಅನುಮೋದಿಸುವ ಮತದಂತೆ ಎಣಿಸಲಾಗುವುದು. ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಪುನರನ್ವಯ ಲಕ್ಷಣ ಹೊಂದಿದೆ ಮತ್ತು ಸಂಖ್ಯೆಯ ಆಧಾರದ ಮೇಲಿದೆ ಮತ್ತು ಎಲ್ಲಾ ಪುಟಗಳ ಪೇಜ್ರ್ಯಾಂಕ್ ಮೆಟ್ರಿಕ್ಗಳು ಇದರ ಜೊತೆ ಸಂಪರ್ಕ ಮಾಡುತ್ತವೆ.ಒಳಬರುವ ಲಿಂಕ್ಗಳು")ಬಹಳ ಪುಟಗಳಿಗೆ ಸಂಪರ್ಕ ಹೊಂದಿರುವ ಒಂದು ಪುಟ ಅಧಿಕ ಪೇಜ್ರ್ಯಾಂಕ್ ಜೊತೆ ತನಗೂ ಹೆಚ್ಚಿನ ಶ್ರೇಣಿ ಪಡೆಯುತ್ತದೆ.ವೆಬ್ ಪೇಜ್ಗೆ ಯಾವುದೇ ಲಿಂಕ್ ಇಲ್ಲದಿದ್ದರೆ ಆಗ ಆ ಪುಟಕ್ಕೆ ಯಾವುದೇ ಬೆಂಬಲವಿರುವುದಿಲ್ಲ. ಇಂಟರ್ನೆಟ್ನಲ್ಲಿ ಪ್ರತಿ ವೆಬ್ಪೇಜ್ಗೆ 0-10ರ ಸಂಖ್ಯಾತ್ಮಕ ಬೆಲೆಯನ್ನು ಗೂಗಲ್ ನಿಗದಿಪಡಿಸುತ್ತದೆ; ಈ ಪೇಜ್ರ್ಯಾಂಕ್ ಗೂಗಲ್ನ ದೃಷ್ಟಿಯಲ್ಲಿ ಸೈಟ್ನ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ತಿಳಿಸುತ್ತದೆ.ರಿಕ್ಟರ್ ಸ್ಕೇಲ್ನಂತಹ ಲಾಗಾರಿದಮಿಕ್ ಅಳತೆಯ ಮೇಲೆ ಸೈದ್ಧಾಂತಿಕ ಸಂಭವನೀಯತೆಯ ಬೆಲೆಯಿಂದ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗಿದೆ.ನಿರ್ಧಿಷ್ಟ ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಸುಮಾರಾಗಿ ಇನ್ಬೌಂಡ್ ಲಿಂಕ್ಗಳ ಪ್ರಮಾಣ ಮತ್ತು ಲಿಂಕ್ಗಳನ್ನು ಒದಗಿಸುವ ಪುಟಗಳ ಪೇಜ್ರ್ಯಾಂಕ್ಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿದೆ.ಇದನ್ನು ಇತರ ವಿಷಯಗಳು ಎನ್ನುವರು ಉದಾಹರಣೆಗೆ ಪುಟಗಳ ಮೇಲೆ ಹುಡುಕು ಶಬ್ದಗಳ ಪ್ರಸಕ್ತತೆ ಮತ್ತು ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ ಮೂಲಕ ವರದಿಯಾದ ಪುಟದ ನಿಜವಾದ ಭೇಟಿಗಳು ಸಹ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಮೇಲೆ ಪ್ರಭಾವ ಬೀರುತ್ತವೆ.[citation needed] ಬದಲಾಯಿಸುವುದು, ವಂಚಿಸುವುದು, ಮತ್ತು ಮೋಸಗಳನ್ನು ತಡೆಗಟ್ಟುವ ಸಲುವಾಗಿ ಇತರ ವಿಷಯಗಳು ಪೇಜ್ರ್ಯಾಂಕ್ನ ಮೇಲೆ ಹೇಗೆ ಪ್ರಭಾವ ಬೀರುತ್ತವೆ ಎನ್ನುವುದರ ಬಗ್ಗೆ ಗೂಗಲ್ ನಿರ್ದಿಷ್ಟವಾದ ಮಾಹಿತಿಯನ್ನು ಒದಗಿಸುವುದಿಲ್ಲ.[citation needed] ಪೇಜ್ ಮತ್ತು ಬ್ರಿನ್ನ ಮೂಲ ಪೇಪರ್ನಿಂದ ಅನೇಕ ಶೈಕ್ಷಣಿಕ ಪೇಪರ್ಗಳು ಪೇಜ್ರ್ಯಾಂಕ್ನ ಬಗ್ಗೆ ಪ್ರಕಟಗೊಳಿಸಿವೆ.[೫] ವಾಸ್ತವವಾಗಿ ಪೇಜ್ರ್ಯಾಂಕ್ ಮೆನಿಪ್ಯುಲೆಶನ್ನನ್ನು ಖಂಡಿಸುವಂತದ್ದು ಎಂದು ಸಾಬೀತುಗೊಳಿಸಿದೆ ಮತ್ತು ತಪ್ಪಾಗಿ ಬೆಲೆಯೇರಿಸಿದ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಮತ್ತು ತಪ್ಪಾಗಿ ಬೆಲೆಯೇರಿಸಿದ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಹೊಂದಿರುವ ಡಾಕ್ಯುಮೆಂಟ್ಗಳಿಂದ ಲಿಂಕ್ಗಳನ್ನು ನಿರ್ಲಕ್ಷಿಸುವ ದಾರಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದರಲ್ಲಿ ವ್ಯಾಪಕವಾದ ಶೋಧನೆ ನಡೆದಿದೆ. ವೆಬ್ಪೇಜ್ಗಳಿಗೆ ಇತರ ಲಿಂಕ್ ಆಧಾರಿತ ರ್ಯಾಂಕಿಂಗ್ ಗಣನಾಶಾಸ್ತ್ರಗಳು, ಜಾನ್ ಕ್ಲೆನ್ಬರ್ಗ್ ಅವರು (ತೆಒಮ ಮತ್ತು ಈಗ ಆಸ್ಕ್.ಕಾಮ್ ನ್ನು ಉಪಯೋಗಿಸಿ) ಸಂಶೋಧಿಸಿದ ಎಚ್ಆಯ್ಟಿಎಸ್ ಗಣನಾಶಾಸ್ತ್ರ, ಆಯ್ಬಿಎಮ್ ಕ್ಲೆವರ್ ಪ್ರಾಜೆಕ್ಟ್, ಮತ್ತು ಟ್ರಸ್ಟರ್ಯಾಂಕ್ ಗಣನಾಶಾಸ್ತ್ರಗಳನ್ನು ಒಳಗೊಂಡಿವೆ.
ಇತಿಹಾಸ[ಬದಲಾಯಿಸಿ]
ಸ್ಟನ್ಫೋರ್ಡ್ ಯುನಿವರ್ಸಿಟಿಯಲ್ಲಿ ಲಾರ್ರಿ ಪೇಜ್ (ಈಗಿನ ಹೆಸರು ಪೇಜ್ -ರ್ಯಾಂಕ್) ಮೂಲಕ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಅಭಿವೃದ್ಧಿಗೊಳಿಸಲಾಯಿತು[೬] ಮತ್ತು ನಂತರ ಸರ್ಜಿ ಬ್ರಿನ್ ಕಂಪನಿ ಹೊಸ ಬಗೆಯ ಸರ್ಚ್ ಇಂಜಿನನ್ನು ಶೋಧಿಸುವ ಯೋಜನೆಯ ಒಂದು ಭಾಗವಾಯಿತು. 1998ರಲ್ಲಿ ಪ್ರಕಟವಾದ ಪ್ರಾಜೆಕ್ಟ್ ಬಗೆಗಿನ ಮೊದಲ ಪೇಪರ್, ಪೇಜ್ರ್ಯಾಂಕ್ ಮತ್ತು ಗೂಗಲ್ ಸರ್ಚ್ ಎಂಜಿನ್ನಿನ ಮೊದಲ ಮಾದರಿಗಳನ್ನು ವಿವರಿಸುತ್ತದೆ:[೫] ಸ್ವಲ್ಪ ನಂತರ ಪೇಜ್ ಮತ್ತು ಬ್ರಿನ್ ಗೂಗಲ್ Inc. (ಗೂಗಲ್ ಸರ್ಚ್ ಎಂಜಿನ್ನಿನ ಹಿಂದಿರುವ ಕಂಪನಿ) ಅನ್ನು ಕಂಡುಹಿಡಿದವು. ಹಲವಾರು ವಿಷಯಗಳಲ್ಲಿ ಒಂದು ಗೂಗಲ್ ಶೋಧನಾ ಫಲಿತಾಂಶಗಳ ಶ್ರೇಣಿಯನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ, ಪೇಜ್ರ್ಯಾಂಕ್ ನಿರಂತರವಾಗಿ ಗೂಗಲ್ನ ಎಲ್ಲಾ ಅಂತರ್ಜಾಲ ಶೋಧನಾ ಟೂಲ್ಗಳಿಗೆ ಆಧಾರ ಒದಗಿಸಿದೆ.[೪] 1950ರ ದಶಕದಲ್ಲಿ ಪೆನ್ಸಿಲ್ವೆನಿಯ ವಿಶ್ವವಿದ್ಯಾಲಯದಲ್ಲಿ ಯುಜೆನ್ ಗಾರ್ಫೀಲ್ಡ್ ಅವರಿಂದ ಮೊದಲು ಅಭಿವೃದ್ಧಿಗೊಳಿಸಲಾದ ಸಿಟೆಶನ್ ವಿಶ್ಲೇಷಣೆ ಮತ್ತು ಪದೋ ವಿಶ್ವವಿದ್ಯಾನಿಲಯದಲ್ಲಿ ಮಸಿಮೋ ಮರ್ಚರಿ ಅವರಿಂದ ಅಭಿವೃದ್ಧಿಗೊಂಡ ಹೈಪರ್ ಶೋಧನೆಗಳಿಂದ ಪೇಜ್ರ್ಯಾಂಕ್ ಪ್ರಭಾವಿತಗೊಂಡಿದೆ (ಗೂಗಲ್ನ ಪ್ರವರ್ತಕರು ಅವರ ಮೂಲ ಪೇಪರಿನಲ್ಲಿ ಗಾರ್ಫೀಲ್ಡ್ರ ಮತ್ತು ಮರ್ಚರಿಯವರ ಕೆಲಸಗಳನ್ನು ಉದಾಹರಿಸಿದ್ದಾರೆ.[೫] ಅದೇ ವರ್ಷದಲ್ಲಿ ಪರಿಚಯಿಸಲಾಯಿತು (1998) ಜಾನ್ ಕ್ಲೆನ್ಬರ್ಗ್ ಅವರು ಎಚ್ಆಯ್ಟಿಎಸ್ನ ಮೇಲೆ ಅವರ ಮುಖ್ಯ ಕೆಲಸವನ್ನು ಪ್ರಕಟಿಸಿದರು. 2010ರಲ್ಲಿ ಹಾರ್ವರ್ಡ್ ಅರ್ಥಶಾಸ್ತ್ರಜ್ಞರ ಪೇಪರ್ ಮತ್ತು 1973ರ ನೊಬೆಲ್ ಪ್ರಶಸ್ತಿ ವಿಜೇತ ವಸ್ಸಿಲಿ ಲಿಯೊಂತಿಫ್ ಪೇಜ್ರ್ಯಾಂಕ್ನ ವಿಧಾನದ ಮೊದಲ ಬೌದ್ಧಿಕ ಮುನ್ಸೂಚಕವಾಗಿತ್ತು ಎಂದು ಅಂಗೀಕರಿಸಲಾಗಿದೆ.[೭][೮][೯]
ಗಣನಶಾಸ್ತ್ರ[ಬದಲಾಯಿಸಿ]
ಪೇಜ್ರ್ಯಾಂಕ್ ಒಂದು ಸಂಭವನೀಯತೆಯ ಹಂಚಿಕೆಯಾಗಿದ್ದು ಸಾಧ್ಯತೆಯನ್ನು ಸೂಚಿಸಲು ಉಪಯೋಗಿಸಲಾಗುತ್ತದೆ. ಇದು ಒಬ್ಬ ಮನುಷ್ಯ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಲಿಂಕ್ಗಳ ಮೇಲೆ ಕ್ಲಿಕ್ ಮಾಡಿದಾಗ ಯಾವುದೇ ನಿರ್ದಿಷ್ಟ ಪುಟದಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ.ಯಾವುದೇ ಅಳತೆಯ ಡಾಕ್ಯುಮೆಂಟ್ಗಳ ಸಂಗ್ರಹಗಳಿಗೆ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಲೆಕ್ಕಹಾಕಬಹುದು. ಗಣನೆಮಾಡುವ ಕಾರ್ಯದ ಪ್ರಾರಂಭದಲ್ಲಿ, ವಿತರಣೆಯನ್ನು ಸಂಗ್ರಹದಲ್ಲಿನ ಎಲ್ಲಾ ಡಾಕ್ಯುಮೆಂಟ್ಗಳ ಮಧ್ಯೆ ಸಮನಾಗಿ ವಿಭಾಗಿಸಲಾಗಿದೆ ಎಂದು ಕೆಲವು ಶೋಧನಾ ಪೇಪರ್ ಗಳಲ್ಲಿ ಭಾವಿಸಲಾಗಿತ್ತು.ಪೇಜ್ರ್ಯಾಂಕ್ನ ಗಣನೆಗಳಿಗೆ "ಪುನರಾವರ್ತನೆಗಳು" ಎನ್ನುವ ಕೆಲವು ಪಾಸ್ಗಳ ಅವಶ್ಯಕತೆಯಿದೆ. ಇದು ಸಂಗ್ರಹದ ಮೂಲಕ ಸಮೀಪದ ಪೇಜ್ರ್ಯಾಂಕ್ ಬೆಲೆಗಳನ್ನು ಹೆಚ್ಚು ಹತ್ತಿರದಿಂದ ಪ್ರತಿಫಲಿಸುವ ಸೈದ್ಧಾಂತಿಕ ನಿಜ ಬೆಲೆಗಳಿಗೆ ಹೊಂದಿಸುತ್ತದೆ. ಸಂಭವನೀಯತೆಯನ್ನು 0 ಮತ್ತು 1ರ ಮಧ್ಯದ ಸಂಖ್ಯಾತ್ಮಕ ಬೆಲೆಯಲ್ಲಿ ಹೇಳಲಾಗುತ್ತದೆ. 0.5 ಸಂಭವನೀಯತೆಯನ್ನು ಏನಾದರೂ ಸಂಭವಿಸುವುದರ "50% ಸಾಧ್ಯತೆ" ಎಂದು ಸಾಮಾನ್ಯವಾಗಿ ನಮೂದಿಸಲಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ, 0.5ರ ಪೇಜ್ರ್ಯಾಂಕ್ ಅಂದರೆ ಒಬ್ಬ ವ್ಯಕ್ತಿ ಯಾದೃಚ್ಛಿಕ ಲಿಂಕ್ ನ ಮೇಲೆ ಕ್ಲಿಕ್ ಮಾಡಿದಾಗ ಅದು 0.5 ಪೇಜ್ರ್ಯಾಂಕ್ ಇರುವ ಡಾಕ್ಯುಮೆಂಟ್ನ್ನು ತೋರಿಸಬಹುದಾದ ಸಾಧ್ಯತೆ 50% ಇದೆ.
ಸಂಕ್ಷಿಪ್ತಗೊಂಡ ಗಣನಾಶಾಸ್ತ್ರ[ಬದಲಾಯಿಸಿ]

ನಾಲ್ಕು ಅಂತರ್ಜಾಲ ಪುಟಗಳ ಒಂದು ಚಿಕ್ಕ ವಿಶ್ವಗಣವನ್ನು ಊಹಿಸಿ: A , B , C , ಮತ್ತು D . ಪೇಜ್ರ್ಯಾಂಕ್ನ ಅಂದಾಜಿನ ಬೆಲೆಯನ್ನು ಈ ನಾಲ್ಕು ಡಾಕ್ಯುಮೆಂಟ್ಗಳ ಮಧ್ಯ ಸಮನಾಗಿ ಹಂಚಲಾಗಿದೆ.ಈ ರೀತಿ, ಪ್ರತಿ ಡಾಕ್ಯುಮೆಂಟ್ ಅಂದಾಜಿಸಿದ 0.25ರ ಪೇಜ್ರ್ಯಾಂಕ್ನಿಂದ ಪ್ರಾರಂಭವಾಗುತ್ತದೆ. ಮೂಲ ಪೇಜ್ರ್ಯಾಂಕ್ನಲ್ಲಿ ಪ್ರಾರಂಭದ ಬೆಲೆ 1 ಆಗಿತ್ತು. ಅಂತರ್ಜಾಲದಲ್ಲಿರುವ ಪುಟಗಳ ಒಟ್ಟೂ ಸಂಖ್ಯೆ ಎಲ್ಲಾ ಪುಟಗಳ ಮೊತ್ತವಾಗಿತ್ತು ಎಂದು ಇದು ಅರ್ಥೈಸುತ್ತಿತ್ತು. 0 ಮತ್ತು 1 ರ ನಡುವಿನ ಸಂಭವನೀಯತೆಯ ಹಂಚಿಕೆಯನ್ನು ಪೇಜ್ರ್ಯಾಂಕ್ನ ನಂತರದ ಆವೃತ್ತಿಗಳು (ಕೆಳಗಿರುವ ಸೂತ್ರಗಳನ್ನು ನೋಡಿ) ಹೊಂದಿವೆ.ಇಲ್ಲಿ ಸರಳ ಸಂಭವನೀಯತೆಯ ಹಂಚಿಕೆಯನ್ನು ಉಪಯೋಗಿಸಲಾಗುವುದು- ಅಂದಿನಿಂದ ಪ್ರಾರಂಭದ ಬೆಲೆ 0.5 ಆಗಿದೆ. B , C , ಮತ್ತು D ಪುಟಗಳು A ಪುಟಕ್ಕೆ ಮಾತ್ರ ಸಂಪರ್ಕ ಹೊಂದಿದ್ದರೆ, ಅವು ಪ್ರತಿಯೊಂದು 0.25 ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಎ ಕ್ಕೆ ಕೊಡುತ್ತವೆ. ಈ ರೀತಿಯಾಗಿ ಈ ಸರಳ ಪದ್ಧತಿಯಲ್ಲಿ ಎಲ್ಲ ಪೇಜ್ರ್ಯಾಂಕ್ PR() A ಯನ್ನು ಸೇರುತ್ತವೆ ಏಕೆಂದರೆ ಎಲ್ಲಾ ಲಿಂಕ್ಗಳು A ಯನ್ನು ಸೂಚಿಸುತ್ತವೆ.
ಇದು 0.75 ಆಗಿದೆ. ಮತ್ತೊಮ್ಮೆ B ಪುಟ ಸಹ C ಪುಟಕ್ಕೆ ಸಂಪರ್ಕ ಹೊಂದಿದ್ದರೆ ಮತ್ತು D ಪುಟ ಎಲ್ಲ ಮೂರು ಪುಟಗಳಿಗೆ ಸಂಪರ್ಕ ಹೊಂದಿದೆ ಎಂದು ಊಹಿಸಿಕೊಳ್ಳಿ.ಲಿಂಕ್-ವೋಟ್ಗಳ ಬೆಲೆಯನ್ನು ಪುಟಗಳಲ್ಲಿನ ಎಲ್ಲ ಹೊರಹೋಗುವ ಲಿಂಕ್ಗಳ ನಡುವೆ ವಿಭಾಗಿಸಲಾಗಿದೆ . ಹೀಗೆ B ಪುಟ 0.125 ಬೆಲೆಯ ವೋಟ್ ಅನ್ನು A ಪುಟಕ್ಕೆ ಮತ್ತು 0.125 ಬೆಲೆಯ ವೋಟ್ ಅನ್ನು C ಪುಟಕ್ಕೆ ಕೊಡುತ್ತದೆ. D ' ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಮೂರನೇ ಒಂದು ಭಾಗವನ್ನು ಮಾತ್ರ A ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಗಣನೆಗೆ ಬರುತ್ತದೆ (ಸುಮಾರು 0.083).
ಬೇರೆ ಪದಗಳಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಡಾಕ್ಯುಮೆಂಟಿನ ಸ್ವಂತ ಪೇಜ್ರ್ಯಾಂಕ್ ಸ್ಕೋರ್ ಅನ್ನು ಹೊರಹೋಗುವ ಲಿಂಕ್ಗಳ L( ) (ನಿರ್ದಿಷ್ಟ ಯು ಆರ್ ಎಲ್ ಗಳನ್ನು ಪ್ರತಿ ಡಾಕ್ಯುಮೆಂಟಿಗೆ ಒಂದೇ ಸಲ ಎಣಿಕೆ ಮಾಡಲಾಗುವುದು) ಸಹಜ ಸಂಖ್ಯೆಯಿಂದ ಭಾಗಿಸಿದಾಗ ಅದು ಹೊರಹೋಗುತ್ತಿರುವ ಲಿಂಕ್ಗೆ ಸಮನಾಗಿರುತ್ತದೆ. ಇದರ ಮೂಲಕ ಪೇಜ್ರ್ಯಾಂಕ್ ಕೊಡಲಾಗುತ್ತದೆ.
- ಸಾಮಾನ್ಯ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಯಾವುದೇ ಪುಟಗಳಿಗೆ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಬೆಲೆಯನ್ನು u ವನ್ನು ಹೀಗೆ ನಮೂದಿಸಬಹುದು:
- ,
ಅಂದರೆ u ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಬೆಲೆ, Bu ಗಣದ( u ಪುಟಕ್ಕೆ ಸಂಪರ್ಕವಿರುವ ಎಲ್ಲಾ ಪುಟಗಳನ್ನೂ ಈ ಗಣ ಹೊಂದಿದೆ) ಹೊರಗಿನ ಎಲ್ಲ v ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಬೆಲೆಗಳನ್ನು v ಪುಟದಿಂದ ಇರುವ ಲಿಂಕ್ಗಳ ಸಂಖ್ಯೆಗಳಿಂದ L (v ) ಭಾಗಿಸುವುದರ ಮೇಲೆ ಆಧಾರವಾಗಿದೆ.
ಡ್ಯಾಂಪಿಂಗ್ ಅಂಶಗಳು[ಬದಲಾಯಿಸಿ]
ಕಾಲ್ಪನಿಕ ಅಂತರ್ಜಾಲ ಶೋಧಿಸುವವನು ಸಹ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಲಿಂಕ್ನ ಮೇಲೆ ಕ್ಲಿಕ್ ಮಾಡಿದಾಗ ಕೊನೆಯಲ್ಲಿ ಕ್ಲಿಕ್ ಮಾಡುವುದನ್ನು ನಿಲ್ಲಿಸುವ ಗುಣವನ್ನು ಪೇಜ್ರ್ಯಾಂಕ್ ಸಿದ್ಧಾಂತ ಹೊಂದಿದೆ. ಯಾವುದೇ ಹಂತದಲ್ಲಿ ಆ ವ್ಯಕ್ತಿ ಮುಂದುವರೆಯುವ ಸಂಭವನೀಯತೆಯು ಡ್ಯಾಂಪಿಂಗ್ ಅಂಶ d ಆಗಿದೆ. ವಿವಿಧ ಅಧ್ಯಯನಗಳು ವಿವಿಧ ರೀತಿಯ ಕುಗ್ಗಿಸುವ ಅಂಶಗಳನ್ನು ಪರೀಕ್ಷಿಸಿವೆ ಆದರೆ ಕುಗ್ಗಿಸುವ ಅಂಶ ಸುಮಾರು 0.85 ನಷ್ಟಿರುತ್ತದೆ ಎಂದು ಸಾಮಾನ್ಯವಾಗಿ ಭಾವಿಸಲಾಗಿದೆ.[೫] ಡ್ಯಾಂಪಿಂಗ್ ಅಂಶವನ್ನು 1ರಿಂದ ಕಳೆಯಲಾಗುತ್ತದೆ.(ಮತ್ತು ಅಲ್ಗಾರಿದಮ್ನ ಪ್ರಕಾರ ಕೆಲವು ಬದಲಾವಣೆಗಳ ಫಲಿತಾಂಶವನ್ನು ಕಡತಗಳ ಒಟ್ಟುಸಂಖ್ಯೆ (N )ನ ಒಟ್ಟೂ ಸಂಗ್ರಹದಿಂದ ಭಾಗಿಸಲಾಗುತ್ತದೆ.) ಮತ್ತು ಈ ನಿಬಂಧನೆಗಳನ್ನು ನಂತರ ಡ್ಯಾಂಪಿಂಗ್ ಫ್ಯಾಕ್ಟರ್ನ ಒಟ್ಟು ಮೊತ್ತಕ್ಕೆ ಅಲ್ಲದೆ ಕೆಲವು ಒಳಮೊತ್ತದ ಪೇಜ್ರ್ಯಾಂಕ್ ಅಂಕಕ್ಕೂ ಸೇರಿಸಲಾಗುತ್ತದೆ. ಅದು ಹೀಗಿರುತ್ತದೆ,
ಆದ್ದರಿಂದ ಬೇರೆ ಪುಟಗಳ ಪೇಜ್ರ್ಯಾಂಕ್ ಗಳ ವಿಸ್ತಾರವಾದ ಭಾಗದಲ್ಲಿ ಯಾವುದೇ ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಪಡೆಯುತ್ತದೆ. ಕುಗ್ಗಿಸುವ ಅಂಶ ಪಡೆದ ಬೆಲೆಯನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಮೂಲ ಪೇಪರ್ ಸ್ವಲ್ಪ ಬೇರೆ ರೀತಿಯ ಸೂತ್ರವನ್ನು ಕೊಟ್ಟಿದೆ, ಇದು ಸ್ವಲ್ಪ ಗೊಂದಲವನ್ನುಂಟುಮಾಡುತ್ತದೆ:
- ಇವುಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸವೇನೆಂದರೆ, ಮೊದಲ ಸೂತ್ರದಲ್ಲಿ ಪೇಜ್ರ್ಯಾಂಕ್ ಬೆಳೆಗಳ ಮೊತ್ತ ಒಂದು, ಎರಡನೇ ಸೂತ್ರದಲ್ಲಿ N ನಿಂದ ಗುಣಿಸಿದಾಗ ಪ್ರತಿ ಪೇಜ್ರ್ಯಾಂಕ್ ಸಿಗುತ್ತದೆ ಮತ್ತು ಮೊತ್ತ N ಆಗುತ್ತದೆ. ಪೇಜ್ ಎಂಡ್ ಬ್ರಿನ್ ಪೇಪರ್ನ ಹೇಳಿಕೆ ಹೀಗಿದೆ "ಎಲ್ಲಾ ಪೇಜ್ರ್ಯಾಂಕ್ಗಳ ಮೊತ್ತ ಒಂದು"[೫] ಮತ್ತು ಇದನ್ನು ಇನ್ನುಳಿದ ಗೂಗಲ್ ಕೆಲಸಗಾರರಿಂದ ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಈ ಮೇಲಿನ ಸೂತ್ರದಂತೆ ಇದಕ್ಕೆ ಒತ್ತಾಸೆ ನೀಡಬೇಕಾಗುತ್ತದೆ.[೧೦]
ಗೂಗಲ್ ಪ್ರತಿ ಸಲ ಅಂತರ್ಜಾಲದಲ್ಲಿ ಹುಡುಕಾಡಿ ಪೇಜ್ರ್ಯಾಂಕ್ ಸ್ಕೋರ್ನ್ನು ಪುನಃ ಲೆಕ್ಕಮಾದುತ್ತದೆ ಮತ್ತು ಇದರ ಸೂಚ್ಯಂಕವನ್ನು ಮತ್ತೆ ತಯಾರಿಸುತ್ತದೆ. ಗೂಗಲ್ ಇದರ ಸಂಗ್ರಹದಲ್ಲಿ ಡಾಕ್ಯುಮೆಂಟ್ ಗಳ ಸಂಖ್ಯೆಯನ್ನು ಹೆಚ್ಚಿಸಿದೆ, ಮತ್ತು ಪೇಜ್ರ್ಯಾಂಕ್ನ ಪ್ರಾರಂಭದ ಅಂದಾಜನ್ನು ಎಲ್ಲಾ ಡಾಕ್ಯುಮೆಂಟ್ಗಳಿಗೆ ಕಡಿಮೆ ಮಾಡಿದೆ. ಸೂತ್ರವು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಅಂತರ್ಜಾಲ ಶೋಧಿಸುವವ ನ ಮಾದರಿಯನ್ನು ಉಪಯೋಗಿಸುತ್ತದೆ, ಇವನು ಬಹಳ ಸಲ ಕ್ಲಿಕ್ ಮಾಡಿದ ನಂತರ ಬೇಸರವಾಗಿ ಯಾದೃಚ್ಛಿಕ ಪುಟಕ್ಕೆ ಬದಲಿಸುತ್ತಾನೆ. ಯಾದೃಚ್ಛಿಕವಾಗಿ ಅಂತರ್ಜಾಲ ಶೋಧಿಸುವವನು ಲಿಂಕ್ ಮೇಲೆ ಕ್ಲಿಕ್ ಮಾಡುವುದರ ಮೂಲಕ ಅದೇ ಪುಟದಲ್ಲಿ ನಿಲ್ಲುವ ಸಾಧ್ಯತೆಯನ್ನು ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಬೆಲೆ ಪ್ರತಿಫಲಿಸುತ್ತದೆ. ಇದನ್ನು ಮಾರ್ಕೊವ್ ಚೈನ್ ರೂಪದಲ್ಲಿ ತಿಳಿಯಬಹುದು ಇದರಲ್ಲಿ ಸ್ಟೇಟ್ಸ್ ಪುಟಗಳಾಗಿವೆ, ಮತ್ತು ಟ್ರಾನ್ಸಿಶನ್ಗಳು ಸಮನಾದ ಸಂಭವನೀಯತೆ ಹೊಂದಿವೆ ಮತ್ತು ಪುಟಗಳ ಮಧ್ಯ ಸಂಪರ್ಕ ಕಲ್ಪಿಸುತ್ತವೆ. ಒಂದು ಪುಟದಿಂದ ಇನ್ನೊಂದು ಪುಟಕ್ಕೆ ಸಂಪರ್ಕ ಇಲ್ಲದಿದ್ದರೆ, ಇವು ಕುಗ್ಗಿ ಹೋಗುತ್ತವೆ ಇದರಿಂದ ಯಾದೃಚ್ಛಿಕ ಅಂತರ್ಜಾಲ ಶೋಧನಾ ಕಾರ್ಯವನ್ನು ಮುಕ್ತಾಯವಾಗುತ್ತದೆ. ಆದರೂ, ಪರಿಹಾರ ಸ್ವಲ್ಪ ಸರಳವಾಗಿದೆ.ಯಾದೃಚ್ಛಿಕ ಶೋಧಕ ಸಿಂಕ್ ಪುಟಕ್ಕೆ ಬಂದಾಗ, ಇದು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಬೇರೆ URL ನ್ನು ಆರಿಸುತ್ತದೆ ಮತ್ತು ಮತ್ತೆ ಶೋಧನಾ ಕೆಲಸವನ್ನು ಮುಂದುವರೆಸುತ್ತದೆ.ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಲೆಕ್ಕಮಾಡುವಾಗ, ಹೊರಹೋಗುವ ಲಿಂಕ್ಗಳು ಇಲ್ಲದೆ ಇರುವ ಪುಟಗಳನ್ನು ಸಂಗ್ರಹದಲ್ಲಿರುವ ಉಳಿದ ಎಲ್ಲ ಪುಟಗಳಿಗೆ ಸಂಪರ್ಕವಿಲ್ಲದ ಪುಟಗಳು ಎಂದು ಭಾವಿಸಲಾಗಿದೆ. ಆದ್ದರಂದ ಅವುಗಳ ಪೇಜ್ರ್ಯಾಂಕ್ ಸ್ಕೋರ್ಗಳನ್ನು ಉಳಿದ ಎಲ್ಲಾ ಪುಟಗಳ ನಡುವೆ ಸಮನಾಗಿ ವಿಭಾಗಿಸಲಾಗಿದೆ. ಇನ್ನುಳಿದಂತೆ, ಉಳಿದ ಪುಟಗಳು ಕಳೆದುಹೋಗದಂತೆ ಕಾಪಾಡಿಕೊಳ್ಳಬೇಕಾಗುತ್ತದೆ. ಈ ಯಾದೃಚ್ಚಿಕ ಪರಿವರ್ತನೆಯನ್ನು ವೆಬ್ನಲ್ಲಿಯ ಎಲ್ಲ ನೋಡ್ಗಳಿಗೆ ಸೇರಿಸಲಾಗಿರುತ್ತದೆ. ಅದರಲ್ಲೂ ಹೆಚ್ಚಾಗಿ d = 0.85 ರೀತಿಯ ಬ್ರೌಸರ್ ಬಳಸುವವರಿಗೆ ಬುಕ್ ಮಾರ್ಕ್ ಸೌಲಭ್ಯವನ್ನು ನೀಡಲಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ ಸಮೀಕರಣ ಕೆಳಗಿನಂತಿದೆ:
ಇಲ್ಲಿ ಇವು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವ ಪುಟಗಳು, ಇದು ಗೆ ಸಂಪರ್ಕ ಕಲ್ಪಿಸುವ ಪುಟಗಳ ಗುಂಪು, ಇದು ಪುಟದಲ್ಲಿರುವ ಹೊರಹೋಗುವ ಲಿಂಕ್ಗಳ ಸಂಖ್ಯೆ, ಮತ್ತು N ಇದು ಒಟ್ಟು ಪುಟಗಳ ಸಂಖ್ಯೆ. ಪೇಜ್ರ್ಯಾಂಕ್ ಮೌಲ್ಯಗಳು ಮುಖ್ಯ ಐಜೆನ್ವೆಕ್ಟರ್ನ ಬದಲಾದ ದಶಮಾಂಶ ಪದ್ದತಿಯಲ್ಲಿರುತ್ತವೆ. ಇದು ಪೇಜ್ರ್ಯಾಂಕ್ನ ಮುಖ್ಯ ದಶಮಾನ ಪದ್ದತಿಯಂತೆ ಇರುತ್ತದೆ: ಇದರ ಪ್ರಕಾರ ಐಜೆನ್ವೆಕ್ಟರ್
ಇಲ್ಲಿ R ಸಮೀಕರಣದ ಪರಿಹಾರ.
ಪ್ರತಿಯೊಂದು i ಗೆ ಪುಟ, ಪುಟ ಕ್ಕೆ ಸಂಬಂಧ ಹೊಂದಿಲ್ಲದಿದ್ದರೆ ಸಾಮಾನ್ಯೀಕರಣಗೊಂಡ ಹೊಂದಾಣಿಕೆಯ ಕಾರ್ಯವು ೦ ಆಗಿರುತ್ತದೆ.
- ,
ಅಂದರೆ ಪ್ರತಿ ಕಾಲಮ್ನ ಒಟ್ಟು ಮೊತ್ತವು 1 ಆಗಿರುತ್ತದೆ. (ಹೆಚ್ಚಿನ ಮಾಹಿತಿಗಾಗಿ ಕೆಳಗಿನ ಕಂಪ್ಯೂಟೇಷನ್ ಭಾಗವನ್ನು ನೋಡಿ.) ಇದು ಹೆಚ್ವಾಗಿ ನೆಟ್ವರ್ಕ್ ಅನಾಲಿಸಿಸ್ನಲ್ಲಿ ಬಳಸಲಾಗುವ ಎಲಿಜೆನ್ವೆಕ್ಟರ್ ಸೆಂಟ್ರಾಲಿಟಿಯಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ. ಮೇಲೆ ತಿಳಿಸಿದ ಬದಲಾವಣೆ ಮಾಡಲಾದ ಹೊಂದಾಣಿಕೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನಲ್ಲಿಯ ದೊಡ್ಡ ಐಜೆನ್ಗ್ಯಾಪ್ನಿಂದಾಗಿ ಇದು ಆಗಿರುತ್ತದೆ. [೧೧] ಪೇಜ್ರ್ಯಾಂಕ್ ಐಜೆನ್ವೆಕ್ಟರ್ನ ಮೌಲ್ಯಗಳು ವೇಗಕ್ಕೆ ಹತ್ತಿರವಾಗಿರುತ್ತವೆ (ಕೇವಲ ಕೆಲವೇ ಪುನರಾವರ್ತನೆಗಳು ಅಗತ್ಯ) ಮಾರ್ಕೊವ್ ಸಿದ್ಧಾಂತದ ಪ್ರಕಾರ ಒಂದು ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಬಹಳ ಸಲ ಕ್ಲಿಕ್ ಮಾಡಿದ ನಂತರ ಅದೇ ಪುಟದಲ್ಲಿ ಉಳಿಯುವ ಸಂಭವನೀಯತೆಯಾಗಿದೆ. ಕ್ಕೆ ಸಮನಾಗಿ ಇದು ಸಂಭವಿಸುತ್ತದೆ ಅಲ್ಲಿ ಇದು ಪುಟದಿಂದ ಅದಕ್ಕೇ ವಾಪಸ್ ಪಡೆಯಲು ಬೇಕಾಗುವ ಕ್ಲಿಕ್ಗಳ ನಿರೀಕ್ಷೆಯ ಸಂಖ್ಯೆ.ಹಳೆಯ ಪುಟಗಳಿಗೆ ಪ್ರಾಮುಖ್ಯತೆ ಕೊಡುವುದು ಇದರ ಮುಖ್ಯವಾದ ಕೊರತೆ. ಏಕೆಂದರೆ ಹೊಸ ಪುಟ ಬಹಳ ಉತ್ತಮವಾಗಿದ್ದರೂ, ಅಸ್ತಿತ್ವದಲ್ಲಿರುವ ಸೈಟ್ನ ಭಾಗವಾಗಿಲ್ಲದಿದ್ದರೆ (ಒಂದು ಸೈಟ್ ವಿಕಿಪಿಡಿಯಾದಂತಹ ಪುಟಗಳ ಗುಂಪಿಗೆ ಸಂಪರ್ಕದಲ್ಲಿರುತ್ತದೆ) ಇದು ಬಹಳ ಲಿಂಕ್ಗಳನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ. ಗೂಗಲ್ ಡೈರೆಕ್ಟರಿ (ಇದು ಓಪನ್ ಡೈರೆಕ್ಟರಿ ಪ್ರೊಜೆಕ್ಟ್ನಿಂದ ತಾನೇ ಪಡೆದ) ಗುಂಪುಗಳಲ್ಲಿ ಪೇಜ್ರ್ಯಾಂಕ್ ವಿಂಗಡಿಸಿದ ಫಲಿತಾಂಶಗಳನ್ನು ಬಳಸುವವರು ನೋಡಲು ಅವಕಾಶ ಮಾಡಿಕೊಡುತ್ತದೆ. ಗೂಗಲ್ ನಿಘಂಟನ್ನು ಗೂಗಲ್ನವರು ಮಾತ್ರ ಒದಗಿಸುತ್ತಾರೆ. ಇಲ್ಲಿ ಪೇಜ್ರ್ಯಾಂಕ್ ನೇರವಾಗಿ ತೋರಿಸುವ ಕ್ರಮವನ್ನು (ಡಿಸ್ಪ್ಲೇ ಆರ್ಡರ್) ನಿರ್ಧರಿಸುತ್ತದೆ.[ಸೂಕ್ತ ಉಲ್ಲೇಖನ ಬೇಕು] ಗೂಗಲ್ನವರ ಬೇರೆ ಶೋಧನಾ ಸೇವೆಗಳಲ್ಲಿ (ಇದರ ಪ್ರಾಥಮಿಕ ಅಂತರ್ಜಾಲ ಶೋಧನೆಯಂತಹ) ಶೋಧನಾ ಫಲಿತಾಂಶಗಳಲ್ಲಿ ತೋರಿಸಿದ ಪುಟಗಳ ಸ್ಕೋರ್ಗಳನ್ನು ಅಳೆಯಲು ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ಉಪಯೋಗಿಸಲಾಗುತ್ತದೆ. ಪೇಜ್ರ್ಯಾಂಕ್ನ ಗಣನೆಯನ್ನು ತ್ವರಿತಗೊಳಿಸಲು ಕೆಲವು ಯೋಜನೆಗಳನ್ನು ಸೂಚಿಸಲಾಗಿದೆ.[೧೨] ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ಮೆನಿಪ್ಯುಲೆಟ್ ಮಾಡುವ ವಿವಿಧ ಯೋಜನೆಗಳು ಶೋಧನಾ ಫಲಿತಾಂಶಗಳ ಶ್ರೇಣಿಗಳನ್ನು ಸುಧಾರಿಸಲು ಮತ್ತು ಜಾಹಿರಾತಿನ ಲಿಂಕ್ಗಳನ್ನು ಕಾನೂನುಬದ್ಧ ಮಾಡುವ ಸಂಘಟಿತ ಪ್ರಯತ್ನದಲ್ಲಿ ಕೆಲಸಮಾಡುತ್ತಿವೆ.ಈ ಯೋಜನೆಗಳು ಬಹಳ ಸಲ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಅರ್ಹತೆಯ ವಿಷಯದಲ್ಲಿ ಮಹತ್ತರ ಪ್ರಭಾವ ಬೀರಿದೆ, ಇದು ಯಾವ ಡಾಕ್ಯುಮೆಂಟ್ಗಳು ಅಂತರ್ಜಾಲ ಸಮುದಾಯದ ದೃಷ್ಟಿಯಿಂದ ಹೆಚ್ಚು ಮುಖ್ಯವಾದದ್ದು ಎಂದು ನಿರ್ಧರಿಸಲು ಹುಡುಕುತ್ತದೆ. ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಕೃತಕವಾಗಿ ಹೆಚ್ಚಿಸಲು ವಿನ್ಯಾಸಗೊಳಿಸಿದ ಇತರ ಯೋಜನೆಗಳನ್ನು ಮತ್ತು ಲಿಂಕ್ ಫಾರ್ಮ್ ಗಳನ್ನು ಗೂಗಲ್ ದಂಡಿಸುತ್ತದೆ.ಡಿಸೆಂಬರ್ 2007ರಲ್ಲಿ ಹಣ ಕೊಟ್ಟ ಟೆಕ್ಸ್ಟ್ ಲಿಂಕ್ಗಳನ್ನು ಮಾರಾಟ ಮಾಡುವ ಸೈಟ್ಗಳನ್ನು ಸಕ್ರಿಯವಾಗಿ ದಂಡಿಸುವುದನ್ನು ಗೂಗಲ್ ಪ್ರಾರಂಭಿಸಿದೆ. ಲಿಂಕ್ ಫಾರ್ಮ್ಗಳನ್ನು ಮತ್ತು ಇತರ ಪೇಜ್ರ್ಯಾಂಕ್ ಮೆನಿಪ್ಯುಲೆಶನ್ ಟೂಲ್ಗಳನ್ನು ಗೂಗಲ್ ಹೇಗೆ ಪತ್ತೆ ಹಚ್ಚುತ್ತದೆ ಎಂಬುದು ಗೂಗಲ್ನ ಟ್ರೇಡ್ಸಿಕ್ರೇಟ್ ಆಗಿದೆ.
ಗಣನೆ[ಬದಲಾಯಿಸಿ]
ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಇಟರೆಟಿವ್ಲಿ ಅಥವಾ ಬೀಜಗಣಿತೀಯವಾಗಿ ಲೆಕ್ಕ ಮಾಡಲಾಗುವುದು. ಪರ್ಯಾಯವಾಗಿ,. ಪವರ್ ಇಟರೇಶನ್ ವಿಧಾನ,[೯][೧೩] ಅಥವಾ ಪವರ್ ವಿಧಾನವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
Iterative[ಬದಲಾಯಿಸಿ]
ಮೊದಲಿನ ಘಟನೆಯಲ್ಲಿ, ಆಗಿತ್ತು, ಸಾಮಾನ್ಯವಾಗಿ ಪ್ರಾರಂಭದ ಸಂಭವನೀಯತೆಯ ಹಂಚಿಕೆಯನ್ನು ಹೀಗೆ ಊಹಿಸಲಾಗಿತ್ತು
- .ಮೇಲೆ ವಿವರಿಸಿದಂತೆ ಪ್ರತಿ ಹಂತದಲ್ಲಿ ಲೆಕ್ಕಾಚಾರ ಹೀಗಿರುತ್ತದೆ,
- ,
ಅಥವಾ ಮಾತೃಕೆ ಸಂಕೇತ ಪದ್ಧತಿಯಲ್ಲಿ :, (*) ಇದರಲ್ಲಿ ಮತ್ತು ಇದು ಉದ್ದದ ಕಾಲಂ ವೆಕ್ಟರ್ ಇದು ಒಂದನ್ನು ಮಾತ್ರ ಒಳಗೊಂಡಿದೆ. ಈ ಮಾತೃಕೆಯನ್ನು ಹೀಗೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ
ಅಂದರೆ,:, ಇದರಲ್ಲಿ ಗ್ರಾಫ್ನ ಹೊಂದಿಕೊಳ್ಳಬಲ್ಲ ಮಾತೃಕೆಯನ್ನು ಸೂಚಿಸಿತ್ತದೆ ಮತ್ತು ಕರ್ಣ ಮಾತೃಕೆಯು ಕರ್ಣದಲ್ಲಿ ಹೊರಹೋದ ರೂಪದಲ್ಲಿರುತ್ತದೆ. ಕೆಲವು ಚಿಕ್ಕ ಗೆ ಗಣನೆ ಮುಗಿಯುತ್ತದೆ.
- ,ಅಂದರೆ ಸಂಯೋಜನೆಯನ್ನು ಊಹಿಸಲಾಗಿದೆ.
ಬೀಜಗಣಿತ[ಬದಲಾಯಿಸಿ]
ನಂತರದ ಹೊಂತದಲ್ಲಿ, ಗೆ (ಅಂದರೆ ಸ್ಥಿರ ಸ್ಥಿತಿಯಲ್ಲಿ), ಮೇಲಿನ ಸಮೀಕರಣ (*) ಹೀಗಿದೆ
- . (**)ಪರಿಹಾರ ಹೀಗೆ ಕೊಟ್ಟಿದೆ :,
ಅಭಿನ್ನತೆ ಮಾತೃಕೆಯ ಜೊತೆ ಕ್ಕೆ ಏಕಮಾತ್ರವಾಗಿರುವ ಪರಿಹಾರವಿದೆ. ಇದನ್ನು ಸ್ಟೊಕಾಸ್ಟಿಕ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಮತ್ತು ಪೆರೊನ್-ಫ್ರೋಬೆನಿಯಸ್ ಪ್ರಮೆಯದ ಕಾರಣದಿಂದಾಗಿ ಇದು ಐಗನ್ವ್ಯಾಲ್ಯೂದ ಒಂದಕ್ಕೆ ಸಮನಾಗಿರುವುದರಿಂದ ಇದನ್ನು ಏನೂ ಅಲ್ಲದರಿಂದ ನೋಡಬಹುದು.
ಪವರ್ ವಿಧಾನ[ಬದಲಾಯಿಸಿ]
ಮಾತೃಕೆ ಪರಿವರ್ತನೆ ಸಂಭವನೀಯತೆಯಾಗಿದ್ದರೆ, ಅದರಿಂದ ಕಾಲಮ್-ಸ್ಟೊಕಾಸ್ಟಿಕ್ನಿಂದಲ್ಲದೆ ಯಾವುದೇ ಕಾಲಮ್ ಇಲ್ಲದೆಯೂ ಕೂಡ ಕೇವಲ ಸೊನ್ನೆಗಳು ಮತ್ತು ಇದು ಒಂದು ಸಂಭವನೀಯತೆಯ ಹಂಚಿಕೆಯಾಗಿದೆ (ಅಂದರೆ, ), ಸಮೀಕರಣ (**) ಇದು ಕೆಳಗಿನದಕ್ಕೆ ಸಮವಾಗಿದೆ :. (***) ಆದ್ದರಿಂದ ಪೇಜ್ರ್ಯಾಂಕ್ ಮುಖ್ಯವಾದ ಐಜೆನ್ವೆಕ್ಟರ್ನ. ಇದು ವೇಗವಾಗಿ ಮತ್ತು ಸುಲಭವಾಗಿ ಪವರ್ ವಿಧಾನ ವನ್ನು ಉಪಯೋಗಿಸಿ ಗಣನೆ ಮಾಡುವ ರೀತಿ: ಆರ್ಬಿಟ್ರರಿ ವೆಕ್ಟರ್ ನಿಂದ ಪ್ರಾರಂಭಿಸಿ, ಈ ನಿರ್ವಾಹಕ ಮುಂದೆ ಅನ್ವಯವಾಗಿದೆ, ಅಂದರೆ,
- ,
ಇಲ್ಲಿಯವರೆಗೆ :. (***) ಸಮೀಕರಣದಲ್ಲಿ ಆವರಣದ ಬಲಬದಿಯಲ್ಲಿರುವ ಮಾತೃಕೆ ವಿವರಿಸಿದಂತೆ:,ಇಲ್ಲಿ, ಪ್ರಾರಂಭದ ಸಂಭವನೀಯತೆಯ ಹಂಚಿಕೆಯಾಗಿದೆ. ಈ ವಿಷಯದಲ್ಲಿ
- .
ಕೊನೆಯದಾಗಿ, ಸೊನ್ನೆ ಮಾತ್ರ ಇರುವ ಕಾಲಂಗಳನ್ನು ಹೊಂದಿರುವ ಇದ್ದರೆ, ಅವುಗಳನ್ನು ಪ್ರಾರಂಭದ ಸಂಭವನೀಯತೆ ವೆಕ್ಟರ್ ಜೊತೆ ಬದಲಾಯಿಸಬೇಕು. ಬೇರೆ ಪದಗಳಲ್ಲಿ
- ,
ಇಲ್ಲಿ ಮಾತೃಕೆಯನ್ನು ಹೀಗೆ ನಿರೂಪಿಸಲಾಗಿದೆ
- ,
ಮತ್ತು : ಇಲ್ಲಿ, ನ್ನು ಉಪಯೋಗಿಸಿ ಮಾಡಿದ ಮೇಲಿನ ಲೆಕ್ಕಾಚಾರಗಳು ಒಂದೇ ರೀತಿಯ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ಕೊಡುತ್ತವೆ ಅವುಗಳ ಫಲಿತಾಂಶಗಳನ್ನು ಸಹಜ ಸ್ಥಿತಿಗೆ ತಂದಾಗ:
- .
ಸಾಮರ್ಥ್ಯ[ಬದಲಾಯಿಸಿ]
ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಉಪಯೋಗಿಸಿದ ರೂಪುರೇಖೆ, ವಿಧಾನಗಳನ್ನು ಸರಿಯಾಗಿ ನಡೆಸುವುದು, ಮತ್ತು ಬೇಕಾದ ಫಲಿತಾಂಶದ ನಿಖರತೆಗಳ ಆಧಾರದ ಮೇಲೆ ಮೂರು ವಿಧಾನಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಬೇಕಾಗುವ ಸಮಯ ಹೆಚ್ಚು ಕಡಿಮೆಯಾಗುತ್ತದೆ.ಸಾಮಾನ್ಯವಾಗಿ ಲೆಕ್ಕಾಚಾರವನ್ನು ಬಹಳ ಸಲ ಮಾಡಬೇಕಾದರೆ (ಅಂದರೆ, ಬೆಳೆಯುತ್ತಿರುವ ನೆಟ್ವರ್ಕ್ ಗಾಗಿ) ಅಥವಾ ನೆಟ್ವರ್ಕ್ ನ ಪ್ರಮಾಣ ವಿಸ್ತಾರವಾಗಿದ್ದರೆ, ಮಾತೃಕೆಯ ವಿಪರ್ಯಯದಿಂದ ಬೀಜಗಣತೀಯ ಗಣನೆ ನಿಧಾನವಾಗುತ್ತದೆ ಮತ್ತು ಮೆಮೊರಿಯ ಕೊರತೆಯಾಗುತ್ತದೆ, ಮತ್ತು ಪವರ್ ವಿಧಾನ ಹೆಚ್ಚು ಪರಿಣಾಮಕಾರಿಯಾಗಿದೆ.
ವ್ಯತ್ಯಯನಗಳು[ಬದಲಾಯಿಸಿ]
ಗೂಗಲ್ ಟೂಲ್ಬಾರ್[ಬದಲಾಯಿಸಿ]
ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ನ ಪೇಜ್ರ್ಯಾಂಕ್, ನೋಡಿದ ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು 0 ಮತ್ತು 10ರ ನಡುವಿನ ಪೂರ್ಣ ಸಂಖ್ಯೆಯಂತೆ ತೋರಿಸುತ್ತದೆ. ಹೆಚ್ಚು ಜನಪ್ರಿಯ ವೆಬ್ಸೈಟ್ಗಳು ಹತ್ತನೇ ಪೇಜ್ರ್ಯಾಂಕ್ ಪಡೆದಿವೆ. ಕಡಿಮೆ ಗುಣಮಟ್ಟದವು 0 ಪೇಜ್ರ್ಯಾಂಕ್ ಪಡೆದಿವೆ.ಟೂಲ್ಬಾರ್ನ ಪೇಜ್ರ್ಯಾಂಕ್ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವ ನಿಖರವಾದ ವಿಧಾನವನ್ನು ಗೂಗಲ್ ತಿಳಿಯಪಡಿಸಿಲ್ಲ, ಮೊದಲು, ಕೆಳಗಿನ ವೆಬ್ಸೈಟ್ಗೆ ಹೋಗಿ ಸಹ ಕಂಡುಹಿಡಿಯಬಹುದಾಗಿದೆ: http://www.google.com/search?client=navclient-auto&ch=6-1484155081&features=Rank&q=info:http://www.wikipedia.org/[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ] (ಗಮನಿಸಿ: ಈ ಲಿಂಕ್ 2010.01.23 ನ ನಿಯಮ ಉಲ್ಲಂಘಿಸಿದ ರೀತಿಯಲ್ಲಿ ಗೂಗಲ್ ತಪ್ಪನ್ನು ತೋರಿಸುತ್ತದೆ) ಇಲ್ಲಿ www.wikipedia.org ಇದು ವೆಬ್ಸೈಟ್ ಹೆಸರಾಗಿದೆ.
ಕೆಳಗಿನ ಒಂದು-ಸಾಲಿನ ಜಾವಾಸ್ಕ್ರಿಪ್ಟ್ ಯುಆರ್ಎಲ್ ನ ಬದಲಾಗಿ ಕೆಲಸ ಮಾಡುತ್ತದೆ ಮತ್ತು ಯಾವುದೇ ಬ್ರೌಸರ್ನ ಬುಕ್ಮಾರ್ಕ್ ಬಾರ್ನಲ್ಲಿ ಉಪಯೋಗವಾಗುವ ಬುಕ್ಮಾರ್ಕ್ಲೆಟ್ ನಂತೆ ಉಪಯೋಗಿಸುತ್ತದೆ (ಸದ್ಯದಲ್ಲಿ ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ನ ಅಭಾವವನ್ನು ಸೇರಿಸುವ ಗೂಗಲ್ ಚ್ರೋಮ್ನ್ನು ಒಳಗೊಂಡಿದೆ)
javascript:location.href='http:\/\/www.google.com\/search?client=navclient-auto&ch=6-1484155081&features=Rank&q=info:'+encodeURIComponent(location.href);
(ಗಮನಿಸಿ: ಮೇಲಿನ ಎರಡು ವಿಧಾನಗಳು ೧೦ ಸಪ್ಟೆಂಬರ್ ೨೦೦೯ ರಂತ ೪೦೩ ನಿಷಿದ್ಧ ತಪ್ಪನ್ನು ಉಂಟುಮಾಡುತ್ತವೆ) ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ನ್ನು ಒಂದು ವರ್ಷದಲ್ಲಿ ಐದು ಸಲ ತಿದ್ದುಪಡಿ ಮಾಡಲಾಗಿದೆ, ಆದ್ದರಿಂದ ಕೆಲವೊಮ್ಮೆ ಹಳೆಯ ಬೆಲೆಗಳನ್ನು ತೋರಿಸುತ್ತದೆ. ಇದರ ಇಲ್ಲಿಯವರೆಗಿನ ಕೊನೆಯ ತಿದ್ದುಪಡಿಯನ್ನು ೧೩/೧೪ ಫೆಬ್ರುವರಿ ೨೦೧೦ರಲ್ಲಿ ಮಾಡಲಾಗಿದೆ.[೧೪]
SERP ರಾಂಕ್[ಬದಲಾಯಿಸಿ]
ಎಸ್ಇಆರ್ಪಿ(ಶೋಧನಾ ಎಂಜಿನ್ನಿನ ಫಲಿತಾಂಶದ ಪುಟ) ಇದು ಕೀವರ್ಡ್ ಕ್ವೆರಿಗೆ ಉತ್ತರವಾಗಿ ಶೋಧನಾ ಎಂಜಿನ್ ನೀಡಿದ ನಿಜವಾದ ಫಲಿತಾಂಶವಾಗಿದೆ. ಟೆಕ್ಸ್ಟ್ ಸ್ನಿಪೆಟ್ ಗಳನ್ನು ಹೊಂದಿರುವ ಅಂತರ್ಜಾಲ ಪುಟಗಳಿಗಿರುವ ಸಂಪರ್ಕಗಳ ಪಟ್ಟಿಯನ್ನು ಎಸ್ಇಆರ್ಪಿ ಹೊಂದಿದೆ.ಅಂತರ್ಜಾಲ ಪುಟದ ಎಸ್ಇಆರ್ಪಿ ರ್ಯಾಂಕ್ ಅಂದರೆ ಎಸ್ಇಆರ್ಪಿನಲ್ಲಿ ಸರಿಹೊಂದುವ ಲಿಂಕ್ನ ನಿಯೋಜನೆ, ಇಲ್ಲಿ ಉನ್ನತ ನಿಯೋಜನೆಯೆಂದರೆ ಉತ್ತಮ ಎಸ್ಇಆರ್ಪಿ ರ್ಯಾಂಕ್. ಅಂತರ್ಜಾಲ ಪುಟದ ಎಸ್ಇಆರ್ಪಿ ರಾಂಕ್ ಇದರ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಕಾರ್ಯ ಮಾತ್ರವಲ್ಲ, ಆದರೆ ತುಲನಾತ್ಮಕವಾಗಿ ವಿಸ್ತಾರವಾಗಿರುವ ಮತ್ತು ನಿರಂತರವಾಗಿ ಹೊಂದಿಕೆಯಾದ ವಿಷಯಗಳ ಮೇಲೆ ಆಧಾರಿತವಾಗಿದೆ,[೧೫][೧೬] ಸಾಮಾನ್ಯವಾಗಿ "ಗೂಗಲ್ ಲವ್" ನಂತಹ ಇಂಟರ್ನೆಟ್ ಮಾರಾಟಗಾರರಿಂದ ಉಲ್ಲೇಖಿಸಲ್ಪಟ್ಟಿದೆ.[೧೭] ಎಸ್ಇಒ (ಸರ್ಚ್ ಎಂಜಿನ್ ಆಪ್ಟಿಮೈಜೆಶನ್), ವೆಬ್ಸೈಟ್ ಅಥವಾ ಅತರಜಾಲ ಪುಟಗಳ ಗುಂಪುಗಳಿಗೆ ಸಾಧ್ಯವಾದಷ್ಟು ಉತ್ತಮ ಎಸ್ಇಆರ್ಪಿ ರಾಂಕ್ ಅನ್ನು ಸಾಧಿಸುವ ಉದ್ದೇಶ ಹೊಂದಿದೆ.
ಗೂಗಲ್ ಡೈರೆಕ್ಟರಿ ಪೇಜ್ರ್ಯಾಂಕ್[ಬದಲಾಯಿಸಿ]
ಗೂಗಲ್ ಡೈರೆಕ್ಟರಿ ಪೇಜ್ರ್ಯಾಂಕ್ ಇದೊಂದು 8-ಘಟಕದ ಮಾಪನ. ಇದರ ಮೌಲ್ಯಗಳನ್ನು ಗೂಗಲ್ ಡೈರೆಕ್ಟರಿಯಲ್ಲಿ ನೋಡಬಹುದು. ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ ಹಸಿರುಗೆರೆಯ ಮೌಸ್ಓವರ್ನಿಂದ ಪೇಜ್ರ್ಯಾಂಕ್ ಮೌಲ್ಯವನ್ನು ತೋರಿಸುವುದಿಲ್ಲ, ಗೂಗಲ್ ಡೈರೆಕ್ಟರಿ ಅಸಂಖ್ಯಾತ ಮೌಲ್ಯಗಳಾಗಿರುವ ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ತೋರಿಸುವುದಿಲ್ಲ,ಆದರೆ ಹಸಿರು ಗೆರೆಯ ಹಾಗೆ ಮಾತ್ರ ತೋರಿಸುತ್ತವೆ.
ದೋಷಪೂರಿತ ಅಥವಾ ವಂಚಕ ಪೇಜ್ರ್ಯಾಂಕ್[ಬದಲಾಯಿಸಿ]
ಟೂಲ್ಬಾರ್ನಲ್ಲಿ ಪೇಜ್ರ್ಯಾಂಕ್ ಕಾಣಿಸಿದ ಸಂದರ್ಭದಲ್ಲಿ, ಅದು ಅನೇಕ ತಾಣಗಳಿಗಾಗಿ ನಿರ್ದಿಷ್ಟ ಪೇಜ್ರ್ಯಾಂಕ್ ಮೌಲ್ಯದಿಂದ (ಕೆಲವು ಸಮಯದಲ್ಲಿ ಗೂಗಲ್ನ ಪ್ರಕಟಣೆ ಸಮಯಕ್ಕೆ ಪೂರ್ವದ್ದಾಗಿರುತ್ತದೆ) ಪಡೆದಿರುವುದಾಗಿ ಪರಿಗಣಿಸಲ್ಪಡುತ್ತದೆ, ಈ ಮೌಲ್ಯವು ಸುಲಭವಾಗಿ ಕುಶಲತೆಯಿಂದ ಬಳಸಲ್ಪಟ್ಟಿದೆ ಎಂಬುದನ್ನು ಅದು ತಿಳಿಸುತ್ತದೆ. ಈ ಮುಂಚಿನ ನ್ಯೂನತೆಯು ಯಾವುದೇ ಕಡಿಮೆ ಮಟ್ಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಆಗಿದ್ದು, ಅದು ಕಡಿಮೆ ಮಟ್ಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಪುಟವು ಪೇಜ್ರ್ಯಾಂಕ್ ಗುರಿಯ ಪುಟವನ್ನು ಹೊಂದಲು ಕಾರಣವಾದ ಅಧಿಕ ಮಟ್ಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಪುಟಕ್ಕೆ HTTP 302 ಪ್ರತಿಕ್ರಿಯೆ ಅಥವಾ "ರಿಫ್ರೆಶ್" ಮೆಟಾ ಟ್ಯಾಗ್ ಮೂಲಕ ಪುನಃನಿರ್ದೇಶಿಸಲ್ಪಟ್ಟಿದೆ. ಹೊಸ ಸಿದ್ದಾಂತದಲ್ಲಿ, ಯಾವುದೇ ಪ್ರವೇಶವಿಲ್ಲದ ಲಿಂಕ್ಗಳೊಂದಿಗಿರುವ PR 0 ಪುಟವು ಗೂಗಲ್ ಮುಖಪುಟಕ್ಕೆ ಪುನಃನಿರ್ದೇಶಿಸಲ್ಪಟ್ಟಿದೆ-ಅದು PR 10ಆಗಿದೆ -ಮತ್ತೆ PRನ ಹೊಸ ಪುಟವು PR10ಗೆ ಏರಿಕೆಯಾಗಿದೆ. ಈ ವಂಚನೆಯ ತಂತ್ರವು, 302 ಗೂಗಲ್ ಜಾಕಿಂಗ್ನ ಹಾಗೆ ಎಂಬುದು ಸಹ ತಿಳಿದಿದೆ, ಅದು ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ವಿಫಲಗೊಳ್ಳುವಿಕೆ ಅಥವಾ ಕಂಪ್ಯೂಟರಿನಲ್ಲಿನ ತೊಂದರೆ ಎಂಬುದು ತಿಳಿದಿತ್ತು. ಯಾವುದೇ ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಅತ್ಯಧಿಕ ಅಥವಾ ಕಡಿಮೆ ಮಟ್ಟದ ಅನೇಕ ವೆಬ್ಮಾಸ್ಟರ್ಗಳ ಆಯ್ಕೆಯನ್ನು ವಂಚನೆಗೊಳಿಸುತ್ತದೆ ಮತ್ತು ಗೂಗಲ್ ಮಾತ್ರ ಪುಟದ ನೈಜ ಪೇಜ್ರ್ಯಾಂಕ್ಗೆ ದಾರಿ ಮಾಡಿಕೊಡುತ್ತದೆ. ಚಾಲನೆಯಾಗುತ್ತಿರುವ ಗೂಗಲ್ ಸರ್ಚ್ನಿಂದ ಪ್ರಶ್ನಾರ್ಹ ಪೇಜ್ರ್ಯಾಂಕ್ನೊಂದಿಗೆ ಯುಆರ್ಎಲ್ಗಾಗಿ ಸಾಮಾನ್ಯವಾಗಿ ವಂಚನೆಯನ್ನು, ಅದರ ಫಲಿತಾಂಶಗಳಲ್ಲಿನ ಸಂಪೂರ್ಣ ವಿವಿಧ ತಾಣ(ಪುನಃನಿರ್ದೇಶಿಸಿದ)ದ ಯುಆರ್ಎಲ್ ಅನ್ನು ಪ್ರದರ್ಶಿಸುವ ಫಲಿತಾಂಶಗಳಂತೆ ಪತ್ತೆಮಾಡಲಾಗುತ್ತದೆ.
ಕುಶಲತೆಯಿಂದ ಬಳಸುವ ಪೇಜ್ರ್ಯಾಂಕ್[ಬದಲಾಯಿಸಿ]
ಸರ್ಚ್-ಎಂಜಿನ್ ಆಪ್ಟಿಮೈಜೇಷನ್ ಉದ್ದೇಶಗಳಿಗಾಗಿ, ಕೆಲವು ಕಂಪನಿಗಳು ಅಧಿಕ ಪೇಜ್ರ್ಯಾಂಕ್ ಲಿಂಕ್ಗಳನ್ನು ವೆಬ್ಮಾಸ್ಟರ್ಗಳಿಗೆ ಮಾರಾಟ ಮಾಡುವ ಕೊಡುಗೆಯನ್ನು ನೀಡಿದವು.[೧೮] ಅತ್ಯಧಿಕ-PR ಪುಟಗಳ ಲಿಂಕ್ಗಳಂತೆ,ಅವು ಅಧಿಕ ಮೌಲ್ಯಯುತವಾದವುಗಳೆಂದು ನಂಬಲಾಗಿದೆ, ಅವುಗಳ ರಕ್ಷಣೆಯು ಅಧಿಕ ದುಬಾರಿಯಾದದ್ದು. ಇದು ಬಹಳ ಪರಿಣಾಮಕಾರಿಯಾಗಿದ್ದು, ಗುಣಮಟ್ಟ ಪ್ರಮಾಣದ ಪುಟಗಳಲ್ಲಿ ಜಾಹೀರಾತುಗಳ ಲಿಂಕ್ಯನ್ನು ಕೊಳ್ಳಲು ಸಮಸ್ಯಾರಹಿತ ಮಾರುಕಟ್ಟೆ ತಂತ್ರವಾಗಿದೆ ಮತ್ತು ಈ ವಿಷಯಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ತಾಣಗಳು ದಟ್ಟಣೆಯನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತವೆ ಮತ್ತು ವೆಬ್ಮಾಸ್ಟರ್ನ ಲಿಂಕ್ಯ ಜನಪ್ರಿಯತೆಯನ್ನು ಹೆಚ್ಚಿಸುತ್ತವೆ. ಹೀಗಿದ್ದರೂ, ಗೂಗಲ್ ವೆಬ್ಮಾಸ್ಟರ್ಗಳಿಗೆ ಬಹಿರಂಗವಾಗಿ ಎಚ್ಚರಿಸುವುದೇನೆಂದರೆ, ಅವರು ಚರ್ಚೆಗೊಳಪಡುವ ಪೇಜ್ರ್ಯಾಂಕ್ ಮತ್ತು ಪ್ರಸಿದ್ಧಿಯ ಉದ್ದೇಶಕ್ಕಾಗಿ ಲಿಂಕ್ಗಳನ್ನು ಮಾರಾಟಮಾಡಲು ಪತ್ತೇಹಚ್ಚಿದ್ದರೆ, ಅವರ ಕೊಂಡಿಗಳ ಬೆಲೆ ತಗ್ಗಿಸಲ್ಪಡುತ್ತವೆ (ಇತರೆ ಪುಟಗಳ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಲೆಕ್ಕಾಚಾರದಲ್ಲಿ ನಿರ್ಲಕ್ಷಿಸಲ್ಪಟ್ಟಿದೆ).ಈ ಲಿಂಕ್ಗಳ ಕೊಳ್ಳುವಿಕೆ ಮತ್ತು ಮಾರುವಿಕೆ ಪ್ರಯತ್ನವು ವೆಬ್ಮಾಸ್ಟರ್ ಸಮುದಾಯದಾದ್ಯಂತ ತೀವ್ರ ಚರ್ಚೆಗೊಳಗಾಗಿದೆ. ಗೂಗಲ್ ವೆಬ್ಮಾಸ್ಟರ್ಗಳಿಗೆ ಪ್ರಾಯೋಜಿತ ಲಿಂಕ್ಗಳಲ್ಲಿ ನೊಫಾಲೊ HTML ಲಕ್ಷಣದ ಮೌಲ್ಯವನ್ನು ಬಳಕೆ ಮಾಡಿಕೊಳ್ಳುವಂತೆ ಸಲಹೆ ನೀಡುತ್ತದೆ.ಮ್ಯಾಟ್ ಕಟ್ಸ್ನ ಪ್ರಕಾರ, ವ್ಯವಸ್ಥೆಯನ್ನು ಆಟವಾಡಲು ಪ್ರಯತ್ನಿಸುತ್ತಿರುವಂತಹ ವೆಬ್ಮಾಸ್ಟರ್ಗಳ ಬಗ್ಗೆ ಗೂಗಲ್ ಕಾಳಜಿ ವಹಿಸುತ್ತಿದೆ ಮತ್ತು ಅದರಿಂದಾಗಿ ಗುಣಮಟ್ಟ ಮತ್ತು ಗೂಗಲ್ ಅನ್ವೇಷಣೆ ಫಲಿತಾಂಶಗಳ ಪ್ರಸಕ್ತತೆ ಕಡಿಮೆಯಾಗುತ್ತಿದೆ.[೧೮]
ಉದ್ದೇಶಪೂರ್ವಕ ಶೋಧಕ ಮಾದರಿ[ಬದಲಾಯಿಸಿ]
ಮೂಲ ಪೇಜ್ರ್ಯಾಂಕ್ ಕ್ರಮಾವಳಿ ಪ್ರತಿಫಲನಗಳನ್ನು ರಾಂಡಮ್ ಶೋಧಕ ಮಾದರಿಯೆಂದು ಕರೆಯುವರು, ಇದರ ಅರ್ಥವೆನೆಂದರೆ ನಿರ್ದಿಷ್ಟ ಪುಟದ ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ರಾಂಡಮ್ನಲ್ಲಿರುವ ಲಿಂಕ್ಯನ್ನು ಆ ಪುಟವು ಕ್ಲಿಕ್ಕಿಸಿದಾಗ ಭೇಟಿ ನೀಡುವ ಸೈದ್ದಾಂತಿಕ ಸಾಧ್ಯತೆಯಿಂದ ಪಡೆಯಲಾಗಿದೆ. ಆದರೆ, ನೈಜ ಬಳಕೆದಾರರು ವೆಬ್ ಅನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಜಾಲಾಡುವುದಿಲ್ಲ, ಆದರೆ ಅವರು ಲಿಂಕ್ಗಳ ಮೂಲಕ ತಮ್ಮ ಹಿತಾಸಕ್ತಿ ಮತ್ತು ಉದ್ದೇಶವನ್ನು ಅನುಸರಿಸುತ್ತಾರೆ. ಪೇಜ್ರ್ಯಾಂಕಿಂಗ್ ಮಾದರಿಯು ಎಷ್ಟು ಜನ ಭೇಟಿನೀಡುತ್ತಾರೆಂಬ ಕಾರ್ಯದಂತೆಯೇ ನಿರ್ದಿಷ್ಟ ಪುಟದ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಪ್ರತಿಫಲಿಸುತ್ತದೆ. ಇದನ್ನು ಉದ್ದೇಶಪೂರ್ವಕ ಶೋಧಕ ಮಾದರಿ ಎಂದು ಕರೆಯಲ್ಪಡುವ ನೈಜ ಬಳಕೆದಾರರಿಂದ ಪಡೆಯಲಾಗುತ್ತದೆ.[೧೯] ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ ಪ್ರತಿಯೊಂದು ಪುಟವನ್ನು ಭೇಟಿ ಮಾಡುವುದಕ್ಕೆ ಗೂಗಲ್ಗೆ ಮಾಹಿತಿಯನ್ನು ರವಾನಿಸುತ್ತದೆ ಮತ್ತು ಅದರಿಂದಾಗಿ ಉದ್ದೇಶಪೂರ್ವಕ ಶೋಧಕ ಮಾದರಿಯನ್ನು ಆಧರಿಸಿದ ಗಣನೆಯಾಗುತ್ತಿರುವ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಮೂಲತತ್ವವನ್ನು ಒದಗಿಸುತ್ತದೆ. ಗೂಗಲ್ನ ನೊಫಾಲೊ ಲಕ್ಷಣದ ಪರಿಚಯವು ಸ್ಪ್ಯಾಮ್ಡೆಕ್ಸಿಂಗ್ನೊಂದಿಗೆ ಹೋರಾಡುವಲ್ಲಿ ಪ್ರತಿ ಪರಿಣಾಮವನ್ನು ಬೀರುತ್ತದೆ , ಇದನ್ನು ವೆಬ್ಮಾಸ್ಟರುಗಳು ಹೊರಹೋಗುವ ಲಿಂಕ್ಯಲ್ಲಿ ತಮ್ಮ ಸ್ವಂತ ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ಹೆಚ್ಚಿಸಿಕೊಳ್ಳುವುದಕ್ಕಾಗಿ ಸಾಮಾನ್ಯವಾಗಿ ಬಳಕೆ ಮಾಡುತ್ತಾರೆ. ಇದು ವೆಬ್ ಕಾಲರ್ಗಳಿಗಾಗಿ ನಿರ್ದಿಷ್ಟ ಲಿಂಕ್ಗಳ ನಷ್ಟವನ್ನು ತಪ್ಪಿಸಲು ಕಾರಣವಾಗುತ್ತದೆ. ಅದರಿಂದಾಗಿ ರಾಂಡಮ್ ಶೋಧಕ ಮಾದರಿಯ ಸಾಮರ್ಥ್ಯವುಳ್ಳ ನಂಬಿಕೆಗೆ ಅರ್ಹವಲ್ಲದವುಗಳನ್ನು ಆಧರಿಸಿದ ಮೂಲ ಪೇಜ್ರ್ಯಾಂಕ್ ಕ್ರಮಾವಳಿಯನ್ನು ಮಾಡಲಾಗಿದೆ. ಬಳಕೆದಾರರ ಬ್ರೌಸಿಂಗ್ ಹವ್ಯಾಸಗಳ ಕುರಿತ ಮಾಹಿತಿ ಬಳಕೆಯನ್ನು ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ ಒದಗಿಸುತ್ತದೆ, ಬಹುಶಃ ಅದು ನೊಫಾಲೊ ಲಕ್ಷಣದಿಂದ ಕಾರಣವಾದ ಮಾಹಿತಿ ನಷ್ಟಕ್ಕೆ ಪರಿಹಾರ ನೀಡುತ್ತದೆ.ಪುಟದ SERP ರಾಂಕ್, ಇದು ಶೋಧನೆಯ ಫಲಿತಾಂಶಗಳಲ್ಲಿ ಪುಟದ ನಿರ್ದಿಷ್ಟ ನಿಯೋಜನೆಯನ್ನು ಖಚಿತಪಡಿಸುತ್ತದೆ, ಇದು ಇತರೆ ಅಂಶಗಳ ಜೊತೆಯಲ್ಲಿ ರಾಂಡಮ್ ಶೋಧಕ ಮಾದರಿ(ಪೇಜ್ರ್ಯಾಂಕ್) ಮತ್ತು ಉದ್ದೇಶಪೂರ್ವಕ ಶೋಧಕ ಮಾದರಿ(ಬ್ರೌಸಿಂಗ್ ಹವ್ಯಾಸ)ಗಳ ಸಂಯೋಜನೆಯ ಮೂಲವಾಗಿದೆ [೨೦].
ಇತರ ಉಪಯೋಗಗಳು[ಬದಲಾಯಿಸಿ]
ಪೇಜ್ರ್ಯಾಂಕ್ ಆವೃತ್ತಿಯನ್ನು ಇತ್ತೀಚೆಗೆ ಸಾಂಪ್ರದಾಯಿಕ ವೈಜ್ಞಾನಿಕ ಮಾಹಿತಿ ಸಂಸ್ಥೆ (ISI) ಪ್ರಭಾವಿ ಪ್ರತಿನಿಧಿಗಾಗಿ ಸ್ಥಳಾಂತರ ಮಾಡಿದಂತೆ ಪ್ರಸ್ಥಾಪಿಸಲಾಗಿದ್ದು,[೨೧] ಅದನ್ನು eigenfactor.org ನಲ್ಲಿ ನೆರವೇರಿಸಲಾಗಿದೆ. ನಿಯತಕಾಲಿಕೆಗೆ ಕೆಲವು ಗಣನೆಯಾಗುತ್ತಿರುವ ಒಟ್ಟು ಉಲ್ಲೇಖದ ಬದಲಾಗಿ, ಪ್ರತಿ ಉಲ್ಲೇಖದ "ಪ್ರಾಮುಖ್ಯತೆ"ಯು ಪೇಜ್ರ್ಯಾಂಕ್ ಮಾದರಿಯಲ್ಲಿ ತೀರ್ಮಾನಿಸಲ್ಪಡುತ್ತದೆ. ಪೇಜ್ರ್ಯಾಂಕ್ನ ಸದೃಶ ಹೊಸ ಬಳಕೆಯು ಬೋಧನ ವಿಭಾಗದ ಸ್ಥಾನದಲ್ಲಿ ತಮ್ಮ ಪದವಿಗಳನ್ನು ಬದಲಾಯಿಸಿರುವ ತಮ್ಮ ದಾಖಲೆಗಳನ್ನು ಆಧರಿಸಿದ ಶೈಕ್ಷಣಿಕ ವೈದ್ಯ ಪದವಿಯ ಕಾರ್ಯಕ್ರಮಗಳನ್ನು ವಿಂಗಡಿಸುವುದಾಗಿದೆ. ಪೇಜ್ರ್ಯಾಂಕ್ ನಿಯಮಗಳಲ್ಲಿ, ಶೈಕ್ಷಣಿಕ ವಿಭಾಗಗಳು ಪ್ರತಿಯೊಬ್ಬರಿಂದಲೂ (ಮತ್ತು ತಾವಾಗಿಯೇ) ತಮ್ಮ ಬೋಧನಾ ವಿಭಾಗವನ್ನು ಗೊತ್ತು ಮಾಡುವುದರಿಂದ ಪ್ರತಿಯೊಬ್ಬರಿಗೂ ಸಂಪರ್ಕಕ್ಕೆ ಸಿಗುತ್ತವೆ. [೨೨] ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ರಾಂಕ್ ಅಂತರಗಳು ಅಥವಾ ಮಾರ್ಗಗಳಿಗೆ ಬಳಸಲ್ಪಡುತ್ತಿದ್ದು, ಅದನ್ನು ಎಷ್ಟು ಜನ (ಪಾದಚಾರಿಗಳು ಅಥವಾ ವಾಹನಗಳು) ಪ್ರತ್ಯೇಕ ಅಂತರಗಳು ಅಥವಾ ಮಾರ್ಗಗಳನ್ನು ಉಪಯೋಗಿಸುತ್ತಾರೆ ಎಂಬುದನ್ನು ಊಹಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ.[೨೩][೨೪]. ನಿಘಂಟಿನ ಅಮುಖ್ಯಾರ್ಥಗಳಲ್ಲಿ ಇದನ್ನು ಪದ ಗ್ರಾಹ್ಯದ ಅಸ್ಪಷ್ಟತೆಯ ನಿವಾರಣೆಯನ್ನು ತೋರಿಸುವಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ[೨೫] ಮತ್ತು ಸ್ವಯಂಚಾಲಿತ ರಾಂಕ್ ವರ್ಡ್ನೆಟ್ ಸೈನ್ಸೆಟ್ಸ್ ಪ್ರಕಾರ, ಸಕಾರಾತ್ಮಕತೆ ಅಥವಾ ನಕಾರಾತ್ಮಕತೆಯಂತಹ ನೀಡಲಾಗಿರುವ ಅಮುಖ್ಯಾರ್ಥ ಹಕ್ಕನ್ನು ಅವರು ಹೇಗೆ ದೃಢವಾಗಿ ಸ್ವಾಧೀನಪಡಿಸಿಕೊಳ್ಳುತ್ತಾರೆ. [೨೬] ಪೇಜ್ರ್ಯಾಂಕ್ಗೆ ಹೋಲಿಕೆಯಾಗುವ ಕ್ರಿಯಾತ್ಮಕ ಅಧಿಕಾನುಕೂಲ ವಿಧಾನವು ವಿಕಿಪೀಡಿಯಾ ಲಿಂಕ್ ರಚನೆಯನ್ನು ಆಧರಿಸಿದ ಗ್ರಾಹಕೀಯಗೊಳಿಸಿದ ಓದುವಿಕೆ ಪಟ್ಟಿಗಳನ್ನು ಸೃಷ್ಟಿಸಲು ಬಳಸಲ್ಪಡುತ್ತದೆ.[೨೭] ವೆಬ್ ಕ್ರಾಲರ್ ಅನೇಕ ಪ್ರಮುಖ ಮೆಟ್ರಿಕ್ಸ್ಗಳಲ್ಲಿ ಒಂದು ಎಂಬಂತೆ ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ಬಳಸಬಲ್ಲದು, ಇದು ವೆಬ್ನ ಕ್ರಾಲ್ ಅವಧಿಯಲ್ಲಿ ಭೇಟಿ ನೀಡುವ URLಅನ್ನು ಖಚಿತಪಡಿಸುವುದಕ್ಕಾಗಿ ಬಳಕೆಯಾಗುತ್ತದೆ. ಆರಂಭದ ಕೆಲಸ ಮಾಡುವ ಪತ್ರಿಕೆಗಳಲ್ಲಿ ಒಂದೂ. [೨೮] ಅವು ಗೂಗಲ್ ರಚನೆಯಲ್ಲಿ ಬಳಸಲ್ಪಟ್ಟಿದ್ದು, ಯುಆರ್ಎಲ್ ಕ್ರಮದ ಮೂಲಕ ಸಮರ್ಥ ಕ್ರಾಲಿಂಗ್ ಆಗಿದೆ . [೨೯] ಅವುಗಳನ್ನು ಅನೇಕ ವಿವಿಧ ಪ್ರಮುಖ ಮೆಟ್ರಿಕ್ಸ್ನ ಬಳಕೆಯು ಹೇಗೆ ಆಳವಾಗಿದೆ ಎಂಬುದನ್ನು ಪತ್ತೇ ಮಾಡಲು ಮತ್ತು ಎಷ್ಟು ಗೂಗಲ್ ತಾಣಗಳು ಕ್ರಾಲ್ (ನಡೆ) ಆಗಬಲ್ಲವು ಎಂಬುದನ್ನು ಚರ್ಚಿಸಲಾಗುತ್ತದೆ. ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ಈ ಅಸಂಖ್ಯಾತ ಪ್ರಮುಖ ಮೆಟ್ರಿಕ್ಸ್ಗಳಲ್ಲಿ ಒಂದೆಂಬಂತೆ ಅರ್ಪಿಸಲಾಗಿದೆ, ಆದರೆ ಅವುಗಳನ್ನು ಯುಆರ್ಎಲ್ಗಾಗಿ ಅಸಂಖ್ಯಾತ ಇನ್ಬೌಂಡ್ ಮತ್ತು ಔಟ್ಬೌಂಡ್ ಲಿಂಕ್ಗಳಂತೆ ಬೇರೆಯವರು ಪಟ್ಟಿ ಮಾಡಿದ್ದಾರೆ ಮತ್ತು ಅವು ಯುಆರ್ಎಲ್ನ ತಾಣದಲ್ಲಿ ಮಾರ್ಗ ಡೈರೆಕ್ಟರಿಯಿಂದ ಅಂತರವನ್ನು ಹೊಂದಿವೆ.ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ಸಂಪೂರ್ಣ ವೆಬ್ನಲ್ಲಿ ಸ್ವತಃ ಬ್ಲಾಗೊಸ್ಪಿಯರ್ನಂತಿರುವ ಸಮುದಾಯದ ಸ್ಪಷ್ಟ ಪ್ರಭಾವವನ್ನು ವಿಧಾನಶಾಸ್ತ್ರ Archived 2010-02-12 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. ದಂತೆ ಅಳೆಯಲು ಸಹ ಬಳಕೆ ಮಾಡಲಾಗುತ್ತದೆ. ಈ ಸಾಮೀಪ್ಯವನ್ನು ಪೇಜ್ರ್ಯಾಂಕ್ಕೋಸ್ಕರ ಬಳಸಲಾಗಿದ್ದು, ಸ್ಕೇಲ್-ಫ್ರೀ ನೆಟ್ವರ್ಕ್ ದೃಷ್ಟಿಕೋನದ ಪ್ರತಿಫಲನದಲ್ಲಿನ ಗಮನದ ವಿತರಣೆಯನ್ನು ಅಳೆಯುವುದಕ್ಕಾಗಿಯೂ ಬಳಸಲಾಗುತ್ತದೆ.ಯಾವುದೇ ಪರಿಸರ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಪೇಜ್ರ್ಯಾಂಕ್ನ ಪರ್ಯಾಯ ಆವೃತ್ತಿಯನ್ನು ಸ್ಥಿರ ಆರೋಗ್ಯದ ಪರಿಸರಕ್ಕೆ ಅಗತ್ಯವಾಗುವ ವರ್ಗಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಬಳಸಲಾಗುವುದು.[೩೦]
ಗೂಗಲ್ನ rel[ಬದಲಾಯಿಸಿ]
"ನೋಫಾಲೋ" ಆಯ್ಕೆ[ಬದಲಾಯಿಸಿ]
2005ರ ಪ್ರಾರಂಭದಲ್ಲಿ ಗೂಗಲ್ "ನೋಫಾಲೋ" [೩೧] ಎಂಬ ಹೊಸ ಆಯ್ಕೆಯನ್ನು ಎಚ್ಟಿಎಮ್ಎಲ್ ಲಿಂಕ್ನ rel ಮತ್ತು ಎಂಕರ್ ಘಟಕಗಳಿಗೆ ಕಾರ್ಯಗತಮಾಡಿತು, ಆದ್ದರಿಂದ ಗೂಗಲ್ ಪೇಜ್ರ್ಯಾಂಕ್ ಮಾಡುವಾಗ ವೆಬ್ಸೈಟನ್ನು ಅಭಿವೃದ್ಧಿಗೊಳಿಸುವವರು ಮತ್ತು ಬ್ಲಾಗ್ ಮಾಡುವವರು ಮಾಡಿದ ಲಿಂಕುಗಳನ್ನು ಪರಿಗಣಿಸುವುದಿಲ್ಲ,- ಈ ಲಿಂಕುಗಳು ಪೇಜ್ರ್ಯಾಂಕ್ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ "ಮತ" ಚಲಾಯಿಸುವುದಿಲ್ಲ. ನೋಫಾಲೋ ಸಂಪರ್ಕವನ್ನು ಸ್ಪ್ಯಾಮ್ಡೆಕ್ಸಿಂಗ್ ಹೋರಾಟಕ್ಕೆ ಸಹಾಯ ಮಾಡುವ ಪ್ರಯತ್ನವಾಗಿ ಸೇರಿಸಲಾಗಿತ್ತು. ಉದಾಹರಣೆಗೆ, ಜನರು ಈ ಹಿಂದೆ ಅನೇಕ ಸಂದೇಶ ಪಲಕಗಳನ್ನು ತಮ್ಮ ವೆಬ್ಸೈಟ್ಗೆ ಕೃತಕವಾಗಿ ಸೇರಿಸುವ ಮೂಲಕ ಹುಟ್ಟುಹಾಕಬಹುದು. ಯಾವುದೇ ಮೌಲ್ಯದ ಆದಾರವಿಲ್ಲದೆ, ಸಂದೇಶ-ಪಲಕದ ನಿರ್ವಾಹಕರು ಅವರ ಕೋಡ್ಗಳನ್ನು ಯಾಂತ್ರಿಕವಾಗಿ ಪೋಸ್ಟ್ಗಳ ಎಲ್ಲಾ ಹೈಪರ್ಲಿಂಕ್ಗಳಿಗೆ "rel='nofollow'" ಬರೆಯುವ ಮೂಲಕ ಪೇಜ್ರ್ಯಾಂಕ್ನಿಂದ ಆ ಪೋಸ್ಟ್ ಅನ್ನು ತಪ್ಪಿಸಬಹುದಾಗಿದೆ. ಈ ರೀತಿಯ ತಪ್ಪಿಸುವಿಕೆಯ ಕ್ರಮದಲ್ಲಿಯೂ ಕೂಡಾ ಕೆಲವೊಂದು ಹಿನ್ನೆಡೆಗಳಿವೆ, ಕೆಲವು ನೈಜ ಕಮೆಂಟ್ಗಳ ಲಿಂಕ್ ಮೌಲ್ಯವನ್ನು ಇದು ತಪ್ಪಿಸುತ್ತದೆ. (ನೋಡಿ: Spam in blogs#nofollow) ಯಾಂತ್ರಿಕವಾಗಲ್ಲದೆ ಪೇಜ್ರ್ಯಾಂಕ್ನ ಚಲನೆಯನ್ನು ವೆಬ್ಸೈಟ್ನ ಇತರೆ ಪೇಜ್ಗಳಲ್ಲಿ, ಹಲವು ವೆಬ್ಮಾಸ್ಟರ್ಗಳು ಪೇಜ್ರ್ಯಾಂಕ್ ಸ್ಕಲ್ಪ್ಟಿಂಗ್[೩೨] ಅನ್ನು ಉಪಯೋಗಿಸುತ್ತಾರೆ. ಇದು ವ್ಯೂಹಾತ್ಮಕವಾಗಿ nofollow ಅನ್ನು ವೆಬ್ಮಾಸ್ಟರ್ ಅತಿ ಮುಖ್ಯ ಎಂದು ಪರಿಗಣಿಸುವ ವೆಬ್ಸೈಟ್ನ ಕೆಲವು ಆಂತರಿಕ ಲಿಂಕ್ಗಳಲ್ಲಿ ಪೇಜ್ರ್ಯಾಂಕ್ ಅನ್ನು ಸೇರಿಸುವ ಪ್ರಕ್ರಿಯೆಯಾಗಿದೆ. ಈ ತಂತ್ರವನ್ನು ನೊಪಾಲೊವ್ ಅಟ್ರಿಬ್ಯೂಟ್ ಕೊಡಲು ಪ್ರಾರಂಭಿಸಿದಾಗಿನಿಂದಲೂ ಬಳಸಲಾಗುತ್ತಿದೆ. ಆದರೆ ಈ ತಂತ್ರವು ಕೆಲವು ಜನರ ಪ್ರಕಾರ ಇದರ ಪ್ರಭಾವವನ್ನು ಕಳೆದುಲಿಂಕ್ದೆ.[೩೩]
ಗೂಗಲ್ ವೆಬ್ಮಾಸ್ಟರ್ ಟೂಲ್ಗಳಿಂದ ತೆಗೆಯುವುದು[ಬದಲಾಯಿಸಿ]
ಕಂಪನಿ ತನ್ನ ವೆಬ್ಮಾಸ್ಟರ್ ಟೂಲ್ಸ್ ವಿಭಾಗದಿಂದ ಪೇಜ್ರ್ಯಾಂಕ್ನ್ನು ತೆಗೆದುಹಾಕಿದೆ ಎಂದು 14 ಅಕ್ಟೋಬರ್ 2009ರಂದು ಗೂಗಲ್ ಕೆಲಸಗಾರ್ತಿ ಸೂಸನ್ ಮೊಸ್ಕ್ವ ಸ್ಪಷ್ಟಪಡಿಸಿದ್ದಾರೆ. "ಪೇಜ್ರ್ಯಾಂಕ್ ಗೆ ಹೆಚ್ಚು ಒತ್ತು ನೀಡಬೇಡಿ ಎಂದು ನಾವು ಬಹಳ ದಿನಗಳಿಂದ ಜನರಿಗೆ ಹೇಳುತ್ತಾ ಇದ್ದೆವು; ಬಹಳ ಸೈಟ್ಗಳ ಮಾಲೀಕರು ಇದು ಅಳತೆ ಮಾಡುವ ಹೆಚ್ಚು ಮಹತ್ವಪೂರ್ಣ ವಿಧಾನ ಎಂದು ತಿಳಿದಂತೆ ತೋರುತ್ತದೆ, ಆದರೆ ಇದು ಸತ್ಯವಲ್ಲ" ಎಂದು ಹೇಳಿದ್ದಾರೆ.[೩೪] ಮೊಸ್ಕ್ವರವರು ದೃಡಪಡಿಸಿದ ಎರಡು ದಿನಗಳ ನಂತರವೂ ಪೇಜ್ರ್ಯಾಂಕ್ ನ್ನು ಗೂಗಲ್ ಟೂಲ್ಬಾರ್ನ ಮೇಲೆ ತೋರಿಸಲಾಗುತ್ತಿತ್ತು.
ಇವನ್ನೂ ಗಮನಿಸಿ[ಬದಲಾಯಿಸಿ]
- EigenTrust — a decentralized ಪೇಜ್ರ್ಯಾಂಕ್ ಗಣನಶಾಸ್ತ್ರ
- ಗೂಗಲ್ ಬಾಂಬ್
- ಗೂಗಲ್ ಮಾರ್ಗದರ್ಶನ ಸೂತ್ರ
- ಗೂಗಲ್ ಹುಡುಕಾಟ
- ಗೂಗಲ್ ಮೇಟ್ರಿಕ್ಸ್
- ಹಿಲ್ಟಾಪ್ ಗಣನಶಾಸ್ತ್ರ
- ಲಿಂಕ್ ಲವ್
- ಪೀಜನ್ Rank
- ಪವರ್ ಮೆಥಡ್ — ಪೇಜ್ರ್ಯಾಂಕ್ ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು iterative eigenvector ಗಣನಶಾಸ್ತ್ರ ಬಳಸಲಾಗುತ್ತದೆ.
- ಸರ್ಚ್ ಎಂಜಿನ್ ಆಪ್ಟಿಮೈಸೇಶನ್
- SimRank - a measure of object-to-object similarity based on random-surfer model
ಸಿಮ್ರ್ಯಾಂಕ್- ರ್ಯಾಂಡಮ್ ಸರ್ಫರ್ ಮಾದರಿ ವಿಷಯದಿಂದ ವಿಷಯಕ್ಕೆ ಸಮಾನತೆಯನ್ನು ಅಳೆಯುವುದಾಗಿದೆ
ಟಿಪ್ಪಣಿಗಳು[ಬದಲಾಯಿಸಿ]
- ↑ ೧.೦ ೧.೧ "Google Press Center: Fun Facts". www.google.com. Archived from the original on 2009-04-24. Retrieved 2009-10-05.
- ↑ Lisa M. Krieger (1 December 2005). "Stanford Earns $336 Million Off Google Stock". San Jose Mercury News, cited by redOrbit. Retrieved 2009-02-25.
- ↑ Richard Brandt. "Starting Up. How Google got its groove". Stanford magazine. Archived from the original on 2009-03-10. Retrieved 2009-02-25.
- ↑ ೪.೦ ೪.೧ ಗೂಗಲ್ ತಂತ್ರಜ್ಞಾನ
- ↑ ೫.೦ ೫.೧ ೫.೨ ೫.೩ ೫.೪ Sergey Brin, Larry Page (1998). The Anatomy of a Large-Scale Hypertextual Web Search Engine. Brisbane, Australia. pp. 107–117. Archived from the original on 2008-09-11. Retrieved 2010-03-29.
{{cite conference}}: Unknown parameter|booktitle=ignored (help) - ↑ David Vise and Mark Malseed (2005). The Google Story. p. 37. ISBN ISBN 0-553-80457-X. Archived from the original on 2006-04-28. Retrieved 2010-03-29.
{{cite book}}: Check|isbn=value: invalid character (help) - ↑ http://science.slashdot.org/story/10/02/17/2317239/ಪೇಜ್ರ್ಯಾಂಕ್-ವಿಧಾನ-ಆಲ್ಗರಿದಮ್-1940ರಿಂದ-ಪತ್ತೇಹಚ್ಚಲಾಗಿದೆ?art_pos=3
- ↑ http://www.technologyreview.com/blog/arxiv/24821/
- ↑ ೯.೦ ೯.೧ http://arxiv.org/abs/1002.2858
- ↑ ಮ್ಯಾಟ್ ಕಟ್ಸ್'ನ ಬ್ಲಾಗ್: ಸ್ಟ್ರೇಟ್ ಫ್ರಾಮ್ ಗೂಗಲ್: ವಾಟ್ ಯು ನೀಡ್ ಟು ನೌ, ಅವರ ಸ್ಲೈಡ್ಸ್ ಪುಟ 15 ನೋಡಿ.
- ↑ Taher Haveliwala and Sepandar Kamvar. (2003). "The Second Eigenvalue of the Google Matrix" (PDF). Stanford University Technical Report.
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Gianna M. Del Corso, Antonio Gullí, Francesco Romani (2005). "Fast PageRank Computation via a Sparse Linear System". Internet Mathematics. 2 (3).
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Arasu, A. and Novak, J. and Tomkins, A. and Tomlin, J. (2002). PageRank computation and the structure of the web: Experiments and algorithms. Brisbane, Australia. pp. 107–117.
{{cite conference}}: Unknown parameter|booktitle=ignored (help)CS1 maint: multiple names: authors list (link) - ↑ {0/ಗೂಗಲ್ ಪೇಜ್ರ್ಯಾಂಕ್ ಡೇಟ್ಸ್ http://www.1websitedesigner.com/google-pagerank#dates
- ↑ Aubuchon, Vaughn, "Google Ranking Factors - SEO Checklist", http://www.vaughns-1-pagers.com/internet/google-ranking-factors.htm
{{citation}}: Missing or empty|title=(help) - ↑ Fishkin, Rand (April 2, 2007). "Search Engine Ranking Factors - Version 2". seomoz.org. Retrieved May 11, 2009.
{{cite web}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ "ಆರ್ಕೈವ್ ನಕಲು". Archived from the original on 2010-02-06. Retrieved 2010-03-29.
- ↑ ೧೮.೦ ೧೮.೧ "How to report paid links". mattcutts.com/blog. April 14, 2007. Retrieved 2007-05-28.
- ↑ Jøsang, A. (2007), "Trust and Reputation Systems", in Aldini, A. (ed.), Foundations of Security Analysis and Design IV, FOSAD 2006/2007 Tutorial Lectures. (PDF), Springer LNCS 4677, pp. 209–245, doi:10.1007/978-3-540-74810-6[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ]
- ↑ SEOnotepad, "Myth of the Google Toolbar Ranking", http://www.seonotepad.com/search-engines/google-seo/myth-of-the-google-toolbar-ranking/
{{citation}}: Missing or empty|title=(help) - ↑ Johan Bollen, Marko A. Rodriguez, and Herbert Van de Sompel. (2006). "Journal Status". Scientometrics. 69 (3).
{{cite journal}}: Unknown parameter|month=ignored (help)CS1 maint: multiple names: authors list (link) - ↑ Benjamin M. Schmidt and Matthew M. Chingos (2007). "Ranking Doctoral Programs by Placement: A New Method" (PDF). PS: Political Science and Politics. 40 (July): 523–529. Archived from the original (PDF) on 2010-08-16. Retrieved 2010-03-29.
- ↑ B. Jiang (2006). "Ranking spaces for predicting human movement in an urban environment" (PDF). International Journal of Geographical Information Science. 23: 823–837.
- ↑ Jiang B., Zhao S., and Yin J. (2008). "Self-organized natural roads for predicting traffic flow: a sensitivity study" (PDF). Journal of Statistical Mechanics: Theory and Experiment. P07008.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ ರೊಬರ್ಟ್ ನವಿಗ್ಲಿ,ಮಿರೆಲ್ಲಾ ಲಾಪಾಟಾ. "ಆಯ್ನ್ ಎಕ್ಸ್ಪೀರಿಮೆಂಟಲ್ ಸ್ಟಡಿ ಆಫ್ ಗ್ರಾಫ್ ಕನೆಕ್ಟಿವಿಟಿ ಫಾರ್ ಅನ್ಸೂಪರ್ವೈಸ್ಡ್ ವರ್ಡ್ ಸೆನ್ಸ್ ಡಿಸ್ಆಯ್೦ಬಿಗೇಷನ್". IEEE ಟ್ರಾನ್ಸಾಕ್ಷನ್ಸ್ ಆನ್ ಪ್ಯಾಟರ್ನ್ ಅನಾಲಿಸೀಸ್ ಆಯ್೦ಡ್ ಮಷಿನ್ ಇಂಟೆಲಿಜೆನ್ಸ್ (ಟಿಪಿಎಎಮ್ಐ), 32(4), IEEE ಪ್ರೆಸ್, 2010, ಪು. 678-692.
- ↑ Andrea Esuli and Fabrizio Sebastiani. "PageRanking WordNet synsets: An Application to Opinion-Related Properties" (PDF). In Proceedings of the 35th Meeting of the Association for Computational Linguistics, Prague, CZ, 2007, pp. 424-431. Retrieved June 30, 2007.
{{cite web}}: Unknown parameter|dateformat=ignored (help) - ↑ Wissner-Gross, A. D. (2006). "Preparation of topical readings lists from the link structure of Wikipedia". Proceedings of the IEEE International Conference on Advanced Learning Technology. Rolduc, Netherlands: 825. doi:10.1109/ICALT.2006.1652568.
{{cite journal}}: External link in|title= - ↑ "Working Papers Concerning the Creation of Google". Google. Retrieved November 29, 2006.
{{cite web}}: Unknown parameter|dateformat=ignored (help) - ↑ Cho, J., Garcia-Molina, H., and Page, L. (1998). "Efficient crawling through URL ordering". Proceedings of the seventh conference on World Wide Web. Brisbane, Australia.
{{cite journal}}: External link in|title= - ↑ ಗೂಗಲ್ ಟ್ರಿಕ್ ಟ್ರಾಕ್ಸ್ ಎಕ್ಸ್ಟಿಂಕ್ಷನ್
- ↑ "Preventing Comment Spam". Google. Retrieved January 1, 2005.
{{cite web}}: Unknown parameter|dateformat=ignored (help) - ↑ http://www.seomoz.org/blog/ ಪೇಜ್ರ್ಯಾಂಕ್ ಶಿಲ್ಪಾಕೃತಿಯು ಶಿಲ್ಪಾಕೃತಿಯ ಮೌಲ್ಯ ಮತ್ತು ಸಮರ್ಥನೀಯ ಅನುಕೂಲಗಳನ್ನು ನೊಫಾಲೊ ಜೊತೆಗೆ ವಿಶ್ಲೇಷಿಸುತ್ತದೆ.
- ↑ http://www.mattcutts.com/blog/ಪೇಜ್ರ್ಯಾಂಕ್-ಶಿಲ್ಪಾಕೃತಿ[ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ] ರಚಿಸುವುದು/
- ↑ Susan Moskwa, "PageRank Distribution Removed From WMT", http://www.google.com/support/forum/p/Webmasters/thread?tid=6a1d6250e26e9e48&hl=en, retrieved October 16, 2009
{{citation}}: Missing or empty|title=(help); Unknown parameter|dateformat=ignored (help)
ಆಕರಗಳು[ಬದಲಾಯಿಸಿ]
- Altman, Alon (2005). Ranking Systems: The PageRank Axioms (PDF). Vancouver, BC. Archived from the original (PDF) on 2008-05-30. Retrieved 2008-02-05.
{{cite conference}}: Check date values in:|date=(help); Unknown parameter|booktitle=ignored (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Cheng, Alice (2006-06-11). Manipulability of PageRank under Sybil Strategies (PDF). Ann Arbor, Michigan. Archived from the original (PDF) on 2010-08-21. Retrieved 2008-01-22.
{{cite conference}}: Unknown parameter|booktitle=ignored (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Farahat, Ayman (2006). "Authority Rankings from HITS, PageRank, and SALSA: Existence, Uniqueness, and Effect of Initialization". SIAM Journal on Scientific Computing. 27 (4): 1181–1201.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Haveliwala, Taher (2003). An Analytical Comparison of Approaches to Personalizing PageRank (PDF).
{{cite conference}}: Check date values in:|date=(help); Unknown parameter|booktitle=ignored (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Langville, Amy N. (2003). "Survey: Deeper Inside PageRank". Internet Mathematics. 1 (3).
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Langville, Amy N. (2006). Google's PageRank and Beyond: The Science of Search Engine Rankings. Princeton University Press. ISBN 0-691-12202-4.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Page, Lawrence (1999). "The PageRank citation ranking: Bringing order to the Web". Archived from the original on 2006-04-27. Retrieved 2010-03-29.
{{cite journal}}: Cite journal requires|journal=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Richardson, Matthew (2002). The intelligent surfer: Probabilistic combination of link and content information in PageRank (PDF). Vol. 14.
{{cite conference}}: Unknown parameter|booktitle=ignored (help); Unknown parameter|coauthors=ignored (|author=suggested) (help)
ಹೊರಗಿನ ಲಿಂಕ್ಗಳು[ಬದಲಾಯಿಸಿ]
- ಗೂಗಲ್ನಿಂದ ಅವರ್ ಸರ್ಚ್: ಗೂಗಲ್ ಟೆಕ್ನೋಲಾಜಿ
- ಅಮೆರಿಕನ್ ಮೆಥಮ್ಯಾಟಿಕಲ್ ಸೊಸೈಟಿಯಿಂದ ಹೌ ಗೂಗಲ್ ಫೈಂಡ್ಸ್ ಯುವರ್ ನೀಡ್ಲ್ ಇನ್ ದ ವೆಬ್ಸ್ ಹೆಸ್ಟಾಕ್
- ಒರಿಜಿನಲ್ ಪೇಜ್ರ್ಯಾಂಕ್ ಯು.ಎಸ್. ಪೇಟೆಂಟ್- ಮೆಥಡ್ ಫಾರ್ ನೋಡ್ ರಾಂಕಿಂಗ್ ಇನ್ ಲಿಂಕ್ಡ್ ಡಾಟಾಬೇಸ್ Archived 2014-08-29 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. - ಸೆಪ್ಟೆಂಬರ್ 4, 2001
- ಒರಿಜಿನಲ್ ಪೇಜ್ರ್ಯಾಂಕ್ ಯು.ಎಸ್. ಪೇಟೆಂಟ್- ಮೆಥಡ್ ಫಾರ್ ಸ್ಕೋರಿಂಗ್ ಡಾಕ್ಯುಮೆಂಟ್ಸ್ ಇನ್ ಲಿಂಕ್ಡ್ ಡಾಟಾಬೇಸ್ Archived 2021-02-24 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. - ಸೆಪ್ಟೆಂಬರ್ 28, 2004
- ಪೇಜ್ರ್ಯಾಂಕ್ ಯು.ಎಸ್. ಪೇಟೆಂಟ್-ಮೆಥಡ್ ಫಾರ್ ನೋಡ್ ರಾಂಕಿಂಗ್ ಇನ್ ಎ ಲಿಂಕ್ಡ್ ಡಾಟಾಬೇಸ್ Archived 2019-08-28 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. - ಜೂನ್ 6, 2006
- ಪೇಜ್ರ್ಯಾಂಕ್ ಯು.ಎಸ್.ಪೇಟೆಂಟ್- ಸ್ಕೋರಿಂಗ್ ಡಾಕ್ಯುಮೆಂಟ್ಸ್ ಇನ್ ಎ ಲಿಂಕ್ಡ್ ಡಾಟಾಬೇಸ್ Archived 2018-03-31 ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. - ಸೆಪ್ಟೆಂಬರ್ 11, 2007
- ಸೈಂಟಿಸ್ಟ್ ಡಿಸ್ಕವರ್ಸ್ ಪೇಜ್ರ್ಯಾಂಕ್-ಟೈಪ್ ಅಲ್ಗಾರಿದಮ್ ಫ್ರಮ್ ದ 1940 [ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಕೊಂಡಿ] - ಫೆಬ್ರುವರಿ 17, 2010
- ವಿಕಿಪೀಡಿಯಾದೊಂದಿಗಿನ ಲಿಂಕ್ ಕಟ್ಟಡವು ಹೇಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ? - ಏಪ್ರಿಲ್ 28, 2019
- Pages using deprecated source tags
- CS1 errors: unsupported parameter
- CS1 errors: ISBN
- CS1 maint: multiple names: authors list
- CS1 errors: missing title
- CS1 errors: bare URL
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಲೇಖನಗಳು from ಆಗಸ್ಟ್ 2021
- ಶಾಶ್ವತವಾಗಿ ಮಡಿದ ಬಾಹ್ಯ ಕೊಂಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಎಲ್ಲಾ ಲೇಖನಗಳು
- CS1: long volume value
- CS1 errors: external links
- Articles with unsourced statements from October 2009
- Articles with invalid date parameter in template
- ವೆಬ್ ಆರ್ಕೈವ್ ಟೆಂಪ್ಲೇಟಿನ ವೇಬ್ಯಾಕ್ ಕೊಂಡಿಗಳು
- CS1 errors: dates
- CS1 errors: missing periodical
- ಗೂಗಲ್
- ಸರ್ಚ್ ಎಂಜಿನ್ ಆಪ್ಟಿಮೈಸೇಶನ್
- ಒಳ್ಳೆಯ ಹೆಸರಾದ ಆಡಳಿತ ಮಂಡಳಿ
- ಅಂತರ್ಜಾಲ ಹುಡುಕಾಟದ ಗಣನಶಾಸ್ತ್ರ
- ಅಮೆರಿಕಾದ ಸಂಶೋಧನೆಗಳು
- ಕ್ರೌಡ್ಸೋರ್ಸಿಂಗ್
- ಮಾರ್ಕೊವ್ ಮಾಡೆಲ್ಸ್
- ಲಿಂಕ್ ಅನಾಲಿಸೀಸ್




















































