ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರ

ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರ ಎಂಬುದು ಕಿಣ್ವಗಳಿಂದ ವೇಗವರ್ಧನೆಗೆ ಒಳಪಡುವಂತಹ ರಾಸಾಯನಿಕ ಪ್ರತಿಕ್ರಿಯೆಗಳ ಅಧ್ಯಯನವಾಗಿದೆ. ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರದಲ್ಲಿ, ಪ್ರತಿಕ್ರಿಯೆಯ ದರವನ್ನು (ವೇಗ) ಅಳತೆಮಾಡಲಾಗುತ್ತದೆ. ಅಲ್ಲದೇ ಈ ಕ್ರಿಯೆಯ ಸ್ಥಿತಿಯಲ್ಲಿ ಉಂಟಾದ ಬದಲಾವಣೆಯಿಂದ ಆಗಬಹುದಾದ ಪರಿಣಾಮಗಳನ್ನು ಕೂಡ ಪರೀಕ್ಷಿಸಲಾಗುತ್ತದೆ. ಕಿಣ್ವದ ಚಲನಶಾಸ್ತ್ರವನ್ನು ಈ ರೀತಿ ಅಧ್ಯಯನ ಮಾಡುವುದರಿಂದ, ಕಿಣ್ವದ ವೇಗವರ್ಧನೆಯ ಕಾರ್ಯಚಟುವಟಿಕೆಯನ್ನು ತಿಳಿಯಬಹುದಾಗಿದೆ. ಇದರ ಜೊತೆಯಲ್ಲಿ ಚಯಾಪಚಯ ಕ್ರಿಯೆಯಲ್ಲಿ ಇದರ ಪಾತ್ರವೇನು, ಹೇಗೆ ಇದರ ಕ್ರಿಯಾಶೀಲತೆಯನ್ನು ನಿಯಂತ್ರಿಸಬಹುದು, ಹಾಗು ಹೇಗೆ ಮಾದಕ ವಸ್ತು ಅಥವಾ ವಿಷ, ಕಿಣ್ವದಲ್ಲಿನ ಕ್ರಿಯೆಯನ್ನು ತಡೆಗಟ್ಟಬಲ್ಲದು ಎಂಬುದರ ಬಗ್ಗೆ ತಿಳಿಯಬಹುದಾಗಿದೆ. ಕಿಣ್ವಗಳು ಸಾಮಾನ್ಯವಾಗಿ ಪ್ರೋಟೀನ್ ಅಣುಗಳಾಗಿದ್ದು, ಇತರ ಅಣುಗಳನ್ನು ಬಳಸಿಕೊಳ್ಳುತ್ತವೆ. ಇತರ ಅಣುಗಳೆಂದರೆ ಕಿಣ್ವಗಳ ತಲಾಧಾರಗಳು (ಸಬ್ ಸ್ಟ್ರೇಟ್ಸ್ )(ಸೂಕ್ಷ್ಮ ಜೀವಿ ಯಾವ ತಲದ ಮೇಲೆ ನೆಲಸಿ ವರ್ಧಿಸುವುದೋ ಆ ಆಧಾರ). ಈ ಬಳಸಿಕೊಳ್ಳುವಂತಹ ಅಣುಗಳು ಕಿಣ್ವದ ಸಕ್ರಿಯ ಸೈಟ್(ತಲಾಧಾರವು ಬಂಧಿಸಲ್ಪಟ್ಟು ಪ್ರಕ್ರಿಯೆಗೆ ಒಳಪಡುವ ಕಿಣ್ವದ ಭಾಗ)ನಲ್ಲಿ ಬಂಧಿಸಲ್ಪಡುತ್ತವೆ; ಅಲ್ಲದೇ ಇವುಗಳನ್ನು ಕ್ರಮಗಳ ಸರಣಿಯ ಮೂಲಕ ಉತ್ಪನ್ನವಾಗಿ ರೂಪಾಂತರಿಸಲಾಗುತ್ತದೆ. ಈ ಕ್ರಮಗಳ ಸರಣಿಯನ್ನು ಕಿಣ್ವಕ ಕಾರ್ಯರೀತಿ (ವಿಧಾನ)ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ಕಾರ್ಯರೀತಿಗಳನ್ನು ಏಕ-ತಲಾಧಾರ ಮತ್ತು ಬಹು-ತಲಾಧಾರದ ಕಾರ್ಯರೀತಿಗಳೆಂದು ವಿಂಗಡಿಸಬಹುದಾಗಿದೆ. ಟ್ರಿಯೊಸ್ ಫಾಸ್ಫೆಟ್ ಐಸೊಮರ್ಸ್ ನಂತಹ ಕೇವಲ ಒಂದು ತಲಾಧಾರವನ್ನು ಮಾತ್ರ ಬಂಧಿಸುವ ಕಿಣ್ವಗಳ ಮೇಲಿನ ಚಲನಶಾಸ್ತ್ರದ ಅಧ್ಯಯನವು, ಕಿಣ್ವವು ಈ ತಲಾಧಾರವನ್ನು ಯಾವುದರಲ್ಲಿ ಬಂಧಿಸುತ್ತದೆಯೋ ಅದರ ಆಕರ್ಷಣ ಬಲವನ್ನು ಅಳತೆ ಮಾಡುವ ಹಾಗು ಉತ್ಪತ್ತಿಯ ದರವನ್ನು ಅಳತೆ ಮಾಡುವ ಗುರಿ ಹೊಂದಿರುತ್ತದೆ. ಡೈಹೈಡ್ರೊಫೊಲೇಟ್ ರಿಡಕ್ಟೇಸ್(ಜೈವಿಕ ರಾಸಾಯನಿಕದ ಬದಲಾವಣೆ)(ಬಲಭಾಗದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ.) ನಂತಹ ಕಿಣ್ವಗಳು ಬಹು ತಲಾಧಾರಗಳನ್ನು ಬಂಧಿಸಿದಾಗ, ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರವು ಈ ತಲಾಧಾರಗಳು ಯಾವ ಸರಣಿಯಲ್ಲಿ ಬಂಧಿಸಲ್ಪಡುತ್ತವೆ ಎಂಬುದನ್ನು ತೋರಿಸಬಲ್ಲದು. ಅಲ್ಲದೇ ಯಾವ ಕ್ರಮಾನುಗತಿಯಲ್ಲಿ ಉತ್ಪನ್ನಗಳನ್ನು ಬಿಡುಗಡೆಮಾಡುತ್ತವೆ ಎಂಬುದನ್ನೂ ಕೂಡ ತೋರಿಸಬಲ್ಲದು. ಏಕ ತಲಾಧಾರವನ್ನು ಬಂಧಿಸಿ ಬಹು ಉತ್ಪನ್ನಗಳನ್ನು ಬಿಡುಗಡೆ ಮಾಡುವ ಕಿಣ್ವಗಳ ಉದಾಹರಣೆಯು ಪ್ರೋಟಿಯೇಸ್(ಪ್ರೋಟೀನ್ ಗಳು) ಆಗಿದೆ, ಇದು ಒಂದು ಪ್ರೋಟೀನ್ ತಲಾಧಾರವನ್ನು ಎರಡು ಪಾಲಿಪೆಪ್ಟೈಡ್ ಆಗಿ ವಿಭಜಿಸುತ್ತದೆ. ಎರಡು ತಲಾಧಾರಗಳನ್ನು ಒಟ್ಟಿಗೆಸೇರಿಸುವ DNA ಪಾಲಿಮರೇಸ್ ನಂತಹ ಇತರ ಕಿಣ್ವಗಳು ನ್ಯೂಕ್ಲಿಯೊಟೈಡ್ ಅನ್ನು DNAಯೊಂದಿಗೆ ಸೇರಿಸುತ್ತವೆ. ಈ ಕಾರ್ಯರೀತಿಯು ಅತ್ಯಂತ ಕಷ್ಟಕರವಾದ ಕ್ರಮಗಳ ಸರಣಿಯಾಗಿದ್ದರೂ ಕೂಡ, ಚಲನೆಗಳನ್ನು ಒಟ್ಟಾಗಿ ನಿರ್ಧರಿಸುವ ಒಂದು ರೇಟ್- ಡಿಟರ್ಮೈನಿಂಗ್ ಸ್ಟೆಪ್ (ದರ ನಿರ್ಧರಿಸುವ ಕ್ರಮ) ಇದೆ. ಈ ದರ-ನಿರ್ಧರಿಸುವ ಕ್ರಮವು ಬಹುಶಃ ರಾಸಾಯನಿಕ ಪ್ರತಿಕ್ರಿಯೆಯಾಗಿರಬಹುದು ಅಥವಾ ಕಿಣ್ವದಿಂದ ಬಿಡುಗಡೆಯಾಗುವ ಉತ್ಪನ್ನ(ಗಳು)ದಲ್ಲಿ ಒಳಗೊಂಡಿರುವ ಕಿಣ್ವದ ಅಥವಾ ತಲಾಧಾರಗಳ ಕನ್ ಫಾರ್ಮೇಷನಲ್ ಐಸಾಮರಿಸಮ್ ನ ಬದಲಾವಣೆಯಾಗಿರಬಹುದು. ಕೋಶಗಳಲ್ಲಿನ ಪ್ರೋಟೀನ್ ರಚನೆಯ ತಿಳಿವಳಿಕೆಯು ಚಲನಶಾಸ್ತ್ರದ ದತ್ತಾಂಶವನ್ನು ವಿವರಿಸಲು ಸಹಾಯಕವಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ರಚನೆಯು ವೇಗವರ್ಧನೆಯ ಸಂದರ್ಭದಲ್ಲಿ ಹೇಗೆ ತಲಾಧಾರಗಳು ಮತ್ತು ಉತ್ಪನ್ನಗಳು ಬಂಧಿಸಲ್ಪಡುತ್ತವೆ ಎಂಬುದನ್ನು ಈ ರಾಚನಿಕತೆ ಸೂಚಿಸಬಲ್ಲದು; ಪ್ರತಿಕ್ರಿಯೆಯ ಸಂದರ್ಭದಲ್ಲಿ ಯಾವ ಬದಲಾವಣೆಗಳು ಉಂಟಾದವು; ಅಲ್ಲದೇ ಈ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ ಉಳಿಯುವ ಶೇಷ ಅಮೈನೊ ಆಮ್ಲದ ಪಾತ್ರವನ್ನು ಕೂಡ ಸೂಚಿಸಬಲ್ಲದು. ಈ ಕಾರ್ಯವಿಧಾನದ ಪ್ರತಿಕ್ರಿಯೆಯ ಸಮಯದಲ್ಲಿ ಕೆಲವು ಕಿಣ್ವಗಳು ಪರಿಣಾಮಕಾರಿಯಾಗಿ ಆಕಾರ ಬದಲಾಯಿಸುತ್ತವೆ; ಇಂತಹ ಸಂದರ್ಭದಲ್ಲಿ ಇದು ಬಂಧಿತ ಮತ್ತು ಬಂಧಿತವಲ್ಲದ ತಲಾಧಾರ ಸದೃಶಯೊಂದಿಗೆ ಕಿಣ್ವದ ರಚನೆಯನ್ನು ನಿರ್ಧರಿಸಲು ಸಹಾಯಮಾಡುತ್ತದೆ. ಎಲ್ಲಾ ಜೈವಿಕ ವೇಗವರ್ಧಕಗಳು ಪ್ರೋಟೀನ್ ಕಿಣ್ವಗಳಾಗಿರುವುದಿಲ್ಲ; ರೈಬೊಸೈಮ್ಸ್ ಮತ್ತು ರೈಬೊಸಮ್ಸ್ ನಂತಹ RNA- ಆಧಾರಿತ ವೇಗವರ್ಧಕಗಳು ಅನೇಕ ಕೋಶಗಳ ಕ್ರಿಯೆಗೆ ಅಗತ್ಯವಾಗಿವೆ. ಉದಾಹರಣೆಗೆ, RNA ಸ್ಪ್ಲೈಸಿಂಗ್ ಮತ್ತು ಟ್ರಾನ್ಸ್ಲೇಷನ್. ರೈಬೊಸೈಮ್ಸ್ ಮತ್ತು ಕಿಣ್ವಗಳ ನಡುವಿನ ಪ್ರಮುಖ ವ್ಯತ್ಯಾಸವೆಂದರೆ, RNA ವೇಗವರ್ಧಕಗಳು ನ್ಯೂಕ್ಲಿಯೊಟೈಡ್ ಗಳಿಂದ ರಚಿತವಾಗಿರುತ್ತವೆ. ಕಿಣ್ವಗಳು ಅಮೈನೊ ಆಮ್ಲಗಳಿಂದ ರಚಿತವಾಗಿರುತ್ತವೆ. ರೈಬೊಸೈಮ್ಸ್ ಹೆಚ್ಚು ಸೀಮಿತ ಪ್ರತಿಕ್ರಿಯೆಗಳ ಸರಣಿಯನ್ನು ಪ್ರದರ್ಶಿಸಿದರೂ ಕೂಡ, ಅವುಗಳ ಯಾಂತ್ರಿಕ ರೀತಿಯ ಕ್ರಿಯಾ ಕಾರ್ಯರೀತಿ ಗಳನ್ನು ಮತ್ತು ಚಲನಶಾಸ್ತ್ರವನ್ನು ಒಂದೇ ರೀತಿಯ ವಿಧಾನದ ಮೂಲಕ ವಿಶ್ಲೇಷಿಸಬಹುದು ಮತ್ತು ವರ್ಗೀಕರಿಸಬಹುದು.

ಸಾಮಾನ್ಯ ತತ್ವಗಳು

ಪ್ರಕ್ರಿಯೆಯ ದರವು ತಲಾಧಾರದ ಸಾರೀಕರಣ ಹೆಚ್ಚಿದಂತೆ ಹೆಚ್ಚಾಗುತ್ತ ಹೋಗುತ್ತದೆ, ಆದರೆ ತಲಾಧಾರದ ಅತ್ಯಂತ ಹೆಚ್ಚು ಸಾರೀಕರಣದಲ್ಲಿ ಇವು ನೆನೆಯುತ್ತವೆ.

ಕಿಣ್ವದಿಂದ ವೇಗವರ್ಧನೆಗೆ ಒಳಪಟ್ಟ ಪ್ರತಿಕ್ರಿಯೆಯು, ಖಚಿತವಾಗಿ ಅದೇ ಪ್ರತಿಕ್ರಿಯಾಕಾರಿಯನ್ನು ಬಳಸುತ್ತದೆ. ಅಲ್ಲದೇ ವೇಗವರ್ಧನೆಗೆ ಒಳಪಡದ ಕಾರ್ಯದಲ್ಲಿ ನೀಡುವ ಉತ್ಪನ್ನವನ್ನೇ ಇದು ಕೂಡ ಒದಗಿಸುತ್ತದೆ. ಇತರ ವೇಗವರ್ಧಕಗಳಂತೆ, ಕಿಣ್ವಗಳು ಕೂಡ ತಲಾಧಾರಗಳು ಮತ್ತು ಉತ್ಪನ್ನಗಳ ನಡುವಿನ ತಟಸ್ಥ ಸ್ಥಾನವನ್ನು ಬದಲಾಯಿಸುವುದಿಲ್ಲ.^[೧] ಆದರೂ, ವೇಗವರ್ಧನೆಗೆ ಒಳಪಡದ ರಾಸಾಯನಿಕ ಪ್ರತಿಕ್ರಿಯೆಗಳಂತೆ, ಕಿಣ್ವ-ವೇಗವರ್ಧನೆಗೆ ಒಳಪಟ್ಟ ಕ್ರಿಯೆಗಳು ಚಲನಶಾಸ್ತ್ರದ ಆದ್ರೀಕರಣವನ್ನು (ಹೀರಿಕೊಳ್ಳುವಿಕೆ)ತೋರಿಸುವುದಿಲ್ಲ. ಕಿಣ್ವದ ಸಾರೀಕರಣಕ್ಕಾಗಿ ಮತ್ತು ತುಲನಾತ್ಮಕವಾಗಿ ಕಡಿಮೆಯಿರುವಂತಹ ತಲಾಧಾರದ ಸಾರೀಕರಣಕ್ಕಾಗಿ, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ದರವು ತಲಾಧಾರದ ಸಾರೀಕರಣದೊಂದಿಗೆ ರೇಖೀಯವಾಗಿ ಹೆಚ್ಚುತ್ತಾಹೋಗುತ್ತದೆ ; ಕಿಣ್ವದ ಅಣುಗಳು ಪ್ರತಿಕ್ರಿಯೆಯ ವೇಗವನ್ನು ವರ್ಧಿಸಲು ಮುಕ್ತವಾಗಿರುತ್ತವೆ. ಅಲ್ಲದೇ ತಲಾಧಾರ ಸಾರೀಕರಣವು ಹೆಚ್ಚುತ್ತಿದೆ ಎಂದರೆ ಕಿಣ್ವ ಮತ್ತು ತಲಾಧಾರದ ಅಣುಗಳು ಒಂದು ಮತ್ತೊಂದನ್ನು ಸಂಧಿಸುವ ದರವು ಹೆಚ್ಚಾಗುತ್ತಿದೆ ಎಂದಾಗುತ್ತದೆ. ಆದರೂ ತಲಾಧಾರದ ಸಾರೀಕರಣವು ತುಲನಾತ್ಮಕವಾಗಿ ಅಧಿಕವಿದ್ದಾಗ, ಒಂದೊಕ್ಕೊಂದರ ವರ್ಧಿತ ದರವು ಅಸಂಪಾತವಾಗಿ(ನಿರ್ದಿಷ್ಟ ರೇಖೆಯನ್ನು ಸ್ಪರ್ಶಿಸುವುದು ಎಂಬಂತೆ, ಆದರೆ ಸ್ಪರ್ಶಿಸದೆ ಅದರ ಬಳಿ ಸಾಗುತ್ತಿರುವ), ಊಹಾತ್ಮಕ ಗರಿಷ್ಠ ಮಟ್ಟವನ್ನು ಮುಟ್ಟುತ್ತದೆ; ಕಿಣ್ವದ ಬಹುತೇಕ ಎಲ್ಲಾ ಸಕ್ರಿಯ ಜಾಗೆಗಳು ಆಕ್ರಮಿಸಲ್ಪಟ್ಟಿರುತ್ತವೆ. ಅಲ್ಲದೇ ಕ್ರಿಯೆಯ ದರವನ್ನು ಕಿಣ್ವದ ಸ್ವಾಭಾವಿಕ ಉತ್ಪಾದನಾ ದರದ ಮೇಲೆ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ಈ ಎರಡು ಸೀಮಿತಗೊಳಿಸುವ ಪ್ರಕರಣಗಳ ನಡುವಿನ ತಲಾಧಾರ ಸಾರೀಕರಣದ ಮಧ್ಯಮ ಗತಿಯ K _M ತತ್ವದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಕಿಣ್ವದ ಚಲನೆಯ ಎರಡು ಅತ್ಯಂತ ಪ್ರಮುಖ ಗುಣಾತ್ಮಕ ಅಂಶಗಳಿವೆ ಅವುಗಳೆಂದರೆ: ಕಿಣ್ವವು ಹೇಗೆ ಅತಿ ಬೇಗ ಪ್ರತ್ಯೇಕ ತಲಾಧಾರದೊಂದಿಗೆ ಆರ್ದ್ರವಾಗುತ್ತದೆ ಹಾಗು ಹೇಗೆ ಅದು ಗರಿಷ್ಠ ದರವನ್ನು ಸಾಧಿಸುತ್ತದೆ. ಈ ವಿಷಯಗಳನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದರಿಂದ ಕಿಣ್ವವು ಕೋಶದಲ್ಲಿ ಏನು ಮಾಡಬಹುದು ಎಂಬುದನ್ನು ಸೂಚಿಸಬಹುದಾಗಿದೆ. ಅಲ್ಲದೇ ಕಿಣ್ವವು ಈ ಸ್ಥಿತಿಯಲ್ಲಿ ಬದಲಾವಣೆಗಳಿಗೆ ಹೇಗೆ ಪ್ರತಿಕ್ರಿಯಿಸುತ್ತದೆ ಎಂಬುದನ್ನು ತೋರಿಸಬಹುದಾಗಿದೆ.

ಕಿಣ್ವದ ವಿಶ್ಲೇಷಣೆಗಳು

ಕಿಣ್ವ ವಿಶ್ಲೇಷಣೆಯೆಂಬುದು, ಪ್ರಯೋಗಾಲಯದ ಕಾರ್ಯವಿಧಾನವಾಗಿದ್ದು, ಇದು ಕಿಣ್ವ ಪ್ರತಿಕ್ರಿಯೆಗಳ ದರವನ್ನು(ವೇಗ) ಅಳೆಯುತ್ತದೆ. ಏಕೆಂದರೆ ಕಿಣ್ವಗಳು ಅವು ವೇಗವರ್ಧಿಸುವ ಪ್ರತಿಕ್ರಿಯೆಗಳಿಂದಾಗಿ ನಾಶವಾಗುವುದಿಲ್ಲ. ಕಿಣ್ವದ ವಿಶ್ಲೇಷಣೆಯು, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಕ್ರಿಯೆಯ ದರವನ್ನು ಅಳೆಯಲು ತಲಾಧಾರಗಳ ಸಾರೀಕರಣದಲ್ಲಿ ಅಥವಾ ಉತ್ಪನ್ನಗಳ ಸಾರೀಕರಣದಲ್ಲಿ ಬದಲಾವಣೆಯನ್ನು ಅನುಸರಿಸುತ್ತವೆ. ಮಾಪನದ ಅನೇಕ ವಿಧಾನಗಳಿವೆ. ರೋಹಿತ ದ್ಯುತಿಮಾಪಕ ವಿಶ್ಲೇಷಣೆಯು, ಉತ್ಪನ್ನಗಳು ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾಕಾರಿಗಳ ನಡುವೆ ಬೆಳಕಿನ ಹೀರುವಿಕೆಯಲ್ಲಿ ನಡೆಯುವ ಬದಲಾವಣೆಯನ್ನು ವೀಕ್ಷಿಸುತ್ತದೆ; ರೇಡಿಯೋಮಾಪನ ವಿಶ್ಲೇಷಣೆಯು, ಸಂಯೋಜನೆಯನ್ನು ಅಥವಾ ಸಮಯದ ಆಧಾರಕ್ಕನುಗುಣವಾಗಿ ಉತ್ಪನ್ನ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಪ್ರಕ್ರಿಯೆಯ ಮೊತ್ತವನ್ನು ಅಳೆಯಲು ವಿಕಿರಣಪಟುತ್ವದ ಬಿಡುಗಡೆಯನ್ನು ಒಳಗೊಂಡಿದೆ. ರೋಹಿತ ದ್ಯುತಿಮಾಪಕ ವಿಶ್ಲೇಷಣೆಯು, ಈ ಕ್ರಿಯೆಯ ದರವನ್ನು ನಿರಂತರವಾಗಿ ಗಣಿಸಿ ಅಳೆಯಲು ಅವಕಾಶನೀಡುತ್ತದೆ ಎಂಬ ಕಾರಣಕ್ಕಾಗಿ ಇದು ಅತ್ಯಂತ ಅನುಕೂಲಕರವಾಗಿದೆ. ರೇಡಿಯೋಮಾಪನ ವಿಶ್ಲೇಷಣೆಯು ಮಾದರಿಗಳನ್ನು (ಸ್ಯಾಂಪಲ್ ಗಳು)(ಉದಾಹರಣೆಗೆ ಇವು ಅನುಕ್ರಮವಾಗಿಲ್ಲದ ವಿಶ್ಲೇಷಣೆಗಳು) ತೆಗೆದುಹಾಕಬೇಕು ಮತ್ತು ಎಣಿಸಬೇಕು ಎಂದು ಅಪೇಕ್ಷಿಸಿದರೂ ಕೂಡ, ಅವು ಅತ್ಯಂತ ಸೂಕ್ಷ್ಮವಾಗಿರುತ್ತವೆ. ಅಲ್ಲದೇ ಇದು ಕಿಣ್ವ ದ್ಯುತಿಪಟುತ್ವದ ಅತ್ಯಂತ ಕೆಳಮಟ್ಟಗಳನ್ನು ಅಳೆಯುತ್ತದೆ .^[೨] ಸಂಯೋಜನೆಯನ್ನು ನಿಯಂತ್ರಿಸಲು ಅಥವಾ ತಲಾಧಾರವು ಉತ್ಪನ್ನವಾಗಿ ಬದಲಾಗುವಂತೆ ರಾಸಾಯನಿಕ ಐಸೋಟೋಪ್ ಗಳನ್ನು ಬಿಡುಗಡೆ ಮಾಡಲು ಮಾಸ್ ಸ್ಪೆಕ್ಟ್ರೋಮೆಟ್ರಿ(ದ್ರವ್ಯರಾಶಿ ಗಾತ್ರ) ಎಂಬ ವಿಧಾನ ಬಳಸುವುದು ಹೋಲಿಕೆಯ ದೃಷ್ಟಿಯಿಂದ ಉತ್ತಮವಾಗಿದೆ. ಅತ್ಯಂತ ಸೂಕ್ಷ್ಮವಾದ ಕಿಣ್ವ ವಿಶ್ಲೇಷಣೆಗಳು,ಸೂಕ್ಷ್ಮದರ್ಶಕದ ಮೂಲಕ ನಾಭೀಕರಿಸಿದ ಲೇಸರ್ ಗಳನ್ನು ಬಳಸುತ್ತದೆ. ಈ ಲೇಸರ್ ಗಳನ್ನು ಕಿಣ್ವವು ಅವುಗಳ ಕ್ರಿಯಾತ್ಮಕ ವೇಗವನ್ನು ವರ್ಧಿಸಿದಾಗ, ಒಂದು ಕಿಣ್ವದ ಅಣುಗಳಲ್ಲಿ ಉಂಟಾಗುವ ಬದಲಾವಣೆಯನ್ನು ವೀಕ್ಷಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ. ಈ ಮಾಪನಗಳು, ಕಿಣ್ವದ ಕ್ರಿಯಾ ಕಾರ್ಯರೀತಿಯ ಸಂದರ್ಭದಲ್ಲಿ ಕೊಫ್ಯಾಕ್ಟರ್ಸ್(ಪ್ರೋಟೀನ್ ಇಲ್ಲದ ರಾಸಾಯನಿಕ ಸಂಯುಕ್ತ) ನ ಪ್ರತಿದೀಪ್ತಿಯಲ್ಲಿ ಬದಲಾವಣೆಯನ್ನು ಬಳಸುತ್ತವೆ. ಅಥವಾ ಪ್ರೋಟೀನ್ ನ ನಿರ್ದಿಷ್ಟ ಭಾಗಗಳಿಗೆ ಪ್ರತಿ ದೀಪಕ ವರ್ಣದ್ರವ್ಯವನ್ನು ಸೇರಿಸುತ್ತವೆ. ಈ ವರ್ಣದ್ರವ್ಯವನ್ನು ವೇಗವರ್ಧನೆಯ ಸಹ ಉತ್ಪನ್ನದ ಕ್ರಿಯೆಯ ಸಂದರ್ಭದಲ್ಲಿ ದೊರೆಯುವ ಕ್ಷಣಗಳನ್ನು (ಟಿಪ್ಪಣಿ)ವರದಿ ಮಾಡಲು ಸೇರಿಸಲಾಗುತ್ತದೆ.^[೩] ಈ ಅಧ್ಯಯನಗಳು ಚಲನಶಾಸ್ತ್ರಗಳ ಬಗ್ಗೆ ಮತ್ತು ಏಕ ಕಿಣ್ವದ ಚಾಲಕಶಕ್ತಿಗಳ ಬಗ್ಗೆ ಹೊಸ ದೃಷ್ಟಿಕೋನವನ್ನು ಒದಗಿಸುತ್ತವೆ. ಈ ಹೊಸ ದೃಷ್ಟಿಕೋನವು ಮಿಲಿಯನ್ ಗಟ್ಟಲೆ ಕಿಣ್ವ ಅಣುಗಳ ಸಾಮಾನ್ಯ ವರ್ತನೆಯನ್ನು ವೀಕ್ಷಿಸುತ್ತಿದ್ದ ಸಾಂಪ್ರದಾಯಿಕ ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರಕ್ಕೆ ವ್ಯತಿರಿಕ್ತವಾಗಿದೆ.^[೪]^[೫] ಕಿಣ್ವ ವಿಶ್ಲೇಷಣೆಗಾಗಿ ಮುಂದುವರೆಯುತ್ತಿರುವ ಉದಾಹರಣೆ ವಿವರಣೆಗಾಗಿ ವಕ್ರರೇಖೆಯನ್ನು ಮೇಲ್ಭಾಗದಲ್ಲಿ ಕೊಡಲಾಗಿದೆ. ಕಿಣ್ವವು ಆರಂಭಿಕ ದರದಲ್ಲಿ ಉತ್ಪನ್ನವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ. ಈ ದರವು ಕ್ರಿಯೆ ಪ್ರಾರಂಭವಾದ ನಂತರ ಅಲ್ಪಾವಧಿಯಲ್ಲಿಯೇ ಹೆಚ್ಚು ಕಡಿಮೆ ರೇಖೀಯವಾಗಿರುತ್ತದೆ. ಪ್ರತಿಕ್ರಿಯೆಯು ನಡೆದಂತೆ ಮತ್ತು ತಲಾಧಾರವು ನಶಿಸುತ್ತಹೋದಂತೆ ದರವು ಸತತವಾಗಿ ಕಡಿಮೆಯಾಗುತ್ತದೆ.ಇಲ್ಲಿನ ರಾಸಾಯನಿಕ ಸ್ಪಂದನಶೀಲತೆ ಹೀರಿಕೆಯ ಮಟ್ಟ ತೋರಿಸುತ್ತದೆ.(ತಲಾಧಾರವು ಆರ್ದ್ರಮಟ್ಟದಲ್ಲಿ ಇರದ ವರೆಗೆ). ಆರಂಭಿಕ(ಮತ್ತು ಗರಿಷ್ಠ) ದರವನ್ನು ಅಳೆಯಲು, ಕಿಣ್ವ ವಿಶ್ಲೇಷಣೆಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಪ್ರತಿಕ್ರಿಯೆಯು ಪ್ರಗತಿಯಲ್ಲಿದ್ದಾಗ ಮಾಡಲಾಗುತ್ತದೆ. ಅದರಲ್ಲೂ ಕ್ರಿಯೆ ಸಂಪೂರ್ಣವಾಗಲು ಕೆಲವೇ ಕೆಲವು ಪ್ರತಿಶತದಷ್ಟು ಬಾಕಿಯಿದ್ದಾಗ ವಿಶ್ಲೇಷಣೆ ಮಾಡಲಾಗುತ್ತದೆ. ಆರಂಭಿಕ ದರದ ಕಾಲಾವಧಿಯು ವಿಶ್ಲೇಷಣಾ ಸ್ಥಿತಿಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಅಲ್ಲದೇ ಇದು ಮಿಲಿಸೆಕೆಂಡ್ ನಿಂದ ಪ್ರತಿ ಗಂಟೆಗೆ ಏರಬಲ್ಲದು. ಆದರೂ, ದ್ರವಗಳನ್ನು ವೇಗವಾಗಿ ಬೆರೆಸಲು ಬಳಸುವ ಸಾಧನವು, ಒಂದು ಸೆಕೆಂಡ್ ಗಿಂತ ಕಡಿಮೆ ಅವಧಿಯಲ್ಲಿ ಆರಂಭಿಕ ದರದಲ್ಲೇ, ವೇಗವಾಗಿ ಚಲನಶಾಸ್ತ್ರದ ಅಳತೆಗೆ ಅವಕಾಶ ಮಾಡಿಕೊಡುತ್ತದೆ.^[೬] ಈ ಅನೇಕ ತೀವ್ರಗತಿಯ ವಿಶ್ಲೇಷಣೆಗಳು ಪೂರ್ವ ಸ್ಥಿರತೆಯ ಚಲನೆಗಳನ್ನು ಮಾಪನ ಮಾಡಲು ಅತ್ಯಗತ್ಯವಾಗಿವೆ.ಇವುಗಳನ್ನು ಕೆಳಗೆ ಚರ್ಚಿಸಲಾಗಿದೆ. ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರದ ಬಹುಪಾಲು ಅಧ್ಯಯನಗಳು ಈ ಆರಂಭಿಕ ಸ್ಥಿತಿಯ ಮೇಲೆ ಹೆಚ್ಚು ಗಮನಹರಿಸುತ್ತವೆ. ಆರಂಭಿಕ ಸ್ಥಿತಿಯೆಂದರೆ ಹೆಚ್ಚು ಕಡಿಮೆ ಕಿಣ್ವ ಪ್ರತಿಕ್ರಿಯೆಗಳ ಅವಲಂಬಿತ ಭಾಗ. ಅದೇನೇ ಆದರೂ, ಪ್ರತಿಕ್ರಿಯೆಯ ಸಂಪೂರ್ಣ ವಕ್ರರೇಖೆಯನ್ನು ಕೂಡ ಅಳೆಯಲು ಸಾಧ್ಯವಿದೆ ಹಾಗು ಈ ದತ್ತಾಂಶವನ್ನು ರೇಖೀಯವಲ್ಲದ ದರ ಸಮೀಕರಣಕ್ಕೂ ಅಳವಡಿಸಬಹುದಾಗಿದೆ. ಈ ರೀತಿಯಲ್ಲಿ ಕಿಣ್ವದ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕಗಳನ್ನು ಅಳೆಯುವುದಕ್ಕೆ ಮುಂದುವರೆಯುತ್ತಿರುವ ವಕ್ರರೇಖೆಯ ವಿಶ್ಲೇಷಣೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.^[೭] ಆರಂಭಿಕವಾಗಿ ದರ ಪ್ರಮಾಣವನ್ನು ಖಚಿತವಾಗಿ ಅಳತೆಮಾಡಲು ಸಾಧ್ಯವಿಲ್ಲದಷ್ಟು ವೇಗವಾಗಿದ್ದಾಗ ಈ ಮಾರ್ಗವು ವೇಗ ಚಲನಶಾಸ್ತ್ರ ಕ್ಕೆ ಪರ್ಯಾಯರೂಪದಲ್ಲಿ ಸಹಾಯಕವಾಗಿದೆ.

ಏಕ-ತಲಾಧಾರ ಪ್ರತಿಕ್ರಿಯೆಗಳು

ಏಕ-ತಲಾಧಾರ ಯಾಂತ್ರೀಕೃತ ಕಾರ್ಯರೀತಿಗಳೊಂದಿಗೆ ಕಿಣ್ವಗಳು ಕೆಳಕಂಡವುಗಳನ್ನು ಒಳಗೊಂಡಿವೆ: ಟ್ರಿಯೊ ಫಾಸ್ ಫೇಟ್ ಐಸೊಮರ್ಸ್ ನಂತಹ ಐಸೊಮರ್ಸ್ ಗಳು ಅಥವಾ ಅಡ್ನಿಲೇಟ್ ಸೈಕ್ಲೇಸ್ ಮತ್ತು ಹ್ಯಾಮರ್ ಹೆಡ್ ರೈಬೊಜಿಮ್ ನಂತಹ ಬಯೋ ಸ್ಪೋಸ್ಪೊ ಗ್ಲಿಸೆರ್ಟ್ ಮ್ಯುಟೇಸ್, ಅಂತರಣುವಿನ ಲೈಸೇಸ್, RNA ಲೈಸೆ.^[೮] ಆದರೂ, ಏಕ ತಲಾಧಾರವನ್ನು ಮಾತ್ರ ಹೊಂದಿರುವ ಕೆಲವು ಕಿಣ್ವಗಳು ಈ ರೀತಿಯ ವರ್ಗ ವ್ಯವಸ್ಥೆಯ ಯಾಂತ್ರಿಕ ವಿಧಾನದ ಭಾಗವಾಗುವುದಿಲ್ಲ. ಕ್ರಿಯಾವರ್ಧಕವು ಇದಕ್ಕೆ ಉದಾಹರಣೆಯಾಗಿದೆ. ಕಿಣ್ವವು ಪ್ರತಿಕ್ರಿಯಿಸುವಂತಹ ಹೈಡ್ರೊಜನ್ ಪರಾಕ್ಸೈಡ್ ತಲಾಧಾರದ ಮೊದಲ ಅಣು ಆಕ್ಸಿಡೀಕರಣಕ್ಕೆ ಒಳಪಡುತ್ತದೆ ಹಾಗು ತರುವಾಯ ತಲಾಧಾರದ ಎರಡನೆಯ ಅಣುವಿನಿಂದ ನಶಿಸಿಹೋಗುತ್ತದೆ. ಏಕ ತಲಾಧಾರಕ್ಕೆ ಒಳಪಟ್ಟಿದ್ದರೂ ಕೂಡ, ಪರಿವರ್ತಿತ ಕಿಣ್ವ ಮಧ್ಯಂತರ ಅಸ್ತಿತ್ವವೆಂದರೆ, ಕ್ರಿಯಾವರ್ಧಕದ ಈ ಕಾರ್ಯರೀತಿಯು ಪಿಂಗ್ ಪಾಂಗ್ ಕಾರ್ಯರೀತಿಯಾಗಿದೆ. ಇದು ಒಂದು ವಿಧದ ಯಾಂತ್ರಿಕ ಕಾರ್ಯವಿಧಾನವಾಗಿದೆ,ಇದನ್ನು ಕೆಳಗೆ ಕೊಟ್ಟಿರುವ ಬಹು-ತಲಾಧಾರ ಪ್ರತಿಕ್ರಿಯೆಗಳ ವಿಭಾಗದಲ್ಲಿ ಚರ್ಚಿಸಲಾಗಿದೆ.

ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನಶಾಸ್ತ್ರ

ಚಿತ್ರ:Mechanism plus rates.svg

ಕಿಣ್ವದ ಪ್ರಕ್ರಿಯೆಗಾಗಿ ಏಕ-ತಲಾಧಾರ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ. k1, k-1 ಮತ್ತು k2 ಗಳು ಪ್ರತ್ಯೇಕ ಹಂತಕ್ಕೆ ಪ್ರಮಾಣದರದ ಸ್ಥಿರಾಂಕಗಳಾಗಿವೆ.

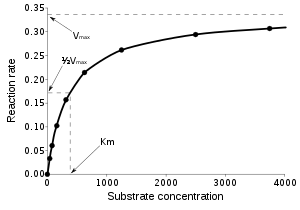
ಕಿಣ್ವ ವೇಗವರ್ಧನೆಗೆ ಒಳಪಟ್ಟ ಕ್ರಿಯೆಗಳು ಕರಗುತ್ತಿದ್ದಂತೆ, ಅವುಗಳ ವೇಗವರ್ಧನೆಯ ದರವು ಹೆಚ್ಚುತ್ತಿರುವ ತಲಾಧಾರಕ್ಕೆ ರೇಖೀಯ ಪ್ರತಿಕ್ರಿಯೆಯನ್ನು ನೀಡುವುದಿಲ್ಲ. ಒಂದು ವೇಳೆ ತಲಾಧಾರದ ಸಾರೀಕರಣಗಳ([S] ಎಂದು ಸೂಚಿಸಲಾಗಿದೆ)ಪ್ರಮಾಣದ ಮೇಲೆ ಆರಂಭಿಕ ದರವನ್ನು ಅಳೆದರೆ, ಬಲಭಾಗದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ದರವು(v ) ತಲಾಧಾರ[S] ಹೆಚ್ಚಿದಂತೆ ಹೆಚ್ಚುತ್ತಹೋಗುತ್ತದೆ. ಆದರೂ, ತಲಾಧಾರದ ಸಾರೀಕರಣವು [S] ಅಧಿಕವಾದಂತೆ ಕಿಣ್ವವು ತಲಾಧಾರದೊಂದಿಗೆ ಕರಗುತ್ತಹೋಗುತ್ತದೆ. ಅಲ್ಲದೇ ದರವು V _max ಅನ್ನು ತಲುಪುತ್ತದೆ. ಇದು ಕಿಣ್ವದ ಗರಿಷ್ಥ ದರವಾಗಿದೆ. ಏಕ-ತಲಾಧಾರ ಕ್ರಿಯೆಯ ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನೆಯ ಮಾದರಿಯನ್ನು ಬಲಬದಿಯಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. ಕಿಣ್ವ-ತಲಾಧಾರ ಸಂಕೀರ್ಣ ES ಅನ್ನು ರೂಪಿಸಲು, ಕಿಣ್ವ E ಮತ್ತು ತಲಾಧಾರ S ನ ನಡುವೆ ರಾಸಾಯನಿಕ ಚಲನೆ ಏರ್ಪಡುತ್ತದೆ. ರಾಸಾಯನಿಕ ಚಲನೆಗಳಿಗೆ $ES{\overset {k_{cat}}{\longrightarrow }}E+P$ ಕಿಣ್ವಕ ಕಾರ್ಯರೀತಿಯು ಸಂಕೀರ್ಣವಾಗಿರಬಹುದಾದರೂ ಕೂಡ, ದರವನ್ನು ನಿರ್ಧರಿಸುವ ಒಂದು ಕಿಣ್ವಕ ಕ್ರಮವಿದೆ. ಈ ಕ್ರಮವು ರಾಸಾಯನಿಕ ಚಲನೆಯ ಗೋಚರವಾಗುವ ಸ್ಥಿರಾಂಕ k _cat ದೊಂದಿಗೆ ಈ ಕ್ರಿಯೆಯನ್ನು ಏಕ ವೇಗವರ್ಧಕ ಕ್ರಮವಾಗಿ ರೂಪಿಸಲು ಅವಕಾಶ ನೀಡುತ್ತದೆ. ಒಂದು ವೇಳೆ ಕ್ರಿಯೆಯ ಮಾರ್ಗವು ಒಂದು ಅಥವಾ ಅನೇಕ ಮಧ್ಯಂತರಗಳ ಮೇಲೆ ನಡೆದರೆ, k _cat ಅನೇಕ ಧಾತ್ವಕ (ಎಲಿಮೆಂಟರಿ)ದರ ಸ್ಥಿರಾಂಕಗಳ ಕಾರ್ಯವಾಗಿದೆ. ಏಕ ರೂಪದ ಕ್ರಿಯೆಯಂತಹ(ಉದಾಹರಣೆಗೆ ಯಾವುದೇ ಮಧ್ಯಂತರಗಳಿಲ್ಲದ) ಸರಳ,ಸ್ಪಂದನಾತ್ಮಕ ವಿಷಯದಲ್ಲಿ ಇದು ಧಾತ್ವಕ ಆಣ್ವಿಕತೆ() ದರ ಸ್ಥಿರಾಂಕಕ್ಕೆ k ₂ ಅಭಿನ್ನವಾಗಿರುತ್ತದೆ. ಗೋಚರವಾಗುವ ಆಣ್ವಿಕತೆಯ ದರ ಸ್ಥಿರಾಂಕ k _catಅನ್ನು ಉತ್ಪಾದನ ಸಂಖ್ಯೆ ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ. ಅಲ್ಲದೇ ಇದು ಪ್ರತಿ ಸೆಕೆಂಡಿಗೆ ವೇಗವರ್ಧಿಸುವ ಕಿಣ್ವಕಗಳ ಗರಿಷ್ಠ ಸಂಖ್ಯೆಯನ್ನು ಕೂಡ ಸೂಚಿಸುತ್ತದೆ. ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನೆಯ ಸಮೀಕರಣ^[೯] ವು ಹೇಗೆ (ಆರಂಭಿಕ) ವೇಗದ ಕ್ರಿಯೆಯ ದರವು v ₀ ತಲಾಧಾರದ ಸ್ಥಾನವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ ಎಂಬುದನ್ನು ವಿವರಿಸುತ್ತದೆ. ತಲಾಧಾರದ ಸ್ಥಾನವೆಂದರೆ ಬಂಧಿತ ಸಮತೋಲನ ಸ್ಥಿತಿ ಮತ್ತು ದರ ಸ್ಥಿರಾಂಕವು k ₂ ಇರುವ ಸ್ಥಿತಿ.

v_{0}={\frac {V_{\max[}{\mbox{S}}]}{K_{M}+[{\mbox{S}}]}}

(ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನೆಯ ಸಮೀಕರಣ)

ನಿಯತಾಂಕಗಳೊಂದಿಗೆ

{\begin{aligned}K_{M}\ &amp;{\stackrel {\mathrm {def} }{=}}\ {\frac {k_{2}+k_{-1}}{k_{1}}}\approx K_{D}\\V_{\max }\ &amp;{\stackrel {\mathrm {def} }{=}}\ k_{cat}{[}E{]}_{tot}\end{aligned}}

ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನೆಯ ಈ ಸಮೀಕರಣವು ಬಹುಪಾಲು ಏಕ-ತಲಾಧಾರ ಕಿಣ್ವ ಚಲನೆಗಳ ಆಧಾರವಾಗಿದೆ. ಎರಡು ಬಹುಮುಖ್ಯವಾದ ಊಹೆಗಳು ಈ ಸಮೀಕರಣದ ಆಧಾರವಾಗಿವೆ. (ಕಾರ್ಯರೀತಿಯ ಬಗೆಗಿನ ಸಾಮಾನ್ಯ ಕಲ್ಪನೆಯನ್ನು ಹೊರತುಪಡಿಸಿ ಯಾವುದೇ ಮಧ್ಯಂತರವಿಲ್ಲದೇ ಅಥವಾ ಕ್ರಿಯೆಯನ್ನು ತಡೆಯುವ ಯಾವುದೇ ವಸ್ತುವಿಲ್ಲದೆ ಹಾಗು ಕಿಣ್ವದ ನಿಯಂತ್ರಣವಿಲ್ಲದೇ ಅಥವಾ ಸಹಕಾರಿ ಬಂಧಕವಿಲ್ಲದೆ ಕ್ರಿಯೆಯಲ್ಲಿ ಒಳಗೊಳ್ಳುವುದು). ಮೊದಲನೆಯ ಊಹೆಯು ಭಾಗಶಃ-ಸ್ಥಿರ ಊಹೆಯಾಗಿದೆ(ಅಥವಾ ಸುಳ್ಳು-ನಿರಾಧಾರ ಊಹೆಯಾಗಿರಬಹುದು), ತಲಾಧಾರ-ಬಂಧಿತ ಕಿಣ್ವದ (ಅಲ್ಲದೇ ಬಂಧಿತವಲ್ಲದ ಕಿಣ್ವವು ಕೂಡ) ಸಾರೀಕರಣವು ಉತ್ಪನ್ನದ ಮತ್ತು ತಲಾಧಾರದ ಸಾರೀಕರಣಕ್ಕಿಂತ ನಿಧಾನವಾಗಿ ಬದಲಾಗುತ್ತದೆ. ಈ ಕಾರಣದಿಂದ ಸಮಯದ ಆಧಾರದ ಮೇಲೆ ನಡೆಯುವ ಸಂಕೀರ್ಣದ ಬದಲಾವಣೆಯನ್ನು ಸೊನ್ನೆಗೆ ನಿಗದಿ ಮಾಡಬಹುದಾಗಿದೆ. $d{[}ES{]}/{dt}\;{\overset {!}{=}}\;0$ . ಕಿಣ್ವದ ಒಟ್ಟು ಸಾರೀಕರಣವು ಸಮಯದ ಆಧಾರದ ಮೇಲೆ ಬದಲಾಗುವುದಿಲ್ಲವೆಂಬುದು ಎರಡನೆಯ ಊಹೆಯಾಗಿದೆ. ಈ ಕಾರಣದಿಂದ Failed to parse (syntax error): {\displaystyle {[}E{]}_\text{tot} = {[}E{]} + {[}ES{]} \; \overset{!} } $=\;{\text{const}}$ . ಇದದ ಸಂಪೂರ್ಣ ವ್ಯುತ್ಪತ್ತಿಯನ್ನು ಇಲ್ಲಿ ನೋಡಬಹುದಾಗಿದೆ. ಮೈಕಲೀಸ್ ಸ್ಥಿರಾಂಕವಾದ K _M ಅನ್ನು ಪ್ರಾಯೋಗಿಕವಾಗಿ ಈ ಕೆಳಕಂಡಂತೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ: ಕಿಣ್ವದ ಕ್ರಿಯೆಯ ದರ V _max ಅರ್ಧವಿದ್ದಾಗ ತಲಾಧಾರ [S] = K _m ಅನ್ನು ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣಕ್ಕೆ ಆದೇಶಿಸುವ ಮೂಲಕ ಸಾರೀಕರಣವನ್ನು ಪರಿಶೀಲಿಸಬಹುದಾಗಿದೆ. ಅಲ್ಲದೇ ಇದನ್ನು ರೇಖಾಚಿತ್ರಗಳಾಗಿ ನೋಡಬಹುದಾಗಿದೆ. ದರವನ್ನು ನಿರ್ಧರಿಸುವ ಕಿಣ್ವಕ ಕ್ರಮವು ತಲಾಧಾರದ ವಿಯೋಜನೆಗಿಂತ (ಡಿಸೋಸಿಯೇಷನ್)( $k_{2}\ll k_{-1}$ ) ನಿಧಾನವಾಗಿದ್ದರೆ, ಮೈಕ್ಯೆಲಿಸ್ ಸ್ಥಿರಾಂಕವು K _M, ಸರಿಸುಮಾರಾಗಿ ES ಸಂಕೀರ್ಣ ಸಂಯುಕ್ತದ ವಿಯೋಜಿತ ಸ್ಥಿರಾಂಕವಾದ K _D ಯಷ್ಟಿರುತ್ತದೆ. ಒಂದು ವೇಳೆ $[S]$ ಹೋಲಿಕೆಯಲ್ಲಿ $K_{M}$ ಕ್ಕಿಂತ ಚಿಕ್ಕದಾಗಿದ್ದರೆ, ಆಗ $[S]/(K_{M}+[S])\approx [S]/K_{M}$ ಮತ್ತು ಅತ್ಯಂತ ಚಿಕ್ಕದಾದ ES ಸಂಕೀರ್ಣವು $[E]_{0}\approx [E]$ ಅನ್ನು ರೂಪಿಸುತ್ತವೆ. ಈ ಕಾರಣದಿಂದ,ಉತ್ಪನ್ನದ ರಚನೆಯ ದರವು

v_{0}\approx {\frac {k_{cat}}{K_{M}}}[E][S]\qquad \qquad {\text{if }}[S]\ll K_{M}

ಹೀಗೆ ಉತ್ಪನ್ನದ ರಚನೆಯ ದರವು ಕಿಣ್ವದ ಸಾರೀಕರಣದ ಮೇಲೆ ಮತ್ತು ತಲಾಧಾರದ ಸಾರೀಕರಣದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ. ಸಮೀಕರಣವು, ಅನುಗುಣವಾದ ಸ್ಯೂಡೋ- ಸೆಕೆಂಡ್ ಆರ್ಡರ್ ದರ ಸ್ಥಿರಾಂಕ $k_{2}/K_{M}$ ನ ಜೊತೆಗೆ ರಾಸಾಯನಿಕ ಚಲನೆಯನ್ನು ಹೋಲುತ್ತದೆ. ಈ ಸ್ಥಿರಾಂಕವು ವೇಗವರ್ಧಕ ಕಾರ್ಯಪಟುತ್ವದ ಮಾಪನವಾಗಿದೆ. ಅತ್ಯಂತ ಕಾರ್ಯಪಟುತ್ವವುಳ್ಳ ಕಿಣ್ವಗಳು 10⁸ - 10¹⁰ M⁻¹ s⁻¹ ನಲ್ಲಿ $k_{2}/K_{M}$ ಅನ್ನು ತಲುಪುತ್ತವೆ. ಈ ಕಿಣ್ವಗಳು ಅತ್ಯಂತ ದಕ್ಷವಾಗಿದ್ದು, ತಲಾಧಾರ ಅಣುವನ್ನು ಸಂಧಿಸಿದ ಪ್ರತಿಸಲವೂ ಪರಿಣಾಮಕಾರಿಯಾಗಿ ಕ್ರಿಯೆಯ ವೇಗವನ್ನು ವರ್ಧಿಸುತ್ತವೆ. ಹೀಗೆ ಕಿಣ್ವಗಳು ಕಾರ್ಯಪಟುತ್ವಕ್ಕಾಗಿ(ವಿಸರಣ ಪರಿಮಿತಿ) ಮೇಲ್ಮಟ್ಟದ ಸೈದ್ಧಾಂತಿಕ ಮಿತಿಯನ್ನು ತಲುಪುತ್ತವೆ; ಈ ಕಿಣ್ವಗಳನ್ನು ಹೆಚ್ಚಾಗಿ ಪರ್ಫೆಕ್ಟ್(ಯಾವುದೇ ಕೊರತೆಯಿಲ್ಲದ) ಕಿಣ್ವಗಳೆಂದು ಕರೆಯಲಾಗುತ್ತದೆ.^[೧೦]

ಸಮಯಾನುಕ್ರಮದ ಚಲನಾ ವಿಶ್ಲೇಷಣೆಗಾಗಿ ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣದ ನೇರ ಬಳಕೆ

ಮೈಕ್ಯಲೀಸ-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣವು ನಿರೀಕ್ಷಿಸಿದ ವೇಗಗಳನ್ನು, ಸ್ವಲ್ಪ ಕಾಲದ ವರೆಗೆ ಅದೃಶ್ಯವಾಗುವ ತಲಾಧಾರದ ಮಾದರಿಯನ್ನು ಮತ್ತು ಉತ್ಪನ್ನದ ಉತ್ಪಾದನೆಯ ಮಾದರಿಯನ್ನು ರೂಪಿಸಲು ನೇರವಾಗಿ ಬಳಸಬಹುದಾಗಿದೆ. ಈ ಮಾದರಿಯನ್ನು ಮೈಕ್ಯಲೀಸ-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣವನ್ನು ಮೊದಲನೆಯ ಸಾಲಿನ ರಾಸಾಯನಿಕ ಚಲನೆಯ ಸಮೀಕರಣವಾಗಿ ಸಂಯೋಜಿಸುವ ಮೂಲಕ ರೂಪಿಸಬಹುದಾಗಿದೆ. ಮೊದಲನೆಯ ಸಾಲಿನ ರಾಸಾಯನಿಕ ಚಲನೆಯ ವಿವರಣೆಯಲ್ಲಿ, ಗಣಿತಶಾಸ್ತ್ರದ ಸ್ಥಿರಾಂಕವನ್ನು ಬಳಸುವುದರೊಂದಿಗೆ ಸಂಬಂಧಿಸಿರುವ ಸಮಸ್ಯೆಯನ್ನು ಗುರುತಿಸಿದರೆ ಮಾತ್ರ ಇದನ್ನು ಸಾಧಿಸಲು ಸಾಧ್ಯ. ಉದಾಹರಣೆಗೆ e ^-k , ಇದು ವಿಭಾಗವಾದ ಸ್ಥಿರಾಂಕವಾಗಿದ್ದು, ಗುಣಾಕಾರಗಳಿಗೆ ಕ್ರಮಬದ್ಧವಾದ ದೋಷಗಳನ್ನು ಪರಿಚಯಿಸಿತು. ಅಲ್ಲದೇ ಇದನ್ನು ಏಕ ಸ್ಥಿರಾಂಕವಾಗಿ ಪುನಃ ಬರೆಯಬಹುದಾಗಿದೆ. ಈ ಏಕ ಸ್ಥಿರಾಂಕವು ಪ್ರತಿ ಕಾಲಾವಧಿಯ ನಂತರ ಉಳಿದ ತಲಾಧಾರವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ.^[೧೧]

[S]=[S]_{0}(1-k)^{t}\,

[S]=[S]_{0}(1-v/[S]_{0})^{t}\,

[S]=[S]_{0}(1-(V_{\max[}S]_{0}/(K_{M}+[S]_{0})/[S]_{0}))^{t}\,

ಮೈಕ್ಯಲೀಸ-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣದ ರೇಖೀಯ ನಕ್ಷೆಗಳು

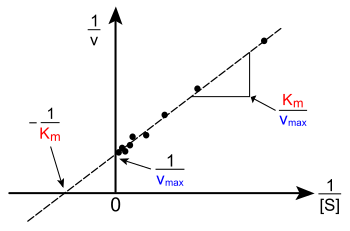
ಪರಸ್ಪರ ವರ್ತಿಸುವ ಮೈಕ್ಯಲೀs-ಮೆನ್ ಟೆನ್ ಚಲನಶಾಸ್ತ್ರದ ಭೋಧನೆಯನ್ನು ವರ್ಜಿನಿಯಾ ವಿಶ್ವವಿದ್ಯಾನಿಲಯದಲ್ಲಿ ಬಳಸುವ ಮೂಲಕ^[α], ಚಲನೆಯ ಬೇರೆ ಬೇರೆ ಸ್ಥಿರಾಂಕವನ್ನು ಹೊಂದಿರುವಂತಹ ಕಿಣ್ವದ ವರ್ತನೆಯ ಮೇಲೆ ಉಂಟಾಗಬಹುದಾದ ಪರಿಣಾಮಗಳನ್ನು ತಿಳಿಸಲಾಗಿದೆ. ಮೇಲೆ ಚಿತ್ರಿಸಲಾದ v ವಿರುದ್ಧದ [S] ರೇಖೀಯ ನಕ್ಷೆ ರೇಖೀಯವಾಗಿಲ್ಲ; ಕೆಳ[S]ನಲ್ಲಿ ಆರಂಭಿಕವಾಗಿ ರೇಖೀಯವಾಗಿದ್ದರೂ ಕೂಡ, ಮೇಲಿನ [S] ನಲ್ಲಿ ಇದು ಕರಗಿರುವ ಕಡೆಗೆ ಬಾಗಿದೆ. ಕಂಪ್ಯೂಟರ್ ನ ಮೇಲೆ ರೇಖೀಯವಲ್ಲದ ಸಮಾಶ್ರಯಣ(ನಾನ್ ಲೀನಿಯರ್ ರಿಗ್ರೆಷನ್)ದ ಆಧುನಿಕ ಯುಗ ಬರುವ ಮೊದಲು, ಈ ರೇಖೀಯವಾಗಿಲ್ಲದಿರುವಿಕೆಯು,K _M ಮತ್ತು V _max ಅನ್ನು ಖಚಿತವಾಗಿ ಅಂದಾಜುಮಾಡಲು ಕಷ್ಟವಾಗಿಸಿತ್ತು. ಆದ್ದರಿಂದ, ಅನೇಕ ಸಂಶೋಧಕರು ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣದ ರೇಖೀಕರಣವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು. ಉದಾಹರಣೆಗೆ, ಲೈನ್ ವೀವರ್-ಬರ್ಕ್ ರೇಖೀಯ ನಕ್ಷೆ, ಈಡಿ-ಹಾಫ್ಸ್ಟೀ ರೇಖಾಚಿತ್ರ ಮತ್ತು ಹ್ಯಾನ್ಸ್ ವುಲ್ಫ್ ರೇಖೀಯ ನಕ್ಷೆ. ಈ ಎಲ್ಲಾ ರೇಖೀಯ ಚಿತ್ರಗಳು ದತ್ತಾಂಶವನ್ನು ದೃಶ್ಯೀಕರಿಸಲು ಸಹಾಯಕವಾಗಿವೆ. ಆದರೆ ಇವುಗಳಲ್ಲಿ ಯಾವುದನ್ನು ಕೂಡ ಚಲನೆಯ ಪ್ರಮಿತಿಯನ್ನು ನಿರ್ಧಿರಿಸಲು ಬಳಸುವುದಿಲ್ಲ. ಕಂಪ್ಯೂಟರ್ ಸಾಫ್ಟ್ ವೇರ್ ಸುಲಭವಾಗಿ ದೊರೆಯುವುದರಿಂದ, ಅದು ರೇಖೀಯವಲ್ಲದ ಸಮಾಶ್ರಯಣ ವಿಧಾನಗಳ ಮೂಲಕ ಚಲನೆಯ ಪ್ರಮಿತಿಯನ್ನು ಅತ್ಯಂತ ಖಚಿತವಾಗಿ ನಿರ್ಧರಿಸಲು ಅವಕಾಶನೀಡುತ್ತದೆ.^[೧೨] ಲೈನ್ ವೀವರ್-ಬರ್ಕ್ ರೇಖೀಯ ನಕ್ಷೆ ಅಥವಾ ಡಬಲ್ ರೆಸಿಪ್ರೊಕಲ್ ರೇಖೀಯ ನಕ್ಷೆ ಎಂಬುದು ಚಲನಾ ದತ್ತಾಂಶವನ್ನು ವಿವರಿಸುವ ಸಾಮಾನ್ಯ ಮಾರ್ಗವಾಗಿದೆ. ಇದನ್ನು ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣದ ಎರಡು ಕಡೆಗಳ ವ್ಯುತ್ಕ್ರಮ(ರೆಸಿಪ್ರೊಕಲ್)(ಯಾವುದರಿಂದ ಗುಣಿಸಿದರೆ ಗುಣಲಬ್ಧ 1 ಬರುವುದು ಅದೋ)ವನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಮೂಲಕ ನಿರ್ಮಿಸಬಹುದಾಗಿದೆ. ಬಲಬದಿಯಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ, ಇದು ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣದ ರೇಖೀಯ ರೂಪವಾಗಿದೆ. ಅಲ್ಲದೇ ಇದು 1/V _maxಅನ್ನು ಅಂತಃ ಛೇಧಿಸಲು (ಇಂಟರ್ ಸೆಪ್ಟ್) ಸಮಾನವಾದ y ನೊಂದಿಗೆ ಮತ್ತು 1/K _M ನ ರೇಖೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುವ x ಸಮಾನದೊಂದಿಗೆ, ಹಾಗು y = mx + c ಸಮೀಕರಣದೊಂದಿಗೆ ದೊಂದಿಗೆ ನೇರವಾದ ಗೆರೆಯನ್ನು ನಿರ್ಮಿಸಿದೆ.

{\frac {1}{v}}={\frac {K_{M}}{V_{\max[}{\mbox{S}}]}}+{\frac {1}{V_{\max }}}

ಸಹಜವಾಗಿ, ನಕಾರಾತ್ಮಕ 1/[S] ನಲ್ಲಿ ಯಾವುದೇ ಪ್ರಾಯೋಗಿಕ ಮೌಲ್ಯಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗುವುದಿಲ್ಲ; ಲೋವರ್ ಲಿಮಿಟಿಂಗ್ ಮೌಲ್ಯವಾದ 1/[S] = 0 (y -ಅಂತಃ ಛೇಧ) ತಲಾಧಾರದ ಅನಿರ್ದಿಷ್ಟ ಸಾರೀಕರಣವನ್ನು ಹೋಲುತ್ತದೆ. ತಲಾಧಾರದ ಸಾರೀಕರಣದಲ್ಲಿ 1/v=1/V_max ಅನ್ನು ಬಲಬದಿಯಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ; ಹೀಗೆ x - ಅಂತಃ ಛೇಧವು, ಸಕಾರಾತ್ಮಕ ಸಾರೀಕರಣದಿಂದ ತೆಗೆದುಕೊಳ್ಳಲಾದ ಪ್ರಾಯೋಗಿಕ ದತ್ತಾಂಶದ ಬಹಿರ್ಗಣನೆಯಾಗಿದೆ. ಲೈನ್ ವೀವರ್-ಬರ್ಕ್ ರೇಖೀಯ ನಕ್ಷೆಯು ಅತ್ಯಂತ ಸಹಜವಾಗಿ, ತಲಾಧಾರದ ಕಡಿಮೆ ಸಾರೀಕರಣದಲ್ಲಿ ತೆಗೆದುಕೊಂಡ ಅಳತೆಯ ಮಹತ್ವವನ್ನು ತಿರುಚುತ್ತದೆ. ಈ ಕಾರಣದಿಂದಾಗಿ ಇದು V _max ಮತ್ತು K _M ನ ತಪ್ಪಾದ ಅಂದಾಜನ್ನು ನೀಡಬಹುದಾಗಿದೆ.^[೧೩] ಇಡಿ-ಹಾಫ್ಸ್ಟೀ ರೇಖೀಯ ನಕ್ಷೆಯು, ಅತ್ಯಂತ ನಿಖರ ರೇಖೀಯ ನಕ್ಷೆಯನ್ನು ತಯಾರಿಸುವ ವಿಧಾನವಾಗಿದೆ. ಈ ಪ್ರಕರಣದಲ್ಲಿ , v ಯನ್ನು v /[S]ವಿರುದ್ಧ ರಚಿಸಲಾಗಿದೆ. ಅತ್ಯಂತ ಸಾಮಾನ್ಯವಾದ ಮೂರನೆಯ ರೇಖಾ ಚಿತ್ರ,ಹ್ಯಾನ್ಸ್-ವೂಲ್ಫ್ ರೇಖೀಯ ನಕ್ಷೆಯಲ್ಲಿ , [S]/v ಯನ್ನು [S] ನ ವಿರುದ್ಧ ರಚಿಸಲಾಗಿದೆ. ಸಾರ್ವತ್ರಿಕವಾಗಿ, ದತ್ತಾಂಶವನ್ನು ಸಾಮಾನ್ಯ ಮಟ್ಟಕ್ಕೆ ತರುವುದು , ಪ್ರಾಯೋಗಿಕ ಕಾರ್ಯದ ಮೊತ್ತ ಕಡಿಮೆ ಮಾಡಲು ಹಾಗು ಉತ್ಪನ್ನದ ಗುಣಮಟ್ಟ ಹೆಚ್ಚಿಸಲು ಸಹಾಯಕವಾಗಿದೆ. ಅಲ್ಲದೇ ಇದು ರೇಖಾಚಿತ್ರಕ್ಕೆ ಮತ್ತು ಸಂಖ್ಯಾತ್ಮಕ ವಿಶ್ಲೇಷಣೆಗೆ ತಕ್ಕದ್ದಾಗಿದೆ.^[೧೪]

ಚಲನೆಯ ಸ್ಥಿರಾಂಕಗಳ ಪ್ರಾಯೋಗಿಕ ಮಹತ್ವ

ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರದ ಅಧ್ಯಯನವು ಎರಡು ಮೂಲಭೂತ ಕಾರಣಗಳಿಂದಾಗಿ ಅತ್ಯಂತ ಮಹತ್ವವಾಗಿದೆ. ಮೊದಲನೆಯದಾಗಿ, ಇದು ಹೇಗೆ ಕಿಣ್ವಗಳು ಕಾರ್ಯ ನಿರ್ವಹಿಸುತ್ತವೆ ಎಂಬುದನ್ನು ವಿವರಿಸಲು ಸಹಾಯಕವಾಗಿದೆ. ಎರಡನೆಯದಾಗಿ ಜೀವಿಗಳಲ್ಲಿ ಕಿಣ್ವಗಳು ಹೇಗೆ ವರ್ತಿಸುತ್ತವೆ ಎಂಬುದನ್ನು ಊಹಿಸಲು ಸಹಾಯ ಮಾಡುತ್ತದೆ. ಚಯಾಪಚಯ ವನ್ನು ನಿಯಂತ್ರಿಸಲು ಕಿಣ್ವಗಳು ಹೇಗೆ ಒಟ್ಟಿಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ ಎಂಬುದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಮೇಲೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಚಲನೆಯ ಸ್ಥಿರಾಂಕಗಳು K _M ಮತ್ತು V _max ಗಳಿಗೆ ಕಷ್ಟವಾಗುತ್ತದೆ. ಈ ಊಹೆಯನ್ನು ಮಾಡಲು ಸರಳವಾದ ವ್ಯವಸ್ಥೆಗಳಿಗೂ ಕೂಡ ಕಷ್ಟವಾಗುವುದು. ಉದಾಹರಣೆಗೆ, ಆಕ್ಸಲೋಸಿಟೇಟ್ ಮೈಟೊಕಾಂಡ್ರಿಯನ್ ನೊಳಗೆ ಮೆಲೇಟ್ ಡಿಹೈಡ್ರೋಗೆನ್ಸ್ ನಿಂದ ಉಂಟಾಗಿದೆ. ಆಕ್ಸಲೋಸಿಟೇಟ್ ಸಿಟ್ರೇಟ್ ಸಿಂಥಸ್,ಫೊಸ್ಫೊಎನಾಲ್ ಲೈರುವೇಟ್ ಕಾರ್ಬಾಕ್ಸಿನೈಸ್ ಅಥವಾ ಆಸ್ಪರ್ಟೇಟ್ ಅಮೈನೊಟ್ರಾನ್ಸ್ಫಾರ್ಸ್ ಗಳಿಂದಲು ಕೂಡ ನಾಶವಾಗಬಲ್ಲದು. ಅಲ್ಲದೇ ಅನುಕ್ರಮವಾಗಿ ಸಿಟ್ರಿಕ್ ಆಸಿಡ್ ಸೈಕಲ್, ಗ್ಲುಕೊನಿಯೊಜೆನ್ಸೀಸ್ ಅಥವಾ ಆಸ್ಪರೆಟಿಕ್ ಆಮ್ಲದ ಜೈವಿಕ ಉತ್ಪತ್ತಿಗಳಿಂದಲೂ ಕೂಡ ನಾಶವಾಗಬಲ್ಲದು. ಎಷ್ಟು ಪ್ರಮಾಣದ ಆಕ್ಸಲೋಸಿಟೇಟ್ ಯಾವ ಪ್ರತಿಕ್ರಿಯಾಸರಣಿಯಲ್ಲಿ ಹೋಗುತ್ತದೆ ಎಂಬುದನ್ನು ಊಹಿಸಲು, ಆಕ್ಸಲೋಸಿಟೇಟ್ ನ ಸಾರೀಕರಣದ ಅರಿವಿರಬೇಕು. ಅಲ್ಲದೇ ಈ ಪ್ರತಿ ಕಿಣ್ವಗಳ ಸಾರೀಕರಣ ಮತ್ತು ಚಲನೆಯ ಬಗೆಗಿನ ಜ್ಞಾನವಿರಬೇಕು. ಚಯಾಪಚಯಿ ಪ್ರತಿಕ್ರಿಯಾಸರಣಿಗಳ ವರ್ತನೆಯನ್ನು ಊಹಿಸುವ ಈ ಗುರಿಯು, ಬೃಹತ್ ಮೊತ್ತದ ಚಲನೆಯ ಸಂಶ್ಲೇಷಣೆಯಲ್ಲಿ ಮತ್ತು ಜೀನ್ ಎಕ್ಸ್ ಪ್ರೆಷನ್ ದತ್ತಾಂಶವನ್ನು ಸಂಪೂರ್ಣ ಜೀವಿಗಳ ಖಚಿತವಾದ ಮಾದರಿಯನ್ನು ರೂಪಿಸುವಲ್ಲಿ ಅದರ ಅತ್ಯಂತ ಸಂಕೀರ್ಣವಾದ ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ತಲುಪುತ್ತದೆ. ಪರ್ಯಾಯವಾಗಿ, ಚಯಾಪಚಯಿ ಮಾದರಿಯನ್ನು ರೂಪಿಸಲು ಇರುವ ಸಮಸ್ಯೆಯನ್ನು ಸರಳಗೊಳಿಸಲು ಕೆಳಗಿರುವ ಕಿಣ್ವದ ಚಲನೆಗಳನ್ನು ಕಡೆಗಾಣಿಸಬೇಕು. ಅಲ್ಲದೇ ಕೇವಲ ಕ್ರಿಯೆಯ ಸಂಪರ್ಕದ ರಸಗಣಿತದ ಬಗೆಗಿನ ಮಾಹಿತಿಯ ಮೇಲೆ ಮಾತ್ರ ಅವಲಂಬಿಸಿರಬೇಕು. ಇದನ್ನು ಫ್ಲಕ್ಸ್ ಬ್ಯಾಲೇನ್ಸ್ ಅನಾಲಿಸಸ್ ವಿಧಾನವೆಂದು ಕರೆಯಲಾಗುತ್ತದೆ.^[೧೫]^[೧೬].

ಮಧ್ಯಂತರ(ಸಂಯುಕ್ತ)ದೊಂದಿಗೆ ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನೆಗಳು

ಅತ್ಯಂತ ಸರಳವಾದ ಮಾದರಿಯನ್ನು ಕೂಡ ಪರಿಗಣಿಬಹುದು

{\begin{aligned}E+S{\underset {k_{-1}}{\overset {k_{1}}{\begin{smallmatrix}\displaystyle \longrightarrow \\\displaystyle \longleftarrow \end{smallmatrix}}}}ES{\overset {k_{2}}{\longrightarrow }}EI{\overset {k_{3}}{\longrightarrow }}E+P\end{aligned}}

ಕಿಣ್ವ ಮತ್ತು ಮಧ್ಯಂತರದ ಅಸ್ತಿತ್ವದೊಂದಿಗೆ ಸಂಕೀರ್ಣವಿದ್ದಾಗ ಮಧ್ಯಂತರವು ಎರಡನೆಯ ಹಂತದಲ್ಲಿ ಉತ್ಪನ್ನವಾಗಿ ಬದಲಾಗುತ್ತದೆ. ಈ ವಿಷಯದಲ್ಲಿ ನಾವು ಅತ್ಯಂತ ಸದೃಶವಾಗಿರುವ ಸಮೀಕರಣವನ್ನು ಹೊಂದಿದ್ದೇವೆ.^[೧೭]

{\begin{aligned}v_{0}&amp;=k_{cat}{\frac {{[}S{]}{[}E{]}_{0}}{K_{M}^{\prime }+{[}S{]}}}\end{aligned}}

ಆದರೆ ಸ್ಥಿರಾಂಕಗಳು ಭಿನ್ನವಾಗಿರುತ್ತವೆ

{\begin{aligned}K_{M}^{\prime }\ &amp;{\stackrel {\mathrm {def} }{=}}\ {\frac {k_{3}}{k_{2}+k_{3}}}K_{M}={\frac {k_{3}}{k_{2}+k_{3}}}\cdot {\frac {k_{2}+k_{-1}}{k_{1}}}\\k_{cat}\ &amp;{\stackrel {\mathrm {def} }{=}}\ {\dfrac {k_{3}k_{2}}{k_{2}+k_{3}}}\end{aligned}}

ನಾವು ಅದನ್ನು ಸೀಮಿತಗೊಳಿಸಿದ ಪ್ರಕರಣದಲ್ಲಿ ನೋಡಬಹುದು. $k_{3}\gg k_{2}$ , ಹೀಗೆ EI to E + P ನಿಂದ ಕೊನೆಯ ಹಂತ ಅದರ ಹಿಂದಿನ ಹಂತಕ್ಕಿಂತ ವೇಗವಾಗಿರುತ್ತದೆಯೋ ಆಗ ನಾವು ಮತ್ತೊಮ್ಮೆ ಮೂಲ ಸಮೀಕರಣವನ್ನು ಪಡೆಯುತ್ತೇವೆ. ತರುವಾಯ ಗಣಿತೀಯವಾಗಿ ನಾವು $K_{M}^{\prime }\approx K_{M}$ ಮತ್ತು $k_{cat}\approx k_{2}$ ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ.

ಬಹು-ತಲಾಧಾರ ಪ್ರತಿಕ್ರಿಯೆಗಳು

ಬಹು-ತಲಾಧಾರ ಕ್ರಿಯೆಗಳು ಸಂಕೀರ್ಣ ದರದ ಸಮೀಕರಣಗಳನ್ನು ಅನುಸರಿಸುತ್ತವೆ. ಇದು ತಲಾಧಾರಗಳು ಹೇಗೆ ಬಂಧಿಸುತ್ತವೆ ಮತ್ತು ಯಾವ ಕ್ರಮಾನುಗತಿಯಲ್ಲಿ ಬಂಧಿಸುತ್ತವೆ ಎಂಬುದನ್ನು ವಿವರಿಸುತ್ತದೆ. ಒಂದುವೇಳೆ ತಲಾಧಾರ A ಯ ಸಾರೀಕರಣವನ್ನು ಸ್ಥಿರವಾಗಿರಿಸಿ ತಲಾಧಾರ B ಯ ಸಾರೀಕರಣವನ್ನು ಬದಲಾಯಿಸಿದರೆ ಈ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕಗಳ ವಿಶ್ಲೇಷಣೆ ಅತ್ಯಂತ ಸುಲಭವಾಗುವುದು. ಇಂತಹ ಸ್ಥಿತಿಯಲ್ಲಿ, ಕಿಣ್ವವು ಕೇವಲ ಏಕ-ತಲಾಧಾರ ಕಿಣ್ವದಂತೆ ವರ್ತಿಸುತ್ತದೆ, ಹಾಗು [S] ನಿಂದ v ನಕ್ಷೆಯು ತಲಾಧಾರ B ಗೆ ಸ್ಪಷ್ಟವಾದ K _Mಮತ್ತು V _max ಸ್ಥಿರಾಂಕಗಳನ್ನು ನೀಡುತ್ತದೆ. ಒಂದುವೇಳೆ ಈ ಅಳತೆಗಳನ್ನು A ಯ ವಿಭಿನ್ನ ಸ್ಥಿರ ಸಾರೀಕರಣಗಳಲ್ಲಿ ಪ್ರದರ್ಶಿಸಿದರೆ, ಈ ದತ್ತಾಂಶವನ್ನು ಪ್ರತಿಕ್ರಿಯೆಯ ಕಾರ್ಯರೀತಿಯನ್ನು ತಿಳಿಯಲು ಬಳಸಿಕೊಳ್ಳಬಹುದಾಗಿದೆ. (ಕಿಣ್ವಗಳ ಪ್ರತಿಸ್ಪಂದನದ ಪೂರಕ ವಿಧಾನದ ಅಳವಡಿಕೆ ಇಲ್ಲಿನ ಪ್ರಮುಖ ಅಂಶವಾಗಿದೆ.) A ಮತ್ತು B ಎಂಬ ಎರಡು ತಲಾಧಾರಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಮತ್ತು ಇಲ್ಲಿ ಇವುಗಳನ್ನು P ಮತ್ತು Q ಎಂಬ ಎರಡು ಉತ್ಪನ್ನಗಳಾಗಿ ಬದಲಾಯಿಸುವ ಕಿಣ್ವಕ್ಕೆ ಎರಡು ಬಗೆಯ ಕಾರ್ಯರೀತಿಗಳಿವೆ: ತ್ರಯಾಧಾರಿತ ಸಂಕೀರ್ಣತೆ ಮತ್ತು ಪಿಂಗ್- ಪಾಂಗ್.

ತ್ರಯಾಧಾರಿತ-ಸಂಕೀರ್ಣ ಕಾರ್ಯರೀತಿಗಳು

ಈ ಕಿಣ್ವಗಳಲ್ಲಿ, EAB ತ್ರಯಾಧಾರಿತ ಸಂಕೀರ್ಣ ಸಂಯುಕ್ತವನ್ನು ಉತ್ಪಾದಿಸುವ ಸಮಯದಲ್ಲಿಯೇ ಎರಡು ತಲಾಧಾರಗಳು ಕಿಣ್ವಕ್ಕೆ ಬಂಧಿಸಲ್ಪಡುತ್ತವೆ. ಬಂಧಕದ ರೀತಿಯು ಯಾದೃಚ್ಛಿಕವಾಗಿರಬಹುದು. (ಯಾದೃಚ್ಛಿಕ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ), ಅಥವಾ ತಲಾಧಾರಗಳು ಪ್ರತ್ಯೇಕವಾದ ಕ್ರಮಾನುಗತಿಯಲ್ಲಿ ಬಂಧಿಸಲ್ಪಡಬೇಕಾಗುತ್ತದೆ. (ಕ್ರಮಾನುಗತಿಯ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ). ಲೈನ್ ವೀವರ್-ಬರ್ಕ್ ರೇಖೀಯ ನಕ್ಷೆಯಲ್ಲಿ ಚಿತ್ರಿಸಲಾದ ,[S] ನಿಂದ v ಯ ಒಂದು ಗುಂಪು ತ್ರಯಾಧಾರಿತ ಸಂಕೀರ್ಣ ಕಾರ್ಯರೀತಿಯೊಂದಿಗೆ ಕಿಣ್ವದಿಂದ ಭಾಗಿಸಲ್ಪಟ್ಟಾಗ (Aಯನ್ನು ಸ್ಥಿರವಾಗಿಸಿ, Bಯನ್ನು ಬದಲಾಯಿಸುವುದು.)ರೇಖೆಗಳ ಒಂದು ಗುಂಪನ್ನು ಛೇದಿಸಲಾಗುತ್ತದೆ. ತ್ರಯಾಧಾರಿತ-ಸಂಕೀರ್ಣ ಕಾರ್ಯವಿಧಾನಗಳೊಂದಿಗೆ ಕಿಣ್ವಗಳು ಕೆಳಕಂಡವುಗಳನ್ನು ಒಳಗೊಂಡಿವೆ: ಗ್ಲೂಟಥಿಯೋನ್ S -ಟ್ರಾನ್ಸ್ಫಾರ್ಸಿ,^[೧೮] ಡೈಹೈಡ್ರೊಫೊಲೇಟ್ ರಿಡಕ್ಟೇಸ್^[೧೯] ಮತ್ತು DNA ಪಾಲಿಮರೇಸ್.^[೨೦](ಡಿಎನ್ ಎ ನಲ್ಲಿರುವ ಕಿಣ್ವಗಳು) ಈ ಕೆಳಕಂಡ ಕೊಂಡಿಗಳು ಕಿಣ್ವಗಳ ಡೈಹೈಡ್ರೊಫೊಲೇಟ್ ರಿಡಕ್ಟೇಸ್^[β] ಮತ್ತು DNA ಪಾಲಿಮರೇಸ್^[γ] ನ ತ್ರಯಾಧಾರಿತ-ಸಂಕೀರ್ಣ ಕಾರ್ಯ ವ್ಯವಸ್ಥೆಯನ್ನು ಕುರಿತ ಕಿರು ಅನಿಮೇಷನ್ ಚಿತ್ರಗಳನ್ನು ತೋರಿಸುತ್ತವೆ.

ಪಿಂಗ್-ಪಾಂಗ್ ಕಾರ್ಯರೀತಿಗಳು

ಕಿಣ್ವ ಪ್ರತಿಕ್ರಿಯೆಗಾಗಿ ಪಿಂಗ್–ಪಾಂಗ್ (ಹಗರು ಪ್ರೊಟೀನ್ ಗಳು) ಕಾರ್ಯರೀತಿಯಲ್ಲಿA ಮತ್ತು B ತಲಾಧಾರಗಳನ್ನು ಅಥವಾ P ಮತ್ತು Q ಉತ್ಪನ್ನಗಳನ್ನು ಒಳಗೊಂಡ ಮಧ್ಯಂತರಗಳು.

ಬಲಬದಿಯಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ, ಪಿಂಗ್-ಪಾಂಗ್ ಕಾರ್ಯ ರೀತಿಯೊಂದಿಗೆ ಕಿಣ್ವಗಳು ಎರಡು ಹಂತಗಳಲ್ಲಿ ಅಸ್ಥಿತ್ವದಲ್ಲಿರಬಹುದು. E ಮತ್ತು ರಾಸಾಯನಿಕವಾಗಿ ಮಾರ್ಪಡಿಸಲಾದ ಕಿಣ್ವ E* ರೂಪದಲ್ಲಿ ಅಸ್ತಿತ್ವದಲ್ಲಿರಬಹುದು; ಈ ಮಾರ್ಪಡಿಸಲಾದ ಕಿಣ್ವವನ್ನು ಮಧ್ಯಂತರವೆಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಇಂತಹ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ,ಕಿಣ್ವವನ್ನು E* ಯಾಗಿ ಬದಲಾಯಿಸಲು ತಲಾಧಾರ A ಬಂಧಿಸಲ್ಪಡುತ್ತದೆ, ಉದಾಹರಣೆಗೆ, ರಾಸಾಯನಿಕ ಗುಂಪುಗಳನ್ನು ಸಕ್ರಿಯ ಸೈಟ್ ಗೆ ವರ್ಗಾಯಿಸುವ ಮೂಲಕ ಮತ್ತು ಅನಂತರ ಬಿಡುಗಡೆ ಹೊಂದುವ ಮೂಲಕ ತಲಾಧಾರ ಬಂಧಿಸಲ್ಪಡುತ್ತದೆ. ಕೇವಲ ಮೊದಲನೆಯ ತಲಾಧಾರ ಬಿಡುಗಡೆಯಾದ ನಂತರವೇ ತಲಾಧಾರ B ಯನ್ನು ಬಂಧಿಸಬಹುದಾಗಿದೆ. ಅಲ್ಲದೇ ಮಾರ್ಪಡಿಸದಂತಹ E ರೂಪವನ್ನು ಮತ್ತೊಮ್ಮೆ ಉತ್ಪಾದಿಸಲು ರೂಪಾಂತರಿತ ಕಿಣ್ವದೊಂದಿಗೆ ಪ್ರತಿಕ್ರಿಯಿಸಬಹುದಾಗಿದೆ. ಪಿಂಗ್-ಪಾಂಗ್ ಕಾರ್ಯರೀತಿಯೊಂದಿಗೆ ಕಿಣ್ವದ ಮೂಲಕ v ಯ ಒಂದು ಗುಂಪನ್ನು [S] ನಿಂದ (Aಯನ್ನು ಸ್ಥಿರವಾಗಿರಿಸಿ, Bಯನ್ನು ಬದಲಾಯಿಸುವುದು) ಬಾಗಿಸುವುದನ್ನು ಲೈನ್ ವೀವರ್-ಬರ್ಕ್ ರೇಖೀಯ ನಕ್ಷೆಯಲ್ಲಿ ರಚಿಸಲಾಗಿದೆ. ಸಮಾಂತರದ ರೇಖೆಗಳನ್ನು ಬಿಡುಗಡೆಮಾಡಲಾಗುವುದು. ಇದನ್ನು ಎರಡನೆಯ ರೇಖೀಯ ನಕ್ಷೆ ಎಂದು ಕರೆಯಲಾಗುವುದು. ಪಿಂಗ್-ಪಾಂಗ್ ಕಾರ್ಯರೀತಿಯಲ್ಲಿಯೊಂದಿಗೆ ಕಿಣ್ವಗಳು ಈ ಕೆಳಕಂಡವುಗಳನ್ನು ಒಳಗೊಂಡಿವೆ:ಪರಾಕ್ಸಿಡೇಸ್: ನಂತಹ ಕೆಲವು ಆಕ್ಸಿಡೋರಿಡಕ್ಟೇಸ್,^[೨೧] , ಅಕ್ಲೆನ್ಯೂರ್ಮಿನೇಟ್ ಸಿಟಿಡಿಲಿಟ್ರಾನ್ಸ್ಫಾರ್ಸಿ^[೨೨] ನಂತಹ ಟ್ರಾನ್ಸ್ಫಾರ್ಸಿಸ್ ಮತ್ತು ಟ್ರಿಪ್ಸಿನ್ಮತ್ತು ಸೈಮೊಟ್ರಿಪ್ಸಿನ್ ನಂತಹ ಸೆರಿನ್ ಪ್ರೋಟಿಯೇಸ್ಸ್.^[೨೩] ಸೆರಿನ್ ಪ್ರೋಟಿಯೇಸ್ ಗಳು(ಪ್ರೋಟೀನ್), ಕಿಣ್ವದ ಅತ್ಯಂತ ಸಾಮಾನ್ಯ ಮತ್ತು ಭಿನ್ನವಾದ ವರ್ಗಳಾಗಿವೆ. ಇವು ಜೀರ್ಣಕಾರಿ ಕಿಣ್ವಗಳು (ಟ್ರಿಪ್ಸಿನ್, ಸೈಮೊಟ್ರಿಪ್ಸಿನ್, ಮತ್ತು ಇಲ್ಯಾಸ್ಟೇಸ್) ರಕ್ತವನ್ನು ಹೆಪ್ಪುಗಟ್ಟಿಸುವ ಅನೇಕ ಕಿಣ್ವಗಳು ಮತ್ತು ಇತರ ಕಿಣ್ವಗಳನ್ನು ಒಳಗೊಂಡಿವೆ. ಈ ಸೆರಿನ್ ಪ್ರೋಟಿಯೇಸ್ ಗಳಲ್ಲಿ, E* ಮಧ್ಯಂತರವು ಆಸಿಲ್ ಆಗಿದೆ.(ಆಮ್ಲೀಯ ರಾಡಿಕಲ್)- ಇದು ಕಿಣ್ವದ ವರ್ಗವಾಗಿದ್ದು, ಪ್ರೋಟೀನ್ ತಲಾಧಾರದಲ್ಲಿ ಪೆಪ್ಟೈಡ್ ಬಂಧದ ಮೇಲೆ ಸಕ್ರಿಯ ಸೈಟ್ ನ ಸೆರಿನ್ ಶೇಷದಿಂದಾಗುವ ದಾಳಿಯಿಂದ ರೂಪುಗೊಳ್ಳುತ್ತದೆ. ಸೈಮೊಟ್ರಿಪ್ಸಿನ್ ನ ಕಾರ್ಯರೀತಿಯನ್ನು ತೋರಿಸುವ ಕಿರು ಚಿತ್ರ(ಅನಿಮೇಷನ್)ಕ್ಕೆ ಇಲ್ಲಿ ಸಂಪರ್ಕ ಕಲ್ಪಿಸಲಾಗಿದೆ.^[δ]

ನಾನ್-ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನಶಾಸ್ತ್ರ

ಕೆಲವು ಕಿಣ್ವಗಳು [S] ರೇಖೆಯಿಂದ ಅರ್ಧವರ್ತುಲಾಕಾರದ v ಯನ್ನು ಬಿಡುಗಡೆಮಾಡಬಲ್ಲವು. ಇವು ಹೆಚ್ಚಾಗಿ ಸಕ್ರಿಯ ಸೈಟ್ ನಲ್ಲಿ ತಲಾಧಾರ ದ ಸಹಕಾರಿ ಬಂಧಕವನ್ನು ಸೂಚಿಸುತ್ತವೆ. ಒಂದು ತಲಾಧಾರ ಅಣುವಿನ ಬಂಧಕವು ಅನಂತರದ ತಲಾಧಾರ ಅಣುಗಳ ಬಂಧಕದ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ. ಈ ವರ್ತನೆಯು ಪ್ರೋಟೀನ್ ಕಿಣ್ವಗಳಲ್ಲಿ, ಪರಸ್ಪರ ಪರಿಣಾಮವನ್ನುಂಟುಮಾಡುವ ಅನೇಕ ಸಕ್ರಿಯ ಸೈಟ್ ಗಳೊಂದಿಗೆ ಅತ್ಯಂತ ಸಾಮಾನ್ಯವಾಗಿದೆ.^[೨೪] ಇಲ್ಲಿ, ಸಹಕಾರಿಸುವ ಕಾರ್ಯರೀತಿಯು ಹಿಮೋಗ್ಲೋಬಿನ್ ಕಾರ್ಯರೀತಿಯನ್ನು ಹೋಲುತ್ತದೆ. ಒಂದು ಸಕ್ರಿಯ ಸೈಟ್ ಗೆ ತಲಾಧಾರವನ್ನು ಬಂಧಿಸುವ ಕ್ರಿಯೆಯಲ್ಲಿ ಮತ್ತು ತಲಾಧಾರದ ಅಣುಗಳಿಗೆ ಇತರ ಸಕ್ರಿಯ ಸೈಟ್ ನ ಆಕರ್ಷಣ ಬಲವನ್ನು ಬದಲಾಯಿಸುವ ಕ್ರಿಯೆಯಲ್ಲಿ ಸದೃಶವಾಗಿದೆ. ಮೊದಲನೆಯ ತಲಾಧಾರ ಅಣುವಿನ ಬಂಧಕವು, ತಲಾಧಾರಕ್ಕಾಗಿ ಇತರ ಸಕ್ರಿಯ ಸೈಟ್ ನ ಆಕರ್ಷಣ ಬಲವನ್ನು ಹೆಚ್ಚಿಸಿದಾಗ ಸಕಾರಾತ್ಮಕ ಸಹಕಾರವು ಉಂಟಾಗುತ್ತದೆ. ಮೊದಲನೆಯ ತಲಾಧಾರದ ಬಂಧಕವು ಇತರ ತಲಾಧಾರದ ಅಣುಗಳಿಗಾಗಿ ಕಿಣ್ವದ ಆಕರ್ಷಣ ಬಲವನ್ನು ಕಡಿಮೆ ಮಾಡಿದಾಗ ನಕಾರಾತ್ಮಕತೆ ಉಂಟಾಗುತ್ತದೆ. ಅಲೊಸ್ಟಿಯರಿಕ್ ಕಿಣ್ವಗಳು, ಮ್ಯಾಮ್ಲಿಯನ್ (ಸಸ್ತನಿಯ) ಟೈರೊಸಿಲ್ tRNA-ಸಿಂಥಟೇಸ್ ಅನ್ನು ಒಳಗೊಂಡಿವೆ, ಇದು ನಕಾರಾತ್ಮಕತೆ ತೋರಿಸುತ್ತದೆ.^[೨೫] ಅಲ್ಲದೇ ಬ್ಯಾಕ್ಟೀರಿಯಾದ ಆಸ್ಪರ್ಟೇಟ್ ಟ್ರಾನ್ಸ್ ಕಾರ್ಬ್ಮೊಲೇಸ್^[೨೬] ಮತ್ತು ಫಾಸ್ಫೊ ಫ್ರುಕ್ಟೊನೈಸೆ,^[೨೭] ಯನ್ನು ಒಳಗೊಂಡಿದೆ. ಇವು ಸಕಾರಾತ್ಮಕ ಸಹಕಾರ ತೋರಿಸುತ್ತವೆ. ಸಹಕಾರವು ಅನಿರೀಕ್ಷಿತವಾಗಿ ಸಾಮಾನ್ಯವಾದುದ್ದಾಗಿದೆ. ಅಲ್ಲದೇ ಇದು ತಲಾಧಾರಗಳ ಸಾರೀಕರಣದಲ್ಲಿ ಬದಲಾವಣೆಯನ್ನು ಉಂಟುಮಾಡುವುದಕ್ಕಾಗಿ ಕಿಣ್ವದ ಪ್ರತಿಕ್ರಿಯೆಯನ್ನು ನಿಯಂತ್ರಿಸಲು ಸಹಾಯಕವಾಗಿದೆ. ಸಕಾರಾತ್ಮಕ ಸಹಕಾರವು [S] ನ ಕಡೆಗೆ ಕಿಣ್ವಗಳು ಅತ್ಯಂತ ಸೂಕ್ಷ್ಮವಾಗುವಂತೆ ಮಾಡುತ್ತವೆ. ಅಲ್ಲದೇ ಅವುಗಳ ಕ್ರಿಯಾಶೀಲತೆಯು ಸಂಕುಚಿತ ಪ್ರಮಾಣದ ತಲಾಧಾರ ಸಾರೀಕರಣದ ಮೇಲೆ ಭಾರಿ ಬದಲಾವಣೆಗಳನ್ನು ತೋರಿಸಬಲ್ಲದು. ಇದಕ್ಕೆ ಪ್ರತಿಯಾಗಿ, ನಕಾರಾತ್ಮಕ ಸಹಕಾರವು [S] ನಲ್ಲಿ ಸಣ್ಣ ಬದಲಾವಣೆಗಳನ್ನು ಮಾಡಲು ಕೂಡ ಕಿಣ್ವಗಳನ್ನು ಪ್ರತಿಕ್ರಿಯೆ ತೋರದಂತೆ ಮಾಡುತ್ತದೆ. ಹಿಲ್ ಸಮೀಕರಣವನ್ನು^[೨೮] ನಾನ್-ಮೈಕ್ಯಲೀಸ್-ಮೆನ್ ಟೆನ್ ಚಲನಶಾಸ್ತ್ರದಲ್ಲಿ ಸಹಕಾರದ ಮಟ್ಟವನ್ನು ವಿವರಿಸಲು ಹೆಚ್ಚಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ. ಹಿಲ್ ಸಮೀಕರಣವು ವ್ಯಾಖ್ಯಾನಿಸಿದ n ಗುಣಾಂಕವು, ಒಂದು ಸಕ್ರಿಯ ಸೈಟ್ ನಲ್ಲಿ ತಲಾಧಾರದ ಬಂಧಕವು ಇತರ ಸಕ್ರಿಯ ಸೈಟ್ ನ ತಲಾಧಾರದ ಬಂಧಕದ ಮೇಲೆ ಎಷ್ಟರ ಮಟ್ಟಿಗೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಎಂಬುದನ್ನು ಅಳೆಯುತ್ತದೆ. <1 ನ ಹಿಲ್ ಗುಣಾಂಕವು ನಕಾರಾತ್ಮಕ ಸಹಕಾರವನ್ನು ಸೂಚಿಸುತ್ತದೆ ಹಾಗು >1 ನ ಗುಣಾಂಕವು ಸಕಾರಾತ್ಮಕ ಸಹಕಾರವನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಪೂರ್ವ ಸ್ಥಿರತೆಯ ಚಲನೆಗಳು

ಕಿಣ್ವವು ತಲಾಧಾರದೊಂದಿಗೆ ಬೆರೆತ ನಂತರ ಮೊದಲನೆಯ ಕ್ಷಣದಲ್ಲಿ, ಯಾವುದೇ ಉತ್ಪನ್ನವು ರೂಪುಗೊಳ್ಳುವುದಿಲ್ಲ ಮತ್ತು ಯಾವುದೇ ಮಧ್ಯಂತರಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿರುವುದಿಲ್ಲ. ಪ್ರತಿಕ್ರಿಯೆಯ ನಂತದ ಕೆಲವು ಮಿಲಿಸೆಕೆಂಡ್ ಗಳ ಅಧ್ಯಯನವನ್ನೇ ಪೂರ್ವಸ್ಥಿರತೆಯ ಚಲನೆಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ ಪೂರ್ವ ಸ್ಥಿರತೆಯ ಚಲನಶಾಸ್ತ್ರವು ಕಿಣ್ವ–ತಲಾಧಾರ ಮಧ್ಯಂತರಗಳ (ಉದಾಹರಣೆಗೆ ES ಅಥವಾ E*) ರಚನೆಗೆ ಮತ್ತು ಬಳಕೆಗೆ ಸಂಬಂಧಿಸಿದೆ. ಇದು ಅವುಗಳ ಪೂರ್ವ ಸ್ಥಿರತೆಯ ಸಾರೀಕರಣಗಳು ತಲುಪುವ ವರೆಗೂ ಸಂಬಂಧಿಸಿರುತ್ತದೆ. ಈ ಮಾರ್ಗವನ್ನು ಮೊದಲನೆಯ ಬಾರಿಗೆ ಸೈಮೊಟ್ರಿಪ್ಸಿನ್ ನ ಮೂಲಕ ಜಲವಿಚ್ಛೇದನೆ ಪ್ರತಿಕ್ರಿಯೆಯ ವೇಗವರ್ಧನೆಗೆ ಅನ್ವಯಿಸಲಾಯಿತು.^[೨೯] ಕಿಣ್ವವು ಯಾವ ಕಾರ್ಯರೀತಿಯನ್ನು ಅನುಸರಿಸುತ್ತದೆ ಎಂಬ ಪರೀಕ್ಷೆಯಲ್ಲಿ ಪತ್ತೆಹಚ್ಚುವ ಮಧ್ಯಂತರವು ಸಾಕ್ಷ್ಯಾಧಾರದ ಮುಖ್ಯ ತುಣುಕಾಗಿದೆ. ಉದಾಹರಣೆಗೆ, ಮೇಲೆ ತೋರಿಸಲಾದ ಪಿಂಗ್-ಪಾಂಗ್ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ ಚಲನೆಗಳ ಅತಿವೇಗದ ಮಾಪನಗಳು P ಉತ್ಪನ್ನದ ಬಿಡುಗಡೆಯನ್ನು ಅನುಸರಿಸಬಹುದು ಹಾಗು ಮಾರ್ಪಾಡಾದ ಕಿಣ್ವ ಮಧ್ಯಂತರ E* ಯ ರಚನೆಯನ್ನು ಅಳೆಯಬಹುದು.^[೩೦] ಸೈಮೊಟ್ರಿಪ್ಸಿನ್ ನ ವಿಷಯದಲ್ಲಿ, ಈ ಮಧ್ಯಂತರವು ಸಕ್ರಿಯ ಸೈಟ್ ನಲ್ಲಿ ತಲಾಧಾರದ ಮೇಲೆ ನ್ಯೂಕ್ಲಿಯೊಫಿಲಿಕ್ ಸೆರಿನ್ ಮಾಡುವ ದಾಳಿಯಿಂದ ಉಂಟಾಗುತ್ತದೆ. ಅಲ್ಲದೇ ಆಸಿಲ್-ಕಿಣ್ವ ಮಧ್ಯಂತರದ ರಚನೆಯಿಂದಲೂ ರೂಪಗೊಳ್ಳುತ್ತದೆ. ಬಲಬದಿಯಲ್ಲಿರುವ ಚಿತ್ರದಲ್ಲಿ, ಕಿಣ್ವವು ಕ್ರಿಯೆಯ ಮೊದಲ ಕೆಲವು ಸೆಕೆಂಡ್ ಗಳಲ್ಲಿ E* ಯನ್ನು ಅತ್ಯಂತ ವೇಗದಲ್ಲಿ ಬಿಡುಗಡೆ ಮಾಡುತ್ತದೆ. ಅನಂತರ ಸ್ಥಿರ ಸ್ಥಿತಿಯನ್ನು ತಲುಪುತ್ತ ಹೋದಂತೆ ದರ ಕಡಿಮೆಯಾಗುತ್ತದೆ. ಕ್ರಿಯೆಯಲ್ಲಿ ಅತಿವೇಗವಾಗಿ ಸಂಭವಿಸುವ ಈ ಒಡೆಯುವ ಹಂತವು ಕಿಣ್ವದ ಏಕ ಕಾರ್ಯವನ್ನು ಮಾತ್ರ ಅಳೆಯುತ್ತದೆ. ಇದರ ಪರಿಣಾಮವಾಗಿ, ಸಿಡಿಯುವಿಕೆಯಿಂದ ಬಿಡುಗಡೆಯಾದ ಉತ್ಪನ್ನದ ಮೊತ್ತವನ್ನು ನಕ್ಷೆಯ y -ರೇಖೆಯ ಮೇಲೆ ಅಂತಃ ಛೇದದಂತೆ ತೋರಿಸಲಾಗಿದೆ. ಅಲ್ಲದೇ ವಿಶ್ಲೇಷಣೆಯಲ್ಲಿರುವ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಕಿಣ್ವದ ಸಂಖ್ಯೆಯನ್ನು ನೀಡಲಾಗಿದೆ.^[೩೧]

ರಾಸಾಯನಿಕ ಕಾರ್ಯರೀತಿ

ಕಿಣ್ವದ ಪ್ರತಿಕ್ರಿಯೆಯ ರಾಸಾಯನಿಕ ಕಾರ್ಯರೀತಿಯನ್ನು ನಿರ್ಧರಿಸುವುದು ಕಿಣ್ವದ ಚಲನೆಗಳನ್ನು ಅಳೆಯುವ ಅತ್ಯಂತ ಮಹತ್ವದ ಗುರಿಯಾಗಿದೆ. ಉದಾಹರಣೆಗೆ, ತಲಾಧಾರವನ್ನು ಉತ್ಪನ್ನವಾಗಿ ವರ್ಗಾಯಿಸುವ ರಾಸಾಯನಿಕ ಹಂತಗಳ ಕ್ರಮಾನುಗತಿ. ಮೇಲೆ ಚರ್ಚಿಸಲಾದ ಚಲನೆಯ ಮಾರ್ಗಗಳು, ಯಾವ ದರದಲ್ಲಿ ಮಧ್ಯಂತರಗಳು ರೂಪುಗೊಳ್ಳುತ್ತವೆ ಹಾಗು ಆಂತರಿಕವಾಗಿ ಪರಿವರ್ತನೆ ಹೊಂದುತ್ತವೆ ಎಂಬುದನ್ನು ತೋರಿಸುತ್ತವೆ. ಆದರೆ ಇವು ಈ ಮಧ್ಯಂತರಗಳೇನೆಂಬುದನ್ನು ಖಚಿತವಾಗಿ ಕಂಡುಹಿಡಿಯಲಾರವು. ಅನೇಕ ವಿಶ್ಲೇಷಣ ಸ್ಥಿತಿಗಳಡಿ ತೆಗೆದುಕೊಂಡ ಚಲನಶೀಲತೆಯ ಅಳತೆಗಳು ಅಥವಾ ಸ್ವಲ್ಪ ಮಟ್ಟಿಗೆ ಮಾರ್ಪಡಿಸಲಾದ ಕಿಣ್ವಗಳು ಅಥವಾ ತಲಾಧಾರಗಳು ಹೆಚ್ಚಾಗಿ ರಾಸಾಯನಿಕ ಕಾರ್ಯರೀತಿಯ ಮೇಲೆ ಬೆಳಕು ಹರಿಸುತ್ತವೆ. ಇವು ಕ್ರಿಯೆಯಲ್ಲಿ ದರ ನಿರ್ಧರಿಸುವ ಕ್ರಮ ಅಥವಾ ಮಧ್ಯಂತರಗಳನ್ನು ಬಹಿರಂಗಪಡಿಸುವ ಮೂಲಕ ರಾಸಾಯನಿಕ ಕಾರ್ಯರೀತಿಯ ಮೇಲೆ ಪರಿಣಾಮಕಾರಿ ಮಧ್ಯಸ್ಥಿಕೆಯ ಪ್ರತಿಕ್ರಿಯೆಗಳಾಗಿವೆ. ಉದಾಹರಣೆಗೆ, ಕೋವೇಲನ್ಸಿ ಬಂಧವು ಹೈಡ್ರೊಜನ್ ಪರಮಾಣು ವಿನ ವಿಭಜನೆಯು ಸರ್ವಸಾಮಾನ್ಯ ದರ ಪ್ರಮಾಣಕದ ನಿರ್ಧಾರಕ ಹಂತವಾಗಿದೆ. ಜಲಜನಕದ ವರ್ಗಾವಣೆಯು ದರ ನಿರ್ಧಾರಕವಾಗಿದ್ದು, ಪ್ರತಿಯೊಂದು ಜಲಜನಕವನ್ನು ಇದರ ಸ್ಥಿರ ಐಸೊಟೋಪ್ ಆದ ಡ್ಯೂಟೀರಿಯಮ್(ಸಾಮಾನ್ಯ ಹೈಡ್ರೋಜನ್ ಪರಮಾಣುವಿನ ಎರಡರಷ್ಟು ತೂಕವಿರುವ ಹೈಡ್ರೋಜನ್ ಐಸೊಟೋಪು)ನಿಂದ ಆದೇಶಿಸುವ ಮೂಲಕ ಇದನ್ನು ತೋರಿಸಬಹುದಾಗಿದೆ.ಇದರಲ್ಲಿ ಚಲನಶೀಲತೆಯ ಪರಿಣಾಮಗಳನ್ನೂ ಅಳತೆಗೆ ಒಡ್ಡಬಹುದಾಗಿದೆ. ವಿಷಮಸ್ಥಿತಿಯಲ್ಲಿರುವ ಜಲಜನಕವನ್ನು ಬದಲಾಯಿಸಿದಾಗ ಪ್ರಾಥಮಿಕ ಕೈನೆಟಿಕ್ ಐಸೊಟೋಪ್ ಎಫೆಕ್ಟ್ ನಿಂದಾಗಿ ದರವು ಬದಲಾಗುತ್ತದೆ. ಏಕೆಂದರೆ ವಿಭಜಿಸಲು ಜಲಜನಕದ ಬಂಧಕ್ಕಿಂತ ಡ್ಯೂಟೀರಿಯಮ್ ಬಂಧವು ಗಟ್ಟಿಯಾಗಿರುತ್ತದೆ.^[೩೨] ಇತರ ಐಸೊಟೋಪ್ ಪರ್ಯಾಯಗಳಿಂದ, ಹೋಲಿಕೆಯ ದೃಷ್ಟಿಯಲ್ಲಿ ಸದೃಶವಾಗಿರುವ ಪರಿಣಾಮಗಳನ್ನು ಅಳೆಯಲು ಕೂಡ ಸಾಧ್ಯ. ಉದಾಹರಣೆಗೆ, ¹³C/¹²C ಮತ್ತು ¹⁸O/¹⁶O, ಆದರೆ ಈ ಪರಿಣಾಮಗಳು ಅತ್ಯಂತ ಸೂಕ್ಷ್ಮವಾಗಿರುತ್ತವೆ.^[೩೩] ಐಸೊಟೋಪ್ ಗಳನ್ನು ಅಂತಿಮ ಉತ್ಪನ್ನದಲ್ಲಿ ತಲಾಧಾರ ಅಣುಗಳ ವಿವಿಧ ಭಾಗಗಳ ಅಳಿವು- ಉಳಿವನ್ನು ಬಹಿರಂಗಪಡಿಸಲು ಕೂಡ ಬಳಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಅಂತಿಮ ಉತ್ಪನ್ನದಲ್ಲಿ ಆಮ್ಲಜನಕದ ಪರಮಾಣುವಿನ ವ್ಯತ್ಯಾಸದ ಮೂಲವನ್ನು ಅರಿತುಕೊಳ್ಳುಲು ಕೆಲವೊಮ್ಮೆ ಕಷ್ಟವಾಗುತ್ತದೆ; ಅದು ನೀರಿನಿಂದ ಬರುವವರೆಗೂ ಅಥವಾ ತಲಾಧಾರದ ಭಾಗದಿಂದ ಬರುವವರೆಗೂ ಅದರ ಮೂಲ ತಿಳಿದುಕೊಳ್ಳಲು ಕಷ್ಟವಾಗುತ್ತದೆ. ಕ್ರಮಬದ್ದ ಆಮ್ಲಜನಕದ ಸ್ಥಿರ ಐಸೊಟೋಪ್ ¹⁸O ಅನ್ನು ಅನೇಕ ಅಣುಗಳಾಗಿಸುವ, ವಿಭಜನೆಯನ್ನು ಆದೇಶಿಸುವ ಮೂಲಕ ಇದನ್ನು ನಿರ್ಧರಿಸಬಹುದಾಗಿದೆ. ಈ ವಿಭಿನ್ನ ಅಣುಗಳು ಪ್ರತಿಕ್ರಿಯೆಯಲ್ಲಿ ಭಾಗವಹಿಸುತ್ತವೆ. ಅಲ್ಲದೇ ಉತ್ಪನ್ನದಲ್ಲಿ ಐಸೊಟೋಪ್ ಗಾಗಿ ಪರೀಕ್ಷೆಗೆ ಒಳಪಡುತ್ತವೆ.^[೩೪] ವಿಭಿನ್ನ pH ಸ್ಥಿತಿಗಳಡಿ ಚಲನೆ ಮತ್ತು ಐಸೊಟೋಪ್ ನ ಪರಿಣಾಮಗಳ ಮೂಲಕವೂ ರಾಸಾಯನಿಕ ಕಾರ್ಯರೀತಿಯನ್ನು(ವಿಧಾನ) ವಿವರಿಸಬಹುದಾಗಿದೆ.^[೩೫] ಲೋಹದ ಅಯಾನುವನ್ನು ಬದಲಾಯಿಸುವ ಮೂಲಕ ಅಥವಾ ಇತರ ಬಂಧಿತ ಕೊ ಫ್ಯಾಕ್ಟರ್ ಗಳ(ಸಹ ಅಂಶಗಳ ಕ್ರಿಯಾಶೀಲತೆ) ಮೂಲಕ ,^[೩೬]. ಸಂರಕ್ಷಿಸಲಾದ ಅಮೈನೊ ಆಮ್ಲದ ಶೇಷಗಳ ಸೈಟ್ -ಡೈರೆಕ್ಟೆಡ್ ಮ್ಯೂಟಜೆನಿಸಿಸ್ ನ ಮೂಲಕ , ಅಥವಾ ತಲಾಧಾರ(ಗಳ)ದ ಹೋಲಿಕೆಯಲ್ಲಿರುವ ಕಿಣ್ವದ ವರ್ತನೆಯನ್ನು ಅಧ್ಯಯನ ಮಾಡುವ ಮೂಲಕ ರಾಸಾಯನಿಕ ಕಾರ್ಯರೀತಿಯನ್ನು ವಿವರಿಸಬಹುದಾಗಿದೆ.^[೩೭] ಸದೃಶ್ಯ ಅಯಾನುಗಳ ಮೂಲಕ ಅದರ ಚಲನಶೀಲತೆಯ ಅಸ್ತಿತ್ವ ಕಾಣಿಸುತ್ತದೆ.ಇದು ಅದರ ಅಧ್ಯಯನಕ್ಕೆ ಪೂರಕವಾಗಿದೆ

ಕಿಣ್ವದ ಪ್ರತಿಬಂಧ ಮತ್ತು ಸಕ್ರಿಯಕರಣ

ಅಣುಗಳು ಕಿಣ್ವದ ಪ್ರತಿಬಂಧಕಗಳಾಗಿವೆ. ಇವು ಕಿಣ್ವದ ಕಾರ್ಯಚಟುವಟಿಕೆಯನ್ನು ಕಡಿಮೆಮಾಡುತ್ತವೆ ಅಥವಾ ನಿಲ್ಲಿಸುತ್ತದೆ. ಈ ಕಾರಣದಿಂದಾಗಿ ಕಿಣ್ವದ ಸಕ್ರಿಯಕಾರಿಗಳನ್ನು ಒಂದೇ ನಾಣ್ಯದ ವಿರುದ್ಧ ಬದಿಯಲ್ಲಿರುವ ಸಕ್ರಿಯಕಾರಿಗಳೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ. ಈ ಬದಿಯಲ್ಲಿ ಅವು ಕಿಣ್ವಗಳ ವೇಗವರ್ಧಕದ ದರವನ್ನು ಹೆಚ್ಚಿಸುವ ಅಣುಗಳಾಗಿರುತ್ತವೆ. ಈ ಪಾರಸ್ಪರಿಕ ಕ್ರಿಯೆಗಳು ಪೂರ್ವ ಸ್ಥಿತಿಗೆ ತರಬಲ್ಲ ವಾಗಿರುತ್ತವೆ. (ಉದಾಹರಣೆಗೆ, ಪ್ರತಿಬಂಧಕವನ್ನು ತೆಗೆದುಹಾಕುವ ಮೂಲಕ ಕಿಣ್ವದ ಕಾರ್ಯವನ್ನು ಪುನಃ ಸ್ಥಾಪಿಸಬಹುದು.) ಅಥವಾ ಪೂರ್ವ ಸ್ಥಿತಿಗೆ ತರಲು ಸಾಧ್ಯವಿಲ್ಲ ದ್ದಾಗಿರುತ್ತದೆ. (ಉದಾಹರಣೆಗೆ ಪ್ರತಿಬಂಧಕವು ಶಾಶ್ವತವಾಗಿ ಕಿಣ್ವವನ್ನು ಕಾರ್ಯನಿರ್ವಹಿಸದಂತೆ ಮಾಡಬಹುದು).

ಪೂರ್ವಸ್ಥಿತಿಗೆ ತರಬಲ್ಲ ಪ್ರತಿಬಂಧಕಗಳು

ಸಾಂಪ್ರದಾಯಿಕವಾಗಿ ಪೂರ್ವ ಸ್ಥಿತಿಗೆ ತರಬಲ್ಲ ಕಿಣ್ವದ ಪ್ರತಿಬಂಧಕಗಳನ್ನು ಸ್ಪರ್ಧಾತ್ಮಕ, ಸ್ಪರ್ಧಾತ್ಮಕವಲ್ಲದ, ಸ್ಪರ್ಧೆಯಿಲ್ಲದ ಅಥವಾ ಮಿಶ್ರಣವೆಂದು ವರ್ಗೀಕರಿಸಲಾಗಿದೆ. ಈ ವರ್ಗೀಕರಣವನ್ನು K _m ಮತ್ತು V _max ನ ಮೇಲೆ ಅವುಗಳ ಪರಿಣಾಮದ ಅನುಸಾರ ಮಾಡಲಾಗಿದೆ. ಈ ವಿಭಿನ್ನ ಪರಿಣಾಮಗಳು ಕಿಣ್ವ E ಯನ್ನು , ಕಿಣ್ವ–ತಲಾಧಾರ ಸಂಕೀರ್ಣ ES ಅನ್ನು ಅಥವಾ ಇವೆರಡನ್ನೂ ಬಂಧಿಸಿದ ಪ್ರತಿಬಂಧಕದ ಫಲಿತಾಂಶದಿಂದ, ಬಲಬದಿಯ ಚಿತ್ರದಲ್ಲಿ ಮತ್ತು ಕೆಳಗಿನ ಟೇಬಲ್ ನಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಉಂಟಾಗಿದೆ. ಪ್ರತಿಬಂಧಕದ ಪ್ರತ್ಯೇಕವಾದ ವಿಧವನ್ನು, ಪ್ರತಿಬಂಧಕದ ಸಾರೀಕರಣದ ಕಾರ್ಯರೂಪದಂತೆ ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರದ ಅಧ್ಯಯನ ಮಾಡುವ ಮೂಲಕ ತಿಳಿಯಬಹುದಾಗಿದೆ. ಲೈನ್ ವೀವರ- ಬರ್ಕ್ ಮತ್ತು ಇಡೈ-ಹಾಫ್ಸ್ಟೀ ನಕ್ಷೆಗಳು^[೧೩] ನಾಲ್ಕು ವಿಧದ ಪ್ರತಿಬಂಧವನ್ನು ಬಿಡುಗಡೆ ಮಾಡಿವೆ. ಇವು ಪ್ರತಿಬಂಧಕದ ಸಾರೀಕರಣದೊಂದಿಗೆ ಭಿನ್ನರೀತಿಯ ವ್ಯತ್ಯಾಸ ಹೊಂದಿವೆ. ಸಂಕ್ಷಿಪ್ತತೆಗಾಗಿ, ಎರಡು ಚಿಹ್ನೆಗಳನ್ನು ಬಳಸಲಾಗಿದೆ:

\alpha =1+{\frac {[{\mbox{I}}]}{K_{i}}}

\alpha = 1 + \frac{[\mbox{I}]}{K_{i}} ಮತ್ತು

\alpha ^{\prime }=1+{\frac {[{\mbox{I}}]}{K_{i}^{\prime }}}

\alpha^{\prime} = 1 + \frac{[\mbox{I}]}{K_{i}^{\prime}}

K _i ಮತ್ತು K_i ಗಳು ಕಿಣ್ವವನ್ನು ಮತ್ತು ಕಿಣ್ವ–ತಲಾಧಾರ ಸಂಕೀರ್ಣವನ್ನು ಬಂಧಿಸಲು ಅನುಕ್ರಮವಾಗಿ ವಿಯೋಜನೆಗೊಂಡ ಸ್ಥಿರಾಂಕಗಳಾಗಿವೆ. ಪೂರ್ವ ಸ್ಥಿತಿಗೆ ತರಬಲ್ಲ ಪ್ರತಿಬಂಧಕದಲ್ಲಿ, ಕಿಣ್ವದ ಸ್ಪಷ್ಟವಾದ K_mಮತ್ತು V_max, (α/α') K_m ಮತ್ತು (1/α') V_max ಆಗುತ್ತವೆ. ಅನುಕ್ರಮವಾಗಿ ಸಾಮಾನ್ಯ ಪ್ರಕರಣಗಳಿಗೆ ಕೆಳಗೆ ತೋರಿಸಿರುವಂತೆ.

width="10%" align="center"	width="10%" align="center"	ಪ್ರತಿಬಂಧದ ವಿಧಗಳು	K _m apparent	V _max apparent
K _i only	(Failed to parse (syntax error): {\displaystyle \ಆಲ್ಫ^{\prime}=1} )	ಸ್ಪರ್ಧಾತ್ಮಕ	$K_{m}\alpha ~$	$~V_{\max }~$
K _i' only	(Failed to parse (syntax error): {\displaystyle \ಆಲ್ಫ=1~} )	ಸ್ಪರ್ಧಾತ್ಮಕವಲ್ಲದ	${\frac {K_{m}}{\alpha ^{\prime }}}$	${\frac {V_{\max }}{\alpha ^{\prime }}}$
K _i = K _i'	(Failed to parse (syntax error): {\displaystyle \ಆಲ್ಫ = \ಆಲ್ಫ^{\prime}} )	ಸ್ಪರ್ಧೆಯಿಲ್ಲದ	$~K_{m}~$	${\frac {V_{\max }}{\alpha ^{\prime }}}$
K _i ≠ K _i'	(Failed to parse (syntax error): {\displaystyle \ಆಲ್ಫ \neq \ಆಲ್ಫ^{\prime}} )	ಮಿಶ್ರಿತ(%)	${\frac {K_{m}\alpha }{\alpha ^{\prime }}}$	${\frac {V_{\max }}{\alpha ^{\prime }}}$

ರೇಖೀಯವಲ್ಲದ ಸಮಾಶ್ರಯಣವು ಕಿಣ್ವದ ಚಲನೆಗಳ ದತ್ತಾಂಶವನ್ನು ಮೇಲೆ ನೀಡಲಾದ ದರ ಸಮೀಕರಣಗಳಿಗೆ ಹೊಂದಿಸುತ್ತದೆ^[೩೮]. ಇದರಿಂದಾಗಿ K _i ಮತ್ತು K_i ವಿಯೋಜನೆಗೊಂಡ ಸ್ಥಿರಾಂಕಗಳ ನಿಖರ ಅಂದಾಜನ್ನು ಪಡೆಯಬಹುದಾಗಿದೆ . ಪ್ರತಿಬಂಧಕದ ಪದಗಳಿಗೆ ಪರ್ಯಾಯವಾಗಿ ಆಲ್ಫ ಸಂಕೇತಗಳ ಬಳಕೆಯು, ಸಾಂಪ್ರದಾಯಿಕವಾಗಿ ಪ್ರತಿಬಂಧ ಚಲನಶಾಸ್ತ್ರದ ಮಾದರಿಯನ್ನು ರೂಪಿಸಲು ಇರುವ ಸಮಸ್ಯೆಗಳನ್ನು ಆವರಣಗೊಳಿಸುತ್ತದೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ ಪ್ರತಿಬಂಧದ ಸ್ಪರ್ಧೆಯಿಲ್ಲದ ರೂಪವು , ಪ್ರತಿಕ್ರಿಯೆಯ ಗರಿಷ್ಠ ವೇಗದ ಬಲದ ಮೇಲೆ ನೇರವಾಗಿ ಪರಿಣಾಮ ಬೀರುವ ಪ್ರತಿಬಂಧಕದ ಬಂಧನ ಸಿದ್ಧಾಂತವನ್ನು ಅವಲಂಬಿಸಿದೆ. ಅದೇನೇ ಆದರೂ ಈ ಪದವನ್ನು ಗರಿಷ್ಠ ವೇಗಕ್ಕೆ ವಿಲೋಮವಾಗಿ ಸಂಬಂಧಿಸಿರುವಂತೆ ಚಿತ್ರಿಸಲಾಗಿದೆ. ಸರಳ ಪುನಸ್ಸಂಯೋಜನೆಯು ಪ್ರತಿಬಂಧಕದ ಬಂಧದ ನಡುವೆ ಮತ್ತು ಗರಿಷ್ಥ ವೇಗವು ಕಡಿಮೆಯಾಗುವುದರ ನಡುವೆ ಇರುವ ನೇರ ಸಂಬಂಧವನ್ನು ತೋರಿಸುತ್ತದೆ.

{\cfrac {V_{\max }}{1+{\cfrac {[I]}{K_{i}}}}}

{\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{K_{i}}}}

ಕೆಳಗೆ ಸೊನ್ನೆಯನ್ನು ಸೇರಿಸುವ ಮೂಲಕ([I]-[I])

{\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{[I]+K_{i}-[I]}}}

[I]+K_i ನಿಂದ ಭಾಗಿಸುವ ಮೂಲಕ

{\cfrac {V_{\max }}{\cfrac {1}{1-{\cfrac {[I]}{[I]+K_{i}}}}}}

V_{\max }-V_{\max }{\cfrac {[I]}{[I]+K_{i}}}

ಈ ಸಂಕೇತವು ಮೈಕ್ಯಲೀಸ-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣಕ್ಕೆ ಸದೃಶವಾಗಿದೆ ಎಂಬುದನ್ನು ತೋರಿಸುತ್ತದೆ. ಅದರಲ್ಲಿ ಪ್ರತಿಕ್ರಿಯೆಯ ದರವು ತಲಾಧಾರದೊಂದಿಗೆ ಪಾರಸ್ಪರಿಕ ಕ್ರಿಯೆಯಲ್ಲಿ ತೊಡಗಿರುವ ಕಿಣ್ವದ ಮೊತ್ತದ ಶೇಕಡಾವಾರುವಿನ ಮೇಲೆ ಅವಲಂಬಿಸಿರುತ್ತದೆ. ತಲಾಧಾರದಿಂದ ಪರಿಮಿತಿಗೊಳಪಟ್ಟ ಕಿಣ್ವದ ಮೊತ್ತದ ಅಪೂರ್ಣಾಂಕ

{\cfrac {[S]}{[S]+K_{m}}}

ಪ್ರತಿಬಂಧಕದಿಂದ ಪರಿಮಿತಿಗೊಳಪಟ್ಟ ಕಿಣ್ವದ ಮೊತ್ತದ ಅಪೂರ್ಣಾಂಕ

{\cfrac {[I]}{[I]+K_{i}}}

ಪ್ರತಿಬಂಧಕದ ಪರಿಣಾಮವು, ಅದರೊಂದಿಗೆ ಪ್ರತಿಕ್ರಿಯಿಸುವ ಕಿಣ್ವ ಮೊತ್ತದ ಶೇಕಡಾವಾರು ಫಲಿತಾಂಶವಾಗಿದೆ. ಈ ಸಮೀಕರಣದ ಪ್ರಸ್ತುತ ರೂಪದಲ್ಲಿರುವ ಒಂದು ಸಮಸ್ಯೆಯೆಂದರೆ, ಇದು ಪ್ರತಿಬಂಧಕದ ಬಂಧದೊಂದಿಗೆ ಕಿಣ್ವದ ಸಂಪೂರ್ಣ ಆಂತರಿಕ ಪ್ರತಿಬಂಧವನ್ನು ಹೊಂದುತ್ತದೆ. ತಲಾಧಾರದ 100 ಪ್ರತಿಶತದಷ್ಟು ಪ್ರತಿಬಂಧನದಿಂದ ಕೇವಲ >0 ಪ್ರತಿಶತದ ವರೆಗೆ ಎಲ್ಲಿಬೇಕಾದರೂ ಬೃಹತ್ ಪ್ರಮಾಣದ ಪರಿಣಾಮಗಳುಂಟಾಗಬಹುದು. ಇದಕ್ಕೆ ಕಾರಣ ಡೆಲ್ಟಾ V _max ಪದವನ್ನು ಒಳಗೊಳ್ಳುವ ಮೂಲಕ ವಿಭಿನ್ನ ಮಟ್ಟದ ಪ್ರತಿಬಂಧದಕ್ಕೆ ಅವಕಾಶ ಮಾಡಿಕೊಡಲು ಸಮೀಕರಣವನ್ನು ಸುಲಭವಾಗಿ ಮಾರ್ಪಡಿಸಬಹುದಾಗಿದೆ.

V_{\max }-\Delta V_{\max }{\cfrac {[I]}{[I]+K_{i}}}

ಅಥವಾ

V_{\max }1-(V_{\max }1-V_{\max }2){\cfrac {[I]}{[I]+K_{i}}}

ಈ ಪದವು ಅನಂತರ ಶೇಷವಾದ ಕಿಣ್ವದ ಚಟುವಟಿಕೆಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಬಲ್ಲದು. ಪ್ರತಿಬಂಧಕವು ಗುಂಪಿನಲ್ಲಿ ಪ್ರತ್ಯೇಕವಾದ ಕಿಣ್ವಗಳೊಂದಿಗೆ ಪ್ರತಿಕ್ರಿಯಿಸುವಾಗ ನಡೆಯುವ ಕಿಣ್ವದ ಚಟುವಟಿಕೆಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಬಹುದಾಗಿದೆ. ಆದರೂ ಈ ಪದದ ಒಳಗೂಡಿಸುವಿಕೆಯು, ಸಕ್ರಿಯಕರಣದ ಸಾಧ್ಯತೆಗೆ ಅವಕಾಶ ನೀಡುವ ಮೂಲಕ ಅಧಿಕ ಮೌಲ್ಯ ಹೊಂದಿರುತ್ತದೆ. ಒಂದು ವೇಳೆ ಎರಡನೆಯ V _max ಪದವು ಆರಂಭಿಕ ಪದಕ್ಕಿಂತ ಹೆಚ್ಚಾದಾಗ ಹೀಗಾಗುತ್ತದೆ. ಸಕ್ರಿಯಕರಣದ ಸಾಧ್ಯತೆಗೆ ಮತ್ತು ಸಂಕೇತಕ್ಕೆ ಕಾರಣವಾಗುವ ಪ್ರತಿಬಂಧಕ "I" ಅನ್ನು ಇಲ್ಲಿ ಸೂಚಿಸಲಾದ ಪರಿವರ್ತಕ ಪದ "X" ದಿಂದ ಬದಲಾಯಿಸುವ ಮೂಲಕ ಪುನಃ ದಾಖಲಿಸಬಹುದು.

V_{\max }1-(V_{\max }1-V_{\max }2){\cfrac {[X]}{[X]+K_{x}}}

ಈ ಪರಿಭಾಷೆಯು ಮೈಕ್ಯಲೀಸ-ಮೆನ್ ಟೆನ್ ಸಮೀಕರಣದ ಗರಿಷ್ಠ ವೇಗಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಚಲನೆಯ ಪರಿಣಾಮಗಳೊಂದಿಗೆ ಸರಳವಾದ ಮಾರ್ಗದಲ್ಲಿ ಸಂಪರ್ಕಿಸುವುದರ ಫಲವಾಗಿದೆ. ಇದು K _m ಕ್ಕೆ ಸಂಧಿಸಿದಂತೆ ಪರಿಮಾಣಗಳನ್ನು ವಿವರಿಸುವ ಪದದ ಪ್ರಮುಖ ಸಮಸ್ಯೆಯ ಮೇಲೆ ಬೆಳಕುಚೆಲ್ಲುತ್ತದೆ. ತಲಾಧಾರಕ್ಕಾಗಿ ಕಿಣ್ವದ ಆಕರ್ಷಣ ಬಲದೊಂದಿಗೆ ಸಂಬಂಧಿಸಿರುವ K _m ಬಹುಪಾಲು ವಿಷಯಗಳಲ್ಲಿ ಕಿಣ್ವದ ಬಂಧಕ ಭಾಗದಲ್ಲಿ ಪ್ರಮುಖ ಸಮಸ್ಯೆಗಳಿಗೆ ಸಂಬಂಧಿಸಿರುತ್ತದೆ. ಇದು ಕಿಣ್ವ ಪ್ರತಿಬಂಧಕದ ಪಾರಸ್ಪರಿಕ ಕ್ರಿಯೆಗಳಿಂದ ನೇರವಾಗಿ ಹೊರಬರುತ್ತದೆ. ಇಂತಹ ಪದವು V _max ಯನ್ನು ಮಾರ್ಪಡಿಸಲು ಮೇಲೆ ಸೂಚಿಸಿದ ಪದಕ್ಕೆ ಸದೃಶವಾಗಿದೆ. ಇದು ಬಹುತೇಕ ಸಂದರ್ಭಗಳಿಗೆ ಸೂಕ್ತವಾಗಿದೆ:^[೩೯]

K_{m}1-(K_{m}1-K_{m}2){\cfrac {[X]}{[X]+K_{x}}}

ಪೂರ್ವ ಸ್ಥಿತಿಗೆ ತರಲಾಗದ ಪ್ರತಿಬಂಧಕಗಳು

ಕಿಣ್ವ ಪ್ರತಿಬಂಧಕಗಳು ಕಿಣ್ವಗಳನ್ನು ಪೂರ್ವ ಸ್ಥಿತಿಗೆ ತರಲಾಗದಂತೆ ನಿಷ್ಕ್ರಿಯಗೊಳಿಸಬಲ್ಲವು. ಇದನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಕೋವೇಲನ್ಸಿಯ ರೀತಿಯಲ್ಲಿ ಮಾರ್ಪಡಿಸಲಾದ ಸಕ್ರಿಯ ಸೈಟ್ ನ ಶೇಷಗಳಿಂದ ಮಾಡಬಲ್ಲವು. ಬಹುಶಃ ಆತ್ಮಹತ್ಯಾ ತಲಾಧಾರಗಳೆಂದು ಕರೆಯಲಾಗುವ ಈ ಪ್ರತಿಕ್ರಿಯೆಗಳು ಘಾತೀಯ ಕ್ಷಯಿಸುವಿಕೆಯ (ಎಕ್ಸ್ ಪೊನೇಷನಲ್ ಡಿಕೇ) ಕಾರ್ಯಗಳನ್ನು ಅನುಸರಿಸಬಹುದು. ಅಲ್ಲದೇ ಅವು ಸಾಮಾನ್ಯವಾಗಿ ಆರ್ದ್ರವಾಗಿರುತ್ತವೆ. ಆರ್ದ್ರೀಕರಣದ ಕೆಳಮಟ್ಟಕ್ಕೆ, ಅವು ಪ್ರತಿಬಂಧಕದೊಂದಿಗೆ ಚಲನಶಾಸ್ತ್ರದ ಪ್ರಕ್ರಿಯಾ ದರವನ್ನು ಅನುಸರಿಸುತ್ತವೆ.

ವೇಗವರ್ಧನೆಯ ಯಾಂತ್ರಿಕ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ

ಘರ್ಷಣೆಯಿಂದ ಸರಿಹೊಂದಿಸುವ ಮಾದರಿಯು(ಇನ್ ಡ್ಯೂಸ್ ಫಿಟ್ ಮಾಡೆಲ್) ಕಿಣ್ವ–ತಲಾಧಾರ ಪಾರಸ್ಪರಿಕ ಕ್ರಿಯೆಯ ಅತ್ಯಂತ ಅನುಕೂಲಕರವಾದ ಮಾದರಿಯಾಗಿದೆ.^[೪೦] ಈ ಮಾದರಿಯು, ಕಿಣ್ವ ಮತ್ತು ತಲಾಧಾರದ ನಡುವೆ ನಡೆಯುವ ಆರಂಭಿಕ ಪಾರಸ್ಪರಿಕ ಕ್ರಿಯೆಯು ಹೋಲಿಕೆಯ ದೃಷ್ಟಿಯಿಂದ ಅತ್ಯಂತ ದುರ್ಬಲವಾಗಿದೆ ಎಂಬುದನ್ನು ಪ್ರಸ್ತಾಪಿಸುತ್ತದೆ. ಆದರೆ ಈ ದುರ್ಬಲ ಪಾರಸ್ಪರಿಕ ಕ್ರಿಯೆಗಳು ಕಿಣ್ವದಲ್ಲಿ ಅತ್ಯಂತ ವೇಗವಾಗಿ ಬಂಧಕಕ್ಕೆ ಬಲನೀಡುವ ರಚನೆಯ ಬದಲಾವಣೆಗಳಿಗೆ(ಕಾನ್ ಫರ್ಮೇಷನಲ್ ಚೇಂಜ್) ಪ್ರೇರಿಪಿಸುತ್ತವೆ ಎಂಬುದನ್ನು ತಿಳಿಸುತ್ತದೆ. ಈ ರಚನೆಯ ಬದಲಾವಣೆಗಳು, ತಲಾಧಾರದಲ್ಲಿ ರಾಸಾಯನಿಕ ಬಂಧಕಗಳಿಗೆ ಸಮೀಪವಾಗಿರುವ ಸಕ್ರಿಯ ಸೈಟ್ ನಲ್ಲಿ ವೇಗವರ್ಧಕದ ಶೇಷಗಳನ್ನು ತರುತ್ತದೆ.ಇವುಗಳನ್ನು ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಬದಲಾಯಿಸಲಾಗುತ್ತದೆ.^[೪೧] ರಚನೆಯ ಬದಲಾವಣೆಗಳನ್ನು ಸರ್ಕ್ಯುಲರ್ ಡೈಕ್ರಾಯಿಸಮ್ ಅಥವಾ ಡ್ಯೂಅಲ್ ಪೊಲರೈಸೇಷನ್ ಇಂಟರ್ ಫರ್ಮೆಟ್ರಿ ಗಳನ್ನು ಬಳಸುವ ಮೂಲಕ ಅಳೆಯ ಬಹುದಾಗಿದೆ.(ಎರಡು ಕೋನಗಳಲ್ಲಿ ಪರೀಕ್ಷಿಸಿದಾಗ ಎರಡು ವಿಧದ ಬಣ್ಣಗಳು ಗೋಚರಿಸುತ್ತವೆ.) ಬಂಧಕವು ಕ್ರಿಯೆ ಉಂಟಾದ ನಂತರ, ವೇಗವರ್ಧನೆಯ ಒಂದು ಅಥವಾ ಹೆಚ್ಚು ಯಾಂತ್ರಿಕ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ ಪ್ರತಿಕ್ರಿಯೆಯ ಸಂಕ್ರಮಣ ಹಂತದ ಸಾಮರ್ಥ್ಯ ಕುಗ್ಗಿಸುತ್ತವೆ. ಪ್ರತಿಕ್ರಿಯೆಗೆ ಪರ್ಯಾಯ ಪ್ರತಿಕ್ರಿಯೆಗಳ ಅನುಕ್ರಮ ಕಲ್ಪಿಸಿಕೊಡುವ ಮೂಲಕ ಅದರ ಸಾಮರ್ಥ್ಯ ಕಡಿಮೆ ಮಾಡುತ್ತವೆ. ವೇಗವರ್ಧನೆಯ ಯಾಂತ್ರಿಕ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ ಬಂಧನದ ಎಳೆತದಿಂದ ಉಂಟಾದ ವೇಗವರ್ಧನೆಯನ್ನು ಒಳಗೊಳ್ಳುತ್ತವೆ; ಸಾಮೀಪ್ಯ ಮತ್ತು ಪೂರ್ವಾಭಿಮುಖಗೊಳಿಸುವ ಮೂಲಕ; ಸಕ್ರಿಯ ಸೈಟ್ ನ ಪ್ರೋಟಾನ್ ದಾನಿಗಳ ಅಥವಾ ಒಪ್ಪಿಕೊಳ್ಳುವವರ ಮೂಲಕ; ಕೋವೇಲನ್ಸಿ ವೇಗವರ್ಧನೆ ಮತ್ತು(ಅಣುಗಳ ಒಂದೆಡೆ ಸೇರಿಸುವಿಕೆ) ಕ್ವಾಂಟಮ್ ಟ್ಯೂನಲಿಂಗ್.^[೩೦]^[೪೨] ಕಿಣ್ವ ಚಲನಶಾಸ್ತ್ರಕ್ಕೆ ವೇಗವರ್ಧನೆಯ ಯಾವ ಕ್ರಮವನ್ನು ಕಿಣ್ವ ಬಳಸುತ್ತದೆ ಎಂಬುದನ್ನು ಸಾಬೀತು ಪಡಿಸಲು ಸಾಧ್ಯವಾಗಿಲ್ಲ. ಆದರೂ ಕೆಲವು ಚಲನಶಾಸ್ತ್ರದ ದತ್ತಾಂಶವು, ಇತರ ತಂತ್ರಜ್ಞಾನ ವಿಧಾನಗಳಿಂದ ಪರೀಕ್ಷಿಸಬಹುದಾದ ಸಾಧ್ಯತೆಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಪಿಂಗ್-ಪಾಂಗ್ (ಹಗುರ ಪ್ರೊಟೀನ್ ಗಳ)ಕಾರ್ಯರೀತಿಯಲ್ಲಿ, ಬರ್ಸ್ಟ್ -ಫೇಸ್ ಪೂರ್ವ ಸ್ಥಿರತೆಯ ಚಲನಶಾಸ್ತ್ರದೊಂದಿಗೆ, ಕಿಣ್ವದ ಈ ಕಾರ್ಯರೀತಿಯಲ್ಲಿ ಕೋವೇಲನ್ಸಿ ವೇಗವರ್ಧನೆಯು ಅತ್ಯಂತ ಮಹತ್ವವಾಗಿದೆ ಎಂಬುದನ್ನು ಸೂಚಿಸಬಹುದು. ಪರ್ಯಾಯವಾಗಿ, ತೀಕ್ಷ್ಣ pH ನ ಹೀರಿಕೊಳ್ಳುವಿಕೆಯು V _max ನ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆಯೇ ಹೊರತು K _m ನ ಮೇಲೆ ಬೀರುವುದಿಲ್ಲ. ಇದು ಬಹುಶಃ ವೇಗವರ್ಧನೆ ಉಂಟಾಗಲು ಸಕ್ರಿಯ ಸೈಟ್ ನಲ್ಲಿರುವ ಶೇಷವು ಅಯಾನೀಕರಣ ಸ್ಥಿತಿಯಲ್ಲಿರಬೇಕಾದ ಅಗತ್ಯವಿದೆ ಎಂಬುದನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಇವನ್ನೂ ಗಮನಿಸಿ

ಪ್ರೋಟೀನ್ ಚಾಲಕಶಕ್ತಿಗಳು

ಅಡಿ ಟಿಪ್ಪಣಿಗಳು

α ^{^} ಲಿಂಕ್: ಇಂಟರಾಕ್ಟೀವ್ ಮೈಕ್ಯಲೀಸ-ಮೆನ್ ಟೆನ್ ಕೈನೆಟಿಕ್ಸ್ ಟುಟೋರಿಯಲ್ (ಜಾವಾ ರಿಕ್ವೈರ್ಡ್) Archived 8 March 2007^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. β ^{^} ಲಿಂಕ್: ಡೈಹೈಡ್ರೊಫೊಲೇಟ್ ರಿಡಕ್ಟೇಸ್ ಮೆಕ್ಯಾನಿಸಮ್ (ಗಿಫ್) Archived 20 August 2006^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. γ ^{^} ಲಿಂಕ್: DNA ಪಾಲಿಮರೇಸ್ ಮೆಕ್ಯಾನಿಸಮ್ (ಗಿಫ್) Archived 14 May 2006^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. δ ^{^} ಲಿಂಕ್: ಸೈಮೊಟ್ರಿಪ್ಸಿನ್ ಮೆಕ್ಯಾನಿಸಮ್ (ಫ್ಲ್ಯಾಷ್ ರಿಕ್ವೈರ್ಡ್) Archived 19 March 2007^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.

ಉಲ್ಲೇಖಗಳು

↑ Wrighton, Mark S.; Ebbing, Darrell D. (1993). General chemistry (4th ed.). Boston: Houghton Mifflin. ISBN 0-395-63696-5.{{cite book}}: CS1 maint: multiple names: authors list (link)
↑ Danson, Michael; Eisenthal, Robert (2002). Enzyme assays: a practical approach. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-963820-9.{{cite book}}: CS1 maint: multiple names: authors list (link)
↑ Xie XS, Lu HP (1999). "Single-molecule enzymology". J. Biol. Chem. 274 (23): 15967–70. doi:10.1074/jbc.274.23.15967. PMID 10347141. Archived from the original on 31 ಮೇ 2009. Retrieved 24 ನವೆಂಬರ್ 2010. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: unflagged free DOI (link)
↑ Lu H (2004). "Single-molecule spectroscopy studies of conformational change dynamics in enzymatic reactions". Current pharmaceutical biotechnology. 5 (3): 261–9. doi:10.2174/1389201043376887. PMID 15180547.
↑ Schnell J, Dyson H, Wright P (2004). "Structure, dynamics, and catalytic function of dihydrofolate reductase". Annual review of biophysics and biomolecular structure. 33: 119–40. doi:10.1146/annurev.biophys.33.110502.133613. PMID 15139807.{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ Gibson QH (1969). "Rapid mixing: Stopped flow". Methods Enzymol. 16: 187–228. doi:10.1016/S0076-6879(69)16009-7.
↑ Duggleby RG (1995). "Analysis of enzyme progress curves by non-linear regression". Methods Enzymol. 249: 61–90. doi:10.1016/0076-6879(95)49031-0. PMID 7791628.
↑ Murray JB, Dunham CM, Scott WG (2002). "A pH-dependent conformational change, rather than the chemical step, appears to be rate-limiting in the hammerhead ribozyme cleavage reaction". J. Mol. Biol. 315 (2): 121–30. doi:10.1006/jmbi.2001.5145. PMID 11779233. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
↑ ಮೈಕೆಲೀಸ್ L. ಅಂಡ್ ಮೆನ್ ಟೆನ್ M.L. ಕೈನೆಟಿಕ್ ಡರ್ ಇನ್ ವರ್ಟಿನ್ ವ್ರಿಂಗ್ಕುಂಗ್ ಬಯೋಕೆಮ್. Z. 1913; 49:333–369 ಇಂಗ್ಲೀಶ್ ಟ್ರಾನ್ಸ್ ಲೇಷನ್ 2007 ರ ಏಪ್ರಿಲ್ 6 ರಂದು ಪ್ರವೇಶಿಸಲಾಯಿತು.
↑ Stroppolo ME, Falconi M, Caccuri AM, Desideri A (2001). "Superefficient enzymes". Cell. Mol. Life Sci. 58 (10): 1451–60. doi:10.1007/PL00000788. PMID 11693526.{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ ವಾಲ್ಷ್ R,ಮಾರ್ಟೀನ್ E, ದ್ಯಾರ್ವೆಷ್ S. ಅ ಮೆಥೆಡ್ ಟು ಡಿಸ್ಕ್ರೈಬ್ ಎನ್ ಸೈಮ್-ಕ್ಯಾಟಲೈಸ್ಡ್ ರಿಯಾಕ್ಷನ್ಸ್ ಬೈ ಕಂಬೈನಿಂಗ್ ಸ್ಟೀಡಿ ಸೇಟ್ ಅಂಡ್ ಟೈಮ್ ಕೋರ್ಸ್ ಎನ್ ಸೈಮ್ ಕೈನೆಟಿಕ್ ಪ್ಯಾರಮೀಟರ್ಸ್. ಬಯೊಕೆಮಿಸ್ಟ್ರಿ ಬಯೊಫಿಸಿಕ್ಸ್ ಆಕ್ಟಾ. 2010 ಜನವರಿ;1800:1-5
↑ Jones ME (1 ಜನವರಿ 1992). "Analysis of algebraic weighted least-squares estimators for enzyme parameters". Biochem. J. 288 (Pt 2): 533–8. PMC 1132043. PMID 1463456.
↑ ^೧೩.೦ ^೧೩.೧ Tseng SJ, Hsu JP (1990). "A comparison of the parameter estimating procedures for the Michaelis-Menten model". J. Theor. Biol. 145 (4): 457–64. doi:10.1016/S0022-5193(05)80481-3. PMID 2246896. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ Bravo IG, Busto F, De Arriaga D; et al. (2001). "A normalized plot as a novel and time-saving tool in complex enzyme kinetic analysis". Biochem. J. 358 (Pt 3): 573–83. PMC 1222113. PMID 11577687. {{cite journal}}: Explicit use of et al. in: |author= (help); Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
↑ Almaas E, Kovács B, Vicsek T, Oltvai ZN, Barabási AL (2004). "Global organization of metabolic fluxes in the bacterium Escherichia coli". Nature. 427 (6977): 839–43. doi:10.1038/nature02289. PMID 14985762. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
↑ Reed JL, Vo TD, Schilling CH, Palsson BO (2003). "An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR)". Genome Biol. 4 (9): R54. doi:10.1186/gb-2003-4-9-r54. PMC 193654. PMID 12952533.{{cite journal}}: CS1 maint: multiple names: authors list (link) CS1 maint: unflagged free DOI (link)
↑ ಸಂಪೂರ್ಣ ಮೂಲಕ್ಕಾಗಿ, ಇಲ್ಲಿ ನೋಡಿ
↑ Dirr H, Reinemer P, Huber R (1994). "X-ray crystal structures of cytosolic glutathione S-transferases. Implications for protein architecture, substrate recognition and catalytic function". Eur. J. Biochem. 220 (3): 645–61. doi:10.1111/j.1432-1033.1994.tb18666.x. PMID 8143720. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
↑ Stone SR, Morrison JF (1988). "Dihydrofolate reductase from Escherichia coli: the kinetic mechanism with NADPH and reduced acetylpyridine adenine dinucleotide phosphate as substrates". Biochemistry. 27 (15): 5493–9. doi:10.1021/bi00415a016. PMID 3052577. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ Fisher PA (1994). "Enzymologic mechanism of replicative DNA polymerases in higher eukaryotes". Prog. Nucleic Acid Res. Mol. Biol. 47: 371–97. doi:10.1016/S0079-6603(08)60257-3. PMID 8016325.
↑ Akerman SE, Müller S (2003). "2-Cys peroxiredoxin PfTrx-Px1 is involved in the antioxidant defence of Plasmodium falciparum". Mol. Biochem. Parasitol. 130 (2): 75–81. doi:10.1016/S0166-6851(03)00161-0. PMID 12946843. Archived from the original on 20 ಫೆಬ್ರವರಿ 2008. Retrieved 24 ನವೆಂಬರ್ 2010. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ Bravo IG, Barrallo S, Ferrero MA, Rodríguez-Aparicio LB, Martínez-Blanco H, Reglero A (2001). "Kinetic properties of the acylneuraminate cytidylyltransferase from Pasteurella haemolytica A2". Biochem. J. 358 (Pt 3): 585–98. PMC 1222114. PMID 11577688. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
↑ Kraut J (1977). "Serine proteases: structure and mechanism of catalysis". Annu. Rev. Biochem. 46: 331–58. doi:10.1146/annurev.bi.46.070177.001555. PMID 332063.
↑ Ricard J, Cornish-Bowden A (1987). "Co-operative and allosteric enzymes: 20 years on". Eur. J. Biochem. 166 (2): 255–72. doi:10.1111/j.1432-1033.1987.tb13510.x. PMID 3301336. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ Ward WH, Fersht AR (1988). "Tyrosyl-tRNA synthetase acts as an asymmetric dimer in charging tRNA. A rationale for half-of-the-sites activity". Biochemistry. 27 (15): 5525–30. doi:10.1021/bi00415a021. PMID 3179266. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ Helmstaedt K, Krappmann S, Braus GH (2001). "Allosteric regulation of catalytic activity: Escherichia coli aspartate transcarbamoylase versus yeast chorismate mutase". Microbiol. Mol. Biol. Rev. 65 (3): 404–21, table of contents. doi:10.1128/MMBR.65.3.404-421.2001. PMC 99034. PMID 11528003. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
↑ Schirmer T, Evans PR (1990). "Structural basis of the allosteric behaviour of phosphofructokinase". Nature. 343 (6254): 140–5. doi:10.1038/343140a0. PMID 2136935. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ ಹಿಲ್, A. V. ದಿ ಪಾಸಿಬಲ್ ಎಫ್ಟೆಕ್ಟ್ ಆಫ್ ದಿ ಅಗ್ರಿಗೇಷನ್ ಆಫ್ ದಿ ಮೊಲ್ಯಾಕ್ಯೂಲ್ಸ್ ಆಫ್ ಹಿಮೊಗ್ಲೋಬಿನ್ ಆನ್ ಇಟ್ಸ್ ಡಿಸೊಸಿಯೇಷನ್ ಕರ್ವ್ಸ್ J. ಫಿಸಾಯ್ಲ್. (Lond.) , 1910 40, iv-vii.
↑ Hartley BS, Kilby BA (1954). "The reaction of p-nitrophenyl esters with chymotrypsin and insulin". Biochem. J. 56 (2): 288–97. PMC 1269615. PMID 13140189. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ ^೩೦.೦ ^೩೦.೧ Fersht, Alan (1999). Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding. San Francisco: W.H. Freeman. ISBN 0-7167-3268-8.
↑ Bender ML, Begué-Cantón ML, Blakeley RL; et al. (1966). "The determination of the concentration of hydrolytic enzyme solutions: alpha-chymotrypsin, trypsin, papain, elastase, subtilisin, and acetylcholinesterase". J. Am. Chem. Soc. 88 (24): 5890–913. doi:10.1021/ja00976a034. PMID 5980876. {{cite journal}}: Explicit use of et al. in: |author= (help); Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
↑ Cleland WW (2005). "The use of isotope effects to determine enzyme mechanisms". Arch. Biochem. Biophys. 433 (1): 2–12. doi:10.1016/j.abb.2004.08.027. PMID 15581561. Archived from the original on 20 ಫೆಬ್ರವರಿ 2008. Retrieved 24 ನವೆಂಬರ್ 2010. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ Northrop D (1981). "The expression of isotope effects on enzyme-catalyzed reactions". Annu. Rev. Biochem. 50: 103–31. doi:10.1146/annurev.bi.50.070181.000535. PMID 7023356.
↑ Baillie T, Rettenmeier A (1986). "Drug biotransformation: mechanistic studies with stable isotopes". Journal of clinical pharmacology. 26 (6): 448–51. PMID 3734135.
↑ Cleland WW (1982). "Use of isotope effects to elucidate enzyme mechanisms". CRC Crit. Rev. Biochem. 13 (4): 385–428. doi:10.3109/10409238209108715. PMID 6759038.
↑ Christianson DW, Cox JD (1999). "Catalysis by metal-activated hydroxide in zinc and manganese metalloenzymes". Annu. Rev. Biochem. 68: 33–57. doi:10.1146/annurev.biochem.68.1.33. PMID 10872443.
↑ Kraut D, Carroll K, Herschlag D (2003). "Challenges in enzyme mechanism and energetics". Annu. Rev. Biochem. 72: 517–71. doi:10.1146/annurev.biochem.72.121801.161617. PMID 12704087.{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ Leatherbarrow RJ (1990). "Using linear and non-linear regression to fit biochemical data". Trends Biochem. Sci. 15 (12): 455–8. doi:10.1016/0968-0004(90)90295-M. PMID 2077683. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ ವಾಲ್ಷ್ R, ಮಾರ್ಟೀನ್ E, ಡ್ಯಾರ್ವೆಷ್ S. A ವರ್ಸಟೈಲ್ ಇಕ್ಯುವೇಷನ್ ಟು ಡಿಸ್ಕ್ರೈಬ್ ರಿವರ್ಸಿಎಬಲ್ ಎನ್ ಸೈಮ್ ಇನ್ ಹೆಬಿಷನ್ ಅಂಡ್ ಆಕ್ಟಿವೇಷನ್ ಕೈನೆಟಿಕ್ಸ್: ಮಾಡೆಲಿಂಗ್ ಬೇಟಾ-ಗ್ಲ್ಯಾಕ್ಟೊಸೈಡ್ಸ್ ಅಂಡ್ ಬಟ್ ರಿಲ್ಕೊಲಿನ್ಸ್ಟ್ರೇಸ್ . ಬಯೊಕೆಮಿಸ್ಟ್ರಿ ಬಯೊಫಿಸಿಕ್ಸ್ ಆಕ್ಟಾ.ಬಯೊಕಿಮ್ Biophys Acta. 2007 1770:733-46.
↑ Koshland DE (1958). "Application of a Theory of Enzyme Specificity to Protein Synthesis". Proc. Natl. Acad. Sci. U.S.A. 44 (2): 98–104. doi:10.1073/pnas.44.2.98. PMC 335371. PMID 16590179. {{cite journal}}: Unknown parameter |month= ignored (help)
↑ Hammes G (2002). "Multiple conformational changes in enzyme catalysis". Biochemistry. 41 (26): 8221–8. doi:10.1021/bi0260839. PMID 12081470.
↑ Sutcliffe M, Scrutton N (2002). "A new conceptual framework for enzyme catalysis. Hydrogen tunnelling coupled to enzyme dynamics in flavoprotein and quinoprotein enzymes". Eur. J. Biochem. 269 (13): 3096–102. doi:10.1046/j.1432-1033.2002.03020.x. PMID 12084049. Archived from the original on 8 ನವೆಂಬರ್ 2006. Retrieved 24 ನವೆಂಬರ್ 2010.

ಹೆಚ್ಚಿನ ಓದಿಗಾಗಿ

ಪರಿಚಯದ

Cornish-Bowden, Athel (2004). Fundamentals of enzyme kinetics (3rd ed.). London: Portland Press. ISBN 1-85578-158-1.
Stevens, Lewis; Price, Nicholas C. (1999). Fundamentals of enzymology: the cell and molecular biology of catalytic proteins. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-850229-X.{{cite book}}: CS1 maint: multiple names: authors list (link)
Bugg, Tim (2004). Introduction to Enzyme and Coenzyme Chemistry. Cambridge, MA: Blackwell Publishers. ISBN 1-4051-1452-5.

ಮುಂದುವರಿದ ಸ್ಥಿತಿ

Segel, Irwin H. (1993). Enzyme kinetics: behavior and analysis of rapid equilibrium and steady state enzyme systems (New ed.). New York: Wiley. ISBN 0-471-30309-7.
Fersht, Alan (1999). Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding. San Francisco: W.H. Freeman. ISBN 0-7167-3268-8.
Santiago Schnell, Philip K. Maini (2004). "A century of enzyme kinetics: Reliability of the K_M and v_max estimates" (PDF). Comments on Theoretical Biology. 8: 169–87. doi:10.1080/08948550302453. Archived from the original (PDF) on 21 ಫೆಬ್ರವರಿ 2006. Retrieved 24 ನವೆಂಬರ್ 2010.
Walsh, Christopher (1979). Enzymatic reaction mechanisms. San Francisco: W. H. Freeman. ISBN 0-7167-0070-0.
Cleland, William Wallace; Cook, Paul (2007). Enzyme kinetics and mechanism. New York: Garland Science. ISBN 0-8153-4140-7.{{cite book}}: CS1 maint: multiple names: authors list (link)

ಬಾಹ್ಯ ಕೊಂಡಿಗಳು

ಅನಿಮೇಷನ್ ಆಫ್ ಆನ್ ಎನ್ ಸೈಮ್ ಅಸೇ Archived 6 October 2011^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. — ಶೋ ಎಫೆಕ್ಟ್ ಆಫ್ ಮ್ಯಾನ್ಯುಪ್ಲೇಟಿಂಗ್ ಅಸೇ ಕಂಡಿಷನ್ಸ್
MACiE Archived 8 August 2011^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. — ಅ ಡೇಟಾ ಬೇಸ್ ಆಫ್ ಎನ್ ಸೈಮ್ ರಿಯಾಕ್ಷನ್ ಮೆಕ್ಯಾನಿಸಮ್ಸ್
ENZYME — ಎಕ್ಸ್ ಪ್ಯಾಸಿ ಎನ್ ಸೈಮ್ ನೋಮೆನ್ ಕಲ್ಚರ್ ಡೇಟಾಬೇಸ್
ExCatDB Archived 13 October 2007^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. — ಅ ಡೇಟಾ ಬೇಸ್ ಆಫ್ ಎನ್ ಸೈಮ್ ಕ್ಯಾಟಲಿಟಿಕ್ ಮೆಕ್ಯಾನಿಸಮ್ಸ್
BRENDA — ಕಾಂಪ್ರಹೆನ್ಸಿವ್ ಎನ್ ಸೈಮ್ ಡೇಟಾ ಬೇಸ್, ಗಿವಿಂಗ್ ಸಬ್ ಸ್ಟ್ರೇಟ್ಸ್ , ಇನ್ ಹೆಬಿಟರ್ಸ್ ಅಂಡ್ ರಿಯಾಕ್ಷನ್ ಡಯಗ್ರಾಮ್ಸ್
SABIO-RK Archived 17 November 2006^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. — ಅ ಡೇಟಾ ಬೇಸ್ ಆಫ್ ರಿಯಾಕ್ಷನ್ ಕೈನಟಿಕ್ಸ್
ಜೋಸೆಫ್ ಕ್ರೌಟ್ಸ್ ರಿಸರ್ಚ್ ಗ್ರೂಪ್, ಯುನಿವರ್ಸಿಟಿ ಆಫ್ ಕ್ಯಾಲಿಫೋರ್ನಿಯ ಸ್ಯಾನ್ ಡಿಗೊ Archived 20 August 2006^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ. — ಅನಿಮೇಷನ್ಸ್ ಆಫ್ ಸೆವರಲ್ ಎನ್ ಸೈಮ್ ರಿಯಾಕ್ಷನ್ ಮೆಕ್ಯಾನಿಸಮ್ಸ್
ಸಿಂಬಾಲಿಸಮ್ ಅಂಡ್ ಟರ್ಮಿನಾಲಜಿ ಇನ್ ಎನ್ ಸೈಮ್ ಕೈನಟಿಕ್ಸ್ — ಅ ಕಾಂಪ್ರಹೆನ್ಸಿವ್ ಎಕ್ಸ್ ಪ್ಲನೇಷನ್ ಆಫ್ ಕಾನ್ಸೆಪ್ಟ್ಸ್ ಅಂಡ್ ಟರ್ಮಿನಾಲಜಿ ಇನ್ ಎನ್ ಸೈಮ್ ಕೈನಟಿಕ್ಸ್
ಆನ್ ಇಂಟರ್ ಡಕ್ಷನ್ ಟು ಎನ್ ಸೈಮ್ ಕೈನಟಿಕ್ಸ್ Archived 12 June 2004^{[Date mismatch]} ವೇಬ್ಯಾಕ್ ಮೆಷಿನ್ ನಲ್ಲಿ.— ಆನ್ ಆಕ್ಸಸೇಬಲ್ ಸೆಟ್ ಆಫ್ ಆನ್-ಲೈನ್ ಟುಟೊರಿಯಲ್ಸ್ ಆನ್ ಎನ್ ಸೈಮ್ ಕೈನಟಿಕ್ಸ್
ಎನ್ ಸೈಮ್ ಕೈನಟಿಕ್ಸ್ ಅನಿಮೇಟೆಡ್ ಟುಟೋರಿಯಲ್ — ಆನ್ ಅನಿಮೇಟೆಡ್ ಟುಟೋರಿಯಲ್ ವಿತ್ ಆಡಿಯೋ

ಟೆಂಪ್ಲೇಟು:Enzymes

[1] Wrighton, Mark S.; Ebbing, Darrell D. (1993). General chemistry (4th ed.). Boston: Houghton Mifflin. ISBN 0-395-63696-5.{{cite book}}: CS1 maint: multiple names: authors list (link)

[2] Danson, Michael; Eisenthal, Robert (2002). Enzyme assays: a practical approach. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-963820-9.{{cite book}}: CS1 maint: multiple names: authors list (link)

[3] Xie XS, Lu HP (1999). "Single-molecule enzymology". J. Biol. Chem. 274 (23): 15967–70. doi:10.1074/jbc.274.23.15967. PMID 10347141. Archived from the original on 31 ಮೇ 2009. Retrieved 24 ನವೆಂಬರ್ 2010. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: unflagged free DOI (link)

[4] Lu H (2004). "Single-molecule spectroscopy studies of conformational change dynamics in enzymatic reactions". Current pharmaceutical biotechnology. 5 (3): 261–9. doi:10.2174/1389201043376887. PMID 15180547.

[5] Schnell J, Dyson H, Wright P (2004). "Structure, dynamics, and catalytic function of dihydrofolate reductase". Annual review of biophysics and biomolecular structure. 33: 119–40. doi:10.1146/annurev.biophys.33.110502.133613. PMID 15139807.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[6] Gibson QH (1969). "Rapid mixing: Stopped flow". Methods Enzymol. 16: 187–228. doi:10.1016/S0076-6879(69)16009-7.

[7] Duggleby RG (1995). "Analysis of enzyme progress curves by non-linear regression". Methods Enzymol. 249: 61–90. doi:10.1016/0076-6879(95)49031-0. PMID 7791628.

[8] Murray JB, Dunham CM, Scott WG (2002). "A pH-dependent conformational change, rather than the chemical step, appears to be rate-limiting in the hammerhead ribozyme cleavage reaction". J. Mol. Biol. 315 (2): 121–30. doi:10.1006/jmbi.2001.5145. PMID 11779233. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

[9] ಮೈಕೆಲೀಸ್ L. ಅಂಡ್ ಮೆನ್ ಟೆನ್ M.L. ಕೈನೆಟಿಕ್ ಡರ್ ಇನ್ ವರ್ಟಿನ್ ವ್ರಿಂಗ್ಕುಂಗ್ ಬಯೋಕೆಮ್. Z. 1913; 49:333–369 ಇಂಗ್ಲೀಶ್ ಟ್ರಾನ್ಸ್ ಲೇಷನ್ 2007 ರ ಏಪ್ರಿಲ್ 6 ರಂದು ಪ್ರವೇಶಿಸಲಾಯಿತು.

[10] Stroppolo ME, Falconi M, Caccuri AM, Desideri A (2001). "Superefficient enzymes". Cell. Mol. Life Sci. 58 (10): 1451–60. doi:10.1007/PL00000788. PMID 11693526.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[11] ವಾಲ್ಷ್ R,ಮಾರ್ಟೀನ್ E, ದ್ಯಾರ್ವೆಷ್ S. ಅ ಮೆಥೆಡ್ ಟು ಡಿಸ್ಕ್ರೈಬ್ ಎನ್ ಸೈಮ್-ಕ್ಯಾಟಲೈಸ್ಡ್ ರಿಯಾಕ್ಷನ್ಸ್ ಬೈ ಕಂಬೈನಿಂಗ್ ಸ್ಟೀಡಿ ಸೇಟ್ ಅಂಡ್ ಟೈಮ್ ಕೋರ್ಸ್ ಎನ್ ಸೈಮ್ ಕೈನೆಟಿಕ್ ಪ್ಯಾರಮೀಟರ್ಸ್. ಬಯೊಕೆಮಿಸ್ಟ್ರಿ ಬಯೊಫಿಸಿಕ್ಸ್ ಆಕ್ಟಾ. 2010 ಜನವರಿ;1800:1-5

[12] Jones ME (1 ಜನವರಿ 1992). "Analysis of algebraic weighted least-squares estimators for enzyme parameters". Biochem. J. 288 (Pt 2): 533–8. PMC 1132043. PMID 1463456.

[Tseng-13] ೧೩.೦ ^೧೩.೧ Tseng SJ, Hsu JP (1990). "A comparison of the parameter estimating procedures for the Michaelis-Menten model". J. Theor. Biol. 145 (4): 457–64. doi:10.1016/S0022-5193(05)80481-3. PMID 2246896. {{cite journal}}: Unknown parameter |month= ignored (help)

[14] Bravo IG, Busto F, De Arriaga D; et al. (2001). "A normalized plot as a novel and time-saving tool in complex enzyme kinetic analysis". Biochem. J. 358 (Pt 3): 573–83. PMC 1222113. PMID 11577687. {{cite journal}}: Explicit use of et al. in: |author= (help); Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

[15] Almaas E, Kovács B, Vicsek T, Oltvai ZN, Barabási AL (2004). "Global organization of metabolic fluxes in the bacterium Escherichia coli". Nature. 427 (6977): 839–43. doi:10.1038/nature02289. PMID 14985762. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

[16] Reed JL, Vo TD, Schilling CH, Palsson BO (2003). "An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR)". Genome Biol. 4 (9): R54. doi:10.1186/gb-2003-4-9-r54. PMC 193654. PMID 12952533.{{cite journal}}: CS1 maint: multiple names: authors list (link) CS1 maint: unflagged free DOI (link)

[17] ಸಂಪೂರ್ಣ ಮೂಲಕ್ಕಾಗಿ, ಇಲ್ಲಿ ನೋಡಿ

[18] Dirr H, Reinemer P, Huber R (1994). "X-ray crystal structures of cytosolic glutathione S-transferases. Implications for protein architecture, substrate recognition and catalytic function". Eur. J. Biochem. 220 (3): 645–61. doi:10.1111/j.1432-1033.1994.tb18666.x. PMID 8143720. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

[19] Stone SR, Morrison JF (1988). "Dihydrofolate reductase from Escherichia coli: the kinetic mechanism with NADPH and reduced acetylpyridine adenine dinucleotide phosphate as substrates". Biochemistry. 27 (15): 5493–9. doi:10.1021/bi00415a016. PMID 3052577. {{cite journal}}: Unknown parameter |month= ignored (help)

[20] Fisher PA (1994). "Enzymologic mechanism of replicative DNA polymerases in higher eukaryotes". Prog. Nucleic Acid Res. Mol. Biol. 47: 371–97. doi:10.1016/S0079-6603(08)60257-3. PMID 8016325.

[21] Akerman SE, Müller S (2003). "2-Cys peroxiredoxin PfTrx-Px1 is involved in the antioxidant defence of Plasmodium falciparum". Mol. Biochem. Parasitol. 130 (2): 75–81. doi:10.1016/S0166-6851(03)00161-0. PMID 12946843. Archived from the original on 20 ಫೆಬ್ರವರಿ 2008. Retrieved 24 ನವೆಂಬರ್ 2010. {{cite journal}}: Unknown parameter |month= ignored (help)

[22] Bravo IG, Barrallo S, Ferrero MA, Rodríguez-Aparicio LB, Martínez-Blanco H, Reglero A (2001). "Kinetic properties of the acylneuraminate cytidylyltransferase from Pasteurella haemolytica A2". Biochem. J. 358 (Pt 3): 585–98. PMC 1222114. PMID 11577688. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

[23] Kraut J (1977). "Serine proteases: structure and mechanism of catalysis". Annu. Rev. Biochem. 46: 331–58. doi:10.1146/annurev.bi.46.070177.001555. PMID 332063.

[24] Ricard J, Cornish-Bowden A (1987). "Co-operative and allosteric enzymes: 20 years on". Eur. J. Biochem. 166 (2): 255–72. doi:10.1111/j.1432-1033.1987.tb13510.x. PMID 3301336. {{cite journal}}: Unknown parameter |month= ignored (help)

[25] Ward WH, Fersht AR (1988). "Tyrosyl-tRNA synthetase acts as an asymmetric dimer in charging tRNA. A rationale for half-of-the-sites activity". Biochemistry. 27 (15): 5525–30. doi:10.1021/bi00415a021. PMID 3179266. {{cite journal}}: Unknown parameter |month= ignored (help)

[26] Helmstaedt K, Krappmann S, Braus GH (2001). "Allosteric regulation of catalytic activity: Escherichia coli aspartate transcarbamoylase versus yeast chorismate mutase". Microbiol. Mol. Biol. Rev. 65 (3): 404–21, table of contents. doi:10.1128/MMBR.65.3.404-421.2001. PMC 99034. PMID 11528003. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

[27] Schirmer T, Evans PR (1990). "Structural basis of the allosteric behaviour of phosphofructokinase". Nature. 343 (6254): 140–5. doi:10.1038/343140a0. PMID 2136935. {{cite journal}}: Unknown parameter |month= ignored (help)

[28] ಹಿಲ್, A. V. ದಿ ಪಾಸಿಬಲ್ ಎಫ್ಟೆಕ್ಟ್ ಆಫ್ ದಿ ಅಗ್ರಿಗೇಷನ್ ಆಫ್ ದಿ ಮೊಲ್ಯಾಕ್ಯೂಲ್ಸ್ ಆಫ್ ಹಿಮೊಗ್ಲೋಬಿನ್ ಆನ್ ಇಟ್ಸ್ ಡಿಸೊಸಿಯೇಷನ್ ಕರ್ವ್ಸ್ J. ಫಿಸಾಯ್ಲ್. (Lond.) , 1910 40, iv-vii.

[29] Hartley BS, Kilby BA (1954). "The reaction of p-nitrophenyl esters with chymotrypsin and insulin". Biochem. J. 56 (2): 288–97. PMC 1269615. PMID 13140189. {{cite journal}}: Unknown parameter |month= ignored (help)

[Fersht-30] ೩೦.೦ ^೩೦.೧ Fersht, Alan (1999). Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding. San Francisco: W.H. Freeman. ISBN 0-7167-3268-8.

[31] Bender ML, Begué-Cantón ML, Blakeley RL; et al. (1966). "The determination of the concentration of hydrolytic enzyme solutions: alpha-chymotrypsin, trypsin, papain, elastase, subtilisin, and acetylcholinesterase". J. Am. Chem. Soc. 88 (24): 5890–913. doi:10.1021/ja00976a034. PMID 5980876. {{cite journal}}: Explicit use of et al. in: |author= (help); Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

[32] Cleland WW (2005). "The use of isotope effects to determine enzyme mechanisms". Arch. Biochem. Biophys. 433 (1): 2–12. doi:10.1016/j.abb.2004.08.027. PMID 15581561. Archived from the original on 20 ಫೆಬ್ರವರಿ 2008. Retrieved 24 ನವೆಂಬರ್ 2010. {{cite journal}}: Unknown parameter |month= ignored (help)

[33] Northrop D (1981). "The expression of isotope effects on enzyme-catalyzed reactions". Annu. Rev. Biochem. 50: 103–31. doi:10.1146/annurev.bi.50.070181.000535. PMID 7023356.

[34] Baillie T, Rettenmeier A (1986). "Drug biotransformation: mechanistic studies with stable isotopes". Journal of clinical pharmacology. 26 (6): 448–51. PMID 3734135.

[35] Cleland WW (1982). "Use of isotope effects to elucidate enzyme mechanisms". CRC Crit. Rev. Biochem. 13 (4): 385–428. doi:10.3109/10409238209108715. PMID 6759038.

[36] Christianson DW, Cox JD (1999). "Catalysis by metal-activated hydroxide in zinc and manganese metalloenzymes". Annu. Rev. Biochem. 68: 33–57. doi:10.1146/annurev.biochem.68.1.33. PMID 10872443.

[37] Kraut D, Carroll K, Herschlag D (2003). "Challenges in enzyme mechanism and energetics". Annu. Rev. Biochem. 72: 517–71. doi:10.1146/annurev.biochem.72.121801.161617. PMID 12704087.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[38] Leatherbarrow RJ (1990). "Using linear and non-linear regression to fit biochemical data". Trends Biochem. Sci. 15 (12): 455–8. doi:10.1016/0968-0004(90)90295-M. PMID 2077683. {{cite journal}}: Unknown parameter |month= ignored (help)

[39] ವಾಲ್ಷ್ R, ಮಾರ್ಟೀನ್ E, ಡ್ಯಾರ್ವೆಷ್ S. A ವರ್ಸಟೈಲ್ ಇಕ್ಯುವೇಷನ್ ಟು ಡಿಸ್ಕ್ರೈಬ್ ರಿವರ್ಸಿಎಬಲ್ ಎನ್ ಸೈಮ್ ಇನ್ ಹೆಬಿಷನ್ ಅಂಡ್ ಆಕ್ಟಿವೇಷನ್ ಕೈನೆಟಿಕ್ಸ್: ಮಾಡೆಲಿಂಗ್ ಬೇಟಾ-ಗ್ಲ್ಯಾಕ್ಟೊಸೈಡ್ಸ್ ಅಂಡ್ ಬಟ್ ರಿಲ್ಕೊಲಿನ್ಸ್ಟ್ರೇಸ್ . ಬಯೊಕೆಮಿಸ್ಟ್ರಿ ಬಯೊಫಿಸಿಕ್ಸ್ ಆಕ್ಟಾ.ಬಯೊಕಿಮ್ Biophys Acta. 2007 1770:733-46.

[40] Koshland DE (1958). "Application of a Theory of Enzyme Specificity to Protein Synthesis". Proc. Natl. Acad. Sci. U.S.A. 44 (2): 98–104. doi:10.1073/pnas.44.2.98. PMC 335371. PMID 16590179. {{cite journal}}: Unknown parameter |month= ignored (help)

[41] Hammes G (2002). "Multiple conformational changes in enzyme catalysis". Biochemistry. 41 (26): 8221–8. doi:10.1021/bi0260839. PMID 12081470.

[42] Sutcliffe M, Scrutton N (2002). "A new conceptual framework for enzyme catalysis. Hydrogen tunnelling coupled to enzyme dynamics in flavoprotein and quinoprotein enzymes". Eur. J. Biochem. 269 (13): 3096–102. doi:10.1046/j.1432-1033.2002.03020.x. PMID 12084049. Archived from the original on 8 ನವೆಂಬರ್ 2006. Retrieved 24 ನವೆಂಬರ್ 2010.

[೧]

[೨]

[೩]

[೪]

[೫]

[೬]

[೭]

[೮]

[೯]

[೧೦]

[೧೧]

[α]

[೧೨]

[೧೩]

[೧೪]

[೧೫]

[೧೬]

[೧೭]

[೧೮]

[೧೯]

[೨೦]

[β]

[γ]

[೨೧]

[೨೨]

[೨೩]

[δ]

[೨೪]

[೨೫]

[೨೬]

[೨೭]

[೨೮]

[೨೯]

[೩೦]

[೩೧]

[೩೨]

[೩೩]

[೩೪]

[೩೫]

[೩೬]

[೩೭]

[೩೮]

[೩೯]

[೪೦]

[೪೧]

[೪೨]